1 Introduction

The sequence of states which a magnetized neutron star in a wind-fed mass-exchange binary system follows as it spins down from the initially very short periods can be expressed in the form of the following chain: ejector $\rightarrow$ propeller $\rightarrow$ accretor. This classification, first suggested by Shvartsman (1970), reflects three different evolutionary stages and three different mechanisms of energy release responsible for the neutron star emission.

The spindown of a neutron star in the state of ejector is governed by the canonical spin-powered pulsar mechanism. The spindown power dominates the star energy budget and is spent predominantly to the generation of magneto-dipole waves and particle acceleration. The pulsar-like spindown ceases when the pressure of the material being ejected by the neutron star can no longer balance the pressure of the surrounding gas. The stellar wind plasma penetrates into the neutron star light cylinder and interacts with the star magnetosphere. This corresponds to the neutron star state transition: ejector $\rightarrow$ propeller.

Neutron star in the state of propeller is spinning down due to the interaction between its fast rotating magnetosphere and the surrounding material. Davies et al. (1979) and Davies & Pringle (1981) have shown that during this state the star magnetosphere is surrounded by a spherical quasi-static envelope in which the plasma temperature is of the order of the free-fall temperature,

$$T(R) \simeq T_{\rm ff}(R)=\frac{GM_{\rm ns} m_{\rm p}}{k R}\cdot$$ (1)

Here $M_{\rm ns}$ is the mass of the neutron star, $m_{\rm p}$ is the proton mass and k is the Boltzmann constant. The rotational energy loss by the neutron star is convected up through the envelope by the turbulent motions and lost through its outer boundary. The structure of the envelope and the spindown rate of the neutron star depend on the value of the ratio:

$$\kappa=\frac{\omega R_{\rm m}}{V_{\rm s}(R_{\rm m})},$$

where $R_{\rm m}$ is the magnetospheric radius, $\omega=2\pi/P_{\rm s}$is the neutron star angular velocity and $V_{\rm s}(R_{\rm m})$ is the sound speed at the magnetospheric radius, which according to Eq. (1) is of the order of the free-fall velocity, $V_{\rm ff}$:

$$V_{\rm s}(R_{\rm m}) \simeq V_{\rm ff}(R_{\rm m})=\sqrt{\frac{2GM_{\rm ns}}{R_{\rm m}}}\cdot$$ (2)

On this basis Davies et al.(1979) distinguished three sub-states of the propeller state: (b) very rapid rotator ( $\kappa \gg 1$); (c) supersonic propeller ( ) and (d) subsonic propeller ( $\kappa < 1$).

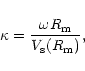
In cases "b'' and "c'' the magnetospheric radius of the neutron star exceeds its corotational radius,

$$R_{\rm cor}= \left(\frac{GM_{\rm ns}}{\omega^2}\right)^{1/3}.$$

This means that the neutron star in these cases is in the centrifugal inhibition regime and hence, the effective accretion onto its surface is impossible.

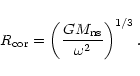
In the case "d'' the magnetospheric radius is smaller than the corotational radius. In this situation the plasma being penetrated from the base of the envelope into the star magnetic field is able to flow along the magnetic field lines and to accrete onto the star surface. However the effective plasma penetration into the magnetosphere does not occur, if the magnetospheric boundary is interchange stable. According to Arons & Lea (1976) and Elsner & Lamb (1976) the onset condition for the interchange instability of the magnetospheric boundary reads

$$T < T_{\rm cr} \simeq 0.3\ T_{\rm ff}.$$

This means that the neutron star can change its state from the subsonic propeller to accretor only when the cooling of the envelope plasma (due to the radiation and convective motions) dominates the energy input to the envelope due to the propeller action by the neutron star.

Investigating this particular situation Davies & Pringle (1981, hereafter DP81) have shown that the energy input to the envelope dominates the energy losses until the spin period of the star reaches the break period, $P_{\rm br}$. Assuming the following values of the neutron star parameters: the magnetic moment $\mu=10^{30} \mu_{30}\,{\rm G\,cm^3}$ and the mass $m= 1 (M_{\rm ns}/M_{\odot})$, and putting the strength of the stellar wind (in terms of the maximum possible accretion rate) $\dot{M}_0=10^{15}~M_{15}\,{\rm g\,s^{-1}}$ they estimated the value of the break period as 60s.

However, putting the same values of parameters and following the same method of calculations I found the value of $P_{\rm br}$ to be of the order of 450s, i.e. by a factor of 7.5 larger than that previously estimated in DP81. In this letter I present the calculations and show that this result forced us to change some basic conclusions about the origin of the long periods X-ray pulsars.