A&A 368, 347-368 (2001)
DOI: 10.1051/0004-6361:20000489

The COMPTEL instrumental line background

G. Weidenspointner^1, - M. Varendorff¹ - U. Oberlack³ - D. Morris² - S. Plüschke¹ - R. Diehl¹ -
S. C. Kappadath⁴ - M. McConnell² - J. Ryan² - V. Schönfelder¹ - H. Steinle¹

1 - Max-Planck-Institut für extraterrestrische Physik, 85740 Garching, Germany
2 - Space Science Center, University of New Hampshire, Durham, NH 03824, USA
3 - Astrophysics Laboratory, Columbia University, New York, NY 10027, USA
4 - Louisiana State University, Baton Rouge, Louisiana, USA

Received 28 July 2000 / Accepted 5 December 2000

Abstract
The instrumental line background of the Compton telescope COMPTEL onboard the Compton Gamma-Ray Observatory is due to the activation and/or decay of many isotopes. The major components of this background can be attributed to eight individual isotopes, namely ²D, ²²Na, ²⁴Na, ²⁸Al, ⁴⁰K, ⁵²Mn, ⁵⁷Ni, and ²⁰⁸Tl. The identification of instrumental lines with specific isotopes is based on the line energies as well as on the variation of the event rate with time, cosmic-ray intensity, and deposited radiation dose during passages through the South-Atlantic Anomaly. The characteristic variation of the event rate due to a specific isotope depends on its life-time, orbital parameters such as the altitude of the satellite above Earth, and the solar cycle. A detailed understanding of the background contributions from instrumental lines is crucial at MeV energies for measuring the cosmic diffuse gamma-ray background and for observing $\gamma$-ray line emission in the interstellar medium or from supernovae and their remnants. Procedures to determine the event rate from each background isotope are described, and their average activity in spacecraft materials over the first seven years of the mission is estimated.

Key words: methods: data analysis - line: identification

  
1 Introduction

Gamma-ray experiments in low-Earth orbit, such as the Compton telescope COMPTEL onboard the Compton Gamma-Ray Observatory (CGRO), operate in an intense and variable radiation environment. The main constituents of the ambient radiation fields are primary cosmic-ray particles, geomagnetically trapped radiation-belt particles, as well as albedo neutrons and $\gamma$-ray photons. The different particle species interact with the spacecraft and detector materials, resulting in the emission of instrumental background photons (for a review, see e.g. Dean et al. 1991). COMPTEL data, dominated by instrumental background, have a typical signal-to-noise ratio of a few percent. Hence, a qualitative and quantitative understanding of the instrumental background is crucial for conducting astrophysical measurements, in particular of the cosmic diffuse gamma-ray background (hereafter CDG), and of the $\gamma$-ray line emission in the interstellar medium or from supernovae and their remnants.

The instrumental background experienced by COMPTEL is subdivided into two major components according to their signature in energy space: first, a continuum background discussed by Ryan et al. (1997); second, the instrumental line background, the focus of this paper. The latter arises from a number of different radioactive isotopes generated in the instrument material. This primarily occurs from activation by trapped protons during passages through the South-Atlantic Anomaly (SAA), from neutron absorption, and from primordial radioactivity. An earlier report on activation in the COMPTEL telescope was given by Morris et al. (1997a).

The discussion is structured as follows. After a brief description of the COMPTEL instrument in Sect. 2, general characteristics of the instrumental (line) background are summarized in Sect. 3. In Sect. 4, identifications of specific isotopes are discussed. In Sect. 5, the variations of the activity of individual isotopes are described. In Sect. 6, a comparison of instrumental line backgrounds in different low-energy $\gamma$-ray experiments is given. Also, average values for the activity of spacecraft materials are presented. The results of this work are summarized and discussed in Sect. 7. Finally, appendices give the event selections used in these line studies, and provide detailed descriptions of the procedures employed for determining the background contributions of individual isotopes in the CDG analysis, and also - with slight modifications - in the analysis of the galactic 1.8 MeV line emission from ²⁶Al.

  
2 Instrument description

COMPTEL is the first double-scattering Compton telescope designed for $\gamma$-ray astronomy to operate on a satellite platform. A detailed description of the COMPTEL instrument, which is sensitive to $\gamma$-rays in the 0.8-30 MeV range, can be found in Schönfelder et al. (1993). Briefly, the instrument consists of two planes of detector arrays, D1 and D2, separated by 1.58 m (see Fig. 1). The D1 detector consists of seven cylindrical modules filled with NE 213A organic liquid scintillator. The D2 detector consists of 14 cylindrical NaI(Tl) crystals. The D1 scintillator material has a low average atomic number to optimize the occurrence of a single Compton scatter, while the D2 scintillator crystals have a high density and average atomic number to maximize their photon absorption properties. Each detector array is surrounded by a pair of overlapping anti-coincidence domes, manufactured of NE 110 plastic scintillator, to reject charged particle triggers of the telescope. The in-flight performance of the instrument is monitored with two calibration (CAL) units, each composed of a ⁶⁰Co-doped scintillator viewed by two 1/2 inch photomultiplier tubes (PMTs), that provide tagged photons for in-flight energy calibration (Snelling et al. 1986). The COMPTEL instrument accepts and registers coincident triggers in a single D1-D2 module pair within the coincidence time window of $\sim 40$ ns in the absence of a veto signal from the four charged particle shields as valid events. These interactions can be caused by a single photon or by multiple photons and/or particles. Among other parameters, a time-of-flight (ToF) value and a so-called pulse shape discriminator (PSD) value in D1 are recorded for each event. The ToF is a measure of the time difference between the triggers in the D1 and D2 detectors and is used to discriminate forward scattered (D1 $\rightarrow$D2) events, such as celestial photons with a ToF value of about 5 ns, from backward scattered (D2 $\rightarrow$D1) background events which cluster around a ToF value of about -5 ns. The PSD is a measure of the shape of the scintillation light pulse in the D1 detector. The energy loss characteristics of recoil electrons resulting from Compton scattering and of recoil protons resulting from neutron scattering are different, allowing one to reject many neutron induced events. The summed energy deposits in the two detectors, E₁ + E₂, are a measure of the total energy of the incident photon, $E_{\rm tot}$, while the photon scatter angle $\bar{\varphi}$ is determined from E₁and E₂ through the Compton-scatter formula:

$$\cos \bar{\varphi} = 1 - \frac{m_{\rm o} c^2}{{E}_{2}} + \fr... ...1} + {E}_{2}}, \; {\rm with} \; m_{\rm o} c^2 = 511~{\rm keV}.$$ (1)

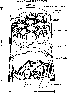	Figure 1: A schematic view of the Compton telescope COMPTEL (from Schönfelder et al. 1993)
Open with DEXTER

   
3 Characteristics of instrumental linebackground

The particle and photon environment of COMPTEL produces coincident interactions in the D1 and D2 detectors that pass all the logic and electronic criteria for a valid event. In the following, an overview is given of different types of instrumental background events in terms of their interaction process and location, as illustrated in Fig. 2. This classification of background events (van Dijk 1996) provides a simple and versatile framework for discussing the COMPTEL instrumental background. ToF is of prime importance in identifying and rejecting instrumental background events. A schematic representation of the ToF distribution of valid events is depicted in Fig. 3.

	Figure 2: An illustration of the main channels for the triggering of valid events due to instrumental background (adopted from van Dijk 1996). For simplicity, BATSE was omitted in this schematic view of CGRO. The various event types are explained in the text
Open with DEXTER

$\bullet$ Event types A and B: events caused by the double scattering of a single photon. Any photon created in CGRO may produce this type of background event, which, if the scattering is from D1 to D2, is identical to a proper celestial event. It follows that the ToF distribution of forward scattered single photon events is identical to that of celestial photons and peaks around 5 ns in the ToF forward peak. Depending on where they originate, forward scattered single photon events may be rejected. In particular, many of the photons that originate from below the D1 detector (such as type B events) can be eliminated by a selection on the scatter angle $\bar{\varphi}$ (see e.g. the event selections in Appendix A). The remaining instrumental background from forward scattered single photons is therefore mostly due to photons originating in, around and above the D1 detector (such as type A events); type B events are negligible. Line emissions appear in energy space, particularly in $E_{\rm tot}$ and E₁-E₂ space (see below).

Single photons may also scatter in D2 before interacting in D1. These backward scattered single photon events, however, are identifiable by their ToF distribution, which is confined in the backward peak at ToF values of about - 5 ns. Finally, high-energy neutrons can undergo a double scattering process analogously to photons, however, many of these neutron events can be rejected by their PSD value.

Figure 3: A schematic representation of the ToF distribution of valid events. Three major components can be discerned: the ToF backward peak and forward peak, centered at ToF values of about -5 ns and +5 ns, respectively, and an underlying continuum distribution. The backward peak is composed of all types of background events originating in and around the D2 detector (these are not specified individually in this illustration). The ToF forward peak contains the celestial signal as well as background events originating in and around the D1 detector, mostly of types A and C. The ToF continuum is dominated by background events of types D, E, and F originating in the instrument structure between the two detectors and the spacecraft structure in general. The relative magnitudes of the different components, which depend on $E_{\rm tot}$, are only represented approximately

Open with DEXTER

$\bullet$ Event types C and D: events caused by two or more photons both spatially and temporally correlated (so-called multiple photon or cascade events). In general, multiple photon events are more efficient in generating a background event than single photon events, since the probability for coincident interactions in both detectors increases with the number of emitted photons. Emission of two or more photons can occur from a small region on a time-scale shorter than the coincidence window of 40 ns. Nucleons that have been excited above the first nuclear level, e.g. by proton or neutron interactions, may promptly emit a cascade of photons. The multitude of nuclear excitation levels often results in a rather featureless continuum distribution in energy space. If, however, only a few transition levels are involved, characteristic features appear in E₂ and E₁-E₂ space (see below). Multiple photons may also arise from $\beta$-particle bremsstrahlung, or the annihilation of a positron. Also, high-energy neutrons may induce the emission of one or more $\gamma$-ray photons outside of the D1 scintillator (thereby eluding rejection by PSD) and some may interact in the D2 detector. More complicated nuclear reactions such as the spallation (break-up) of a nucleus or the initiation of a shower of secondaries by an incident cosmic-ray particle or neutron may also produce multiple photons.

Frequently, the emission of photons is nearly simultaneous, i.e. on time-scales much shorter than the coincidence window. The ToF value of these event types is determined by the location of the emitting nucleus relative to the D1 and D2 detectors. Multiple photons originating in the vicinity of the D1 detector (such as type C events) will peak slightly below a ToF value of 5 ns (see Sect. 4.2) and therefore contribute to the ToF forward peak. Photons emitted by nuclei in the spacecraft material between the D1 and D2 detectors (such as type D events) will interact in the two detectors near-simultaneously and have ToF values that are broadly distributed around zero, while photons originating in and around the D2 detector will contribute to the ToF backward peak. The full, double-peaked ToF distribution of all multiple photon events not only reflects the location of the emitting nucleus, but also the mass distribution of the entire spacecraft relative to the D1 and D2 detectors.

$\bullet$ Event type E: events that are both spatially and temporally uncorrelated (the so-called random coincidences). The COMPTEL detectors are continuously exposed to a large flux of $\gamma$-ray photons. This inevitably leads to coincident interactions that qualify as valid events. The photons producing these random coincidences are mostly of local or atmospheric origin. Since the two photons creating the event are unrelated to one another, and, in particular, not correlated in time, these events are uniformly distributed in ToF. Type E events may also involve a neutron instead of a photon triggering the D2 detector, which has no PSD capability.

$\bullet$ Event type F: events caused by two photons that are temporally correlated, but spatially uncorrelated. High-energy cosmic-ray particles or atmospheric neutrons may interact at several different locations along their path through CGRO. Individual interactions include those generating type C and D events (e.g. spallations or showers). The whole interaction chain creating type F events is similar to multiple photon events, the main difference being that their ToF distribution depends on both the location of the interactions as well as the (relativistic) velocity of the primary particle. The ToF distribution of this type of event is broad and covers the entire coincidence window (also reflecting the spacecraft mass distribution).

$\bullet$ Other processes, such as the interaction of a neutron in the D2 detector after producing a photon in the D1 system, or direct ionization losses of $\beta$-particles created in the housings of the D1 scintillators, may also play a role. The event signatures of these and other, more complicated processes, however, will be similar to the event types described above.

Event types A - D may arise from activation by primary cosmic-ray protons or secondary particles as well as atmospheric neutrons. The time between the interaction of the proton or neutron within the telescope material and the actual triggering of a background event varies, since it depends on the decay time of the radio-isotopes produced. These processes and the resulting background events can be crudely separated into "prompt'' and "delayed'' components. For prompt background events the time delay between the primary particle interaction in the instrument and the resulting emission of background photons is shorter than the coincidence window of 40 ns for the triggering of a valid event. Thus the intensity of prompt background components instantaneously follows the (time-variable) incident local cosmic-ray flux (see Sect. 5). For delayed events the time delay is longer than the typical length of the fast-logic veto signal of $\sim$200 ns. In contrast to protons, neutrons can travel to any location in the spacecraft to produce $\gamma$-ray photons without triggering the veto system. Inside the veto domes, particularly in the D1 detector, prompt events can therefore only be produced by neutrons. Both protons and neutrons, however, can produce delayed background events inside as well as outside the veto domes.

As described in Sect. 2, events due to incident celestial photons have ToF values around 5 ns. Only background events with a similar ToF value will therefore interfere with astrophysical analyses. As illustrated in Fig. 3, a major portion of the instrumental background events, including those in the backward peak, can be eliminated by a ToF selection. The most important background event types in the ToF forward peak region around ToF = 5 ns are those originating in the D1 detector (types A and C), and some of the background events produced in the satellite structure (types D, E, and F).

After ToF selection, the majority of the instrumental line background is expected to arise from activation of the D1 detector material because of the relatively high mass density and probability for triggering a background event as compared to the general spacecraft structure. The material composition of the D1 detector system therefore provides important clues as to which radioactive isotopes can effectively be produced and ultimately contribute to the instrumental line background in the low-Earth orbit of CGRO. The D1 support structure and the D1 module and PMT housings are mostly aluminium, the most abundant element in the instrument. The liquid scintillator NE 213A is composed of hydrogen and carbon. The quartz windows in the module housings contain silicon and oxygen. The PMTs and electronics boxes contain, among other elements, copper, nickel, and iron.

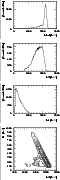	Figure 4: The $E_{\rm tot}$, E2, E1, and E1-E2 distribution of instrumental 2.22 MeV photons from 2D production for CDG event selections as determined from Monte Carlo simulations
Open with DEXTER

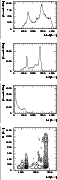	Figure 5: The $E_{\rm tot}$, E2, E1, and E1-E2 distribution of instrumental 24Na events for CDG data selections as determined from Monte Carlo simulations
Open with DEXTER

Events from the instrumental line background produce conspicuous and characteristic features in energy space that can be exploited to distinguish them from the general (continuum) background. The ToF distributions of the line background and the continuum background are also different: the instrumental line background is concentrated in the forward peak region, while the continuum background in energy is throughout the ToF continuum as well as the ToF forward peak. In the following, the characteristics of single photon (type A) events and multiple photon or cascade (type C) events are illustrated with examples of (background) events from ²D and ²⁴Na, respectively, both major contributors to the instrumental line background (see Sect. 4).

The instrumental 2.22 MeV photons emitted when ²D is produced in the D1 scintillators (see Sect. 4.1) are single photon (type A) background events. The $E_{\rm tot}$, E₂, E₁, and E₁-E₂ distributions of instrumental 2.22 MeV photons for CDG event selections (described in Appendix A.1) as determined from Monte Carlo simulations are depicted in Fig. 4. The $E_{\rm tot}$ distribution exhibits a peak at the energy of the primary photon, while the distributions in E₂ and E₁ are broad and relatively featureless. In E₁-E₂ space the event distribution of type A events follows the diagonal ${E}_1 + {E}_2 = {E}_\gamma$, with ${E}_\gamma = 2.22$ MeV for ²D. The distributions in $E_{\rm tot}$ and E₁-E₂ are the most important characteristics of single photon background events.

The $\beta^-$-decay of ²⁴Na results in the emission of two photons with energies 1.37 MeV and 2.75 MeV causing type C line background events (see Sect. 4.2). The $\beta^-$-particle is of minor importance for the generation of a background event. Since it rarely escapes the support structure, it contributes to the background only through secondary bremsstrahlung photons. The ²⁴Na signature in $E_{\rm tot}$, E₂, E₁, and E₁-E₂ as determined from Monte Carlo simulations is shown, for CDG event selections (see Appendix A.1), in Fig. 5. The most important characteristic of ²⁴Na, and any other isotope emitting multiple photons, is the E₂ distribution, which exhibits peaks at the energies of each of the primary photons. In E₁ the only conspicuous feature is the Compton edge of the 1.37 MeV photon (the Compton edge of the 2.75 MeV photon is suppressed by the CDG data selections). The $E_{\rm tot}$ spectrum is more complex and exhibits less pronounced, line-like features just above the individual photon energies. These come from the absorption of one photon in D2 with the other photon scattering in D1 with an energy deposit near the D1 threshold. In addition, in $E_{\rm tot}$ a shoulder is present at about 3.9 MeV. This is analogous to the sum peak in standard spectroscopy employing a single detector. Under CDG data selections, this shoulder is due to the absorption of the 2.75 MeV photon in D2, with the 1.37 MeV photon scattering in D1 with an energy deposit at the Compton edge. The ²⁴Na event distribution in E₁-E₂ space is also very characteristic: the events cluster along two bands parallel to the E₁ axis located in E₂ at the energies of the two decay photons. The band at 2.75 MeV in E₂ extends in E₁ from the threshold up to the Compton edge of the 1.37 MeV photon. The band at 1.37 MeV in E₂ is suppressed by the CDG data selections.

For other isotopes, if the energy of one of a pair of cascade photons is below the D2 threshold, then the two photons produce a cascade (type C) event only if the lower-energy photon scatters in D1, and the higher-energy photon interacts in D2. The E₂ and E₁-E₂ distribution of such a cascade photon pair is simple: there is only one photopeak in E₂ and only one band in E₁-E₂.

Radioactive decays that result in the (simultaneous) emission of two or more photons can produce line background events other than of type C. For example, an individual photon of the emitted photon multiple can produce a type A event, provided all other photons escape from the instrument without interacting in any of the detectors. As apparent in the E₁-E₂ event distribution of ²⁴Na, however, the $E_{\rm tot}$ signatures corresponding to the photon energies 1.37 MeV and 2.75 MeV are much weaker than the cascade structure. Monte Carlo simulations show that less than 10% of the ²⁴Na background events are due to type A events. This illustrates the fact that multiple photon decays in the D1 detector material are more efficient in generating a background event than decays that result in the emission of a single photon only.

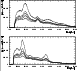Figure 6: An illustration of the spectral distributions in $E_{\rm tot}$(top) and E2 (bottom) as a function of time. The two spectra plotted with thick lines represent the times of highest (after the second reboost in May 1997) and lowest (from the beginning of the mission until the first reboost, May 1991 - Nov. 1993) contributions from long-lived background isotopes. The three intermediate spectra, plotted with thin lines, cover the time periods Nov. 1993 - Oct. 1994 (lowest), Oct. 1994 - Oct. 1995 (middle), and Oct. 1995 - May 1997 (highest)

Open with DEXTER

  
4 Identified radioactive isotopes

  

Table 1: A summary of the isotopes identified in the COMPTEL instrumental line background. For simplicity, only the photon energies of the most frequent decay modes are listed. If $\beta$-decays are involved, the $\beta$-particles have been included in the response simulations. The identification of ²⁰⁸Tl has to be considered tentative. The label "prompt'' for the half-life of the stable isotope ²D refers to the time-scale for the emission of the 2.22 MeV photon

Isotope	Half-Life	Decay Modes and	Main
		Photon Energies [MeV]	Production Channels
2D	prompt	2.224	1H(n $_{\rm ther}$,$\gamma$)
22Na	2.6 y	$\beta^+$ (91%): 0.511, 1.275	27Al(p,3p3n),
		EC (9%) : 1.275	Si(p,4pxn)
24Na	14.96 h	$\beta^-$: 1.37, 2.75	27Al(n,$\alpha$),
			27Al(p,3pn)
28Al	2.2 min	$\beta^-$: 1.779	27Al(n $_{\rm ther}$,$\gamma$)
40K	1.28 109 y	EC (10.7%): 1.461	primordial
52Mn	5.6 d	EC (64%): 0.744, 0.935, 1.434	Fe(p,x), Cr(p,x),
		$\beta^+$ (27%): 0.511, 0.744, 0.935, 1.434	Ni(p,x)
57Ni	35.6 h	$\beta^+$ (35%): 0.511, 1.377	Ni(p,x), Cu(p,x)
		EC (30%): 1.377
208Tl	1.4 1010 y	$\beta^-$ (50%): 0.583, 2.614	primordial
	(232Th)	$\beta^-$ (25%): 0.511, 0.583, 2.614

The major components of the COMPTEL instrumental line background can be attributed to eight individual isotopes, namely ²D, ²²Na, ²⁴Na, ²⁸Al, ⁴⁰K, ⁵²Mn, ⁵⁷Ni, and ²⁰⁸Tl (Weidenspointner 1999). Identification of these isotopes was achieved in an iterative process, starting from the most prominent lines. The $E_{\rm tot}$ and E₂ spectra (see Fig. 6) are particularly useful for the identification of isotopes that give rise to single photon (type A) or multiple photon (type C) events, respectively. The diagnostic power of E₁ spectra is limited since they do not exhibit line features at the energy of the incident photons, but only rather broad features at the corresponding Compton edges. Due to the correlated signatures in E₁-E₂ space, individual spectral features can be accentuated by applying suitable event selections. Viable isotope identifications are required to account self-consistently for spectral features in selected regions of the E₁-E₂ dataspace (see the detailed explanations in Appendix B), as well as for their variation with time and/or incident cosmic-ray intensity (discussed in Sect. 5). The telescope response to individual isotopes was modelled through Monte Carlo simulations. The isotopes, their half-lifes, most important decay channels, and main production channels are summarized in Table 1. Below, a review of the isotope identifications is given (a more detailed account on the COMPTEL instrumental line background can be found in, e.g., Weidenspointner 1999).

  
4.1 ²D

Thermal-neutron capture on hydrogen results in the production of a stable ²D nucleus and the emission of a single 2.22 MeV photon, as seen in $E_{\rm tot}$ (see top panel in Fig. 6). The liquid scintillator NE 213A in the D1 detector modules consists of 9.2% H and 90.8% C by mass, making it an efficient moderator for neutrons. The instrumental 2.22 MeV photons are isotropically emitted from the D1 scintillators and constitute single photon (type A) background events. The average moderation and absorption times in the D1 scintillator for an incident neutron are a few $\mu$s and about 3 10^-4 s, respectively, hence the instrumental 2.22 MeV line is a quasi-prompt background component that follows the local, instantaneous cosmic-ray intensity (Weidenspointner et al. 1996). This quasi-prompt nature of the production/emission of the 2.22 MeV line is the reason for treating, in the following, the stable isotope ²D as if it were unstable, and for referring to it as "short-lived''. In principle, the initial scatterings of the incident neutrons could be identified by their PSD values. However, the time-scale for the moderation and absorption of an incident high-energy neutron is too long to associate the initial scatterings with the delayed neutron capture producing the $\gamma$-ray. The instrumental 2.22 MeV events therefore cannot be rejected by a selection on PSD.

The bulk of the neutrons producing ²D are expected to be of atmospheric origin, with secondary neutrons produced in the spacecraft being of minor importance. This follows from measurements of the fast-neutron flux in the D1 detector and Monte Carlo simulations of the production of secondary neutrons in cosmic-ray interactions (Morris et  al. 1995a), as well as from an estimate for the neutron absorption efficiency of the D1 detector.

  
4.2 ²⁴Na

The main production channels for ²⁴Na are neutron-capture reactions such as ²⁷Al(n, $\alpha$)²⁴Na and proton reactions such as ²⁷Al(p, 3pn)²⁴Na. The Al structure of the D1 detector system is the primary source of ²⁴Na activation. As described in Sect. 3, spectral features of the ²⁴Na background in both the $E_{\rm tot}$ and E₂ spectra can be understood by considering its cascade nature (type C events). In particular, the two photons with energies of 1.37 MeV and 2.75 MeV produce line features at about 1.3 MeV and 2.7 MeV in E₂ (see bottom panel in Fig. 6).

In addition, the time-variation of the ²⁴Na event rate is consistent with expectations for an isotope with a half-life of 15 h that is produced during SAA passages (see Sect. 5.1). Also, ToF distributions summed using data selections that favour ²⁴Na events have the characteristics of type C background events, i.e. they peak slightly below a ToF value of 5 ns (see Fig. 7), corresponding to an average distance of the location of the photon emission from the D1 module of about 20-30 cm.

	Figure 7: The measured ToF distribution of 24Na events from the vicinity of the D1 detector
Open with DEXTER

  
4.3 ⁴⁰K

⁴⁰K is one of the contributors to the spectral line feature at about 1.4 MeV in $E_{\rm tot}$ (see top panel of Fig. 6). A prominent line at this energy was present before launch in some of the calibration data, and at that time was tentatively identified with primordial ⁴⁰K radioactivity, contained e.g. in the concrete of the buildings. The 1.4 MeV line was still present after launch, however, and did not vary with any orbital parameter, indicating an instrumental origin as well.

A viable explanation for the instrumental 1.4 MeV line was the potassium in the glass of the D1 PMTs (van Dijk 1996). Electron capture by ⁴⁰K results in the emission of a single 1.46 MeV photon (type A event). This origin is supported by the fact that a disproportionate fraction of the photons at 1.46 MeV interact in the outer sections of the D1 scintillator, indicating that the photons enter the D1 detectors from the sides, consistent with the location of the D1 PMTs. Also, the observed $\bar{\varphi}$distribution at 1.46 MeV peaks at high $\bar{\varphi}$ values, again indicating that the photons enter from the sides. These characteristics were reproduced in Monte Carlo simulations. Furthermore, the potassium content in the D1 PMTs derived from the observed 1.4 MeV line rate is consistent with the manufacturer's specifications, as was confirmed by radiological measurements of a PMT in the laboratory. The mass of the PMT front window (made of Corning France 801.51) is about 24.9 g, with a potassium mass fraction of 6%; the mass of the PMT side and back glass (both made of Schott 8245) is about 40.7 g and 9.1 g, respectively, both with a potassium mass fraction of 0.14%. The front window contains more than 95% of the potassium in the PMTs and is closest to the detectors. The ⁴⁰K background therefore is dominated by the front window. The ⁴⁰K activity of the front window, normalized to its mass, is about 0.2 decays s^-1 g^-1.

  
4.4 ²²Na

Routine data processing and the investigation of galactic 1.8 MeV line emission from radioactive ²⁶Al indicated the build-up of a broad background component at about 1.5 MeV in $E_{\rm tot}$ (see top panel of Fig. 6). Investigations of the energy distribution of this background feature, as well as of its ToF dependence, led to its identification with the $\beta^+$-decay of ²²Na produced in the D1 detector material (Oberlack 1997). This background component is produced by a two photon cascade (type C event) with energies of $\sim$500 keV and $\sim$1.3 MeV, consistent with the absorption of the 1.275 MeV photon in D2, and the scattering of an annihilation 511 keV photon in D1 (the reverse process, involving absorption of the 511 keV photon in D2, is suppressed because 511 keV is below the D2 threshold). The ToF distribution of the 1.275 MeV ²²Na line in E₂ is consistent with the ToF signature of the ²⁴Na cascade. The build-up of the feature is consistent with an isotope of half-life of 2.6 y (see Sect. 5.1).

The most important process for the production of ²²Na in the D1 detector are proton interactions in the aluminium structure, the main channel being ²⁷Al(p, 3p3n)²²Na. Based on the production cross-sections, some ²²Na should also be produced in proton interactions with silicon, found in the glass of the D1 PMTs, such as Si(p, 4pxn). It is expected that most of the ²²Na production occurs during SAA passages (see Sect. 5.1).

  
4.5 ²⁸Al

The isotope ²⁸Al is produced by thermal-neutron capture on aluminium, the most abundant element in the D1 detector. The existence of the strong ²D line due to thermal-neutron capture on hydrogen indicates the presence of a thermal-neutron flux in the D1 scintillators. The cross-section for thermal-neutron capture on aluminium has a value of 0.28 mb (cf. 0.33 mb for hydrogen). Upon its $\beta^-$-decay, ²⁸Al can generate a type C background event: the 1.78 MeV photon is absorbed in D2, with a bremsstrahlung photon (from the $\beta^-$) scattering in D1. A small fraction of the ²⁸Al decays result in type A background events from the double scattering of the 1.78 MeV photon.

From the beginning of the mission a weak, albeit significant, line feature at about 1.8 MeV has consistently been present in the E₂ distribution (see bottom panel of Fig. 6). The position of this feature is independent of E₁, as expected for a type C event. Additional support for the identification of ²⁸Al comes from the fact that, as expected, the 1.8 MeV feature is short-lived (see Sect. 5.2).

  
4.6 ⁵²Mn and ⁵⁷Ni

The above mentioned isotopes were not sufficient to account entirely for the pronounced and broad $\sim$1.4 MeV feature in E₂ that built up over the mission. After subtracting the effects of the other isotopes, there was clear evidence for a build-up of the 1.4 MeV residual, whose half-life was estimated to be between that of ²⁴Na and that of ²²Na (assuming that it is due to a single isotope). The E₁ dependence of the 1.4 MeV residual in E₂ suggested that the line is due to a $\beta^+$-decay and therefore arises from type C background events. After detailed modelling of the E₂ and $E_{\rm tot}$spectra, taking into account the material composition of the D1 detector, it was concluded that the 1.4 MeV residual is due to a blend of two different isotopes, namely ⁵²Mn (1.43 MeV) and ⁵⁷Ni (1.38 MeV).

The isotope ⁵²Mn is produced in SAA-proton interactions with the Fe, Cr, and Ni in the D1 detector, found mainly in the electronics. Matters are complicated by the fact that ⁵²Mn can be produced in either its ground state or an isomeric state. These two states have different half-lifes and decay schemes. The time variation of the ⁵²Mn event rate suggests that this isotope is more likely produced in the ground state ( T_1/2 = 5.6 d) than in the isomeric state ( T_1/2 = 21.1 min), as described in Sect. 5.1. In this case, most ⁵²Mn events are due to the absorption of a 1.43 MeV photon in D2, accompanied by the scattering of another photon, from the radioactive decay or positron annihilation, in D1.

The isotope ⁵⁷Ni is expected to be mostly produced by proton interactions with Ni and Cu in the D1 detector during SAA passages. The ⁵⁷Ni background is mainly produced by the absorption of the 1.38 MeV photon in D2, with one of the 511 keV annihilation photons scattering in D1 (type C event). Similar to ⁵²Mn, the identification of ⁵⁷Ni, which has a half-life of about 36 h, is supported by modelling the observed long-term variation of its background contribution (see Sect. 5.1).

  
4.7 ²⁰⁸Tl

Similar to the 1.4 MeV feature, the 2.7 MeV feature in E₂represents a blend of lines from more than a single isotope. In addition to ²⁴Na, at least one component with a very long half-life (exceeding that of ²²Na) is present. The position of the residual is about 2.6 MeV. ²⁰⁸Tl, which is part of the natural ²³²Th decay chain, is the most viable candidate.

The isotope ²⁰⁸Tl undergoes $\beta^-$-decay through several channels, all of which involve the emission of at least two photons, implying that the ²⁰⁸Tl multiple photon (type C) events are efficient in triggering the telescope. The half-life of ²⁰⁸Tl is only 3.1 min. If the isotope is part of a natural decay chain, however, then its effective half-life is equal to the longest half-life of any of its parent isotopes, which in this case is the isotope ²³²Th with a half-life of 1.4 10¹⁰ y. The main channel for the production of background events by ²⁰⁸Tl is the absorption of the 2.61 MeV photon in D2, with another photon scattering in D1.

It was assumed that ²⁰⁸Tl is distributed like ⁴⁰K and is only present in the front glass of the D1 PMTs. This was tested by recording $\gamma$-ray spectra of a spare D1 PMT using a Ge spectrometer. Taking the COMPTEL results for the ⁴⁰K and ²⁰⁸Tl lines at face value, and assuming that both isotopes are equally distributed in the D1 PMTs, one expects that the ²⁰⁸Tl activity is about 10^-2 decays s^-1 g^-1 in the front window or about 6% of that of ⁴⁰K, based on the simulated efficiencies, corresponding to a ²³²Th mass fraction of a few 10^-8. Unfortunately, the laboratory measurement of ²⁰⁸Tl was inconclusive. The 1.46 MeV ⁴⁰K line is detected at the 12$\sigma$ level above the general background ( $1700 \pm 140$ counts). The strongest ²⁰⁸Tl lines at 2.61 MeV and 0.58 MeV, however, with intensities of 100% and 85.5%, were only detected at the 0.9$\sigma$ ($50 \pm 56$ counts) and 1.4$\sigma$ ( $128 \pm 92$ counts) level, respectively. Although consistent with expectations, these numbers are insufficient to test the assumptions. Much longer integration times are needed.

  
5 Variability of instrumental lines

The activity of isotopes contributing to the COMPTEL background (except for the primordial radio-isotopes ⁴⁰K and ²⁰⁸Tl) in general varies in time. They are produced by interactions of primary and secondary cosmic-ray particles and radiation-belt (SAA) particles within the instrument material. The intensity of each of these particle species, and hence the level of activation, changes in time due to orbit details (e.g. the satellite's altitude, the geomagnetic cut-off rigidity, the SAA radiation dose) and the solar cycle. The activity of a specific radioactive isotope then results from the competing processes of activation (production) and decay.

The variation of the activity of a specific isotope is complex in general. If the isotope's half-life T_1/2 and the typical time-scale(s) $\tau$ for the intensity variation of the particle population(s) producing it are very different, however, the activity variations can be described rather simply. For $T_{1/2} \ll \tau$, the isotope's activity approximatly follows the incident cosmic-ray particle intensity and its orbital variation (see Sect. 5.2). This is, e.g., the case for short-lived isotopes ( $T_{1/2} \stackrel{\textstyle _<}{_{\sim}}$ a few minutes) produced by primary cosmic-ray particles or neutrons, such as ²D and ²⁸Al. For $T_{1/2} \gg \tau$, a long-term build-up occurs since the activated nuclei do not decay away between consecutive SAA transits (see Sect. 5.1). This is, e.g., the case for long-lived isotopes ( $T_{1/2} \gg 90$ min, i.e. the orbital period) produced during SAA passages (which occur 6-8 times each day), such as ²²Na and ²⁴Na. Intermediate half-lifes produce more complicated variability.

The long-term and orbital variations of spectral features are useful in identifying their physical origin. Spectral features arising from primordial radioactivity will show no variation. Prompt and short-lived components will vary with incident cosmic-ray intensity, i.e. on time-scales shorter than an orbital period. In addition, prompt and short-lived components may also vary over long time-scales if their production is sensitive to changes in the cosmic-ray intensity due to the solar cycle or the orbit altitude. Spectral features due to long-lived isotopes will exhibit variations on time-scales that reflect their half-life as well as the changes in SAA dosage. With regard to a spectral feature not yet identified, these long-term variations provide a crude estimate of its half-life. With regard to a tentatively identified isotope, comparison of its time-dependent activity with an empirical model serves as an important cross-check for the correctness of its identification.

  
5.1 Long-term variation

The long-term variation of the activity of long-lived radio-nuclides arises from the combined effects of the isotopes' decay and the time history of the activation episodes during SAA transits. Activation outside the SAA by cosmic-ray particles is negligible (see e.g. Kurfess et al. 1989), since the average daily fluence due to SAA particles by far exceeds that of cosmic-ray particles. The count rate in the CAL-units can be used to model the production of long-lived radio-nuclides (Varendorff et al. 1997, hereafter referred to as "activity model''). The small plastic scintillators (thickness 3 mm, diameter 12 mm) of the CAL-units are sensitive to protons and other charged particles, but insensitive to secondary $\gamma$-ray photons. They therefore provide a measure of the charged-particle flux at the instrument (Snelling et al. 1986). The trigger rates of the two CAL-units above both a low and a high threshold value are available for all times, including SAA transits. Most other instrument systems are switched off during SAA passages, including the veto shields which therefore cannot be used as charged particle monitors for the activity model. The high-threshold trigger rate of CAL-unit B ( ${r}_{\rm BH}$) is most useful because it is the least affected by noise and long-term efficiency degradation. Only telemetry data gaps interrupt this measure of the cosmic-ray intensity.

To achieve continuous information on the charged-particle flux during every SAA passage, the activity model employs a neural net to describe ${r}_{\rm BH}$ as a function of orbit altitude, geographic longitude and latitude, time since launch (to include variations due to the solar cycle), and orientation (azimuth and zenith) of the satellite relative to its velocity vector (to account for asymmetries in the incident SAA-proton flux, see e.g. Watts et al. 1989). The number of nuclei of a specific isotope as a function of time, N(t), is then given by:

 

$$N(t + \delta t) N(t) \cdot {\rm e}^{-\lambda \cdot \delta t} + N_{\rm new}(t)$$ =

$${\rm and}$$ (2)

$$N_{\rm new}(t) \alpha \cdot \delta t \cdot ({r}_{\rm BH}(t) - {r}_{\rm BH,0})$$ =

where the time interval $\delta t$ usually is 16.384 s, $\lambda = \ln 2 / T_{1/2}$ is the decay constant of the isotope with half-life T_1/2, $\alpha$ is the proportionality factor between the CAL-unit trigger rate and the isotope activation, and ${r}_{\rm BH,0}$ is the value of ${r}_{\rm BH}$outside the SAA. The isotope activity A(t) then is

$$A(t) = \lambda \cdot N(t).$$ (3)

The value of $\alpha$ is not well known as it depends on the cross-sections for the production of the isotope in the telescope material, particularly in the D1 detector. For each isotope, a scaling factor, which is the product of $\alpha$ and the efficiency for triggering a background event (see Sect. 6), must be determined from a measurement of the event rate from the COMPTEL data.

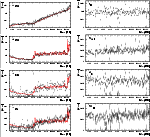Figure 8: The measured event rates due to the long-lived isotopes 22Na, 24Na, 52Mn, and 57Ni, the short-lived isotopes 2D and 28Al, and the primordial isotopes 40K and 208Tl as a function of time for the first 6 years (May 1991 through July 1997) of the CGRO mission for imaging event selections. In addition, the predictions of the normalized activity model for the long-lived isotopes is depicted with solid grey lines

Open with DEXTER

	Figure 9: The altitude of the CGRO orbit as a function of time from May 1991 through July 1997. The two reboosts of the orbit around TJD 9280 (Oct.-Dec. 1993) and TJD 10560 (Apr.-May 1997) are clearly seen. The rapid decay of the orbit at the beginning of the mission results from the increased drag of the expanded atmosphere at solar maximum
Open with DEXTER

A comparison of the measured event rates due to the long-lived isotopes ²²Na, ²⁴Na, ⁵²Mn, and ⁵⁷Ni with the predictions of the normalized activity model from May 1991 through July 1997 is depicted in the left panels of Fig. 8. In addition, the long-term variation determined for the event rates arising from the short-lived isotopes ²D and ²⁸Al, as well as from the primordial radio-nuclides ⁴⁰K and ²⁰⁸Tl are shown in the right panels of Fig. 8. These rates were obtained from the study of the galactic ²⁶Al 1.8 MeV line emission, which requires a measure of the isotopes' background contributions for each observation period (see Appendix B.2) under imaging event selections (see Appendix A.2). The scatter of the eight sets of event rates, particularly those for the primordial radio-isotopes ⁴⁰K and ²⁰⁸Tl, is larger than what is expected from statistics alone. Part of the additional scatter is expected from intrinsic inadequacies of the fitting procedure (such as the correction for the Earth-horizon angle selection, see Appendix B.2) and of the fit models employed (these cannot account for all structures in the E₂ and $E_{\rm tot}$ spectra, which particularly affects weak components, see below and Appendix B). Partly, however, the additional scatter may be attributed to known physical effects. Due to the precession of the satellite orbit the radiation dose from SAA transits may vary considerably between observation periods. In addition, the orientation of the satellite relative to the anisotropic SAA-particle flux affects the radiation dose in the D1 detector, which is the major source of instrumental line background. The resulting differences in SAA radiation dose between observation periods contribute to the scatter in the event rates of the long-lived isotopes. Since the CAL-units are located half-way between the D1 and D2 detectors, shielding effects due to surrounding spacecraft materials may result in less variation in ${r}_{\rm BH}$ than in the D1 radiation dose, so that the activity model would underpredict this variation. Orientation effects may also result in variations of the effective cosmic-ray particle flux between observation periods and add some scatter to the event rates of short-lived isotopes.

The long-term variation of the long-lived isotopes reflects the variation of the SAA radiation dose, which depends, among other parameters, on orbit altitude and solar cycle. ²⁴Na is the best tracer of the changing intensity of the encountered SAA-particle fluxes, as it is the strongest component of the line background and has a half-live of about 15 h. From the beginning of the mission until the first reboost (around TJD 9280), the decay of the orbital altitude (see Fig. 9) results in a monotonic decrease of the incident SAA-particle fluxes. The SAA radiation dose increased after the first reboost; the effect of the slow decrease of the orbital altitude is probably more than compensated by the solar cycle, which proceeded towards solar minimum, resulting in the observed net increase of SAA radiation dose over time. The second reboost (around TJD 10560) again resulted in a significant increase of activation during SAA passages. The long-term variation of the ⁵²Mn and ⁵⁷Ni event rates is similar to that of ²⁴Na, since the half-lifes of these isotopes are of the same order. The long-term behaviour of the ²²Na event rate is quite different. Its 2.6 y half-life is significantly longer than the typical time-scale of the changes in SAA radiation dose. Therefore ²²Na never reaches an equilibrium between activation and decay, but is continuously built up, with the two reboosts resulting in increases in the slope of the ²²Na activity trend.

The fact that the activity model reproduces the long-term variation of the event rates from long-lived isotopes confirms the model assumptions, in particular that activation predominantly occurs during SAA transits. The model can also verify the isotope identifications, as the activity of an isotope depends, among other parameters, on its half-life (see Eqs. (2) and (3)).

The background produced by the short-lived isotopes ²D and ²⁸Al is not expected to be influenced by SAA radiation dose, rather, any long-term trends will arise from variations in the average cosmic-ray intensity. The count rate in the 2.22 MeV line does not exhibit any significant long-term variation. The orbital variation of the event rate in the 2.22 MeV line (Weidenspointner et al. 1996) is similar to that of the fast-neutron flux ( ${E}_{\rm n} > 12.8$ MeV) in the D1 detector (Morris et al. 1995a), as discussed in Sect. 5.2. In addition, Morris et al. (1995a) demonstrated that the solar cycle variation of the fast-neutron flux is much less than its orbit variation. It is therefore expected that the relatively weak solar cycle dependence of the 2.22 MeV line is dominated by the much greater orbital variations, which presumably accounts for much of the observed scatter. Similar to ²D, the isotope ²⁸Al is predominantly produced by thermal-neutron captures. Hence ²⁸Al is expected to exhibit the same long-term variation as ²D. However, the low count rate from ²⁸Al exhibits a slight, increasing trend, hinting at deficiencies of the fit models and/or contributions from yet unidentified isotopes.

The activity of the primordial radio-nuclides ⁴⁰K and ²⁰⁸Tl is constant over the duration of the mission. Both data sets are consistent with this fact, although a small long-term increase may be present for ²⁰⁸Tl. Again, this apparent increase may be due to deficiencies of the fitting procedure and/or due to yet unidentified line background components.

The activity model can not only be used to predict the number of nuclei activated during SAA passages, but also to estimate the average daily SAA-proton fluence from the daily increase in the number of proton-produced nuclei. For example, based on the measured ²²Na event rate a daily average SAA-proton fluence ( ${E}_{\rm p} > 100$ MeV) of 2.3 10⁵ protons cm^-2 was inferred by Varendorff et al. (1997) for the beginning of the mission during solar maximum at an altitude of 440 km. Considering the uncertainties in this measurement, and the large altitude gradient of the SAA-proton flux (Stassinopoulos 1989), this value is in good agreement with the prediction of 5 10⁵ protons cm^-2 for an altitude of 462 km (Dyer et al. 1994).

  
5.2 Variation with cosmic-ray intensity

The prompt instrumental background closely tracks the local, instantaneous cosmic-ray intensity, which can, e.g., be parameterized by a geomagnetic cut-off rigidity. Another way of parameterizing the incident cosmic-ray intensity is to use the count rate of the anti-coincidence domes of the COMPTEL instrument, referred to as "veto rate'' in the following. To a good approximation, the prompt background components vary in proportion to the incident cosmic-ray intensity as monitored by the veto rate. The best example of this are ²D and ²⁸Al (Fig. 10), determined for CDG event selections (see Appendix A.1). In the following discussion, "veto rate'' and "incident cosmic-ray intensity'' are therefore used interchangeably. In contrast to prompt background components, the activity of the primordial radio-isotopes ⁴⁰K and ²⁰⁸Tl is independent of incident cosmic-ray intensity and hence does not vary with veto rate. The activity variation of long-lived isotopes such as ²²Na with veto rate is complex and depends on the isotopes' half-life as well as on the geophysical environment. Similar to the study of the long-term variation, the study of the variation of the event rate of a background component with cosmic-ray intensity can be helpful in identifying the responsible isotope.

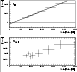	Figure 10: The veto rate variation of the count rate due the background isotopes 2D and 28Al as measured for CDG event selections. The dashed line is a linear fit to the measured 2D event rate
Open with DEXTER

In the following, the physical origin of the complex and - in general - non-linear variation of the event rate of long-lived isotopes with incident cosmic-ray intensity as monitored by veto rate is illustrated with the isotope ²²Na, which has a half-life of 2.6 y. To investigate the variation of a line background component with veto rate over a given time period the events are sorted in energy spectra, one for each of a set of veto rate intervals, according to the veto rate value at the time the events were recorded. The event rate due to the background isotope under study is then determined for each veto rate bin in an iterative line fitting procedure described in Appendix B.1. Each of these rates represents the "average'' event rate due to the isotope in a given veto rate interval over a given time period.

The veto rate variation of the event rate due to ²²Na over relatively short periods of time, during which the geophysical environment did not change significantly, is illustrated in Fig. 11 for data from 1991-1993 (CGRO Phases I and II) and from 1994-1995 (CGRO Cycle 4). To a good approximation, the ²²Na event rate is independent of veto rate, as expected for a half-life of 2.6 years. The average ²²Na event rate increased with time due to the build-up of this isotope during successive SAA passages (see Fig. 8). An increasing background contribution is also observed for long-lived isotopes with shorter half-lifes, such as ²⁴Na with T_1/2 = 15 h. However, due to a correlation between the encountered geomagnetic cut-off rigidity and the time since the last SAA transit, there is some correlation between the event rate of these isotopes and veto rate, which is generally complex even over relatively short periods of time. Nevertheless, the following conclusions drawn from the veto rate variation of the ²²Na event rate apply to long-lived isotopes with shorter half-lifes such as ²⁴Na as well.

	Figure 11: The count rate from 22Na, determined under CDG event selections, as a function of veto rate for data from 1991-1993 and from 1994-1995
Open with DEXTER

	Figure 12: The count rate from 22Na, determined under CDG event selections, as a function of veto rate for data from 1991-1996
Open with DEXTER

The average variation of the event rate arising from ²²Na over the extended time period from 1991-1996 (CGRO Phase I through Cycle 5), during which the geophysical environment changed significantly due to the first reboost (see Fig. 9) and the solar cycle, is depicted in Fig. 12. Typically, a bump-like feature, hereafter referred to as the veto rate bump, appears at low veto rate values when studying the veto rate variation of the background contribution of long-lived isotopes over extended periods of time that include at least one reboost. This is even true for an isotope such as ²²Na, whose event rate is independent of veto rate over short periods of time. It must be emphasized, however, that changes in the geophysical environment do not always produce a bump-like feature, but rather result in a complex, non-linear variation of the contribution from long-lived background components with veto rate.

	Figure 13: The variation of the normalized veto rate frequency distribution with time, exemplified for veto dome 2. Depicted are the normalized veto rate frequency distributions, in units of 16.384 s time intervals (superpackets, SP) per veto rate bin, for the time periods 1991/1992 (thin black line), 1994/1995 (grey line), and 1997/1998 (thick black line)
Open with DEXTER

To understand the origin of the veto rate bump it is necessary to realize that the changing geophysical environment not only affects the activity of long-lived isotopes (see Fig. 8), but also the veto rate frequency distribution, mostly due to variations of the incident cosmic-ray intensity with orbit altitude and solar cycle. This is illustrated in Fig. 13, depicting the normalized veto rate frequency distributions for the time periods 1991/1992, 1994/1995, and 1997/1998 (i.e. CGRO Phase I, Cycle 4, and Cycle 7, respectively). For clarity, the distributions for other Phases/Cycles were omitted as they are fully consistent with the trend described in the following. The generic veto rate distribution is characterized by a pronounced peak at low veto rates, with a flat tail extending to higher veto rate values. To a good approximation, the time variation of this generic veto rate frequency distribution can be described by a slow but steady shift of the peak to higher veto rate values, with some slight changes of the shape of the distribution such as an increasing extension of the tail.

	Figure 14: Illustration of the origin of the veto rate bump. Features such as the veto rate bump result from the combined effects of the time variation of the isotope activity (see Fig. 8) and of the veto rate frequency distribution (see Fig. 13), as explained in detail in the text
Open with DEXTER

As is illustrated in Fig. 14, the veto rate bump is nothing more than an artifact of the combined effects of the long-term variation in the activity of long-lived isotopes (see Fig. 8) and of the long-term shift of the veto rate frequency distribution (see Fig. 13). For simplicity, let us consider a long-lived isotope whose activity is independent of veto rate over periods of time during which the geophysical conditions do not change, such as ²²Na. Let us further consider a combination of two such time intervals of equal duration from early and late in the mission. Late in the mission the isotope activity is higher than early in the mission, and the veto rate distribution is shifted to higher veto rate values. The two sets of data are represented by the two bars in Fig. 14, with the grey-shading indicating the veto rate distribution in terms of the number of 16.384 s sampling intervals (superpackets, see Footnote 4) per veto rate interval, i.e. dark grey indicates that the corresponding veto rate values occurred more often (compare Fig. 13). The average activity (determined as described above) then increases from interval 1 through interval 4 as the late-mission data become relatively more important. In interval 5 both sets of data contribute equally and the average activity is the mean of the individual activities. Finally, only data from the late mission contribute to veto rate interval 6. The net result for the average activity exhibits a general tendency to increase with increasing veto rate with a pronounced bump superimposed - similar to what has been measured for ²²Na (compare to Fig. 12). It can easily be demonstrated, following the above example, that the veto rate bump is an almost universal indicator for the presence of radio-isotopes with half-lifes ranging from several minutes to several years when combining data covering extended periods of time during which the geophysical environment inevitably changed. However, the veto rate bump cannot be used to estimate the half-life of an isotope, as can be done with the activity model. Also, it should be noted that non-linear variations of the event rate due to a long-lived isotope with veto rate other than the veto rate bump are to be expected once the isotope activity decreases and/or the veto rate frequency distribution shifts towards lower values as the mission continues.

Among other things, a detailed understanding of the variation of the background contribution of long-lived isotopes with veto rate is necessary for a reliable measurement of the cosmic diffuse gamma-ray background (CDG) at MeV energies. The COMPTEL analyses make use of the variable nature of the instrument background to isolate the CDG signal, which is assumed to be constant (see e.g. Kappadath et al. 2000; Weidenspointner et al. 2001). In particular, above about 4 MeV the instrumental background is exclusively due to prompt processes. These are also present in the background at lower energies, but with large contributions from long-lived radioactive isotopes. Because prompt background components vary, to a good approximation, linearly with incident cosmic-ray intensity as monitored by veto rate, they can be eliminated from the data by an extrapolation technique (Kappadath et al. 1996). In contrast, the event rate of long-lived isotopes does not vary linearly with veto rate. The contributions of long-lived isotopes must therefore be subtracted, as a function of veto rate, before the veto rate extrapolation (Weidenspointner 1999). The validity of a veto rate extrapolation for removing prompt instrumental backgrounds thus depends on the absence of any long-lived background components, since only then can the event rate be assumed to vary linearly with veto rate. Subtraction of non-prompt background components after the veto rate extrapolation is only possible for constant background components, such as primordial radioactivity.

   
6 Background line intensities: Comparisonsand implications

The instrumental line background of an instrument is determined by its material composition, the radiation environment, and the employed detection principle. In this respect it is interesting to compare the COMPTEL instrumental lines with those identified in the data from other low-energy $\gamma$-ray experiments on satellite platforms such as the NaI Gamma-Ray Spectrometer (GRS) onboard the Solar Maximum Mission (SMM) and the Ge Gamma-Ray Spectrometer (GRS) flown on HEAO 3. In doing so, one must keep in mind that an instrument's energy resolution is important for resolving lines. At 1 MeV, the energy resolution (FWHM) of COMPTEL is 9.8% and 8.8% in $E_{\rm tot}$and E₂, respectively (Schönfelder et al. 1993). At the same energy, the resolution of GRS-SMM was about 5.4% (Forrest et al. 1981), and that of GRS-HEAO 3 was $\stackrel{\textstyle _<}{_{\sim}}$0.3% (Mahoney et al. 1980). Therefore, the Ge spectrometer onboard HEAO 3 is far superior for $\gamma$-ray line studies compared to COMPTEL and GRS-SMM, which have similar resolution. The CGRO satellite is kept in a circular orbit of 28.5$^\circ$ inclination at altitudes between about 330 km and 515 km (see Fig. 9). The SMM and HEAO 3 missions were operated in circular orbits of 28.5$^\circ$ inclination at about 490-570 km altitude, and 43.6$^\circ$ inclination at about 500 km altitude, respectively. Similar to COMPTEL, the most abundant element in the material composition of both GRS-SMM (E. Chupp, priv. comm., 1999) and GRS-HEAO 3 (Wheaton et al. 1989) is Al in the instrument structures. Also, all instruments contain significant amounts of Fe, Ni, Cu, and Cr in, e.g., electronics components.

Five of the eight isotopes identified in the COMPTEL line background, namely ²²Na, ²⁴Na, ²⁸Al, ⁵²Mn, and ⁵⁷Ni, are due to activation of Al and Fe, Ni, Cu, and Cr nuclei in the instrument structure. As expected, each of these isotopes has also been identified in GRS-SMM (Share et al. 1989) and GRS-HEAO 3 (Wheaton et al. 1989) data. For GRS-SMM, however, an additional production channel for ²²Na and ²⁴Na were proton and neutron reactions, respectively, on ²³Na in the NaI detectors. Other isotopes identified in GRS-SMM and GRS-HEAO 3 that result from activation of the five elements and which have major lines below about 1 MeV should in principle also be present in the COMPTEL background, however, their events are suppressed by the D1 and D2 detector thresholds used in COMPTEL analyses. On the other hand, instrumental lines due to activation of Cs and I (GRS-SMM) or Ge (GRS-HEAO 3) are absent in COMPTEL since they exhibit a ToF value not used in the analysis (I) or since these elements are not present in the instrument (Cs, Ge).

The different detection principles employed in the three instruments result in significant differences in the relative importance of specific isotopes, their detectability, and rejectability. COMPTEL requires coincident interactions in the D1 and D2 detector and therefore is particularly susceptible to multiple photon events such as the $\beta^+$-decay of ²²Na or the $\beta^-$-decay of ²⁴Na (see Sect. 3). Consequently, multiple photon events are relatively more important than single photon events. On the other hand, individual photons from these decays produce photopeaks in E₂ that can be used for identifying individual isotopes and for determining their background contribution. In addition, the characteristic E₁-E₂ signature of multiple photon events provides a wide range of options for their rejection (or enhancement). In the SMM and HEAO 3 spectrometers events are triggered by individual photons. Unlike the COMPTEL veto system, which consists of plastic scintillator domes, the anti-coincidence systems of the SMM and HEAO 3 spectrometers were made of CsI crystals and therefore sensitive to photons at $\gamma$-ray line energies. For these two detectors therefore the probability for a radioactive decay to trigger the detectors is proportional to the number of emitted photons, as is the probability to trigger the anti-coincidence systems. To first order, the net probability of a radioactive decay for generating a background event is therefore independent of the photon multiplicity for GRS-SMM and GRS-HEAO 3. As long as the decays occur outside the detectors, individual photons will give rise to photopeaks in the latter two instruments, and these backgrounds are harder to suppress by event selections than in COMPTEL. As far as decays inside the detectors are concerned, $\beta$-decays are particularly hard to identify for GRS-SMM (e.g. activation of Na) and GRS-HEAO 3 (activation of Ge) since the added $\beta$-continuum will broaden $\gamma$-ray lines beyond recognition. In COMPTEL, activation in the D2 detector is effectively eliminated by event (ToF) selection.

Since COMPTEL is the first double-scattering Compton telescope operated in a near-Earth orbit, the instrumental background experienced during this mission may provide guidance for the design of future instruments. Below, some implications of the COMPTEL instrumental line background for conducting $\gamma$-ray line studies with this and future instruments are discussed.

The by far strongest astrophysical $\gamma$-ray line signal detected by COMPTEL is 1.8 MeV line emission from ²⁶Al in the interstellar medium (Diehl et al. 1995a). When observing along the galactic plane, the average event rate due to this extended line source is about 7 10^-4 s^-1 for imaging selections (see Appendix A.2). Typical event rates due to point sources observed by COMPTEL in the light of $\gamma$-ray lines, such as the supernova remnant Cas A (⁴⁴Ti at 1.12 MeV, Iyudin et al. 1997), or the type Ia supernova 1991T (⁵⁶Co at 0.85 MeV and 1.24 MeV, Morris et al. 1997b), or the Vela region (²⁶Al at 1.8 MeV, Diehl et al. 1995b) are about 3 10^-5 s^-1. Typical event rates arising from individual background isotopes are about 10^-1 s^-1 (see Fig. 8). Below 3 MeV, instrumental background lines account for 10-50% of the total background rate (see Fig. B.8). It follows that the signal-to-background ratio for astrophysical $\gamma$-ray lines in general is less than 1%, which can be enhanced to a few percent by fine-tuning the imaging event selections described in Appendix A.2 for analyzing a specific $\gamma$-ray line.

 

 

Table 2: Background isotope properties relevant for astrophysical $\gamma$-ray line studies. For each isotope the following quantities are listed: the efficiency for producing a background event under imaging event selections, the material(s) in which the isotope is produced, and the mission-averaged activity. Further details are given in the text

Isotope	Efficiency	Material	Activity
	(Imaging Sel.)		[g-1s-1]
2D	7 10-4	D1 scintillator	3.4 10-3
22Na	8 10-4	D1 Al structure	7 10-4
24Na	9 10-4	D1 Al structure	9 10-4
28Al	2 10-4	D1 Al structure	2 10-3
40K	2 10-4	D1 PMT glass	0.2
52Mn	2 10-3	Fe around D1	4 10-4
		Cr around D1	3 10-4
		Ni around D1	2 10-4
		Cu around D1	7 10-5
57Ni	5 10-4	Ni around D1	5 10-4
		Cu around D1	6 10-5
208Tl	2 10-3	D1 PMT glass	10-2

In this respect it is interesting to take a look at the efficiency, determined by Monte Carlo simulation, for various isotopes to produce a background event (see Table 2). For imaging selections, this efficiency is about 7 10^-4 and 2 10^-4 for ²D and ⁴⁰K, both of which give rise to type A (single photon) background events. A major source of type C multiple photon events is ²⁴Na with an efficiency of about 9 10^-4. The efficiency for ²⁰⁸Tl, a minor source of type C events which is assumed to have the same spatial distribution as ⁴⁰K, is about 2 10^-3. This is an order of magnitude larger than the efficiency for ⁴⁰K and again illustrates that COMPTEL is more susceptible to multiple photon decays than to single photon decays. The more stringent CDG event selections reduce these efficiencies by factors of 4-7 and 2-3 for type A and type C background events, respectively. For comparison, the detection efficiencies for celestial lines around 1-2 MeV are about 2 10^-4 using imaging event selections.

A goal for future Compton telescopes is to minimize background production by design. Passive material should be reduced, and manufactured from materials with low activation. Based on simulated efficiencies and the COMPTEL mass model, "mission-averaged'' activities (in decays per g of material per s) were derived for the eight identified isotopes using data representing the first 7 years of the mission (June 1991 to April 1998). These activities, together with the above mentioned simulated efficiencies and the activated materials, are summarized in Table 2. The relative yields for ⁵²Mn and ⁵⁷Ni were determined in hadron simulations (P. Jean, priv. comm., 1997). The numbers for the average activities are accurate within factors of 2-3. Their major sources of uncertainty are the simulated efficiencies and the mass normalization, which are currently based on the assumption that the activation is homogeneous in a particular material. This may not be accurate for isotopes produced by thermal neutrons, in particular ²⁸Al. As a cross-check, the average activities were compared to simulations of activation of COMPTEL materials, neglecting the contributions of secondary particles, for a solar-maximum radiation environment (P. Jean, priv. comm., 1997). The measured and the simulated activities are generally consistent within factors of a few for isotopes mainly produced by SAA protons. Hence these average activities may be used for estimating the line background rates of future instruments in a similar orbit, taking into account how the mass distribution differs from that of COMPTEL.

  
7 Summary and discussion

We have identified eight different isotopes in the COMPTEL instrumental line background, namely ²D, ²²Na, ²⁴Na, ²⁸Al, ⁴⁰K, ⁵²Mn, ⁵⁷Ni, and ²⁰⁸Tl. These isotopes can account for the major instrumental background lines. Some minor instrumental lines, however, remain unidentified at this time. In addition, we have studied the variation of the event rate of these isotopes with time and incident cosmic-ray intensity, and determined the average activity of spacecraft materials.

These results provide valuable insight into the physical processes that give rise to instrumental background lines in $\gamma$-ray detectors in low-Earth orbits. Because of their importance for MeV astronomy, these issues have repeatedly been studied (see, e.g., Dean et al. 1991 and references therein). Obviously, each detector has its own, unique instrumental background. Nevertheless, background investigations such as those reported in this work add to a growing pool of background experience to be found in the literature, which will prove to be important for the design of future instruments and the understanding of their data.

The successful modelling of the time variation of the background contributions from the long-lived isotopes ²²Na, ²⁴Na, ⁵²Mn, and ⁵⁷Ni in COMPTEL supports the conclusion that activation occurs predominantly during SAA passages. On average, CGRO passes through the SAA 6-8 times each day. In 1991 (at solar maximum and hence at minimum SAA-proton flux) the daily average of the incident flux of SAA protons with ${E}_{\rm p} > 100$ MeV was about 38 times higher than the corresponding incident galactic cosmic-ray proton flux (Dyer et al. 1994), illustrating the importance of SAA passages with respect to the total deposited radiation dose. The SAA-proton flux varies strongly with altitude and solar cycle. For example, during its mission the altitude of CGRO ranged from 350-500 km, which corresponds to a variation of the SAA-proton flux of a factor $\sim$10, while the solar activity results in a variation by a factor $\sim$2 at these altitudes (Stassinopoulos 1989). According to our activity model (Varendorff et al. 1997) the anisotropy of the SAA-proton flux at low satellite altitudes (Watts et al. 1989) has an important effect on the radiation dose and hence on activation. These findings are consistent with earlier studies of GRS-SMM instrumental lines, in which activation due to (anisotropic) radiation-belt protons during SAA transits has been identified as major source of (long-lived) line background and its variation with time (see Kurfess et al. 1989; Share et al. 1989, and references therein).

In contrast, the activities of short-lived isotopes are mostly determined by the incident primary cosmic-ray and albedo-neutron fluxes. The enhanced production of these isotopes during SAA transits is of little importance for their background contribution outside the SAA, where astrophysical data are recorded, because of their rapid decay, which precludes build-up.

Two strategies for reducing instrumental line background in future low-energy $\gamma$-ray detectors due to activation of long-lived isotopes present themselves. First, care should be taken to avoid detector materials which are easily activated by SAA protons (such as aluminium) or which carry primordial radioactivity. Second, instruments should be placed in orbits that minimize radiation-belt proton dosage, such as a low-altitude equatorial orbit below the radiation belts and outside the SAA, or a high-altitude orbit above the radiation belts (as scheduled for the INTEGRAL observatory). The flux of (low-energy) cosmic rays is significantly lower in a low-altitude orbit as compared to a high-altitude orbit - at the cost of a much higher albedo-neutron flux. Another strategy for limiting the impact of remaining instrumental lines in future instruments is, e.g., to exploit the expected improvement in energy resolution to identify (and model) a large number of instrumental background components. A comprehensive treatment of the implications of the COMPTEL instrumental line (and continuum) background for future Compton telescopes is beyond the scope of this paper and will be given in a separate publication.

Finally, although investigations of background lines are of interest in their own right, they are ultimately motivated by the struggle to eliminate background events in astrophysical analyses. The COMPTEL instrumental background lines, particularly those from long-lived isotopes, are a concern below about 4 MeV. At these energies detailed understanding of the dataspace structure and variability of the instrumental lines is indispensable for optimizing many astrophysical investigations, such as that of the cosmic diffuse gamma-ray background (see e.g. Kappadath et al. 2000; Weidenspointner et al. 2001) or of the galactic 1.8 MeV line emission from ²⁶Al (see e.g. Oberlack 1997; Plüschke et al. 2000).

Comparing event rates due to $\gamma$-ray line sources and due to instrumental background it is evident that source fluxes cannot be derived from global event rates with COMPTEL. This is only possible in imaging analysis, which exploits the characteristic cone-like distribution of source events in a three-dimensional data space spanned by the scatter angle $\bar{\varphi}$ and the direction (zenith and azimuth) of the scattered photon (see Schönfelder et al. 1993). Instrumental background components exhibit comparatively smooth distributions in this data space, allowing for their separation from the signal. Further exploitation of existing knowledge on the dataspace structure of instrumental lines will remedy some of the difficulties in the search for astrophysical $\gamma$-ray lines (see e.g. Morris et al. 1997b). Nevertheless, data selections that increase the signal-to-background ratio are clearly of great value.

The importance of instrumental background suppression/rejection can be illustrated with the original report of nuclear de-excitation lines from the Orion region (Bloemen et al. 1994), which would have corresponded to an event rate of about 6 10^-4 s^-1 spread over a rather broad energy range of 3-7 MeV. As was recognized in our recent analyses, the variations in the ²⁴Na event rate over the different observation periods of this galactic region are capable of producing spatial inhomogeneities in the background of that order, which then can be falsely attributed to a celestial signal. Only correlations of the supposed Orion signal with data space domains where ²⁴Na contamination is strongest provided the hints to suspect an instrumental background artifact as the origin of the claimed detection (Bloemen et al. 1999).

Acknowledgements

It is a pleasure to acknowledge laboratory efforts of J. Macri, and of R. Georgii, C. Wunderer, and W. Plass in measuring primordial radioactivity in D1 PMTs. We are also pleased to acknowledge work on hadron simulations for estimating activation of spacecraft materials by P. Jean. The COMPTEL project is supported by the German government through DARA grant 50 QV 90968, by NASA under contract NAS5-26645, and by The Netherlands Organization for Scientific Research NWO.

  
Appendix A Event selections

The results on the COMPTEL instrumental lines given in the main body of this paper have been derived using two different sets of event selections, described below.

  
A.1 CDG analysis

In the COMPTEL analysis of the cosmic diffuse gamma-ray background (CDG), the intense atmospheric $\gamma$-ray background is eliminated by selecting data from times when the Earth was sufficiently far outside a circular field-of-view defined by event selections. Detailed descriptions of these selections can be found in, e.g., Kappadath (1998) and Weidenspointner (1999).

The standard set of CDG event selections used in this paper are as follows:

 

$$70~{\rm keV} \le {E}_{1} \le 20~{\rm MeV}$$

$$730~{\rm keV} \le {E}_{2} \le 30~{\rm MeV}$$

$$800~{\rm keV} \le {E}_{\rm tot} \le 30~{\rm MeV}$$

$$110~{\rm ch} \le {\rm ToF} \le 130~{\rm ch}$$ (A.1)

$${\rm PSD}_{\rm low}({E}_{1}) \le {\rm PSD} \le {\rm PSD}_{\rm high}({E}_{1})$$

$$6^\circ \le \bar{\varphi} \le 38^\circ$$

$$\zeta + \bar{\varphi} = \xi \le 40^\circ$$

where $\bar{\varphi}$ is the photon scatter angle (see Eq. (1)), and $\zeta$ is the angle between the direction of the scattered photon and the telescope z-axis. The selection on $\xi$ defines a field-of-view of half opening angle 40$^\circ$. The values of PSD $_{\rm low}$ and PSD $_{\rm high}$are 40 ch and 110 ch at 70 keV, 55 ch and 95 ch at 1 MeV, 55 ch and 92 ch at 10 MeV, and 40 ch and 90 ch at 20 MeV. At intermediate E₁ energies, these boundaries are linearly interpolated. In addition, the horizon of the Earth, as seen by the instrument, is required to be at least 5$^\circ$ outside the field-of-view.

  
A.2 Imaging analysis

In COMPTEL imaging analyses such as that of the ²⁶Al 1.8 MeV line emission from the galaxy, $\gamma$-ray albedo photons from the Earth's atmosphere are rejected by determining for each event the minimal angular distance between its possible origins in the sky and the Earth horizon. This angular distance, denoted $\epsilon$ below, is required to exceed a minimum value (see e.g. Schönfelder et al. 1993). Hence, the effective field-of-view in imaging analysis changes with time as the instrument orbits the Earth.

The standard set of imaging event selections used in this paper are as follows:

 

$$70~{\rm keV} \le {E}_{1} \le 20~{\rm MeV}$$

$$650~{\rm keV} \le {E}_{2} \le 30~{\rm MeV}$$

$$750~{\rm keV} \le {E}_{\rm tot} \le 30~{\rm MeV}$$

$$115~{\rm ch} \le {\rm ToF} \le 130~{\rm ch}$$ (A.2)

$$0~{\rm ch} \le {\rm PSD} \le 110~{\rm ch}$$

$$0^\circ \le \bar{\varphi} \le 50^\circ$$

$$\epsilon \ge 5^\circ.$$

  
Appendix B Line fitting procedures in analyses of CDG and ²⁶Al

Many astrophysical analyses, such as that of the cosmic diffuse gamma-ray background (CDG), of the galactic 1.8 MeV line emission from ²⁶Al, or of $\gamma$-ray line emission from supernovae, can be optimized by detailed modelling of the instrumental line background. Below, the (similar) procedures used to determine the background event rates due to individual isotopes employed by Weidenspointner et al. (2001); Oberlack (1997) and Plüschke et al. (2000) in investigations of the CDG and of the ²⁶Al emission, respectively, are described.

  
B.1 CDG analysis

Figure B.1: A schematic representation of the simulated E1-E2 distributions of the eight isotopes identified in the instrumental line background for CDG event selections. The "vertical'' and "diagonal'' bands represent multiple photon and single photon events, respectively (compare to the detailed individual diagrams in Sect. 4)

Figure B.2: An illustration of the E1-E2 ranges of the three E2 spectra and the $E_{\rm tot}$ spectrum used to determine the event rates due to the background isotopes. Also plotted are lines of constant $\bar{\varphi}$ (solid) and $E_{\rm tot}$ (dashed)

Accounting for the event rates due to the instrumental line background, in particular its long-lived components, is important for measuring the CDG at MeV energies (e.g. Kappadath et al. 2000; Weidenspointner et al. 2001). As explained above, the background contributions of long-lived isotopes have to be subtracted before prompt and short-lived backgrounds can be eliminated by veto rate extrapolation. The event rates due to the eight identified background isotopes producing the major instrumental lines are determined, as a function of veto rate, in an iterative procedure by fitting a set of three E₂ spectra and one $E_{\rm tot}$ spectrum for each veto rate interval.

The rationale of the iterative fitting procedure is illustrated in Figs. B.1 and B.2. The E₁-E₂ distributions of the eight isotopes as obtained from Monte Carlo simulations are schematically depicted for CDG event selections in Fig. B.1. In general, there is considerable overlap in the E₁-E₂distributions of individual isotopes (in particular around 1.3 MeV in E₂), which precludes an independent determination of the isotopes' background contributions. Therefore, an iterative procedure was introduced, which starts at the highest energies in E₁ and E₂, where ambiguities are minimal, and then proceeds down to the increasingly complex structures at lower E₁ and E₂energies. The E₁-E₂ ranges of the three E₂ spectra and the $E_{\rm tot}$ spectrum, chosen such as to enhance or suppress individual lines or spectral features, are indicated in Fig. B.2. The E₁-E₂ ranges covered by the second and third E₂ fit and by the $E_{\rm tot}$ fit overlap, hence the results of these fits are not statistically independent. The overlap is caused by the $E_{\rm tot}$ fit, which was introduced to properly separate the background events from ²D and ²⁸Al. Inclusion or omission of the $E_{\rm tot}$ fit therefore is a trade-off between systematic and statistical uncertainty. By iteratively fitting the second and third E₂ spectrum and the $E_{\rm tot}$ spectrum, both the systematic and the statistical uncertainty in the ²D and ²⁸Al event rates are minimized (other isotopes are hardly affected by the overlap, see below). In additon, the iterative approach ensures the self-consistency of the determined isotope background contributions. Also included in Fig. B.2 are lines of constant $\bar{\varphi}$ and $E_{\rm tot}$. Comparison of Figs. B.1 and B.2 provides a first indication of the many options for fitting individual lines, which can be enhanced or suppressed through the choice of the fit regions, and in addition through selections on $E_{\rm tot}$ and/or $\bar{\varphi}$. In particular, event selections may be used to suppress unidentified, long-lived spectral features, which cannot be eliminated by veto rate extrapolation (see Kappadath et al. 2000; Weidenspointner et al. 2001).

The E₁-E₂ ranges of the three E₂spectra and the $E_{\rm tot}$ spectrum indicated in Fig. B.2 were chosen for the iterative fitting procedure for the following reasons. The first E₂ spectrum, covering the E₁-E₂region of 950-1250 keV in E₁ and 2000-3500 keV in E₂(see Figs. B.1 and B.2), allows us to determine the event rate from ²⁴Na. The signal from this isotope is optimized by selecting E₁ energies around the Compton edge of the 1.37 MeV photon interacting in D1 and around the photopeak of the 2.75 MeV photon interacting in D2 (see Fig. 5). The ²D event rate is determined from fitting the $E_{\rm tot}$spectrum ( $E_{\rm tot}$ 1810-2800 keV, E₁ 70-950 keV, and E₂ 730-2800 keV, see Figs. B.1 and B.2). The second E₂ spectrum (E₁ 500-950 keV, E₂1500-3500 keV, see Figs. B.1 and B.2) is used to determine the event rate from ²⁸Al. Finally, the third E₂spectrum is intended for determining the background contributions from the $\beta^+$-decays of ²²Na, ⁵²Mn, and ⁵⁷Ni, with the 270-350 keV range in E₁ being optimized for the Compton edge of 511 keV photons, and the E₂ range covering the energies 1100-3500 keV (see Figs. B.1 and B.2). To optimize the signal of the instrumental lines, which originate in the D1 detector material, a ToF range of 2.5-7.5 ns was selected for the spectra (compare Fig. 3).

The three E₂ spectra and the $E_{\rm tot}$ spectrum are analyzed in an iterative procedure consisting of eight fits, listed below. The contributions from the primordial radio-nuclides ⁴⁰K and ²⁰⁸Tl are not determined from the fits, but calculated from their known (⁴⁰K, see Sect. 4.3) or estimated (²⁰⁸Tl, see Sect. 4.7) activities based on Monte Carlo simulations. Similarly, once the background contribution of an isotope has been determined from any spectrum, the isotope's contribution to any other spectrum can be predicted based on Monte Carlo simulations. The eight identified isotopes can account for the major instrumental lines, however, some weak lines or spectral features remain unidentified at this time. In the fits, some of these unidentified lines were described by Gaussians to minimize systematic errors in the determination of the event rates of the identified components. The unidentified components are genuinely different from those identified since their variation with cosmic-ray intensity, as well as their dependence on event parameter selections, are different (see Kappadath et al. 2000; Weidenspointner et al. 2001). The identified isotopes are represented by templates obtained from Monte Carlo simulation. These templates have not been smoothed as smoothing inevitably increases the systematic uncertainty due to distortions of the template shape. The small "spikes'' in the templates in Figs. B.3-B.6 are an artifact of the plotting software. The eight fit steps are:

Figure B.3: An example of a fit of the first E2 spectrum, which is used to determine the event rate due to 24Na. In addition to the total fit, the 24Na template (solid line), the two unidentified features (dashed and dash-dotted lines), and the exponential continuum are indicated

Figure B.4: An example of a fit of the $E_{\rm tot}$ spectrum for determining the count rate in the 2D 2.22 MeV line. In additon to the total fit, the 2D template (solid line), an unidentifed component at about 2.3 MeV (dashed line), the continuum contributions from 24Na and 208Tl (solid and dash-dotted lines), and the exponential continuum (dashed line) are indicated

1.

E₂ Fit 1: The event rate due to the isotope ²⁴Na is determined (see Fig. B.3);

2.

$E_{\rm tot}$ Fit: The ²D event rate is estimated; the contributions from ²⁴Na and ²⁰⁸Tl are fixed. All other isotopes are neglected;

3.

E₂ Fit 2: The ²D and ²⁸Al event rates are estimated; the contributions from ²⁴Na and ²⁰⁸Tl are fixed;

4.

E₂ Fit 3: The background contributions due to the $\beta^+$-decays of ²²Na, ⁵²Mn, and ⁵⁷Ni are estimated; the contributions from ²D, ²⁴Na, ²⁸Al, ⁴⁰K, and ²⁰⁸Tl are fixed;

5.

$E_{\rm tot}$ Fit: The ²D event rate is determined; the contributions from all other isotopes (²²Na, ²⁴Na, ²⁸Al, ⁴⁰K, ⁵²Mn, ⁵⁷Ni, and ²⁰⁸Tl) are fixed (see Fig. B.4);

6.

E₂ Fit 2: The event rate due to the isotope ²⁸Al is determined; the contributions from ²D, ²⁴Na, and ²⁰⁸Tl are fixed (see Fig. B.5);

7.

E₂ Fit 3: The event rates due to the $\beta^+$-decays of ²²Na, ⁵²Mn, and ⁵⁷Ni are determined; all other isotopes are fixed (see Fig. B.6);

8.

$E_{\rm tot}$ Fit: The ²D event rate is re-determined as in Fit 5.

In this procedure, Fits 5-7 re-iterate Fits 2-4 to ensure convergence, which is tested by comparing the results of Fits 5 and 8. In general, the two fits yield nearly identical results. This self-consistent determination of the event rates of long-lived isotopes inevitably requires the determination of all isotope contributions, whether long-lived, short-lived, or prompt. In the CDG analysis, subtraction of the contributions from ²D, ²⁴Na, and ²⁸Al are based on Fits 8, 1, and 6, respectively (see Weidenspointer et al. 2001). The event rates due to the $\beta^+$-decays of ²²Na, ⁵²Mn, and ⁵⁷Ni are derived from the results of Fit 7. As pointed out before, the contributions from the primordial radio-nuclides ⁴⁰K and ²⁰⁸Tl need not be determined from the line fits, but can be computed based on the known or estimated activities.

Figure B.5: An example for a fit of the second E2 spectrum, which is used to determine the event rate from 28Al. In addition to the total fit, the templates for 2D (the line feature at $\sim$1.6 MeV, fixed), 28Al (the 1.78 MeV line), 24Na (the strong line at 2.75 MeV, fixed) and 208Tl (the weaker line at 2.61 MeV, fixed), the three unidentified features (dashed, dashed-dotted, and dashed lines), and the exponential continuum are indicated

Figure B.6: An example for a fit of the third E2 spectrum, which is used to determine the event rates from 22Na (dotted line), 52Mn (thick solid line), and 57Ni (thin solid line). Also depicted are the fixed components (2D: solid line at 1.9 MeV, 24Na: dash-dotted line, 28Al: weak solid component below 1.9 MeV, 40K: dashed line, 208Tl: solid line at 2.6 MeV), as well as the total fit, the exponential continuum, and the unidentified 2.93 MeV feature

  
B.2 ²⁶Al analysis

The analysis of the galactic 1.8 MeV line emission from ²⁶Al is, similar to that of the CDG, affected by the instrumental line background and its temporal variation. The galactic 1.8 MeV line emission is determined in the energy band 1.7-1.9 MeV, using adjacent energy bands for constructing a model for the background in this so-called line interval (comprehensive descriptions of this approach can be found in, e.g., Knödlseder 1997 & Oberlack 1997). In particular, the scatter angle $(\bar{\varphi})$ distribution of the 1.7-1.9 MeV background model is derived from an interpolation of the $\bar{\varphi}$ distributions in narrow adjacent energy intervals (1.6-1.7 MeV and 1.9-2.0 MeV). Due to the long-term variation of the instrumental line background (see e.g. Fig. 8), the ratio of the number of counts in the line interval and in the adjacent energy intervals is decreasing with time (see Fig. B.7), mostly due to the build-up of ²²Na, a major component in the 1.6-1.7 MeV band in $E_{\rm tot}$ (Oberlack 1997). To eliminate the time dependent contamination of the background reference from adjacent energies, the number of counts due to each component of the instrumental line background has to be determined for each individual observation period, employing a procedure outlined below. After subtraction of the instrumental line background, the ratio of counts in the line interval and the adjacent energy intervals to a good approximation is constant in time (see Fig. B.7), and data from individual observation periods can be summed to analyze the galactic 1.8 MeV line emission.

Figure B.7: Count ratios (number of counts in the line interval divided by the number of counts in the adjacent energy intervals) as determined for observations at galactic latitude $\vert b\vert > 40^{\circ }$. The ratios, and a linear model of their time variation, are shown before (grey) and after (black) subtraction of the instrumental line background

The procedure used in the ²⁶Al analysis to determine the background contributions of the eight identified background isotopes is a modified version of the CDG procedure described in Appendix B.1. The modifications are motivated by differences in the event selections applied in the two analyses, particularly differences in the elimination of atmospheric background (see Appendix A.1 and A.2). One of the consequences is that in the ²⁶Al imaging analysis events with larger $\bar{\varphi}$values are accepted than in the CDG analysis. For some isotopes, notably ²⁴Na, this results in significant changes of the E₁-E₂ distribution as compared to that for CDG event selections. Consequently, the optimal fit regions in E₁-E₂ space are somewhat different. Also, in contrast to the CDG analysis, in the ²⁶Al analysis the $\bar{\varphi}$ distribution of the accepted events is different for each observation period due to the orbit dependent rejection of atmospheric background. The simulated energy distributions for each background isotope therefore have to be corrected for the specific $\bar{\varphi}$ distribution of each individual observation period (Oberlack 1997). The correction for selections to reject atmospheric background has been calculated assuming a homogeneous illumination of the D1 detector. Since there is a certain edge enhancement in the illumination of the D1 modules for background produced in the D1 structure, slight differences in these corrections result in small distortions of the templates, and thus add to the observed scatter in the determined isotope event rates (see Fig. 8). As each observation period is independently analyzed for its instrumental line background contamination, the background modelling in the ²⁶Al analysis yields as a welcome by-product the long-term variation of the event rates due to the eight identified background isotopes depicted in Fig. 8.

Figure B.8: An example for an $E_{\rm tot}$ fit in the 26Al analysis. The upper panel depicts the $E_{\rm tot}$ spectrum before (line histogram) and after (data points) subtracting the contributions from the identified background isotopes (indicated by smooth curves with different line types). The middle panel shows the $E_{\rm tot}$ spectrum after isotope subtraction, together with the continuum background fit. The bottom panel gives the residuum of the fit

The four steps of the iterative line fitting procedure in the ²⁶Al analysis are similar to those in the CDG analysis, hence we content ourselves with describing only the differences. In the first step, two E₁-E₂ regions are fitted simultaneously to obtain the ²⁴Na event rate (Oberlack 1997): the E₁-E₂ region depicted in Fig. B.2, and an additional E₁-E₂ region extending from 2000 to 2700 keV in E₁ and from 1100 to 2000 keV in E₂. Analogous to the first E₁-E₂region, the additional E₁-E₂ region optimizes the ²⁴Na signal from simultaneous interactions of the 1.37 MeV and 2.75 MeV photons in D2 and D1, respectively, which are no longer suppressed due to the larger accepted $\bar{\varphi}$ values for imaging selections. The E₁-E₂ region for the second step extends down to 700 keV in E₁, and is used for determining the ²⁸Al rate and for obtaining start parameters to determine the event rates of the remaining isotopes, particularly ²²Na, in Fit 3. However, unlike in the CDG analysis, the contributions of the primordial isotopes ⁴⁰K and ²⁰⁸Tl are not fixed in the ²⁶Al analysis, but determined in Fit 3 and 1, respectively. As far as determining the contributions of each individual isotope is concerned, the procedure ends here, since it has been demonstrated in the CDG analysis that one fit cycle is sufficient to obtain self-consistent isotope rates. This advanced background treatment provided the basis for the latest COMPTEL ²⁶Al all-sky maps (e.g. Oberlack 1997; Plüschke et al. 2000).

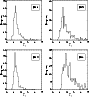Figure B.9: The distribution of the $\chi ^2_{\nu }$ values for each of the four fit steps in determining the instrumental line contamination in the 26Al analysis (Plüschke et al. 2000)

To investigate the extent to which the identified isotopes can account for spectral features in $E_{\rm tot}$, an additional fit is performed (see Fig. B.8). In this $E_{\rm tot}$fit ( E₁ > 70 keV, E₂ > 650 keV), the contributions from the eight background isotopes are fixed at the values obtained from the three previous E₂ fits; only the continuum background, modelled by a power law with an exponential turn-over at low energies, is varied. As can be seen, the major spectral features are accounted for by the eight identified isotopes, however, some minor features remain unidentified at this time.

The distribution of the $\chi ^2_{\nu }$ values for each of the four fit steps, as obtained in the analysis of Plüschke et al. (2000), is shown in Fig. B.9. The quality of Fits 1 and 3, in which the event rates of most of the background isotopes are determined, is acceptable. The $\chi ^2_{\nu }$distribtion for the $E_{\rm tot}$ fit, however, indicates that further improvement of the instrumental line background modelling is still possible.

References

 
• Bloemen, H., et al. 1994, A&A, 281, L5 In the text NASA ADS  
• Bloemen, H., et al. 1999, ApJ, 512, L137 In the text  
• Dean, A. J., et al. 1991, Space Sci. Rev., 57, 109 In the text NASA ADS  
• Diehl, R., et al. 1995a, A&A, 298, 445 In the text NASA ADS  
• Diehl, R., et al. 1995b, A&A, 298, L25 In the text NASA ADS  
• Dyer, C. S., et al. 1994, IEEE Trans. Nucl. Sci., 41, No. 3, 438 In the text  
• Forrest, D. J., et al. 1981, Solar Phys., 65, 15 In the text  
• Iyudin, A. F., et al. 1997, ESA, SP-382, 37 In the text  
• Kappadath, S. C., et al. 1996, A&AS, 120, C619 In the text NASA ADS  
• Kappadath, S. C., 1998, Ph.D. Thesis, University of New Hampshire, USA In the text  
• Kappadath, S. C., et al. 2000, ApJ, in preparation In the text  
• Knödlseder, J. 1997, Thèse de l'Université Paul Sabatier, Toulouse, France In the text  
• Kurfess, J. D., et al. 1989, in High-energy radiation background in space (AIP 186), ed. A. Rester, Jr., & J. I. Trombka, 250 In the text  
• Mahoney, W. A., et al. 1980, NIM A, 178, 363 In the text  
• Morris, D. J., et al. 1995a, J. Geophys. Res., 100, 12243 In the text  
• Morris, D. J., et al. 1997a, in 1997 Conference on the High-Energy Background in Space, ed. J. I. Trombka, J. S. Schweitzer, & G. P. Lasche, Institute of Electrical and Electronic Engineers (IEEE), 26 In the text  
• Morris, D. J., et al. 1997b, in Proc. of the Fourth Compton Symposium (AIP 410), ed. C. D. Dermer, M. S. Strickman, & J. D. Kurfess 1084 In the text  
• Oberlack, U. 1997, Dissertation, Technical University Munich, Germany In the text  
• Plüschke, S., et al. 2000, in Proc. of 5th Compton Symposium (AIP 510), ed. M. McConnell, & J. M. Ryan, 35 In the text  
• Ryan, J., et al. 1997, in 1997 Conference on the High-Energy Background in Space, ed. J. I. Trombka, J. S. Schweitzer, & G. P. Lasche, Institute of Electrical and Electronic Engineers (IEEE), 13 In the text  
• Schönfelder, V., et al. 1993, ApJS, 86, 657 In the text NASA ADS  
• Share, G. H., et al. 1989, in High-energy radiation background in space (AIP 186), ed. A. Rester, Jr., & J. I. Trombka, 266 In the text  
• Snelling, M., et al. 1986, NIM A, 248, 545 In the text  
• Stassinopoulos, E. G. 1989, in High-energy radiation background in space (AIP 186), ed. A. Rester, Jr., & J. I. Trombka, 3-63 In the text  
• van Dijk, R. 1996, Ph.D. Thesis, University of Amsterdam, The Netherlands In the text  
• Varendorff, M., et al. 1997, in Proc. of the Fourth Compton Symposium (AIP 410), ed. C. D. Dermer, M. S. Strickman, & J. D. Kurfess 1577 In the text  
• Watts, J. W., et al. 1989, in High-energy radiation background in space (AIP 186), ed. A. Rester, Jr., & J. I. Trombka, 75 In the text  
• Weidenspointner, G., et al. 1996, A&AS, 120, C631 In the text NASA ADS  
• Weidenspointner, G. 1999, Dissertation, Technical University Munich, Germany In the text  
• Weidenspointner, G., et al. 2001, A&A, in preparation In the text  
• Wheaton, W. A., et al. 1989, in High-energy radiation background in space (AIP 186), ed. A. Rester, Jr., & J. I. Trombka, 304 In the text