5 Modelisation of the kinematics

For each galaxy, we wish to reconstruct the entire velocity field, projected on the sky, and constrain it with the observed velocity profiles along the short and long axis of the nuclear bar (or disc for NGC 1365). Three of the four galaxies observed here have embedded nuclear bars, and the orbits are then not expected to be circular. To interpret these profiles, in a first approximation, we build simple models of the orbital structure, based on the epicyclic theory, assuming that the departures from circular motions are small.

5.1 Linear approximation

We introduce the usual coordinate system ($\xi$, $\eta$), rotating with the angular speed of rotation $\Omega - \Omega_{\rm p}$ in the frame co-rotating with the bar perturbation ( $\Omega_{\rm p}$).

$$r = r_0 + \xi$$

$$\theta = \theta_0 + (\Omega - \Omega_{\rm p}) t + \eta/r_0$$

where $\theta$ is the azimuthal angle in the rotating frame.

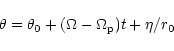
The bar potential is modelled by the function:

$$\Phi(r,\theta) = -\Phi_2(r) \cos{ 2\theta} + ...$$

with small harmonic terms ( $\Phi_4, \Phi_6 \le \Phi_2$). The shape of the bar potential is taken from the k=3 bar of the surface density-potential pairs generated by Kalnajs (1976):

$$\Phi_2(r) = 0.53 q_{\rm bar} x (1.-2.5 x+2.1875 x^2-0.65625 x^3)$$

when $x = r^2/r_{\rm bar}^2 < 1$. Outside $r_{\rm bar}$, the potential is extrapolated by continuity, with an inverse power law (in r^-4). The strengths of the bars $q_{\rm bar}$ are chosen such that the perturbations in the velocity field match at best the data. The strength of the perturbation is best quantified by the maximum over the disc of the ratio of the tangential force to the radial force, $P2_{\max}$. This quantity is given in Table 4 for the four galaxies.

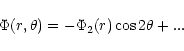
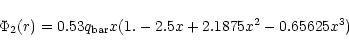
The equations of motion are linearized; in order to take into account the transition at the inner Lindblad resonances, an artificial frictional force is introduced, with a damping coefficient $\lambda$, as is usually done to simulate gas orbits (Lindblad & Lindblad 1994; Wada 1994). The motion is that of an harmonic oscillator, forced by an imposed external perturbation. The equations can be solved, at the neighborhood of the ILR (and OLR) and far from corotation, and give the coordinates and velocities of the orbit of the guiding centre, the epicyclic motions around this centre being damped by the frictional force.

This formulation (see Appendix A) accounts for the change of orientation of orbits at the crossing of resonances (parallel or perpendicular to the bar), and when the damping parameter $\lambda$ is not zero, of a gradual orientation change, corresponding to the gas spiral arms. We also use models with spiral configurations, since some young supergiant stars, just formed out of the gas, share its dynamics (and are indeed observed in the NIR range).

5.2 Galaxy models

The mass model for the spiral galaxies is made of three components:

• a small bulge, of Plummer shape potential
  
  $$\Phi_{\rm b}(r) = - {{G M_{\rm b} }\over {\sqrt{r^2 +r_{\rm b}^2}}}$$
  
  
  with characteristic mass $M_{\rm b}$ and radius $r_{\rm b}$;
• a Toomre disc, representing the main stellar disc, of surface density
  
  $$\Sigma(r) = \Sigma_0 ( 1 +r^2/r_{\rm d}^2 )^{-3/2}$$
  
  
  truncated at $r_{\rm t}$;
• a nuclear disc, which corresponds to the decoupled nuclear bar, and is required to account for the large gradients of velocity profiles, observed at kpc scale in the present work. Its shape is also taken as a Toomre function:
  
  $$\Sigma(r) = \Sigma_0 ( 1 +r^2/r_{\rm nd}^2 )^{-3/2}$$
  
  
  with a characteristic mass $M_{\rm nd}$ and radius $r_{\rm nd}$.

Let us emphasize that within the centre of spiral galaxies, the presence of dark matter is not required (e.g. Freeman 1992): the spherical dark matter halo, usually added to flatten rotation curves at large radii, have such a large characteristic radius that it has no influence on the inner parts considered here. All parameters are displayed in Table 4. From these analytical components, it is easy to compute the critical velocity dispersion for axisymmetric instability at each radius. We assume that the radial velocity dispersion $\sigma_{\rm r}$is everywhere proportional to this critical velocity, with a constant Toomre parameter Q as a function of radius. The value of Q is also indicated in Table 4. The tangential velocity dispersion $\sigma_{\theta}$ is assumed to verify the epicyclic relation:

$$\sigma_{\theta} = \frac{\kappa}{2\Omega} \sigma_{\rm r}.$$

The disc plane is assumed to have a constant scale-height h_zwith radius, and the z-velocity dispersion is derived from the surface density in the disc $\Sigma(r)$ by:

$$\sigma_z^2(r)=2 \pi G \Sigma(r) h_z.$$

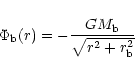
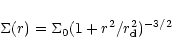
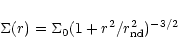
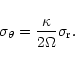
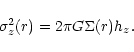
For each observed slit, we have computed the velocity dispersion along the line-of-sight in combining the local dispersion, and the contribution of the velocity gradient in the observed spatial resolution. Even in the very centre of the galaxies, this second contribution was always negligible.

Figure 7: Model velocity profiles for NGC 1097. Top left: the shape of the orbits in the linear epicyclic approximation, projected on the sky plane. Top right: the deduced velocity field, with the orientation of the nuclear bar indicated. Bottom: The corresponding velocity profiles, along the nuclear bar (left), and perpendicular to it (right) overimposed on the ISAAC kinematical profiles and their corresponding error bars. Two lines are plotted for the modeled velocity dispersion profiles, including or not the velocity gradients in the resolution elements. Most of the time, the two profiles are coinciding

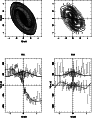Figure 8: Model velocity profiles for NGC 1365. (See Fig. 7 for caption)

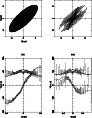Figure 9: Model velocity profiles for NGC 1808. (See Fig. 7 for caption)

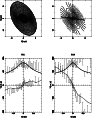Figure 10: Model velocity profiles for NGC 5728. (See Fig. 7 for caption)

5.3 Fits of the observations

The results of the modelisation can be seen in Figs. 7-10 for the four galaxies. In all cases, the presence of the nuclear disc is necessary to account for the large velocities at the kpc scale. The small bulges allowed by the photometry are insufficient, and in general bring a negligible contribution to the rotation curve. To limit the number of free parameters, we have fixed the mass and radius of the bulges to the statistical relation found by de Jong (1996) through NIR photometry. According to the types of the present galaxies, the bulge-to-disc ratio is 0.1, and the bulge radius is about 10 times lower than the disc radius. The main stellar disc are truncated at $r_{\rm disc} = R_{25}$, and their radial scale-lengths are deduced, assuming a central surface brightness of 21 B-mag arcsec^-2. The scale-heights of the discs are chosen to be 0.2 times the radial scale-length (e.g. Bottema 1993). The remaining free parameters to fit are therefore:

• $M_{\rm d}$ the disc mass, which is constrained by the outer parts of the velocity curve;
• $M_{\rm nd}$ and $r_{\rm nd}$ the mass and characteristic size of the circumnuclear disc. These parameters are constrained by the inner parts of the rotation curve;
• The strength and radius of the bar, $q_{\rm bar}$ (or equivalently $P2_{\max}$) and $r_{\rm bar}$, together with the pattern speed $\Omega_{\rm p}$, constrained by the shape and amplitude of the velocity profile;
• Q the Toomre parameter, constrained by the observed dispersion.

Since we are concerned here only with the circumnuclear regions, there is no corotation inside the model, but most of the time the best fit of $\Omega_{\rm p}$ is such that there are one or two inner Lindblad resonances.

 

 

Table 4: Model parameters for the 4 galaxies

Galaxy	$M_{\rm b}$	$r_{\rm b}$	$M_{\rm nd}$	$r_{\rm nd}$	$M_{\rm d}$	$r_{\rm d}$	$r_{\rm t}$	Q	hz	$r_{\rm bar}$	$\Omega_{\rm p}$	$P2_{\max}$
	1010 $M_\odot$	kpc	1010 $M_\odot$	kpc	1010 $M_\odot$	kpc	kpc		kpc	kpc	kms-1/kpc
NGC1097	1.3	0.6	1.6	0.9	13	5.9	22	1.5	1.2	3	78	0.06
NGC1365	1.0	0.8	1.1	1.2	10	8.0	30	1.8	1.6	5	25	0.23
NGC1808	0.3	0.3	0.9	0.4	2.7	2.7	10	1.4	0.5	0.9	60	0.07
NGC5728	0.4	0.4	0.9	0.6	3.8	4.3	16	1.6	0.9	3	50	0.06

For all galaxies except NGC 1365, the best fit is obtained with a nuclear bar, oriented differently than the primary bar, and parallel to the apparent nuclear bar. For NGC 1365 however, it was better to keep the primary bar potential orientation, with its low pattern speed, and rely on the different phase orientation of the orbits, to form a spiral nuclear structure, between the two ILRs. This confirms the observation that NGC 1365 does not include a secondary bar, as previously claimed, but a decoupled nuclear disc surrounded by spiral arms within the ILR of the primary bar.

In no case was it possible to find any central drop for the velocity dispersion. Of course, there is still a certain latitude in the fitting procedure, but some features are certain: it is not possible to reproduce the observations without a circumnuclear disc component, or with an axisymmetric potential. Elliptical orbits are required, and the fits give an order of magnitude of their importance. Also the required mass of the circumnuclear disc component is comparable, and sometimes even greater, than the bulge mass. The present models are simple first approximations, with bi-symmetry imposed (there is no m=1 components, although in NGC 1808, such an asymmetry is clearly observed); more realistic models constrained by further detailed kinematical data are needed to precise the dynamics of the double-bar galaxies. New models will also help to examine the issue of the central mass concentrations, for which we cannot, at the moment, give a lower limit.