

Up: Confirmation of the existence scales
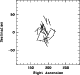 |
Figure 1:
A map of the polarization vectors of all significantly
polarized (
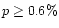 and
and
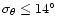 )
quasars
with right ascensions )
quasars
with right ascensions
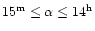
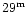 ,
and redshifts ,
and redshifts
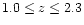 .
The vector length is arbitrary.
The 13 new objects are indicated by additional points .
The vector length is arbitrary.
The 13 new objects are indicated by additional points |
We first want to test the hypothesis that the polarization position
angles of quasars located in region A1 preferentially lie in the
interval [146
 -46
-46
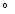 ]
instead of being uniformly
distributed. This angular sector was selected prior to the new
observations - on the basis of the results of Paper I-, and the
polarization position angles have been measured for a sample of
quasars different from that one at the origin of the detection of the
effect. Out of the 13 new significantly polarized quasars in region
A1 (Table 1), 10 have their polarization position angles in the
expected range. To test the null hypothesis H0 of uniform
distribution of circular observations against the alternative of
sectoral preference, we may use a simple binomial test (e.g. Lehmacher
& Lienert 1980; Siegel 1956). If
]
instead of being uniformly
distributed. This angular sector was selected prior to the new
observations - on the basis of the results of Paper I-, and the
polarization position angles have been measured for a sample of
quasars different from that one at the origin of the detection of the
effect. Out of the 13 new significantly polarized quasars in region
A1 (Table 1), 10 have their polarization position angles in the
expected range. To test the null hypothesis H0 of uniform
distribution of circular observations against the alternative of
sectoral preference, we may use a simple binomial test (e.g. Lehmacher
& Lienert 1980; Siegel 1956). If
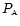 is the
probability under H0 that a polarization position angle falls in
the angular sector [146
is the
probability under H0 that a polarization position angle falls in
the angular sector [146
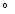 -46
-46
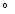 ], then
], then
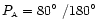 .
If L denotes the number of polarization position
angles falling in [146
.
If L denotes the number of polarization position
angles falling in [146
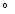 -46
-46
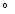 ], L has a binomial
distribution under H0, such that the probability to have
], L has a binomial
distribution under H0, such that the probability to have
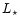 or more polarization angles in [146
or more polarization angles in [146
 -46
-46
 ]
is
]
is
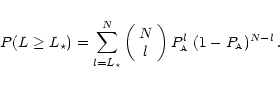 |
(1) |
With N=13 and
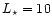 ,
we compute
,
we compute
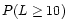 =
1.8%. This indicates that the hypothesis of uniform distribution of
polarization position angles may be rejected at the 1.8% significance
level in favour of coherent orientation.
A map of the quasar polarization vectors is illustrated in Fig. 1,
including the objects from Paper I. An alignment is clearly seen, with
a net clustering of polarization vectors around
=
1.8%. This indicates that the hypothesis of uniform distribution of
polarization position angles may be rejected at the 1.8% significance
level in favour of coherent orientation.
A map of the quasar polarization vectors is illustrated in Fig. 1,
including the objects from Paper I. An alignment is clearly seen, with
a net clustering of polarization vectors around
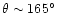 -
-
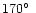 .
Altogether, there are 29 significantly polarized quasars
in this region, and 25 of them have their polarization vectors aligned
i.e. their polarization position angles in the range 146
.
Altogether, there are 29 significantly polarized quasars
in this region, and 25 of them have their polarization vectors aligned
i.e. their polarization position angles in the range 146
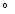 -46
-46
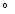 (Tables 1 and
2, and Paper I). It is interesting to note
that the effect is stable when we increase the polarization degree
cutoff (then decreasing the probability of a possible contamination):
out of 22 quasars with
(Tables 1 and
2, and Paper I). It is interesting to note
that the effect is stable when we increase the polarization degree
cutoff (then decreasing the probability of a possible contamination):
out of 22 quasars with
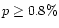 ,
19 have their polarization
vectors aligned, and out of 17 quasars with
,
19 have their polarization
vectors aligned, and out of 17 quasars with
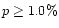 ,
16 have
their polarization vectors aligned.
,
16 have
their polarization vectors aligned.
Since in total 43 new polarized objects were found all over the sky,
it is also interesting to re-run the global statistical tests used in
Paper I. These tests are applied to the whole sample of 213
objects. The statistics basically measure the dispersion of
polarization position angles for groups of 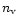 neighbours in the
3-dimensional space, the significance being evaluated through
Monte-Carlo simulations, shuffling angles over positions. It is not
our purpose to repeat here what was done in Paper I, but only to
illustrate the trend with the larger sample. The significance
levels of the statistical tests, i.e. the probabilities that the test
statistics would have been exceeded by chance only, are given in
Fig. 2 for the four tests considered in Paper I. Compared to Figs. 9
and 10 of Paper I, all the statistical tests indicate a net decrease
of the significance level for the larger sample, strengthening the
view that polarization vectors are not randomly distributed over the
sky but are coherently oriented in groups of 20-30 objects. We
note a shift of the minimum significance level towards slightly higher
values of
neighbours in the
3-dimensional space, the significance being evaluated through
Monte-Carlo simulations, shuffling angles over positions. It is not
our purpose to repeat here what was done in Paper I, but only to
illustrate the trend with the larger sample. The significance
levels of the statistical tests, i.e. the probabilities that the test
statistics would have been exceeded by chance only, are given in
Fig. 2 for the four tests considered in Paper I. Compared to Figs. 9
and 10 of Paper I, all the statistical tests indicate a net decrease
of the significance level for the larger sample, strengthening the
view that polarization vectors are not randomly distributed over the
sky but are coherently oriented in groups of 20-30 objects. We
note a shift of the minimum significance level towards slightly higher
values of 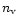 ,
as expected from the increase of the number density
of the objects.
,
as expected from the increase of the number density
of the objects.
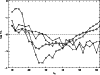 |
Figure 2:
The logarithmic significance level (S.L.) of the four
statistical tests defined in Paper I, S with
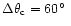
 , ,
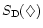 , ,
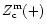 , ,
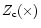 ,
when applied to the new sample of 213 polarized quasars. ,
when applied to the new sample of 213 polarized quasars.
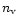 is the number of nearest neighbours around each quasar; it is
involved in the calculation of averaged quantities. The dashed
horizontal line indicates the 1% significance level
is the number of nearest neighbours around each quasar; it is
involved in the calculation of averaged quantities. The dashed
horizontal line indicates the 1% significance level |
All these results confirm the existence of orientation effects in the
distribution of quasar polarization vectors, and more particularly in
the high-redshift region A1 where an independent test was performed.


Up: Confirmation of the existence scales
Copyright ESO 2001
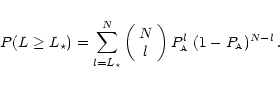
![]() neighbours in the
3-dimensional space, the significance being evaluated through
Monte-Carlo simulations, shuffling angles over positions. It is not
our purpose to repeat here what was done in Paper I, but only to
illustrate the trend with the larger sample. The significance
levels of the statistical tests, i.e. the probabilities that the test
statistics would have been exceeded by chance only, are given in
Fig. 2 for the four tests considered in Paper I. Compared to Figs. 9
and 10 of Paper I, all the statistical tests indicate a net decrease
of the significance level for the larger sample, strengthening the
view that polarization vectors are not randomly distributed over the
sky but are coherently oriented in groups of 20-30 objects. We
note a shift of the minimum significance level towards slightly higher
values of
neighbours in the
3-dimensional space, the significance being evaluated through
Monte-Carlo simulations, shuffling angles over positions. It is not
our purpose to repeat here what was done in Paper I, but only to
illustrate the trend with the larger sample. The significance
levels of the statistical tests, i.e. the probabilities that the test
statistics would have been exceeded by chance only, are given in
Fig. 2 for the four tests considered in Paper I. Compared to Figs. 9
and 10 of Paper I, all the statistical tests indicate a net decrease
of the significance level for the larger sample, strengthening the
view that polarization vectors are not randomly distributed over the
sky but are coherently oriented in groups of 20-30 objects. We
note a shift of the minimum significance level towards slightly higher
values of ![]() ,
as expected from the increase of the number density
of the objects.
,
as expected from the increase of the number density
of the objects.