

Up: A new analysis of Lacertae
Subsections
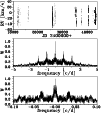 |
Figure 1:
Spectroscopic observations of EN Lac. Top: time sampling. Center: window
function. Bottom: window function zoomed at low frequencies |
Details on sources of data and instruments used.
Column "A":
A:
Frost et al. (1926) (cf. also Lee
1910 and Struve & Bobrovnikoff 1925),
B:
Beardsley (1969),
C:
Struve et al. (1952),
D:
McNamara (1957),
E:
Bloch et al. (1970),
F:
LeContel et al. (1983),
G:
Abt et al. (1990),
H: Sato & Hayasaka (1986)
I: Chapellier et al. (1995),
J: this paper.
Column "I":
I: Yerkes 1.02-m refractor, Bruce 1-prism spg.,
II: Allegheny 0.79-m Keeler Memorial reflector, 1-prism Mellon spg.,
III: Mt. Wilson 1.52-m reflector, Cassegrain spg.,
IV: Mt. Wilson 2.54-m reflector, coudé grating spg.,
V: Lick 0.91-m refractor, new Mills 3-prism spg.,
VI: Lick 0.30-m refractor, 2-prism spg.,
VII: Haute Provence 1.20-m reflector, prism spg.,
VIII: Haute Provence 1.52-m reflector, grating spg.,
IX: Kitt Peak National Observatory 1-m coudé feed grating spg.,
X: Okayama 1.88-m reflector, coudé grating spg.,
XI: Haute Provence 1.93-m reflector, grating spg.,
XII: this paper: Ondrejov 2.0-m reflector, coudé grating spg. with
a Reticon RL 1872F/30 detector with 15
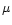
m pixels,
XIII: this paper: Tautenburg 2.0-m reflector, coudé echelle spectrograph
with a Tektronix
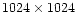
CCD with 24
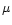
m pixels,
XIV: this paper: DAO 1.22-m reflector, coudé grating spg.
with a thick Loral
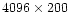
CCD with 15
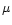
m pixels,
XV, XVI: this paper: OHP 1.52-m reflector, Aurélie coudé grating spg. with
a TH 7832 detector with 13
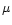
m pixels,
XVII: this paper: DAO 1.83-m reflector, Cassegrain grating spg.
Table 2 gives the journal of all RV observations at our disposal.
Our own observations more than doubled the existing body of the data.
Derived RVs are listed in Table 3![[*]](/icons/foot_motif.gif) .
New spectra were obtained at four observatories:
.
New spectra were obtained at four observatories:
- 1.
- The dominant data set consists of 942 echelle spectra from
the Thüringer Landessternwarte (TLS) Tautenburg. They were reduced with
the help of MIDAS software by HL. The standard MIDAS software was modified
for the wavelength calibration to obtain a perfect fit also at
the overlapping edges of the echelle orders. RVs were obtained from
the comparison of the synthetic and observed line profiles for the three
cleanest (least blended) He I lines: 5015, 5875, and 6678 Å;
- 2.
- The second largest set is a series of blue (4400-4700 Å) and
green (4750-5050 Å) Aurelie spectra secured with the 1.52-m reflector
of the Haute Provence Observatory (OHP) during 8 consecutive nights.
Their initial reduction (bias subtraction, flat-fielding)
was done by PM. The wavelength calibration and RV measurements were
carried out by PH who used the SPEFO program - see Horn et al. (1996) and
Skoda (1996). RVs of symmetric and stronger metallic lines (mostly O II,
N II and C II), H
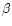 and He I 4472 and 4923 Å lines were measured. Their wavelengths were derived from measurements
of synthetic spectra broadened to the projected rotational velocity
of EN Lac. Only lines which were symmetric in the synthetic spectra were
used;
and He I 4472 and 4923 Å lines were measured. Their wavelengths were derived from measurements
of synthetic spectra broadened to the projected rotational velocity
of EN Lac. Only lines which were symmetric in the synthetic spectra were
used;
- 3.
- Four red (6280-6720 Å) Reticon spectra were obtained in
the coudé focus of the Ondrejov 2.0-m reflector. They were completely
reduced with SPEFO by PH. RVs were derived from He I 6678 Å, H
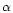 and several stronger and symmetric metallic lines;
and several stronger and symmetric metallic lines;
- 4.
- Several red (6100-6750 Å) CCD spectrograms were obtained
at the Dominion Astrophysical Observatory (DAO). They were completely reduced
within IRAF and MIDAS by SY and DH. Only RV of the He I 6678 Å line was
measured.
For all spectra covering the red wavelength region the instrumental
RV zero-points were derived with the help of a large set of telluric
O2 and H2O lines. This allows us to assume that the above
datasets 1, 3 and 4 (sets 15, 16, 17 and 20 of Table 2) are
on exactly the same heliocentric wavelength scale. Note that due to the
fitting procedures all RVs correspond to the RVs of line centroids and not
of line minima.
We compiled all series of RV observations available in the astronomical
literature and used a computer program to derive heliocentric Julian dates
(HJDs hereafter) from the tabulated dates of mid-exposures or geocentric
Julian dates for all of them. This way we found a few misprints in
tabulated JDs for RVs of EN Lac published by Beardsley (1969). For convenience of
future investigators, they are summarized in Table 4.
For JD 2420038 it is not clear whether the misprint occurred for
the date or the Julian date and we omitted this observation from our data
set. Figure 1 shows the sampling of all RVs in time and also
the window function of the data which will be discussed later.
Table 4:
Misprints detected in tabulated times of observations of
EN Lac in Beardsley (1969)
|
Date (G.M.T.) |
Tabulated JD |
Correct JD |
| |
-2400000 |
-2400000 |
|
1913 Sep. 27.621 |
20038.671 |
? |
| 1914 Sep. 22.746 |
20389.746 |
20398.746 |
| 1916 Sep. 02.631 |
21107.631 |
21109.631 |
Our compilation of RVs is very inhomogeneous. Spectra were observed with
different instruments and have very different linear dispersions and
resolutions. Also RVs were derived by different authors and rest on different
sets of spectral lines. A part of them comes from photographic plates and
another one from electronic spectra. So we have a set of RVs of different
accuracy and probably also of a slightly different zero point of the RVscale.
To take these differences at least partly into account, we attempted
to find out a suitable weighting scheme. This is not simple in our
particular case. Due to steady improvements of the observational and
reduction techniques, the accuracy, and therefore the weights would,
on average, increase with time. We have recent observations of a high
accuracy, well suited for precise RV measurements. However, the older,
less accurate observations are invaluable to a search for the long-term
amplitude changes over the periods of years or even decades.
The trouble is that any weighting scheme with a steep dependence on, say,
the dispersion of the spectra (a strong weighting hereafter) almost completely
suppresses the older observations. Consequently, we used three different
weighting schemes: unweighted data, weak weighting, and strong weighting.
Unweighted data will be used to derive a complete multiple-frequency fit
and to include long-term amplitude modulation of rapid oscillations.
Weighted data will be used to verify and improve the frequencies found in
the first step and to derive an accurate orbital solution.
Strong weighting:
The error of a RV value derived from a single spectral line profile I(RV)follows from the photon statistics (Butler et al. 1996):
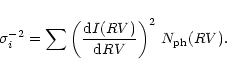 |
(1) |
The accuracy of a RV measurement at a certain point of the line profile is
determined by the local gradient of the profile and the number of photons
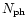 collected at this point. The sum extends over all discrete
measurements (steps in RV) taken to derive the RV of line i. Assuming
a Gaussian line profile and a small central line depth Ai,
it follows that
collected at this point. The sum extends over all discrete
measurements (steps in RV) taken to derive the RV of line i. Assuming
a Gaussian line profile and a small central line depth Ai,
it follows that
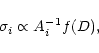 |
(2) |
where f is a function of the dispersion, but also of 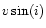 and of the
resolution of measurement limited by the projected slit width of
the spectrograph, or possibly by the pixel size of the electronic
detector or the point spread function of the photographic
plates. Petrie (1962) tabulated the mean RV errors found from single-line
measurements in photographic spectra of various dispersions.
A least squares fit to his values for B-type stars give
and of the
resolution of measurement limited by the projected slit width of
the spectrograph, or possibly by the pixel size of the electronic
detector or the point spread function of the photographic
plates. Petrie (1962) tabulated the mean RV errors found from single-line
measurements in photographic spectra of various dispersions.
A least squares fit to his values for B-type stars give
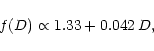 |
(3) |
where D is in Åmm-1 and f is in kms-1.
If the mean RV, based on measurements of N lines, is computed from
unweighted data, as we will assume here, the error of the mean follows as
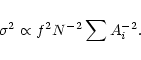 |
(4) |
To estimate the sum in Eq. (4) we will assume that in any spectrum the Nstrongest lines were used. In that case the sum can be estimated from the inverse
frequency distribution of line depths in the spectrum. For EN Lac we obtain from an
analysis of the TLS spectra an approximate distribution of
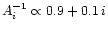 ,
where i=1 stands for the strongest metal line
(the 11th strongest line of the spectrum has a line depth of about half of the depth
of the strongest line).
,
where i=1 stands for the strongest metal line
(the 11th strongest line of the spectrum has a line depth of about half of the depth
of the strongest line).
The weight w of a RV value should be
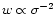 which leads
to the final formula
which leads
to the final formula
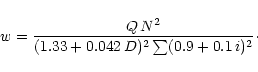 |
(5) |
The summation goes over the N lines measured in a given spectrum.
The superior S/N ratio of the electronic spectra is taken into account
via an additional multiplicative factor Q. We set Q=1 for photographic
and Q=4 for electronic spectra.
Since we assumed that unweighted mean RVs are derived by most of the authors,
the approximately assumed steadily decrease
of line depth with increasing N results in a maximum of the weights for
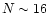 .
We, therefore, set in Eq. (3) N=16for all RVs derived from more than 16 lines.
.
We, therefore, set in Eq. (3) N=16for all RVs derived from more than 16 lines.
Weak weighting: To test the influence of weighting on the obtained
results we also used a weak weighting for a comparison. We assumed that
the accuracy of RVs depends only on the linear dispersions and use
Eq. (3) to calculate the weights, with
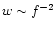 .
The adopted weights for the individual data sets and for both weighting
schemes are also given in Table 2. Weights were normalized
in such a way that w=10 for the TLS data.
.
The adopted weights for the individual data sets and for both weighting
schemes are also given in Table 2. Weights were normalized
in such a way that w=10 for the TLS data.
The question of different instrumental RV zero-points will be discussed
later in connection with the multiple period search.


Up: A new analysis of Lacertae
Copyright ESO 2001


![]() .
New spectra were obtained at four observatories:
.
New spectra were obtained at four observatories:
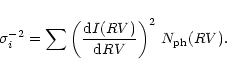
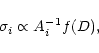
![]() which leads
to the final formula
which leads
to the final formula
![]() .
We, therefore, set in Eq. (3) N=16for all RVs derived from more than 16 lines.
.
We, therefore, set in Eq. (3) N=16for all RVs derived from more than 16 lines.
![]() .
The adopted weights for the individual data sets and for both weighting
schemes are also given in Table 2. Weights were normalized
in such a way that w=10 for the TLS data.
.
The adopted weights for the individual data sets and for both weighting
schemes are also given in Table 2. Weights were normalized
in such a way that w=10 for the TLS data.