The second program uses a multiple period finding technique which is able to optimize arbitrary frequencies and its harmonics. It is based on a least-squares fit of sinusoids. For very low eccentricities, as in the case of EN Lac, the program fits the orbital curve very well using only the fundamental period and its first harmonic. It is, therefore, possible to obtain a simultaneous fit of orbital as well as pulsational periods at one iterative process. All but one of the periods are fixed. To optimize the whole family of frequencies involved, the procedure is iteratively repeated for individual frequencies. In a sense, the program represents an extension of the well-known CLEAN algorithm since not only one single period but also the amplitudes and phases of all included periods are optimized.
The third program computes a modified Scargle periodogram the ordinate of which corresponds to the reduction of the sum of squares by the least squares fit of sinusoids used. A detailed description of the periodogram and a discussion of its statistical properties can be found in Lehmann et al. (1999). The program is used to search in the residuals of an assumed multiple frequency model for possible additional frequencies.
Some principal results were also independently verified with the help of program FOTEL - see Hadrava (1990).
When the oscillations show constructive interference, the
amplitude of the observed short-term RV variations is nearly comparable to
the semi-amplitude of the orbital RV curve. This complicates the determination
of truly reliable orbital elements. One can of course make use of the fact
that the three periods of oscillations,
P1 = 0
![]() 1691678, P2 = 0
1691678, P2 = 0
![]() 1707769, and P3 = 0
1707769, and P3 = 0
![]() 1817331,
have been well established from photometric observations. However,
the amplitudes of these oscillations are known to vary with time which
represents an extra complication for the frequency analysis.
1817331,
have been well established from photometric observations. However,
the amplitudes of these oscillations are known to vary with time which
represents an extra complication for the frequency analysis.
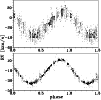 |
Figure 2: Top: orbital solution I derived from raw data. Bottom: orbital solution II derived from the same data but prewhitened for the short-term variations found in selected data groups |
| Solution I | Solution II | |||||
| P [d] | 12.096860 | 0.000026 | 12.096844 | 0.000010 | ||
| K [kms-1] | 23.66 | 0.18 | 23.818 | 0.033 | ||
| -12.52 | 0.13 | -12.289 | 0.026 | |||
| e | 0.0347 | 0.0090 | 0.0392 | 0.0017 | ||
| 65 | 12 | 63.7 | 2.1 | |||
|
|
39053.77 | 0.41 | 39053.71 | 0.07 | ||
|
|
39054.55 | 0.78 | 39054.53 | 0.14 | ||
| rms | 6.03 kms-1 | 1.10 kms-1 | ||||
| group | set | mean JD | P1 | K1 | P2 | K2 | P3 | K3 | P4 | K4 | ||
| 1 | 2 | 19699.6 | 39 | 39 | .16918 | 8.6 | .17078 | 3.0 | .18165 | 2.4 | ||
| 2 | 2 | 20054.0 | 52 | 52 | .16920 | 7.9 | .17092 | 3.4 | .18169 | 5.6 | ||
| 3 | 3 | 33923.4 | 327 | 15 | .16915 | 15.5 | .17070 | 2.9 | .18179 | 1.6 | ||
| 4 | 4 | 33874.9 | 47 | 4 | .16865 | 11.7 | 1.733 | 1.9 | ||||
| 5 | 5 | 33904.9 | 68 | 7 | .16917 | 13.7 | .17081 | 4.5 | .18106 | 1.0 | ||
| 6 | 6 | 34795.8 | 36 | 4 | .16924 | 15.1 | .17078 | 4.1 | .18173 | 4.2 | ||
| 7 | 8 | 34913.0 | 26 | 2 | .16961 | 18.9 | ||||||
| 8 | 10 | 43057.3 | 51 | 4 | .18193 | 4.5 | .16961 | 7.4 | ||||
| 9 | 11 | 43425.0 | 118 | 7 | .16931 | 5.2 | .17076 | 1.9 | .18173 | 2.6 | ||
| 10 | 13 | 43739.3 | 82 | 3 | .16831 | 7.5 | .18073 | 4.8 | .2896 | 2.1 | ||
| 11 | 14 | 45627.6 | 47 | 5 | .16916 | 4.2 | .17348 | 1.0 | .18166 | 5.2 | ||
| 12 | 18+19 | 48453.8 | 250 | 6 | .16986 | 5.7 | .18179 | 6.4 | .19701 | 1.1 | ||
| 13 | 16 | 51110.4 | 229 | 6 | .16917 | 1.9 | .17323 | 4.4 | .19545 | 2.2 | ||
| 14 | 16 | 51437.1 | 714 | 9 | .16917 | 3.9 | .17083 | 3.1 | .18171 | 2.0 | .17258 | 2.0 |
| 15 | 17 | 51449.5 | 33 | 4 | .16921 | 3.7 | .17084 | 4.0 | .18193 | 0.8 |
To disentangle the orbital motion and short-term RV changes, we proceeded in two different ways. In the first step, we derived an initial solution (solution I of Table 5) using all the original RVs of Table 2 and adopting the weak weighting. This is why the scatter around the mean orbital RV curve displayed in the upper panel of Fig. 2 looks larger than the calculated mean rms per one observation: the scatter is mainly caused by low-dispersion data with small weights. A small part of the scatter is also due to the fact that we assumed one joint systemic velocity for all RVs at this stage.
To proceed further, we created subsets of RV data, spanning not more than 180 d. Moreover, each subset was formed in such a way that it contains data from only one source and from one spectrograph and also enough RVs with a sufficient sampling in time to allow a separate period search for rapid changes. This way, we formed 15 different subsets which are listed in Table 6. Then we subjected the O-C velocity residuals from solution I for each of the subsets to a period search in the neighbourhood of the known periods P1 to P3. Using a least-squares sinusoidal fit of these three periods within each subset, we prewhitened the original RVs for the rapid changes. Prewhitened RVs from all subsets were then combined and used to calculate a new orbital solution. The process was iterated until convergence was achieved. The final orbital solution is given as solution II in Table 5. No evidence of apsidal motion was found. It is seen that the decrease of the mean rms error per 1 observation between solutions I and II is quite substantial.
| |
Figure 3: A plot of the semi-amplitude of the P1-variation of Table 6 vs. time. The solid curve is a sinusoid with a period of 23000 d |
Table 6 shows that for a few subsets, we arrived at rather peculiar values of the short periods. In some cases, only one or two periods are detectable. A significant result of our analysis is the finding that the amplitude of P1 varies with an apparent cycle of about 23000 d - see Fig. 3. Possible time scales for the amplitude variation of P3 are 237, 473 or 673 d, the latter value being reported already by Jerzykiewicz & Pigulski (1996) from their analysis of photometric data. There is no evidence of a periodic modulation of the amplitude of P2.
Note that our approach differs from that used by Jerzykiewicz & Pigulski (1996) who fixed the values of the three short periods at their values known from photometry and fitted only their amplitudes. They concluded that the amplitudes are strongly variable with time. For completeness, we repeated their analysis using all our RVs prewhitened for orbital variation via solution II. The results are compared in Table 7. It is seen that a free fit of the periods leads to much larger semiamplitudes for all three considered periods than a fit with fixed values of the periods from photometry. Moreover, the phase diagram of the data prewhitened for P2 and P3 and folded with P1 shows a clear phase shift between the older, more scattered RVs of higher amplitude and the CCD data with a lower amplitude - see the upper panel in Fig. 4.
If one allows for a free convergence of all three periods, it is possible to arrive at somewhat larger amplitudes and a better phase coherence for P1. There are remaining phase shifts, however, especially for P2 and P3, and it is clear that the three known frequencies are unable to model the large amplitudes of P1 (up to 18 kms-1 during certain epochs) properly. For P2 we arrived at a one-year alias of the reported photometric period. This value was also found by others, as already mentioned in Sect. 2.
| periods fixed | periods optimized | ||
| P [d] | K [kms-1] | P [d] | K [kms-1] |
| .1691678 | 3.8 | .16916714 | 5.7 |
| .1707769 | 0.9 | .17085757 | 2.6 |
| .1817331 | 2.1 | .18171870 | 2.7 |
The varying accuracy of the RVs was taken into account through the weighting schemes already described. To check on possible differences in the RVzero-points of individual data sets, we will now include only data sets with large enough RVs, with a good orbital-phase coverage. Applying these requirements, we finally selected all data sets from Table 2 with the exception of subsets 7, 9, and 12. We may assume that the RV zero-point of our own measurements, calibrated via telluric lines (data sets 15, 16, and 17) is identical and equal to zero in the RV residuals. We will further assume that the subsets 3 and 8 have a common zero point, similarly as subsets 5, 6, 3, and 8, 10, 11, and 18, 19. All these groups were obtained with the same instruments and have comparable weights.
We started with prewhitening the selected set of RVs, formed by all of above-mentioned subsets, for orbital solution II. The RV residuals from this prewhitening were then subjected to a period search over the frequency range from 0 to 10 d-1. The frequency corresponding to the strongest peak in the periodogram was then improved via sinusoidal fit and removed from the data. The new residuals were again subjected to a period search and the sinusoidal fit was repeated, now for two free periods. After finding three short periods near to the photometric periods P1 to P3, a multiperiodic fit was applied to the original RVs and allowed to calculate also the orbital frequency and its first harmonics. (Note that this procedure is legitimate as long as there is no detectable apsidal motion present in the system.)
Since the results could be sensitive to possible differences in the RV zero points, parallel analyses were carried out for original data and for data where the zero-point corrections were taken into account. To compute the zero-point corrections the residuals from the multiperiodic fit were averaged within each data subset and the mean value was subtracted from all RVs of the subset in question. As long as the same new frequency was found in both parallel analyses, it was adopted as a real one, i.e. not caused by differing RVzero-points only.
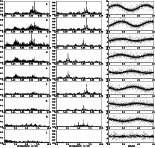 |
Figure 5: Left column: periodograms obtained during the process of successive prewhitening. The following detected periods of Table 9 are indicated: a) P1, b) P1-, c) P2, d) P3, e) P3+, f) P1+, g) P2+, h) P1++, i) P4. Middle and right column: periodograms and phase diagrams for the same periods are also shown, based on the final solution, after the RVs were prewhitened for all other contributions |
| Order | P | K |
|
|
| [d] | [kms-1] | |||
| P1 | 1 | 0.16916707 | 7.6 | |
| P1+ | 4 | 0.16916605 | 5.0 | 76.7 y |
| P1- | 2 | 0.16916809 | 3.2 | 76.7 y |
| P2 | 7 | 0.17085553 | 2.7 | |
| P2+ | 3 | 0.17077074 | 1.4 | 344 d |
| P3 | 5 | 0.18173251 | 2.6 | |
| P3+ | 6 | 0.18168352 | 2.4 | 674 d |
| Order | P | K |
|
|
| [d] | [kms-1] | |||
| P1 | 1 | 0.16916703 | 5.9 | |
| P1+ | 4 | 0.16916596 | 5.2 | 73.6 y |
| P1- | 2 | 0.16916810 | 3.5 | 73.6 y |
| P1++ | 8 | 0.16916078 | 2.3 | 12.5 y |
| P2 | 7 | 0.17085554 | 2.2 | 331 d |
| P2+ | 3 | 0.17076729 | 1.6 | |
| P3 | 5 | 0.18173256 | 2.8 | 674 d |
| P3+ | 6 | 0.18168357 | 2.3 | |
| P4 | 9 | 1.91985 | 0.7 |
The obtained results are summarized in Tables 8
and 9.
The periods which were detected in our analyses and which are very close
to the three known photometric periods are denoted here as P1, P2and P3. Newly found periods, which are very close to P1, P2 or P3and which can be responsible for the amplitude modulation of the
periods P1, P2 and P3, are denoted ![]() in such a way that
in such a way that
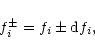 |
(6) |
We stopped at the point when different new frequencies were detected from different weighting schemes. Table 8 summarizes the results for this stage of reduction. Beside the values of P1 to P3, two "sidelobes'' of P1, responsible for the amplitude modulation of P1 with a period of 76.7 years, and two frequencies very close to P2 and P3 and corresponding to their amplitude modulation with 344-d and 674-d periods, respectively, were detected.
| Solution III | Solution IV | |||||
| P [d] | 12.096867 | 0.000010 | 12.096864 | 0.000011 | ||
| K [kms-1] | 23.858 | 0.051 | 23.853 | 0.051 | ||
| -12.694 | 0.039 | -12.446 | 0.039 | |||
| e | 0.0435 | 0.0026 | 0.0539 | 0.0026 | ||
| 59.4 | 2.9 | 61.4 | 2.1 | |||
|
|
39053.59 | 0.10 | 39053.65 | 0.10 | ||
|
|
39054.54 | 0.20 | 39054.52 | 0.17 | ||
| rms | 1.7 kms-1 | 1.5 kms-1 | ||||
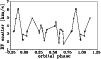 |
Figure 7: The RV phase scatter vs. orbital phase with phase zero at periastron passage - see the text for details |
No other periods could be detected in the residuals from this solution
for the unweighted data. In the weakly weighted data, the strongest peak
suggests yet another period of 0
![]() 202, which, however, does not seem
to be significant (semi-amplitude of 0.4 kms-1 and a very unconvincing
phase diagram). From the strongly weighted data, another period very close
to P1 was indicated. A free fit for all detected periods
changes the period of the amplitude modulation of P2 from 344 d to 331 d,
however. The solution derived from the strongly weighted data is
summarized in Table 9 and the successive periodograms
are shown in Fig. 5. Middle panels show the periodograms
for each of the periods resulting after subtraction of all other
contributions obtained in the final solution. Comparing panels
a to g of this column (panels h and i are on enlarged frequency
scale) one can recognize the window function of the data shown in
Fig. 1. The one-month aliases can clearly be seen.
In all periodograms also the one-year alias peaks can be found (not resolved
in Fig. 1).
Note that the difference of the two frequencies found for the P2 variation
corresponds to 331 d so that the two frequencies are not one-year aliases
of each other.
In the right column of Fig. 5 the phase diagrams
of each period, after prewhitening the data for all other periods,
are shown.
202, which, however, does not seem
to be significant (semi-amplitude of 0.4 kms-1 and a very unconvincing
phase diagram). From the strongly weighted data, another period very close
to P1 was indicated. A free fit for all detected periods
changes the period of the amplitude modulation of P2 from 344 d to 331 d,
however. The solution derived from the strongly weighted data is
summarized in Table 9 and the successive periodograms
are shown in Fig. 5. Middle panels show the periodograms
for each of the periods resulting after subtraction of all other
contributions obtained in the final solution. Comparing panels
a to g of this column (panels h and i are on enlarged frequency
scale) one can recognize the window function of the data shown in
Fig. 1. The one-month aliases can clearly be seen.
In all periodograms also the one-year alias peaks can be found (not resolved
in Fig. 1).
Note that the difference of the two frequencies found for the P2 variation
corresponds to 331 d so that the two frequencies are not one-year aliases
of each other.
In the right column of Fig. 5 the phase diagrams
of each period, after prewhitening the data for all other periods,
are shown.
The orbital solutions, based on RVs prewhitened for all short periods
of Tables 8 and 9, are presented in Table 10
as solutions III and IV, respectively. For comparison we also give the
calculated epochs of primary mid-eclipse. Pigulski & Jerzykiewicz (1988) derived
![]() and
and
![]() from the light-curve
analysis. Note that the epoch of the primary mid-eclipse from all of
our orbital solutions agrees with their epoch within the errors of its
determination. A phase diagram corresponding to solution IV is shown in
Fig. 6.
from the light-curve
analysis. Note that the epoch of the primary mid-eclipse from all of
our orbital solutions agrees with their epoch within the errors of its
determination. A phase diagram corresponding to solution IV is shown in
Fig. 6.
Solutions III and IV are based on RVs corrected for the zero-point shifts and on
strong weights. The results are almost identical to those derived without the zero-point
corrections. In particular, there is only a marginal difference of 0
![]() 000007
in the orbital period. The adopted zero-point
corrections are summarized in Table 2.
000007
in the orbital period. The adopted zero-point
corrections are summarized in Table 2.
To demonstrate that the rapid variations of EN Lac are somehow related to the binary nature of the star is not an easy task, especially given the fact that the amplitude of the strongest mode of oscillations varies secularly. Fortunately, the rich collection of new spectra analyzed here was obtained over a limited period of time and seems suitable to such an analysis.
Using all 1315 original RVs from
spectrograms of sets 16 to 20, we formed phase bins 0.![]() 07 wide in three
sliding representations - similar to three different "covers'' in the phase
dispersion minimization method of Stellingwerf (1978). (The width of the
bins was chosen in such a way as to ensure numerous enough representation
in most of them.) We then calculated mean RV and its rms error
within each such phase bin. The rms error characterizes the total scatter
at given orbital phase and should be proportional to the total amplitude
of rapid changes at that phase. Omitting all bins defined by less than
30 RVs, we plot the phase scatter versus orbital phase calculated from
periastron in Fig. 7. There seems to be a rapid increase of
the scatter prior and perhaps also after each periastron passage, though the
effect is only marginal. Still more data will be needed to verify that
it is a real effect dependent on orbital phase and not, e.g., an accidental
effect of positive interference of several pulsational modes.
07 wide in three
sliding representations - similar to three different "covers'' in the phase
dispersion minimization method of Stellingwerf (1978). (The width of the
bins was chosen in such a way as to ensure numerous enough representation
in most of them.) We then calculated mean RV and its rms error
within each such phase bin. The rms error characterizes the total scatter
at given orbital phase and should be proportional to the total amplitude
of rapid changes at that phase. Omitting all bins defined by less than
30 RVs, we plot the phase scatter versus orbital phase calculated from
periastron in Fig. 7. There seems to be a rapid increase of
the scatter prior and perhaps also after each periastron passage, though the
effect is only marginal. Still more data will be needed to verify that
it is a real effect dependent on orbital phase and not, e.g., an accidental
effect of positive interference of several pulsational modes.
Copyright ESO 2001