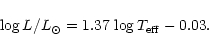![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{1896F21new.eps} %
\end{figure}](/articles/aa/full/2001/05/aads1896/Timg50.gif) |
Figure 21:
The structure of the S Dor area on the HR-diagram. It shows amongst others the SD-triangle in which the s-a S Dor variables move to-and-fro during the SD-phases, the SD-minimum strip (fat dashed line) with the thinly dashed lines as its bandwidth, and the Yellow Void |