![\begin{figure}
\par\includegraphics[width=6cm,clip]{sdfig13.eps}\end{figure}](/articles/aa/full/2001/05/aads1896/Timg38.gif) |
Figure 13:
The schematic light curve ( )
versus JD-2400000
of the w-a S Dor variable R85 in the LMC. Note that
the magnitude HDEptg 1925 = 10.9 (Table 5) is not indicated in
the figure. The broken curve represents the L-SD phase.
The S-SD phase and the )
versus JD-2400000
of the w-a S Dor variable R85 in the LMC. Note that
the magnitude HDEptg 1925 = 10.9 (Table 5) is not indicated in
the figure. The broken curve represents the L-SD phase.
The S-SD phase and the 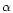 Cyg-type microvariations are
schematically sketched on scale (based on VBLUW monitoring,
while the dots are in most cases individual observations by various authors),
see for further details van Genderen et al. (1998b). The epochs of the three
spectral type determinations are indicated by arrows and are from Feast et al.
(1960), viz. around 1959, and Massey et al. (2000),
viz. in 1996 and 1999 (Tables 4, 5 and 6) Cyg-type microvariations are
schematically sketched on scale (based on VBLUW monitoring,
while the dots are in most cases individual observations by various authors),
see for further details van Genderen et al. (1998b). The epochs of the three
spectral type determinations are indicated by arrows and are from Feast et al.
(1960), viz. around 1959, and Massey et al. (2000),
viz. in 1996 and 1999 (Tables 4, 5 and 6) |