

Up: The ATCA/VLA OH 1612
Subsections
In this section we analyse the global completeness of the survey
and discuss the statistical accuracy of the quantities given
in Table 2. The discussion and figures follow closely that of the
corresponding section in Paper I, but is adapted to treat some
VLA-specific details. We will assume errors
are normally distributed, unless stated otherwise.
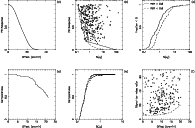 |
Figure 7:
a-f)
Representation of the completeness of the data (Sect. 5.1.2).
a) The primary beam response (PBR)
of the VLA antennae at 18 cm, as a function of
radial offset from the pointing centre, taken from
Napier & Rots (1982).
b) The PBR calculated for the detected sources
plotted against the highest peak-OH flux densities, corrected for primary beam
attenuation. The solid line indicates the lowest flux densities detected
in PBR bins. The dashed line indicates the expected inner
boundary calculated from the PBR curve in a) for a limiting
flux density of 120 mJy (chosen to fit observed extremes).
c) The cumulative flux density distribution for stars with PBR values
> 0.8 (solid line) and < 0.6 (dashed line). The solid line is taken to
be the intrinsic OH flux density distribution for the sources in the survey.
d) The completeness, relative to the pointing centres,
of the survey as a function of position offsets from the field centres.
e) The completeness of the sample as a function of flux density.
The offset out to which a source with certain flux density can be
observed is determined from the dashed line in b). Then we determine
the area covered inside that offset, as a fraction of the total
area of the survey. The solid curve gives this for the ideal case
of no missing pointings, the dashed curve takes the gaps (Fig. 1 )
into account.
f) The signal-to-noise ratio for all sources, plotted
against their radial offset from the pointing centre. The dashed
line shows the (observed) lower limit at a certain offset |
The empirical noise levels (defined as the rms in the
 cubes after the last pass
of source subtraction) for all 965 fields are shown
in Fig. 3. The median noise is 25 mJy (mean 32 mJy: the same
as the ATCA Bulge region);
90% of the fields have noise levels below 50 mJy.
cubes after the last pass
of source subtraction) for all 965 fields are shown
in Fig. 3. The median noise is 25 mJy (mean 32 mJy: the same
as the ATCA Bulge region);
90% of the fields have noise levels below 50 mJy.
In this section we treat the global completeness of the sample.
There was no absolute lower detection limit set in the
searching routines (opposed to the strategy for the ATCA survey).
The half-power beam width (HPBW) of the VLA antennae at 1612 MHz
is 13
 5. Approximately 55% of the total area of the VLA survey
would be covered within the HPBW (this includes the fact that 8% of pointings
are missing).
For fields that are not on the boundary of the surveyed region,
the largest possible offset from the nearest pointing
for any source is 21
5. Approximately 55% of the total area of the VLA survey
would be covered within the HPBW (this includes the fact that 8% of pointings
are missing).
For fields that are not on the boundary of the surveyed region,
the largest possible offset from the nearest pointing
for any source is 21
 2,
which corresponds to a primary-beam response (PBR) of 0.16 (Fig. 7 a).
In Fig. 6 we see that this typically guarantees
that the main lobe of a detected source is measured to be stronger than
any of its sidelobes, even in other fields, provided we cover
the entire survey region with our image sizes
(square in
2,
which corresponds to a primary-beam response (PBR) of 0.16 (Fig. 7 a).
In Fig. 6 we see that this typically guarantees
that the main lobe of a detected source is measured to be stronger than
any of its sidelobes, even in other fields, provided we cover
the entire survey region with our image sizes
(square in
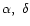 ), which is the case where there are
no gaps (Fig. 1). Note that the field separation is the
absolute maximum, given the primary-beam response, to still
guarantee proper identification of the main lobes of all sources.
In fields at the perimeter of the
survey region (cf. Fig. 1), sources could be
found in principle at offsets up to 29
), which is the case where there are
no gaps (Fig. 1). Note that the field separation is the
absolute maximum, given the primary-beam response, to still
guarantee proper identification of the main lobes of all sources.
In fields at the perimeter of the
survey region (cf. Fig. 1), sources could be
found in principle at offsets up to 29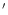 .
In practice, the largest offset was 21
.
In practice, the largest offset was 21
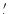 3 (Table 2);
only four sources were found more than 20
3 (Table 2);
only four sources were found more than 20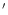 away from the
nearest pointing centre.
away from the
nearest pointing centre.
In Fig. 7 b we plot the PBR of each source against its peak flux density.
The solid line connects stars with the lowest detected OH
flux densities, determined in bins of PBR.
The dashed curve indicates the expected relation between
PBR and flux-density cut-off
for an absolute detection limit of 120 mJy (cf. 160 mJy, 140 mJy for
the ATCA survey regions). Note that the empirical detection level
is clearly not as constant across the VLA region as across the
ATCA regions.
The global limit is closer to 150 mJy, but there are a few
detections that clearly are outliers (limit 90 mJy). This is due to the gaps
in the coverage, that increase the area covered by large offsets
from what it would normally be, combined with a larger
spread in the noise levels (see above; Fig. 3).
In Fig. 7 c we plot the cumulative flux-density distributions
for all detected sources with PBR > 0.8 (solid)
and, for comparison, with PBR < 0.6 (dashed).
We postulate that the survey is essentially complete for PBR > 0.8,
for flux densities above the sensitivity limit,
and take the solid curve in Fig. 7 c as
the intrinsic cumulative flux-density distribution
for the present sample.
We use this distribution to determine the fraction of the
"flux-density function" seen at a given offset (Fig. 7 d),
with the absolute limit of 120 mJy to determine the cut-off in
flux density at the offset.
In short, the curve in Fig. 7 d shows what fraction of
the flux-density distribution we see if we select sources with
a certain offset from Table 2![[*]](/icons/foot_motif.gif) .
.
![\begin{figure}
{\psfig{figure=ms10125f8.ps,width=10truecm} }
\parbox[b]{8cm}{}\end{figure}](/articles/aa/full/2001/05/aa10125/Timg44.gif) |
Figure 8:
a-d)
With the channel width of 2.27kms-1, the
intrinsic velocity structure of the maser features,
of order 0.2kms-1 wide, is undersampled. Hence, aliassing
and measurement errors are introduced, that depend on the
offset of the true spectral peak from the centre
of the channel it is detected in.
This figure gives the difference between "measured" and
"perfect" OH/IR-type spectrum in stellar velocity a),
outflow velocity b),
flux density c) and peak-flux-density ratio d). The "perfect"
spectrum has an outflow velocity 15kms-1 and unit
flux density for both peaks.
We "observed" it 100 times, adding random noise
so that the resulting signal-to-noise ratio was between 0.0 and 0.3,
shifting the stellar velocity (abscissae) by random amounts
within one channel width, convolving with
the spectral-response sinc function and binning to
the resolution of the observations.
The combined errors are
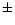 0.8kms-1 in velocity, mostly -0.24kms-1 in outflow velocity
(independent of the value of the outflow velocity) and of
the order of +35% in flux density (the measured value is
lower than the true one, mostly due
to the wide bins) with 0.8kms-1 in velocity, mostly -0.24kms-1 in outflow velocity
(independent of the value of the outflow velocity) and of
the order of +35% in flux density (the measured value is
lower than the true one, mostly due
to the wide bins) with 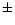 5% due to noise and aliassing.
In the fourth plot we see that the intrinsically symmetric
spectrum may be distorted by > 20%.
None of these quantities show
any trend with signal-to-noise ratio 5% due to noise and aliassing.
In the fourth plot we see that the intrinsically symmetric
spectrum may be distorted by > 20%.
None of these quantities show
any trend with signal-to-noise ratio |
The solid curve in Fig. 7e shows what fraction of the searched
area we cover
if we select all sources with a certain flux density from Table 2.
The dashed curve in Fig. 7e shows the same distribution, but this
time properly corrected for the gaps in the coverage and the corresponding
redistribution of area from small offsets to large offsets.
The dashed curve reaches 99% completeness for 2 Jy,
the solid curve for 0.5 Jy. The latter is virtually the same as
the 99% completeness of the ATCA surveys. The survey is
80% complete for sources of 320 mJy or 285 mJy, respectively,
again similar to the ATCA surveys.
This should be interpreted as follows. If we select all sources
brighter than 2 Jy (after correction for PBR), the distribution
on the sky will be entirely uninfluenced by our observations
and only reflect the real surface-density distribution. If we
select all sources brighter than 0.5 Jy, the distribution will
show holes at the missing pointings, but will not be influenced
by the variable sensitivity within fields. If one selects
even fainter sources, the distribution will be a complicated
function of both intrinsic surface density and survey sensitivity.
Finally, in Fig. 7f, we plot the signal-to-noise ratio for
all detected sources against offset. The limiting signal-to-noise ratio
is 7 (the corresponding ratios for the ATCA surveys are 4 and 6, respectively)
at low offsets.
Summarizing, the lower sensitivity limit is 120 mJy 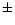 30 mJy, with
the most sensitive detections made at 7
30 mJy, with
the most sensitive detections made at 7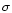 .
The survey is 99% complete for flux densities higher than
0.5 Jy (or 2 Jy, when taking into account holes in the survey area) and
90% complete in flux density for offsets lower than 13
.
The survey is 99% complete for flux densities higher than
0.5 Jy (or 2 Jy, when taking into account holes in the survey area) and
90% complete in flux density for offsets lower than 13
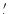 2.
2.
The positions given in Table 2 (Cols. 4, 5) are
determined by fitting a parabola over 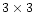 1
1
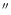 cells
around the peak pixel in the cleaned and restored
map of the peak channel (MAXFIT), made
around the position of the object found by the searching routine.
This ensures that the inaccurate handling by Miriad
of the third coordinate of the visibility domain
does not influence our final positions.
The errors in Table 2 (Col. 6) are the formal errors determined
by fitting a point-source object (IMFIT) to the
centre of the above-mentioned map.
They are typically negligible with respect to the errors
introduced by the low resolution of some of the observations.
cells
around the peak pixel in the cleaned and restored
map of the peak channel (MAXFIT), made
around the position of the object found by the searching routine.
This ensures that the inaccurate handling by Miriad
of the third coordinate of the visibility domain
does not influence our final positions.
The errors in Table 2 (Col. 6) are the formal errors determined
by fitting a point-source object (IMFIT) to the
centre of the above-mentioned map.
They are typically negligible with respect to the errors
introduced by the low resolution of some of the observations.
Firstly, the positional accuracy varies dramatically from source
to source, as the maximum baseline length varies from 7 k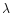 (see Table 1) to 55 k
(see Table 1) to 55 k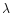 ,
corresponding to a resolution
of 29
,
corresponding to a resolution
of 29
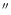 and 4
and 4
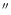 ,
respectively.
With 1
,
respectively.
With 1
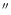 cells for the imaging of all fields,
the positional errors for sources observed with
the lowest resolution would go to infinity (see Fig. 5 in Paper I).
As an example, for a
maximum baseline length of 25 k
cells for the imaging of all fields,
the positional errors for sources observed with
the lowest resolution would go to infinity (see Fig. 5 in Paper I).
As an example, for a
maximum baseline length of 25 k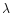 the half width of the synthesized beam at half maximum would
be
the half width of the synthesized beam at half maximum would
be 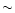 8
8
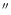 ,
or 5.5 cells, giving an error of <2 cells
or 2
,
or 5.5 cells, giving an error of <2 cells
or 2
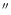 ,
following Fig. 5 in Paper I.
,
following Fig. 5 in Paper I.
Secondly, since we discard baselines below 5 k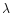 (Sect. 3),
for observations with compact array
configurations (Aug., Sep. 1993) the synthesized-beam shape
was severely compromised, given the minimal hour-angle coverage
(cf. #237, 280 with infinite beam size).
However, our position for #280 differs only 11
(Sect. 3),
for observations with compact array
configurations (Aug., Sep. 1993) the synthesized-beam shape
was severely compromised, given the minimal hour-angle coverage
(cf. #237, 280 with infinite beam size).
However, our position for #280 differs only 11
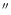 of that
given in the literature (Braz & Epchtein 1983),
which is entirely within their errors.
of that
given in the literature (Braz & Epchtein 1983),
which is entirely within their errors.
In short, the typical error in the positions
is of the order of 2
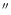 ,
in agreement with our findings
in Sect. 5.7.
,
in agreement with our findings
in Sect. 5.7.
The flux densities in Table 2 (Cols. 12, 13)
were determined from the same cubes as described in Sect. 5.2.
The data were summed over 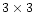 1
1
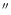 cells around the maximum cell and divided by the
corresponding sum of the synthesized beam (IMSPEC).
The formal errors (Col. 14) were determined
by IMFIT, in the peak channel.
Errors marked with
cells around the maximum cell and divided by the
corresponding sum of the synthesized beam (IMSPEC).
The formal errors (Col. 14) were determined
by IMFIT, in the peak channel.
Errors marked with 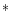 (mostly 0.0 mJy) indicate
that the absolute flux-density calibration was not carried out properly
in the corresponding field.
We applied a fudge factor of 16 to all flux
densities measured in those fields, which introduces
an error of 25% for those sources (in properly calibrated fields
this factor ranges from 12 to 20).
In all other fields, the error from the absolute
calibration is of the order of 1%, except for
those observed on 260594 where it is 20%.
From the time-dependent calibration solutions, we expect
errors of 10% - 20% in the flux densities.
(mostly 0.0 mJy) indicate
that the absolute flux-density calibration was not carried out properly
in the corresponding field.
We applied a fudge factor of 16 to all flux
densities measured in those fields, which introduces
an error of 25% for those sources (in properly calibrated fields
this factor ranges from 12 to 20).
In all other fields, the error from the absolute
calibration is of the order of 1%, except for
those observed on 260594 where it is 20%.
From the time-dependent calibration solutions, we expect
errors of 10% - 20% in the flux densities.
An addional error is introduced by random noise and binning.
In Fig. 5.1.2c we show that this amounts to
35% (binning) 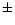 5% (noise).
The corresponding errors in the peak-flux-density ratio (Fig. 5.1.2d) is
5% (noise).
The corresponding errors in the peak-flux-density ratio (Fig. 5.1.2d) is
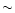 20% (0.7/0.6 instead of 1/1, Fig. 5.1.2c).
20% (0.7/0.6 instead of 1/1, Fig. 5.1.2c).
Summarizing, the relevant errors
are on average 15% (calibration) plus
5% (noise) plus for some sources 25% (fudging).
Multiplying, we find a typical accuracy
for the flux densities in Table 2 of 20%,
which is in agreement our findings in Sect. 5.7, or 40% for fudged
sources.
As the VLA has on-line Doppler tracking, the velocity band
is always centered on 0kms-1 (LSR), but the bandpass calibration,
in frequency space, changes the velocity range
slightly with position and date. However, all
detections are within the range that
was covered on all dates (-200kms-1, +210kms-1), so
sensitivity and errors are independent of the value of the velocity.
In Fig. 5.1.2a we show the difference between measured stellar
velocity, combining the effects of binning, noise and aliassing,
and the true stellar velocity of a perfect spectrum, as a function
of true stellar velocity with respect to the centre of the
channel of detection.
The typical errors are less than 1kms-1, in agreement with
our finding in Sect. 5.7.
The same arguments as given in Paper I apply, that for double-peaked
sources the outflow velocity will be systematically
slightly underestimated (see also Fig. 5.1.2b)
due to undersampling of the spectra.
For single-peaked sources there is an
uncertainty in the stellar velocity of typically 14kms-1.
The fraction of such single-peak sources in this VLA set is low (3%)
compared to the ATCA sets in Papers I, II (9%, 18%).
Due to the variable data quality and remnant RFI, fewer
single-peaked detections were significant according
to our criteria. For instance, a detection in three
separate channels at the same spatial position was more readily
accepted if it was in two neighbouring channels plus one at a certain
velocity interval than if it was in three neighbouring channels, even
if statistically those two scenarios may have the same probability.
Empirically, the single-peaked configuration is more likely
to turn out not to be a source, but remnant RFI.
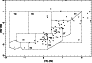 |
Figure 9:
The IRAS two-colour diagram for sources with an IRAS identification
lying within the IRAS error ellipse (Col. 17,  1)
with well-determined IRAS 12, 25 and 60
1)
with well-determined IRAS 12, 25 and 60  m flux densities (i.e.
no upper limits). The colours are defined as m flux densities (i.e.
no upper limits). The colours are defined as
![$[12]-[25]\equiv 2.5$](/articles/aa/full/2001/05/aa10125/img12.gif)
 log( log(
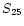 / /
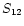 ) ) |
In Col. 17, the distance from the OH source to the position
of the IRAS point source (Col. 16) is given
in fractional radii of the IRAS error ellipse in the direction of the OH
position (see Paper I). N=1 means the position of the
OH source can be identified
with the position of the IRAS source with 95% confidence.
The IRAS PS in Col. 16 is in fact the one that is most likely to
be connected to the OH source, i.e. with the smallest value of N.
Of the 286 sources, 207 (72%) have an IRAS PS counterpart within the IRAS
error ellipse (N < 1). This fraction is comparable to those found
in Papers I, II (65%, 75%), as well as to the 68% found
by Blommaert et al. (1994).
In Fig. 9 we show the IRAS two-colour diagram (van der Veen & Habing 1988)
for sources with an IRAS identification with N<1 and reliable IRAS colours.
Note that this two-colour diagram is very similar to that of the
ATCA Bulge OH/IR stars (Paper I), rather than of the ATCA Disk stars,
in terms of the population of region V and the scatter on the
evolutionary track (regions III). This similarity remains the same
when leaving out the source with longitude below 10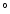 .
It could be due to the orientation of the Bar, that
causes it to extend to higher longitudes in the northern galactic plane.
However, it should be realized that by plotting only those sources that
have well-determined IRAS flux densities in three bands, a selection
effect is introduced. The distribution is influenced by the levels of
background confusion.
.
It could be due to the orientation of the Bar, that
causes it to extend to higher longitudes in the northern galactic plane.
However, it should be realized that by plotting only those sources that
have well-determined IRAS flux densities in three bands, a selection
effect is introduced. The distribution is influenced by the levels of
background confusion.
We searched the SIMBAD data base for previous OH detections
within 1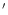 from each position in Table 2.
In Col. 16, as well as in Fig. 10, an "
from each position in Table 2.
In Col. 16, as well as in Fig. 10, an " " indicates
a reference to Paper I;
if not in that catalogue, an "x" indicates a reference
to te Lintel et al. (1989);
if not in that catalogue, a "+" indicates another OH reference
and a "-" no OH reference at all.
In total, there are 26 "
" indicates
a reference to Paper I;
if not in that catalogue, an "x" indicates a reference
to te Lintel et al. (1989);
if not in that catalogue, a "+" indicates another OH reference
and a "-" no OH reference at all.
In total, there are 26 " " references, which is one less
than determined from the actual Paper I source list (see next section)
since entries in SIMBAD are not always entirely correct.
Note that we did not check for coincidence in velocity.
By this definition, 161 sources in Table 2, or 56% (cf. 47, 55% for
the ATCA survey regions),
are new detections; see Paper I for a more elaborate discussion.
" references, which is one less
than determined from the actual Paper I source list (see next section)
since entries in SIMBAD are not always entirely correct.
Note that we did not check for coincidence in velocity.
By this definition, 161 sources in Table 2, or 56% (cf. 47, 55% for
the ATCA survey regions),
are new detections; see Paper I for a more elaborate discussion.
The strip of
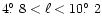 was observed in both the VLA- and the ATCA parts of the survey, to
allow direct comparison between the two resulting data sets.
In that region, there are 47 stars detected in the ATCA survey and
36 in the VLA survey, of which 27 stars are actually in common.
With another two sources in common between the two parts of the ATCA survey
(Papers I, II), the total number of sources in the combined survey is 766.
was observed in both the VLA- and the ATCA parts of the survey, to
allow direct comparison between the two resulting data sets.
In that region, there are 47 stars detected in the ATCA survey and
36 in the VLA survey, of which 27 stars are actually in common.
With another two sources in common between the two parts of the ATCA survey
(Papers I, II), the total number of sources in the combined survey is 766.
Taking into account the intrinsic variability of the sources and
the varying primary-beam responses in systematic observations, even
two surveys with exactly the same flux-density limits would not
yield the same detections unless they were carried out simultaneously
and with the same pointing pattern.
The redetection
rate of the VLA is 27/47=57% and of the ATCA 27/36=75%.
The difference between those numbers is a direct measure of the relative
"efficiency''
((number of detected sources)/(number of detectable sources within limits))
of the two surveys, provided the overlap region is
representative of the whole area. The ATCA
survey is 30% more "efficient'' than the VLA survey.
This is entirely in agreement with the ratio of FWHM coverages:
the ATCA Bulge survey covers 73% of the
survey area within a PBR of 0.5, the VLA 55%, including the missing
pointings.
If we compare this VLA data set to the ATCA Disk data set,
there are 250 and 202 stars, respectively,
in the strips from  10
10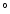 to
to 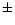 45
45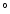 in
longitude, even though the VLA survey is
less efficient. This could again be interpreted as a sign of
the Bar extending to much higher longitudes on the northern
side of the galactic Centre (see Sect. 5.5).
in
longitude, even though the VLA survey is
less efficient. This could again be interpreted as a sign of
the Bar extending to much higher longitudes on the northern
side of the galactic Centre (see Sect. 5.5).
For the 27 sources in common, the average difference in position
is 1
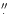 66 (0
66 (0
 04-2
04-2
 91) and in velocity 0.68kms-1.
The latter value excludes two
sources (#010 = SCHB268, #021 = SCHB286)
for which one of the two peaks was not detected in the ATCA survey
and source #020 (SCHB285) which is known to have a very variable
velocity profile (Sevenster & Chapman in preparation).
91) and in velocity 0.68kms-1.
The latter value excludes two
sources (#010 = SCHB268, #021 = SCHB286)
for which one of the two peaks was not detected in the ATCA survey
and source #020 (SCHB285) which is known to have a very variable
velocity profile (Sevenster & Chapman in preparation).
For 8 sources, the observing date (200293) was relatively close to
that of the ATCA, so that a flux-density comparison could be made.
Taking into account the differences in velocity resolution and
the typical variability of sources, the flux densities are the same
to about 20% (cf. Sect. 5.3).


Up: The ATCA/VLA OH 1612
Copyright ESO 2001

![\begin{figure}
{\psfig{figure=ms10125f8.ps,width=10truecm} }
\parbox[b]{8cm}{}\end{figure}](/articles/aa/full/2001/05/aa10125/Timg44.gif)
