

Up: Orbital eccentricity growth through
Subsections
5 A simple analytic model
In order to help understand some of the simulation results
described above, we consider a simplified model system
of primary, orbiting companion and disc.
We suppose the companion orbits inside a disc with truncated
inner edge. We make the additional simplification
that the central star remains fixed at the origin
of the coordinate system. The disc itself is taken to be inviscid with
a simple relation between vertically integrated pressure, Pand surface density, 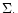 Much of the complex nonlinear dynamics involving
the balance between tides and viscosity determining
the structure of the inner disc edge is thus omitted.
However, enough content remains in order
to display an instability leading to eccentricity growth
in both disc and companion orbit, as well as the excitation
of an outward propagating density wave with half the pattern speed.
The existence of this has been described above.
Much of the complex nonlinear dynamics involving
the balance between tides and viscosity determining
the structure of the inner disc edge is thus omitted.
However, enough content remains in order
to display an instability leading to eccentricity growth
in both disc and companion orbit, as well as the excitation
of an outward propagating density wave with half the pattern speed.
The existence of this has been described above.
We are concerned here with the situation when the companion
orbit becomes eccentric. In general it will
precess with a period very much longer than
the orbital period. In an inertial frame the
time averaged orbit then appears as a perturbation
of the unperturbed circular orbit with azimuthal
mode number m=1.
Because we are interested in modes that appear to change slowly
in the inertial frame, we adopt the approach of secular perturbation theory.
We thus perform a time average over an interval
long compared to the orbital period
but short compared to the orbital precession period.
The companion then acts gravitationally as if
it mass were continuously
distributed along its orbit with line density inversely
proportional to its speed. In an average sense it behaves
like a continuous mass distribution and can be regarded as an infinitesimally
thin annular extension of the disc. In this respect we suppose that
we have a disc with well defined inner edge, interior to which there
is a gap or hole
in which the companion orbits. In the secular theory, we shall regard
the companion as equivalent to an annular extension of the disc orbiting
inside the
gap and consider an eccentric companion orbit as
a non axisymmetric perturbation of the initially
axisymmetric combined disc-companion system.
In this way an eccentric disc is produced also as comprising the normal mode.
Good coupling results in eccentricities of comparable magnitudes
in both components, while weak coupling enables them to exhibit
eccentricities separately. The condition for good coupling is that
the precession period induced in disc orbits by the companion
and its own pressure and self-gravity
be comparable to the precession period induced in the companion orbit
by the disc. This is met when the disc mass,
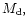 contained in a radial
scale
comparable to the gap radius (or 1:3 resonance radius as
taken below) is comparable to the mass of the companion.
When these masses are very different, the situation will favour
either an eccentric companion orbit or an eccentric disc.
contained in a radial
scale
comparable to the gap radius (or 1:3 resonance radius as
taken below) is comparable to the mass of the companion.
When these masses are very different, the situation will favour
either an eccentric companion orbit or an eccentric disc.
This occurs because the
slowly precessing nonaxisymmetric pattern in the disc
makes it behave similarly to a planet of mass
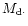 From standard secular perturbation theory (Brouwer & Clemence 1961)
eccentricity is freely exchanged between this planet and the companion
when their orbital angular momenta are comparable, a situation
that occurs here when the masses are comparable.
From standard secular perturbation theory (Brouwer & Clemence 1961)
eccentricity is freely exchanged between this planet and the companion
when their orbital angular momenta are comparable, a situation
that occurs here when the masses are comparable.
The slowly varying m=1 modes described above are found to be negative
angular momentum modes. This means that if they induce an angular
momentum transfer
to outer disc material from the region where they are located,
they will grow unstably.
Within the framework of secular perturbation theory of an initially
axisymmetric
disc this does not occur. However, if the high frequency components
of the companion potential are now allowed to act, their coupling
with the m=1 secular mode induces an angular momentum loss and hence growth.
This occurs through the coupling of the m=1 low frequency mode
with an m=1 potential component with pattern speed equal to the orbital
frequency. This produces a forcing potential with m=2 and pattern speed
one half the orbital frequency. As we shall see this can produce
a density wave resonantly excited at the 1:3 resonance located at
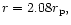
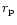 being the companion semi-major axis,
provided that resonance is contained within the disc, and hence mode growth.
A favourable situation occurs when the gap or inner hole is large enough that
possibly stabilizing corotation resonances are absent (Goldreich & Tremaine
1980; Artymowicz 1993; Lin & Papaloizou 1993a).
When growth occurs we find two limiting cases. When the companion mass
dominates that of the disc, an eccentric disc is produced.
This situation is illustrated by our run in which the companion
was maintained on a fixed circular orbit. In the opposite case,
an eccentric companion orbit is expected as has
been previously discussed by e.g. Artymowicz (1992) and
Lin & Papaloizou (1993a).
In the intermediate case
eccentricities in both components are produced.
We consider linear perturbations of a two dimensional
flat axisymmetric disc and time averaged planet.
The dependence on time, t, and azimuthal angle,
being the companion semi-major axis,
provided that resonance is contained within the disc, and hence mode growth.
A favourable situation occurs when the gap or inner hole is large enough that
possibly stabilizing corotation resonances are absent (Goldreich & Tremaine
1980; Artymowicz 1993; Lin & Papaloizou 1993a).
When growth occurs we find two limiting cases. When the companion mass
dominates that of the disc, an eccentric disc is produced.
This situation is illustrated by our run in which the companion
was maintained on a fixed circular orbit. In the opposite case,
an eccentric companion orbit is expected as has
been previously discussed by e.g. Artymowicz (1992) and
Lin & Papaloizou (1993a).
In the intermediate case
eccentricities in both components are produced.
We consider linear perturbations of a two dimensional
flat axisymmetric disc and time averaged planet.
The dependence on time, t, and azimuthal angle, 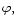 is taken
to be through a factor
is taken
to be through a factor
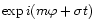 henceforth
taken as read. Here the
azimuthal mode number m=1 and the mode frequency
henceforth
taken as read. Here the
azimuthal mode number m=1 and the mode frequency
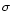 is such that
is such that
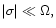 where
where 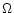 is the angular
velocity
in the unperturbed disc
where the unperturbed surface density is
is the angular
velocity
in the unperturbed disc
where the unperturbed surface density is 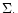 The Lagrangian displacement
The Lagrangian displacement
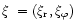 obeys the perturbed equations of motion
obeys the perturbed equations of motion
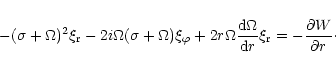 |
(1) |
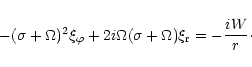 |
(2) |
Equations (1) and (2) can be combined to give
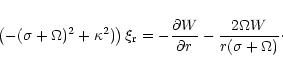 |
(3) |
Here
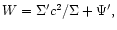 where
where 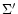 and
and 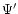 are the
surface density and gravitational potential perturbations respectively.
The vertically integrated pressure P is assumed to be a function of
are the
surface density and gravitational potential perturbations respectively.
The vertically integrated pressure P is assumed to be a function of
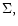
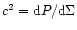 is the square of the sound speed,
and
is the square of the sound speed,
and
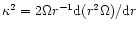 is the square of
the epicyclic frequency.
The perturbation to the gravitational
potential
may be written (temporarily restoring the
is the square of
the epicyclic frequency.
The perturbation to the gravitational
potential
may be written (temporarily restoring the 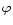 dependence)
dependence)
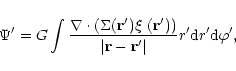 |
(4) |
where this and similar integrals are taken over the active mass distribution.
We may apply (4) to both the distributed disc
mass and the separated, time averaged, but initially
radially localized companion mass
for which
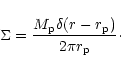 |
(5) |
Here 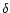 denotes a delta function and
denotes a delta function and 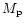 the companion mass.
Before so doing, we use the fact that
the companion mass.
Before so doing, we use the fact that
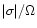 is small to
make some simplifications. In this limit and for a thin disc
for which forces due to internal pressure and self-gravity
are small, Eq. (2) becomes
is small to
make some simplifications. In this limit and for a thin disc
for which forces due to internal pressure and self-gravity
are small, Eq. (2) becomes
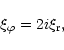 |
(6) |
which is the limiting form for purely epicyclic motion.
We use this to evaluate the pressure and self-gravity terms
on the right hand side of (3). The error in doing this, for a
gravitationally
stable disc, is measured
by the greater of
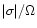 and H/r, where H is the semi-thickness
of the disc.
Then we have
and H/r, where H is the semi-thickness
of the disc.
Then we have
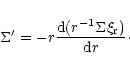 |
(7) |
Equation (4) can then be written
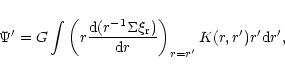 |
(8) |
with
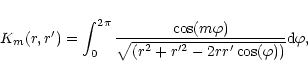 |
(9) |
and noting that for m=1 we shall drop the subscript from
Km(r,r'),thus
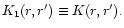 We finally obtain a normal mode equation for
We finally obtain a normal mode equation for
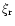 by using
(8),
and (7) in (3) in the form
by using
(8),
and (7) in (3) in the form
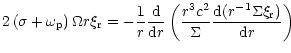 |
|
|
|
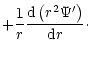 |
|
|
(10) |
Here we have used the fact that
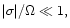 and the precession frequency
and the precession frequency
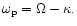
Although Eq. (10) applies to the joint disc and companion system,
we shall separate the contributions to the potential from
the companion and disc, writing
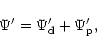 |
(11) |
where
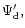 and
and
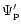 are the contributions
from the disc and planet obtained from the appropriate
surface density distributions respectively.
Using (5), we find
are the contributions
from the disc and planet obtained from the appropriate
surface density distributions respectively.
Using (5), we find
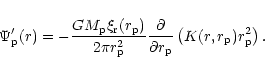 |
(12) |
Here the eccentricity of the companion orbit is related to the displacement by
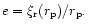
If we replace 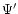 in (10) by the disc contribution
in (10) by the disc contribution
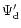 only, we obtain an equation for the normal modes of the
disc only. In fact under reasonable boundary conditions
that
only, we obtain an equation for the normal modes of the
disc only. In fact under reasonable boundary conditions
that
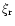 is well behaved at the inner boundary and vanishes
at large distances, (10) gives a self-adjoint eigenvalue problem
for the eigenvalue
is well behaved at the inner boundary and vanishes
at large distances, (10) gives a self-adjoint eigenvalue problem
for the eigenvalue 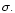 The right hand side gives a self-adjoint
operator with weight
The right hand side gives a self-adjoint
operator with weight 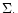 Denoting, the eigenvalues by
Denoting, the eigenvalues by 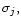 and corresponding eigenfunctions,
and corresponding eigenfunctions,
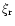 by
uj, j= 1,2,...,we have the orthogonality condition
by
uj, j= 1,2,...,we have the orthogonality condition
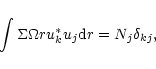 |
(13) |
with this and later integrals being taken over the disc.
We comment that the eigenvalues are all real and the local dispersion relation
associated with (10) is the low frequency limit
of the well known relation for spiral density waves (Lin & Shu 1964)
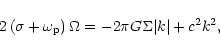 |
(14) |
where k is the radial wavenumber and of course m=1.Each mode propagates with a prograde pattern speed
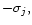 which is also the precession frequency.
which is also the precession frequency.
The effect of the companion may be incorporated by adding
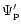 into
into 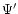 in (10). Regarding the companion potential so added
as giving an external forcing term, Eq. (10) may be solved using the
standard method of eigenfunction expansion to give interior to the disc
in (10). Regarding the companion potential so added
as giving an external forcing term, Eq. (10) may be solved using the
standard method of eigenfunction expansion to give interior to the disc
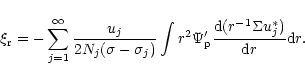 |
(15) |
Omitting the pressure term, Eq. (10) gives
for the equation of motion of the companion
![\begin{displaymath}2\left[\sigma + \omega_{\rm p}(r_{\rm p}) \right] \Omega(r_{\...
...si'_{\rm d}(r) \right) \over {\rm d} r}
\right]_{r=r_{\rm p}}
\end{displaymath}](/articles/aa/full/2001/04/aa9988/img114.gif) |
(16) |
with
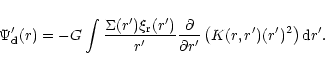 |
(17) |
Combining (16), (15) and (17)
gives an equation for the eigenvalue 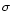 for the joint
normal mode in the form
for the joint
normal mode in the form
![\begin{displaymath}\left[\sigma + \omega_{\rm p}(r_{\rm p}) \right] \Omega(r_{\r...
...t^2 M_{\rm p} \over 8\pi r_{\rm p}^2 N_j (\sigma - \sigma_j)},
\end{displaymath}](/articles/aa/full/2001/04/aa9988/img116.gif) |
(18) |
with the coupling coefficient given by
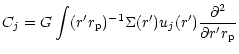 |
|
|
|
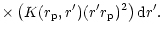 |
|
|
(19) |
The schematic behaviour of the eigenvalues is that, when the coupling
coefficient Cj is negligible, the solutions are
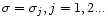 and
and
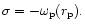 In this case the companion
and disc are
decoupled
and precess independently. In contrast when the coupling is non negligible
the precession of companion orbit and disc are linked. One induces
eccentricity in the other. To estimate when this occurs, one needs that
In this case the companion
and disc are
decoupled
and precess independently. In contrast when the coupling is non negligible
the precession of companion orbit and disc are linked. One induces
eccentricity in the other. To estimate when this occurs, one needs that
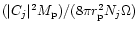 be
of the same order as the square of the difference in disc
and companion orbit
precession frequencies
be
of the same order as the square of the difference in disc
and companion orbit
precession frequencies
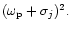 If the companion
and disc mutually induce eccentricity and precession,
simple
estimates, assuming there is a single radial scale length, indicate
this requires that
If the companion
and disc mutually induce eccentricity and precession,
simple
estimates, assuming there is a single radial scale length, indicate
this requires that
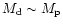 for good coupling.
for good coupling.
We comment that although the gravity
of the disc acting on both itself and the companion
has been included in the above formalism, the self-interaction
only affects the precise determination of the 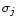 and uj.The above discussion still applies if that is neglected,
as long as the interaction
with the companion is retained. This is the case for the simulations
presented here.
and uj.The above discussion still applies if that is neglected,
as long as the interaction
with the companion is retained. This is the case for the simulations
presented here.
The effective angular momentum content in the joint mode can be
evaluated using standard methods (e.g. Goodman & Ryu 1992;
Lin & Papaloizou 1993b).
For the low frequency modes considered here, we obtain after
a straightforward calculation
 |
(20) |
where the integral is over the entire system.
We comment that, using (5), the contribution from the companion
to
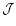 is
is
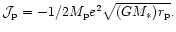 This is negative corresponding to a negative
angular momentum mode and it is also minus the radial action.
If angular momentum is drained from the mode, the companion orbit
eccentricity
and radial action grow. In general the total angular momentum content
is
This is negative corresponding to a negative
angular momentum mode and it is also minus the radial action.
If angular momentum is drained from the mode, the companion orbit
eccentricity
and radial action grow. In general the total angular momentum content
is
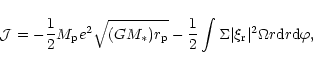 |
(21) |
where the second contribution now comes from the disc only, involving
the radial component of the Lagrangian displacement
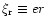 there.
there.
5.10 Angular momentum loss due to resonant torques
The modes discussed above, in the time averaging approximation,
do not lose angular momentum. However,
only the time averaged potential due to the companion has been included.
When the effects of the full potential are included,
additional perturbation of the disc occurs. This can lead to
angular momentum loss through resonant torques
(Goldreich & Tremaine 1978).
In that case, the mode eccentricities grow and instability occurs.
The full potential due to the companion located
at
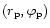 can be written
can be written
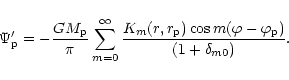 |
(22) |
When the disc and companion orbit are eccentric, with small eccentricities,
to evaluate the companion potential at the location of a perturbed fluid
element in the disc,
we set
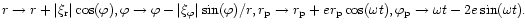 Here, arbitrary phases are chosen
such that all ellipses have apsidal lines aligned at
Here, arbitrary phases are chosen
such that all ellipses have apsidal lines aligned at
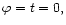 consistently with the joint mode. The orbital frequency is
consistently with the joint mode. The orbital frequency is 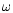 and we have neglected the small precession frequency.
The simulations suggest an alignment such the eccentricities of the
disc and orbit are of opposite sign. In this case the disc pericentre
is closest to the orbital apocentre.
The contribution
to the companion potential that is first order in the eccentricities
and we have neglected the small precession frequency.
The simulations suggest an alignment such the eccentricities of the
disc and orbit are of opposite sign. In this case the disc pericentre
is closest to the orbital apocentre.
The contribution
to the companion potential that is first order in the eccentricities
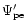 is given by
is given by
where
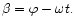 We comment that for zero eccentricities, all time dependent
components of the companion
potential have pattern speed
We comment that for zero eccentricities, all time dependent
components of the companion
potential have pattern speed 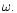 In the outer disc, there are
possible outer Lindblad resonances where
In the outer disc, there are
possible outer Lindblad resonances where
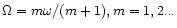 However, as the inner edge approaches the 1:2 resonance,
only the resonance with m=1 remains eventually.
When eccentricities are included,
contributions occur in (23) with pattern speeds
However, as the inner edge approaches the 1:2 resonance,
only the resonance with m=1 remains eventually.
When eccentricities are included,
contributions occur in (23) with pattern speeds
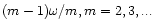 The outer Lindblad resonances associated with these are at
The outer Lindblad resonances associated with these are at
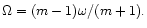 For m=2, this gives
the smallest value of
For m=2, this gives
the smallest value of
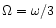 which
occurs at the 1:3 resonance.
The corresponding pattern speed of the resonant forcing is
which
occurs at the 1:3 resonance.
The corresponding pattern speed of the resonant forcing is 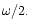 As the material at the outer Lindblad
resonance rotates more slowly than the pattern speed,
resonant torques cause angular momentum loss leading to
eccentricity growth of the joint disc-companion system.
For discs with inner edges approaching the 1:2 resonance
such that the disc surface density becomes depressed there, potentially
damping corotation torques (Goldreich & Tremaine 1980)
and coorbital Lindblad torques (Artymowicz 1993) are weakened.
Here we shall assume that
only the 1:3 resonance needs to be considered.
The resonant forcing occurs through terms produced by
a nonlinear coupling
between the secular m=1 mode and disturbances with m=1moving with the orbital pattern speed
As the material at the outer Lindblad
resonance rotates more slowly than the pattern speed,
resonant torques cause angular momentum loss leading to
eccentricity growth of the joint disc-companion system.
For discs with inner edges approaching the 1:2 resonance
such that the disc surface density becomes depressed there, potentially
damping corotation torques (Goldreich & Tremaine 1980)
and coorbital Lindblad torques (Artymowicz 1993) are weakened.
Here we shall assume that
only the 1:3 resonance needs to be considered.
The resonant forcing occurs through terms produced by
a nonlinear coupling
between the secular m=1 mode and disturbances with m=1moving with the orbital pattern speed
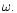 We begin by
calculating the resonant forcing using (23)
as a forcing potential on the unperturbed axisymmetric disc.
However, it is important
to note that not all the effective forcing terms are included in this way.
They arise also by coupling between the secular m=1 mode
and the tidal distortion of the disc produced by
the circular orbit tide propagating with a pattern speed
We begin by
calculating the resonant forcing using (23)
as a forcing potential on the unperturbed axisymmetric disc.
However, it is important
to note that not all the effective forcing terms are included in this way.
They arise also by coupling between the secular m=1 mode
and the tidal distortion of the disc produced by
the circular orbit tide propagating with a pattern speed 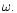 Evaluation of these is lengthy and depends on the detailed disc model which
has here been simplified.
Instead of such evaluation,
we replace the disc eccentricity in (23) by
Evaluation of these is lengthy and depends on the detailed disc model which
has here been simplified.
Instead of such evaluation,
we replace the disc eccentricity in (23) by
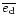 to indicate additional forcing. Although such forcing is not necessarily
through a potential, it can still be taken into account by defining
a suitable
to indicate additional forcing. Although such forcing is not necessarily
through a potential, it can still be taken into account by defining
a suitable
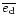 which is proportional to the
disc eccentricity
amplitude (see Eq. [24]).
This procedure will enable eccentricity growth rates
to be qualitatively discussed and estimated.
The component of (23) with pattern speed
which is proportional to the
disc eccentricity
amplitude (see Eq. [24]).
This procedure will enable eccentricity growth rates
to be qualitatively discussed and estimated.
The component of (23) with pattern speed
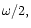 is then given by
is then given by
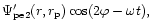 where
where
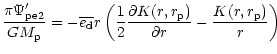 |
|
|
|
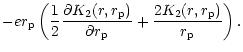 |
|
|
(24) |
Here we have set
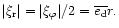 We calculate the rate of loss of angular momentum as a result
of resonant torques using the torque formula of
Goldreich & Tremaine (1978, 1980) to obtain
We calculate the rate of loss of angular momentum as a result
of resonant torques using the torque formula of
Goldreich & Tremaine (1978, 1980) to obtain
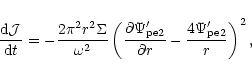 |
(25) |
where r and the disc quantities are evaluated at the 1:3 resonance.
The angular momentum is transported outwards via a wave with pattern speed
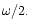 It has to be extracted from the m=1 joint mode
and the companion orbit which have combined together to give
the resonant forcing.
It has to be extracted from the m=1 joint mode
and the companion orbit which have combined together to give
the resonant forcing.
Extraction from an eccentric companion orbit can occur directly through
the excited m=2 wave.
Extraction from the m=1 mode can occur through a recoupling of the
m=2 wave with
the tidal potential with pattern speed 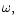 to produce a time independent forcing with m=1.
Similarly extraction from the orbit can occur through recoupling of the m=2wave to
the m=1 joint mode to produce an m=1 disturbance with the circular
orbit pattern speed
to produce a time independent forcing with m=1.
Similarly extraction from the orbit can occur through recoupling of the m=2wave to
the m=1 joint mode to produce an m=1 disturbance with the circular
orbit pattern speed 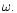
If the resonantly excited m=2 wave carries an angular momentum
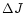 ,
the associated energy is
,
the associated energy is
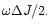 If this energy is supplied by the circular orbit tide, then
the angular momentum supplied along with it will be
If this energy is supplied by the circular orbit tide, then
the angular momentum supplied along with it will be
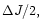 leaving
leaving
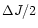 to be extracted from the joint m=1 mode.
to be extracted from the joint m=1 mode.
The above discussion suggests
the growth rate of this mode can be obtained by
assuming half the
resonantly induced angular momentum loss
is extracted from it.
The growth rate of the combined mode is then estimated as
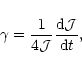 |
(26) |
with
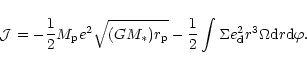 |
(27) |
Evaluating (25) we obtain
where
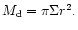
Note that here we neglect any change in the companion
semi-major axis due to the time dependent terms in the disc potential.
To set the magnitudes of typical growth rates, we first
set the terms involving the disc eccentricity
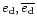 to zero.
We find from (28)
that for the 1:3 resonance with
to zero.
We find from (28)
that for the 1:3 resonance with
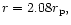
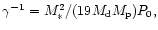 with P0 being the
orbital period. Thus for
with P0 being the
orbital period. Thus for
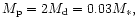 here we allow a factor of two surface density enhancement above
the initial value at the 1:3 resonance,
we find a growth time
here we allow a factor of two surface density enhancement above
the initial value at the 1:3 resonance,
we find a growth time
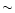 120 companion orbital periods.
This is comparable, but a factor of
120 companion orbital periods.
This is comparable, but a factor of 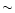 3 smaller,
than the eccentricity growth rate
obtained for calculation N5, and is consistent with the idea
that the orbital
eccentricity driving arises through effects due to
both the orbital eccentricity itself and the eccentricity
induced in the disc,
the latter actually giving stronger effects.
We comment that for these parameters the disc and companion orbit
eccentricities are likely to be coupled. This is because
typically
3 smaller,
than the eccentricity growth rate
obtained for calculation N5, and is consistent with the idea
that the orbital
eccentricity driving arises through effects due to
both the orbital eccentricity itself and the eccentricity
induced in the disc,
the latter actually giving stronger effects.
We comment that for these parameters the disc and companion orbit
eccentricities are likely to be coupled. This is because
typically
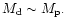 Then the precession frequency
induced by the companion in externally orbiting disc matter
is given by
Then the precession frequency
induced by the companion in externally orbiting disc matter
is given by
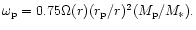 Similarly the precession frequency induced by the
disc (assumed to have constant surface density)
in the companion orbit is
Similarly the precession frequency induced by the
disc (assumed to have constant surface density)
in the companion orbit is
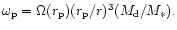 These are comparable leading to the likely setting up of a joint mode.
We comment that this condition is the same as
requiring that the companion orbital angular momentum and the orbital
angular momentum contained in
These are comparable leading to the likely setting up of a joint mode.
We comment that this condition is the same as
requiring that the companion orbital angular momentum and the orbital
angular momentum contained in 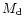 assumed in circular orbit
be comparable.
assumed in circular orbit
be comparable.
Under the conditions of the simulations considered here,
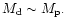 Then it is also likely that the radial action in the disc is comparable
to that of the companion and so modifies the growth rate.
However, as long as they are comparable our estimate is probably
reasonable. Note that
Then it is also likely that the radial action in the disc is comparable
to that of the companion and so modifies the growth rate.
However, as long as they are comparable our estimate is probably
reasonable. Note that
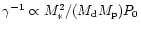 as long as
as long as 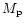 is comparable to or less than
is comparable to or less than
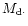 If the companion mass dominates, so fixing it in a circular orbit,
then e=0, in (28) and
If the companion mass dominates, so fixing it in a circular orbit,
then e=0, in (28) and
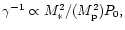 attaining a limiting value independent of the disc mass.
Our simulation with fixed
companion orbit indicates that the growth rate does not change very much
as
attaining a limiting value independent of the disc mass.
Our simulation with fixed
companion orbit indicates that the growth rate does not change very much
as 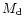 is reduced significantly below
is reduced significantly below


Up: Orbital eccentricity growth through
Copyright ESO 2001
![]() Much of the complex nonlinear dynamics involving
the balance between tides and viscosity determining
the structure of the inner disc edge is thus omitted.
However, enough content remains in order
to display an instability leading to eccentricity growth
in both disc and companion orbit, as well as the excitation
of an outward propagating density wave with half the pattern speed.
The existence of this has been described above.
Much of the complex nonlinear dynamics involving
the balance between tides and viscosity determining
the structure of the inner disc edge is thus omitted.
However, enough content remains in order
to display an instability leading to eccentricity growth
in both disc and companion orbit, as well as the excitation
of an outward propagating density wave with half the pattern speed.
The existence of this has been described above.
![]() From standard secular perturbation theory (Brouwer & Clemence 1961)
eccentricity is freely exchanged between this planet and the companion
when their orbital angular momenta are comparable, a situation
that occurs here when the masses are comparable.
From standard secular perturbation theory (Brouwer & Clemence 1961)
eccentricity is freely exchanged between this planet and the companion
when their orbital angular momenta are comparable, a situation
that occurs here when the masses are comparable.
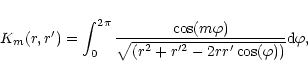
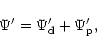
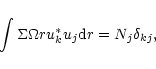
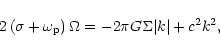
![]() and uj.The above discussion still applies if that is neglected,
as long as the interaction
with the companion is retained. This is the case for the simulations
presented here.
and uj.The above discussion still applies if that is neglected,
as long as the interaction
with the companion is retained. This is the case for the simulations
presented here.
![]() can be written
can be written
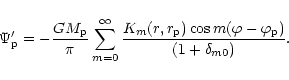
![]() It has to be extracted from the m=1 joint mode
and the companion orbit which have combined together to give
the resonant forcing.
It has to be extracted from the m=1 joint mode
and the companion orbit which have combined together to give
the resonant forcing.
![]() to produce a time independent forcing with m=1.
Similarly extraction from the orbit can occur through recoupling of the m=2wave to
the m=1 joint mode to produce an m=1 disturbance with the circular
orbit pattern speed
to produce a time independent forcing with m=1.
Similarly extraction from the orbit can occur through recoupling of the m=2wave to
the m=1 joint mode to produce an m=1 disturbance with the circular
orbit pattern speed ![]()
![]() ,
the associated energy is
,
the associated energy is
![]() If this energy is supplied by the circular orbit tide, then
the angular momentum supplied along with it will be
If this energy is supplied by the circular orbit tide, then
the angular momentum supplied along with it will be
![]() leaving
leaving
![]() to be extracted from the joint m=1 mode.
to be extracted from the joint m=1 mode.
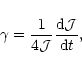
![]() to zero.
We find from (28)
that for the 1:3 resonance with
to zero.
We find from (28)
that for the 1:3 resonance with
![]()
![]() with P0 being the
orbital period. Thus for
with P0 being the
orbital period. Thus for
![]() here we allow a factor of two surface density enhancement above
the initial value at the 1:3 resonance,
we find a growth time
here we allow a factor of two surface density enhancement above
the initial value at the 1:3 resonance,
we find a growth time
![]() 120 companion orbital periods.
This is comparable, but a factor of
120 companion orbital periods.
This is comparable, but a factor of ![]() 3 smaller,
than the eccentricity growth rate
obtained for calculation N5, and is consistent with the idea
that the orbital
eccentricity driving arises through effects due to
both the orbital eccentricity itself and the eccentricity
induced in the disc,
the latter actually giving stronger effects.
We comment that for these parameters the disc and companion orbit
eccentricities are likely to be coupled. This is because
typically
3 smaller,
than the eccentricity growth rate
obtained for calculation N5, and is consistent with the idea
that the orbital
eccentricity driving arises through effects due to
both the orbital eccentricity itself and the eccentricity
induced in the disc,
the latter actually giving stronger effects.
We comment that for these parameters the disc and companion orbit
eccentricities are likely to be coupled. This is because
typically
![]() Then the precession frequency
induced by the companion in externally orbiting disc matter
is given by
Then the precession frequency
induced by the companion in externally orbiting disc matter
is given by
![]() Similarly the precession frequency induced by the
disc (assumed to have constant surface density)
in the companion orbit is
Similarly the precession frequency induced by the
disc (assumed to have constant surface density)
in the companion orbit is
![]() These are comparable leading to the likely setting up of a joint mode.
We comment that this condition is the same as
requiring that the companion orbital angular momentum and the orbital
angular momentum contained in
These are comparable leading to the likely setting up of a joint mode.
We comment that this condition is the same as
requiring that the companion orbital angular momentum and the orbital
angular momentum contained in ![]() assumed in circular orbit
be comparable.
assumed in circular orbit
be comparable.
![]() Then it is also likely that the radial action in the disc is comparable
to that of the companion and so modifies the growth rate.
However, as long as they are comparable our estimate is probably
reasonable. Note that
Then it is also likely that the radial action in the disc is comparable
to that of the companion and so modifies the growth rate.
However, as long as they are comparable our estimate is probably
reasonable. Note that
![]() as long as
as long as ![]() is comparable to or less than
is comparable to or less than
![]() If the companion mass dominates, so fixing it in a circular orbit,
then e=0, in (28) and
If the companion mass dominates, so fixing it in a circular orbit,
then e=0, in (28) and
![]() attaining a limiting value independent of the disc mass.
Our simulation with fixed
companion orbit indicates that the growth rate does not change very much
as
attaining a limiting value independent of the disc mass.
Our simulation with fixed
companion orbit indicates that the growth rate does not change very much
as ![]() is reduced significantly below
is reduced significantly below
![]()