

Up: Orbital eccentricity growth through
4 Numerical calculations
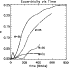 |
Figure 1:
This figure shows the evolution of the eccentricity versus time
(measured in units of P0) for the calculations, N2, N3, N4, N5 listed
in Table 1. The lines corresponding to each companion of different
mass are indicated on the figure in units of 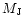
|
Recent simulations of protoplanets with
0.001 < q < 0.01,interacting with
discs with physical parameters similar to those adopted
here, being thought to be appropriate to protoplanetary
discs, have been carried out by Bryden et al. (1999), Kley (1999),
and Lubow et al. (1999). Fixed circular orbits were
assumed. It was found that a gap was formed that deepened
and widened with increasing q. The disc interior to the orbit
accreted onto the central star forming an inner cavity.
Subsequent work by NPMK which allowed the orbit to evolve
found that it remained essentially circular while migrating
towards the central star.
We remark that Artymowicz (1992) indicated that
orbital eccentricity growth might occur for sufficiently large
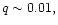 while Lin & Papaloizou (1993a) argued that for sufficiently wide gaps,
eccentricity growth could be induced by interaction at the 1:3
resonance in the outer disc and the 3:1 resonance in the inner disc.
As the latter is absent in the work presented here, only
the 1:3 resonance in the outer disc will concern us.
while Lin & Papaloizou (1993a) argued that for sufficiently wide gaps,
eccentricity growth could be induced by interaction at the 1:3
resonance in the outer disc and the 3:1 resonance in the inner disc.
As the latter is absent in the work presented here, only
the 1:3 resonance in the outer disc will concern us.
The aim of the work presented here is to examine for what value of
the companion-star mass ratio, if any, eccentricity growth of the companion
orbit is induced by its interaction with the disc model that we assume.
Should it occur, we wish
to understand the dominant mechanism by which growth occurs
and in particular whether the 1:3 resonance is involved.
The numerical calculations are summarised in Table 1.
The case of q=10-3 was considered in some detail in NPMK.
The planet/companion in this case was found to migrate in towards the central
star on a time scale given by the viscous evolution time at the initial
position of the planet (also see Lin & Papaloizou 1986)
remaining on an essentially circular orbit.
We will not give further discussion here on this case, since eccentricity
growth was not observed.
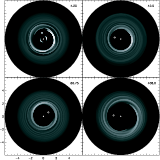 |
Figure 2:
This figure shows the evolution of the surface density
profile of the disc in calculation N5 described in Table 1. The time,
in units of P0, is shown at the top right hand corner of each panel.
The initial clearing of a gap is shown in the first and second
panel, and the growth of
eccentricity of the disc interior to the 1:3 resonance (located at
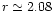 )
may be observed in the third panel. The fourth panel shows the
disc at a later time when the companion has developed an eccentricity of )
may be observed in the third panel. The fourth panel shows the
disc at a later time when the companion has developed an eccentricity of
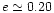 ,
and indicates that the behaviour of the disc becomes
more complicated and unsteady during these later times ,
and indicates that the behaviour of the disc becomes
more complicated and unsteady during these later times |
The evolution of the eccentricity for the remaining cases listed
in Table 1 is shown in Fig. 1. It is apparent
from this figure that strong eccentricity growth occurs for
mass ratios in the range
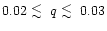 ,
with the strongest eccentricity
growth being observed at the higher end of this range. From here onwards we
will concentrate on describing the evolution of the q=0.03 case.
,
with the strongest eccentricity
growth being observed at the higher end of this range. From here onwards we
will concentrate on describing the evolution of the q=0.03 case.
A plot of the surface density evolution of run N5 described in Table 1
is shown in Fig. 2. The times corresponding to each panel
are shown in the top right hand corner in units of P0.
It can be seen that the disc interior to
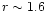 is cleared out
by the action of the companion tides on a relatively short
time scale, and remains tidally truncated.
Further evolution of the system leads to the formation
of an eccentric outer disc, as may be observed in the third panel of
Fig. 2. Figure 4 also shows the formation of an eccentric
disc for a companion on a fixed circular orbit, and is described below.
As the eccentricity of the companion increases
beyond
is cleared out
by the action of the companion tides on a relatively short
time scale, and remains tidally truncated.
Further evolution of the system leads to the formation
of an eccentric outer disc, as may be observed in the third panel of
Fig. 2. Figure 4 also shows the formation of an eccentric
disc for a companion on a fixed circular orbit, and is described below.
As the eccentricity of the companion increases
beyond
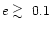 ,
we observe
that the disc response becomes non steady as the companion orbits between
apocentre and pericentre. The evolution of the orbital radius of
the companion and its eccentricity evolution (on both linear and log scales)
are presented in Fig. 3.
This figure shows that the eccentricity undergoes a period
of rapid growth after a time of
,
we observe
that the disc response becomes non steady as the companion orbits between
apocentre and pericentre. The evolution of the orbital radius of
the companion and its eccentricity evolution (on both linear and log scales)
are presented in Fig. 3.
This figure shows that the eccentricity undergoes a period
of rapid growth after a time of 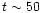 P0. The logarithmic
plot of e versus t shown in the second panel of this figure shows that
the growth rate is initially constant (approximately), but then decreases as
the system evolves beyond
P0. The logarithmic
plot of e versus t shown in the second panel of this figure shows that
the growth rate is initially constant (approximately), but then decreases as
the system evolves beyond
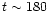 P0, indicating exponential growth
during these early stages. Analysis of the torques being exerted
on the companion between the times
P0, indicating exponential growth
during these early stages. Analysis of the torques being exerted
on the companion between the times
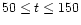 P0 shows that the
angular momentum is removed from the companion orbit
and transferred to the disc as it approaches
apocentre, leading to further growth of the orbital
eccentricity. This, however,
does not explain why the disc itself becomes eccentric during its early
evolution. At a later time
P0 shows that the
angular momentum is removed from the companion orbit
and transferred to the disc as it approaches
apocentre, leading to further growth of the orbital
eccentricity. This, however,
does not explain why the disc itself becomes eccentric during its early
evolution. At a later time
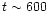 P0, the eccentricity
reaches a maximum value
P0, the eccentricity
reaches a maximum value 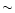 0.25. It subsequently enters
into a sequence of cyclic variations, decreasing
to small values at
0.25. It subsequently enters
into a sequence of cyclic variations, decreasing
to small values at
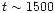 P0, before increasing again.
After the initial saturation the disc is always very eccentric
and in contact with the companion at some orbital phases.
This interaction of the companion
with material with higher specific
angular momentum causes the early net inward orbital migration
to reverse such that the final semi-major axis
at
P0, before increasing again.
After the initial saturation the disc is always very eccentric
and in contact with the companion at some orbital phases.
This interaction of the companion
with material with higher specific
angular momentum causes the early net inward orbital migration
to reverse such that the final semi-major axis
at
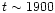 P0 exceeds the initial one.
But note that the details of this evolution depend
on the manner in which the disc interacts with the companion
and will be discussed by one of us in a future publication.
Clearly the disc-companion interaction is very
different in the brown dwarf regime from the planetary one.
P0 exceeds the initial one.
But note that the details of this evolution depend
on the manner in which the disc interacts with the companion
and will be discussed by one of us in a future publication.
Clearly the disc-companion interaction is very
different in the brown dwarf regime from the planetary one.
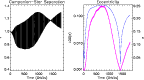 |
Figure 3:
This figure shows the evolution of the companion-star
orbital separation as a function of time in the first panel,
and the orbital eccentricity plotted as a log function (dotted line)
and linear function (solid line) in the second panel.
It is apparent that the eccentricity undergoes a period
of rapid growth after 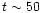 P0. Between
P0. Between 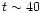 and 100 P0,
the growth is approximately exponential, as indicated by the plot
of
and 100 P0,
the growth is approximately exponential, as indicated by the plot
of 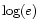 in the second panel which is close to being a straight line
during these times. At later times, the growth rate decreases and the plots
show a change of behaviour at
in the second panel which is close to being a straight line
during these times. At later times, the growth rate decreases and the plots
show a change of behaviour at
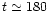 P0 when
P0 when
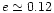 .
This change in the growth of e is accompanied by a change in the behaviour
of the disc surface density response, which becomes very unsteady.
This latter point was discussed
in the caption of Fig. 2.
On average there is net inward orbital migration
until .
This change in the growth of e is accompanied by a change in the behaviour
of the disc surface density response, which becomes very unsteady.
This latter point was discussed
in the caption of Fig. 2.
On average there is net inward orbital migration
until
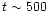 P0. After this time the eccentricity
starts to decrease before increasing again in a cyclic variation.
During these later phases
the companion has contact with material with higher specific
angular momentum from the eccentric disc. The interaction
causes the inward migration to reverse
P0. After this time the eccentricity
starts to decrease before increasing again in a cyclic variation.
During these later phases
the companion has contact with material with higher specific
angular momentum from the eccentric disc. The interaction
causes the inward migration to reverse |
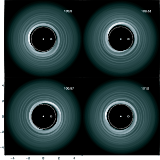 |
Figure 4:
This figure shows the eccentricity of the inner parts
of the outer disc for a run in which the companion was maintained on a
fixed circular orbit, with
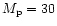
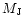 .
The times of each panel are shown
in the top right corner in units of the orbital period. The figure is plotted
in a frame that is corotating with the binary orbit, and the dotted line
indicates the position of the 1:2 outer Lindblad resonance .
The times of each panel are shown
in the top right corner in units of the orbital period. The figure is plotted
in a frame that is corotating with the binary orbit, and the dotted line
indicates the position of the 1:2 outer Lindblad resonance |
 |
Figure 5:
This figure shows the evolution of the m=2 component
of the Fourier transform of the surface density, in the inertial frame,
for the case of
a
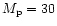
 companion on a fixed circular orbit.
The time elapsed when moving between the panels is shown in
the top right hand corner, in units of P0, where we have arbitrarily
denoted the time of the first panel to be t=0.0.
From the discussion in the text, it is expected that an m=2 spiral density wave will be excited at the 1:3 outer eccentric
Lindblad resonance, located at
companion on a fixed circular orbit.
The time elapsed when moving between the panels is shown in
the top right hand corner, in units of P0, where we have arbitrarily
denoted the time of the first panel to be t=0.0.
From the discussion in the text, it is expected that an m=2 spiral density wave will be excited at the 1:3 outer eccentric
Lindblad resonance, located at
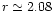 (shown by the dashed line), if the
eccentricity growth of the disc arises because
of a period doubling instability.
This wave should have a pattern speed
(shown by the dashed line), if the
eccentricity growth of the disc arises because
of a period doubling instability.
This wave should have a pattern speed
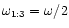 .
For an m=2 feature, the observed pattern should
repeat every P0, but not
every P0/2 (as would be the case if the wave had a frequency .
For an m=2 feature, the observed pattern should
repeat every P0, but not
every P0/2 (as would be the case if the wave had a frequency
 ).
Comparing the first and fifth panels, it is apparent that the m=2 pattern does indeed repeat after every P0. Comparing the
first and third panels, it is obvious that the m=2 feature does not repeat
every P0/2 ).
Comparing the first and fifth panels, it is apparent that the m=2 pattern does indeed repeat after every P0. Comparing the
first and third panels, it is obvious that the m=2 feature does not repeat
every P0/2 |
In order to explore why the disc itself becomes eccentric, an identical
simulation to N5 was performed, except that the companion was maintained
on a fixed circular orbit. According to
the discussion given below,
non linear coupling between an eccentric disc mode (with small e)
corresponding to an essentially time independent m=1 pattern
and the m=1component of the tidal potential and its disc response
propagating with pattern speed equal to the orbital frequency,
is expected to give rise to the excitation of an
m=2 spiral density wave emitted at the 1:3 outer eccentric
Lindblad resonance. The pattern speed of this wave is half the orbital
frequency. This wave can in turn couple back through the tidal
potential to produce a time independent wave and associated
potential with m=1. The removal of angular momentum from the disc
through such a potential
will cause the disc eccentricity to increase. This is because
no energy is removed along with the angular momentum,
from the fluid orbits, so they cannot remain circular.
If a wave with pattern speed equal to half the orbital frequency
is present and launched from the 1:3 resonance,
in a simulation with a companion on a fixed circular orbit, then it
accounts naturally for
the growth of disc eccentricity. Wave excitation is also expected
to cause a growth in orbital eccentricity when that is present
(see Lin & Papaloizou 1993a, and below).
The excited wave is expected to have a
pattern speed equal to
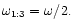 Because the disc configuration changes to one in which
the pattern rotation period has doubled, the instability
produces a period doubling and so resembles a parametric instability.
Because the disc configuration changes to one in which
the pattern rotation period has doubled, the instability
produces a period doubling and so resembles a parametric instability.
A plot of the disc surface density for the run with the companion on a fixed
circular orbit is shown in Fig. 4, in a frame corotating with the orbit.
The panels are separated by one third of the orbital period.
The 1:2 outer Lindblad resonance is shown by the dotted line, and the
eccentricity of the inner parts of the disc that lie just exterior
to this resonance may be observed.
The disc surface density that resulted from the simulation
in which the companion remained on a fixed circular orbit
was Fourier transformed in azimuth, and the m=2 component was examined.
In line with our expectations, it was observed that once the inner disc was
cleared of material, the presence of the m=2 wave being launched from
the 1:3 outer eccentric Lindblad resonance became apparent, travelling with
a pattern speed 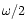 .
This m=2 component of
.
This m=2 component of 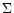 is plotted in Fig. 5 at different
times during an orbit.
Comparison between the first, fifth, and ninth panels, which are separated by an
orbital period of the star-companion system, show that the pattern does indeed
repeat after this time interval. Comparison between panels separated by
half an orbital period, such as the first and third, shows that the pattern
does not repeat after half an orbital period. An m=2 wave travelling
with the orbital frequency
is plotted in Fig. 5 at different
times during an orbit.
Comparison between the first, fifth, and ninth panels, which are separated by an
orbital period of the star-companion system, show that the pattern does indeed
repeat after this time interval. Comparison between panels separated by
half an orbital period, such as the first and third, shows that the pattern
does not repeat after half an orbital period. An m=2 wave travelling
with the orbital frequency 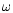 would repeat after every half an orbital
period. The fact that the m=2 wave only repeats after every orbital period
indicates that it is being excited at the 1:3 resonance (indicated by the dashed
line in Fig. 5) with a pattern speed
would repeat after every half an orbital
period. The fact that the m=2 wave only repeats after every orbital period
indicates that it is being excited at the 1:3 resonance (indicated by the dashed
line in Fig. 5) with a pattern speed
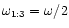 .
We conclude that a parametric instability is operating to excite this wave,
giving rise to an eccentric disc.
In calculation N5 where the star-companion orbit
is able to evolve, the interaction between the companion and the eccentric
disc leads to the growth of eccentricity of the companion orbit.
.
We conclude that a parametric instability is operating to excite this wave,
giving rise to an eccentric disc.
In calculation N5 where the star-companion orbit
is able to evolve, the interaction between the companion and the eccentric
disc leads to the growth of eccentricity of the companion orbit.
As described above, previous work on orbital eccentricity growth through
disc-companion interactions indicated that direct resonant wave excitation at
inner and outer eccentric Lindblad resonances should drive eccentricity, whereas
interaction with material at corotating Lindblad resonances should cause
it to damp (Artymowicz 1993; Lin & Papaloizou 1993a). In the simulations
presented here, only the outer 1:3 resonance is important, and it is of
interest to ask whether direct wave excitation at this resonance, or
interaction with the disc eccentricity, is primarily responsible for
the eccentricity growth of the companion orbit. To address this question,
we performed simulations
similar to run N5, but in which the surface density of the disc was
Fourier analysed in azimuth. In these calculations the gravitational
force of the disc acting on the star-companion orbit only included a
contribution from an individual Fourier component (m=1, 2, 3, or 4),
though the full potential of the star-companion system acting on the disc was
included. We expect that if the interaction of the companion with the disc
eccentricity is dominant in driving the companion eccentricity then the
calculation including only the m=1 component of the disc gravitational
potential will show more rapid growth of orbital eccentricity.
Conversely, if resonant wave excitation of an m=2 wave at the 1:3 resonance was
primarily responsible, then the calculation
including only the m=2 component of the disc
potential will show more rapid eccentricity growth.
In fact, we find that the m=1 run showed a moderately larger eccentricity
growth than the m=2 run, suggesting that the orbital
interaction with the eccentric disc
produces the stronger growth. This conclusion is further suggested
by the estimates of the eccentricity growth rates presented in Sect. 5.10.
The runs including only the m=3 and m=4 terms showed negligible
eccentricity growth.


Up: Orbital eccentricity growth through
Copyright ESO 2001




