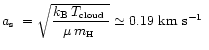 (where
(where
The millimeter continuum maps and radial profiles presented in Sects. 3 and 4 allow us to test, in Sect. 5.1.2 below, several theoretical predictions which we first summarize in Sect. 5.1.1.
In the self-similar collapse theory of Shu and co-workers, the
instantaneous structure of a protostellar dense core is primarily
determined by the position of the expansion wavefront (see Sect. 1).
For a typical cloud temperature
![]() K (e.g. Myers &
Benson 1983), the isothermal sound speed is
K (e.g. Myers &
Benson 1983), the isothermal sound speed is
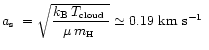 (where
(where ![]() is the
Boltzman constant,
is the
Boltzman constant,
![]() the mean molecular weight, and
the mean molecular weight, and
![]() the mass of atomic hydrogen). At the distance of the Taurus cloud,
the head of the expansion wave should be located at angular radii
the mass of atomic hydrogen). At the distance of the Taurus cloud,
the head of the expansion wave should be located at angular radii
![]() ,
,
![]()
![]() and
and ![]()
![]() ,
when t=104 yr, t=105 yr, and t=106 yr, respectively. A
power-law density profile of the form
,
when t=104 yr, t=105 yr, and t=106 yr, respectively. A
power-law density profile of the form
![]() is
expected, with
is
expected, with
![]() inside the expansion wavefront, and
inside the expansion wavefront, and
![]() further out.
More generally, the work of Whitworth & Summers (1985) shows
that, during the protostellar phase (i.e.,
further out.
More generally, the work of Whitworth & Summers (1985) shows
that, during the protostellar phase (i.e., ![]() ),
all isothermal similarity solutions converge at small radii
toward a free-fall density profile of the type
),
all isothermal similarity solutions converge at small radii
toward a free-fall density profile of the type
![]() ,
where
,
where
![]() is the accretion rate with w0 ranging
from 0.975 for the Shu case to
is the accretion rate with w0 ranging
from 0.975 for the Shu case to ![]() 47 for the Larson-Penston
case
47 for the Larson-Penston
case![]() .
.
Hence, in all self-similar isothermal models, the mass enclosed within
a given radius of the infall envelope should roughly scale as
![]() ,
where t is the age of the central
protostar (i.e., the time elapsed since point mass formation). When
the sound speed is
,
where t is the age of the central
protostar (i.e., the time elapsed since point mass formation). When
the sound speed is
![]() ,
the envelope masses predicted by
the Shu model are:
,
the envelope masses predicted by
the Shu model are:
![]() ,
,
![]() ,
and
,
and
![]() (see e.g. Fig. 5a). For t > 0, the
envelope masses are expected to be a factor
(see e.g. Fig. 5a). For t > 0, the
envelope masses are expected to be a factor ![]() 7 larger in the
Larson-Penston solution than in the Shu model. For comparison, at
point mass formation (t=0), the mass enclosed by the (static) SIS at
7 larger in the
Larson-Penston solution than in the Shu model. For comparison, at
point mass formation (t=0), the mass enclosed by the (static) SIS at
![]() K is
K is
![]() for
for
![]() ,
while the mass enclosed by
the (dynamic) Larson-Penston flow is
,
while the mass enclosed by
the (dynamic) Larson-Penston flow is ![]() 4.4 times larger. In the
magnetized case, a similar overdensity factor exists between the
dynamical similarity solution of Contopoulos et al. (1998) around t = 0 and the (equilibrium) singular isothermal magnetic disk (see discussion in Basu 1998).
When the collapse initial conditions are not self-similar but
correspond to pressure-truncated Bonnor-Ebert isothermal spheres, the
(inner) density profile is expected to approach that of the
Larson-Penston similarity solution near point mass formation (
4.4 times larger. In the
magnetized case, a similar overdensity factor exists between the
dynamical similarity solution of Contopoulos et al. (1998) around t = 0 and the (equilibrium) singular isothermal magnetic disk (see discussion in Basu 1998).
When the collapse initial conditions are not self-similar but
correspond to pressure-truncated Bonnor-Ebert isothermal spheres, the
(inner) density profile is expected to approach that of the
Larson-Penston similarity solution near point mass formation (
![]() )
but to relax toward the Shu density profile at later times,
until the expansion wavefront reaches the finite outer radius of the
cloud core (see Foster & Chevalier 1993).
)
but to relax toward the Shu density profile at later times,
until the expansion wavefront reaches the finite outer radius of the
cloud core (see Foster & Chevalier 1993).
In the alternative, non-isothermal description of the collapse by
McLaughlin & Pudritz (1996, 1997), based on a logotropic equation of
state of the type
![]() ln
ln
![]() (where
(where
![]() ,
and
,
and ![]() and
and
![]() are the
central values of the pressure and density), the initial conditions
are taken to be a singular logotropic sphere with
are the
central values of the pressure and density), the initial conditions
are taken to be a singular logotropic sphere with
![]() ,
truncated by external pressure at some outer
radius
,
truncated by external pressure at some outer
radius
![]() .
When the collapse of such a logotrope is initiated
(by, e.g., a small increase in external pressure), the density
distribution also approaches a free-fall
.
When the collapse of such a logotrope is initiated
(by, e.g., a small increase in external pressure), the density
distribution also approaches a free-fall
![]() power-law
power-law![]() inside the head of the expansion wave. The envelope mass enclosed
within
inside the head of the expansion wave. The envelope mass enclosed
within
![]() AU remains essentially constant during a
first "redistribution'' phase. For a critical logotrope of total mass
AU remains essentially constant during a
first "redistribution'' phase. For a critical logotrope of total mass
![]() and outer radius
and outer radius
![]() AU, this phase lasts for approximately 106 yr and the
enclosed mass is
AU, this phase lasts for approximately 106 yr and the
enclosed mass is
![]() ,
assuming the nominal parameters adopted by McLaughlin &
Pudritz (i.e.,
,
assuming the nominal parameters adopted by McLaughlin &
Pudritz (i.e.,
![]() K and a surface pressure
K and a surface pressure
![]() ). Thereafter, the stellar
mass increases roughly as
). Thereafter, the stellar
mass increases roughly as
![]() and the envelope
mass decreases accordingly [
and the envelope
mass decreases accordingly [
![]() ], until all the mass has been accreted and the
accretion phase is terminated at
], until all the mass has been accreted and the
accretion phase is terminated at
![]() yr. The
accretion history predicted by this model is thus very different from
that of the Shu et al. model.
yr. The
accretion history predicted by this model is thus very different from
that of the Shu et al. model.
Given observational uncertainties, the power-law density structure
derived in Sect. 4 for the envelopes of bona-fide protostars in Taurus
and Bok globules [
![]() with
with
![]() ]
is
consistent with that expected for either a SIS (p = 2) or a
free-fall configuration (p = 1.5). In the context of the standard
protostellar model, the median circumstellar mass
]
is
consistent with that expected for either a SIS (p = 2) or a
free-fall configuration (p = 1.5). In the context of the standard
protostellar model, the median circumstellar mass
![]() estimated for our complete sample of Taurus
candidate protostars corresponds to a collapse age of
estimated for our complete sample of Taurus
candidate protostars corresponds to a collapse age of
![]() yr. This value is in rough agreement with the typical lifetime
inferred for Taurus Class I sources based on statistical arguments (
yr. This value is in rough agreement with the typical lifetime
inferred for Taurus Class I sources based on statistical arguments (
![]() yr - see, e.g., KHSS90). Furthermore, the
median envelope mass of the "bona-fide'' Class I/0 protostars of
Taurus,
yr - see, e.g., KHSS90). Furthermore, the
median envelope mass of the "bona-fide'' Class I/0 protostars of
Taurus,
![]() ,
is within a factor of
,
is within a factor of
![]() of
of
![]() ,
suggesting
that these objects are still well into the main accretion phase with
estimated collapse ages
,
suggesting
that these objects are still well into the main accretion phase with
estimated collapse ages
![]() yr. By contrast, the
median mass measured for the 11 undetected or unresolved Class I
sources of Taurus (see e.g. Fig. 3g), is very low
(
yr. By contrast, the
median mass measured for the 11 undetected or unresolved Class I
sources of Taurus (see e.g. Fig. 3g), is very low
(
![]() ), and corresponds to a very old
collapse age
), and corresponds to a very old
collapse age
![]() yr. This is much longer than the
estimated lifetime of the protostellar embedded phase, implying that
the peculiar Class I sources cannot be genuine protostars.
Altogether, except perhaps for these peculiar sources (see also
Sect. 5.2.1 below), our Taurus results are in fairly good agreement with
the predictions of the standard collapse model.
yr. This is much longer than the
estimated lifetime of the protostellar embedded phase, implying that
the peculiar Class I sources cannot be genuine protostars.
Altogether, except perhaps for these peculiar sources (see also
Sect. 5.2.1 below), our Taurus results are in fairly good agreement with
the predictions of the standard collapse model.
On the other hand, the envelopes of Class 0 protostars in both Perseus
and isolated globules tend to be a factor of ![]() 2 to
2 to ![]() 12
more massive than is predicted by the standard model, even if
very young collapse ages are assumed:
12
more massive than is predicted by the standard model, even if
very young collapse ages are assumed:
![]() is
measured, while a maximum of
is
measured, while a maximum of
![]() is expected. As the gas temperature in the initial cloud core
cannot be much larger than 10 K (e.g. Ladd et al. 1994),
such large masses cannot be explained in the SIS picture unless
non-thermal sources of support are included. A factor of
is expected. As the gas temperature in the initial cloud core
cannot be much larger than 10 K (e.g. Ladd et al. 1994),
such large masses cannot be explained in the SIS picture unless
non-thermal sources of support are included. A factor of ![]() 2
increase in mass can be accommodated by the standard model if a
significant (static) magnetic field is present (e.g. Li & Shu 1996).
In principle, turbulence may also contribute to the support of the
initial dense core (e.g. Myers & Fuller 1992). However, the
small-scale condensations or "kernels'' corresponding to the
progenitors of protostars in star-forming clusters (e.g. MAN98) appear
to be essentially "coherent'', i.e., largely devoid of turbulence
(Goodman et al. 1998; Myers 1998; Belloche et al. 2001). We conclude
that variants of the standard model can probably account for the
masses measured in most Bok globules but are clearly insufficient to
explain the
2
increase in mass can be accommodated by the standard model if a
significant (static) magnetic field is present (e.g. Li & Shu 1996).
In principle, turbulence may also contribute to the support of the
initial dense core (e.g. Myers & Fuller 1992). However, the
small-scale condensations or "kernels'' corresponding to the
progenitors of protostars in star-forming clusters (e.g. MAN98) appear
to be essentially "coherent'', i.e., largely devoid of turbulence
(Goodman et al. 1998; Myers 1998; Belloche et al. 2001). We conclude
that variants of the standard model can probably account for the
masses measured in most Bok globules but are clearly insufficient to
explain the
![]() envelopes observed toward L1157-MM and the
Class 0 objects of Perseus. The most likely explanation in the latter
cases is that the collapse started from non-singular initial
conditions, resulting in a nonequilibrium density configuration
similar to the Larson-Penston flow near point mass formation (see
Sect. 5.1.1 above). Such a conclusion, which is consistent with the
large accretion/ejection rates inferred for Perseus Class 0 objects
(Bontemps et al. 1996 - hereafter BATC96), could be tested if direct
observational constraints on the infall velocity field of these
sources are obtained: large infall velocities are indeed expected.
envelopes observed toward L1157-MM and the
Class 0 objects of Perseus. The most likely explanation in the latter
cases is that the collapse started from non-singular initial
conditions, resulting in a nonequilibrium density configuration
similar to the Larson-Penston flow near point mass formation (see
Sect. 5.1.1 above). Such a conclusion, which is consistent with the
large accretion/ejection rates inferred for Perseus Class 0 objects
(Bontemps et al. 1996 - hereafter BATC96), could be tested if direct
observational constraints on the infall velocity field of these
sources are obtained: large infall velocities are indeed expected.
In contrast to isothermal models, the logotropic model of McLaughlin
& Pudritz (1997) accounts only marginally for our Taurus results: the
radial density structure we observe (
![]() )
is somewhat
steeper than the predictions (i.e., p=0.5-1.5). The disagreement is
most serious for the Taurus YSOs with the most massive envelopes,
namely the young Class 0 objects IRAM 04191, K04166, and L1527, which
have
)
is somewhat
steeper than the predictions (i.e., p=0.5-1.5). The disagreement is
most serious for the Taurus YSOs with the most massive envelopes,
namely the young Class 0 objects IRAM 04191, K04166, and L1527, which
have
![]() ,
while p=0.5-1 is expected at
,
while p=0.5-1 is expected at
![]() yr in this model. Moreover, the envelope mass predicted by the
nominal critical model of McLaughlin & Pudritz during the collapse
[
yr in this model. Moreover, the envelope mass predicted by the
nominal critical model of McLaughlin & Pudritz during the collapse
[
![]() at most] is significantly lower
than that implied by our observations in both Taurus and isolated
globules. The case of B335 is discussed by McLaughlin & Pudritz
(1997) who conclude that this object may correspond to a
at most] is significantly lower
than that implied by our observations in both Taurus and isolated
globules. The case of B335 is discussed by McLaughlin & Pudritz
(1997) who conclude that this object may correspond to a
![]() collapsing logotrope at the end of its accretion phase. However, our
measurements of the envelope mass [
collapsing logotrope at the end of its accretion phase. However, our
measurements of the envelope mass [
![]() ]
]![]() and power-law density index [
and power-law density index [
![]() ]
are
not consistent with such a model which predicts
]
are
not consistent with such a model which predicts
![]() and p=1.5.
and p=1.5.
Furthermore, none of the low-mass pre-stellar cores studied in detail up to now has a density structure consistent with a pressure-truncated logotrope (Bacmann et al. 2000).
Our
![]() -
-
![]() diagram for the embedded YSOs of Taurus is
displayed in Figs. 5a,b, along with two sets of
evolutionary tracks. The values of
diagram for the embedded YSOs of Taurus is
displayed in Figs. 5a,b, along with two sets of
evolutionary tracks. The values of
![]() (from Sect. 3.2) and
(from Sect. 3.2) and
![]() (from the literature) used in this diagram can be found in
Tables 1 and 2, respectively. Rather
than the total masses detected in the maps, we have preferred to use
our estimates of the inner envelope mass,
(from the literature) used in this diagram can be found in
Tables 1 and 2, respectively. Rather
than the total masses detected in the maps, we have preferred to use
our estimates of the inner envelope mass,
![]() (see Sect. 3.2).
Our maps suggest that the envelopes of bona-fide protostars in Taurus
have a power-law density structure up to a fairly large radius,
(see Sect. 3.2).
Our maps suggest that the envelopes of bona-fide protostars in Taurus
have a power-law density structure up to a fairly large radius,
![]() -
-![]() AU (cf. Col. 7 of Table 4). But the
total mass measured within
AU (cf. Col. 7 of Table 4). But the
total mass measured within
![]() ,
which has a median value
,
which has a median value
![]() ,
is unlikely to be entirely
accreted by the central object. As pointed out by, e.g., Ladd et al. (1998), the outflow will probably disperse a significant
fraction of this mass. Our map of the L1527 envelope, which shows
some evidence for a bipolar cavity oriented along the outflow axis
(Fig. 1l), is consistent with this view. As the star
formation efficiency in a single isolated core is expected to be
,
is unlikely to be entirely
accreted by the central object. As pointed out by, e.g., Ladd et al. (1998), the outflow will probably disperse a significant
fraction of this mass. Our map of the L1527 envelope, which shows
some evidence for a bipolar cavity oriented along the outflow axis
(Fig. 1l), is consistent with this view. As the star
formation efficiency in a single isolated core is expected to be ![]() 30% on theoretical grounds (Matzner & Mckee 2000), we believe that
the initial core mass within
30% on theoretical grounds (Matzner & Mckee 2000), we believe that
the initial core mass within
![]() AU should provide a better
indicator of the final stellar mass than the total core mass.
AU should provide a better
indicator of the final stellar mass than the total core mass.
The first set of evolutionary tracks, shown in Fig. 5a,
corresponds to the predictions of the standard protostellar model
(e.g. Adams et al. 1987) and assumes that
![]() ,
with
,
with
![]() (i.e.,
(i.e.,
![]() )
and
)
and
![]() .
.
The second set of evolutionary tracks (Fig. 5b) shows
the predictions of the accretion scenario advocated by BATC96 and
AWB2000, in which protostars form from dense cores with finite
initial masses, M0, and both the envelope mass and the accretion
rate are assumed to decline exponentially with time according to
![]() ,
where
,
where
![]() yr is a characteristic time. Such a decline of
yr is a characteristic time. Such a decline of
![]() is consistent with the decrease of outflow power observed from
Class 0 to Class I protostars (BATC96), and is theoretically expected
in the case of non-singular collapse initial conditions (e.g. Foster
& Chevalier 1993; HAB97). The tracks of Fig. 5b
further assume that the observed bolometric luminosities result from a
combination of accretion and stellar contributions:
is consistent with the decrease of outflow power observed from
Class 0 to Class I protostars (BATC96), and is theoretically expected
in the case of non-singular collapse initial conditions (e.g. Foster
& Chevalier 1993; HAB97). The tracks of Fig. 5b
further assume that the observed bolometric luminosities result from a
combination of accretion and stellar contributions:
![]() ,
where
,
where
![]() is the stellar radius and
is the stellar radius and
![]() the
stellar luminosity on the birthline for PMS stars
the
stellar luminosity on the birthline for PMS stars![]() (Stahler 1988).
(Stahler 1988).
It can be seen that the "standard'' tracks based on the self-similar
theory of Shu et al. (1987) account relatively well for the locations
of the bona-fide protostars of Taurus in the
![]() -
-
![]() diagram
(see Fig. 5a). Furthermore, there is a good continuity
between Class 0 and (bona-fide) Class I objects: In regions of
isolated star formation, Class 0 objects (open circles in
Fig. 5a) may merely correspond to extreme versions of
bona-fide Class I sources (filled circles). A similar conclusion was
reached by HAB97 based on a discussion of the outflow properties (see
Fig. 10 of HAB97). In this respect, it is noteworthy that more than
half of the bona-fide Class I sources of Fig. 5 lie above the solid straight lines marking the border zone between
diagram
(see Fig. 5a). Furthermore, there is a good continuity
between Class 0 and (bona-fide) Class I objects: In regions of
isolated star formation, Class 0 objects (open circles in
Fig. 5a) may merely correspond to extreme versions of
bona-fide Class I sources (filled circles). A similar conclusion was
reached by HAB97 based on a discussion of the outflow properties (see
Fig. 10 of HAB97). In this respect, it is noteworthy that more than
half of the bona-fide Class I sources of Fig. 5 lie above the solid straight lines marking the border zone between
![]() and
and
![]() in the diagram: They match the
conceptual definition of the Class 0 stage given by AWB93 (see above).
Our observations are thus consistent with the idea that all of
the bona-fide Class 0 and Class I objects of Fig. 5 are
in the main accretion phase of YSO evolution.
in the diagram: They match the
conceptual definition of the Class 0 stage given by AWB93 (see above).
Our observations are thus consistent with the idea that all of
the bona-fide Class 0 and Class I objects of Fig. 5 are
in the main accretion phase of YSO evolution.
Despite this reasonably good agreement, two problems should be pointed
out. First, as noticed by Kenyon et al. (1993a, hereafter KCH93) and
summarized by Hartmann (1998), the accretion luminosities predicted by
the standard model tend to be larger than the observed bolometric
luminosities by up to an order of magnitude: the luminosity predicted
at a typical collapse age of ![]() 2 105 yr is
2 105 yr is
![]() ,
while the median Class I/0 luminosity in our sample is
,
while the median Class I/0 luminosity in our sample is
![]() .
This discrepancy is quite severe
even though it can be reduced by a factor of
.
This discrepancy is quite severe
even though it can be reduced by a factor of
![]() if
non-spherical accretion effects and wind driving are properly taken
into account (cf. Shu et al. 1996). The solution proposed by
KCH93 is that envelope material does not fall directly onto the
central star but piles up in a disk whose radius is substantially
larger than the stellar radius, thereby reducing the infall
luminosity. It remains to be seen, however, whether short episodes of
high disk accretion ("FU Ori'' outbursts) can be made frequent enough
to maintain
if
non-spherical accretion effects and wind driving are properly taken
into account (cf. Shu et al. 1996). The solution proposed by
KCH93 is that envelope material does not fall directly onto the
central star but piles up in a disk whose radius is substantially
larger than the stellar radius, thereby reducing the infall
luminosity. It remains to be seen, however, whether short episodes of
high disk accretion ("FU Ori'' outbursts) can be made frequent enough
to maintain
![]() throughout the embedded
phase, as measured by millimeter interferometers (e.g. Terebey et al. 1993; Looney et al. 2000).
throughout the embedded
phase, as measured by millimeter interferometers (e.g. Terebey et al. 1993; Looney et al. 2000).
A second problem with the evolutionary tracks of the standard model is
that they do not account for the properties of the peculiar Class I
sources identified here (open star markers in Fig. 5a).
In spite of their Class I infrared SEDs (Adams et al. 1987; KCH93) and
low bolometric temperatures (
![]() K according to
Chen et al. 1995), these objects cannot be interpreted as
accreting protostars in the framework of the inside-out collapse
model. Possible interpretations are given in Sect. 5.2.3 below.
K according to
Chen et al. 1995), these objects cannot be interpreted as
accreting protostars in the framework of the inside-out collapse
model. Possible interpretations are given in Sect. 5.2.3 below.
The tracks assuming an exponential decrease in the rate of envelope dissipation with time (Fig. 5b) explain the luminosities of the bona-fide Class 0/I protostars better than do the standard tracks (see also HAB97 and Myers et al. 1998), and account even marginally for the locations of the peculiar Class I sources.
Although obviously idealized, this time-dependent accretion scenario
hints that the peculiar Class I sources may correspond to low-mass
objects at the very end of the protostellar accretion phase. In this
view, they would be the descendants of the lowest mass bona-fide
protostars of Fig. 5. Physically, an exponential
termination of the accretion phase may result from the finite mass
reservoir available in the initial pre-collapse core. Indeed, our
1.3 mm continuum maps suggest that, even in Taurus, the initial core
is bounded with
![]() AU (see, e.g.,
Fig. 3f). When the collapse expansion wave reaches
AU (see, e.g.,
Fig. 3f). When the collapse expansion wave reaches
![]() (which occurs at
(which occurs at
![]() yr in
the standard picture), the circumstellar evolution is likely to change
drastically in character: the central YSO should enter a phase of
residual accretion and its remnant envelope may be quickly dispersed
by the outflow. The peculiar Class I sources may be representative of
this late accretion phase.
yr in
the standard picture), the circumstellar evolution is likely to change
drastically in character: the central YSO should enter a phase of
residual accretion and its remnant envelope may be quickly dispersed
by the outflow. The peculiar Class I sources may be representative of
this late accretion phase.
For direct comparison with Fig. 5, we show in
Fig. 6 the
![]() -
-
![]() diagram constructed for
the self-embedded YSOs of
diagram constructed for
the self-embedded YSOs of ![]() Ophiuchi using data from AM94, MAN98,
and Wilking et al. (1989). Since the protostars of
Ophiuchi using data from AM94, MAN98,
and Wilking et al. (1989). Since the protostars of
![]() Ophiuchi are surrounded by compact, finite-sized envelopes
(cf. MAN98),
Ophiuchi are surrounded by compact, finite-sized envelopes
(cf. MAN98),
![]() is here simply taken to be the total mass
enclosed within a relatively well-defined envelope outer radius
(cf. AM94). The same evolutionary tracks as in Fig. 5
are superposed. In this case, a clear contrast between Class 0 and
Class I objects is apparent. The standard tracks, which would imply a
continuum of protostars rather than two separate classes, do not fit
the
is here simply taken to be the total mass
enclosed within a relatively well-defined envelope outer radius
(cf. AM94). The same evolutionary tracks as in Fig. 5
are superposed. In this case, a clear contrast between Class 0 and
Class I objects is apparent. The standard tracks, which would imply a
continuum of protostars rather than two separate classes, do not fit
the ![]() Oph diagram and cannot account for the observed Class I
sources with
Oph diagram and cannot account for the observed Class I
sources with
![]() and
and
![]() 1-2
1-2
![]() .
.
On the other hand, the time-dependent accretion tracks explain all of
the ![]() Oph objects reasonably well. It is also noteworthy that
the sources are on average more luminous (by a factor
Oph objects reasonably well. It is also noteworthy that
the sources are on average more luminous (by a factor ![]() 3-10)
in Ophiuchus than in Taurus (see also Chen et al. 1995). This,
coupled with the fact that the standard accretion scenario is
satisfactory in Taurus, supports the suggestion of HAB97 (see also
André 1997) that embedded YSOs follow different accretion histories
in
3-10)
in Ophiuchus than in Taurus (see also Chen et al. 1995). This,
coupled with the fact that the standard accretion scenario is
satisfactory in Taurus, supports the suggestion of HAB97 (see also
André 1997) that embedded YSOs follow different accretion histories
in ![]() Ophiuchi and in Taurus. This is presumably the result of a
marked difference in fragmentation lengthscale between the two clouds:
Ophiuchi and in Taurus. This is presumably the result of a
marked difference in fragmentation lengthscale between the two clouds:
![]() AU in
AU in ![]() Oph (cf. MAN98) versus
Oph (cf. MAN98) versus
![]() AU in Taurus (this paper).
AU in Taurus (this paper).
Comparing Fig. 5 with Fig. 6, and Fig. 1 with the ![]() Oph 1.3 mm maps of AM94 and
MAN98, we suggest that the circumstellar evolutionary state of the
peculiar Class I YSOs of Taurus may be similar to that of the typical
Class I sources of Ophiuchus: in both cases, only remnant, compact
envelopes are present.
Oph 1.3 mm maps of AM94 and
MAN98, we suggest that the circumstellar evolutionary state of the
peculiar Class I YSOs of Taurus may be similar to that of the typical
Class I sources of Ophiuchus: in both cases, only remnant, compact
envelopes are present.
![\begin{figure}
\par\includegraphics[angle=0,width=8.8cm,clip]{ms10015f6.eps}\end{figure}](/articles/aa/full/2001/03/aa10015/Timg483.gif) |
Figure 6:
Same as Fig. 5 for the embedded YSOs of the |
On the other hand, the near-infrared spectra observed by Greene &
Lada (1996) for L1489, M04295, M04489 and M04181+2655 differ from
those of T Tauri stars. If the near-IR spectroscopy scheme developped
by Greene & Lada (1996) is correct, M04295, M04489 and M04181+2655
should be intermediate objects between protostars and PMS stars and
L1489 should be surrounded by significant envelope material. We also
note that Z04260 is not strictly point-like in our 1.3 mm data (see
Fig. 11k). Furthermore, millimeter interferometric
mapping of L1489 (e.g. Hogerheijde et al.1997, 1998; Ohashi 1999)
reveals a ![]() 1000 AU rotating structure with possible infall
motions, which is apparently different from the more compact disks
typically observed in T Tauri stars (see, e.g., Dutrey et al. 1996).
1000 AU rotating structure with possible infall
motions, which is apparently different from the more compact disks
typically observed in T Tauri stars (see, e.g., Dutrey et al. 1996).
Several peculiar Class I sources may thus be highly reddened PMS stars while others could be objects in transition between protostars and T Tauri stars. These sources illustrate that the interpretation of YSO SEDs is non unique and that mapping information, preferably at several wavelengths, is crucial to get at a proper physical picture (see also Miroshnichenko et al. 1999).
As mentioned in Sect. 3, our 1.3 mm maps reveal the presence of at
least seven new dense cores/condensations in the vicinity of the
targeted YSOs (see Table 3). Since these cold cores do
not coincide with IRAS point sources, they are good candidates for
being at either the pre-stellar stage or the Class 0 protostellar
stage of evolution (cf. AWB2000). One of these objects, IRAM 04191,
has been studied in more detail (AMB99) and corresponds to the first
clear-cut example of a Class 0 protostar in Taurus: It has a large
envelope mass (
![]() ), very low bolometric
luminosity and bolometric temperature (
), very low bolometric
luminosity and bolometric temperature (
![]() ,
,
![]() K), and features a jet-like CO outflow as well as
extended infall motions. Some of the cores of Table 3
may also be associated with very young accreting protostars. On the
other hand, the fact that five of these sources have flat inner
intensity profiles (see Sect. 4.1 and Fig. 3h) suggests
that they rather correspond to pre-stellar dense cores similar to
those discussed by Ward-Thompson et al. (1994, 1999). Follow-up
observations are required to assess their nature more firmly. In any
event, the serendipitous discovery of these cold objects in the course
of a pointed 1.3 mm mapping study of IRAS YSOs clearly emphasizes the
need for deep, unbiased surveys of molecular clouds in the
submillimeter band. Such surveys should soon become possible with,
e.g., the Far InfraRed and Submillimeter Telescope (FIRST) of ESA.
K), and features a jet-like CO outflow as well as
extended infall motions. Some of the cores of Table 3
may also be associated with very young accreting protostars. On the
other hand, the fact that five of these sources have flat inner
intensity profiles (see Sect. 4.1 and Fig. 3h) suggests
that they rather correspond to pre-stellar dense cores similar to
those discussed by Ward-Thompson et al. (1994, 1999). Follow-up
observations are required to assess their nature more firmly. In any
event, the serendipitous discovery of these cold objects in the course
of a pointed 1.3 mm mapping study of IRAS YSOs clearly emphasizes the
need for deep, unbiased surveys of molecular clouds in the
submillimeter band. Such surveys should soon become possible with,
e.g., the Far InfraRed and Submillimeter Telescope (FIRST) of ESA.
Copyright ESO 2001