 |
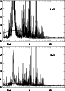
Figure 2:
Collision strength for
3s23p5 2P
|
Figures 2 to 4 show some illustrative plots of the calculated collision strength at low scattering energies. All these transitions are affected by resonances in the first 2 or 3 Rydbergs above threshold: these resonances arise primarily from the 3s23p43d states, with resonances arising from the 3s3p53d and higher states having negligible effect on transitions from the ground state (Figs. 2, 3). However, Fig. 4 show significant resonance structure up to 6 Ryd above threshold for excitation out of the 3s3p6 initial state, and this justifies the inclusion of the 3s3p53d and higher levels in the 180-level BPRM calculation in order to obtain accurate data for these transitions.
 |
Figure 2:
Collision strength for
3s23p5 2P
|
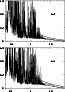 |
Figure 3:
Collision strength for
3s23p5 2P
|
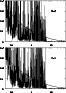 |
Figure 4:
Collision strength for
3s3p6 2S
|
Collision strengths are computed for the required fine-structure
transitions over a sufficiently wide and fine energy mesh
in order to be able to
integrate over a Maxwellian distribution to obtain the
effective collision strength ![]() ,
from which the excitation and de-excitation rate coefficients
can easily be obtained (Hummer et al. 1993).
Our energy mesh was determined by increasing the number of
points until the integration converged:
resulting in an energy spacing of 0.001-0.002 Ryd
in the resonance regions,
a total of 7460 energy points.
The range of temperatures chosen was
,
from which the excitation and de-excitation rate coefficients
can easily be obtained (Hummer et al. 1993).
Our energy mesh was determined by increasing the number of
points until the integration converged:
resulting in an energy spacing of 0.001-0.002 Ryd
in the resonance regions,
a total of 7460 energy points.
The range of temperatures chosen was
![]() 0.8 dex of the temperature
of maximum ionic abundance given by Shull & Van Steenberg (1982),
and our final results are tabulated in Table 6.
0.8 dex of the temperature
of maximum ionic abundance given by Shull & Van Steenberg (1982),
and our final results are tabulated in Table 6.
| i | BD | Present | i | BD | Present |
| 1 | 7.23E-01 | 6.19E-01 | 17 | 1.16E-08 | 1.31E-08 |
| 2 | 1.36E-01 | 1.73E-01 | 18 | 1.97E-02 | 1.55E-02 |
| 3 | 1.86E-09 | 1.39E-09 | 19 | 5.36E-09 | 1.31E-08 |
| 4 | 1.46E-06 | 3.70E-07 | 20 | 1.31E-02 | 1.28E-02 |
| 5 | 2.92E-02 | 4.10E-02 | 21 | 1.33E-02 | 1.05E-02 |
| 6 | 1.03E-07 | 1.19E-07 | 22 | 5.67E-08 | 4.48E-08 |
| 7 | 2.30E-08 | 4.43E-08 | 23 | 1.02E-08 | 6.11E-09 |
| 8 | 4.24E-02 | 8.68E-02 | 24 | 4.81E-03 | 3.88E-03 |
| 9 | 1.14E-09 | 1.66E-09 | 25 | 5.37E-10 | 5.73E-10 |
| 10 | 1.86E-02 | 3.69E-02 | 26 | 3.81E-08 | 7.29E-09 |
| 11 | 4.11E-08 | 3.09E-08 | 27 | 8.40E-11 | 7.83E-11 |
| 12 | 2.18E-08 | 1.90E-09 | 28 | 1.65E-10 | 3.25E-12 |
| 13 | 1.72E-09 | 6.33E-09 | 29 | 3.88E-11 | 4.92E-11 |
| 14 | 1.11E-09 | 1.85E-09 | 30 | 2.23E-10 | 2.08E-10 |
| 15 | 2.30E-09 | 2.16E-09 | 31 | 6.26E-11 | 7.48E-11 |
| 16 | 7.91E-09 | 3.32E-08 |
Our effective collision strengths ![]() are also plotted in Figs. 2-4
as a function of kT Rydbergs,
alongside the collision strength
are also plotted in Figs. 2-4
as a function of kT Rydbergs,
alongside the collision strength ![]() :
the figures illustrate that the enhancement of
:
the figures illustrate that the enhancement of
![]() due to low-energy resonances extends
to surprisingly large temperatures (
due to low-energy resonances extends
to surprisingly large temperatures (
![]() K).
Typical enhancements are factors of two or three for transitions from
the ground state (Figs. 2-3) and up to an order of magnitude
for the optically forbidden transitions
out of the excited 3s3p6 level (Fig. 4).
K).
Typical enhancements are factors of two or three for transitions from
the ground state (Figs. 2-3) and up to an order of magnitude
for the optically forbidden transitions
out of the excited 3s3p6 level (Fig. 4).
For comparison we also plot the DW ![]() from Bhatia & Doshek (1995)
and the early R-matrix calculation of
from Bhatia & Doshek (1995)
and the early R-matrix calculation of ![]() of Mohan et al. (1994),
showing that although our present results agree well with these
at higher energies
(see also Table 4), these other calculations
appear to underestimate or ignore the resonance contribution at low temperatures.
of Mohan et al. (1994),
showing that although our present results agree well with these
at higher energies
(see also Table 4), these other calculations
appear to underestimate or ignore the resonance contribution at low temperatures.
To see the effect of the resonance enhancement more clearly,
we recalculate in Table 5 the level populations given by
Bhatia & Doschek (1995) for electron density 1010 cm-3 and 106 K,
with no proton excitation or blackbody radiative excitation.
We use all our radiative and collisonal rates from Tables 2 and 6
(i.e. for transitions involving levels 1, 2 and 3),
and complete the dataset up to level 31 using Bhatia and Doschek's data:
the rate equations are then solved as in their Eq. (3) for the level populations.
Our resonance-enhanced ![]() for 1-2 (2P
3/2-1/2),
which we published in an earlier IP paper
(Pelan & Berrington 1995), gives some redistribution
of population between level 1 and 2.
But the total 2P ground population drops 7% when the
for 1-2 (2P
3/2-1/2),
which we published in an earlier IP paper
(Pelan & Berrington 1995), gives some redistribution
of population between level 1 and 2.
But the total 2P ground population drops 7% when the
![]() from the ground state to higher levels also includes resonances
as in the present work,
and the population of 4F9/2 and 4F7/2
(levels 8 and 10 in Table 5) doubles.
from the ground state to higher levels also includes resonances
as in the present work,
and the population of 4F9/2 and 4F7/2
(levels 8 and 10 in Table 5) doubles.
| i-i' | 5.4 | 5.6 | 5.8 | 6.0 | 6.2 | 6.4 | 6.6 | 6.8 | 7.0 |
| 1-2 | 2.97 | 2.69 | 2.27 | 1.79 | 1.35 | 0.99 | 0.73 | 0.54 | 0.40 |
| 1-3 | 0.7939 | 0.6812 | 0.5868 | 0.5133 | 0.4602 | 0.4241 | 0.4008 | 0.3867 | 0.3792 |
| 1-4 | 0.1742 | 0.1496 | 0.1262 | 0.1045 | 0.0849 | 0.0674 | 0.0522 | 0.0394 | 0.0291 |
| 1-5 | 0.2389 | 0.2063 | 0.1755 | 0.1468 | 0.1203 | 0.0963 | 0.0749 | 0.0566 | 0.0415 |
| 1-6 | 0.0993 | 0.0856 | 0.0722 | 0.0597 | 0.0484 | 0.0384 | 0.0298 | 0.0226 | 0.0168 |
| 1-7 | 0.0418 | 0.0360 | 0.0304 | 0.0250 | 0.0201 | 0.0158 | 0.0121 | 0.0091 | 0.0067 |
| 1-8 | 0.1702 | 0.1480 | 0.1252 | 0.1036 | 0.0839 | 0.0664 | 0.0514 | 0.0390 | 0.0291 |
| 1-9 | 0.0715 | 0.0625 | 0.0523 | 0.0428 | 0.0349 | 0.0284 | 0.0232 | 0.0189 | 0.0154 |
| 1-10 | 0.1281 | 0.1097 | 0.0913 | 0.0744 | 0.0595 | 0.0469 | 0.0368 | 0.0291 | 0.0234 |
| 1-11 | 0.0846 | 0.0722 | 0.0599 | 0.0488 | 0.0391 | 0.0308 | 0.0239 | 0.0184 | 0.0141 |
| 1-12 | 0.1132 | 0.1001 | 0.0863 | 0.0729 | 0.0606 | 0.0500 | 0.0411 | 0.0340 | 0.0286 |
| 1-13 | 0.0697 | 0.0603 | 0.0507 | 0.0419 | 0.0338 | 0.0264 | 0.0199 | 0.0146 | 0.0105 |
| 1-14 | 0.0944 | 0.0814 | 0.0682 | 0.0573 | 0.0480 | 0.0392 | 0.0311 | 0.0241 | 0.0185 |
| 1-15 | 0.0792 | 0.0729 | 0.0661 | 0.0574 | 0.0476 | 0.0380 | 0.0295 | 0.0225 | 0.0169 |
| 1-16 | 0.0543 | 0.0469 | 0.0394 | 0.0329 | 0.0283 | 0.0255 | 0.0240 | 0.0232 | 0.0228 |
| 1-17 | 0.1343 | 0.1209 | 0.1065 | 0.0930 | 0.0816 | 0.0726 | 0.0659 | 0.0611 | 0.0580 |
| 1-18 | 0.1351 | 0.1206 | 0.1054 | 0.0907 | 0.0785 | 0.0699 | 0.0648 | 0.0625 | 0.0621 |
| 1-19 | 0.1619 | 0.1375 | 0.1140 | 0.0953 | 0.0820 | 0.0732 | 0.0676 | 0.0644 | 0.0629 |
| 1-20 | 0.1627 | 0.1438 | 0.1257 | 0.1100 | 0.0974 | 0.0882 | 0.0823 | 0.0793 | 0.0787 |
| 1-21 | 0.1177 | 0.0995 | 0.0815 | 0.0650 | 0.0507 | 0.0387 | 0.0289 | 0.0211 | 0.0150 |
| 1-22 | 0.1101 | 0.0933 | 0.0768 | 0.0622 | 0.0500 | 0.0403 | 0.0330 | 0.0277 | 0.0241 |
| 1-23 | 0.1045 | 0.0891 | 0.0758 | 0.0648 | 0.0560 | 0.0493 | 0.0447 | 0.0420 | 0.0409 |
| 1-24 | 0.1288 | 0.1096 | 0.0943 | 0.0822 | 0.0728 | 0.0661 | 0.0622 | 0.0608 | 0.0614 |
| 1-25 | 0.0580 | 0.0530 | 0.0489 | 0.0453 | 0.0425 | 0.0406 | 0.0394 | 0.0388 | 0.0386 |
| 1-26 | 0.0594 | 0.0526 | 0.0473 | 0.0435 | 0.0416 | 0.0415 | 0.0424 | 0.0437 | 0.0450 |
| 1-27 | 1.908 | 1.917 | 1.925 | 1.933 | 1.939 | 1.943 | 1.950 | 1.963 | 1.982 |
| 1-28 | 3.856 | 3.870 | 3.898 | 3.934 | 3.966 | 3.992 | 4.018 | 4.053 | 4.101 |
| 1-29 | 0.4783 | 0.4762 | 0.4802 | 0.4924 | 0.5122 | 0.5362 | 0.5608 | 0.5839 | 0.6047 |
| 1-30 | 6.805 | 6.883 | 6.963 | 7.032 | 7.083 | 7.124 | 7.171 | 7.236 | 7.323 |
| 1-31 | 0.2161 | 0.2216 | 0.2240 | 0.2274 | 0.2363 | 0.2512 | 0.2690 | 0.2863 | 0.3018 |
| 2-3 | 0.3508 | 0.3111 | 0.2762 | 0.2481 | 0.2274 | 0.2131 | 0.2039 | 0.1985 | 0.1958 |
| 2-4 | 0.0596 | 0.0504 | 0.0418 | 0.0342 | 0.0274 | 0.0216 | 0.0166 | 0.0125 | 0.0092 |
| 2-5 | 0.0539 | 0.0444 | 0.0358 | 0.0284 | 0.0222 | 0.0170 | 0.0127 | 0.0093 | 0.0067 |
| 2-6 | 0.0532 | 0.0460 | 0.0389 | 0.0324 | 0.0264 | 0.0210 | 0.0163 | 0.0122 | 0.0090 |
| 2-7 | 0.0321 | 0.0283 | 0.0244 | 0.0206 | 0.0170 | 0.0137 | 0.0108 | 0.0082 | 0.0061 |
| 2-8 | 0.0292 | 0.0240 | 0.0192 | 0.0151 | 0.0116 | 0.0088 | 0.0066 | 0.0048 | 0.0034 |
| 2-9 | 0.0312 | 0.0282 | 0.0249 | 0.0216 | 0.0183 | 0.0150 | 0.0118 | 0.0090 | 0.0067 |
| 2-10 | 0.0498 | 0.0424 | 0.0352 | 0.0286 | 0.0227 | 0.0177 | 0.0136 | 0.0105 | 0.0082 |
| 2-11 | 0.0539 | 0.0461 | 0.0385 | 0.0314 | 0.0251 | 0.0196 | 0.0151 | 0.0114 | 0.0085 |
| 2-12 | 0.0787 | 0.0692 | 0.0588 | 0.0484 | 0.0386 | 0.0299 | 0.0226 | 0.0169 | 0.0127 |
| 2-13 | 0.0468 | 0.0399 | 0.0329 | 0.0271 | 0.0228 | 0.0200 | 0.0184 | 0.0173 | 0.0166 |
| 2-14 | 0.0360 | 0.0313 | 0.0262 | 0.0216 | 0.0175 | 0.0138 | 0.0106 | 0.0079 | 0.0057 |
| 2-15 | 0.0308 | 0.0270 | 0.0232 | 0.0194 | 0.0156 | 0.0122 | 0.0093 | 0.0070 | 0.0051 |
| 2-16 | 0.0516 | 0.0453 | 0.0386 | 0.0327 | 0.0285 | 0.0258 | 0.0240 | 0.0227 | 0.0216 |
| i-i' | 5.4 | 5.6 | 5.8 | 6.0 | 6.2 | 6.4 | 6.6 | 6.8 | 7.0 |
| 2-17 | 0.0471 | 0.0399 | 0.0329 | 0.0266 | 0.0212 | 0.0166 | 0.0128 | 0.0096 | 0.0070 |
| 2-18 | 0.0866 | 0.0710 | 0.0568 | 0.0452 | 0.0357 | 0.0275 | 0.0205 | 0.0149 | 0.0106 |
| 2-19 | 0.0757 | 0.0677 | 0.0592 | 0.0503 | 0.0424 | 0.0362 | 0.0317 | 0.0284 | 0.0260 |
| 2-20 | 0.0924 | 0.0798 | 0.0677 | 0.0563 | 0.0458 | 0.0364 | 0.0281 | 0.0211 | 0.0154 |
| 2-21 | 0.1118 | 0.0979 | 0.0852 | 0.0745 | 0.0661 | 0.0600 | 0.0561 | 0.0542 | 0.0539 |
| 2-22 | 0.0845 | 0.0726 | 0.0608 | 0.0501 | 0.0411 | 0.0339 | 0.0285 | 0.0247 | 0.0222 |
| 2-23 | 0.0642 | 0.0544 | 0.0458 | 0.0392 | 0.0348 | 0.0328 | 0.0325 | 0.0334 | 0.0352 |
| 2-24 | 0.0611 | 0.0532 | 0.0467 | 0.0414 | 0.0370 | 0.0337 | 0.0316 | 0.0308 | 0.0309 |
| 2-25 | 0.0381 | 0.0343 | 0.0304 | 0.0261 | 0.0215 | 0.0168 | 0.0125 | 0.0090 | 0.0062 |
| 2-26 | 0.0447 | 0.0399 | 0.0356 | 0.0316 | 0.0276 | 0.0238 | 0.0207 | 0.0183 | 0.0167 |
| 2-27 | 0.6641 | 0.6596 | 0.6610 | 0.6714 | 0.6911 | 0.7169 | 0.7446 | 0.7714 | 0.7961 |
| 2-28 | 0.1400 | 0.1386 | 0.1371 | 0.1393 | 0.1488 | 0.1646 | 0.1828 | 0.1999 | 0.2147 |
| 2-29 | 1.520 | 1.530 | 1.540 | 1.548 | 1.551 | 1.550 | 1.549 | 1.553 | 1.564 |
| 2-30 | 0.0292 | 0.0267 | 0.0242 | 0.0219 | 0.0197 | 0.0178 | 0.0162 | 0.0150 | 0.0142 |
| 2-31 | 4.289 | 4.335 | 4.386 | 4.431 | 4.462 | 4.481 | 4.500 | 4.533 | 4.583 |
| 3-4 | 0.0732 | 0.0606 | 0.0474 | 0.0351 | 0.0250 | 0.0173 | 0.0118 | 0.0079 | 0.0053 |
| 3-5 | 0.0749 | 0.0621 | 0.0486 | 0.0361 | 0.0259 | 0.0180 | 0.0123 | 0.0083 | 0.0055 |
| 3-6 | 0.0572 | 0.0480 | 0.0380 | 0.0285 | 0.0204 | 0.0142 | 0.0096 | 0.0064 | 0.0043 |
| 3-7 | 0.0337 | 0.0296 | 0.0244 | 0.0188 | 0.0137 | 0.0095 | 0.0065 | 0.0043 | 0.0028 |
| 3-8 | 0.0452 | 0.0356 | 0.0268 | 0.0193 | 0.0134 | 0.0090 | 0.0060 | 0.0039 | 0.0025 |
| 3-9 | 0.1418 | 0.1254 | 0.1036 | 0.0795 | 0.0575 | 0.0397 | 0.0266 | 0.0175 | 0.0113 |
| 3-10 | 0.0435 | 0.0347 | 0.0263 | 0.0189 | 0.0131 | 0.0088 | 0.0058 | 0.0038 | 0.0025 |
| 3-11 | 0.0400 | 0.0320 | 0.0243 | 0.0176 | 0.0123 | 0.0084 | 0.0057 | 0.0038 | 0.0026 |
| 3-12 | 0.1864 | 0.1659 | 0.1386 | 0.1074 | 0.0783 | 0.0545 | 0.0368 | 0.0245 | 0.0161 |
| 3-13 | 0.0519 | 0.0426 | 0.0332 | 0.0245 | 0.0174 | 0.0119 | 0.0080 | 0.0053 | 0.0034 |
| 3-14 | 0.0768 | 0.0657 | 0.0523 | 0.0395 | 0.0287 | 0.0203 | 0.0141 | 0.0098 | 0.0068 |
| 3-15 | 0.0655 | 0.0568 | 0.0471 | 0.0367 | 0.0270 | 0.0191 | 0.0132 | 0.0091 | 0.0063 |
| 3-16 | 0.0578 | 0.0521 | 0.0435 | 0.0338 | 0.0250 | 0.0181 | 0.0132 | 0.0099 | 0.0077 |
| 3-17 | 0.0858 | 0.0739 | 0.0599 | 0.0463 | 0.0347 | 0.0257 | 0.0193 | 0.0148 | 0.0118 |
| 3-18 | 0.0880 | 0.0722 | 0.0561 | 0.0417 | 0.0299 | 0.0209 | 0.0143 | 0.0097 | 0.0065 |
| 3-19 | 0.0956 | 0.0817 | 0.0659 | 0.0506 | 0.0383 | 0.0296 | 0.0240 | 0.0206 | 0.0186 |
| 3-20 | 0.0776 | 0.0654 | 0.0523 | 0.0398 | 0.0292 | 0.0209 | 0.0147 | 0.0103 | 0.0073 |
| 3-21 | 0.0742 | 0.0599 | 0.0463 | 0.0343 | 0.0245 | 0.0171 | 0.0117 | 0.0080 | 0.0055 |
| 3-22 | 0.0670 | 0.0558 | 0.0437 | 0.0322 | 0.0227 | 0.0154 | 0.0103 | 0.0067 | 0.0044 |
| 3-23 | 0.0485 | 0.0409 | 0.0325 | 0.0245 | 0.0177 | 0.0123 | 0.0084 | 0.0056 | 0.0037 |
| 3-24 | 0.0481 | 0.0401 | 0.0328 | 0.0259 | 0.0196 | 0.0142 | 0.0099 | 0.0067 | 0.0045 |
| 3-25 | 0.0415 | 0.0376 | 0.0328 | 0.0282 | 0.0241 | 0.0208 | 0.0184 | 0.0166 | 0.0154 |
| 3-26 | 0.0521 | 0.0470 | 0.0419 | 0.0372 | 0.0331 | 0.0298 | 0.0273 | 0.0256 | 0.0244 |
| 3-27 | 0.2772 | 0.2710 | 0.2328 | 0.1819 | 0.1331 | 0.0930 | 0.0632 | 0.0422 | 0.0280 |
| 3-28 | 0.1967 | 0.1746 | 0.1408 | 0.1057 | 0.0754 | 0.0520 | 0.0351 | 0.0234 | 0.0154 |
| 3-29 | 0.1179 | 0.1042 | 0.0839 | 0.0629 | 0.0449 | 0.0309 | 0.0208 | 0.0138 | 0.0091 |
| 3-30 | 0.1712 | 0.1370 | 0.1046 | 0.0772 | 0.0558 | 0.0398 | 0.0283 | 0.0203 | 0.0146 |
| 3-31 | 0.1199 | 0.0960 | 0.0736 | 0.0545 | 0.0396 | 0.0285 | 0.0205 | 0.0149 | 0.0110 |
Thus, we conclude that it is not safe to calculate rates from earlier tabulations of the collision strength without taking into account resonance enhancement. We believe that, by including resonance structure associated with 180 levels, we have included the most significant resonance effects on transitions to the 31 lowest levels.
Acknowledgements
This work was done with the support of a PPARC grant GR/K97608. We would like to thank Drs. P. Young and H. Mason for providing the level populations code.
© ESO 2001