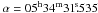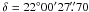| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A11 | |
| Number of page(s) | 6 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201016301 | |
| Published online | 17 February 2011 | |
A sensitive upper limit to the circular polarization of the Crab nebula at λ3 mm
1
Institut de Radioastronomie Millimétrique
300 rue de la Piscine, 38406
Saint Martin d’Hères
France
e-mail: hwiese@mpifr.de
2
Institut d’Astrophysique Spatiale, Centre Universitaire d’Orsay,
Bât. 121,
91405
Orsay Cedex,
France
3
Astroparticule et Cosmologie, Université Paris-Diderot,
Bâtiment Condorcet, 10 rue Alice
Domon et Léonie Duquet, 75205
Paris Cedex 13,
France
Received:
13
December
2010
Accepted:
29
December
2010
A new observation of the distribution of the circular polarization over the Crab Nebula supernova remnant yields an upper limit of <0.2% at a radio frequency of 89.2 GHz. This limit is set by the uncertainty in correcting for the instrumental polarization. The raw data were dominated by the conversion of the strong linear polarization to circular in the crosspolarized sidelobes of the 30 m telescope. They were modeled as due to a differential phase gradient between the orthogonally linearly polarized far-field radiation patterns of the two receivers. As the source is tracked these rotate with respect to the radio source distribution on the sky since the telescope has an alt-azimuth mount and a Nasmyth focus. This allows the model to be fit to the raw data and a correction can be made. Our limit of <0.2% is to be compared with <0.03% derived at 610 MHz (Wilson & Weiler 1997, ApJ, 475, 661) and <6% measured at 23 GHz (Wright & Forster 1980, ApJ, 239, 873). These limits are consistent with the polarization expected from an optically thin synchrotron source with the known physical properties of the Crab Nebula. This non-detection does not allow an estimate to be made of the relative contribution to the radio emission from electrons and positrons.
Key words: ISM: supernova remnants / radiation mechanisms: non-thermal / polarization
© ESO, 2011
1. Introduction
The Crab nebula (with its radiosource Tau A) is a plerion-type supernova remnant, consisting of the following components (see Hester 2008, for a review):
-
1.
The pulsar that formed 955 years ago is the engine powering(with a remarkable efficiency, Kennel & Coroniti 1984) thesynchrotron emission from the nebula.
-
2.
The pulsar jet transfers this power from the pulsar to the synchrotron nebula, which is confined by the ejecta from the SN explosion. Near the center of the nebula a shock is formed where the jet is thermalized and ultra-relativistic particles are released into the surrounding nebula. The shock appears as features like the X-ray ring (Weisskopf et al. 2000) and the wisps (Scargle 1969) visible in optical and radio images (Bietenholz et al. 2004). There is also an X-ray torus, being magnetically confined as it pushes into the nebula: the magnetic field in the torus is traced by the wisps there (i.e., is toroidal), whereas the magnetic field in the synchrotron nebula has a more complex structure.
-
3.
The synchrotron nebula expands into the swept-up supernova ejecta where another shock forms and Rayleigh-Taylor instabilities lead to the formation of filaments, visible optically.
The work presented here aims at a detection of circular polarization at λ3 mm. Several previous observations at lower radio frequency have been reported. Wright & Foster (1980) reported an upper limit of 6% at 23 GHz, and Wilson & Weiler (1997) found an upper limit of 0.03% at 610 MHz. The small circular polarization (%) measured by Martin et al. (1972) in the optical waveband towards the synchrotron nebula is of interstellar origin, namely by dielectric dust particles.
Our measurements of the linear polarization in the synchrotron emission from Tau A and its position angle provide a polarization calibration standard for the high-frequency instrument of the Planck satellite and are published separately (Aumont et al. 2010). Here we present the circular polarization data, aquired at the same time.
2. Observations and data reduction
2.1. Observations
The observations were made with the correlation polarimeter XPOL at the IRAM 30m telescope, from 05 to 09 September 2007 and from 09 to 12 January 2009. The orthogonally polarized receivers were tuned to the frequency of the HCO+(J = 1–0) transition at 89.2 GHz, and made coherent by a common local oscillator reference (for details see Thum et al. 2008). Our polarimeter allows the measurement of four Stokes parameters simultaneously. The incoming beam from the subreflector is directed into two orthogonally linearly polarized beams, by a wire grid polarizer at 45°. There are two possible orientations of the wires of the grid, either parallel or perpendicular to the plane of incidence. Only in the latter case is the polarization of the reflected beam pure linear, with no crosspolarization. This optimum orientation was only used in 2007, and in consequence these observations suffer from fewer systematic errors than the 2009 data.
The images were taken in “on-the-fly” mode, scanning along pairwise orthogonal
directions. The half power beam size was 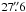 ,
and the frequency bandpass was 500 MHz wide. The 2009 maps extend to beyond the edge of
the synchrotron nebula, such that spatial baselines could be removed from the individual
subscans and separate measurements of an emission-free atmospheric reference were
unnecessary. In January 2009, the total observing time spent on Tau A was 13ḥ5, to produce
in total 40 maps with median system temperature 113 K, yielding an image size of
510′′ × 440′′. The resulting Stokes I image is shown in Fig. 1. The noise level σv (rms) in the corresponding
unprocessed Stokes V image is 4.8 mJy per beam.
,
and the frequency bandpass was 500 MHz wide. The 2009 maps extend to beyond the edge of
the synchrotron nebula, such that spatial baselines could be removed from the individual
subscans and separate measurements of an emission-free atmospheric reference were
unnecessary. In January 2009, the total observing time spent on Tau A was 13ḥ5, to produce
in total 40 maps with median system temperature 113 K, yielding an image size of
510′′ × 440′′. The resulting Stokes I image is shown in Fig. 1. The noise level σv (rms) in the corresponding
unprocessed Stokes V image is 4.8 mJy per beam.
In September 2007, smaller maps were taken, and the atmospheric emission was removed
using a dedicated reference measurement and destriping the Stokes I map with the
Plait algorithm (Emerson & Gräve 1988). The four final Stokes images were obtained by a weighted mean of the
individual images, each weighted by 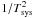 , i.e., the
inverse squared system temperature. Such weighting yields an optimum signal-to-noise ratio
in the resulting image. A sensitivity of σv = 3.6 mJy was
achieved, after 10ḥ1 observing time, taking 66 smaller (455′′ × 330′′) maps, at a median
system temperature of 123 K. Because total power fluctuations cancel out in cross
correlations, this sensitivity is an order of magnitude below that of the corresponding
Stokes I and Q images. More details on the observations and the raw data processing can be
found in Aumont et al. (2010).
, i.e., the
inverse squared system temperature. Such weighting yields an optimum signal-to-noise ratio
in the resulting image. A sensitivity of σv = 3.6 mJy was
achieved, after 10ḥ1 observing time, taking 66 smaller (455′′ × 330′′) maps, at a median
system temperature of 123 K. Because total power fluctuations cancel out in cross
correlations, this sensitivity is an order of magnitude below that of the corresponding
Stokes I and Q images. More details on the observations and the raw data processing can be
found in Aumont et al. (2010).
 |
Fig. 1 Stokes I image of Tau A (2009 data). Contours are at
0.2 × 2j − 1 Jy per beam, with
j = 1 to 10. Lowest contour: 200 mJy
(corresponding to 6σrms). Highest
contour: 4.5 Jy. The beam’s fwhm is indicated in the lower left
corner. The cross marks the Pulsar’s position. Map center:
|
2.2. Data reduction
2.2.1. Analysis of the instrumental polarization
Owing to the convolution of the intrinsic brightness distribution of the Stokes parameters with the telescope’s instrumental response, the Stokes V map, obtained after weighting and gridding the individual maps, is dominated by instrumental artefacts. This can be demonstrated by splitting the set of maps into two subsets whose position angles χ0 of the vertical direction in the Nasmyth reference frame, after projection onto the sky, are spaced by roughly 90°1. The two resulting Stokes V images clearly show different emission patterns, with a circularly polarized flux density ranging between − 58 and + 50 mJy for the first ensemble of maps, and between − 46 and + 35 mJy for the second one. This finding immediately shows that the dominant Stokes V signal in the λ3 mmcontinuum emission from Tau A is of instrumental origin: unlike Stokes Q and Stokes U, the Stokes I and V parameters are invariant under rotations of the coordinate system defining the orthogonal componentes of the E vector2. Therefore, the Stokes V maps are contaminated by a leakage from linear to circular polarization, while the invariant component is either due to an intrinsic circular polarization, or due to an instrumental generation of Stokes V from Stokes I. This requires crosspolarization in the far-field radiation patterns such as that produced by a non-optimum orientation of the polarizer (for details, see Thum et al. 2008, Appendix). In the case of the 2007 data this effect was negligible. Towards unpolarized sources Stokes V almost vanished ( ≤ 0.05%), unlike for the 2009 observations. Generating V from U on the other hand demands a differential phase. In the absence of cross-talk between receivers with orthogonal polarizations and housed in separate dewars (there is no cross talk down to − 40 dB, Thum et al. 2008), the major contribution to the instrumental Stokes V is expected to be from small errors in the calibration of the phase difference between the horizontally and vertically polarized signals (since absolute phases do not matter here, in the following phase means “differential phase”).
The differential phase can be separated into two components: a small one due to the limited accuracy inherent to our phase calibration scheme (rms better than 1°, Thum et al. 2008), and a systematic contribution owing to the fact that we measure the instrumental phase within the receiver cabin and therefore miss instrumental contributions arising between the phase calibration unit and the far-field. A measurement of the differential phase would only be possible with a celestial point source of strong and well known Stokes U and V continuum signals, which is not available. The data are therefore affected by a direction-dependent differential phase error in the far-field, probably owing to an asymmetric and different illumination of the subreflector by the orthogonally polarized horns, and therefore to a spurious conversion of Stokes U to Stokes V (Müller matrix element MUV).
Because correlation polarimetry with orthogonally polarized feed horns yields the
Stokes U and V parameters as the real and imaginary part, respectively, of the cross
correlation between the input signals, such a phase error affects Stokes V much more
than Stokes U, where it is a second order effect. This is so because the circular
polarization of virtually all polarized continuum sources on the sky is much weaker than
their linear polarization. This can be shown by the following analysis where
A denotes the amplitude of the complex cross correlation,
φ the intrinsic phase of the vertically polarized component of the
E vector of the incident wave with respect to the horizontally
polarized one and Δφ the phase error. U0,
V0 are the intrinsic Stokes U and V parameters of the
observed object, and Um and Vm
the measured ones, i.e., including a phase error describing the spurious conversion of
Stokes U to Stokes V. The coordinate system for the definition of both the intrinsic and
the observed Stokes parameters is fixed in the plane of the Nasmyth focus:
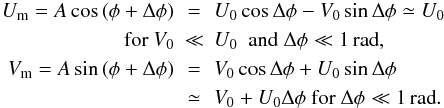 (1)The
result shows that Um is, to first order, not affected by
phase errors, and that the contamination of Stokes V by the phase error is additive. In
order to retrieve V0 from Vm, a
model of the distribution of the phase error across the far field beam pattern is thus
needed.
(1)The
result shows that Um is, to first order, not affected by
phase errors, and that the contamination of Stokes V by the phase error is additive. In
order to retrieve V0 from Vm, a
model of the distribution of the phase error across the far field beam pattern is thus
needed.
2.2.2. A model description of the polarization leakage
In the following, we describe the simplified model for the variation of the differential phase Δφ on the sky and its use to correct the data. It consists of a constant phase offset and a linear variation with angle, assumed due to misalignments on the Nasmyth platform. Here misalignment should be understood as having two components, one being the linear displacements of the receivers from the secondary focus. This produces differential pointing of the main beams on the sky. The second being mispointing of the receivers themselves so that they do not point at the center of the subreflector, and so give rise to asymmetric illuminations of the aperture plane. To a first approximation this will give a linear variation of differential phase between the two orthogonally polarized beams as a function of angle in the far-field.
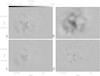 |
Fig. 2 Demonstration of the image reconstruction process, for the 2007 observations. The
cross denotes the position of the pulsar. The grayscale wedge (with
|
The relevant measurement equation reads, for a single map j and
assuming that the intrinsic (Q0 and
U0) and measured (Qm and
Um) Stokes Q and U parameters are stationary while the map
is taken (e.g., ignoring parallactic and Nasmyth rotation on a timescale of 0ḥ5),
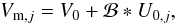 (2)where ∗ denotes the
convolution product and ℬ the distribution of the phase error Δφ
weighted by the telescope’s cross-correlation beam pattern. ℬ is derived from a generic
model comprising a constant phase gradient ∇φ that results from the
unequal illumination of the secondary mirror by the slightly mispointed receivers and
therefore assumed to be stationary in the Nasmyth reference frame:
(2)where ∗ denotes the
convolution product and ℬ the distribution of the phase error Δφ
weighted by the telescope’s cross-correlation beam pattern. ℬ is derived from a generic
model comprising a constant phase gradient ∇φ that results from the
unequal illumination of the secondary mirror by the slightly mispointed receivers and
therefore assumed to be stationary in the Nasmyth reference frame:
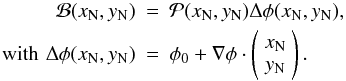 (3)Here
(3)Here
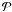 is the cross-correlation beam pattern normalized to 1 at peak, given as a Gaussian
function of the angular coordinates
(xN,yN) in the Nasmyth
reference frame,
is the cross-correlation beam pattern normalized to 1 at peak, given as a Gaussian
function of the angular coordinates
(xN,yN) in the Nasmyth
reference frame, ![\begin{equation} \frac{\Theta^2 \ln {\mathcal P}(x_{\rm N},y_{\rm N})}{2\ln 2} = - \sum_{k=1,2}\left[(x_{\rm N}-x_{0,k})^2+(y_{\rm N}-y_{0,k})^2\right] \end{equation}](/articles/aa/full_html/2011/04/aa16301-10/aa16301-10-eq51.png) (4)with
the half-maximum full beamwidth Θ and the offsets of the receivers from the rotation
axis, x0,k and y0,k (the index
k = 1,2 labels the receivers). φ0 is the
phase difference between the orthogonal polarizations on the rotation axis defining the
origin of the Nasmyth reference frame. The image shown in Fig. 2a is a sensitivity weighted average of the
Nmap = 66 individual maps observed in 2007, i.e.,
(4)with
the half-maximum full beamwidth Θ and the offsets of the receivers from the rotation
axis, x0,k and y0,k (the index
k = 1,2 labels the receivers). φ0 is the
phase difference between the orthogonal polarizations on the rotation axis defining the
origin of the Nasmyth reference frame. The image shown in Fig. 2a is a sensitivity weighted average of the
Nmap = 66 individual maps observed in 2007, i.e.,
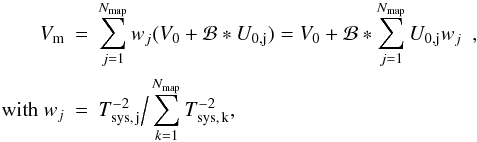 (5)where
we assume that V0 is stationary (see next subsection), i.e.
the contamination of Stokes V is given by the convolution of the phase error beam with
the Stokes U images, the latter being rotated with respect to the Nasymyth reference
system as the source is tracked, and with weights
wj. Because the reference system for
the on-the-fly maps is the equatorial system (right ascension and declination offsets
Δα, Δδ), it is customary to perform the
convolution there rather than in the Nasmyth reference frame. Their respective
coordinates are related by the angles ηj
(the mean parallactic angle for map j) and
χ0,j = ϵj − ηj
(where ϵj is the mean elevation for
map j),
(5)where
we assume that V0 is stationary (see next subsection), i.e.
the contamination of Stokes V is given by the convolution of the phase error beam with
the Stokes U images, the latter being rotated with respect to the Nasymyth reference
system as the source is tracked, and with weights
wj. Because the reference system for
the on-the-fly maps is the equatorial system (right ascension and declination offsets
Δα, Δδ), it is customary to perform the
convolution there rather than in the Nasmyth reference frame. Their respective
coordinates are related by the angles ηj
(the mean parallactic angle for map j) and
χ0,j = ϵj − ηj
(where ϵj is the mean elevation for
map j), 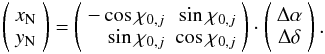 (6)The variance
χ2 among the pixels of the difference image
(6)The variance
χ2 among the pixels of the difference image 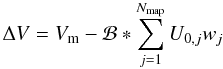 (7)was then
minimized by varying four free parameters, namely the phase gradient
(∂φ/∂x,∂φ/∂y) and the position
of the horizontally polarized reference receiver with respect to the axis on which the
phase difference disappears
(x0,y0), assumed to coincide
with the rotation axis (i.e., φ0 = 0 rad). The differential
offset of the receivers was measured independently from pointing observations of strong
point sources. Because of the many image processing steps involved in calculating
χ2 for each set of parameters, preference was given to a
simulated annealing method (Metropolis algorithm, see Press et al. 1994), using χ2 as the “energy” to be
minimized in the annealing process. This approach is less accurate than other methods,
but turned out to be sufficient for our purposes after repeating the minimization of
χ2 with different search options. In an attempt to confirm
the fit result, the resulting phase gradient was then fixed, and the receiver offset
obtained is within ≃ 1′′ of the measured one, i.e., rather insensitive to the receiver
misalignment within these limits. The results of our analysis are summarized in
Table 1. The results of simulations suggest
that such effects can be accounted for by an offset of the aperture plane illumination
by about 8% of the diameter of the subreflector, or a mis-pointing of the receivers of
about
(7)was then
minimized by varying four free parameters, namely the phase gradient
(∂φ/∂x,∂φ/∂y) and the position
of the horizontally polarized reference receiver with respect to the axis on which the
phase difference disappears
(x0,y0), assumed to coincide
with the rotation axis (i.e., φ0 = 0 rad). The differential
offset of the receivers was measured independently from pointing observations of strong
point sources. Because of the many image processing steps involved in calculating
χ2 for each set of parameters, preference was given to a
simulated annealing method (Metropolis algorithm, see Press et al. 1994), using χ2 as the “energy” to be
minimized in the annealing process. This approach is less accurate than other methods,
but turned out to be sufficient for our purposes after repeating the minimization of
χ2 with different search options. In an attempt to confirm
the fit result, the resulting phase gradient was then fixed, and the receiver offset
obtained is within ≃ 1′′ of the measured one, i.e., rather insensitive to the receiver
misalignment within these limits. The results of our analysis are summarized in
Table 1. The results of simulations suggest
that such effects can be accounted for by an offset of the aperture plane illumination
by about 8% of the diameter of the subreflector, or a mis-pointing of the receivers of
about 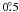 .
Then MUV ≃ 0.1. For a given observing epoch, the maximum
value of | pC | is reproduced by the different approaches.
The comparison between the results from 2007 and 2009 shows that the image resulting
from the campaign in September 2007 has a lower degree of contamination in Stokes V,
owing to the optimum orientation of the beam-splitting grid in 2007, and because the
receiver alignment was somewhat better. A map of planet Mars (which is unresolved by the
telescope and can safely be considered as unpolarized) confirmed that the instrumental
conversion of Stokes I to Stokes V disappeared in the 2007 data
(MIV < 3σrms = 0.05%).
The excess of the residual pCin 2009 stems from the
MIV term not taken into account explicitly, and agrees
with the model result from Thum et al. (2008,
their Fig. 7) for the non-optimized beam splitter and
.
Then MUV ≃ 0.1. For a given observing epoch, the maximum
value of | pC | is reproduced by the different approaches.
The comparison between the results from 2007 and 2009 shows that the image resulting
from the campaign in September 2007 has a lower degree of contamination in Stokes V,
owing to the optimum orientation of the beam-splitting grid in 2007, and because the
receiver alignment was somewhat better. A map of planet Mars (which is unresolved by the
telescope and can safely be considered as unpolarized) confirmed that the instrumental
conversion of Stokes I to Stokes V disappeared in the 2007 data
(MIV < 3σrms = 0.05%).
The excess of the residual pCin 2009 stems from the
MIV term not taken into account explicitly, and agrees
with the model result from Thum et al. (2008,
their Fig. 7) for the non-optimized beam splitter and
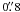 misalignment. Our analysis requires that the intrinsic polarizations in Stokes U and V,
as measured in the equatorial reference frame, remain stationary within either observing
campaign. This requirement is fulfilled here: although the outward motion of the radio
wisps can be up to ~ 0.3c (Bietenholz et al. 2004), it leads, after two months, to a position shift
of
misalignment. Our analysis requires that the intrinsic polarizations in Stokes U and V,
as measured in the equatorial reference frame, remain stationary within either observing
campaign. This requirement is fulfilled here: although the outward motion of the radio
wisps can be up to ~ 0.3c (Bietenholz et al. 2004), it leads, after two months, to a position shift
of 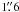 (for a distance to Tau A of 2 kpc, Trimble 1968),
which is still unresolved by our observations.
(for a distance to Tau A of 2 kpc, Trimble 1968),
which is still unresolved by our observations.
Figure 2 demonstrates the image reconstruction for the 2007 observations: the raw Stokes V image (Vm), the mean Stokes U image (weighted average of the U0,j), the averaged model images B ∗ U0,j for the parameters minimizing the χ2 of the difference image ΔV (Eq. (7)), and the resulting reconstructed image of V0. The dominating antisymmetric pattern of the raw Stokes V image has now disappeared. The noise in the reconstructed Stokes V image of Fig. 2 is about 4 mJy. At the position of the pulsar, we obtain | pC | ≤ 0.20%, corresponding to about 3σV. This upper limit is more sensitive than the 23 GHz limit of Wright & Forster (1980) by a factor of 30.
Summary of fitted parameters. Bold text indicates fixed parameters.
3. Discussion
Astronomical circular polarization can be produced in two ways, either in the cyclotron- or synchrotron emission process itself that also generates the strong linearly polarized continuum (see e.g., Weiler 1974, for a review), or when the latter crosses a magnetized plasma. Although these processes can be co-spatial, we treat them separately.
3.1. Circular polarization of synchrotron and cyclotron radiation
The absence of a detectable circular polarization in the synchrotron emission from Tau A
is not surprising, because the sign of Stokes V depends on whether the velocity vector of
an electron emitting synchrotron emission is between the magnetic field direction and the
line-of-sight, or outside (i.e., whether the angle ψ between the velocity
vector and the line-of-sight is positive or negative). For an isotropic distribution of
electrons, there is a small term of the order of
O(ψ2). The linear term in
ψ does not cancel either, because the solid angles in which electrons
with ψ > 0 and ψ < 0 radiate are unequal
by a factor of | ψ | sinθ (Pacholczyk 1977; θ is the angle between the
magnetic field direction and the line-of-sight). If self-absorption becomes important, the
circular polarization has a sign change at a frequency
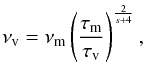 (8)where
νm is the frequency of the maximum of the spectral energy
distribution and τm is the optical depth at that frequency
(and τv the optical depth at νv).
The spectral index s of the assumed power-law energy distribution of
electrons,
Ne(E) = Ne(E0)(E/E0) − s,
can be determined from the spectral index of the synchrotron spectrum. The
λ1.3 mmimage of Tau A taken with the same telescope (Bandiera et al.
2002) is too close in frequency to ours and
therefore does not allow us to estimate the spectral index, because the accuracy of the
flux scale is about 20% at both frequencies. Our flux calibration is consistent with a
spectral index between λ20 cmand λ1.3 mmof
α = −0.28 to − 0.2 (comparing Bandiera et al. 2002 with a λ20 cmmap, Bietenholz et al. 1997). For frequencies well above the cyclotron turnover
(which is below 81.5 MHz, Baars & Hartsuijker 1972), this yields s = 1 − 2α ≃ 1.5. The
average magnetic field ⟨ B ⟩ has been determined from the break of the
radio spectrum, at ν ~ 1013 Hz (Marsden et al. 1984), to be 0.3 mG, corresponding to equipartition
between thermal and magnetic pressure. With these values, the sign change of Stokes V due
to synchrotron self-absorption occurs at about 0.6 MHz. The intrinsic circular
polarization at 89.2 GHz is therefore of the order of 0.01% (using Pacholczyk 1977, Eq. (3.124)). This is for an isotropic
distribution of electron energies and optically thin conditions, in a unifrom magnetic
field aligned at 45° to the line-of-sight, i.e., an order of magnitude below our upper
limit. We note that for a (e + ,e − ) plasma, as usually assumed to
be present (Hester 2008, p. 130; Gaensler &
Slane 2006) the intrinsic circular polarization
would be even smaller. Wilson & Weiler (1997) conclude that their upper limit to | pC | at
610 MHz is still too high for an estimate of the contribution to the radio emission from
positrons with respect to that of electons. The same holds for our upper limit.
(8)where
νm is the frequency of the maximum of the spectral energy
distribution and τm is the optical depth at that frequency
(and τv the optical depth at νv).
The spectral index s of the assumed power-law energy distribution of
electrons,
Ne(E) = Ne(E0)(E/E0) − s,
can be determined from the spectral index of the synchrotron spectrum. The
λ1.3 mmimage of Tau A taken with the same telescope (Bandiera et al.
2002) is too close in frequency to ours and
therefore does not allow us to estimate the spectral index, because the accuracy of the
flux scale is about 20% at both frequencies. Our flux calibration is consistent with a
spectral index between λ20 cmand λ1.3 mmof
α = −0.28 to − 0.2 (comparing Bandiera et al. 2002 with a λ20 cmmap, Bietenholz et al. 1997). For frequencies well above the cyclotron turnover
(which is below 81.5 MHz, Baars & Hartsuijker 1972), this yields s = 1 − 2α ≃ 1.5. The
average magnetic field ⟨ B ⟩ has been determined from the break of the
radio spectrum, at ν ~ 1013 Hz (Marsden et al. 1984), to be 0.3 mG, corresponding to equipartition
between thermal and magnetic pressure. With these values, the sign change of Stokes V due
to synchrotron self-absorption occurs at about 0.6 MHz. The intrinsic circular
polarization at 89.2 GHz is therefore of the order of 0.01% (using Pacholczyk 1977, Eq. (3.124)). This is for an isotropic
distribution of electron energies and optically thin conditions, in a unifrom magnetic
field aligned at 45° to the line-of-sight, i.e., an order of magnitude below our upper
limit. We note that for a (e + ,e − ) plasma, as usually assumed to
be present (Hester 2008, p. 130; Gaensler &
Slane 2006) the intrinsic circular polarization
would be even smaller. Wilson & Weiler (1997) conclude that their upper limit to | pC | at
610 MHz is still too high for an estimate of the contribution to the radio emission from
positrons with respect to that of electons. The same holds for our upper limit.
3.2. Circular polarization due to radiative transfer effects in a magnetized plasma
Is it conceivable that at high frequency circular polarization can be produced by a more
efficient mechanism than the synchrotron emission process itself? The sought-after effect
would then be a manifestation of magnetic birefringence. While the Faraday rotation of
linear polarization in a magnetized plasma is the most efficient mechanism to convert
Stokes parameters into each other, it is only a special case of what is now known as
“generalized Faraday effect” (Wilson 1980; Melrose
& Robinson 1994). Under the optical thin
conditions which apply to the λ3 mm emission from Tau A, the transfer of
polarized radiation in a collisionless plasma can be described as the motion of a
polarization point on the surface of the Poincaré sphere at constant latitude, where the
zenith of the coordinate system on the sphere is defined by the natural mode of the
medium. The latter depends on the angle ϑ between the magnetic field
direction and the line-of-sight. If the natural mode changes along the line-of-sight, the
coordinate system changes, too, and the polarization point on the Poincaré sphere follows
a complicated trajectory. If the propagation is quasi-longitudinal
( | ϑ | ≪ 1 rad), the natural mode is circularly polarized, and the
radiative transfer leads to the well-known Faraday rotation. If the natural mode is
quasi-transversal (i.e. if the line-of-sight crosses a region where ϑ
passes through π/2, a so-called quasi-transversal QT layer), the
natural mode is linearly polarized, and the transfer of radiation in such a zone leads to
the conversion between linear and circular polarization (dubbed “Faraday pulsation”3 by Pacholczyk & Swihart 1970; Rosenberg 1972) and leads
to a “circular repolarization” of intrinsically linearly polarized radiation (Pacholczyk
1973, considering a cold plasma with an admixture
of relativistic electrons). The synchrotron emission observed by us is from a plasma,
consisting mainly of relativistic electrons, and for which the natural radiative
propagation mode is elliptical (with an axis ratio determined by the number density ratio
of cold and relativistic particles, Kennett & Melrose 1998), making the generation of circular polarization easier than in a
cold plasma. Detailed calculations for a synchrotron nebula are seemingly yet to be
carried out. However, the following estimate may be instructive here. The plasma can be
considered stationary with respect to the propagating radiation, since both the plasma
frequency 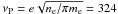 kHz and the electron
gyrofrequency
νG = eB/2πmec = 0.84 kHz
are orders of magnitude below our observing frequency of
νobs = 89.2 GHz, for the 0.3 mG magnetic field, and
ne = 1.3 × 104 cm-3 (Fesen &
Kirshner 1982, from forbidden SII line ratios in
the filaments). For such conditions, Segre & Zanza (2001) estimate the production of circular polarization in a QT layer,
assuming a constant gradient of the line-of-sight component of the magnetic field,
Bcosϑ, and a constant component
B0 perpendicular to it. Such a situation could apply between
the X-ray torus and the body of the synchrotron nebula with their crossed respective
fields mentioned in the introduction. For ϑ linearly increasing from 84°
to 96° along a line-of-sight element of 0.03 pc (the approximate thickness of the inner
X-ray ring seen by Chandra, and of the knots in it, Weisskopf et al. 2000), one obtains , which is several orders of magnitude below our
upper limit. Circular repolarization is therefore insignificant, because it is of the
order of (νG/νobs)2,
whereas Faraday rotation is a first order effect (and most likely, except for some
filaments, of interstellar origin, Bietenholz & Kronberg 1990). We infer that the features in the reconstructed Stokes V image
(Fig. 2d) are to be attributed to the phase error.
They originate most likely from the higher-order effects, neglected in our linear
analysis, that can only be considered with a detailed model of the response of telescope
and receiver cabin optics to partially polarized radiation.
kHz and the electron
gyrofrequency
νG = eB/2πmec = 0.84 kHz
are orders of magnitude below our observing frequency of
νobs = 89.2 GHz, for the 0.3 mG magnetic field, and
ne = 1.3 × 104 cm-3 (Fesen &
Kirshner 1982, from forbidden SII line ratios in
the filaments). For such conditions, Segre & Zanza (2001) estimate the production of circular polarization in a QT layer,
assuming a constant gradient of the line-of-sight component of the magnetic field,
Bcosϑ, and a constant component
B0 perpendicular to it. Such a situation could apply between
the X-ray torus and the body of the synchrotron nebula with their crossed respective
fields mentioned in the introduction. For ϑ linearly increasing from 84°
to 96° along a line-of-sight element of 0.03 pc (the approximate thickness of the inner
X-ray ring seen by Chandra, and of the knots in it, Weisskopf et al. 2000), one obtains , which is several orders of magnitude below our
upper limit. Circular repolarization is therefore insignificant, because it is of the
order of (νG/νobs)2,
whereas Faraday rotation is a first order effect (and most likely, except for some
filaments, of interstellar origin, Bietenholz & Kronberg 1990). We infer that the features in the reconstructed Stokes V image
(Fig. 2d) are to be attributed to the phase error.
They originate most likely from the higher-order effects, neglected in our linear
analysis, that can only be considered with a detailed model of the response of telescope
and receiver cabin optics to partially polarized radiation.
3.3. Circular polarization due to the pulsar emission
Last, but not least, we examine that the Crab pulsar itself does not contribute a strong circularly polarized flux. The optical depth at 89.2 GHz in the foreground synchrotron nebula being negligible, the question arises whether the almost complete circular polarization of the giant pulses (for the Crab pulsar: Hankins et al. 2003; Popov et al. 2006; for PSR B1937+21: Cognard et al. 1996) yields an observable signature at λ3 mm. However, it is unlikely that giant pulses contribute to our Stokes V emission, although they constitute the main component of the radio emission from Tau A (Popov et al. 2006): a single giant pulse consists of hundreds of sometimes unresolved nanopulses, but left- and right-circular polarization have a similar occurrence, and the circular polarization therefore tends to cancel out in observations that are unresolved in time. Even if there was a residual Stokes V at radio wavelengths, it would probably be undetectable at mm wavelengths: simultaneous observations of the giant pulses at 0.6 GHz and 1.4 GHz (Sallmen et al. 1999) yield steep spectral indices (between − 2.2 and − 4.9, average main pulse value ~4) for them. Extrapolating the typical flux density of a nanopulse of 1000 Jy from 5.5 GHz to 86.2 GHz leaves a flux of 260 mJy, but the time-averaged pulsed flux density would be much lower, at most ~1 mJy, on top of the synchrotron flux from the nebula towards the pulsar, 5.3 Jy. The sensitivity of our measurements of the fractional circular polarization is 0.1% to 0.2%, still an order of magnitude above the sensitivity needed if the time-averaged pulsed flux density was significantly (i.e., >10%) circularly polarized.
4. Conclusions
This analysis was aimed at an accurate measurement of the circularly polarized component of the λ3 mm continuum emission from Tau A. Owing to the strong linear polarization of the emission from the synchrotron nebula, useful results were only obtained after a correction for a differential phase gradient across the far-field beams. Such a gradient most likely arises from the differential illumination of the subreflector by the slightly misaligned, orthogonally polarized receivers whose signals are cross-correlated to detect the linearly and circularly polarized flux. Our corrected data yield an upper limit to the fractional circular polarization towards the Crab pulsar, i.e., near the peak of the radio emission, of 0.2% at 89.2 GHz. This upper limit is not surprising bearing in mind: (1) the weakness of the intrinsic circular polarization of the synchrotron emission at high radio frequency; (2) the disorder and changes in magnetic field direction over the body of the nebula; (3) the high probability that most
of the synchrotron radiation comes from a relativistic positron-electron plasma; (4) the low efficiency, at high frequency, of the conversion from linear to circular polarization by radiative transfer effects; (5) the time averaging of the strongly circularly polarized giant pulses from the neutron star. It has been suggested (Kennel & Coroniti 1984) that the radio emission is due to a population of electrons which are accelerated in the filaments which might therefore radiate significant circular polarization. Our sensitivity and angular resolution do not enable a test of this proposition to be made however.
In vapors the effect is known as Voigt effect (Voigt 1898), in liquids as Cotton-Mouton effect.
Acknowledgments
We acknowledge the assistance of the technical staff of IRAM Granada, and wish to express our gratitude to Pierre Cox, the director of IRAM, for his grant of observing time, and to the colleagues from the Planck CTWG6 for their help with the observations.
References
- Aumont, J., Conversi, L., Thum, C., et al. 2010, A&A, 514, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baars, J. W. M., & Hartsuijker, A. P. 1972, A&A, 17, 172 [NASA ADS] [Google Scholar]
- Bandiera, R., Neri, R., & Cesaroni, R. 2002, A&A, 386, 1044 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bietenholz, M. F., & Kronberg, P. P. 1990, ApJ, 357, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Bietenholz, M. F., Kassim, N., Frail, D. A., et al. 1997, ApJ, 490, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Bietenholz, M. F., Hester, J. J., Frail, D. A., & Bartel, N. 2004, ApJ, 615, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Cocke, W. J., Muncaster, G. W., & Gehrels, T. 1971, ApJ, 169, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Cognard, I., Shrauner, J. A., Taylor, J. H., & Thorsett, S. E. 1996, ApJ, 457, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Emerson, D. T., & Gräve, R. 1988, A&A, 190, 353 [NASA ADS] [Google Scholar]
- Fesen, R. A., & Kirshner, R. P. 1982, ApJ, 258, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Gaensler, B. M., & Slane, P. O. 2006, ARA&A, 44, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Hester, J. J. 2008, ARA&A, 46, 127 [Google Scholar]
- Kennel, C. F., & Coroniti, F. V. 1984, ApJ, 283, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Kennett, M., & Melrose, D. 1998, Publications of the Astronomical Society of Australia, 15, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Marsden, P. L., Gillett, F. C., Jennings, R. E., et al. 1984, ApJ, 278, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, P. G., Illing, R., & Angel, J. R. P. 1972, MNRAS, 159, 191 [NASA ADS] [Google Scholar]
- Melrose, D. B., & Robinson, P. A. 1994, Proceedings of the Astronomical Society of Australia, 11, 16 [NASA ADS] [Google Scholar]
- Pacholczyk, A. G. 1977, Radio Galaxies, Vol. 89, Pergamon Press International Series on Natural Philosophy [Google Scholar]
- Pacholczyk, A. G. 1973, MNRAS, 163, 29P [NASA ADS] [Google Scholar]
- Pacholczyk, A. G., & Swihart, T. L. 1970, ApJ, 161, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Popov, M. V., Soglasnov, V. A., Kondrat’Ev, V. I., et al. 2006, Astron. Rep., 50, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1994, Numerical Recipes in C. The Art of Scienctific Computing, 2nd edn. (Cambridge University Press) [Google Scholar]
- Rosenberg, H. 1972, A&A, 19, 66 [NASA ADS] [Google Scholar]
- Sallmen, S., Backer, D. C., Hankins, T. H., Moffett, D., & Lundgren, S. 1999, ApJ, 517, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Scargle, J. D. 1969, ApJ, 156, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Segre, S. E., & Zanza, V. 2001, ApJ, 554, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Thum, C., Wiesemeyer, H., Paubert, G., Navarro, S., & Morris, D. 2008, PASP, 120, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Trimble, V. 1968, AJ, 73, 535 [Google Scholar]
- Voigt, W. 1898, Nachr. der K. Gesellsch. der Wiss. zu Göttingen [Google Scholar]
- Weiler, K. W. 1974, Mem. Soc. Astron. Ital., 45, 573 [NASA ADS] [Google Scholar]
- Weisskopf, M. C., Hester, J. J., Tennant, A. F., et al. 2000, ApJ, 536, L81 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wilson, A. S., & Weiler, K. W. 1997, ApJ, 475, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, D. B. 1980, MNRAS, 192, 787 [NASA ADS] [Google Scholar]
- Wright, M. C. H., & Forster, J. R. 1980, ApJ, 239, 873 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Stokes I image of Tau A (2009 data). Contours are at
0.2 × 2j − 1 Jy per beam, with
j = 1 to 10. Lowest contour: 200 mJy
(corresponding to 6σrms). Highest
contour: 4.5 Jy. The beam’s fwhm is indicated in the lower left
corner. The cross marks the Pulsar’s position. Map center:
|
| In the text | |
 |
Fig. 2 Demonstration of the image reconstruction process, for the 2007 observations. The
cross denotes the position of the pulsar. The grayscale wedge (with
|
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.