A&A 390, 1115-1118 (2002)
DOI: 10.1051/0004-6361:20020749
The age of the Sun and the relativistic corrections in the EOS
A. Bonanno1 - H. Schlattl2,3 -
L. Paternò3
1 - INAF - Osservatorio Astrofisico di Catania, Città Universitaria,
95123 Catania, Italy
2 -
Astrophysics Research Institute, Liverpool John Moores
University, Twelve Quays House, Egerton Wharf, Birkenhead CH41 1LD,
UK
3 -
Dipartimento di Fisica e Astronomia
dell'Università, Sezione Astrofisica, Città Universitaria, 95123 Catania, Italy
Received 18 April 2002 / Accepted 13 May 2002
Abstract
We show that the inclusion of special relativistic
corrections in the revised OPAL and MHD equations of state has a
significant impact on the helioseismic determination of the solar age.
Models with relativistic corrections included lead to a reduction of about
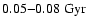 with respect
to those obtained with the old OPAL or MHD EOS. Our best-fit value is
with respect
to those obtained with the old OPAL or MHD EOS. Our best-fit value is
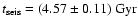 which is in remarkably good agreement
with the meteoritic value for the solar age.
We argue that the inclusion of relativistic corrections is important for
probing the evolutionary state of a star
by means of the small frequency separations
which is in remarkably good agreement
with the meteoritic value for the solar age.
We argue that the inclusion of relativistic corrections is important for
probing the evolutionary state of a star
by means of the small frequency separations
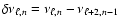 ,
for spherical harmonic degrees
,
for spherical harmonic degrees
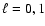 and radial order
and radial order
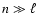 .
.
Key words: Sun: interior - Sun: oscillations - equation of state
The possibility of using helioseismology to constrain the solar age has been
discussed by several authors in the past.
Very recently Dziembowski et al. (1999) have shown that the most robust and accurate method is
provided by the small frequency separation analysis (SFSA),
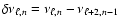 ,
for spherical harmonic degrees
,
for spherical harmonic degrees
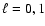 and radial order
and radial order
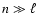 (Tassoul 1980).
(Tassoul 1980).
The important property of this quantity is its
strong sensitivity to the sound-speed gradient
near the solar centre and its weak dependence on
the details of the treatment of the outer layers. Despite our ignorance of
a reliable convection model for the solar envelope we are
therefore able to verify how well our models are able to
reproduce the deep radiative regions, in particular the solar core.
Since the properties of the core are mainly determined by
the present central hydrogen abundance, and the latter is influenced
by the solar age, SFSA is a reliable tool to
examine the seismic age of the Sun.
Adopting the OPAL equation of state (Rogers
et al. 1996) a seismic age of
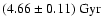 has been obtained by
Dziembowski et al. (1999), which is consistent with the
meteoritic age
has been obtained by
Dziembowski et al. (1999), which is consistent with the
meteoritic age
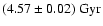 of Bahcall et al. (1995).
of Bahcall et al. (1995).
The aim of this paper is to show that an important ingredient in this
type of analysis is the usage of an accurate equation of state (EOS).
In particular, by the inclusion of the special relativistic corrections,
like in the updated version of the OPAL EOS, the helioseismic age of
the Sun is reduced to
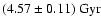 ,
which is in
remarkable agreement with the meteoritic value.
,
which is in
remarkable agreement with the meteoritic value.
Elliott & Kosovichev (1998) have demonstrated that
the inclusion of relativistic corrections in
the EOS leads to a better agreement between the solar models and
the seismic Sun. By inverting SOI-MDI/SOHO p-mode frequencies
they found that the solar adiabatic exponent 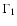 is much
better reproduced by solar models including the relativistic contribution
to the Fermi-Dirac statistics. Since the improved EOS
causes a decrease of
is much
better reproduced by solar models including the relativistic contribution
to the Fermi-Dirac statistics. Since the improved EOS
causes a decrease of 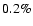 in the adiabatic index
in the adiabatic index 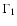 in the solar centre, the sound speed (
in the solar centre, the sound speed (
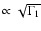 )
is
reduced by about 0.1%. Therefore, the influence of the
relativistic corrections should also be visible in the
small frequency separations
)
is
reduced by about 0.1%. Therefore, the influence of the
relativistic corrections should also be visible in the
small frequency separations
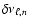 .
Indeed,
Bonanno et al. (2001) have found that including this effect in the value
of
.
Indeed,
Bonanno et al. (2001) have found that including this effect in the value
of 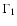 improves the
agreement in
improves the
agreement in
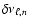 between solar models and observations,
thereby confirming the results of Elliott & Kosovichev (1998).
between solar models and observations,
thereby confirming the results of Elliott & Kosovichev (1998).
In addition to the age, the central hydrogen abundance is also
crucially dependent on the precise value of
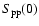 ,
the zero-energy
astrophysical S-factor for the proton-proton fusion cross section.
Schlattl et al. (1999) and Antia & Chitre (1999) have shown, using the old
version of the OPAL EOS, that an increase of
,
the zero-energy
astrophysical S-factor for the proton-proton fusion cross section.
Schlattl et al. (1999) and Antia & Chitre (1999) have shown, using the old
version of the OPAL EOS, that an increase of
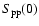 by about 4%
with
respect to Adelberger et al.'s (1998) value yields a
better agreement with the observed frequencies for an age of 4.57 Gyr.
For this reason we consider in our analysis also different values of
by about 4%
with
respect to Adelberger et al.'s (1998) value yields a
better agreement with the observed frequencies for an age of 4.57 Gyr.
For this reason we consider in our analysis also different values of
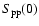 .
.
Including the updated OPAL EOS the best agreement between
meteoritic and seismic age could be achieved with Adelberger
et al.'s (1998)
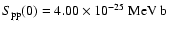 .
Hence, by taking into account the relativistic corrections in the EOS
there is no need for an artificial increase of
.
Hence, by taking into account the relativistic corrections in the EOS
there is no need for an artificial increase of
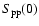 ,
as suggested by
previous works, in order to obtain a better agreement between seismic
and meteoritic age.
,
as suggested by
previous works, in order to obtain a better agreement between seismic
and meteoritic age.
The code and physics used to compute the various solar models are
described briefly in the next section, followed by the consequences
for the seismic age obtained by means of the SFSA
(Sect. 3). In the final part the results are discussed.
We computed a large number of solar models using the GARching
SOlar Model (GARSOM) code which has been described in its latest
version in Schlattl (2001).
Our standard model has been compared with other contemporary solar models
by Turck-Chièze et al. (1998), who found a good agreement between
various programs.
The solar photospheric radius and luminosity have been assumed to be
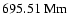 (Brown & Christensen-Dalsgaard 1998) and
(Brown & Christensen-Dalsgaard 1998) and
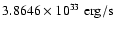 ,
respectively. The surface
metal ratio
has been taken from Grevesse & Noels (1993), thus
Z/X=0.0245.
The mixing length parameter (Böhm-Vitense 1958), initial helium and metal
content have been adjusted in all models to reproduce these values
with an accuracy better than 10-4.
,
respectively. The surface
metal ratio
has been taken from Grevesse & Noels (1993), thus
Z/X=0.0245.
The mixing length parameter (Böhm-Vitense 1958), initial helium and metal
content have been adjusted in all models to reproduce these values
with an accuracy better than 10-4.
In the actual calculations the latest OPAL-opacities (Iglesias &
Rogers 1996) completed in the low-temperature regime by tables of
Alexander & Fergusson (1994) have been implemented.
The outer boundary condition was determined assuming an Eddington grey
atmosphere.
Microscopic diffusion of hydrogen, helium and all major metals is
taken into account. For the EOS we used either the OPAL- (Rogers
et al. 1996) or the MHD-tables (Hummer & Mihalas 1988; Mihalas et al. 1988;
Däppen et al. 1988). The original OPAL EOS (OPAL96) has been updated by treating
electrons relativistically and by improving the activity expansion
method for repulsive interactions (Rogers 2001), denoted OPAL01 in the
following.
In the case of MHD EOS the relativistic corrections are not directly
included in the tables. We have therefore corrected the adiabatic index 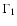 employing the expression of Elliott & Kosovichev (1998),
employing the expression of Elliott & Kosovichev (1998),
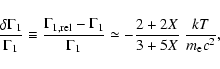 |
(1) |
where T is the temperature, 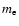 the electron mass,
c the light speed in vacuum, k the Boltzmann constant,
and X the hydrogen mass fraction.
As expected, the correction to
the electron mass,
c the light speed in vacuum, k the Boltzmann constant,
and X the hydrogen mass fraction.
As expected, the correction to
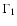 is negative,
since its value is 5/3 for the non-relativistic and 4/3
for the extremely relativistic case.
is negative,
since its value is 5/3 for the non-relativistic and 4/3
for the extremely relativistic case.
The nuclear reaction rates are taken either from Bahcall et al. (1995) or
from Adelberger et al. (1998) with
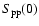 being
being
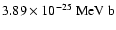 in the first and
in the first and
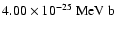 in the latter case. Other differences in the reaction rates are not
very significant in determining the evolutionary stage of the solar core.
in the latter case. Other differences in the reaction rates are not
very significant in determining the evolutionary stage of the solar core.
We have computed solar models following the evolution from the zero-age main sequence
with ages ranging from 4.40 to 5.00 Gyr in steps of 0.1 Gyr.
Some basic quantities of a selection of models are summarized in
Table 1.
![\begin{figure}
\par\resizebox{9.4cm}{!}{\includegraphics[clip]{profile.ps}}
\end{figure}](/articles/aa/full/2002/30/aa2598/Timg45.gif) |
Figure 1:
The differences of 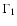 (solid line) and
(solid line) and 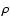 (dashed) between two models which either neglect (model 1) or contain the
relativistic corrections (model 2) in the sense (dashed) between two models which either neglect (model 1) or contain the
relativistic corrections (model 2) in the sense
 . . |
| Open with DEXTER |
For the higher ages the initial helium content has to be reduced to obtain
the correct solar luminosity (compare models 1 and 5). Nevertheless, a
larger lifetime leads to a steeper He profile toward the centre
causing a larger central He abundance.
The consequent increase of the opacity near the core demands an
higher central temperature to produce the
same amount of energy. This effect is further
enhanced by
diffusion which is operating longer for greater ages and is further
increasing the central He content.
Since the relativistic correction to 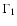 increases with temperature
(Eq. (1)), the inclusion of relativistic effects has a larger
influence on older models. The
relative differences in the profiles of
increases with temperature
(Eq. (1)), the inclusion of relativistic effects has a larger
influence on older models. The
relative differences in the profiles of 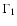 and the density are shown
in Fig. 1.
and the density are shown
in Fig. 1.
Models with greater
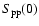 ,
but the same age, have a smaller
,
but the same age, have a smaller 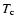 (see models 1 and 6 in Table 1), as
the hydrogen burning in the core is more efficient.
(see models 1 and 6 in Table 1), as
the hydrogen burning in the core is more efficient.
In order to determine the seismic age, we calculated for all the
solar models the small frequency separations
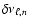 for
for
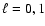 and
and
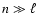 .
These values have been compared with latest GOLF/SOHO data for
.
These values have been compared with latest GOLF/SOHO data for
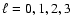 ,
which have been obtained from long time series, and where the
asymmetric line profile has been taken into account during the data reduction
(Thiery et al. 2000). Only the frequencies of the mean multiplet (m=0)
are used, as for them the influence of rotation is smallest.
,
which have been obtained from long time series, and where the
asymmetric line profile has been taken into account during the data reduction
(Thiery et al. 2000). Only the frequencies of the mean multiplet (m=0)
are used, as for them the influence of rotation is smallest.
For the analysis, the 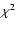 method has been used, as in
Dziembowski et al. (1999) or Schlattl et al. (1999);
method has been used, as in
Dziembowski et al. (1999) or Schlattl et al. (1999);
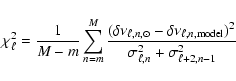 |
(2) |
with M=31 for 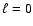 and M=27 for
and M=27 for 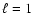 ,
and m being 10 in both cases.
It is interesting to notice that including the relativistic
corrections leads to a reduction of
,
and m being 10 in both cases.
It is interesting to notice that including the relativistic
corrections leads to a reduction of
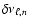 of about
of about
 for low frequencies (Fig. 2).
for low frequencies (Fig. 2).
![\begin{figure}
\par\resizebox{9.4cm}{!}{\includegraphics[clip]{diff.ps}}
\end{figure}](/articles/aa/full/2002/30/aa2598/Timg55.gif) |
Figure 2:
The differences of the quantity
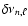 between two models which either neglect (model 1) or contain the
relativistic correction (model 2) in the sense
between two models which either neglect (model 1) or contain the
relativistic correction (model 2) in the sense
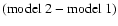 for an age of for an age of
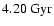 (solid line) and
(solid line) and
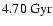 (dashed line).
(dashed line). |
| Open with DEXTER |
The results for the 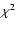 -values in models with different ages
are shown in Figs. 3 and 4. The best-fit age
given by the minimal
-values in models with different ages
are shown in Figs. 3 and 4. The best-fit age
given by the minimal 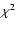 -value (
-value (
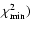 and the
error determined by the condition
and the
error determined by the condition
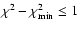 are summarized in Table 2.
are summarized in Table 2.
![\begin{figure}
\par\resizebox{9.4cm}{!}{\includegraphics[clip]{chi0.ps}}
\end{figure}](/articles/aa/full/2002/30/aa2598/Timg72.gif) |
Figure 3:
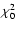 for models with different age, neglecting (dashed
line) or including the relativistic correction (solid line). The MHD-EOS
has been used for the models in the left panel, the OPAL-EOS in the ones
of the right panel.
for models with different age, neglecting (dashed
line) or including the relativistic correction (solid line). The MHD-EOS
has been used for the models in the left panel, the OPAL-EOS in the ones
of the right panel. |
| Open with DEXTER |
Regardless of whether MHD or OPAL EOS is used, the best-fit age is reduced
by about 0.05-0.08
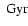 when the relativistic corrections are included.
The minimal value of
when the relativistic corrections are included.
The minimal value of 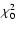 is not significantly
different for all the cases, although the models with OPAL96
EOS have a slightly smaller
is not significantly
different for all the cases, although the models with OPAL96
EOS have a slightly smaller
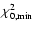 than those obtained with OPAL01 EOS.
than those obtained with OPAL01 EOS.
It is worth noticing that with
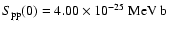 the minimum
the minimum 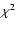 -value slightly improves for both
-value slightly improves for both 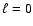 and
and
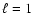 (Table 2).
Using OPAL01 EOS, which includes the relativistic corrections
in a consistent way, we obtain in this case as the best-fit age
(Table 2).
Using OPAL01 EOS, which includes the relativistic corrections
in a consistent way, we obtain in this case as the best-fit age
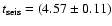 Gyr, where we have taken
the mean of the best-fit value for
Gyr, where we have taken
the mean of the best-fit value for 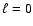 and
and 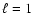 .
This
provides our most reliable value for the seismic solar age.
.
This
provides our most reliable value for the seismic solar age.
By using updated versions of the OPAL and MHD EOS the seismic age of
the Sun has been redetermined using SFSA with the
latest GOLF/SOHO data. The important new ingredient in both equations
of state is the
inclusion of the special relativistic corrections. In both cases
almost the same age has been obtained.
A crucial quantity in the determination of the seismic age is the
proton-proton fusion rate. With the older
versions of the equations of state, a rate about 4% higher as
the value of Adelberger et al. (1998) appears to be favoured, in
order to obtain a better agreement between seismic and meteoritic
ages. However, with the updated versions of the OPAL and MHD EOS the
seismic age obtained with
Adelberger et al.'s (1998)
value for
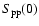 is
is
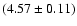 Gyr, which is
in excellent agreement with the meteoritic age of 4.57 Gyr (Bahcall
et al. 1995).
Gyr, which is
in excellent agreement with the meteoritic age of 4.57 Gyr (Bahcall
et al. 1995).
Therefore, the presently favoured value for
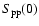 is
is
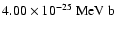 .
However, since the uncertainties, in particular,
in the opacities are supposed to be of the order of a few percent,
.
However, since the uncertainties, in particular,
in the opacities are supposed to be of the order of a few percent,
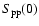 can only be determined with a similar accuracy by comparing
seismic and meteoritic ages.
can only be determined with a similar accuracy by comparing
seismic and meteoritic ages.
A further source of uncertainty is the centrifugal and magnetic
distortion, but these effects can be neglected for the Sun, as discussed by
Dziembowski et al. (1999).
We expect to have asteroseismic data on solar-type
stars with a precision of about
 from future space missions or
high-precision ground-based multi-site spectrographic observations.
We thus think that this effect must be included in the
standard modelling of solar-like stars when discussing the
evolutionary changes in the stellar core.
from future space missions or
high-precision ground-based multi-site spectrographic observations.
We thus think that this effect must be included in the
standard modelling of solar-like stars when discussing the
evolutionary changes in the stellar core.
Acknowledgements
We thank H. M. Antia for many helpful discussions.
The work of H. S. is supported by a Marie Curie
Fellowship of the European Community programme "Human Potential''
under contract number HPMF-CT-2000-00951.
- Adelberger, E. G., Austin, S. M., Bahcall,
J. N., et al. 1998, Rev. Mod. Phys., 70, 1265
In the text
NASA ADS
- Alexander, D. R., & Fergusson, J. W. 1994, ApJ, 437, 879
In the text
NASA ADS
- Antia, H. M., & Chitre, S. M. 1999, A&A, 347, 1000
In the text
NASA ADS
- Antia, H. M., Chitre, S. M., & Thompson, M. J.
2001, A&A, 360, 335
NASA ADS
- Bahcall, J. N., Pinsonneault, M. H., & Wasserburg,
G. J. 1995, Rev. Mod. Phys., 67, 781
In the text
NASA ADS
- Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108
In the text
NASA ADS
- Bonanno, A., Murabito, A., & Paternò, L. 2001, A&A, 375, 1062
In the text
NASA ADS
- Brown, T. M., & Christensen-Dalsgaard, J. 1998, ApJ, 500, L195
In the text
NASA ADS
- Däppen, W., Mihalas, D., Hummer, D. G., & Mihalas, B. W. 1988, ApJ, 332, 261
In the text
NASA ADS
- Dziembowski, W. A., Fiorentini, G., Ricci, B.,
& Sienkiewicz, R. 1999, A&A, 343, 990
In the text
NASA ADS
- Elliott, J. R., & Kosovichev, A. G. 1998, ApJ,
500, L199
In the text
NASA ADS
- Grevesse, N., & Noels,
A. 1993, Phys. Scr., T47, 133
In the text
- Hummer, D. G., & Mihalas, D. 1988, ApJ, 331, 794
In the text
NASA ADS
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943
In the text
NASA ADS
- Mihalas, D., Däppen, W., & Hummer, D. G. 1988, ApJ, 331, 815
In the text
NASA ADS
- Rogers, F. J. 2001, Contrib. Plasma
Phys., 41, 179
In the text
- Rogers, F. J., Swenson, F. J., & Iglesias, C. A. 1996, ApJ, 456, 902
In the text
NASA ADS
- Schlattl, H., Bonanno, A., & Paternò,
L. 1999, Phys. Rev. D, 60, 113002
In the text
- Schlattl, H. 2001, Phys. Rev. D, 64, 013009
In the text
- Tassoul, M. 1980, ApJS, 43, 469
In the text
NASA ADS
- Thiery, S., Boumier, P., Gabriel, A. H., et al.
2000, A&A, 355, 743
In the text
NASA ADS
-
Turck-Chièze, S., Basu, S., Berthomieu, G., et al. 1998, in
Structure and Dynamics of the Interior of the Sun and Sun-like Stars, ed.
S. Korzennik, & A. Wilson, ESA SP-418 (ESA Publication Division, Noordwijk,
The Netherlands), 555
In the text
Copyright ESO 2002
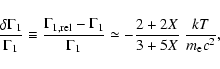
![\begin{figure}
\par\resizebox{9.4cm}{!}{\includegraphics[clip]{profile.ps}}
\end{figure}](/articles/aa/full/2002/30/aa2598/Timg45.gif)
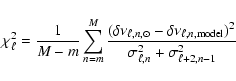
![\begin{figure}
\par\resizebox{9.4cm}{!}{\includegraphics[clip]{diff.ps}}
\end{figure}](/articles/aa/full/2002/30/aa2598/Timg55.gif)
![\begin{figure}
\par\resizebox{9.4cm}{!}{\includegraphics[clip]{chi0.ps}}
\end{figure}](/articles/aa/full/2002/30/aa2598/Timg72.gif)
![\begin{figure}
\par\resizebox{9.4cm}{!}{\includegraphics[clip]{chi1.ps}}
\end{figure}](/articles/aa/full/2002/30/aa2598/Timg73.gif)