M. Murgia^1,2 - P. Parma¹ - H. R. de Ruiter ^1,4 - M. Bondi ¹ - R. D. Ekers ⁵ - R. Fanti ^1,3 - E. B. Fomalont ⁶

1 - Istituto di Radioastronomia del CNR, via Gobetti 101, 40129, Bologna, Italy
2 - Dipartimento di Astronomia, Università di Bologna, via Ranzani 1, 40127 Bologna, Italy
3 - Dipartimento di Fisica, Università di Bologna, via B. Pichat 6/2, 40127 Bologna, Italy
4 - Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
5 - Australia Telescope National Facility, CSIRO, PO Box 76, Epping, NSW 2121, Australia
6 - National Radio Astronomy Observatory, 520 Edgemont Road, Charlottesville, VA 2293, USA

Abstract
We present the results of a multi-frequency study of the inversion symmetric radio galaxy NGC 326 based on Very Large Array observations at 1.4, 1.6, 4.8, 8.5 and 14.9 GHz. The morphological, spectral and polarization properties of this peculiar object are studied at different levels of spatial resolutions. The interpretation of the data will be discussed in forthcoming papers.

Key words: radio continuum: galaxies - galaxies: active - galaxies: individual: NGC 326

1 Introduction

The radio source B2 0055+26 was identified with the elliptical galaxy NGC 326 during a program directed at the identifications of the optical counterparts of radio sources selected from the B2 catalogue (Colla et al. 1975). Basic properties of NGC 326 are reported in Table 1. The radio source was first mapped by Fanti et al. (1977) at 1.4 GHz with the Westerbork Synthesis Radio Telescope (WRST) in the snapshot mode. Because of the interesting structure seen, this observation was followed up by a more sensitive WRST observation at 5 GHz with an angular resolution of $6\hbox{$^{\prime\prime}$ }\times 13\hbox{$^{\prime\prime}$ }$ (Ekers et al. 1978). At this resolution the radio source was found to be composed of two curving tails with a striking 180 $^\circ$ symmetry. NGC 326 was recognized as one of the most spectacular examples of inversion symmetric radio galaxy. The authors explained the unusual structure as being due to the slow precession of the radio jets during the lifetime of the radio source. Rees (1978) suggested that the beam direction precesses due to a realignment caused by the accretion of gas with a different angular momentum direction with respect to the central black hole axis.

Distorted radio galaxies can by classified according to two broad schemes: the mirror symmetric ("C''-shape) and the inversion symmetric ("Z''-shape). A sub-class, called "X''-shape, is characterized by two separate low brightness wings, almost perpendicular to the currently active lobes. There is a broad consensus concerning the dynamical interpretation of the "C''-shape. This kind of distortion is either caused by the translational motion of the galaxy through the intergalactic medium (wide and narrow angle tails) or by the orbital motion of the galaxy around a nearby companion (Blandford & Icke 1978). The explanation of the "Z''-shape and "X''-shape is still uncertain. Along with the secular jet precession (Rees 1978), other two alternative scenarios have been proposed: the sudden realignment of the jet (Wirth et al. 1982) and the buoyancy of the material from the lobes (Worrall et al. 1995).

Battistini et al. (1980) found that NGC 326 is a double system composed of two nearly equally bright elliptical galaxies in a common envelope ("dumbbell'' galaxy). Wirth et al. (1982) investigated the connection between the optical and the radio morphology for a sample of $\sim$ 100 radio emitting dumbbell galaxies. They found about a dozen of sources with "Z'' or "X''-shape and suggested that the presence of another equally massive galaxy within 10-30 kpc of a radio galaxy would strongly influence the jet properties. Particularly, they argue that in the case of bound circular orbits the continuous tidal interaction can produce mirror-symmetric wiggling jets as previously suggested by Blandford & Icke (1978). In the case of unbound orbits an impulsive interaction between the two galaxies can lead to an inversion-symmetric radio source like NGC 326. The "Z''-shape occurs when the duration of the impulsive torque is longer than the jet outflow time to the lobes, while the "X''-shape results when the crossing time is so fast, as compared to the jet outflow time, as to cause an instantaneous change in the jet direction. Wirth et al. (1982) studied in detail the case of NGC 326, using a new optical image. By examining the isophotes they found a brightness difference <1 mag between the two galaxies and very little deviation from pure ellipticity. Indeed they proposed NGC 326 as a prototype for the class of undisturbed dumbbell galaxies. They also pointed the attention to the quite high velocity difference between the two galaxies: $\Delta v \simeq 750$ kms^-1 (Sargent 1973). In the meantime the first 20-cm Very Large Array (VLA) image of the radio source became available (Fomalont 1981; Ekers 1982). In the light of the new optical and radio data, Wirth et al. (1982) reviewed the morphological classification and the interpretation of the source made by Ekers et al. (1978). They suggested that NGC 326 describe an "X''-shape in which the old jet direction was from NE to SW and the actual jet direction is from SE to NW. Moreover, both the old and the new lobes show a "C''-symmetry but with a difference in the position angle of about 120 $^\circ$ , suggesting that the radio galaxy has abruptly changed its velocity direction during its transient interaction with the other galaxy. In the Wirth et al. (1982) picture the velocity of the jet flow cannot be much greater than the $\Delta v$ of the galaxies. More recent redshift measures give $\Delta v=509\pm 44 ~\rm km ~\rm s^{-1}$ (Davoust & Considère 1995) and $\Delta v=549\pm 38 ~\rm km ~\rm s^{-1}$ (Werner et al. 1999).

NGC 326 is the brightest member of a small group of galaxies, Zwicky 0056.9+2636. Werner et al. (1999) measured the redshift for eight galaxies of the group (including NGC 326) confirming the presence of a cluster with a mean redshift of $z_{\rm mean}=0.0477 \pm 0.0007$ and line-of-sight velocity dispersion $\sigma_{z}=599^{+230}_{-110}$ kms^-1. Werner et al. (1999) showed that the brightest of the two optical galaxies (the radio source) is a slowly-moving member of the cluster while its companion has a velocity of about 500 km s^-1 relative to the cluster velocity.

The first detailed studies of the intergalactic medium surrounding NGC 326 were done by Worrall et al. (1995) and Worrall & Birkinshaw (2000). The region containing the source was imaged in soft X-ray with the ROSAT PSPC. Surprisingly, they discovered that the galaxy is embedded in a bright asymmetric X-ray-emitting gaseous medium with properties more typical of a cluster, rather than of a group. They report a gas temperature of kT $\sim 2$ keV and a 0.1-2.4 keV luminosity of $7.5 \times 10^{36} ~h^{-2}$ W. From the PSPC image the emitting gas has a full extent of $\ge$ 400 h^-1 kpc, stretching north-east of the peak, which coincides with the position of NGC 326. The best description of the radial profile they obtained is a combination of a cluster $\beta$ -model and an unresolved component (possibly a hot galactic corona). They obtained a cluster core radius of 171 h^-1 kpc. Because of the presence of the compact hot corona centered on NGC 326, Worrall et al. (1995) proposed that buoyancy effects of the radio plasma in the X-ray atmosphere could be responsible for the bending of the radio lobes. They suggested that, in projection, each radio lobe bends sideways into a tail as the backflow approaches the galactic corona. In order to explain the observed source shape, the buoyancy condition requires a backflow velocity for the lobes material of $v \simeq 3000$ kms^-1.

Table 1: Basic properties of NGC 326.
Optical position $(\alpha_{\rm J2000})$ 00 $^{\rm h}$ 58 $^{\rm m}$ 22 $.\!\!^{\prime\prime}$ 6

Optical position $(\delta_{\rm J2000})$ +26 $^\circ$ 51 $^\prime$ 58 $.\!\!^{\prime\prime}$ 3

Redshift 0.0477

Distance 141 h^-1 Mpc

Magnitude ( $B_{{\rm T}^{0}}$ ) 13.9

1.4 GHz total flux density 1.77 Jy

1.4 GHz total radio luminosity 10^24.6 h^-2 W/Hz

Integrated rotation measure $-25\pm 5$ rad m^-2

Overall spectral index 0.8

Radio source largest linear size 180 h^-1 kpc

Arcsec to kpc conversion factor 1 $^{\prime \prime }$ = 0.63 h^-1 kpc

$h={\rm H}_{0}/100 {\rm ~km~s^{-1} Mpc^{-1}}$ , q₀=0.5.

We use the convention $S_{\nu}\propto \nu^{-\alpha}$ .

This is Paper I of a series of papers dedicated to the radio galaxy NGC326. Here we give a description of the morphological, spectral and polarization characteristics of this radio galaxy. In Sect. 2 we summarize the observations used in this paper. A description of the source morphology and its connections with the polarization and spectral properties is presented in Sect. 3. In Sects. 4 and 5 we analyze the jet collimation properties and the source physical parameters, respectively. A summary of the paper is given in Sect. 6.

We will discuss the interpretation of the spectral and polarization properties respectively in the forthcoming Papers II and III.

**Table 1:** Basic properties of NGC 326.
Optical position $(\alpha_{\rm J2000})$	00 $^{\rm h}$ 58 $^{\rm m}$ 22 $.\!\!^{\prime\prime}$ 6
Optical position $(\delta_{\rm J2000})$	+26 $^\circ$ 51 $^\prime$ 58 $.\!\!^{\prime\prime}$ 3
Redshift	0.0477
Distance	141 h^-1 Mpc
Magnitude ( $B_{{\rm T}^{0}}$ )	13.9
1.4 GHz total flux density	1.77 Jy
1.4 GHz total radio luminosity	10^24.6 h^-2 W/Hz
Integrated rotation measure	$-25\pm 5$ rad m^-2
Overall spectral index	0.8
Radio source largest linear size	180 h^-1 kpc
Arcsec to kpc conversion factor	1 $^{\prime \prime }$ = 0.63 h^-1 kpc
$h={\rm H}_{0}/100 {\rm ~km~s^{-1} Mpc^{-1}}$ , q₀=0.5.
We use the convention $S_{\nu}\propto \nu^{-\alpha}$ .

2 The VLA observations and data reduction

A summary of the observations, including the VLA configuration, frequency, bandwidth, date and length of observations, is reported in Table 2.

Table 2: VLA observations summary.
Array Frequency Bandwidth Date Duration

GHz MHz hours

A 1.41/1.66 12.5 02-Dec.-1984 8.0

A 4.86 12.5 03-Dec.-1984 1.0

B 4.86 25.0 22-May-1985 3.0

B 14.96 25.0 22-May-1985 0.9

C 1.41/1.66 50.0 28-Sep.-1985 0.5

C 4.86 50.0 28-Sep.-1985 0.5

C 14.96 50.0 28-Sep.-1985 7.1

D 4.83 50.0 28-Sep.-2000 0.5

D 8.46 50.0 28-Sep.-2000 1.4

D 14.96 50.0 23-Nov.-1985 0.4

**Table 2:** VLA observations summary.
Array	Frequency	Bandwidth	Date	Duration
	GHz	MHz		hours
A	1.41/1.66	12.5	02-Dec.-1984	8.0
A	4.86	12.5	03-Dec.-1984	1.0
B	4.86	25.0	22-May-1985	3.0
B	14.96	25.0	22-May-1985	0.9
C	1.41/1.66	50.0	28-Sep.-1985	0.5
C	4.86	50.0	28-Sep.-1985	0.5
C	14.96	50.0	28-Sep.-1985	7.1
D	4.83	50.0	28-Sep.-2000	0.5
D	8.46	50.0	28-Sep.-2000	1.4
D	14.96	50.0	23-Nov.-1985	0.4

The flux densities were brought to the scale of Baars et al. (1997) using 3C48 as primary flux density calibrator. The instrumental polarization and the polarization position angle were calibrated using the sources 0116+319 (0042+233 for 6 and 3.5 cm D array) and 3C 138 respectively. The 3C 138 polarization angle was assumed to have a value of -18 $^\circ$ at L band and -24 $^\circ$ at higher frequencies. Post calibration reduction was done using the National Radio Observatory (NRAO) AIPS package. The data for each observation were reduced using the standard self-calibration and cleaning procedures. The C array observation at 20 cm, already presented by Parma et al. (1991), has been reanalyzed for the purposes of this project.

Table 3: Image parameters summary.
Array Frequency Beam $\sigma_{\rm I}$

GHz arcsec mJy/beam

A 1.41 $1\hbox{$.\!\!^{\prime\prime}$ }47 \times 1\hbox{$.\!\!^{\prime\prime}$ }24$ 0.05

A 1.66 $1\hbox{$.\!\!^{\prime\prime}$ }32 \times 1\hbox{$.\!\!^{\prime\prime}$ }05$ 0.05

B 4.86 $1\hbox{$.\!\!^{\prime\prime}$ }19 \times 1\hbox{$.\!\!^{\prime\prime}$ }14$ 0.029

C 1.41 $13\hbox{$.\!\!^{\prime\prime}$ }82 \times 12\hbox{$.\!\!^{\prime\prime}$ }77$ 0.024

C 1.66 $11\hbox{$.\!\!^{\prime\prime}$ }51 \times 10\hbox{$.\!\!^{\prime\prime}$ }71$ 0.021

C 4.86 $3\hbox{$.\!\!^{\prime\prime}$ }99 \times 3\hbox{$.\!\!^{\prime\prime}$ }77$ 0.025

C 14.96 $1\hbox{$.\!\!^{\prime\prime}$ }46 \times 1\hbox{$.\!\!^{\prime\prime}$ }25$ 0.034

D 4.83 $14\hbox{$.\!\!^{\prime\prime}$ }08 \times 12\hbox{$.\!\!^{\prime\prime}$ }81$ 0.06

D 8.46 $8\hbox{$.\!\!^{\prime\prime}$ }97 \times 7\hbox{$.\!\!^{\prime\prime}$ }83$ 0.05

D 14.96 $7\hbox{$.\!\!^{\prime\prime}$ }31 \times 4\hbox{$.\!\!^{\prime\prime}$ }16$ 0.08

$\textstyle \parbox{7.5cm}{Column 4: total intensity image noise.}$

**Table 3:** Image parameters summary.
Array	Frequency	Beam	$\sigma_{\rm I}$
	GHz	arcsec	mJy/beam
A	1.41	$1\hbox{$.\!\!^{\prime\prime}$ }47 \times 1\hbox{$.\!\!^{\prime\prime}$ }24$	0.05
A	1.66	$1\hbox{$.\!\!^{\prime\prime}$ }32 \times 1\hbox{$.\!\!^{\prime\prime}$ }05$	0.05
B	4.86	$1\hbox{$.\!\!^{\prime\prime}$ }19 \times 1\hbox{$.\!\!^{\prime\prime}$ }14$	0.029
C	1.41	$13\hbox{$.\!\!^{\prime\prime}$ }82 \times 12\hbox{$.\!\!^{\prime\prime}$ }77$	0.024
C	1.66	$11\hbox{$.\!\!^{\prime\prime}$ }51 \times 10\hbox{$.\!\!^{\prime\prime}$ }71$	0.021
C	4.86	$3\hbox{$.\!\!^{\prime\prime}$ }99 \times 3\hbox{$.\!\!^{\prime\prime}$ }77$	0.025
C	14.96	$1\hbox{$.\!\!^{\prime\prime}$ }46 \times 1\hbox{$.\!\!^{\prime\prime}$ }25$	0.034
D	4.83	$14\hbox{$.\!\!^{\prime\prime}$ }08 \times 12\hbox{$.\!\!^{\prime\prime}$ }81$	0.06
D	8.46	$8\hbox{$.\!\!^{\prime\prime}$ }97 \times 7\hbox{$.\!\!^{\prime\prime}$ }83$	0.05
D	14.96	$7\hbox{$.\!\!^{\prime\prime}$ }31 \times 4\hbox{$.\!\!^{\prime\prime}$ }16$	0.08

The angular size of NGC 326 exceeds 4.4 arcmin. This represents a problem for high frequency imaging since the radio structure size is comparable to the field of view of a single VLA antenna. The old 2 cm observations suffered from this effect. Learning from experience, we followed a specific observation strategy with the more recent 3.5 cm observations. In order to reduce the problems due to the strong primary beam attenuation we splitted the observations into two different pointings centered at appropriate positions on the wings of the source. The two data sets were reduced independently and the resulting couple of images was then combined using the task LTESS in AIPS. Table 3 summarize the relevant parameters of the single-array images.

Data from different arrays were combined to improve uv-coverage and sensitivity. We combined the A and C arrays at 20 cm, the B, C and D at 6 cm, and the C and D at 2 cm. Each combined data set was self-calibrated. The images at different frequencies were cleaned and restored with the same beam using the AIPS task IMAGR. The "original'' beams were very similar to the finally adopted ones. For the purposes of the spectral and polarization analysis we made data sets composed of matched resolution images, using natural and uniform weighting. Finally we obtained four distinct resolution data sets with exactly the same cut in the maximum uv baseline at each frequency. Their resolutions are 10 $^{\prime \prime }$ , 4 $^{\prime \prime }$ , 2 $^{\prime \prime }$ , and 1 $.\!\!^{\prime\prime}$ 2.

Table 4: Combined array image parameters. The uv weighting function is indicated just after the frequency. UW and NW stand for uniform and natural weights, respectively.
Array Frequency $\sigma_{I}$ $\sigma_{Q,U}$

GHz mJy/beam mJy/beam

$10\hbox{$^{\prime\prime}$ }\times 10\hbox{$^{\prime\prime}$ }$ beam

A+C 1.41 UW 0.22 0.13

A+C 1.66 UW 0.24 0.14

C+D 4.86 NW 0.07 0.06

D 8.46 NW 0.07 0.01

C+D 14.96 NW 0.20 0.07

$4\hbox {$^{\prime \prime }$ }\times 4\hbox {$^{\prime \prime }$ }$ beam

A+C 1.41 NW 0.07 0.04

A+C 1.66 NW 0.08 0.05

B+C 4.86 NW 0.05 0.03

C+D 14.96 NW 0.04 0.04

$2\hbox {$^{\prime \prime }$ }\times 2\hbox {$^{\prime \prime }$ }$ beam

A+C 1.41 NW 0.04 0.03

A+C 1.66 NW 0.05 0.04

B+C 4.86 NW 0.04 0.03

C+D 14.96 NW 0.03 0.03

$1\hbox{$.\!\!^{\prime\prime}$ }2 \times 1\hbox{$.\!\!^{\prime\prime}$ }2$ beam

A 1.41 UW 0.06 0.06

A 1.66 UW 0.07 0.07

B+C 4.86 UW 0.04 0.05

C+D 14.96 UW 0.04 0.06

$\textstyle \parbox{8cm}{ Column 3: total intensity image noise;\\ Column 4: polarization image noise.}$

**Table 4:** Combined array image parameters. The uv weighting function is indicated just after the frequency. UW and NW stand for uniform and natural weights, respectively.
Array	Frequency	$\sigma_{I}$	$\sigma_{Q,U}$
	GHz	mJy/beam	mJy/beam
$10\hbox{$^{\prime\prime}$ }\times 10\hbox{$^{\prime\prime}$ }$ beam
A+C	1.41 UW	0.22	0.13
A+C	1.66 UW	0.24	0.14
C+D	4.86 NW	0.07	0.06
D	8.46 NW	0.07	0.01
C+D	14.96 NW	0.20	0.07
$4\hbox {$^{\prime \prime }$ }\times 4\hbox {$^{\prime \prime }$ }$ beam
A+C	1.41 NW	0.07	0.04
A+C	1.66 NW	0.08	0.05
B+C	4.86 NW	0.05	0.03
C+D	14.96 NW	0.04	0.04
$2\hbox {$^{\prime \prime }$ }\times 2\hbox {$^{\prime \prime }$ }$ beam
A+C	1.41 NW	0.04	0.03
A+C	1.66 NW	0.05	0.04
B+C	4.86 NW	0.04	0.03
C+D	14.96 NW	0.03	0.03
$1\hbox{$.\!\!^{\prime\prime}$ }2 \times 1\hbox{$.\!\!^{\prime\prime}$ }2$ beam
A	1.41 UW	0.06	0.06
A	1.66 UW	0.07	0.07
B+C	4.86 UW	0.04	0.05
C+D	14.96 UW	0.04	0.06

$\begin{figure} \par\includegraphics[angle=-90, width=18cm]{H3092F1.ps}\end{figure}$	Figure 1: 1.4 GHz C array (contours) overlayed onto the optical image from the red Palomar Digitized Sky Survey. The contour levels are 0.5, 0.71, 1, 1.4, 2, 2.8, 4, 5.7, 8, 11, 16, 23, 32, 45, 64, 91, 130, 180 mJy (beam area)^-1 and the restoring beam is $13\hbox{$.\!\!^{\prime\prime}$ }8 \times 12\hbox{$.\!\!^{\prime\prime}$ }8$ with position angle $-16.9\hbox {$^\circ $ }$ .
Open with DEXTER

The equal resolution data sets are given in Table 4. All the images were corrected for primary beam attenuation. NGC 326 is significantly polarized at all frequencies and resolutions. We produced images of the scalar fractional polarization ( $P_{\nu}$ ), depolarization ( $DP^{\nu_{1}}_{\nu_{2}}$ , defined as the ratio between the fractional polarization at $\nu_{1}$ and $\nu_{2}$ ) and rotation measure (RM). The polarization images were corrected for the non-Gaussian noise distribution of the polarized intensity. The RM was obtained using the AIPS task RM by a weighted fit of the position angle to the square wavelength at four frequencies.

The spectral analysis has been performed with the program Synage++ (Murgia 2001).

3 Source morphology, spectrum and polarization

$\begin{figure} \par\includegraphics[width=10cm, angle=-90]{H3092F2.ps}\end{figure}$

Figure 2: 8.5 GHz D array image of NGC 326. The contour levels are 0.15, 0.34, 0.69, 1.4, 2.9, 5.8, 12, 24 mJy (beam area)^-1 and the restoring beam is $9\hbox{$^{\prime\prime}$ }\times 7\hbox{$.\!\!^{\prime\prime}$ }8$ . The vectors lengths are proportional to the degree of polarization, with 100 per cent corresponding to 20 arcsec on the sky, and their directions are those of the ${\vec E}$ -vector. The unresolved source at the tip of the east wing is a flat-spectrum background object.

Open with DEXTER

3.1 Wings and plume

The wings bend and extend away from the lobe axis almost by the same extent ( $2^{\prime}$ ). As already noted by Worrall et al. (1995), the overall "Z''-shape symmetry of the source is broken by a low surface brightness plume located just above the end of east wing. This plume, evident only in the 20 cm and 6 cm images, does not follow the source symmetry. Figure 1 shows a galaxy which is located, in projection, in the middle of the plume. This corresponds to galaxy G6 of Werner et al. (1999) with a radial velocity difference of 1026 km s^-1 with respect to the center of the cluster. If G6 is a cluster member it moves very fast relatively to the intra-cluster medium (slightly more than twice the line-of-sight velocity dispersion). Since the sound speed in the cluster is $\sim$ 650 km s^-1, the motion of G6 would be supersonic. Anyway, the association of G6 to the plume is unclear.

$\begin{figure} \par\includegraphics[width=13.5cm, angle=-90]{H3092F5.ps}\end{figure}$	Figure 5: 1.4 GHz A+C array. The contour levels are 0.25, 0.39, 0.61, 0.96, 1.5, 2.3, 3.7, 5.7, 9, 14, 22 mJy (beam area)^-1 and the restoring beam is $4\hbox {$^{\prime \prime }$ }\times 4\hbox {$^{\prime \prime }$ }$ .
Open with DEXTER

Figure 2 presents the 8.5 GHz map, with the ${\vec E}$ -field vectors superimposed (not corrected for RM, see below). The mean polarization percentage (10 $\hbox{$^{\prime\prime}$ }$ beam) in the wings is $\simeq$ 4% at 1.4 GHz and $\simeq$ 17% at 4.8 and 8.5 GHz. Both wings show depolarization between 4.8 and 1.4 GHz: the mean values of DP^1.4_4.8 (10 $^{\prime \prime }$ beam) are 0.3 and 0.2 for the east and west wing respectively. We calculated the RM at 10 $^{\prime \prime }$ resolution between the frequencies 1.4, 1.6, 4.8 and 8.5 GHz. We found a mean value of $-25\pm 5$ rad m^-2, which is consistent with the galactic value (Simard-Normandin et al. 1981), and a standard deviation $\sigma_{\rm RM}=52$ rad m^-2. Given this value for the rotation measure, the apparent magnetic field direction at 8.5 and 4.8 GHz is within few degrees from the real one.

The apparent magnetic field is longitudinal and highly aligned along the main ridge of emission in both the east and, at least in the first part of, the west wing. At the wing edges the magnetic field bends to a circumferential configuration.

The surface brightness of the plume is too low to give a reliable polarization measure.

At a resolution of 10 $^{\prime \prime }$ , the radio spectrum of the wings between 1.4 and 8.5 GHz can be computed out to their full extent. Figure 4 shows a plot of the two-frequency spectral indices, $\alpha ^{1.4}_{4.8}$ and $\alpha ^{4.8}_{8.5}$ , as a function of the position along the two wings. The spectral indices have been sampled in circular boxes, of the same size as the beam, centered on the ridge lines of maximum emission. In the east wing there is a clear monotonically steepening of the radio spectrum from the south lobe to the end of the wing: $\alpha ^{1.4}_{4.8}$ and $\alpha ^{4.8}_{8.5}$ increase from 0.6 and 0.7 up to 1.3 and 1.9, respectively. The west wing shows a different spectral behavior: $\alpha ^{1.4}_{4.8}$ and $\alpha ^{4.8}_{8.5}$ , increase respectively from 0.6 and 0.7, close to north lobe, up to 1.3 and 1.5, at a distance of $\sim$ $60\hbox{$^{\prime\prime}$ }$ (38 h^-1 kpc). In the remaining part of the wing, $\alpha ^{1.4}_{4.8}$ and $\alpha ^{4.8}_{8.5}$ decrease and saturate to 1.0 and 1.3, respectively.

The resolution of our images allows us to trace spectral index trends also along directions perpendicular to the wing ridge lines. There are significant lateral spectral index gradients with marked differences between the two wings.

The detailed analysis of these spectral index profiles will be presented in Paper II.

$\begin{figure} \par\includegraphics[width=17cm, angle=0]{H3092F6.ps}\end{figure}$

Figure 6: Top panel: 4.8 GHz B+C array total intensity image. The contour levels are 0.14, 0.22, 0.36, 0.58, 0.93, 1.5, 2.4, 3.9, 6.2, 10 mJy (beam area)^-1. The vectors lengths are proportional to the degree of polarization, with 100 per cent corresponding to 10 arcsec on the sky, and their directions are those of the ${\vec E}$ -vector. Bottom panel: 1.4 GHz A+C array gradient image (AIPS task NINER). In both images the restoring beam is $2\hbox {$^{\prime \prime }$ }\times 2\hbox {$^{\prime \prime }$ }$ .

Open with DEXTER

3.2 Lobes

The mean polarization percentage at 8.5 GHz (10 $^{\prime \prime }$ beam) is 12% and 14% in the south and north lobe, respectively (see Fig. 2). Figure 6 presents the 4.8 GHz image at 2 $^{\prime \prime }$ resolution, with the ${\vec E}$ -field vectors superimposed (not corrected for RM, see Sect. 3.1). The mean scalar fractional polarization at 4.8 GHz is 23% and 29% for the south and north lobe, respectively. The variation of the fractional point to point polarization at 4.8 GHz is strongly correlated with the enhancements seen in the total intensity gradient image. In the lateral edges of the northern lobe and in the frontal head of the southern lobe, the fractional polarization P_4.8 is about 43%. In the sharp western edge of the east wing P_4.8 reaches a value of $\sim$ 50%. The mean values of DP^1.4_4.8 (10 $\hbox{$^{\prime\prime}$ }$ beam) are 0.23 and 0.17 in south and north lobe, respectively, while at 2 $^{\prime \prime }$ resolution they go up to 0.52 and 0.48. In both lobes, the mean RM at 10 $^{\prime \prime }$ resolution is about -20 rad m^-2. As a consequence the Faraday rotation is negligible at 4.8 GHz and the apparent magnetic field in the lobes is circumferential, consistently with the configuration deduced from the lower resolution 8.5 GHz map. The magnetic field configuration is also circumferential around the shell structure, where the fractional polarization P_4.8 is about 30%.

The mean fractional polarization of the lobes as function of frequency and beam area is shown in Fig. 7.

Table 5: Lobes and wings properties. The corresponding regions are those indicated in Fig. 3.
South Lobe North Lobe East Wing West Wing Plume

$S_{\rm 20cm}$ (mJy) 213 576 536 288 18

$\theta_{1}\times\theta_{2}$ (arcsec) $30\times 22$ $60\times 32$ $100\times 50$ $110\times 60$ $90\times 60$

$d_{1} \times d_{2}$ (kpc) $22\times 14$ $38\times 20$ $63\times 32$ $69\times 38$ $57\times 38$

$\langle\alpha_{4.8}^{1.4}\rangle$ $0.60 \pm 0.04$ $0.64 \pm 0.02$ $0.90\pm 0.01$ $1.04\pm 0.01$ $2.37\pm 0.02$

$\langle P_{1.4} \rangle$ , 10 $^{\prime \prime }$ beam
3% 2.5% 6% 3% -

$\langle P_{4.8} \rangle$ , 10 $^{\prime \prime }$ beam 13% 15% 22% 16% -

$\langle P_{8.5} \rangle$ , 10 $^{\prime \prime }$ beam 12% 14% 17% 14% -

$\langle P_{1.4} \rangle$ , 2 $^{\prime \prime }$ beam
12% 14% - - -

$\langle P_{4.8} \rangle$ , 2 $^{\prime \prime }$ beam 23% 29% - - -

$\langle DP^{1.4}_{4.8} \rangle$ , 10 $^{\prime \prime }$ beam
0.23 0.17 0.27 0.18 -

$\langle DP^{1.4}_{4.8} \rangle$ , 2 $^{\prime \prime }$ beam 0.52 0.48 - - -

$\langle RM \rangle$ (rad m^-2) $-21\pm 6$ $-18 \pm 4$ $-34 \pm 2$ $-32\pm 6$ -

$\langle \sigma_{\rm RM} \rangle$ (rad m^-2) 57 52 35 65 -

**Table 5:** Lobes and wings properties. The corresponding regions are those indicated in Fig. 3.
	South Lobe	North Lobe	East Wing	West Wing	Plume
$S_{\rm 20cm}$ (mJy)	213	576	536	288	18
$\theta_{1}\times\theta_{2}$ (arcsec)	$30\times 22$	$60\times 32$	$100\times 50$	$110\times 60$	$90\times 60$
$d_{1} \times d_{2}$ (kpc)	$22\times 14$	$38\times 20$	$63\times 32$	$69\times 38$	$57\times 38$
$\langle\alpha_{4.8}^{1.4}\rangle$	$0.60 \pm 0.04$	$0.64 \pm 0.02$	$0.90\pm 0.01$	$1.04\pm 0.01$	$2.37\pm 0.02$
$\langle P_{1.4} \rangle$ , 10 $^{\prime \prime }$ beam	3%	2.5%	6%	3%	-
$\langle P_{4.8} \rangle$ , 10 $^{\prime \prime }$ beam	13%	15%	22%	16%	-
$\langle P_{8.5} \rangle$ , 10 $^{\prime \prime }$ beam	12%	14%	17%	14%	-
$\langle P_{1.4} \rangle$ , 2 $^{\prime \prime }$ beam	12%	14%	-	-	-
$\langle P_{4.8} \rangle$ , 2 $^{\prime \prime }$ beam	23%	29%	-	-	-
$\langle DP^{1.4}_{4.8} \rangle$ , 10 $^{\prime \prime }$ beam	0.23	0.17	0.27	0.18	-
$\langle DP^{1.4}_{4.8} \rangle$ , 2 $^{\prime \prime }$ beam	0.52	0.48	-	-	-
$\langle RM \rangle$ (rad m^-2)	$-21\pm 6$	$-18 \pm 4$	$-34 \pm 2$	$-32\pm 6$	-
$\langle \sigma_{\rm RM} \rangle$ (rad m^-2)	57	52	35	65	-

$\begin{figure} \par\includegraphics[width=18cm]{H3092F8.ps}\end{figure}$	Figure 8: Spectral index profiles along the lobes at 2 $.\!\!^{\prime\prime}$ resolution. The filled and open dots refer to $\alpha ^{1.4}_{4.8}$ and $\alpha ^{4.8}_{14.9}$ , respectively. The shaded box indicates the region excluded from the spectral index calculation.
Open with DEXTER

We have computed the average two-frequency spectral indices $\alpha ^{1.4}_{4.8}$ and $\alpha ^{4.8}_{14.9}$ along slices perpendicular to the lobe axis from the lobe head back to the core using the 2 $^{\prime \prime }$ resolution images. Slices are 3 $^{\prime \prime }$ wide, so that the spectral index measures are practically independent. The regions containing the core and the jet in the northern lobe have been excluded from the statistics. Figure 8 shows the spectral index trends in the lobes. In the south lobe $\alpha ^{1.4}_{4.8}$ is roughly constant around a value of 0.6 with a moderate increase to 0.7 at the lobe end; $\alpha ^{4.8}_{14.9}$ increases from 0.7 to 1.3. The spectral behavior of the north lobe is somewhat complex: $\alpha ^{1.4}_{4.8}$ and $\alpha ^{4.8}_{14.9}$ decrease respectively from 0.75 and 1.35, at the lobe head, to 0.65 and 0.9, stay constant from 10 $^{\prime \prime }$ to 30 $^{\prime \prime }$ , and then increase again up to 1.0 and 1.6 in proximity of the core. The interpretation of the spectral profiles in the north lobe should be considered with caution since it is quite possible that the lobe, the jet and part of the west wing are overlapping each other because of projection effects.

3.3 Jets

The fractional polarization P_4.8 is about 14% in the east jet. The overlap with the lobe and the wing precludes estimation of the fractional polarization in the west jet. The apparent magnetic field is transverse in the east jet, whereas in the west jet it is initially transverse and becomes longitudinal in correspondence with the shell.
We derived the spectral index between 1.4 and 4.8 GHz along the two jets as a function of the distance from the core using the 2 $^{\prime \prime }$ resolution images. The resulting trends are shown in Fig. 10. The spectral index stays almost constant at a value of 0.6 along both jets, although a significant scatter is present in the east jet.

3.4 Radio cores

$\begin{figure} \par\includegraphics[width=14.5cm, angle=0]{H3092F9.ps}\end{figure}$	Figure 9: 1.4 GHz A array (contours) overlaid with the HST image of the dumbbell galaxies (grayscale). The contour levels are 0.23, 0.33, 0.48, 0.71, 0.85, 1.1, 1.6, 2.3, 3.4, 4.8 mJy (beam area)^-1 and the restoring beam is $1\hbox{$.\!\!^{\prime\prime}$ }2 \times 1\hbox{$.\!\!^{\prime\prime}$ }2$ .
Open with DEXTER

The radio spectra of the two cores between 1.4 and 14.9 GHz are shown in Fig. 11. Core 1 has a convex radio spectrum which peaks at about 10 GHz. Core 2 has a powerlaw radio spectrum with an index of 0.3.

Table 6 summarizes the parameters of the two cores derived from the images at 1 $.\!\!^{\prime\prime}$ 2 resolution.

4 Collimation and surface brightness of the jets

We analyzed the evolution of jet collimation and surface brightness as a function of the distance from core.

Table 6: Core properties.
core 1 core 2

1.4 GHz position ( $\alpha_{\rm J2000})$ 00 $^{\rm h}$ 58 $^{\rm m}$ 22 $.\!\!^{\prime\prime}$ 6 00 $^{\rm h}$ 58 $^{\rm m}$ 22 $.\!\!^{\prime\prime}$ 9

1.4 GHz position ( $\delta_{\rm J2000})$ +26 $^\circ$ 51 $^\prime$ 58 $.\!\!^{\prime\prime}$ 7 +26 $^\circ$ 51 $^\prime$ 52 $.\!\!^{\prime\prime}$ 7

$S_{\rm {1.4~GHz}}$ (mJy) $5.33\pm 0.04$ $1.16\pm 0.04$

$S_{\rm {4.8~GHz}}$ (mJy) $10.42\pm 0.03$ $0.78\pm 0.03$

$\alpha_{4.8}^{1.4}$ -0.5 0.3

$P_{\rm {1.4~GHz}}$ (h^-2 WHz^-1) $1.2\times10^{22}$ $2.7\times10^{21}$

$P_{\rm {4.8~GHz}}$ (h^-2 WHz^-1) $2.3\times10^{22}$ $1.8\times10^{21}$

**Table 6:** Core properties.
	core 1	core 2
1.4 GHz position ( $\alpha_{\rm J2000})$	00 $^{\rm h}$ 58 $^{\rm m}$ 22 $.\!\!^{\prime\prime}$ 6	00 $^{\rm h}$ 58 $^{\rm m}$ 22 $.\!\!^{\prime\prime}$ 9
1.4 GHz position ( $\delta_{\rm J2000})$	+26 $^\circ$ 51 $^\prime$ 58 $.\!\!^{\prime\prime}$ 7	+26 $^\circ$ 51 $^\prime$ 52 $.\!\!^{\prime\prime}$ 7
$S_{\rm {1.4~GHz}}$ (mJy)	$5.33\pm 0.04$	$1.16\pm 0.04$
$S_{\rm {4.8~GHz}}$ (mJy)	$10.42\pm 0.03$	$0.78\pm 0.03$
$\alpha_{4.8}^{1.4}$	-0.5	0.3
$P_{\rm {1.4~GHz}}$ (h^-2 WHz^-1)	$1.2\times10^{22}$	$2.7\times10^{21}$
$P_{\rm {4.8~GHz}}$ (h^-2 WHz^-1)	$2.3\times10^{22}$	$1.8\times10^{21}$

In order to quantify the variations of surface brightness and width along the jets, we produced intensity profiles perpendicular to the jet axis for distances up to 40 $^{\prime \prime }$ and 20 $^{\prime \prime }$ from the core, for the east and west jet, respectively. After having removed a baseline component, the transverse brightness profiles are well fitted by a simple Gaussian over most of the jet length.

We used both the 2 $^{\prime \prime }$ and 1 $.\!\!^{\prime\prime}$ 2 resolution images at 20 cm. We measured the peak surface brightness I₀ and FWHM $\Phi_{0}$ and derived the deconvolved values I and $\Phi$ by the first-order corrections:

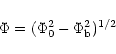
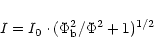
Apart for the initial region ( $\Theta<~12\hbox{$^{\prime\prime}$ }$ ), where the jets are quite symmetric (see below), the dependence of $\Phi$ and I on $\Theta$ are very different for the east and the west jet. The east jet spreads gradually up to 40 $^{\prime \prime }$ from the core, but has local regions that deviate significantly from the mean. Its deconvolved surface brightness drops by an order of magnitude going from the core to a distance of 15 $^{\prime \prime }$ . Then, after a local knot of emission at $\Theta= 20\hbox{$^{\prime\prime}$ }$ , I decreases slowly for the remaining 20 $^{\prime \prime }$ . On the contrary, the west jet expands abruptly at 12 $^{\prime \prime }$ from the core. Its deconvolved brightness initially decreases to a local minimum at $\Theta= 12\hbox{$^{\prime\prime}$ }$ and then raises again peaking at $\Theta= 14\hbox{$^{\prime\prime}$ }$ . Beyond this peak the jet decollimates originating the shell-like structure.

The east/west width ratio within 12 $^{\prime \prime }$ from the core has a mean value of 0.98 and a range from 0.7 to 1.4. The surface brightness ratio has a mean value of 1.2 and a range from 0.49, at 2 $.\!\!^{\prime\prime}$ 4 from the core, to 2, at 4 $.\!\!^{\prime\prime}$ 2 from the core. The overall jet symmetry for $\Theta< 12\hbox{$^{\prime\prime}$ }$ suggests that the jet axes, at least at their base, lie in the plane of the sky. The asymmetry observed at larger distances may be due to strong projection effects and/or differences in the density of the gas surrounding the source.

Both jets exhibit an average flat $I(\Phi )$ relation ( $I \propto \Phi^{-1.35}$ , see Fig. 13). This behaviour indicates either that they depart significantly from the assumption of adiabatic flow, or they must be subject to a rapid longitudinal deceleration (Fanti et al. 1982). For example, for a jet with no longitudinal component of magnetic field and a spectral index of 0.6 the adiabatic condition implies $I \propto \Phi^{-3.4} v_{\rm j}^{-3}$ , where $v_{\rm j}$ is the jet velocity; in this case the required deceleration would be $v_{\rm j}\propto \Phi^{-0.68}$ .

5 Physical parameters of the source

5.1 Lobes and wings

$\begin{figure} \par\includegraphics[width=18cm]{H3092F12.ps}\end{figure}$	Figure 12: Top: deconvolved jets FWHM $\Phi$ (left panel) and brightness I (right panel) profiles from the 2 $^{\prime \prime }$ resolution 20 cm image. Bottom: deconvolved FWHM (left panel) and brightness (right panel) ratios from the 1 $.\!\!^{\prime\prime}$ 2 resolution 20 cm image.
Open with DEXTER

Table 7: Global equipartition parameters.
$U_{\rm tot}$ $u_{\rm min}$ $P_{\rm eq}$ $B_{\rm eq}$

erg erg/cm³ dyne/cm² $\mu$ G

N-Lobe $6.2\times10^{56}$ $9.3\times10^{-12}$ $3.1\times10^{-12}$ 10.0

S-Lobe $3.4\times10^{56}$ $5.1\times10^{-12}$ $1.7\times10^{-12}$ 7.4

W-Wing $3.3\times10^{57}$ $1.4\times10^{-12}$ $4.8\times10^{-13}$ 3.9

E-Wing $3.1\times10^{57}$ $2.1\times10^{-12}$ $6.9\times10^{-13}$ 4.7

**Table 7:** Global equipartition parameters.
	$U_{\rm tot}$	$u_{\rm min}$	$P_{\rm eq}$	$B_{\rm eq}$
	erg	erg/cm³	dyne/cm²	$\mu$ G
N-Lobe	$6.2\times10^{56}$	$9.3\times10^{-12}$	$3.1\times10^{-12}$	10.0
S-Lobe	$3.4\times10^{56}$	$5.1\times10^{-12}$	$1.7\times10^{-12}$	7.4
W-Wing	$3.3\times10^{57}$	$1.4\times10^{-12}$	$4.8\times10^{-13}$	3.9
E-Wing	$3.1\times10^{57}$	$2.1\times10^{-12}$	$6.9\times10^{-13}$	4.7

Table 8: Wings equipartition parameters ( $\alpha =0.6$ ).
distance $u_{\rm min}$ $P_{\rm eq}$ $B_{\rm eq}$

arcsec erg/cm³ dyne/cm² $\mu$ G

West Wing

26 $2.3\times10^{-12}$ $7.7\times10^{-13}$ 5.0

36 $1.7\times10^{-12}$ $5.7\times10^{-13}$ 4.3

43 $8.2\times10^{-13}$ $2.7\times10^{-13}$ 3.0

53 $7.5\times10^{-13}$ $2.5\times10^{-13}$ 2.8

62 $7.1\times10^{-13}$ $2.4\times10^{-13}$ 2.8

72 $7.3\times10^{-13}$ $2.4\times10^{-13}$ 2.8

83 $8.2\times10^{-13}$ $2.7\times10^{-13}$ 3.0

93 $8.1\times10^{-13}$ $2.7\times10^{-13}$ 2.9

103 $7.7\times10^{-13}$ $2.6\times10^{-13}$ 2.9

113 $1.8\times10^{-12}$ $5.9\times10^{-13}$ 4.4

East Wing

16 $3.3\times10^{-12}$ $1.1\times10^{-12}$ 5.9

28 $3.6\times10^{-12}$ $1.2\times10^{-12}$ 6.2

38 $3.6\times10^{-12}$ $1.2\times10^{-12}$ 6.2

45 $2.2\times10^{-12}$ $7.5\times10^{-13}$ 4.9

53 $2.0\times10^{-12}$ $6.8\times10^{-13}$ 4.7

63 $2.0\times10^{-12}$ $6.7\times10^{-13}$ 4.6

73 $1.6\times10^{-12}$ $5.4\times10^{-13}$ 4.2

82 $1.2\times10^{-12}$ $3.9\times10^{-13}$ 3.6

93 $1.2\times10^{-12}$ $4.0\times10^{-13}$ 3.6

103 $1.4\times10^{-12}$ $5.2\times10^{-13}$ 4.1

**Table 8:** Wings equipartition parameters ( $\alpha =0.6$ ).
distance	$u_{\rm min}$	$P_{\rm eq}$	$B_{\rm eq}$
arcsec	erg/cm³	dyne/cm²	$\mu$ G
West Wing
26	$2.3\times10^{-12}$	$7.7\times10^{-13}$	5.0
36	$1.7\times10^{-12}$	$5.7\times10^{-13}$	4.3
43	$8.2\times10^{-13}$	$2.7\times10^{-13}$	3.0
53	$7.5\times10^{-13}$	$2.5\times10^{-13}$	2.8
62	$7.1\times10^{-13}$	$2.4\times10^{-13}$	2.8
72	$7.3\times10^{-13}$	$2.4\times10^{-13}$	2.8
83	$8.2\times10^{-13}$	$2.7\times10^{-13}$	3.0
93	$8.1\times10^{-13}$	$2.7\times10^{-13}$	2.9
103	$7.7\times10^{-13}$	$2.6\times10^{-13}$	2.9
113	$1.8\times10^{-12}$	$5.9\times10^{-13}$	4.4
East Wing
16	$3.3\times10^{-12}$	$1.1\times10^{-12}$	5.9
28	$3.6\times10^{-12}$	$1.2\times10^{-12}$	6.2
38	$3.6\times10^{-12}$	$1.2\times10^{-12}$	6.2
45	$2.2\times10^{-12}$	$7.5\times10^{-13}$	4.9
53	$2.0\times10^{-12}$	$6.8\times10^{-13}$	4.7
63	$2.0\times10^{-12}$	$6.7\times10^{-13}$	4.6
73	$1.6\times10^{-12}$	$5.4\times10^{-13}$	4.2
82	$1.2\times10^{-12}$	$3.9\times10^{-13}$	3.6
93	$1.2\times10^{-12}$	$4.0\times10^{-13}$	3.6
103	$1.4\times10^{-12}$	$5.2\times10^{-13}$	4.1

Therefore the inner radio lobes appear to be close to the pressure of the external gas while the wings appear to be under-pressured by a factor of 10.

5.2 Jets

From the X-ray luminosity reported by Worrall et al. (1995) for the hot galactic corona (i.e. 10⁴¹ h^-2 erg/s), we computed the expected external pressure on the jets. We assumed for the corona a temperature of 1 keV and a gas density profile $n=n_{0}\cdot\left(1+(r/r_{\rm c})^{2} \right)^{-b}$ , where n₀ is the central density while r and $r_{\rm c}$ are the distance from the galaxy and the corona core radius, respectively. We found that the jets are roughly in pressure equilibrium with the surrounding gas (see Fig. 15) for a corona core radius $r_{\rm c}= 3~h^{-1}$ kpc and b=3; in this case the central density results $n_{0}\simeq 0.2 ~h^{1/2}$ cm^-3. A model with $r_{\rm c}= 2~h^{-1}$ kpc, b=2 and $n_{0}\simeq 0.3 ~h^{1/2}$ cm^-3 gives an equivalent result.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{H3092F15.ps}\end{figure}$	Figure 15: Minimum energy magnetic field (solid line, left y-axis) and pressure (dashed line, right y-axis) in the jets. The dotted line represents the expected thermal pressure from the cluster gas and from the hot galactic corona model described in the text.
Open with DEXTER

6 Summary

The source structure is complex at all resolutions and may be dominated by projection effects.

At the lowest resolution the twin wings appear fairly symmetric but the "Z''-shape is disturbed by a plume of low surface brightness and very steep spectral index ( $\alpha > 2$ ). The plume overlaps, in projection, a possible fast-moving member of the galaxy cluster.

At the intermediate resolution of about 4 $^{\prime \prime }$ the source lobes appear asymmetric in shape, size, brightness and projected distance from the core. No compact components (hostspots) are present in the lobes.

At higher resolution, the jets are very symmetric in both flux density and width within the inner 12 $^{\prime \prime }$ from the core. This indicates that the axis of the jets, at least at their base, lies on the plane of the sky. Beyond this distance, the east jet bends gradually with a curvature radius of about 70 $^{\prime \prime }$ reaching the south lobe. The west jet is straight but, after recollimation expands abruptly, giving rise to a shell-like structure embedded in the north lobe.

Overlapping our highest resolution VLA images of the core region with the HST image of the dumbbell, we found that also the companion of the radio galaxy hosts a radio core.

NGC 326 is significantly polarized at all frequencies and resolutions. The magnetic field configuration is circumferential in the lobes and highly aligned with the ridge of emission in the wings. We traced the profile of the spectral index between 1.4 and 8.5 GHz for the entire wing length. The spectral index increases gradually going from the regions in proximity of the lobes to the wing ends. The spectral index distribution in the lobes is complicated, presumably due to the mixing with the wings. Both jets show a constant spectral index profile with a mean value of 0.6.

Finally, we computed the minimum energy, magnetic field and pressure in wings, lobes and jets. We found that the lobes are close to equilibrium with the external gas pressure while the wings are under-pressured by a factor of 10.

These observations allow us to investigate in detail the spectral and polarizarion properties of this peculiar object at different levels of spatial resolution and constitute an excellent data set which permits testing the "standard'' theory of the synchrotron aging analysis.

A multi-frequency study of the radio galaxy NGC 326

I. The data