A&A 368, L8-L12 (2001)
DOI: 10.1051/0004-6361:20010145

Seismic detection of stellar tachoclines

A. Mazumdar - H. M. Antia

Tata Institute of Fundamental Research, Homi Bhabha Road, Mumbai 400005, India

Received 2 January 2001 / Accepted 29 January 2001

Abstract
Helioseismic inversions for the rotation rate have established the presence of a tachocline near the base of the solar convection zone. We show that the tachocline produces a characteristic oscillatory signature in the splitting coefficients of low degree modes, which could be observed on distant stars. Using this signature it may be possible to determine the characteristics of the tachocline using only low degree modes. The limitations of this technique in terms of observational uncertainties are discussed, to assess the possibility of detecting tachoclines on distant stars.

Key words: stars: interiors - stars: oscillations - stars: rotation


   
1 Introduction

Helioseismic inversions of observed splitting coefficients have enabled us to study the rotation rate inside the Sun (Thompson et al. 1996; Schou et al. 1998). From these inversions it has been established that there is a shear layer near the base of the convection zone where the rotation rate undergoes a transition from differential rotation inside the convection zone to almost uniform rotation in the radiative interior. This layer has been referred to as the tachocline (Spiegel & Zahn 1992). The characteristics of this layer have been studied using helioseismic data (Kosovichev 1996; Basu 1997; Antia et al. 1998; Charbonneau et al. 1999; Corbard et al. 1999). Nevertheless, the origin of this shear layer is not yet clear and it would be instructive to probe the possible existence of these layers in distant stars. Such a study would help us in understanding the formation of tachoclines and to test the theories of angular momentum transport in stellar interiors.

The solar tachocline has been detected using frequency splittings for modes of low and intermediate degree, $\ell $. All these modes are not expected to be detected on other stars. In order to detect a tachocline on distant stars we have to look for the signature of a tachocline in low degree modes ($\ell\le3$), which are the only modes that can be detected on these stars. It has been shown that rapid variations in the sound speed in the stellar interior, like those arising at the base of the convection zone leave a characteristic oscillatory signature in the mean frequencies of low degree modes (Gough 1990; Monteiro et al. 1994; Roxburgh & Vorontsov 1994; Basu et al. 1994). From this oscillatory signature it has been possible to put limits on the extent of overshoot below the solar convection zone (Basu 1997). Monteiro et al. (2000) have pointed out that this oscillatory signature can be used to study the location of the base of the convection zone as well as the extent of overshoot below this base in other stars using asteroseismic data for only low degree modes.

In this work we study the signature of a tachocline in the low degree modes. Since the tachocline is a narrow layer where the rotation rate varies rapidly, we would expect an oscillatory signature in the corresponding splitting coefficients. Using a model for the solar tachocline, we show that this oscillatory signature is indeed present in frequency splitting coefficients of the low degree modes. Further, it is, in principle, possible to determine the characteristics of the tachocline, like its location, width and the extent of variation in the rotation rate across the tachocline using this oscillatory signature.

   
2 The technique

The frequency of an eigenmode of a given degree $\ell $, radial order, n, and azimuthal order, m can be expressed in terms of the splitting coefficients, using the expansion

 \begin{displaymath}\nu_{n\ell m} = {\omega_{n\ell m}\over 2\pi} = \nu_{n\ell} + \sum_{j=1}^{j_{\rm max}} c_j (n,\ell) \, {\cal P}_j^{(\ell)}(m). \end{displaymath} (1)

Here $\nu_{n\ell}$ is the mean frequency of the $(n,\ell)$ multiplet, $c_j(n,\ell)$ are the splitting coefficients and ${\cal P}_j^{(\ell)}(m)$ are orthogonal polynomials in m(Ritzwoller & Lavely 1991). If the rotation energy in the star is much smaller than the gravitational energy, then rotation can be treated as a small perturbation over the non-rotating spherically symmetric star. In this approximation the splitting coefficients can be determined by the corresponding component of the rotation rate. Following Ritzwoller & Lavely (1991), we express the rotation rate as

 \begin{displaymath}\Omega(r,\theta)= -\sum_j {w_{2j+1}(r)\over r\sin\theta} {{\rm d}\over {\rm d}\theta}P_{2j+1}(\cos\theta), \end{displaymath} (2)

where $\theta$ is the colatitude, Pj are the Legendre polynomials and wj(r) are expansion coefficients for the rotation rate which are related to the splitting coefficients $c_j(n,\ell)$ by

 \begin{displaymath}c_j(n,\ell)=\int_0^R w_j(r)K_j^{(n,\ell)}(r)r^2\;{\rm d}r, \end{displaymath} (3)

where the kernels $K_j^{(n,\ell)}(r)$ are defined in terms of eigenfunctions of the mode (Ritzwoller & Lavely 1991). For the Sun it is found that a major part of the transition in the tachocline is determined by the splitting coefficient $c_3(n,\ell)$(Antia et al. 1998). The corresponding component of the rotation rate is defined by

 \begin{displaymath}\Omega_3(r,\theta)=-{w_3(r)\over r\sin\theta}{{\rm d}\over {\... ...a}P_3(\cos\theta)={w_3(r)\over r}{3\over 2} (5\cos^2\theta-1). \end{displaymath} (4)

The variation in the other components across the tachocline turns out to be an order of magnitude smaller. The splitting coefficient $c_3(n,\ell)$is defined only for $\ell\ge2$ and hence only these modes can be used to study this component. In the absence of any theoretical understanding of formation of a tachocline, it is difficult to predict the expected form or magnitude of variation for other stars. In this work, we assume that in other stars too the dominant variation is in the $\Omega_3$ component. Although, the analysis is similar for all splitting coefficients, the higher order coefficients can only be determined for modes of higher degree. Since for other stars we can only expect to detect modes with degree l=0,1,2,3, it is not possible to study transition in higher order terms. On the other hand, if the dominant variation in other stars is found in the spherically symmetric component corresponding to $c_1(n,\ell)$ it will be easier to detect the tachocline, but we will not consider this possibility in this work. In the asymptotic limit (Christensen-Dalsgaard & Berthomieu 1991) we can approximate the kernel as $~\cos^2(\omega\tau+\phi)$, where $\tau$ is the acoustic depth given by

 \begin{displaymath}\tau=\int_r^R {1 \over c(r)}\; {\rm d}r. \end{displaymath} (5)

From Eq. (3) it is clear that if we have a rotation rate which is piecewise constant with transition at $r=r_{\rm d}$, then the corresponding splitting coefficient will have an oscillatory term of the form $\sin(2\omega\tau+\phi)$, similar to that observed in the mean frequency due to transition in the sound speed (Monteiro et al. 1994; Basu et al. 1994). The oscillatory part arises because the integral over the region covering an entire wavelength of oscillation will give an average value, while the last part between the nearest node of the eigenfunction and the location of transition, $r_{\rm d}$ will give an oscillatory contribution. Thus we can express the splitting coefficient as

 \begin{displaymath}c_j(n,\ell)=c_j^{(s)}(n,\ell)+A(\omega)\sin\!\left(2\omega\tau+\phi- {\gamma \ell(\ell+1)\over \omega}\right)\!\!, \end{displaymath} (6)

where $c_j^{(s)}(n,\ell)$ is the smooth part of the coefficient, which may arise from possible smooth variations in the rotation rate with depth. The amplitude $A(\omega)$ is a smooth function of $\omega$, while $\gamma$ is a constant. The term involving $\gamma$ arises from a more accurate expression for the vertical wavenumber kr (Monteiro et al. 1994). This term can be neglected while considering only low degree modes, since it is very small for low $\ell $. In general, the amplitude also may depend on $\ell $, but at low degrees these terms are likely to be small.

Following Basu et al. (1994), we take the fourth difference of the splitting coefficients with respect to nto enhance the oscillatory signal. Another advantage of taking the fourth difference is that the smooth part of the splitting coefficients becomes negligible and we do not need to include it in our analysis. This will of course, depend on the smooth component of variation of the rotation rate, but even for a realistic solar rotation profile this component is found to be negligible.

In order to illustrate this oscillatory signature we assume a model tachocline rotation profile of the form

 \begin{displaymath}\Omega(r,\theta)={\delta\Omega (5\cos^2\theta -1)\over 1+\exp[(r_{\rm d}-r)/w]}, \end{displaymath} (7)

where $\delta\Omega$ is the extent of variation in the rotation rate across the tachocline, w is the half-width of the transition layer and $r_{\rm d}$ is its mid-point. It may be noted that this form is different from that used by Kosovichev (1996) and Charbonneau et al. (1999), and in particular, as explained by Antia et al. (1998), the definition of width is also different. The half-width w in our definition should be multiplied by 4.9 to obtain the width as defined by them. Using this model rotation profile we can calculate the corresponding splitting coefficients for the Sun. Because of the choice of latitudinal dependence only the splitting coefficient $c_3(n,\ell)$is found to be non-zero and Fig. 1a shows the fourth difference of these coefficients. For illustration we have included modes with $2 \le \ell \le 10$. The oscillatory trend is clearly seen in these differences. The "wavelength'' of these oscillations depends on the depth $r_{\rm d}$, while the amplitude is determined by the width and $\delta\Omega$. Since the splitting coefficients and hence the fourth differences scale linearly with $\delta\Omega$ we have used only one value $\delta \Omega =20$ nHz which is the typical variation across the solar tachocline. In order to characterize the oscillatory signal we fit the following form to these differences:
 
$\displaystyle \delta^4 c_3(\!n,\ell)\!=\!\left(\!a_0+{a_1\over \omega}+{a_2\ove... ...t) \sin\!\left(\!2\omega\tau+\phi-{\gamma \ell(\ell+1)\over \omega}\!\right)\!.$     (8)

The parameters $a_0,a_1,a_2,\tau,\phi,\gamma$can be determined by a nonlinear least squares fit.
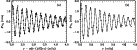  \begin{figure} \leavevmode \hbox to \hsize{\hfil \resizebox{\figwidth}{!}{\incl... ...resizebox{\figwidth}{!}{\includegraphics{Da023_f1b.eps}}\hfil}\par\end{figure} Figure 1: Fourth difference of the splitting coefficient c3, for $\delta \Omega =20$ nHz, $w=0.005~R_\odot$and $r_{\rm d}=0.7~R_\odot$. The continuous line shows a fit according to Eq. (8). a) Modes with $2 \le \ell \le 10$ have been included. The frequency has been shifted to account for the $\ell $-dependence of the term in sine function. b) Only modes with $\ell =2$ and $\ell = 3$ have been included
Open with DEXTER

For distant stars it will be possible to detect modes with $\ell=0,1,2,3$only and hence the number of modes will be highly restricted. Even then it is possible to fit the oscillatory part and Fig. 1b shows one such fit. In this case the parameter $\gamma$ is not relevant as the corresponding term is very small and we fit only the five parameters a0, a1, a2, $\tau$ and $\phi$. All the results presented in this paper are obtained using modes for $\ell = 2,3$ only, unless mentioned otherwise.

   
3 Results

In order to study the signature of the tachocline in the splitting coefficients we calculate $c_3(n,\ell)$ with rotation profiles defined by Eq. (7) using different values of half-width w, and position $r_{\rm d}$ of the tachocline. We fit the oscillatory form defined by Eq. (8) to each of these data sets. It turns out that the position of the tachocline affects mainly the parameter $\tau$, which is close to the acoustic depth of the transition layer. Therefore, in this work we have only shown results with $r_{\rm d}=0.7~R_\odot$. Conversely, the location of the tachocline may be determined from the parameter $\tau$. In order to study the effect of width we use different values of w and the fitted amplitude ( $A(\omega)=a_0+a_1/\omega+a_2/\omega^2$) is shown in Fig. 2. It can be seen that in all cases the amplitude decreases with increasing $\omega$, which may be expected as the modes with higher frequency have larger number of nodes in radial direction and hence the radial wavelength will be smaller, thus giving a smaller contribution to the integral in Eq. (3). At larger width the amplitude reduces and the tachocline profile also gives a contribution to the smooth part at low frequencies and it is not possible to use the simple form to fit the data. It turns out that the extent of variation in the amplitude across the frequency range depends on the width of the tachocline. For small width the variation is smaller, while with increasing width, the variation in amplitude increases. For example, for $w=0.002~R_\odot$, $0.003~R_\odot$, $0.005~R_\odot$ and $0.01~R_\odot$, the ratios of amplitudes at the two limits in Fig. 2 are 2.5, 3.0, 5.5 and 100 respectively. Thus, if we have data covering the entire frequency range it should be possible to determine the width using the extent of variation in amplitude. Once the width is determined, we can determine $\delta\Omega$ from the amplitude of the oscillatory term at the low frequency end. Thus we should be able to determine the characteristics like position, width and $\delta\Omega$ of the tachocline using only low degree modes.

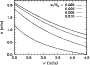  \begin{figure} \par\resizebox{\figwidth}{!}{\includegraphics{Da023_f2.eps}}\par \end{figure} Figure 2: Comparison of amplitude of oscillatory signal as a function of frequency for different widths of the transition region for $\delta \Omega =20$ nHz and $r_{\rm d}=0.7~R_\odot$
Open with DEXTER

In all the foregoing calculations we have used the exact splitting coefficients as calculated for a given rotation profile. In real data, there would naturally be errors associated with each splitting coefficient. In order to simulate real data we have constructed artificial data sets where random errors with standard deviation $\sigma$ are added to all the splitting coefficients. For simplicity, we assume that error is same in all these coefficients. Using 100 different realizations of errors we can estimate the expected errors in each of the fitted parameters, the results of which are summarized in Table 1. For low errors ( $\sigma\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displayst... ...offinterlineskip\halign{\hfil$\scriptscriptstyle ... nHz) it is indeed possible to determine all the parameters to reasonable accuracy and the error in each parameter is proportional to the assumed error in the splitting coefficients.

 

 
Table 1: Values of fitted parameters in oscillatory signal for $\delta \Omega =20$ nHz, $w=0.005~R_\odot$, $r_{\rm d}=0.7~R_\odot$
Error ($\sigma$) a0 $\tau$ $\phi$
(nHz) (nHz) (sec) (rad)
0.010 $0.68 \pm 0.02$ $2323 \pm 5\ensuremath{\phantom{0}}\ensuremath{\phantom{0}} $ $4.70 \pm 0.14$
0.020 $0.68 \pm 0.04$ $2324 \pm 10\ensuremath{\phantom{0}} $ $4.68 \pm 0.28$
0.050 $0.70 \pm 0.10$ $2331 \pm 32\ensuremath{\phantom{0}} $ $4.59 \pm 0.81$
0.100 $0.81 \pm 0.19$ $2330 \pm 135 $ $4.53 \pm 1.40$
0.200 $1.25 \pm 0.45$ $2290 \pm 242 $ $4.79 \pm 1.63$
0.200 $0.79 \pm 0.36$ 2323 $4.70 \pm 0.78$


However, as error increases it is not possible to determine the amplitude variation correctly, but if we fix a1=0 and a2=0then we can still determine the mean amplitude of the oscillatory part. For $\delta \Omega =20$ nHz, we find that it is possible to detect the oscillatory signal reliably when the error $\sigma\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displayst... ...\offinterlineskip\halign{\hfil$\scriptscriptstyle ... nHz, which corresponds to an error of about 1.6 nHz in the fourth differences. If we assume that the tachocline in other stars would also be located close to the base of the convection zone, then its depth can be determined by looking at the oscillatory part in the mean frequencies (Monteiro et al. 2000) which determines the base of the convection zone. In that case we can fix $\tau$ to the value determined from the convection zone base to improve the detectability of the oscillatory signal. The last line in Table 1 shows the results of simulations obtained when $\tau$ was kept fixed. It is clear that the estimated errors in this case are smaller. If we have the splitting coefficients for only $\ell =2$ modes then the errors are found to be $\sqrt{2}$ times larger. For the solar case we can use higher degree modes also, but even in that case the error in the observed splitting coefficients is slightly larger than this limit and it is not possible to detect the signal reliably.

   
4 Discussion

We have shown that a sharp transition in the rotation rate that is expected in the tachocline region gives rise to an oscillatory signal in the splitting coefficients of the low degree modes. The "wavelength'' of the oscillatory signal is determined by the position of the tachocline, while the variation in amplitude across the frequency range is determined by its width. The amplitude of signal is of course proportional to the extent of the variation in the rotation rate. Thus from this oscillatory signal it is, in principle, possible to determine the position, width and $\delta\Omega$ for the tachocline. We are looking for the signal in odd splitting coefficients, which can arise only due to rotation, and not from magnetic fields or structural variations in the stellar interior. In this discussion we have not included any possible latitudinal variation in the characteristics of the tachocline. The solar tachocline is known to be prolate (Charbonneau et al. 1999) and this variation would also affect the oscillatory signal in low degree modes. Using only low degree modes it may not be possible to disentangle all variations in the tachocline, but so long as the latitudinal variation is small, as is the case for the Sun, the mean properties of the tachocline can be determined from the low degree modes.

Since the amplitude of the oscillatory signal is very small, it will be necessary to find the splitting coefficients accurately to determine the characteristics of the tachocline. From our simulations it appears that the required accuracy in the splitting coefficients is $\sim$0.2 nHz for $\delta \Omega =20$ nHz. Even for the Sun, this level of accuracy has not been achieved so far and we do not expect it to be achieved for other stars in near future. But there is no reason to assume that the variation in rotation rate in all stars will be comparable to that in the Sun. In particular, for stars which are fast rotators, we would expect $\delta\Omega$ to be correspondingly larger. Even for stars with similar rotation rate there may be some variation in $\delta\Omega$ or in the amplitude of oscillatory signal for the same $\delta\Omega$. In this work, all the calculations have been done for a solar model. In other stars the amplitude may be somewhat different. If the star is rotating very rapidly, the linear approximation used to relate the splitting coefficients to the rotation rate may not be admissible. But we would expect that for a star which is rotating about 50 times faster than the Sun, this approximation may still be applicable and in that case an accuracy of about 10 nHz may be sufficient to detect the oscillatory signal. For stars with larger M/R3, this limit may also be larger. Similarly, if we choose stars with larger differential rotation, or with favourable amplitude, this number may go up further. Even if stars are rotating more rapidly the oscillatory signal may still be present, but mode identification and interpretation may be more difficult. The upcoming asteroseismic missions like COROT (Baglin et al. 1998), MOST (Matthews 1998) and MONS (Kjeldsen & Bedding 1998) have a planned frequency resolution of 100 nHz, which may not be sufficient to detect this oscillatory signal. But with some improvements in instruments and longer observations of a few selected stars, which are known to be rotating fast and preferably having larger differential rotation, it may be possible to detect this signal in not too distant future.

References

 
Copyright ESO 2001