A&A 494, 379-389 (2009)
DOI: 10.1051/0004-6361:20079225

The rotation and coma profiles of comet C/2004 Q2 (Machholz)

M. Reyniers^1,2, - P. Degroote² - D. Bodewits^3,4 - J. Cuypers⁵ - C. Waelkens²

1 - Royal Meteorological Institute of Belgium, Observations Department, Ringlaan 3, 1180 Brussels, Belgium
2 - Institute of Astronomy, Department of Physics and Astronomy, K.U. Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
3 - KVI Atomic Physics, University of Groningen, Zernikelaan 25, 9747AA Groningen, The Netherlands
4 - NASA Postdoctoral Fellow, Goddard Space Flight Center, Solar System Exploration Division, Mailstop 693, Greenbelt, MD 20771, USA
5 - Royal Observatory of Belgium, Ringlaan 3, 1180 Brussels, Belgium

Received 10 December 2007 / Accepted 14 November 2008

Abstract
Aims. Rotation periods of cometary nuclei are scarce, though important when studying the nature and origin of these objects. Our aim is to derive a rotation period for the nucleus of comet C/2004 Q2 (Machholz).
Methods. C/2004 Q2 (Machholz) was monitored using the Merope CCD camera on the Mercator telescope at La Palma, Spain, in January 2005, during its closest approach to Earth, implying a high spatial resolution (50km per pixel). One hundred seventy images were recorded in three different photometric broadband filters, two blue ones (Geneva U and B) and one red (Cousins I). Magnitudes for the comet's optocentre were derived with very small apertures to isolate the contribution of the nucleus to the bright coma, including correction for the seeing. Our CCD photometry also permitted us to study the coma profile of the inner coma in the different bands.
Results. A rotation period for the nucleus of $P=9.1\pm0.2$h was derived. The period is on the short side compared to published periods of other comets, but still shorter periods are known. Nevertheless, comparing our results with images obtained in the narrowband CN filter, the possibility that our method sampled P/2 instead of P cannot be excluded. Coma profiles are also presented, and a terminal ejection velocity of the grains $v_{\rm gr}=1609\pm48$ms^-1 is found from the continuum profile in the I band.

Key words: comets: general - comets: individual: C/2004 Q2 (Machholz)

1 Introduction

Comets are at the same time both the largest and the smallest celestial bodies in our solar system. While the nucleus of a comet is typically 1 to 15 km, the ion tail can easily extend over more than 1 AU (e.g. Jones et al. 2000). Cometary nuclei are chemically and morphologically complex bodies, consisting of non-volatile ices and frozen grains. When these nuclei approach the sun, gases start to sublimate from them, forming the cloud of gas and dust known as the coma. For comets in the inner solar system, this coma is much brighter than the nucleus, making the nucleus hidden from our view. Yet, information on the dynamics of this nucleus is important to study not only the nature and origin of these objects, but also more generally the origins of our solar system itself. In the first place, it is of a statistical importance to determine cometary periods, since a representative sample of periods could give important clues on possible statistical dependencies with other properties, like orbital period or mass, and with similar objects like asteroids. Moreover, information on the rotational state of a comet gives important clues on the recent history of the comet; fast rotation for example can point to strong recent activity in which the comet changed its own rotation state, or alternatively (but less likely) to a recent interaction with other solar system objects. Finally, rotational periods are also an important parameter in the development of sublimation models for nuclei (Schleicher et al. 1998).

In this paper, we present a study of the Oort Cloud comet C/2004 Q2 (Machholz). Some basic properties of this comet are summarised in Table 1. It was discovered on August 27, 2004 by Machholz (Machholz et al. 2004), and reached a visual brightness of $\sim$3.5 mag at its closest approach to Earth, making it one of the most spectacular astronomical events of that year. The observations presented in this paper are taken around this close encounter, providing a high spatial resolution. In this paper, we concentrate both on the nucleus, and on the inner (10⁵ km) coma. Our observational data consist of CCD images in three photometric bands. Our first objective is to derive a rotation period of the nucleus from our intensive photometric monitoring, while our second goal is to study the profiles of the inner coma. These profiles are relatively simple to determine, and directly lead to some interesting properties, like the terminal ejection velocity of the dust grains.

Published rotation periods of cometary nuclei are scarce (see Samarasinha et al. 2004, for a summary), since the nucleus of a comet situated in the inner solar system is always hidden in an opaque and overwhelming coma. Several techniques have been developed, each with their own drawbacks. One possible technique is to search for structures in the inner coma that emerge on the nucleus, like fans or jets, and search for periodicities in their morphology. This technique was employed to search for the rotation state of C/2004 Q2 (Machholz) by Farnham et al. (2007) and will be discussed later in this paper (Sect. 5.3). The technique used in this paper is aperture photometry using extremely small aperture radii. The idea is that in the vicinity of the optocentre of the coma, a small but observable contribution of the nucleus to the total brightness is expected. In the formalism of Licandro et al. (2000), if the brightness measured in an aperture $\rho$ around the optocentre is given by

$$B(\rho) = B_{\rm N} + B_{\rm C}(\rho)$$

where $B_{\rm C}(\rho)$ is the brightness of the coma captured in a radius $\rho$ and $B_{\rm N}$ the nucleus brightness. The amplitude of the light curve is then

$$\Delta m (\rho) = -2.5 \log [{\rm min}(B_{\rm N}) + B_{\rm C}(\rho)] / [{\rm max}(B_{\rm N}) + B_{\rm C}(\rho)].$$ (1)

Note that in this equation, we implicitly assume that $B_{\rm C}(\rho)$ is constant during the time span of the observations. In practice, changes in the activity can imply large coma variabilities, especially near perihelion. Nevertheless, from Eq. (1), it is easily seen that when taking large apertures, the contribution of the coma $B_{\rm C}(\rho)$ cancels out the amplitude of the light curve induced by the variability of the nucleus. Therefore, very small apertures around the comet's optocentre are usually employed to detect variability induced by the nucleus (Meech et al. 1993,1997; Jewitt 1990; Jewitt & Meech 1985). However, a problem arises when taking apertures smaller than the seeing disc of the observation. This problem was studied in detail by Licandro et al. (2000), who dubbed this problem the seeing effect. They found that several published periods were in fact contaminated, or even attributable, to this seeing effect. In our study, we will take this effect into account.

Table 1: Basic properties of comet C/2004 Q2 (Machholz).

Figure 1: The low-resolution spectrum of comet C/2004 Q2 (Machholz) taken with the EFOSC2 instrument taken with the ESO 3.6 m at La Silla on 9 december 2004. See the text for the line identification. The passbands of the three photometric filters of the Merope instrument used in this paper are shown in red. It is obvious that these broad filters cover a mix of continuum and emission features, with the I filter having the most emission-free passband. The two spectra are ESO archive data, and are taken under programme 274.C-5020 (Weiler).

Open with DEXTER

The reduction of the data, as well as its correction for the seeing effect, are an important part of our work, since it will ultimately determine the quality of our analysis. Therefore, the technical part of our analysis will be a considerable fraction of this paper: the observations are described in Sect. 2, while the reduction is discussed in Sect. 3; Sect. 4 is devoted to the extraction of the cometary magnitudes, including the correction for the seeing effect; next, the variability analysis and its results are presented in Sect. 5; in Sect. 6 we construct the coma profiles in the three filters that we used for this programme. The general discussion of the obtained results is found in Sect. 7; we end with the conclusions (Sect. 8).

Table 2: Observational log. For each night, the number of observations is given for each filter U, B and I. Also the heliocentric ($r_{\rm h}$) and geocentric ($\Delta$) distances are given (in AU, at 0:00 UT), together with the correction factor $f_{\rm a}$ (see Eq. (2) in Sect. 4.2).

  
2 Observations

Comet C/2004 Q2 (Machholz) was intensively monitored with the 1.2 m Mercator telescope at Roque de los Muchachos at La Palma (Spain), between January 7 and January 15, 2005. The telescope is equipped with a photometric camera Merope (Davignon et al. 2004), consisting of a 2 k $\times$ 2 k EEV CCD with a filter wheel consisting of the traditional 7-band Geneva system (Rufener & Nicolet 1988; Golay 1966), added with a Gunn R (Thuan & Gunn 1976) and a Cousins I(Cousins 1975) filter. The field of view is a square 6 $.\mkern -4mu^\prime$5, resulting in a 0 $.\mkern -4mu^\prime$19 sampling.

181 Images were taken, in three different bands: 61 observations in both the Geneva U and B band, and 59 in the Cousins I band. A log of the observations is given in Table 2, while three typical observations are shown in Fig. 2. Integration times were fixed at 60 s for B and I exposures, and 600 s for U band exposures. Each set of observations was accompanied with a standard star observation, immediately before, after or inbetween the comet observations. Standard stars were taken from the Geneva catalogue of standard stars (Rufener 1999). Special care was taken to ensure that the standard stars were not situated in the extended coma or tail of the comet. Standard stars are used to accurately determine the extinction conditions of the time of observation. In addition, 40 sky flats in the three used filters were taken in this observing run, 16 in U, 11 in B and 13 in I. Few comet observations ($\sim$10) could not be used for further analysis, mostly due to a wrong tracking or pointing of the telescope. Weather conditions were exceptionally good with clear nights and a superb seeing throughout the whole observing run.

Before we continue in discussing the actual reduction of the CCD frames, it is a very useful exercise to get an idea which cometary emission these three filters include. For this purpose, we downloaded low-resolution optical spectra of C/2004 Q2 (Machholz) from the ESO archive (http://archive.eso.org). These archive data are taken on December 9, 2004, with the EFOSC2 instrument that is mounted on the ESO 3.6 m telescope, under observation programme 274.C-5020 (Weiler). Reduction was done in the available ESO-MIDAS routines by ourselves, and included the standard steps of a long-slit reduction. Extraction was done over the whole spatial direction. We succeeded to identify all major emission features in these spectra, taking laboratory wavelengths from different sources (Kawakita & Watanabe 2002; O'dell 1971; Lara et al. 2004). High resolution atlases of cometary emission lines (e.g. Cochran & Cochran 2002) indicate that many more emission features are present, but these are not resolved at this relatively low resolution. From a simple inspection of this figure, it is clear that the Geneva U and B bands are sampling both continuum radiation and emission features: NH (and most probably also the very strong OH emission at 3085 Å) in the U band; in the B band the strong CN ( $\Delta\nu=0$) feature, but also C₃ and CH features. The I filter, however, does not contain such strong emission features, and mainly samples the dust continuum.

  
3 Reduction

Figure 2: Three observations, one in each band, taken on January 11, 2005. The frames are shown here to give an idea of the type of data. They are taken consecutively, and hence under very similar ambient conditions. In the U filter, the very clear signature of the ion tail is visible, in B this tail is only marginally visible, and in I it is absent. The field of view of these images is $3\hbox {$.\mkern -4mu^\prime $ }6\times 5\hbox {$.\mkern -4mu^\prime $ }0$ of the total square 6 $.\mkern -4mu^\prime$5 of the CCD; the scale is shown in the lower left corner. Note that on these images, the core of the coma seems to be saturated, which is obviously not the case, but solely a consequence of the chosen colour scale.

Open with DEXTER

The reduction of CCD frames involves the bias correction, the construction of a master flat field, the correction of the raw science frames by this master flat field, and the correction for the background.

Bias correction was done by using the pre- and overscan regions of the image. It was not possible to construct one master flat per filter for the entire observing run, since a few dust particles situated in front of the CCD were clearly visible on the flats. Therefore, several master flats were created per filter, each of them constructed with raw flats that show the same pattern of dust particles. Flats were combined by a median and sigma-clipping method, while special attention was drawn to an adequate removal of the few weak stars present in some raw flats. Note that none of the pixels that were affected by the removal of those weak stars, coincide with pixels that were used in the extraction of the comet's optocentre (Sect. 4.4).

The background correction was also not straightforward. In the case of the standard stars, a clear gradient is present in the background, probably caused by the electronics involved in the windowed ( $300\times300$ pixels) read-out of these frames. The gradient was, however, efficiently removed by the construction and subtraction of a second degree polynomial. In the case of the comet frames, the background could not be determined on the frame, since the coma of the comet is much larger than the field of view of our detector. No dedicated sky frames were taken during the observing run. Consequently, no background correction was done on the comet frames. This choice can be motivated by two arguments. First, a rough estimate of the sky contribution could be made on science frames of other science programmes that night, and we concluded that on all frames the sky contribution is several orders of magnitude weaker than the coma, even on the borders of the CCD. Second, if we fit the decline of the coma with a polynomial f($\rho$) of nth degree, starting from the centre of the coma, then the limit of f($\rho$) for $\rho \rightarrow \infty$ is a useable estimate of the background contribution (e.g. Schulz & A'Hearn 1995). In all our fits, this limit a₀ is significantly small, although there is some difference in a₀ for different polynomial degrees, and for different fitting directions away from the centre. Moreover, the observations were carried out around new moon (January 10), assuring a minimal sky contribution. In any case, the background does certainly not exceed a few thousandths of the pixel values around the centre of the coma. Therefore, background subtraction can be safely neglected when concentrating on the central luminosity, as we do in this paper.

  
4 Extraction

4.1 Extraction of standard stars

Due to their brightness, standard stars are observed out of focus. Standard stars are extracted using SourceExtractor (Bertin & Arnouts 1996). The method of extraction is a simple addition of the flux above a certain threshold (1.4$\sigma$), with a Gaussian correction for the wings of the star. From these standard star magnitudes, extinction coefficients $k_{\lambda}$are derived in each filter. These extinction values were then interpolated to the observation times of the comet.

The extinction values in the U and B filters correlate very well, which is an independent check for their accuracy. The mean $\overline{k_{\lambda}}$, the range (1$\sigma$) and the peak-to-peak of the extinction values in the U filter for the whole observing period are as follows: $\overline{k_{\lambda}} = 0.55 \pm 0.03$ with peak-to-peak 0.12. For the B filter, these values are $\overline{k_{\lambda}}=0.30\pm0.02$ and peak-to-peak 0.07. These basic statistics show that the extinction values are very stable throughout the observing run. We have also performed a frequency analysis of the extinction values for these two filters, but no significant frequencies were found in the range [0, 10] c d^-1.

The extinction values in the I filter are much more variable than the values for U and B. Moreover, they do not correlate with the two other filters. Since we could not find an explanation for this result, we chose to derive the extinction in the I band from a linear combination of the U and B band extinctions. Luckily, the extinction correction is not so critical for the I band, since it is generally very small ($\la$0.1 mag).

  
4.2 Distance correction of the comet frames

Before the actual extraction of the coma centre, one has to correct for the motion of the comet both relative to the observer and the sun. During our observing run, both effects have an opposite effect, as the comet approaches the sun while it recedes from the earth. To correct for the luminosity change caused by the motion of the comet, we have multiplied the science frames by

$$f_{\rm a} = \left(\frac{\Delta}{\Delta_0}\right)^2 \left(\frac{r_{\rm h}}{r_{{\rm h}_0}}\right)^2$$ (2)

with $\Delta$ the distance comet-earth, and $r_{\rm h}$ the distance comet-sun, whereas the subscript 0 denotes these distances on the first night of our observations. The values of these quantities were retrieved from the Horizons On-Line Ephemeris System from the Solar System Dynamics Group of JPL (NASA) (http://ssd.jpl.nasa.gov/horizons.cgi) and are given in Table 2. The factor $f_{\rm a}$ reaches a value of 1.09 in the last night, resulting in a magnitude decrease of $\sim$0.04.

  
4.3 Correction for the seeing effect

In this particular case, especially the extraction of the science frames (see Sect. 4.4) is a delicate step, since we will deal with extremely small aperture sizes, much smaller than the seeing disc. Since seeing conditions are expected to be variable throughout the night, extraction with a aperture size smaller than a typical seeing will introduce artificial variability. In a paper devoted to this seeing effect, Licandro et al. (2000) claim that several published rotational periods of comets are doubtful, and are probably affected by this seeing effect. It is therefore extremely important to account for the variation in the seeing.

Detailed and accurate seeing measurements are available on the Roque de los Muchachos site, provided by the dedicated RoboDIMM telescope (O'Mahony 2003; Augusteijn 2001) of the ING. RoboDIMM forms four images of the same star, measuring image motion in two orthogonal directions from each of the two pairs of images, from which it derives four simultaneous and independent estimates of the seeing. The values are automatically corrected for the zenith distance and a wavelength of 550 nm. The time resolution of these measurements is 2 min, and therefore very well suited for our project. We will use these data for an adequate correction of the seeing effect. The idea is to degrade the seeing of each science frame to the worst seeing that was recorded during the comet observations. While this method seems to be quite rough, its application can be motivated by two facts. First, thanks to the good seeing conditions, the ``worst seeing'' was not that bad at all. In Fig. 4, the RoboDIMM seeing values interpolated to the comet observation times are shown. It is clear that the least favourable seeing does not exceed a FWHM of $\sim$2 $.\!\!^{\prime\prime}$2. Second, the reverse process, in which frames taken in bad seeing conditions are deconvolved to an average or a very good seeing, is a much less robust process. The comets frames were degraded to the worst seeing in that filter, by convolution of a twodimensional Gaussian kernel. As a consequence, images taken in good seeing conditions are convolved with a broad kernel, while images taken in worse conditions, only need a small kernel to be degraded with. In Fig. 3, two examples are show of such a convolution. The left column shows the technique for a frame taken in good conditions, while the right column shows the same set of frames for a frame taken in bad conditions. From top to bottom this figure shows: the frames as they come out from the reduction (upper row), the Gaussian kernel to convolve with (middle row), and the resulting, convolved frames (lower row). The upper left frame shows the optocentre of a comet frame taken at good conditions. Consequently it needs quite a broad kernel (middle left frame) to degrade it to desired seeing. The reverse applies to the right set of frames, with the raw frame taken in less good conditions.

Note that an objection could be made against the use of seeing data originating from another source than our own telescope. Indeed, the seeing is computed for a region of the sky that is not necessary the same as the region containing the comet. Nevertheless, we chose this option for several reasons. (i) A large part of the observing run was photometric, and hence only small spatial variations of the seeing value are expected; (ii) our own observational data do not permit to deduce a seeing value: the standard stars are taken out of focus (to prevent saturation), the science frames are tracked on the comet, and no other science frames are available inbetween the comet observations.

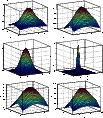Figure 3: Correction for the seeing effect for a frame taken in optimal conditions ( left column of figures), and for a frame taken in less favourable conditions ( right column). The upper row shows the optocentres of the reduced frames (but not yet seeing-corrected). To degrade these frames to the same seeing, the left one has to be convolved with a broad Gaussian kernel ( middle left panel), while the right one with a very narrow Gaussian kernel ( middle right panel). The resulting optocentres are show in the bottom panels.

Open with DEXTER

	Figure 4: The evolution of the seeing during our observational run as recorded by the RoboDIMM telescope (O'Mahony 2003; Augusteijn 2001), interpolated to the times of our comet observations.
Open with DEXTER

  
4.4 Extraction of the comet

Now that all comet frames are degraded to the same seeing, we can safely extract the optocentre of the comet with small apertures well below the seeing disc. This technique poses, on its own turn, two specific problems to deal with. The first one is the determination of the exact location of the optocentre, while the second one involves the discretisation of the pixels when using very small apertures. The extraction is then done using three different extraction radii (1, 3 and 6 pixels).

4.4.1 Determination of the centre

Several solutions can be put forward to determine the optocentre of the coma. The most simple one is obviously taking the position of the brightest pixel in the coma. A second one is to fit a twodimensional Gaussian in the proximity of the optocentre. A third possibility is to take the barycentre of a limited region around the optocentre. We chose this last method, since some tests showed that the first method was a too rough determination, while the Gaussian method did not give good results either. The Gaussian method obviously assumes a Gaussian profile for the optocentre. While this is indeed the case for the immediate surroundings of the optocentre due to the effect of the seeing, it is not the case for a larger area since the coma shows a profile different from Gaussian (see Sect. 6).

4.4.2 Discretisation of pixels

In the case of extraction with small apertures, flux has to be added from the sub-pixel level. Common extraction programs, such as SExtractor, divide each pixel in a certain number of virtual sub-pixels ($5\times5$ in the case of SExtractor), and add the flux in those sub-pixels lying in the predefined aperture radius. Here we chose to work strictly analytic. For each pixel lying at the border of the aperture radius, we calculated the exact fraction of that pixel in the radius.

  
5 Variability analysis

The final magnitudes for the optocentre of the comet are graphically presented in Fig. 5. A detailed frequency analysis was performed on this data set, using two different algorithms: the Jurkevich-Stellingwerf PDM method (Stellingwerf 1978; Jurkevich 1971), and the Lomb-Scargle (Scargle 1982; Lomb 1976) periodogram. The latter one is essentially a Fourier technique, hence it is more sensitive for harmonic periodicities. The former technique searches for the frequency for which the periodogram, devided into a certain number of bins, shows the smallest spread per bin.

	Figure 5: Overview of the magnitudes for the extracted optocentre of the comet in the three different bands. Shown here are the results for an aperture radius of 1 and 6 pixels (0 $.\!\!^{\prime\prime}$19 and 1 $.\!\!^{\prime\prime}$14).
Open with DEXTER

As a first step, a frequency interval has to be defined. A conservative choice would be the interval between zero and the Nyquist frequency. In our case, when taking the inverse of the average time gap between neighboring points while ignoring large gaps, the value of the Nyquist frequency is 44 c d^-1(P=0.55 h). Such a high frequency will, however, lead to a break-up of the comet. A rough estimate of the break-up frequency $f_{\rm b}$ can easily be calculated by stating that at the equatorial velocity $v_{\rm b}$ the centrifugal acceleration equals the gravitational acceleration, and that there is no internal strength to the body. If one assumes a typical density of 1 g cm^-3, then the break-up frequency will be $f_{\rm b} = 7.3$ c d^-1( $P_{\rm b} = 3.3$ h). For smaller densities, the break-up frequency will obviously be smaller; the same is true for aspherical nuclei (Jewitt & Meech 1988). Here, we adopt a safe upper limit for our frequency interval of f = 20 c d^-1 ( $P_{\rm b} = 1.2$ h). The cometary rotation frequencies that are found up to now (Samarasinha et al. 2004) all fall safely in this range.

5.1 Non-periodic variability

As already seen from Fig. 5, there is a remarkable increase in brightness in the nights 12, 13 and 13, 14 January of the observing run. The brightness increase in those two nights leads to a frequency of f = 0.20 c d^-1 (P = 5 d) in the Lomb-Scargle periodograms (Fig. 6), in each filter, and for each of the three radii (1, 3 and 6 pixels). This frequency is also present in the Jurkevich-Stellingwerf results, but somewhat less clear.

The increase in brightness is also seen in the ``raw'' magnitudes, i.e. the magnitudes that are not seeing-corrected. Hence, the brightness increase is certainly not an artifact of our convolution technique explained in Sect. 4.2. However, since the convolution technique is certainly not perfect, it might still be possible that the brightness increase is related to the seeing values that are somewhat higher than average for these two nights. We studied this possibilty by making a variability analysis of the seeing values, and concluded that none of the variability that was found in the seeing, was still present in the seeing-corrected magnitudes, while the raw magnitudes showed the same trends as the seeing values, as expected. Hence we are confident that the seeing effect is adequately accounted for.

Since the total time span of our observational run is only 8 nights, it is not possible to judge whether this frequency is real (implying that the brightness increase is a periodic phenomenon), or it is just a unique event. In any case, since the typical rotational frequencies of cometary nuclei are much higher, it is unlikely that this frequency is linked to the rotation of the nucleus. The brightness increase is more likely a non-periodic event, like an outburst. Possibly it is connected to the sudden change in the solar wind velocity around that period (Degroote et al. 2008). It is, however, unlikely that the solar wind has a direct impact on the comet's nucleus, since it is believed that solar wind cannot enter the so-called contact surface (<10³ km, Ip 2004) of the comet.

  
5.2 Rotation frequency

In order to search for an acceptable rotation frequency, the brightness increase should be removed. This can be done in several ways: e.g. by means of removing (``prewhitening'') the data with the 5 days periodic component found earlier. Another possibility is to subtract the mean value of every night. Since these means are often ill-defined because of the scarcity of the data, we tried to model the data with a combination of unknown nightly means and a periodic component. A third possibility is to perform a simultaneous fit of two frequencies together, one long-term component and one short-term. We will briefly discuss these three methods and their results.

  
5.2.1 Prewithening

When the frequency f = 0.20 c d^-1 (P = 5 d) was removed from the data, we did not find any significant frequencies anymore in the B filter magnitudes. Two different frequencies pop up in the U and I filter periodograms. In the U filter, the most significant frequency is present near f = 6.03 c d^-1 (P = 4.0 h), but after inspection of the periodogram, this frequency and some other frequency close to integer values, seem to be aliases of the frequency 1 c d^-1. There is little doubt that this frequency is an artifact, probably introduced by the imperfect extinction corrections. Moreover, the probable contribution of OH emission in the U filter (see Sect. 2) could explain why this one-day alias is so prominent for this filter. Indeed, the extinction at OH is very high ($\sim$2 mag/airmass), so as the comet rises or sets, the signal from OH can change dramatically. In the I filter, where overall extinction is much less, a significant frequency is seen at f = 2.64 c d^-1 (P = 9.1 h) in both the 1 and 3 pixel size apertures; for the 6 pixel magnitudes, a frequency of f = 3.64 c d^-1 (P = 6.6 h), which is a one-day alias of the former one. The frequency of 2.64 c d^-1 (P = 9.1 h) is also found in this filter and apertures when using the Jurkevich-Stellingwerf method. The variance reduction by this frequency is another 14% (from 50% to 64%).

Figure 6: Jurkevich-Stellingwerf PDM ( left panels) $\theta$-statistic and Lomb-Scargle ( right panels) periodogram for the I magnitudes of 1 pixel aperture. In the two upper panels, the diagrams for the original data are shown, while in the lower panels, the diagrams for the magnitudes prewhitened with f1 = 0.20 c d-1 (P = 5 d) are shown (method #1 in Table 3). On each figure, the frequency f = 2.64 c d-1 (P = 9.1 h) is shown with a red line.

Open with DEXTER

5.2.2 Free nightly means

Table 3: Summary of the frequency analysis results. Three different methods were used to get rid of the brightness increase during two nights of our observational run (12, 13 and 13, 14 January); see Sect. 5.2 for more details.

After subtracting the mean values of every night from the data, the results of the frequency analysis around 2.5 c d^-1 (P around 9.5 h) were not different from the results obtained after prewhitening. However, some spurious, mostly higher, frequencies are present as well. They appear because the nightly mean values are not necessarily the true mean values of the light curve, since the rotation period could be longer than the time span of the comet observations in one night and since only few observations per night were available. A solution to this is to perform a harmonic fit through the data, while taking the mean value for each night as a free parameter. This technique gave no results for the U filter data, but now a frequency near f = 2.50 c d^-1 (P = 9.6 h) appears in the B filter data and near f = 2.59 c d^-1 (P = 9.3 h) in the I filter. These results should be looked at with some caution, since 11 unknowns (three for the harmonic fit, and one for every night) were to be determined in data sets of only about 50 observations.

5.2.3 Two frequencies simultaneously

Finally we looked also for the best two-frequency fit in the data. We searched for the best description of the data in the least squares sense with one long-period component (f between 0.1 and 0.3 c d^-1, corresponding to P between 3.3 d and 10 d) and a shorter-period component (f between 0.3 and 3.0 c d^-1, corresponding to P between 8 h and 3.3 d). The f = 1.00 c d^-1 frequency and its aliases are still too dominant in the U filter data to give reliable results. In the I filter data, a long term component of 0.18 c d^-1 (P = 5.6 d) combined with the frequency f = 2.67 c d^-1 (P = 9.0 h) reduces the variance of the data with 65%. In the B data the combination of 0.22 c d^-1 (P = 4.5 d) and 2.56 c d^-1 (P = 9.4 h) describes the observations best and leads to a variance reduction of 83%.

5.2.4 Final rotation frequency

A summary of the frequency analysis is given in Table 3. In this table, the results are given in cycles per day (c d^-1), since this notation allows us to immediately detect one-day aliases, and to compare directly with the periodograms of Fig. 6. The results of the different methods indicate that a short-term periodicity is present in the data, with a period between 9.0 and 9.4 h. Since not all methods gave consistent results for the B filter data, probably also due to imperfect extinction correction, we take the value found in the I filter data (9.1 h on average) as the best estimate for the rotation period from these data. The spread of the results given by different techniques, indicates that the error (1$\sigma$) on this value can be as high as 0.25 h.

  
5.3 Rotation of Machholz in literature

Sastri et al. (2005) analysed R band images of C/2004 Q2 (Machholz) taken in the same period as our observations (January 2005), and report the same period as ours: P = 9.12 $\pm$ 1.9 h (f = 2.63 c d^-1). The period was derived by studying dust fans visible in these small band images, and adoption of Fulle's formula (Fulle 1987) between grain velocity and the forces on each grain. It is a remarkable result that two such different methods lead to the same value for the rotation period, strengthening of course the confidence in our results.

Farnham et al. (2007) observed C/2004 Q2 (Machholz) intensively during several observing campaigns from January to June 2005, in different filters of the HB narrowband comet filter system (Farnham et al. 2000). The paper concentrates on the CN band images, which reveal two clear jets in roughly opposite directions relative to the nucleus. The presence of the jets were confirmed by images taken with the 1-m telescope at the Lulin Observatory, Taiwan, and the 3.6 m at ESO, La Silla (Lin et al. 2007). Farnham et al. (2007) found that the morphology of these jets repeated itself on the timescale of hours, and through an intensive monitoring in April 2005, the authors could phase the jet morphology on a period of $17.6\pm0.05$ h, which is then also identified as the rotation period of the nucleus. Farnham et al. (2007) explicitly excludes the possibility of a period shorter than 17.6 h, since they did not find similar morphologies of the CN jets with a time span shorter than this period. Also their March observations are consistent with this 17.6 h period. They argue that it is unlikely that the rotation period of the nucleus should have evolved from 9.1 h to 17.6 h between January and March. Hence, the period of Sastri et al., as well as the period found by us, is seemingly in contradiction with the one from Farnham et al.

There might be, however, a possible explanation that could reconcile the two results. The method of Farnham et al. is based on the visual inspection of the morphology of the CN jets that emerge from the nucleus. Since it concerns two opposite jets, there is always one jet dominant in the direction of the observer. If we assume the jets, or more precise, the regions on the comet's nucleus where the jets emerge, to be the main contributors in the comet's variability, then it is obvious that our method catches P/2 and not P. If this interpretation is correct, the results of Farnham et al. are in agreement with ours and the one of Sastri et al. Note that the latter period was derived by modelling the structure and position of the observed dust fans, and not by a periodicity search in a series of images, as was done by Farnham et al.

In the assumption that our method leads to an estimate of P/2 and not P, even then a small difference persists between our P/2 = 9.1 h and Farnham et al.'s P/2 = 8.8 h. This difference can have different explanations. Surely, the measurement errors will account for an important part in this difference, but also another effect can be of importance. Table 2 shows a 7% change in $\Delta$ from the first to the last night's data. This produces a commensurate change in the aperture sizes when measured in km at the comet. If the variability is caused by changes in the comet's activity, then the period determination could be affected by this difference. For example, a burst of activity is seen as a brightening of the coma. When the leading edge of that burst leaves the aperture, the light curve has reached its peak and starts fading again. Because a given aperture is smaller (in km) on earlier nights, the observed peak will occur earlier than it should relative to the last night. This produces a period measurement that is longer than the actual periodicity (defined by the burst of activity reaching the same distance from the nucleus). Given the small pixel dimensions at the comet and the high emission velocities, this could have a significant effect, and thus may help to explain the difference between our 9.1 h and Farnham et al.'s 8.8 h half-periods.

	Figure 7: Phase diagrams of the comet's optocentre magnitudes in the I filter with an aperture radius of 1 pixel. upper panel: phase plot with f1 = 0.20 c d-1 (P = 5 d); lower panel: phase plot with f2=2.64 c d-1 (P = 9.1 h) on the magnitudes prewhitened with f1 (method #1 in Table 3).
Open with DEXTER

  
6 Coma profiles

The first objective of our observational programme was to study the rotation of the nucleus through extremely small aperture photometry. The use of the CCD camera implies, however, that we sample a large part of the inner coma at each observation. Therefore, we decided to initiate a study of the coma profile in the three spectral bands at our disposal. In Sect. 6.2 we will deduce some physical properties of the coma from these profiles, but first a small introduction is given of what can be expected theoretically.

6.1 Theoretical profiles

Historically, the first quantitative model of a cometary coma was elaborated by Eddington (1910). In Eddington's fountain model the comet is assumed to be a uniform and isotropic source of emitting particles such that their density (e.g., gas or dust) would fall as the inverse square of the distance from the source, except the emitters are also subject to a uniform acceleration that pushes on them from a given direction, presumably from the Sun's direction (Combi et al. 2004). Continuing Eddington's work, Wallace et al. (1958) showed that the column density N in the line of sight, and hence the brightness B in the case of an optically thin coma, is given by

$$N = Q / (4 v \rho)$$

where Q is the global particle production rate, v is the initial uniform outflow speed and $\rho$ is the projected distance on the sky plane of the nucleus. Generally the logarithmic derivative m =  ${\rm d}\log B(\rho$)/ ${\rm d}\log \rho$ is used to describe the coma profile, and hence m = -1 in Wallace et al.'s equation. Deviations from the m = -1 profile are expected at distances where the solar radiation pressure becomes important. More specifically, Jewitt & Meech (1987) showed that this distance is of the order of

$$X_{\rm R} \approx {v}_{\rm gr}^2 r_{\rm h}^2 / [2 \beta g_{\rm sun}(1) ]$$ (3)

where $v_{\rm gr}$ is the terminal ejection velocity of a grain, $g_{\rm sun}$is the solar gravity at 1 AU, and $\beta$ is the ratio of the acceleration of a grain due to radiation pressure to the local solar gravity. Beyond this point $X_{\rm R}$, one enters the outer coma where |m| > 1. Jewitt & Meech (1987) derive from both Monte Carlo simulations, as well as from an analytical derivation, that $m \simeq -$1.5 in this region, slightly varying depending on the phase angle and the radiation pressure.

The theoretical profiles that are discussed here assume that the coma has constant (though not necessarily isotropic) activity. In reality, C/2004 Q2 (Machholz) is known to have significant jet activity (Farnham et al. 2007), and jets produce structures that can affect the radial profiles in the coma. Jets on rotating nuclei frequently produce curved or spiral shaped jets. Radial profiles may cross these curved features, causing the inner or outer region to be brighter than otherwise might be expected. This is especially true in the inner coma we are measuring. Since activity changes are invoked as the cause of the variability that defines the cometary period (Sect. 5.3), the profiles are expected to be influenced by this effect.

  
6.2 Coma profiles of C/2004 Q2 (Machholz)

To construct representative coma profiles of C/2004 Q2 (Machholz), we took for each filter one observation taken in the night 08, 09 January 2005, which was a night with optimal conditions and seeing (see Fig. 4). For each of these three observations, we constructed two coma profiles, one in the direction of the sun, and one in the direction of the ion tail. The profiles were constructed by dividing the coma into concentric annuli, with radii that are (logarithmically) equidistant. For each of these annuli, two medians were taken: one of the sunward half of the annulus (sunward profiles in Fig. 8) and one of the tailward half of the annulus (tailward profiles in Fig. 8). The profiles were normalised so that the brightness of the optocentre reaches unity, and plotted on a logarithmic scale. The resulting profiles are shown in Fig. 8, and linear fits were made in the two regimes $2.6 < \log \rho < 4$ and $4 < \log \rho$ ($\rho$ in km). The values for m are also given in this figure.

While the profiles in the I are fully compatible with the basic models presented in the previous section, the profiles in U and B are clearly deviating from these predictions. From Fig. 1 it is clear that in both the U and B bands strong emissions are present, while the I filter is relatively free from strong emission lines. The presence of these emissions breaks the assumption of conservation of mass of a certain species, since the gas can dissociate and/or ionise to other species. The development of theoretical profiles taking these effects into account were initiated by Haser (1957), and are specifically valid when using small band filters concentrated on those emission described in the profile. Since we are using broadband filters in this study, sampling both continuum and emission features, it is very difficult to construct a valid profile for the U and B filters. The I filter, however, is dominated by the continuum, leading to a clean m = -1 profile in the inner coma.

From the change in m from -1 to -1.5 at a distance of $X_{\rm R} = 21.6 \pm 1.3 \times 10^4$ km, we can estimate the terminal ejection velocity of the grains using formula (3). Typically, one assumes $\beta \simeq 1$, which corresponds at 1 AU to spherical grains with a diameter of about 1 $\mu$m. This way, we can estimate $v_{\rm gr}=1609\pm48$ m s^-1, which is much more than we expect from the empirical law of Bobrovnikoff-Delsemme (Delsemme 1982): $v_{\rm gr} = 580/\sqrt{r_{\rm h}} = 524$ m s^-1(e.g. Schulz et al. 1993). Deviations from this law of this magnitude may be attributed to stages of high activity. For distances smaller than $\log \rho \la 2.6$, there is also a clear deviation from the m = -1 trend. At this scale ( $\rho \la 400$ km), other effects come into play. The acceleration zone close to the nucleus has certainly some influence at this scale (Jewitt & Meech 1987), but most importantly it is the seeing that wipes out the m = -1 profile close to the optocentre.

By calculating these m-values for all observations, we can search for temporal variations or global trends in the profiles. We concentrate on the profiles in the I band because of their agreement with the theoretical profiles. We did not use observations containing bright background stars for this purpose, since the profiles of such observations are heavily disturbed by the star tracks. For the determination of the inner and outer coma profiles, respectively 56 and 51 observations were used, and the fitted m-values are shown in Fig. 9. From these m-values, it is clear that the profiles show some variation indeed, but overall we can safely state that the profiles are quite stable throughout our observational run. The spread on the m-value for the inner coma for example, is $m = -1.01\pm0.03$; for the outer coma this is $m = -1.49\pm0.08$. The seemingly periodic behaviour of the inner coma profile (Fig. 9, upper panel) is very peculiar, as we cannot link it to another phenomenon: not with the global brightness trend we encountered previously, nor with the deduced period (P or P/2), nor with any solar wind events. The observed trend is also noticeable for the inner coma in the U and B band, but not in any of the m-values of the outer coma. The fact that we cannot match the variations in the slopes to any known periodicity might be explained if the slopes are being affected by coma structures, as discussed earlier. If the slopes are affected by temporary structures, then sparsely sampling the slope at various times may not reveal variations that change with the rotation period.

In Fig. 9 the evolution of the terminal ejection velocity of the grains $v_{\rm gr}$ is also shown. This quantity is related to the heliocentric distance $r_{\rm h}$ of the comet, but the difference for $r_{\rm h}$ between the beginning and ending of our observational run is too small to see any noticeable effect.

Figure 8: Coma profiles of three representative observations for the three filters used in our programme. Crosses represent the profile in the sunward direction, while the $\times$es show the profile in the direction of the ion tail. The coma in the I filter shows a clean m = -1 profile for $\rho$ < 104 km and m = -1.5 for $\rho$ > 104 km, the profiles in the U and B filter have smaller values for |m|, indicating the influence of gas emissions in these spectral bands.

Open with DEXTER

Figure 9: Temporal evolution (in function of the heliocentric distance $r_{\rm h}$) of the inner and outer coma profiles represented by their m-values, and of the terminal ejection velocity determined with formula (3). The terminal ejection velocity is related to the heliocentric distance $r_{\rm h}$ of the comet, but the difference of $\Delta r_{\rm h}$ $\simeq$ 0.02 AU between the beginning and ending of our observational run is too small to establish global trends.

Open with DEXTER

  
7 Discussion

Rotation periods or periodicities are currently known for about 25 comets. A comprehensive inventory of the currently known or suspected rotation periods is given in Samarasinha et al. (2004), while a more critical list of 15 comets is given in Jorda & Gutiérrez (2000). The mean of the spin periods given in Jorda & Gutiérrez's list is 20 h, but decreases to 12 h when constrained to the short-period comets. Moreover, there seems to be a hint for a relation between rotation period and the size of the nucleus, with larger nuclei having longer periods. However, the small number of published periods does certainly not allow us to draw any final conclusions concerning statistical dependencies.

The difference between the period found by Sastri et al. (2005) that we confirmed here, and the period found by Farnham et al. (2007) is puzzling. Crifo & Rodionov (1999) claim that the present circumnuclear models have too uncertain or even contradictory assumptions, implying that physical properties for the nucleus derived from observations of jets or fans, can deviate considerably from reality. However, in the case of C/2004 Q2 (Machholz), the CN jets observed by Farnham et al. (2007) are bright, and the rotation is obvious from a simple inspection of the phased observations (http://www.astro.umd.edu/~farnham/Machholz/). The authors reject a period shorther than 17.6 h, but, as explained in Sect. 5.3, there is a possibility that our method picked up P/2 instead of P. However, a somewhat uncomfortable inconsistency persists: if the periodicity of 9.1 h that we found in the light curve, is induced by the periodicity in the morphology of the CN jets, then it is not clear why the period is best seen in the I band, and less clear in the B band (see Table 3), which contains the CN emission feature (Fig. 1). A possible explanation for why the periodic variations are visible in the I filter, but not in the B filter, which captures the CN emission, is through the dust production. Farnham et al. (2007) observed full CN spirals in C/2004 Q2 (Machholz), indicating that they remain active throughout the rotation. Dust production, on the other hand, tends to shut down when a source passes into darkness. Thus, the brightness in the B filter, which has a significant signal from CN, may remain fairly constant, while the I filter, which is dominated by continuum, reflects the dust turning on and off. In Farnham et al. (2007) a future paper is announced in which also the observations of C/2004 Q2 (Machholz) in the other HB narrowband comet filters are to be discussed. This could hopefully clarify the different results.

It is clear that a light curve analysis of a comet's optocentre is hampered by several uncertainties. Particularly, the correction for the seeing effect is a delicate step, and the introduced uncertainties are difficult to quantify. Our observational setup is, however, unique in the sense that our spatial resolution of $\sim$48 km pixel^-1 is much higher than papers using the same technique of aperture photometry. Therefore, it is not surpirising that the period is also recovered even when using a relatively large aperture of 6 pixels.

  
8 Conclusion

Comet C/2004 Q2 (Machholz) was monitored using the Merope CCD camera on the Mercator telescope at La Palma, Spain, in January 2005, during its closest approach to Earth. 170 Images were recorded in three different bands. Our main goal was to find a rotation period of the nucleus through aperture photometry using very small apertures. This technique was already succesfully applied to other bright comets, but it was recently criticised by Licandro et al. (2000). These authors studied the effect of aperture radii smaller than the seeing disc, and concluded that many periods published in literature that make use of this technique are contaminated by this seeing effect. In our analysis of comet C/2004 Q2 (Machholz), we took this effect into account by degrading our images to the least favourable seeing. Luckily, since the ambient conditions during our observational run were very good, only the images with a superb seeing had to be degraded slightly.

We searched in each filter and three aperture radii (1, 3 and 6 pixels) for frequencies between 0 and 20 c d^-1 (i.e. periods down to 1.2 h), and this with different algorithms. After taking into account that a long term trend is in our data (which is possibly linked to a solar wind event, see Degroote et al. 2008), a period near $9.1\pm 0.2$ h was found. While this rotation period is in perfect agreement with the one of Sastri et al. (2005), it clearly deviates from the 17.6 h found by Farnham et al. (2007). However, the methodology of both methods could explain the possibility that our method in fact finds P/2 and not P.

Also coma profiles for the inner coma ( $\log \rho < 4.6$, $\rho$ in km) were constructed for each photometric band. In the I-band, a clear m = -1 for $\rho < 10^{4}$ km and m = -1.5 for $\rho$ > 10⁴ km was found, in agreement with a steady state coma without creation or destruction of particles. From this regime change, a terminal ejection velocity of the grains $v_{\rm gr} = 1609$ m s^-1 was derived. In the other filters, smaller m-values were found, due to the contamination of strong gas features in those bands, while the I filter is relatively free from those emissions.

Acknowledgements

The authors are indebted to the referee (Farnham) for his extensive and detailed report that significantly improved the paper. Hans Van Winckel and the Mercator staff at La Palma are acknowledged for their generous and continuous support. M.R. wants to thank Steven Dewitte and Laurent Delobbe of the Royal Meteorological Institute of Belgium for the opportunity to finish this paper, and the warm welcome at my new institute. M.R. acknowledges financial support from the Fund for Scientific Research - Flanders (Belgium) and from the Belgian Federal Science Policy Office.

References

• Augusteijn, T. 2001, The Newsletter of the Isaac Newton Group of Telescopes (ING Newsl.), 4, 27
• Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Bonev, B. P., Mumma, M. J., DiSanti, M. A., et al. 2006, ApJ, 653, 774 [NASA ADS] [CrossRef]
• Cochran, A. L., & Cochran, W. D. 2002, Icarus, 157, 297 [NASA ADS] [CrossRef] (In the text)
• Combi, M. R., Harris, W. M., & Smyth, W. H. 2004, Comets II, 523 [NASA ADS] [CrossRef] (In the text)
• Cousins, A. W. J. 1975, Monthly Notes Astron. Soc. South Africa, 34, 68 (In the text)
• Crifo, J. F., & Rodionov, A. V. 1999, Planet. Space Sci., 47, 797 [NASA ADS] [CrossRef] (In the text)
• Davignon, G., Blecha, A., Burki, G., et al. 2004, in Ground-based Instrumentation for Astronomy, ed. A. F. M. Moorwood, & I. Masanori, Proc. SPIE, 5492, 871 (In the text)
• Degroote, P., Bodewits, D., & Reyniers, M. 2008, A&A, 477, L41 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Delsemme, A. H. 1982, Icarus, 49, 438 [NASA ADS] [CrossRef] (In the text)
• Eddington, A. S. 1910, MNRAS, 70, 442 [NASA ADS] (In the text)
• Farnham, T. L., Schleicher, D. G., & A'Hearn, M. F. 2000, Icarus, 147, 180 [NASA ADS] [CrossRef] (In the text)
• Farnham, T. L., Samarasinha, N. H., Mueller, B. E. A., & Knight, M. M. 2007, AJ, 133, 2001 [NASA ADS] [CrossRef] (In the text)
• Fulle, M. 1987, A&A, 171, 327 [NASA ADS] (In the text)
• Golay, M. 1966, in Spectral Classification and Multicolour Photometry, ed. K. Loden, L. O. Loden, & U. Sinnerstad, IAU Symp., 24, 262
• Haser, L. 1957, Bull. Soc. Roy. Sci. Liege, 43, 740 [NASA ADS] (In the text)
• Ip, W.-H. 2004, Comets II, 605 [NASA ADS] (In the text)
• Jewitt, D. 1990, ApJ, 351, 277 [NASA ADS] [CrossRef]
• Jewitt, D., & Meech, K. J. 1985, Icarus, 64, 329 [NASA ADS] [CrossRef]
• Jewitt, D. C., & Meech, K. J. 1987, ApJ, 317, 992 [NASA ADS] [CrossRef] (In the text)
• Jewitt, D. C., & Meech, K. J. 1988, ApJ, 328, 974 [NASA ADS] [CrossRef] (In the text)
• Jones, G. H., Balogh, A., & Horbury, T. S. 2000, Nature, 404, 574 [NASA ADS] [CrossRef] (In the text)
• Jorda, L., & Gutiérrez, P. 2000, Earth Moon and Planets, 89, 135 [NASA ADS] [CrossRef] (In the text)
• Jurkevich, I. 1971, Ap&SS, 13, 154 [NASA ADS] [CrossRef]
• Kawakita, H., & Watanabe, J.-I. 2002, ApJ, 572, L177 [NASA ADS] [CrossRef]
• Lara, L.-M., Rodrigo, R., Tozzi, G. P., Boehnhardt, H., & Leisy, P. 2004, A&A, 420, 371 [NASA ADS] [CrossRef] [EDP Sciences]
• Licandro, J., Serra-Ricart, M., Oscoz, A., Casas, R., & Osip, D. 2000, AJ, 119, 3133 [NASA ADS] [CrossRef] (In the text)
• Lin, Z. Y., Weiler, M., Rauer, H., & Ip, W. H. 2007, A&A, 469, 771 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Lomb, N. R. 1976, Ap&SS, 39, 447 [NASA ADS] [CrossRef]
• Machholz, D. E., Garradd, G., & McNaught, R. H. 2004, IAU Circ., 8394, 1 (In the text)
• Meech, K. J., Belton, M. J. S., Mueller, B. E. A., Dicksion, M. W., & Li, H. R. 1993, AJ, 106, 1222 [NASA ADS] [CrossRef]
• Meech, K. J., Bauer, J. M., & Hainaut, O. R. 1997, A&A, 326, 1268
• O'dell, C. R. 1971, ApJ, 164, 511 [NASA ADS] [CrossRef]
• O'Mahony, N. 2003, The Newsletter of the Isaac Newton Group of Telescopes (ING Newsl.), 7, 22 [NASA ADS]
• Rufener, F. 1999, VizieR Online Data Catalog, 2169 (In the text)
• Rufener, F., & Nicolet, B. 1988, A&A, 206, 357 [NASA ADS]
• Samarasinha, N. H., Mueller, B. E. A., Belton, M. J. S., & Jorda, L. 2004, Comets II, 281 [NASA ADS] (In the text)
• Sastri, J. H., Vasundhara, R., Kuppuswamy, K., & Velu, C. 2005, IAU Circ., 8480, 3 (In the text)
• Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef]
• Schleicher, D. G., Millis, R. L., Osip, D. J., & Lederer, S. M. 1998, Icarus, 131, 233 [NASA ADS] [CrossRef] (In the text)
• Schulz, R., & A'Hearn, M. F. 1995, Icarus, 115, 191 [NASA ADS] [CrossRef] (In the text)
• Schulz, R., A'Hearn, M. F., Birch, P. V., et al. 1993, Icarus, 104, 206 [CrossRef] (In the text)
• Stellingwerf, R. F. 1978, ApJ, 224, 953 [NASA ADS] [CrossRef]
• Thuan, T. X., & Gunn, J. E. 1976, PASP, 88, 543 [CrossRef] (In the text)
• Wallace, L. V., Miller, I., & Freeman, D. 1958, AJ, 63, 213 [NASA ADS] [CrossRef] (In the text)