A&A 494, 311-315 (2009)
DOI: 10.1051/0004-6361:200811109
Firehose instability in space plasmas with bi-kappa distributions
M. Lazar
- S. Poedts
Center for Plasma Astrophysics, Celestijnenlaan 200B, 3001 Leuven, Belgium
Received 8 October 2008 / Accepted 21 November 2008
Abstract
Context. The existence of suprathermal charged particle populations in space plasma is frequently confirmed by interplanetary missions. In general, the velocity distribution functions are anisotropic, field aligned (gyrotropic) with two temperatures, parallel (
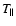 )
and perpendicular (
)
and perpendicular (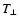 )
to the ambient magnetic field
)
to the ambient magnetic field 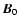 .
.
Aims. Here, the dispersion properties of the firehose instability, which relaxes an anisotropic electron distribution function (
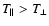 )
of bi-kappa type, are investigated for the first time.
)
of bi-kappa type, are investigated for the first time.
Methods. The Solar wind is generally accepted to be a collisionless plasma and, therefore, the dispersion formalism is constructed on the basis of the kinetic Vlasov-Maxwell equations. The general dispersion relations are derived in terms of the modified plasma dispersion function.
Results. Simple analytical forms are obtained for the dispersion relation of the firehose instability and the instability criterion is derived. The exact numerical evaluation shows a significant departure of the dispersion curves from those obtained for a bi-Maxwellian plasma.
Conclusions. While the maximum growth rate is slightly diminished, the instability extends to large wave-numbers in the presence of suprathermal particles. Thus, this instability is more likely to be found in space plasmas with an anisotropic distribution of bi-kappa type. If all other parameters are known, measuring the instability growth time enables the determination of the spectral index 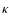 .
.
Key words: plasmas - instabilities - Sun: coronal mass ejections (CMEs) -
Sun: flares - Sun: solar wind
There is consistent observational evidence that nonthermal particle
populations are ubiquitous in the near Earth space plasma (for an
overview, see in Zouganelis et al. 2005, and the references
therein). Suprathermal populations are described by the so-called
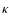 distribution function (introduced by Vasyliunas
1968), i.e. a power law in particle speed, with high-energy
tails, and which degenerates into a Maxwellian distribution function
as the spectral index becomes very large (
distribution function (introduced by Vasyliunas
1968), i.e. a power law in particle speed, with high-energy
tails, and which degenerates into a Maxwellian distribution function
as the spectral index becomes very large (
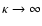 ).
Moreover, such deviations from the Maxwellian distribution are
expected to exist in any low-density plasma in our Universe, where
binary collisions are sufficiently rare. Instead, the wave-particle
interactions can be responsible for the energization of plasma
particles and the occurrence of
).
Moreover, such deviations from the Maxwellian distribution are
expected to exist in any low-density plasma in our Universe, where
binary collisions are sufficiently rare. Instead, the wave-particle
interactions can be responsible for the energization of plasma
particles and the occurrence of 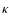 distributions. In an
ambient magnetic field, plasma particles gain energy through the
cyclotron resonance and transit time damping (Landau resonance) of
the linear waves (Fisk 1976). Thus, the small (linear)
amplitude MHD modes, Alfvén and fast magnetosonic waves are able
to accelerate both the electrons and the protons in the solar flares
(Miller 1991, 1997), and in the inner magnetosphere
(Summers & Ma 2000), while the whistler mode can enhance
the energy of the electrons in the Earth's foreshock (Ma & Summers
1998). In the presence of large amplitude waves and plasma
turbulence the nonlinear mechanisms of dissipation (e.g., the
nonlinear Landau damping) also can be responsible for the
energization of plasma particles (Miller 1991, Leubner
2000, Shizgal 2007). However, the MHD turbulent
cascades channel the energy to small scales where the quasi-linear
interactions with particles are again possible (Miller 1991,
1997). The non-thermal features of the particle distribution
functions can also result from heat flows and temperature
anisotropies (Leubner & Viñas 1986). The use of the
generalized kappa-type distribution functions enables a more
realistic description of the turbulent fields and the acceleration
of plasma particles in such environments (Summers & Thorne
1991; Maksimovic et al. 1997; Mace & Hellberg
2003; Lazar et al. 2008b).
distributions. In an
ambient magnetic field, plasma particles gain energy through the
cyclotron resonance and transit time damping (Landau resonance) of
the linear waves (Fisk 1976). Thus, the small (linear)
amplitude MHD modes, Alfvén and fast magnetosonic waves are able
to accelerate both the electrons and the protons in the solar flares
(Miller 1991, 1997), and in the inner magnetosphere
(Summers & Ma 2000), while the whistler mode can enhance
the energy of the electrons in the Earth's foreshock (Ma & Summers
1998). In the presence of large amplitude waves and plasma
turbulence the nonlinear mechanisms of dissipation (e.g., the
nonlinear Landau damping) also can be responsible for the
energization of plasma particles (Miller 1991, Leubner
2000, Shizgal 2007). However, the MHD turbulent
cascades channel the energy to small scales where the quasi-linear
interactions with particles are again possible (Miller 1991,
1997). The non-thermal features of the particle distribution
functions can also result from heat flows and temperature
anisotropies (Leubner & Viñas 1986). The use of the
generalized kappa-type distribution functions enables a more
realistic description of the turbulent fields and the acceleration
of plasma particles in such environments (Summers & Thorne
1991; Maksimovic et al. 1997; Mace & Hellberg
2003; Lazar et al. 2008b).
In magnetized interplanetary plasmas, the particle distribution
functions are in general anisotropic, i.e. depend on the direction
in velocity space (Pilipp et al. 1990; Salem et al.
2003), and, therefore, unstable to the excitation of plasma
instabilities (Paesold & Benz 1999; Fahr & Siewert
2007, for a review of the fundamental properties of
anisotropic plasma instabilities and their applications in space
plasma physics, we recommend the textbook of Gary 1993).
Although considerable progress has been made, questions still exist
about the origin of the particle velocity anisotropies and the
relaxation mechanisms in space plasmas (Stverak et al.
2008). Recently it has been shown how the bulk energy of the
solar wind ions is converted by developing pronounced pitchangle
anisotropies when the ions pass over the solar wind MHD termination
shock (Fahr & Siewert 2007). Such anisotropic distribution
functions are mirror-mode unstable and up to 60 percent of the
thermal ion energy can be converted by this instability into
magnetoacoustic turbulence energy. However, at large solar distances
mechanisms of adiabatic cooling can be identified (e.g., the
conservation of the two magnetic CGL invariants), which prevent the
solar wind from developing strong pressure anisotropies (Fahr &
Siewert 2008).
The preference for the acceleration of plasma particles along the
background magnetic field is a common feature of the different
acceleration models in solar flares and in the solar wind (see the
Introduction of Paesold & Benz 1999, for a brief
description of these mechanisms of acceleration). Thus, the velocity
distribution function becomes anisotropic with a substantial amount
of free energy residing in the direction of the magnetic field that
may give rise to the excitation of the firehose instability.
The electron firehose mode propagates along the ambient magnetic
field and the instability typically arises when the parallel
temperature is much larger than the transverse temperature
(
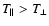 ). In this case, the approximate
instability criterion of Hollweg & Völk (1970) is
fulfilled:
). In this case, the approximate
instability criterion of Hollweg & Völk (1970) is
fulfilled:
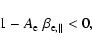 |
(1) |
where
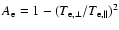 is the electron
temperature anisotropy, and
is the electron
temperature anisotropy, and
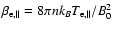 is the ratio of the thermal to the magnetic
pressure. According to condition (1), an instability can
occur only for positive but sub-unitary anisotropies, i.e.
is the ratio of the thermal to the magnetic
pressure. According to condition (1), an instability can
occur only for positive but sub-unitary anisotropies, i.e.
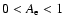 ,
and consequently, for a parallel beta larger than unity.
,
and consequently, for a parallel beta larger than unity.
Since the frequency of the firehose mode is in the range of the ion
gyrofrequency, the electrons are non-resonant and the instability is
non-resonantly driven by the electron temperature anisotropy
(Hollweg & Völk 1970). The ions, however, are resonant
and they can gain energy making the firehose instability responsible
for the transfer of the electron energy to the ions. The first
simulations of the electron firehose instability have also shown
that the generated magnetic field fluctuations scatter the
electrons, reducing their anisotropy (Gary & Nishimura
2003; Paesold & Benz 2003).
Presently, it is believed that the electron firehose instability
presents two branches (Li & Habbal 2000): one with a finite
real frequency,
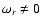 and quasi-parallel propagation
(
and quasi-parallel propagation
(
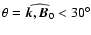 ), and another
one that is non-resonant, with
), and another
one that is non-resonant, with
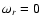 and
quasi-perpendicular propagation (
and
quasi-perpendicular propagation (
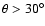 ). Both of
these branches have recently been confirmed by two-dimensional
Particle-In-Cell (PIC) simulations with a physical mass-ratio
(Camporeale & Burges 2008). Here, we should remark that
the second branch describing a purely-growing and
quasi-perpendicular instability is a Weibel-like instability (Weibel
1959), as long as it is non-resonantly excited by a
temperature anisotropy and has the wave-vector normal to the high
temperature axis.
). Both of
these branches have recently been confirmed by two-dimensional
Particle-In-Cell (PIC) simulations with a physical mass-ratio
(Camporeale & Burges 2008). Here, we should remark that
the second branch describing a purely-growing and
quasi-perpendicular instability is a Weibel-like instability (Weibel
1959), as long as it is non-resonantly excited by a
temperature anisotropy and has the wave-vector normal to the high
temperature axis.
Potential applications of the kinetic electron firehose instability
to solar flares or to the solar wind are discussed in Paesold &
Benz (1999) and Li & Habbal (2000). The main idea
is that this instability can constrain the increase of the electron
temperature anisotropy, thus explaining the observations. Indeed,
the anisotropic velocity distribution can be subjected to a
pitchangle isotropisation by quasilinear interactions of electrons
with plasma waves and other dissipative processes. The electron
firehose instability itself can be the most efficient mechanism of
temperature isotropisation in solar flares limiting electron
anisotropy and thus providing the necessary condition for further
acceleration (Messmer 2002).
In the present paper, we briefly describe the dispersion properties
of the electron firehose instability driven by an anisotropic
electron distribution function (
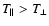 )
of the
bi-kappa type, and propagating along the ambient magnetic
field (
)
of the
bi-kappa type, and propagating along the ambient magnetic
field (
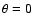 ). The plasma is assumed to be quiescent, without
large amplitude oscillations and turbulence, so that we restrict
this discussion to a quasilinear description of this instability.
). The plasma is assumed to be quiescent, without
large amplitude oscillations and turbulence, so that we restrict
this discussion to a quasilinear description of this instability.
For the transverse waves propagating along the ambient magnetic field, i.e.,
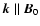 ,
(along the y-axis in the present model), we take the general dispersion relation from Tautz & Schlickeiser (2005)
,
(along the y-axis in the present model), we take the general dispersion relation from Tautz & Schlickeiser (2005)
![\begin{displaymath}1 -{k^2c^2 \over \omega^2} + {\pi \over \omega^2} \sum_a
\ome...
...artial
F_{a,\kappa} \over \partial v_{\parallel}} \right] = 0,
\end{displaymath}](/articles/aa/full/2009/04/aa11109-08/img23.gif) |
(2) |
where 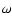 and k denote the frequency and the wave number of
the plasma modes, respectively, and c is the speed of light in a
vacuum,
and k denote the frequency and the wave number of
the plasma modes, respectively, and c is the speed of light in a
vacuum,
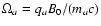 is the (non-relativistic)
gyrofrequency,
is the (non-relativistic)
gyrofrequency,
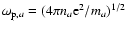 is the
plasma frequency for the particles of species a, and the
is the
plasma frequency for the particles of species a, and the 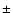 are
used to identify the circularly polarized electromagnetic waves
with right-hand and left-hand polarizations, respectively.
are
used to identify the circularly polarized electromagnetic waves
with right-hand and left-hand polarizations, respectively.
We consider a bi-kappa velocity distribution function of plasma
particles
![\begin{displaymath}F_{\kappa} = {1 \over \pi^{3/2} \theta_{\perp}^2 \theta_{\par...
...v_{\perp}^2 \over \kappa \theta_{\perp}^2}\Biggr]^{-\kappa -1}
\end{displaymath}](/articles/aa/full/2009/04/aa11109-08/img28.gif) |
(3) |
that describes the initially unperturbed plasma system, and which is normalized
by
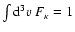 .
We use polar coordinates in the particle velocity space
.
We use polar coordinates in the particle velocity space
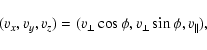 |
(4) |
and the corresponding thermal velocities take different values as
follows
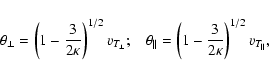 |
(5) |
where
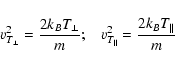 |
(6) |
denote the perpendicular and parallel thermal velocities,
respectively. Such an anisotropic distribution function, known as a
bi-kappa distribution function, has been introduced by Summers and
Thorne (1991), and it approaches the bi-Maxwellian
distribution function as the spectral index reaches the limit
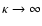 .
.
The electron firehose instability arises when the plasma is hotter
along the direction of the stationary magnetic field, i.e. when
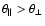 .
This instability is left-handed
(LH) circularly polarized at
.
This instability is left-handed
(LH) circularly polarized at
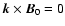 ,
and the
electrons are non-resonant,
,
and the
electrons are non-resonant,
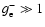 .
Only the ions are
cyclotron resonant, but their contribution is minimized here
assuming that, initially, the ion distribution function is
isotropic. The ion firehose instability develops for similar
conditions of the ion temperature anisotropy,
.
Only the ions are
cyclotron resonant, but their contribution is minimized here
assuming that, initially, the ion distribution function is
isotropic. The ion firehose instability develops for similar
conditions of the ion temperature anisotropy,
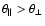 ,
and saturates at maximum growth rates comparable to
the electron firehose instability (viz. of the order of the ion
gyrofrequency). However, because the ion response could be either
inhibited or enhanced by the resonant dissipation of the electron
firehose instability, the interplay of these two instabilities is
more complex and it will be investigated in detail separately.
,
and saturates at maximum growth rates comparable to
the electron firehose instability (viz. of the order of the ion
gyrofrequency). However, because the ion response could be either
inhibited or enhanced by the resonant dissipation of the electron
firehose instability, the interplay of these two instabilities is
more complex and it will be investigated in detail separately.
We now insert the distribution function (3) in Eq. (2) and derive the dispersion relation of the LH transverse modes
![\begin{displaymath}1- {k^2c^2 \over \omega^2} + \sum_a {\omega_{{\rm p},a}^2 \ov...
...) - A_a ~ \left[1+ g_a Z^0_{\kappa} (g_a)\right] \right\} = 0,
\end{displaymath}](/articles/aa/full/2009/04/aa11109-08/img36.gif) |
(7) |
with
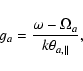 |
(8) |
and where the temperature anisotropy is defined as
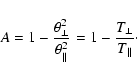 |
(9) |
The new modified dispersion function
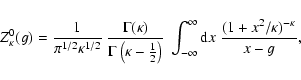 |
(10) |
for 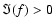 ,
usually describes the dispersion properties of the transverse
waves and instabilities (Lazar et al. 2008a), and is related to the modified
dispersion function
,
usually describes the dispersion properties of the transverse
waves and instabilities (Lazar et al. 2008a), and is related to the modified
dispersion function
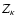 of Summers & Thorne (1991) by (Lazar et al. 2008a)
of Summers & Thorne (1991) by (Lazar et al. 2008a)
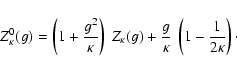 |
(11) |
Both of these modified dispersion functions approach the
standard plasma dispersion function Z of Fried & Conte (1961) in
the limit of
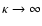 ,
and Eq. (7) reduces
exactly to the dispersion relation of parallel transverse waves in a plasma
with bi-Maxwellian anisotropic distribution functions, see Eq. (7.1.6) from
Gary (1993).
,
and Eq. (7) reduces
exactly to the dispersion relation of parallel transverse waves in a plasma
with bi-Maxwellian anisotropic distribution functions, see Eq. (7.1.6) from
Gary (1993).
Consider a plasma with anisotropic electrons and isotropic ions (protons),
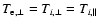 .
The dispersion relation (7) then simplifies to
.
The dispersion relation (7) then simplifies to
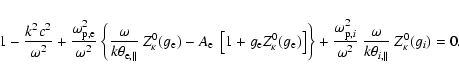 |
(12) |
For Maxwellian
distributions, with the same assumption of anisotropic electrons and
isotropic ions, the dispersion relation (12) transforms, in
the limit of
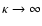 ,
to
,
to
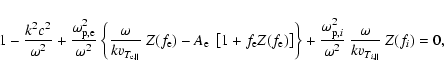 |
(13) |
where Z (f) is the standard plasma dispersion function Z of Fried & Conte (1961) with
the argument
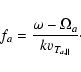 |
(14) |
The electrons are non-resonant and, therefore, the
arguments (8) or (14) can be considered sufficiently large,
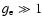 .
This allows us to use the power series of the modified
plasma dispersion function from Summers & Thorne (1991),
and to find, for example, for two values of
.
This allows us to use the power series of the modified
plasma dispersion function from Summers & Thorne (1991),
and to find, for example, for two values of
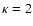 ,
4,
,
4,
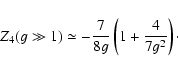 |
(15) |
Combining the last Eqs. (15) with (11), we obtain
for both values of 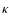 the same expression of
the same expression of
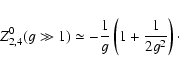 |
(16) |
In the limit of large arguments, 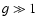 ,
the second-order
approximation of the modified dispersion function
,
the second-order
approximation of the modified dispersion function
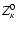 does not depend explicitly on the spectral index
does not depend explicitly on the spectral index 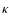 ,
but only
through the factor
,
but only
through the factor
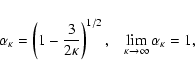 |
(17) |
which relates 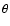 to the thermal velocity, vT, in
Eq. (5). Thus, we can use Eq. (16) to simplify
Eq. (12) and obtain
to the thermal velocity, vT, in
Eq. (5). Thus, we can use Eq. (16) to simplify
Eq. (12) and obtain
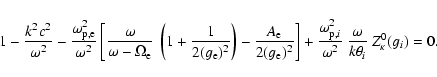 |
(18) |
This is the dispersion relation of the firehose mode, which is unstable under
certain conditions that we derive below.
Here we follow the same formalism as Hollweg & Völk
(1970) and generalize the firehose instability criterion for
anisotropic particle velocity distributions of the bi-kappa
type. We use some reasonable simplifications based on what we are
looking for: the firehose instability has a frequency (
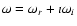 )
in the vicinity of the ion cyclotron
frequency, and therefore
)
in the vicinity of the ion cyclotron
frequency, and therefore
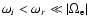 ,
and
,
and
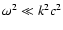 .
Moreover, for simplicity, the protons can be
considered Maxwellian (as sustained by many observations) and
isotropic in the velocity space without any contribution to the
instability. Besides that, the protons are resonant and we can
assume a small argument fi < 1 of the dispersion function
(Maxwellian) that in this case approaches
.
Moreover, for simplicity, the protons can be
considered Maxwellian (as sustained by many observations) and
isotropic in the velocity space without any contribution to the
instability. Besides that, the protons are resonant and we can
assume a small argument fi < 1 of the dispersion function
(Maxwellian) that in this case approaches
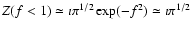 .
With these
presumptions, the dispersion relation (18) becomes
.
With these
presumptions, the dispersion relation (18) becomes
![\begin{displaymath}{k^2c^2 \over \omega_{{\rm p},i}^2} + {\omega_{\rm p,e}^2 \ov...
...} \right] - \imath ~
\pi^{1/2} \; {\omega \over k v_{T_i}} = 0
\end{displaymath}](/articles/aa/full/2009/04/aa11109-08/img61.gif) |
(19) |
and for the real and imaginary part of the frequency scaled to the
ion cyclotron frequency, we derive
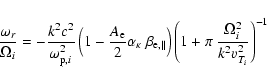 |
(20) |
and
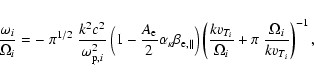 |
(21) |
respectively. The firehose instability will occur for
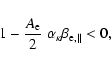 |
(22) |
and for a given anisotropy, condition (22) is satisfied only
for spectral indexes larger than the threshold
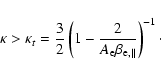 |
(23) |
If the anisotropy chosen here (in accordance with the earlier
estimates of Paesold & Benz 1999) is
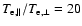 ,
we find
,
we find
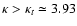 ,
and
indeed, in Fig. 1b, the instability exists only for
,
and
indeed, in Fig. 1b, the instability exists only for
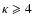 .
For high values of the parallel beta, the
spectral index is sufficiently large
.
For high values of the parallel beta, the
spectral index is sufficiently large
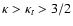 ,
so
that we keep away from the critical value
,
so
that we keep away from the critical value
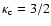 ,
where
the distribution function (3) collapses and the
temperature (5) becomes undefined.
,
where
the distribution function (3) collapses and the
temperature (5) becomes undefined.
While Eq. (22) gives the instability criterion in a plasma with a bi-kappa
temperature anisotropy, for an infinitely large
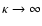 we find the exact criterion of firehose instability for a bi-Maxwellian distribution
we find the exact criterion of firehose instability for a bi-Maxwellian distribution
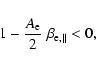 |
(24) |
which upgrades the approximative condition (1) of Hollweg & Völk (1970).
Keeping an ion distribution function of the kappa-type (as suggested
by the recent works of Fisk & Gloeckler 2006,
2007), only the numerical factor
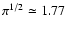 in
the last term of the dispersion relation (19) will increase
slightly, for example, to 2.02 and 2.82 for
in
the last term of the dispersion relation (19) will increase
slightly, for example, to 2.02 and 2.82 for
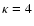 and
and
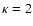 ,
respectively. But this term has no influence on the
instability criterion in Eq. (22). This is confirmed in the
next section by comparing the exact numerical solutions.
,
respectively. But this term has no influence on the
instability criterion in Eq. (22). This is confirmed in the
next section by comparing the exact numerical solutions.
![\begin{figure}
\par\includegraphics[width=73mm]{11109f1a.eps}\\
\vspace{0.5cm}
\includegraphics[width=70mm]{11109f1b.eps}
\end{figure}](/articles/aa/full/2009/04/aa11109-08/Timg76.gif) |
Figure 1:
The real and imaginary solutions of Eq. (25) are plotted with
solid lines for three values of
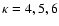 ,
and with dashed lines for
an infinitely large ,
and with dashed lines for
an infinitely large
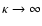 .
The electron-proton plasma parameters are .
The electron-proton plasma parameters are
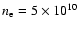 cm-3, cm-3,
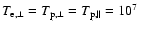 K, K,
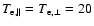 , ,
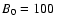 G. G. |
| Open with DEXTER |
In the previous section, we derived the analytical (approximative)
forms of the frequency and the growth rate. Here, however, to be
rigorous, we present the exact numerical solutions of the firehose
instabilities. If the protons are Maxwellian, Eq. (18)
transforms in terms of the standard dispersion function (Fried &
Conte 1961) into
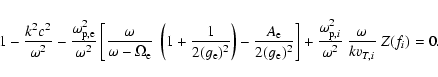 |
(25) |
The real and imaginary solutions of Eq. (25) are shown with
solid lines in Fig. 1. We consider three different cases of
bi-kappa distributions of electrons, corresponding to
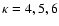 .
For comparison, we indicated with dashed lines the reproduced
numerical solutions from Paesold & Benz (1999) obtained
for the same values of plasma parameters (typical for solar flares),
but for a bi-Maxwellian distribution function (
.
For comparison, we indicated with dashed lines the reproduced
numerical solutions from Paesold & Benz (1999) obtained
for the same values of plasma parameters (typical for solar flares),
but for a bi-Maxwellian distribution function (
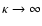 )
of the electrons.
)
of the electrons.
In this case, the maximum growth rates cannot be obtained by simply
imposing d
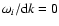 in Eq. (21), or
Eq. (25), because the instability is saturated by two
mechanisms at the same time, either by scattering electrons or by
heating ions (Messmer 2002; Paesold & Benz 2003).
However, the growth rates shown in Fig. 1 are only slightly
diminished by the non-Maxwellian distributions of the electrons.
Contrary to this, the range of instability is extended to larger
wave-numbers. Again, the so-called cutoff wave number,
in Eq. (21), or
Eq. (25), because the instability is saturated by two
mechanisms at the same time, either by scattering electrons or by
heating ions (Messmer 2002; Paesold & Benz 2003).
However, the growth rates shown in Fig. 1 are only slightly
diminished by the non-Maxwellian distributions of the electrons.
Contrary to this, the range of instability is extended to larger
wave-numbers. Again, the so-called cutoff wave number, 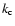 ,
which
limits the existence of the firehose instability to wave numbers
,
which
limits the existence of the firehose instability to wave numbers
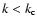 ,
cannot be found by simply imposing condition
,
cannot be found by simply imposing condition
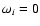 in Eq. (25), because the growth rate decreases drastically
but it does not vanish completely at
in Eq. (25), because the growth rate decreases drastically
but it does not vanish completely at
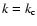 .
Therefore, here, we
only suppose that
.
Therefore, here, we
only suppose that 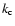 can be derived from the resonance condition
for the ions,
can be derived from the resonance condition
for the ions,
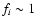 ,
in the dispersion Eq. (25),
and we leave the exact calculation of the maximum growth rates and
the cutoff wave numbers for a detailed analysis elsewhere.
,
in the dispersion Eq. (25),
and we leave the exact calculation of the maximum growth rates and
the cutoff wave numbers for a detailed analysis elsewhere.
![\begin{figure}
\par\includegraphics[width=73mm]{11109f2a.eps}\\
\vspace{0.3cm}
\includegraphics[width=70mm]{11109f2b.eps}
\end{figure}](/articles/aa/full/2009/04/aa11109-08/Timg84.gif) |
Figure 2:
Comparison of numerical solutions given by the Eqs. (18) (dotted lines)
and (25) (solid lines) for an index
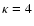 .
The plasma parameters are
the same as in Fig. 1. .
The plasma parameters are
the same as in Fig. 1. |
| Open with DEXTER |
In Fig. 2, with dotted and solid lines, the dispersion
curves (a) and the growth rates (b) given by Eqs. (18)
and (25), respectively, are compared. We have assumed that the
electrons are described by a bi-
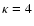 anisotropic
distribution function, and in Eq. (18), the ions are
described by an isotropic
anisotropic
distribution function, and in Eq. (18), the ions are
described by an isotropic
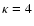 distribution function. A
small deviation is observed only for the growth rates, which are
slightly decreased by the non-Maxwellian ions.
distribution function. A
small deviation is observed only for the growth rates, which are
slightly decreased by the non-Maxwellian ions.
The dispersion relations provided above, for example
Eqs. (18) and (25), allow for a more extensive
analysis of the dispersion properties and the stability of different
plasma systems if we combine electron and ion distribution functions
with diverse spectral indexes as given by the observations.
- 1.
- We have investigated the dispersion properties of the
firehose instability driven by an anisotropic bi-kappa type electron distribution function
(
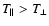 ).
).
- 2.
- The general integral dispersion relations have been derived
in terms of the modified plasma dispersion function.
- 3.
- Simple analytical forms of the dispersion relations are obtained
and the firehose instability criterion is provided.
- 4.
- The exact numerical evaluation of the dispersion curves and the growth rates
have proved a strong dependence on the spectral index
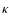 ,
and a
significant departure from the unstable solutions of a bi-Maxwellian plasma.
,
and a
significant departure from the unstable solutions of a bi-Maxwellian plasma.
- 5.
- While the maximum growth rate is slightly diminished, the instability
extends to large wave-numbers. In the presence of suprathermal particles,
the wave-number corresponding to the maximum growth rate as well as the
cutoff wave-number increase considerably.
- 6.
- This instability is thus more likely to be found in space plasmas with
an anisotropic distribution of the bi-kappa type.
- 7.
- If all other parameters are known, measuring the instability growth time makes
it possible to determine the spectral
index
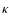 .
.
Acknowledgements
The authors acknowledge financial support from the Research Foundation
Flanders - FWO Belgium. These results were obtained in the framework
of the projects GOA/2009-009 (K.U. Leuven), G.0304.07 (FWO-Vlaanderen) and C 90205 (ESA Prodex 9).
Financial support by the European Commission through the SOLAIRE Network (MTRN-CT-2006-035484)
is gratefully acknowledged. The numerical results were obtained on the HPC cluster VIC of the K.U. Leuven.
We are grateful to the referee (Prof. Fahr) for his insightful
comments and the constructive suggestions.
- Camporeale, E., &
Burgess, D. 2008, JGR, 113, A07107 [CrossRef]
(In the text)
- Fahr, H.-J., &
Siewert, M. 2007, Astrophys. Space Sci. Trans., 3, 21 [NASA ADS]
(In the text)
- Fahr, H.-J., &
Siewert, M. 2008, A&A, 484, L1 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Fisk, L. A. 1976, JGR, 81,
4633 [NASA ADS] [CrossRef]
(In the text)
- Fisk, L. A., &
Gloeckler, G. 2006, ApJ, 640, L79 [NASA ADS] [CrossRef]
(In the text)
- Fisk, L. A., &
Gloeckler, G. 2007, Space Sci. Rev., 130, 153 [NASA ADS] [CrossRef]
(In the text)
- Fried, B. D., & Conte,
S. D. 1961, The Plasma Dispersion Function (New York: Academic
Press)
(In the text)
- Gary, S. P. 1993, Theory of
Space Plasma Microinstabilities (Cambridge: University Press)
(In the text)
- Gary, S. P., &
Nishimura, K. 2003, Phys. Plasmas, 10, 3571 [NASA ADS] [CrossRef]
(In the text)
- Hollweg, J. V., &
Völk, H. J. 1970, JGR, 75, 5297 [CrossRef]
(In the text)
- Lazar, M., Schlickeiser,
R., & Shukla, P. K. 2008, Phys. Plasmas, 15, 042103 [NASA ADS] [CrossRef]
(In the text)
- Lazar, M.,
Schlickeiser, R., Poedts, S., & Tautz, R. C. 2008, MNRAS, 390,
168 [NASA ADS] [CrossRef]
(In the text)
- Leubner, M. P. 2000,
Planet. Space Sci., 48, 133 [NASA ADS] [CrossRef]
(In the text)
- Leubner, M. P., &
Viñas, A. F. 1986, JGR, 91, 13 [CrossRef], 366
(In the text)
- Li, X., & Habbal, S. R.
2000, JGR, 105, 27377 [NASA ADS] [CrossRef]
(In the text)
- Ma, C., & Summers, D.
1998, Geophys. Res. Lett., 25, 4099 [NASA ADS] [CrossRef]
(In the text)
- Mace., R. L., &
Hellberg, M. A. 2003, Phys. Plasmas, 10, 21 [NASA ADS] [CrossRef]
(In the text)
- Maksimovic, M., Pierrard,
V., & Lemaire, J. F. 1997, A&A, 324, 725
(In the text)
- Messmer, P. 2002,
A&A, 382, 301 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Miller, J. A. 1991, ApJ,
376, 342 [NASA ADS] [CrossRef]
(In the text)
- Miller, J. A. 1997, ApJ,
491, 939 [NASA ADS] [CrossRef]
(In the text)
- Paesold, G., & Benz,
A. O. 1999, A&A, 351, 741
(In the text)
- Paesold, G., & Benz,
A. O. 2003, A&A, 401, 711 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Pilipp, W. G.,
Miggenrieder, H., Montgomery, M. D., et al. 1990, JGR, 95,
6305 [NASA ADS] [CrossRef]
(In the text)
- Salem, C., Hubert, D.,
Lacombe, C., et al. 2003, ApJ, 585, 1147 [NASA ADS] [CrossRef]
(In the text)
- Shizgal, B. D. 2007,
Astrophys. Space Sci., 312, 227 [NASA ADS] [CrossRef]
(In the text)
- Stverak, S., Travnicek,
P., Maksimovic, M., et al. 2008, JGR, 113, A03103 [CrossRef]
(In the text)
- Summers, D., & Thorne,
R. M. 1991, Phys. Fluids B, 3, 1835 [NASA ADS]
(In the text)
- Summers, D., & Ma, C.
2000, JGR, 105 [CrossRef] (15), 887
(In the text)
- Tautz, R. C., &
Schlickeiser, R. 2005, Phys. Plasmas, 12, 122901 [NASA ADS] [CrossRef]
(In the text)
- Vasyliunas, V. M. 1968, JGR,
73, 2839 [NASA ADS] [CrossRef]
(In the text)
- Weibel, E. S. 1959, PRL, 2,
83 [NASA ADS] [CrossRef]
(In the text)
- Zouganelis, I.,
Meyer-Vernet, N., Landi, S., Maksimovic, M., & Pantellini, F.
2005, ApJ, 626, L117 [NASA ADS] [CrossRef]
(In the text)
Copyright ESO 2009
![\begin{displaymath}1 -{k^2c^2 \over \omega^2} + {\pi \over \omega^2} \sum_a
\ome...
...artial
F_{a,\kappa} \over \partial v_{\parallel}} \right] = 0,
\end{displaymath}](/articles/aa/full/2009/04/aa11109-08/img23.gif)
![\begin{displaymath}F_{\kappa} = {1 \over \pi^{3/2} \theta_{\perp}^2 \theta_{\par...
...v_{\perp}^2 \over \kappa \theta_{\perp}^2}\Biggr]^{-\kappa -1}
\end{displaymath}](/articles/aa/full/2009/04/aa11109-08/img28.gif)
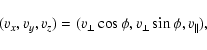
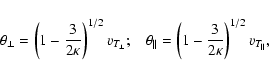
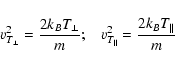
![\begin{displaymath}1- {k^2c^2 \over \omega^2} + \sum_a {\omega_{{\rm p},a}^2 \ov...
...) - A_a ~ \left[1+ g_a Z^0_{\kappa} (g_a)\right] \right\} = 0,
\end{displaymath}](/articles/aa/full/2009/04/aa11109-08/img36.gif)
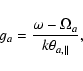
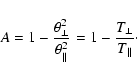
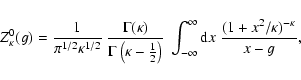
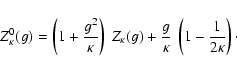
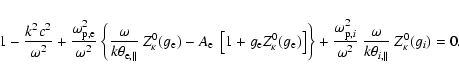
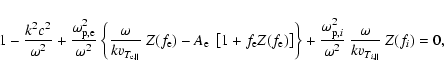
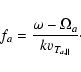
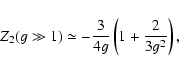
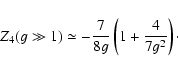
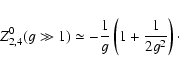
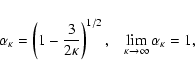
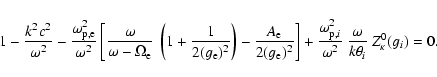
![\begin{displaymath}{k^2c^2 \over \omega_{{\rm p},i}^2} + {\omega_{\rm p,e}^2 \ov...
...} \right] - \imath ~
\pi^{1/2} \; {\omega \over k v_{T_i}} = 0
\end{displaymath}](/articles/aa/full/2009/04/aa11109-08/img61.gif)
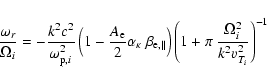
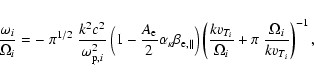
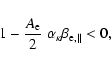
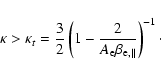
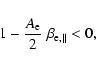
![\begin{figure}
\par\includegraphics[width=73mm]{11109f1a.eps}\\
\vspace{0.5cm}
\includegraphics[width=70mm]{11109f1b.eps}
\end{figure}](/articles/aa/full/2009/04/aa11109-08/Timg76.gif)
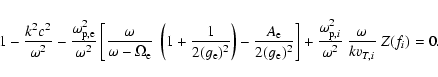
![\begin{figure}
\par\includegraphics[width=73mm]{11109f2a.eps}\\
\vspace{0.3cm}
\includegraphics[width=70mm]{11109f2b.eps}
\end{figure}](/articles/aa/full/2009/04/aa11109-08/Timg84.gif)