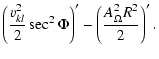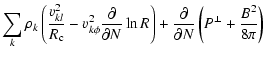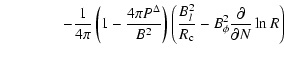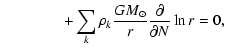A&A 494, 361-371 (2009)
DOI: 10.1051/0004-6361:200810992
Angular momentum transport in a multicomponent solar wind with differentially flowing, thermally anisotropic ions
B. Li - X. Li
Institute of Mathematics and Physics, Aberystwyth University, SY23 3BZ, UK
Received 19 September 2008 / Accepted 27 November 2008
Abstract
Context. The Helios measurements of the angular momentum flux L of the fast solar wind lead to a tendency for the fluxes associated with individual ion angular momenta of protons and alpha particles,  and
and 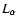 ,
to be negative (i.e., in the sense of counter-rotation with the Sun). However, the opposite holds for the slow wind, and the overall particle contribution
,
to be negative (i.e., in the sense of counter-rotation with the Sun). However, the opposite holds for the slow wind, and the overall particle contribution
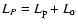 tends to exceed the magnetic contribution
tends to exceed the magnetic contribution  .
These two aspects are at variance with previous models.
.
These two aspects are at variance with previous models.
Aims. We examine whether introducing realistic ion temperature anisotropies can resolve this discrepancy.
Methods. From a general set of multifluid transport equations with gyrotropic species pressure tensors, we derive the equations governing both the meridional and azimuthal dynamics of outflows from magnetized, rotating stars. The equations are not restricted to radial flows in the equatorial plane but valid for general axisymmetric winds that include two major ion species. The azimuthal dynamics are examined in detail, using the empirical meridional flow profiles for the solar wind, constructed mainly according to measurements made in situ.
Results. The angular momentum flux L is determined by the requirement that the solution to the total angular momentum conservation law is unique and smooth in the vicinity of the Alfvén point, defined as where the combined Alfvénic Mach number
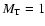 .
.
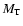 has to consider the contributions from both protons and alpha particles. Introducing realistic ion temperature anisotropies may introduce a change of up to
has to consider the contributions from both protons and alpha particles. Introducing realistic ion temperature anisotropies may introduce a change of up to 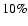 in L and up to
in L and up to  1.8
1.8
 in azimuthal speeds of individual ions between 0.3 and 1 AU, compared with the isotropic case. The latter has strong consequences on the relative importance of LP and
in azimuthal speeds of individual ions between 0.3 and 1 AU, compared with the isotropic case. The latter has strong consequences on the relative importance of LP and  in the angular momentum budget.
in the angular momentum budget.
Conclusions. However, introducing ion temperature anisotropies cannot resolve the discrepancy between in situ measurements and model computations. For the fast-wind solutions, while in extreme cases LP may become negative,  never does. On the other hand, for the slow solar wind solutions examined, LP never exceeds
never does. On the other hand, for the slow solar wind solutions examined, LP never exceeds  ,
even though
,
even though  may be less than the individual ion contribution, since
may be less than the individual ion contribution, since  and
and 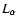 always have opposite signs for the slow and fast wind alike.
always have opposite signs for the slow and fast wind alike.
Key words: Sun: rotation - Sun: magnetic fields - solar wind - stars: rotation - stars: winds, outflows
The angular momentum loss of a rotating star due to its outflow influences the rotational evolution of the star considerably, and is therefore of astrophysical significance in general (see e.g., Weber & Davis 1967; Mestel & Spruit 1987; Belcher & MacGregor 1976; Bouvier et al. 1997). However, direct tests of in situ measurements against theories such as those presented by Weber & Davis (1967) are only possible for the present Sun. A substantial number of studies have been conducted and were compiled in the comprehensive paper by Pizzo et al. (1983), who themselves paid special attention to the Helios measurements of specific angular momentum fluxes. The measurements, further analyzed by Marsch & Richter (1984), are unique in that they allow the individual ion contribution from protons  and alpha particles
and alpha particles 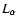 to the solar angular-momentum loss rate per steradian L to be examined. For instance, despite the significant scatter, the data exhibit a distinct trend for
to the solar angular-momentum loss rate per steradian L to be examined. For instance, despite the significant scatter, the data exhibit a distinct trend for
 to be positive (negative) for solar winds with proton speeds
to be positive (negative) for solar winds with proton speeds 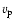 below (above) 400
below (above) 400
 .
A similar trend for
.
A similar trend for
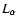 is also found on average. The magnetic contribution
is also found on average. The magnetic contribution
 ,
on the other hand, is remarkably constant. A mean value of
,
on the other hand, is remarkably constant. A mean value of
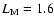
 1029
1029
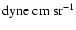 can be quoted for the solar winds of all flow speeds and throughout the region from 0.3 to 1 AU. For comparison, the mean values of angular momentum fluxes carried by ion flows in the slow solar wind are
can be quoted for the solar winds of all flow speeds and throughout the region from 0.3 to 1 AU. For comparison, the mean values of angular momentum fluxes carried by ion flows in the slow solar wind are
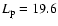 and
and
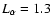
 1029
1029
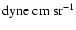 (see Table II of Pizzo et al. 1983). The overall particle contribution to L is then
(see Table II of Pizzo et al. 1983). The overall particle contribution to L is then
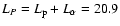
 1029
1029
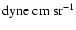 ,
which tends to be larger than
,
which tends to be larger than
 .
It is noteworthy that a more recent study by Scherer et al. (2001) showed how examining the long-term variation of the non-radial components of the solar wind velocity and the corresponding angular momentum fluxes can help us understand the heliospheric magnetic field better.
.
It is noteworthy that a more recent study by Scherer et al. (2001) showed how examining the long-term variation of the non-radial components of the solar wind velocity and the corresponding angular momentum fluxes can help us understand the heliospheric magnetic field better.
Alpha particles should be placed on the same footing as protons from the perspective of solar wind modeling, given their non-negligible abundance and the fact that there tends to exist a substantial differential speed
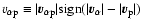 .
As shown by the Helios measurements, a
.
As shown by the Helios measurements, a
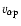 amounting to up to
amounting to up to 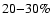 of the local proton speed may occur in both the fast and slow solar winds (Marsch et al. 1982a,b), with the latter being exemplified by an event that took place on day 117 of 1978, when a positive
of the local proton speed may occur in both the fast and slow solar winds (Marsch et al. 1982a,b), with the latter being exemplified by an event that took place on day 117 of 1978, when a positive
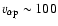
 was found at 0.3 AU (Marsch et al. 1981). That on the average
was found at 0.3 AU (Marsch et al. 1981). That on the average
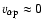 in the slow wind simply reflects that the events with positive and negative
in the slow wind simply reflects that the events with positive and negative
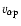 occur with nearly equal frequency (Marsch et al. 1982a). As for the alpha abundance relative to protons, a value of
occur with nearly equal frequency (Marsch et al. 1982a). As for the alpha abundance relative to protons, a value of 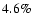 (
(
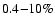 )
is well-established for the fast (slow) solar wind (e.g., McComas et al. 2000). Therefore alpha particles can play an important role as far as the energy and linear momentum balance of the solar wind are concerned.
When it comes to the problem of angular momentum transport, it was shown that in interplanetary space not only the angular momentum flux carried by the alpha particles
)
is well-established for the fast (slow) solar wind (e.g., McComas et al. 2000). Therefore alpha particles can play an important role as far as the energy and linear momentum balance of the solar wind are concerned.
When it comes to the problem of angular momentum transport, it was shown that in interplanetary space not only the angular momentum flux carried by the alpha particles 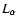 but also that convected by the protons
but also that convected by the protons  are determined by the terms associated with
are determined by the terms associated with
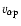 (Li & Li 2006). This essentially derives from the requirement that the proton-alpha velocity difference vector be aligned with the instantaneous magnetic field. As a consequence, these terms have no contribution to the overall angular momentum flux convected by the ion flow LP, which turns out to be smaller than
(Li & Li 2006). This essentially derives from the requirement that the proton-alpha velocity difference vector be aligned with the instantaneous magnetic field. As a consequence, these terms have no contribution to the overall angular momentum flux convected by the ion flow LP, which turns out to be smaller than  in all the models examined in the parameter study by Li et al. (2007). This, together with the fact that
in all the models examined in the parameter study by Li et al. (2007). This, together with the fact that  is always positive (i.e., in the sense of corotation with the Sun), is at variance with the Helios measurements.
is always positive (i.e., in the sense of corotation with the Sun), is at variance with the Helios measurements.
A possible means to reconcile the measurements and the model computation is to incorporate the species temperature anisotropies. This is because the total pressure tensor
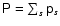 summed over all species s participates in the problem of angular momentum transport via the component
summed over all species s participates in the problem of angular momentum transport via the component
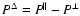 where
where 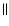 and
and 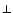 are relative to the magnetic field
are relative to the magnetic field 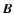 (see e.g., Weber 1970, hereafter referred to as W70). While the overall loss rate per steradian L may not be significantly altered, the azimuthal speed of the solar wind and therefore the particle part of L may be when compared with the isotropic case.
Note that in the treatment of W70 the solar wind was seen as a bulk flow and the ion species are not distinguished. On the other hand, the formulation by Li & Li (2006) did not take into account the pressure anisotropy, which is a salient feature of the velocity distribution functions for both protons and alpha particles as revealed by the Helios measurements (Marsch et al. 1982a,b). It therefore remains to be seen how introducing the pressure anisotropy influences individual ion azimuthal speeds. Moreover, the simple, prescribed functional form for
(see e.g., Weber 1970, hereafter referred to as W70). While the overall loss rate per steradian L may not be significantly altered, the azimuthal speed of the solar wind and therefore the particle part of L may be when compared with the isotropic case.
Note that in the treatment of W70 the solar wind was seen as a bulk flow and the ion species are not distinguished. On the other hand, the formulation by Li & Li (2006) did not take into account the pressure anisotropy, which is a salient feature of the velocity distribution functions for both protons and alpha particles as revealed by the Helios measurements (Marsch et al. 1982a,b). It therefore remains to be seen how introducing the pressure anisotropy influences individual ion azimuthal speeds. Moreover, the simple, prescribed functional form for 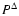 assumed in W70 needs to be updated in light of the more recent particle measurements.
assumed in W70 needs to be updated in light of the more recent particle measurements.
The aim of the present paper is to extend the W70 study in three ways. First, we shall follow a multicomponent approach and examine the angular momentum transport in a solar wind comprising protons, alpha particles and electrons where a substantial proton-alpha particle velocity difference exists. Second, although following W70 we use a prescribed form of 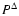 for simplicity, this prescription is based on the Helios measurements, and also takes into account other in situ and remote sensing measurements. Third, unlike W70 where the model equations are restricted to the equatorial plane, the equation set we shall derive is appropriate for a rather general axisymmetrical, time-independent, multicomponent, thermally anisotropic flow emanating from a magnetized rotating star. We note that a similar set of equations, which was also restricted to radial flows, was derived by Isenberg (1984) who worked in the corotating frame of reference and neglected the azimuthal dynamics altogether. The functional dependence on the radial distance and flow speed of the magnetic spiral angle was prescribed instead. His approach is certainly justifiable for the present Sun, but a self-consistent treatment of the azimuthal dynamics is required when flows from other stars are examined. This is because many stars either have a stronger magnetic field or rotate substantially faster than the Sun.
for simplicity, this prescription is based on the Helios measurements, and also takes into account other in situ and remote sensing measurements. Third, unlike W70 where the model equations are restricted to the equatorial plane, the equation set we shall derive is appropriate for a rather general axisymmetrical, time-independent, multicomponent, thermally anisotropic flow emanating from a magnetized rotating star. We note that a similar set of equations, which was also restricted to radial flows, was derived by Isenberg (1984) who worked in the corotating frame of reference and neglected the azimuthal dynamics altogether. The functional dependence on the radial distance and flow speed of the magnetic spiral angle was prescribed instead. His approach is certainly justifiable for the present Sun, but a self-consistent treatment of the azimuthal dynamics is required when flows from other stars are examined. This is because many stars either have a stronger magnetic field or rotate substantially faster than the Sun.
The paper is organized as follows. We start with Sect. 2 where a description is given for the general multifluid, gyrotropic transport equations, based on which the azimuthal dynamics of the multicomponent solar wind is examined. Then Sect. 3 describes the adopted meridional magnetic field and flow profiles. The numerical solutions to the angular momentum conservation law are given in Sect. 4. In Sect. 5, we shall discuss how examining the angular momentum transport in a multicomponent solar wind can also shed some light on the spectra of ion velocity fluctuations induced by Alfvénic activities.
Finally, Sect. 6 summarizes the results. The equations of and a discussion on the poloidal dynamics are presented in the Appendix.
2 Mathematical formulation
Presented in this section is the mathematical development of the equations that govern the angular momentum transport in a time-independent solar wind which consists of electrons (e), protons (p) and alpha particles (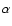 ). Each species s (
). Each species s (
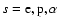 )
is characterized by its mass ms, electric charge es, number density ns, mass density
)
is characterized by its mass ms, electric charge es, number density ns, mass density
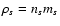 ,
velocity
,
velocity 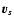 ,
and partial pressure tensor
,
and partial pressure tensor
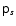 .
If measured in units of the electron charge e, es may be expressed by
es = Zs e with
.
If measured in units of the electron charge e, es may be expressed by
es = Zs e with
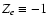 by definition.
by definition.
To simplify the mathematical treatment, a number of assumptions have been made and are collected as follows:
- 1.
- Symmetry about the magnetic axis is assumed, i.e.,
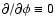 in a heliocentric spherical coordinate system (
in a heliocentric spherical coordinate system (
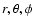 ).
).
- 2.
- The velocity distribution function (VDF) of each species is close to a bi-Maxwellian, and the pressure tensor is gyrotropic, i.e.,
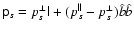 ,
where
,
where  is the unit dyad and
is the unit dyad and  is the unit vector along the magnetic field
is the unit vector along the magnetic field 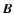 .
The temperatures pertaining to the degrees of freedom parallel and perpendicular to
.
The temperatures pertaining to the degrees of freedom parallel and perpendicular to  follow from the relation
follow from the relation
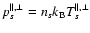 ,
where
,
where 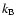 is the Boltzmann constant.
is the Boltzmann constant.
- 3.
- Quasi-neutrality is assumed, i.e.,
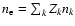 .
.
- 4.
- Quasi-zero current is assumed, i.e.,
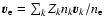 (
(
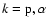 ), except when the reduced meridional momentum equation is derived.
), except when the reduced meridional momentum equation is derived.
2.1 Multi-fluid equations
The equations appropriate for a multi-component solar wind plasma with gyrotropic species pressure tensors may be found by neglecting the electron inertia (
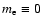 )
in the equations given by Barakat & Schunk (1982). Following the same procedure as given in the Appendix A.1 in Li & Li (2006), one may find
)
in the equations given by Barakat & Schunk (1982). Following the same procedure as given in the Appendix A.1 in Li & Li (2006), one may find
where the subscript s refers to all species (
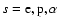 ), while k stands for ion species only (
), while k stands for ion species only (
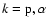 ). The gravitational constant is denoted by G,
). The gravitational constant is denoted by G, 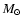 is the mass of the Sun, and c is the speed of light. The momentum and energy exchange rates due to the Coulomb collisions of species s with the remaining ones are denoted by
is the mass of the Sun, and c is the speed of light. The momentum and energy exchange rates due to the Coulomb collisions of species s with the remaining ones are denoted by
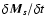 and
and
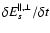 ,
respectively. The third-rank tensor
,
respectively. The third-rank tensor
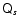 ,
together with the heat flux vectors
,
together with the heat flux vectors
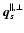 associated with parallel and perpendicular degrees of freedom, arises from the deviation of species VDFs from an exact bi-Maxwellian (Barakat & Schunk 1982). Moreover,
associated with parallel and perpendicular degrees of freedom, arises from the deviation of species VDFs from an exact bi-Maxwellian (Barakat & Schunk 1982). Moreover,
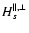 stands for the heating rates applied to species s in the parallel and perpendicular directions from some non-thermal processes. They may be determined by assuming that the heating derives from the dissipation of Alfvén-ion cyclotron waves (e.g., Hollweg & Isenberg 2002), or more simply in some ad hoc fashion such as employed in Leer & Axford (1972). The operators
stands for the heating rates applied to species s in the parallel and perpendicular directions from some non-thermal processes. They may be determined by assuming that the heating derives from the dissipation of Alfvén-ion cyclotron waves (e.g., Hollweg & Isenberg 2002), or more simply in some ad hoc fashion such as employed in Leer & Axford (1972). The operators
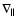 and
and
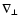 are defined by
are defined by
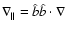 and
and
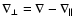 ,
respectively.
,
respectively.
In Eq. (2), the subscript j stands for the ion species other than k, namely, 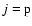 for
for 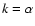 and vice versa. As can be seen, in addition to the term
and vice versa. As can be seen, in addition to the term
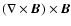 ,
the Lorentz force possesses a new term in the form of the cross product of the ion velocity difference and magnetic field. Physically, this new term represents the mutual gyration of one ion species about the other, the axis of gyration being in the direction of the instantaneous magnetic field. Furthermore, Eq. (5) is the time-independent version of the magnetic induction law, which states that the magnetic field is frozen in the electron fluid. It may be readily shown that the effects of the electron pressure gradient, the Hall term, and the momentum exchange rates as contained in the generalized Ohm's law can be safely neglected given the large spatial scale in question (a formal evaluation of the different terms can be found in Sect. 2.1 of Li et al. 2006).
,
the Lorentz force possesses a new term in the form of the cross product of the ion velocity difference and magnetic field. Physically, this new term represents the mutual gyration of one ion species about the other, the axis of gyration being in the direction of the instantaneous magnetic field. Furthermore, Eq. (5) is the time-independent version of the magnetic induction law, which states that the magnetic field is frozen in the electron fluid. It may be readily shown that the effects of the electron pressure gradient, the Hall term, and the momentum exchange rates as contained in the generalized Ohm's law can be safely neglected given the large spatial scale in question (a formal evaluation of the different terms can be found in Sect. 2.1 of Li et al. 2006).
To proceed, we choose a flux tube coordinate system, in which the base vectors are
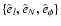 ,
where
,
where
with the subscript P denoting the poloidal component. Moreover, the independent variable l is the arclength along the poloidal magnetic field line measured from its footpoint at the Sun.
This choice permits the decomposition of the magnetic field and species velocities as follows,
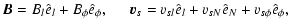 |
|
|
(6) |
where
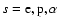 .
From the assumption of azimuthal symmetry, and the assumption that the solar wind is time-independent, one can see from the poloidal component of Eq. (5) that
.
From the assumption of azimuthal symmetry, and the assumption that the solar wind is time-independent, one can see from the poloidal component of Eq. (5) that
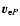 should be strictly in the direction of
should be strictly in the direction of 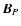 .
In other words,
.
In other words,
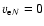 to a good approximation. Now let us consider the
to a good approximation. Now let us consider the 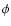 component of the momentum Eq. (2). Since the frequencies associated with the spatial dependence are well below the ion gyro-frequency
component of the momentum Eq. (2). Since the frequencies associated with the spatial dependence are well below the ion gyro-frequency
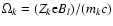 (
(
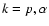 ), from an order-of-magnitude estimate one can see that
), from an order-of-magnitude estimate one can see that
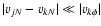 .
Combined with the fact that
.
Combined with the fact that
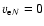 ,
this leads to that both
,
this leads to that both
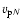 and
and
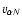 should be very small and can be safely neglected unless they appear alongside the ion gyro-frequency. With this in mind, one can find from the N component of Eq. (2) that
should be very small and can be safely neglected unless they appear alongside the ion gyro-frequency. With this in mind, one can find from the N component of Eq. (2) that
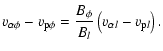 |
|
|
(7) |
That is, the ion velocity difference is strictly aligned with the magnetic field. This alignment condition further couples one ion species to the other.
The fact that vs N (
 )
is negligible means that the system of vector equations may be decomposed into a force balance condition across the poloidal magnetic field and a set of transport equations along it. In the present paper, however, we simply replace the force balance condition by prescribing an analytical meridional magnetic field configuration. Moreover, we examine in detail only the azimuthal dynamics, leaving a brief discussion on the poloidal one in the Appendix.
)
is negligible means that the system of vector equations may be decomposed into a force balance condition across the poloidal magnetic field and a set of transport equations along it. In the present paper, however, we simply replace the force balance condition by prescribing an analytical meridional magnetic field configuration. Moreover, we examine in detail only the azimuthal dynamics, leaving a brief discussion on the poloidal one in the Appendix.
2.2 Azimuthal dynamics
The  component of the magnetic induction law (5) gives
component of the magnetic induction law (5) gives
![$\displaystyle %
\nabla\cdot \left[\frac{1}{R}\left(B_\phi \vec{v}_{{\rm e} P} - v_{{\rm e} \phi} \vec{B}_{P}\right)\right] =0.$](/articles/aa/full/2009/04/aa10992-08/img102.gif) |
|
|
(8) |
Now that
 ,
one may readily integrate Eq. (8) along a magnetic line of force to yield
,
one may readily integrate Eq. (8) along a magnetic line of force to yield
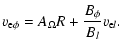 |
|
|
(9) |
Here
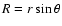 is a geometrical factor to be evaluated along a given line of force (see Fig. 1), and
is a geometrical factor to be evaluated along a given line of force (see Fig. 1), and 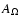 is a constant of integration and should be identified as the angular rotation rate of the footpoint of the magnetic flux tube. Taking into account the alignment condition (7), one may find that
is a constant of integration and should be identified as the angular rotation rate of the footpoint of the magnetic flux tube. Taking into account the alignment condition (7), one may find that
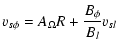 |
|
|
(10) |
where
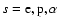 .
Therefore in a frame of reference that corotates with the Sun, the velocities of all species are aligned with the magnetic field.
.
Therefore in a frame of reference that corotates with the Sun, the velocities of all species are aligned with the magnetic field.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0992fig1.eps}
\end{figure}](/articles/aa/full/2009/04/aa10992-08/Timg110.gif) |
Figure 1:
Adopted meridional magnetic field configuration in the inner corona.
Here only a quadrant is shown in which the magnetic axis points upward, and the thick contours
labeled F and S delineate the lines of force along which the fast and slow solar wind solutions are examined, respectively. Also shown is how to define the geometrical factor R, and the base vectors
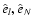 and
and
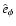 of the flux tube coordinate system
(see Sect. 2).
of the flux tube coordinate system
(see Sect. 2). |
| Open with DEXTER |
Another equation that enters into the azimuthal dynamics is the 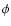 component of the total momentum. In the present case, it reads
component of the total momentum. In the present case, it reads
![$\displaystyle %
\frac{1}{R}\left\{\sum_k \rho_k v_{k l} \left(R v_{k \phi}\righ...
... \pi}\left[\left(1-\frac{4\pi P^\Delta}{B^2}\right)R B_\phi\right]'\right\} =0,$](/articles/aa/full/2009/04/aa10992-08/img111.gif) |
|
|
(11) |
where
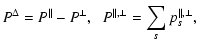 |
|
|
(12) |
and the prime
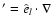 is the directional derivative along the poloidal magnetic field.
is the directional derivative along the poloidal magnetic field.
For a time-independent flow
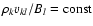 .
It then follows that
.
It then follows that
![$\displaystyle %
R\left[ v_{{\rm p} \phi} + \eta v_{\alpha \phi} -
\frac{B_l B_\...
...rho_{\rm p} v_{{\rm p}l}}\left(1-\frac{4\pi P^\Delta}{B^2}\right)\right] = A_L,$](/articles/aa/full/2009/04/aa10992-08/img115.gif) |
|
|
(13) |
where the constant
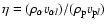 is the ion mass flux ratio, and AL is a constant of integration. Physically, AL is related to the angular momentum loss rate per steradian L by
is the ion mass flux ratio, and AL is a constant of integration. Physically, AL is related to the angular momentum loss rate per steradian L by
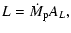 |
|
|
(14) |
where
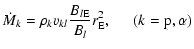 |
|
|
(15) |
is the ion mass loss rate per steradian scaled to the Earth orbit
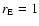 AU, with
AU, with
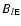 denoting the strength of the poloidal magnetic field at
denoting the strength of the poloidal magnetic field at 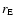 .
It follows that the angular momentum loss rate of the Sun due to the solar wind
.
It follows that the angular momentum loss rate of the Sun due to the solar wind
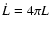 if L is independent of colatitude. Equation (13) shows that L consists of the contributions due to
individual ion angular momenta Lk, the magnetic stresses
if L is independent of colatitude. Equation (13) shows that L consists of the contributions due to
individual ion angular momenta Lk, the magnetic stresses  and the total pressure anisotropy
and the total pressure anisotropy
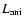 , where
, where
![$\displaystyle %
\left[L_k, L_{\rm M}, L_{\rm ani}\right] = R\left(\frac{B_{l{\r...
...k l}v_{k\phi}, \frac{-B_l B_\phi}{4\pi}, \frac{B_l B_\phi P^\Delta}{B^2}\right]$](/articles/aa/full/2009/04/aa10992-08/img123.gif) |
|
|
(16) |
with
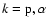 .
.
Substituting Eqs. (10) into (13), one may find
![$\displaystyle %
\tan\Phi \left[M_{\rm T}^2 - \left(1-\beta^\Delta\cos^2\Phi\right)\right]
= \epsilon \left[\frac{A_L}{(1+\eta)A_\Omega R^2}-1\right],$](/articles/aa/full/2009/04/aa10992-08/img124.gif) |
|
|
(17) |
where
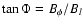 defines the magnetic azimuthal angle
defines the magnetic azimuthal angle 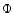 , and
, and
| |
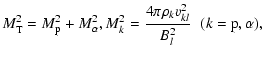 |
|
| |
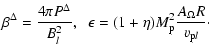 |
(18) |
By definition, 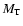 is the combined poloidal Alfvénic Mach number, which involves both ion species. For a typical solar wind, between 1
is the combined poloidal Alfvénic Mach number, which involves both ion species. For a typical solar wind, between 1  and 1 AU there exists a point where
and 1 AU there exists a point where
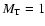 ,
which is to be called the Alfvén point and denoted by
,
which is to be called the Alfvén point and denoted by 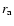 .
.
As discussed in detail by Li & Li (2006), when species temperature anisotropy is absent (
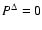 and therefore
and therefore
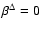 ), for Eq. (17) to possess a solution that passes smoothly through
), for Eq. (17) to possess a solution that passes smoothly through 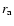 the two constants AL and
the two constants AL and 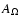 have to be related by
have to be related by
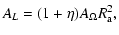 |
|
|
(19) |
where the subscript a denotes quantities evaluated at the Alfvén point. When
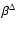 is not zero, a direct relation between AL and
is not zero, a direct relation between AL and 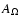 is not as obvious since now Eq. (17) becomes cubic in
is not as obvious since now Eq. (17) becomes cubic in  .
Nevertheless, one may write AL as
.
Nevertheless, one may write AL as
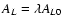 ,
where AL 0 is determined through Eq. (19) and therefore
,
where AL 0 is determined through Eq. (19) and therefore 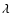 stands for the correction due to a finite
stands for the correction due to a finite
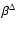 .
It then follows that
.
It then follows that
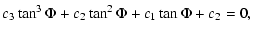 |
|
|
(20) |
where
| |
![$\displaystyle c_3 = M_{\rm T}^2-1, c_2 = \epsilon\left[1-\lambda\left(\frac{R_{\rm a}}{R}\right)^2\right],$](/articles/aa/full/2009/04/aa10992-08/img137.gif) |
|
| |
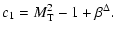 |
(21) |
Given the meridional flow profiles along a prescribed magnetic field line, Eq. (20) possesses only one real root at locations far away from  .
However, in the vicinity of
.
However, in the vicinity of 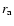 ,
there exists in general three real roots and they diverge near
,
there exists in general three real roots and they diverge near 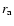 .
The requirement that there exists a unique solution that is smooth from 1
.
The requirement that there exists a unique solution that is smooth from 1  out to 1 AU determines
out to 1 AU determines 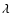 (Weber 1970; Weber & Davis 1970).
(Weber 1970; Weber & Davis 1970).
3 Meridional magnetic field and flow profiles
In principle, one needs to solve Eqs. (A.1) to (A.4) together with Eq. (17) simultaneously to gain a a quantitative insight. In the present paper, we refrain from doing so because from previous experience it proves difficult to yield the flow profiles that satisfactorily reproduce in situ measurements such as made by Helios. Take the proton-alpha speed difference
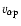 in the fast solar wind for example. It is observationally established that
in the fast solar wind for example. It is observationally established that
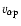 closely tracks the local Alfvén speed in the heliocentric range r> 0.3 AU (Marsch et al. 1982a). So far this fact still poses a theoretical challenge: adjusting the ad hoc heating parameters, or fine-tuning the cyclotron resonance mechanism is unable to produce such a behavior (see, e.g. Hu & Habbal 1999). We therefore adopt an alternative approach by prescribing the background meridional flow profiles that mimic the observations and then examining what consequences the species anisotropies have on the azimuthal dynamics.
closely tracks the local Alfvén speed in the heliocentric range r> 0.3 AU (Marsch et al. 1982a). So far this fact still poses a theoretical challenge: adjusting the ad hoc heating parameters, or fine-tuning the cyclotron resonance mechanism is unable to produce such a behavior (see, e.g. Hu & Habbal 1999). We therefore adopt an alternative approach by prescribing the background meridional flow profiles that mimic the observations and then examining what consequences the species anisotropies have on the azimuthal dynamics.
3.1 Background meridional magnetic field
For the meridional magnetic field, we adopt an analytical model given by Banaszkiewicz et al. (1998).
In the present implementation, the model magnetic field consists of the dipole and current-sheet components only. A set of parameters M=2.2265, Q=0, K=0.9343 and a1=1.5 are chosen such that the last open magnetic field line is anchored at heliocentric colatitude
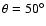 on the Sun, while at the Earth orbit, the meridional magnetic field strength Bl is 3
on the Sun, while at the Earth orbit, the meridional magnetic field strength Bl is 3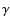 and independent of colatitude
and independent of colatitude 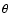 ,
consistent with Ulysses measurements (Smith & Balogh 1995).
,
consistent with Ulysses measurements (Smith & Balogh 1995).
The background magnetic field configuration is depicted in Fig. 1, where the thick contours labeled F and S represent the lines of force along which we examine the
fast and slow solar wind solutions, respectively. Tube F (S), which intersects the Earth orbit at 70 (89
(89 )
colatitude, originates from
)
colatitude, originates from
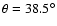 (
(
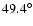 )
at the Sun where the meridional magnetic field strength Bl is 3.93 (3.49) G.
)
at the Sun where the meridional magnetic field strength Bl is 3.93 (3.49) G.
3.2 Prescribed meridional flow profiles
The background meridional flow parameters are found by adopting a three-step approach described as follows:
- 1.
- Using some ad hoc heating parameters, we solve along flux tube F (S) the isotropic version of Eqs. (A.1) to (A.4) (see Eqs. (8) to (10) in Li & Li 2007, for details) to yield the distribution between 1
 and 1 AU of the ion number densities nk and meridional speeds vk l (
and 1 AU of the ion number densities nk and meridional speeds vk l (
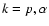 ), as well as the isotropic species temperatures Ts (
), as well as the isotropic species temperatures Ts (
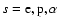 )
for the fast (slow) solar wind.
Specifically, the heating rates are of the same format as in Sect. 3.2 in Li & Li (2008). To generate the fast and slow solar wind solutions, the parameters
)
for the fast (slow) solar wind.
Specifically, the heating rates are of the same format as in Sect. 3.2 in Li & Li (2008). To generate the fast and slow solar wind solutions, the parameters
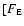 (in
(in
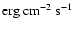 ), ld (in
), ld (in  ),
), ![$\chi]$](/articles/aa/full/2009/04/aa10992-08/img147.gif) are chosen to be
[1.9, 2.2, 2.2] and
[1, 1.8, 3.7], respectively.
By simply adjusting the heating parameters it proves difficult to produce a reasonable
are chosen to be
[1.9, 2.2, 2.2] and
[1, 1.8, 3.7], respectively.
By simply adjusting the heating parameters it proves difficult to produce a reasonable 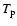 profile in that if
profile in that if 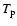 in the inner corona is close to observations then
in the inner corona is close to observations then 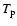 at 1 AU is usually only a fraction of the typically measured values. Moreover, the derived speed difference
at 1 AU is usually only a fraction of the typically measured values. Moreover, the derived speed difference
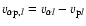 varies little between 0.3 and 1 AU, in contrast to the Helios measurements. Therefore some additional steps are employed to make the flow profiles more realistic. Specifically, all the parameters except
varies little between 0.3 and 1 AU, in contrast to the Helios measurements. Therefore some additional steps are employed to make the flow profiles more realistic. Specifically, all the parameters except 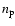 and
and
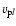 are required to undergo a smooth transition from the profiles for the region
are required to undergo a smooth transition from the profiles for the region 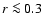 AU derived so far
to those specified in next step for the outer region.
AU derived so far
to those specified in next step for the outer region.
- 2.
- The desired profiles, given in Table 1, for
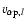 ,
,
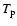 and
and 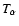 for the region
for the region 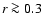 AU (denoted by subscript o) are based on the in situ measurements to be detailed shortly. Once
AU (denoted by subscript o) are based on the in situ measurements to be detailed shortly. Once
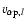 is known, the meridional alpha speed
is known, the meridional alpha speed
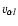 is given by
is given by
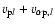 ,
and the alpha density
,
and the alpha density 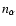 by
by
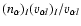 ,
where the subscript I denotes the values obtained in the first step. The distributions of nk, vkl (
,
where the subscript I denotes the values obtained in the first step. The distributions of nk, vkl (
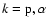 )
and Ts (
)
and Ts (
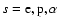 )
thus constructed are for the isotropic model.
)
thus constructed are for the isotropic model.
- 3.
- Now the ion temperatures
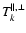 can be constructed by prescribing the temperature anisotropy
can be constructed by prescribing the temperature anisotropy
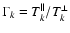 (
(
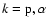 ). Note that the electron temperature is assumed to be isotropic. For the region within several solar radii,
). Note that the electron temperature is assumed to be isotropic. For the region within several solar radii, 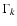 is required to decrease with r from 1 at 1
is required to decrease with r from 1 at 1  ,
where the Coulomb self-collisions are still frequent enough to suppress a temperature anisotropy, to some value less than unity. This inner profile is not directly constrained by observations but constructed by noting that the processes operational in the inner corona tend to heat the ions preferentially in the perpendicular direction
(e.g., Hollweg & Isenberg 2002). On the other hand, for
,
where the Coulomb self-collisions are still frequent enough to suppress a temperature anisotropy, to some value less than unity. This inner profile is not directly constrained by observations but constructed by noting that the processes operational in the inner corona tend to heat the ions preferentially in the perpendicular direction
(e.g., Hollweg & Isenberg 2002). On the other hand, for 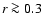 AU,
AU, 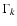 follows a power law dependence on r with the exponent determined by the Helios measurements (see Table 1). Specifying the temperature anisotropies of protons and alpha particles at 1 AU,
follows a power law dependence on r with the exponent determined by the Helios measurements (see Table 1). Specifying the temperature anisotropies of protons and alpha particles at 1 AU,
 and
and
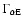 ,
determines
,
determines 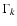 in the outer region.
The inner and outer profiles are then connected smoothly to yield the desired
in the outer region.
The inner and outer profiles are then connected smoothly to yield the desired 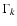 .
The temperatures
.
The temperatures
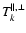 follow from the relations
follow from the relations
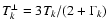 and
and
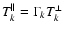 .
.
A detailed description of Table 1 is necessary. Note that throughout this table
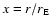 where
where
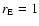 AU. Let us first focus on the adopted values for the fast solar wind. For the isotropic proton and alpha temperatures at 1 AU, we adopted the typical values of
AU. Let us first focus on the adopted values for the fast solar wind. For the isotropic proton and alpha temperatures at 1 AU, we adopted the typical values of
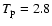
 105 K and
105 K and
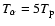 (see e.g., McComas et al. 2000; Schwenn 1990, hereafter Sch90 and Mc00). Furthermore, Figs. 18 and 19 in Marsch et al. (1982b, hereafter M82b) indicate that
(see e.g., McComas et al. 2000; Schwenn 1990, hereafter Sch90 and Mc00). Furthermore, Figs. 18 and 19 in Marsch et al. (1982b, hereafter M82b) indicate that
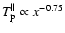 ,
and
,
and
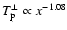 .
A power law dependence for
.
A power law dependence for 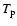 of
of
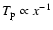 is therefore consistent with such a behavior, and also consistent with the Ulysses measurements (see Table 2 in Mc00). Furthermore, Fig. 5 in Marsch et al. (1982a, hereafter M82a) indicates that
is therefore consistent with such a behavior, and also consistent with the Ulysses measurements (see Table 2 in Mc00). Furthermore, Fig. 5 in Marsch et al. (1982a, hereafter M82a) indicates that
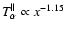 ,
and
,
and
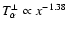 .
A profile of
.
A profile of
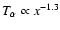 is consistent with this behavior, but differs substantially from that measured by Ulysses, which yields that
is consistent with this behavior, but differs substantially from that measured by Ulysses, which yields that
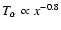 (see Table 2 in Mc00). Moving on to the slow solar wind, we note that values of
(see Table 2 in Mc00). Moving on to the slow solar wind, we note that values of
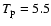
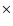 104 K and
104 K and
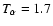
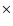 105 K are typically found at 1 AU (see e.g., Sch90). In addition, Figs. 18 and 19 in M82b indicate that
105 K are typically found at 1 AU (see e.g., Sch90). In addition, Figs. 18 and 19 in M82b indicate that
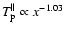 ,
and
,
and
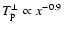 .
Therefore we adopted a
.
Therefore we adopted a 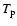 profile of
profile of
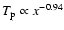 .
On the other hand, we adopted a profile for
.
On the other hand, we adopted a profile for 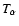 in the form
in the form
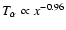 ,
which is consistent with the measured alpha temperature anisotropies which indicate that
,
which is consistent with the measured alpha temperature anisotropies which indicate that
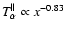 ,
and
,
and
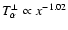 (see Fig. 5 in M82a).
(see Fig. 5 in M82a).
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0992fig2.eps}
\end{figure}](/articles/aa/full/2009/04/aa10992-08/Timg180.gif) |
Figure 2:
Radial distribution between 1  and 1 AU of the adopted meridional flow parameters for the fast ( left column) and slow ( right) solar wind. a) and c), the meridional flow speeds of protons (
and 1 AU of the adopted meridional flow parameters for the fast ( left column) and slow ( right) solar wind. a) and c), the meridional flow speeds of protons (
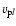 )
and alpha particles ( )
and alpha particles (
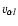 ). b) and d), the ion temperatures ). b) and d), the ion temperatures
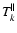 (dotted lines),
(dotted lines),
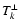 (dashed lines), and
(dashed lines), and
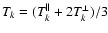 (solid lines) where
(solid lines) where
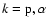 .
The construction of .
The construction of
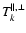 is described in Sect. 3.2.
The error bars in b) and d) represent the uncertainties of the UVCS measurements of the effective proton temperature as reported by Kohl et al. (1998) for a coronal hole, and by Frazin et al. (2003) for a streamer, respectively. Note that both measurements are typical of solar minimum conditions. Moreover, the asterisks in a) and c) denote the Alfvén point, where the meridional Alfvénic Mach number (defined by Eq. (18)) equals unity.
is described in Sect. 3.2.
The error bars in b) and d) represent the uncertainties of the UVCS measurements of the effective proton temperature as reported by Kohl et al. (1998) for a coronal hole, and by Frazin et al. (2003) for a streamer, respectively. Note that both measurements are typical of solar minimum conditions. Moreover, the asterisks in a) and c) denote the Alfvén point, where the meridional Alfvénic Mach number (defined by Eq. (18)) equals unity. |
| Open with DEXTER |
In this study
 and
and
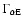 will serve as free parameters.
The Helios measurements indicate that
will serve as free parameters.
The Helios measurements indicate that
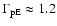
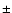 0.3 and
0.3 and
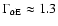
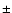 0.6 for the fast solar wind with
0.6 for the fast solar wind with
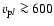
 ,
while
,
while
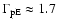
 0.7 and
0.7 and
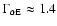
 0.6 for the slow solar wind with
0.6 for the slow solar wind with
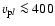
 (Marsch et al. 1982a,b). Theoretically, one may expect that the
(Marsch et al. 1982a,b). Theoretically, one may expect that the
![$[\Gamma_{\rm p E}, \Gamma_{\rm\alpha E}]$](/articles/aa/full/2009/04/aa10992-08/img188.gif) pair may not occupy the whole rectangle bounded by the given values in the
pair may not occupy the whole rectangle bounded by the given values in the
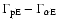 space, since too strong an anisotropy can drive the system unstable with respect to a number of instabilities when the plasma
space, since too strong an anisotropy can drive the system unstable with respect to a number of instabilities when the plasma 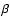 is comparable to unity. Given that the lower limit of
is comparable to unity. Given that the lower limit of
 or
or
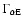 is only slightly lower than 1, the ion-cyclotron instability can be shown to be unlikely to occur (see, e.g., Eq. (3) in Gary et al. 1994). However, the firehose instability may be relevant since it happens when
is only slightly lower than 1, the ion-cyclotron instability can be shown to be unlikely to occur (see, e.g., Eq. (3) in Gary et al. 1994). However, the firehose instability may be relevant since it happens when
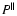 is sufficiently larger than
is sufficiently larger than 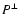 and
and
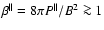 .
Note that the alpha particles with a non-negligible abundance drifting relative to protons may complicate the situation considerably given that in addition to the firehose, electromagnetic ion/ion instabilities may also be relevant and the occurrence of such instabilities is not restricted to the cases where the parallel
.
Note that the alpha particles with a non-negligible abundance drifting relative to protons may complicate the situation considerably given that in addition to the firehose, electromagnetic ion/ion instabilities may also be relevant and the occurrence of such instabilities is not restricted to the cases where the parallel 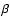 is large (Hellinger & Trávnícek 2006). Nevertheless, we only compare the modeled
is large (Hellinger & Trávnícek 2006). Nevertheless, we only compare the modeled
![$[\Gamma_{\rm p}, \Gamma_\alpha]$](/articles/aa/full/2009/04/aa10992-08/img194.gif) with the non-resonant firehose criterion such as found via the dispersion relation of Alfvén waves (see Eq. (23) in Isenberg 1984). Specializing to an electron-proton-alpha plasma, the dispersion relation dictates that instability occurs when
with the non-resonant firehose criterion such as found via the dispersion relation of Alfvén waves (see Eq. (23) in Isenberg 1984). Specializing to an electron-proton-alpha plasma, the dispersion relation dictates that instability occurs when
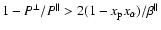 where
where
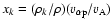 (
(
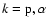 )
with
)
with
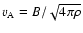 being the Alfvén speed determined by the bulk mass density
being the Alfvén speed determined by the bulk mass density
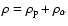 .
Using this criterion it is found that the modeled flow profiles are all stable with the only exception being for the segment
.
Using this criterion it is found that the modeled flow profiles are all stable with the only exception being for the segment 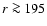
 in the fast wind with the largest values of
in the fast wind with the largest values of
 and
and
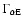 .
.
Figure 2 gives the radial distributions between 1  and 1 AU of the flow parameters for the fast and slow solar wind in the left and right panels, respectively. Figures 2a and c depict the meridional ion speeds
and 1 AU of the flow parameters for the fast and slow solar wind in the left and right panels, respectively. Figures 2a and c depict the meridional ion speeds
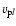 and
and
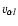 ,
while the ion temperatures
,
while the ion temperatures
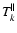 (the dotted curves),
(the dotted curves), 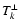 (dashed) and Tk (solid) are given in Figs. 2b and d (
(dashed) and Tk (solid) are given in Figs. 2b and d (
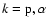 ). The values for the temperature anisotropy adopted for the construction are
). The values for the temperature anisotropy adopted for the construction are
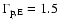 and
and
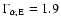 for the fast wind, and
for the fast wind, and
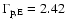 and
and
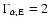 for the slow wind. In Fig. 2b, the error bars represent the uncertainties of the UVCS measurements for the proton effective temperature, made for a polar coronal hole as reported by Kohl et al. (1998). Similar measurements by Frazin et al. (2003) along the edges of an equatorial streamer are given in Fig. 2d. Moreover, the asterisks in Figs. 2a and c mark the location of the Alfvén point as defined by Eq. (18).
for the slow wind. In Fig. 2b, the error bars represent the uncertainties of the UVCS measurements for the proton effective temperature, made for a polar coronal hole as reported by Kohl et al. (1998). Similar measurements by Frazin et al. (2003) along the edges of an equatorial streamer are given in Fig. 2d. Moreover, the asterisks in Figs. 2a and c mark the location of the Alfvén point as defined by Eq. (18).
For the fast (slow) solar wind it is found that at 1 AU the meridional proton speed
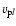 is 607 (304)
is 607 (304)
 ,
the proton flux
,
the proton flux
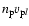 is 2.8 (3.84) in units of 108
is 2.8 (3.84) in units of 108
 ,
the alpha abundance
,
the alpha abundance
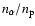 is 4.56% (3.6%), and the meridional component of the proton-alpha velocity difference
is 4.56% (3.6%), and the meridional component of the proton-alpha velocity difference
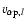 is 23 (5)
is 23 (5)
 .
These values are consistent with in situ measurements such as made by Ulysses (McComas et al. 2000). Moreover, the fast (slow) solar wind reaches the Alfvén point at 10.7 (13.3)
.
These values are consistent with in situ measurements such as made by Ulysses (McComas et al. 2000). Moreover, the fast (slow) solar wind reaches the Alfvén point at 10.7 (13.3)  ,
beyond which
,
beyond which
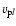 increases only slightly with increasing r. On the other hand, for
increases only slightly with increasing r. On the other hand, for 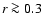 AU the meridional alpha speed
AU the meridional alpha speed
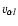 decreases rather than increases with r as a consequence of the prescribed
decreases rather than increases with r as a consequence of the prescribed
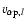 profile. If examining the ratio of
profile. If examining the ratio of
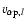 to the meridional Alfvén speed
to the meridional Alfvén speed
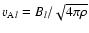 ,
one may find that for the fast solar wind this ratio decreases only slightly from 0.98 at 0.3 AU to 0.82 at 1 AU, while for the slow wind it shows a substantial variation from 0.88 at 0.3 AU to 0.29 at 1 AU. The modeled
,
one may find that for the fast solar wind this ratio decreases only slightly from 0.98 at 0.3 AU to 0.82 at 1 AU, while for the slow wind it shows a substantial variation from 0.88 at 0.3 AU to 0.29 at 1 AU. The modeled
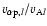 can be seen to agree with the Helios measurements as given by Fig. 11 of Marsch et al. (1982a). Note that a value of
can be seen to agree with the Helios measurements as given by Fig. 11 of Marsch et al. (1982a). Note that a value of
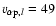
 at 0.3 AU is not unrealistic for slow solar winds, even larger values have been found by Helios 2 when approaching perihelion (Marsch et al. 1981).
Moving on to the temperature profiles, one may see that the
at 0.3 AU is not unrealistic for slow solar winds, even larger values have been found by Helios 2 when approaching perihelion (Marsch et al. 1981).
Moving on to the temperature profiles, one may see that the
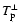 profiles inside 5
profiles inside 5  are in reasonable agreement with the UVCS line-width measurements for both the fast and slow solar wind.
are in reasonable agreement with the UVCS line-width measurements for both the fast and slow solar wind.
4 Numerical results
Having described the meridional magnetic field and flow profiles, we may now address the following questions: to what extent is the total angular momentum loss of the Sun affected by the ion temperature anisotropies? and how is the angular momentum budget distributed among particle momenta, the magnetic torque, and the torque due to ion temperature anisotropies? To this end, let us first examine the fast and then the slow solar wind solutions. In the computations, we take
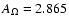
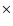 10-6 rad s-1, which corresponds to a sidereal rotation period of 25.38 days.
10-6 rad s-1, which corresponds to a sidereal rotation period of 25.38 days.
4.1 Fast solar wind
Figure 3 presents the radial profiles of (a) the proton azimuthal speed
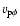 ;
(b) the alpha one
;
(b) the alpha one
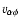 ;
and (c) the ion angular momentum fluxes Lk (
;
and (c) the ion angular momentum fluxes Lk (
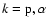 ), their sum LP, the flux due to the magnetic torque
), their sum LP, the flux due to the magnetic torque  ,
and that due to temperature anisotropies
,
and that due to temperature anisotropies
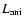 (see Eq. (16)). Note that the dash-dotted curves in Fig. 3c plot negative values. In Figs. 3a and b, the ion azimuthal speeds for the isotropic model with identical meridional flow parameters are given by the dashed lines for comparison. The fast wind profile corresponds to
(see Eq. (16)). Note that the dash-dotted curves in Fig. 3c plot negative values. In Figs. 3a and b, the ion azimuthal speeds for the isotropic model with identical meridional flow parameters are given by the dashed lines for comparison. The fast wind profile corresponds to
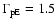 and
and
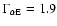 .
.
For the chosen
 and
and
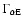 ,
it is found that
,
it is found that
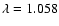 .
Consequently, the total angular momentum loss rate per steradian L is 1.8 (here and hereafter in units of 1029
.
Consequently, the total angular momentum loss rate per steradian L is 1.8 (here and hereafter in units of 1029
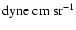 )
in the anisotropic case, and is only modestly enhanced compared with the isotropic case, for which L=1.71. Furthermore, Figs. 3a and b indicate that the radial dependence of the ion azimuthal speed
)
in the anisotropic case, and is only modestly enhanced compared with the isotropic case, for which L=1.71. Furthermore, Figs. 3a and b indicate that the radial dependence of the ion azimuthal speed
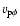 or
or
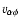 in the anisotropic model is similar to that in the isotropic one. For instance, both models yield that with increasing distance the alpha particles develop an azimuthal speed in the direction of counterrotation with the Sun:
in the anisotropic model is similar to that in the isotropic one. For instance, both models yield that with increasing distance the alpha particles develop an azimuthal speed in the direction of counterrotation with the Sun:
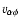 becomes negative beyond 7.95 (8.35)
becomes negative beyond 7.95 (8.35)  in the anisotropic (isotropic) model. The difference between the isotropic and anisotropic cases becomes more prominent at large distances where
in the anisotropic (isotropic) model. The difference between the isotropic and anisotropic cases becomes more prominent at large distances where
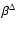 becomes increasingly significant, as would be expected from Eq. (17). Take the values of
becomes increasingly significant, as would be expected from Eq. (17). Take the values of
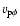 and
and
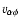 at 1 AU. The isotropic (anisotropic) model yields that
at 1 AU. The isotropic (anisotropic) model yields that
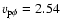 (3.46)
(3.46)
 and that
and that
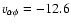 (-11.7)
(-11.7)
 at 1 AU. Note that the changes introduced to the ion azimuthal speeds by pressure anisotropies (
at 1 AU. Note that the changes introduced to the ion azimuthal speeds by pressure anisotropies (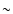 0.9
0.9
 for both protons and alpha particles) play an important role in the distribution of the angular momentum budget L among different contributions, as shown by Fig. 3c. The proton contribution
for both protons and alpha particles) play an important role in the distribution of the angular momentum budget L among different contributions, as shown by Fig. 3c. The proton contribution  exceeds
exceeds  for
for
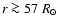 and
and  attains 5.07 at 1 AU, significantly larger than the magnetic part
attains 5.07 at 1 AU, significantly larger than the magnetic part
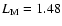 at the same location. In fact, the overall particle contribution LP, which increases with distance, overtakes the magnetic contribution
at the same location. In fact, the overall particle contribution LP, which increases with distance, overtakes the magnetic contribution  from 170.5
from 170.5  onwards, despite the fact that the alpha contribution tends to offset the proton one. The dominance of LP over
onwards, despite the fact that the alpha contribution tends to offset the proton one. The dominance of LP over  happens in conjunction with the increasing importance of
happens in conjunction with the increasing importance of
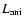 ,
the flux due to total pressure anisotropy which is in the direction of counterrotation with the Sun. In contrast, without pressure anisotropies, at 1 AU it turns out that even though a value of 3.73 is found for
,
the flux due to total pressure anisotropy which is in the direction of counterrotation with the Sun. In contrast, without pressure anisotropies, at 1 AU it turns out that even though a value of 3.73 is found for  ,
it is almost cancelled by an
,
it is almost cancelled by an 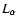 of -3.49. The resulting LP is thus 0.23, substantially smaller than
of -3.49. The resulting LP is thus 0.23, substantially smaller than  ,
which is nearly identical to the value found in the anisotropic model. This contrast between anisotropic and isotropic cases is understandable since it follows from Eq. (13) that, given that the constant AL does not vary much from the isotropic to anisotropic model, the change of LP should be largely offset by that of
,
which is nearly identical to the value found in the anisotropic model. This contrast between anisotropic and isotropic cases is understandable since it follows from Eq. (13) that, given that the constant AL does not vary much from the isotropic to anisotropic model, the change of LP should be largely offset by that of
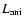 .
.
Figure 4 expands the obtained results by displaying the dependence on
 and
and
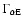 of (a) the factor
of (a) the factor 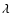 ,
(b) the proton azimuthal speed
,
(b) the proton azimuthal speed
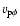 and (c) the alpha one
and (c) the alpha one
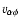 at two different distances plotted by the different linestyles indicated in (b), as well as (d) the constituents comprising the angular momentum flux at 1 AU. In addition to the individual ion contributions
at two different distances plotted by the different linestyles indicated in (b), as well as (d) the constituents comprising the angular momentum flux at 1 AU. In addition to the individual ion contributions  and
and 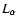 ,
and the magnetic one
,
and the magnetic one  ,
the overall particle contribution
,
the overall particle contribution
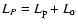 is also given. Note that
is also given. Note that 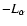 instead of
instead of 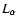 is plotted in Fig. 4d.
Moreover, the horizontal bars on the left of Figs. 4b and c represent the azimuthal ion speeds derived in the isotropic case at the corresponding locations for comparison. The open circles correspond to the cases where
is plotted in Fig. 4d.
Moreover, the horizontal bars on the left of Figs. 4b and c represent the azimuthal ion speeds derived in the isotropic case at the corresponding locations for comparison. The open circles correspond to the cases where
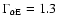 .
It turns out that at any given
.
It turns out that at any given
 each parameter varies monotonically from the value with
each parameter varies monotonically from the value with
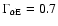 ,
represented by the end of the arrow, to the value with
,
represented by the end of the arrow, to the value with
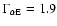 given by the arrow head. In Fig. 4b the arrows have been slightly shifted from one another to avoid overlapping.
given by the arrow head. In Fig. 4b the arrows have been slightly shifted from one another to avoid overlapping.
Table 1:
Profiles for some solar wind parameters in the region r> 0.3 AU.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0992fig3.eps}
\end{figure}](/articles/aa/full/2009/04/aa10992-08/Timg232.gif) |
Figure 3:
Radial distributions of a) the proton azimuthal speed
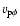 ,
b) the alpha one ,
b) the alpha one
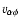 ,
and c) various contributions to the angular momentum budget in an ,
and c) various contributions to the angular momentum budget in an
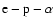 solar wind with ion temperature anisotropies. In a) and b), the profiles derived for a solar wind with identical flow parameters where ion temperature anisotropies are neglected are given by dashed lines for comparison. Panel c) depicts the individual ion angular momentum fluxes
solar wind with ion temperature anisotropies. In a) and b), the profiles derived for a solar wind with identical flow parameters where ion temperature anisotropies are neglected are given by dashed lines for comparison. Panel c) depicts the individual ion angular momentum fluxes  and
and 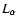 ,
their sum LP, and the fluxes associated with the magnetic stresses ,
their sum LP, and the fluxes associated with the magnetic stresses  ,
and with the temperature anisotropies ,
and with the temperature anisotropies
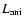 (see Eq. (16)). The dash-dotted lines represent negative values.
(see Eq. (16)). The dash-dotted lines represent negative values. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0992fig4.eps}
\end{figure}](/articles/aa/full/2009/04/aa10992-08/Timg233.gif) |
Figure 4:
Values of several parameters as a function of
 ,
the proton temperature anisotropy at 1 AU. a) The factor ,
the proton temperature anisotropy at 1 AU. a) The factor 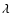 ,
the deviation of which from unity represents the correction to the total angular momentum loss due to the introduction of ion pressure anisotropies; b) and c) the proton and alpha azimuthal speeds ,
the deviation of which from unity represents the correction to the total angular momentum loss due to the introduction of ion pressure anisotropies; b) and c) the proton and alpha azimuthal speeds
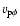 and
and
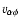 at two different heliocentric distances given by different line styles as indicated in b); d) various components in the angular momentum flux at 1 AU including individual ion contribution
at two different heliocentric distances given by different line styles as indicated in b); d) various components in the angular momentum flux at 1 AU including individual ion contribution  and
and 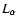 ,
the overall particle contribution ,
the overall particle contribution
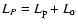 ,
as well as the contribution from magnetic stresses ,
as well as the contribution from magnetic stresses  .
Note that .
Note that 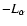 instead of
instead of 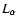 is given in d). The short horizontal bars in panels b) and c) represent the azimuthal ion speeds derived in the isotropic model for comparison. Furthermore, in panel b) the curve corresponding to 1 AU is slightly shifted relative to that for 0.3 AU to avoid the two overlapping each other. The open circles correspond to the cases where
is given in d). The short horizontal bars in panels b) and c) represent the azimuthal ion speeds derived in the isotropic model for comparison. Furthermore, in panel b) the curve corresponding to 1 AU is slightly shifted relative to that for 0.3 AU to avoid the two overlapping each other. The open circles correspond to the cases where
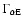 is fixed at 1.3, where
is fixed at 1.3, where
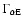 is the alpha temperature anisotropy at 1 AU. At a given
is the alpha temperature anisotropy at 1 AU. At a given
 each parameter varies monotonically from the value with
each parameter varies monotonically from the value with
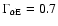 ,
represented by the end of the arrow, to the value with ,
represented by the end of the arrow, to the value with
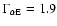 given by the arrow head. The ranges in which
given by the arrow head. The ranges in which
 and
and
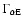 vary are determined from the Helios measurements (see text for details).
vary are determined from the Helios measurements (see text for details). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0992fig5.eps}
\end{figure}](/articles/aa/full/2009/04/aa10992-08/Timg234.gif) |
Figure 5:
Similar to Fig. 4 but for the slow solar wind. Here the open circles correspond to the cases where
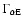 is fixed at 1.4, and the arrow represents how the specific parameter varies at a given
is fixed at 1.4, and the arrow represents how the specific parameter varies at a given
 when when
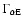 increases from 0.8 to 2.0.
increases from 0.8 to 2.0. |
| Open with DEXTER |
From Fig. 4a one can see that 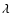 decreases with increasing
decreases with increasing
 or
or
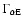 ,
ranging from 1.101 at the upper left to 1.058 at the lower right corner. The deviation of
,
ranging from 1.101 at the upper left to 1.058 at the lower right corner. The deviation of 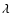 from unity, albeit modest, indicates that the changes introduced in the total angular momentum loss due to the ion pressure anisotropies are not negligible. From Figs. 4b and c one can see that between 0.3 to 1 AU, the magnitude of the azimuthal speeds of both species decreases with increasing distance. Furthermore, at either 0.3 or 1 AU, both
from unity, albeit modest, indicates that the changes introduced in the total angular momentum loss due to the ion pressure anisotropies are not negligible. From Figs. 4b and c one can see that between 0.3 to 1 AU, the magnitude of the azimuthal speeds of both species decreases with increasing distance. Furthermore, at either 0.3 or 1 AU, both
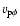 and
and
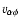 increase when
increase when
 or
or
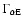 increases. Take the values at 1 AU for instance. One can see that
increases. Take the values at 1 AU for instance. One can see that
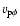 ranges from 2.36 to 3.46
ranges from 2.36 to 3.46
 ,
while
,
while
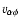 varies between -12.8 and -11.7
varies between -12.8 and -11.7
 .
For the majority of the solutions both
.
For the majority of the solutions both
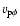 and
and
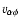 tend to be larger in the algebraic sense than the corresponding values in the isotropic model, which yield 2.54 and -12.6
tend to be larger in the algebraic sense than the corresponding values in the isotropic model, which yield 2.54 and -12.6
 for protons and alpha particles, respectively. However, at 0.3 AU
for protons and alpha particles, respectively. However, at 0.3 AU
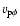 or
or
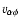 tends to be smaller in the anisotropic than in the isotropic case. Now
tends to be smaller in the anisotropic than in the isotropic case. Now
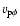 and
and
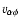 vary in the intervals
[2.37, 3.77] and
[-15.8, -14.2]
vary in the intervals
[2.37, 3.77] and
[-15.8, -14.2]
 ,
respectively. For comparison, the isotropic model yields a
,
respectively. For comparison, the isotropic model yields a
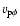 (
(
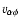 )
of 3.33 (-14.7)
)
of 3.33 (-14.7)
 .
Now let us examine the specific angular momentum fluxes
.
Now let us examine the specific angular momentum fluxes  ,
,
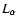 and
and  at 1 AU. Figure 4d indicates that
at 1 AU. Figure 4d indicates that  has the weakest parameter dependence, which is easily understandable given that to a good approximation
has the weakest parameter dependence, which is easily understandable given that to a good approximation
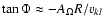 where k may be taken to be p or
where k may be taken to be p or 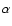 (see Eq. (10)). Besides, the parameter dependence of
(see Eq. (10)). Besides, the parameter dependence of 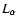 is rather modest, varying by
is rather modest, varying by 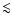 10% from -3.55 to -3.23 when
10% from -3.55 to -3.23 when
 or
or
 changes. On the other hand,
changes. On the other hand,  changes substantially, ranging between 3.46 and 5.07. Hence the overall particle contribution LP also shows a significant parameter dependence. In particular, LP may exceed
changes substantially, ranging between 3.46 and 5.07. Hence the overall particle contribution LP also shows a significant parameter dependence. In particular, LP may exceed  when
when
 .
For the solutions examined, LP can be found to be positive and attain its maximum of LP=1.84 when
.
For the solutions examined, LP can be found to be positive and attain its maximum of LP=1.84 when
![$[\Gamma_{\rm pE}, \Gamma_{\rm\alpha E}]=[1.5, 1.9]$](/articles/aa/full/2009/04/aa10992-08/img238.gif) .
Only for the lowest values of
.
Only for the lowest values of
 and
and
 can one find a negative LP of -0.084. Moreover, the protons always show a partial corotation, i.e.,
can one find a negative LP of -0.084. Moreover, the protons always show a partial corotation, i.e.,
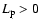 .
From this we conclude that the ion temperature anisotropies are unlikely the cause of the tendency for
.
From this we conclude that the ion temperature anisotropies are unlikely the cause of the tendency for  or LP to be negative for the fast solar wind as indicated by the Helios measurements (Marsch & Richter 1984; Pizzo et al. 1983).
or LP to be negative for the fast solar wind as indicated by the Helios measurements (Marsch & Richter 1984; Pizzo et al. 1983).
4.2 Slow solar wind
Figure 5 presents, in the same fashion as Fig. 4, the dependence on
 and
and
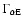 of various quantities derived for the slow solar wind. A comparison with Fig. 4 indicates that nearly all the features in Fig. 5 are reminiscent of those obtained for fast solar wind solutions. However, some quantitative differences exist nonetheless. For instance, when
of various quantities derived for the slow solar wind. A comparison with Fig. 4 indicates that nearly all the features in Fig. 5 are reminiscent of those obtained for fast solar wind solutions. However, some quantitative differences exist nonetheless. For instance, when
 is held fixed, all the examined parameters for the slow wind vary little even though
is held fixed, all the examined parameters for the slow wind vary little even though
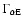 changes considerably from 0.8 to 2. In contrast, the parameters for the fast wind show an obvious
changes considerably from 0.8 to 2. In contrast, the parameters for the fast wind show an obvious
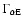 dependence. This difference can be largely attributed to the fact that in the slow wind the ions are substantially cooler than in the fast wind. Figure 5a shows that
dependence. This difference can be largely attributed to the fact that in the slow wind the ions are substantially cooler than in the fast wind. Figure 5a shows that 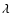 ranges from 0.94 to 1.016. In other words, relative to the isotropic case, the solar angular momentum loss rate per steradian in the anisotropic models may be enhanced or reduced by up to
ranges from 0.94 to 1.016. In other words, relative to the isotropic case, the solar angular momentum loss rate per steradian in the anisotropic models may be enhanced or reduced by up to 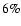 .
If examining Figs. 5b and c, one may find that at both 0.3 and 1 AU, the azimuthal speeds of both ion species,
.
If examining Figs. 5b and c, one may find that at both 0.3 and 1 AU, the azimuthal speeds of both ion species,
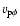 and
and
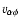 ,
are larger algebraically in the anisotropic models than in the isotropic one. The difference between the two is more prominent at 0.3 AU, where the isotropic model yields that
,
are larger algebraically in the anisotropic models than in the isotropic one. The difference between the two is more prominent at 0.3 AU, where the isotropic model yields that
![$[v_{\rm p\phi}, v_{\alpha\phi}]=[3.49, -18.1]$](/articles/aa/full/2009/04/aa10992-08/img241.gif)
 ,
whereas the anisotropic models yield that with increasing
,
whereas the anisotropic models yield that with increasing
 ,
,
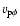 increases from 3.76 to 5.04
increases from 3.76 to 5.04
 ,
and
,
and
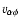 varies between -17.8 to -16.3
varies between -17.8 to -16.3
 .
As for the ion azimuthal speeds at 1 AU, one can see that varying
.
As for the ion azimuthal speeds at 1 AU, one can see that varying
 leads to a
leads to a
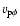 varying between 1.18 and 1.72
varying between 1.18 and 1.72
 ,
and a
,
and a
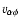 ranging from -5.85 to -5.31
ranging from -5.85 to -5.31
 .
The corresponding changes in the specific ion angular momentum fluxes are shown by Fig. 5d, which indicates that the proton one
.
The corresponding changes in the specific ion angular momentum fluxes are shown by Fig. 5d, which indicates that the proton one  increases with increasing
increases with increasing
 from 2.52 to 3.67, and likewise, the alpha one
from 2.52 to 3.67, and likewise, the alpha one 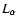 increases from -1.83 to -1.66. On the other hand, the flux associated with magnetic stresses
increases from -1.83 to -1.66. On the other hand, the flux associated with magnetic stresses  hardly varies, and a value of 3.36 can be quoted for all the models examined. Therefore in the parameter space explored,
hardly varies, and a value of 3.36 can be quoted for all the models examined. Therefore in the parameter space explored,  may be smaller than
may be smaller than  ,
which is however offset by the alpha contribution that is always in the direction of counter-rotation to the Sun. In fact, the alpha contribution is so significant that the overall particle contribution LP never exceeds
,
which is however offset by the alpha contribution that is always in the direction of counter-rotation to the Sun. In fact, the alpha contribution is so significant that the overall particle contribution LP never exceeds  .
In other words, incorporating ion temperature anisotropy cannot resolve the outstanding discrepancy between previous models and observations concerning the relative importance of particle and magnetic contributions in the angular momentum budget of the solar wind.
.
In other words, incorporating ion temperature anisotropy cannot resolve the outstanding discrepancy between previous models and observations concerning the relative importance of particle and magnetic contributions in the angular momentum budget of the solar wind.
5 Discussion
As demonstrated by Li & Li (2008), the discussion on the angular momentum transport also allows us to say a few words on the frequency spectra Sk (f) (
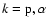 )
of the ion velocity fluctuations during Alfvénic activities in the fast solar wind in the super-Alfvénic portion where
)
of the ion velocity fluctuations during Alfvénic activities in the fast solar wind in the super-Alfvénic portion where
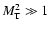 .
This is due to the well-known change of the properties of Alfvénic fluctuations around some
.
This is due to the well-known change of the properties of Alfvénic fluctuations around some
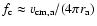 ,
where
,
where
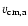 is the speed of center of mass evaluated at the Alfvén point
is the speed of center of mass evaluated at the Alfvén point 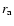 (see e.g., Li & Li 2008; Heinemann & Olbert 1980). For typical fast wind parameters,
(see e.g., Li & Li 2008; Heinemann & Olbert 1980). For typical fast wind parameters,
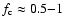
 10-5
10-5
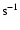 .
While the fluctuations with frequencies
.
While the fluctuations with frequencies
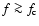 are genuinely wave-like and may be described by the WKB limit given the slow spatial variation of flow parameters in the region in question, those with
are genuinely wave-like and may be described by the WKB limit given the slow spatial variation of flow parameters in the region in question, those with
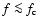 behave in a quasi-static manner and may be described by the solutions to the angular momentum conservation law which also governs the zero-frequency fluctuations. As shown by Li & Li (2008) who neglected the species temperature anisotropy, in the region
behave in a quasi-static manner and may be described by the solutions to the angular momentum conservation law which also governs the zero-frequency fluctuations. As shown by Li & Li (2008) who neglected the species temperature anisotropy, in the region 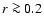 AU which will be explored by the Solar Orbiter and Solar Probe, the ratio of the alpha to proton velocity fluctuation amplitude
AU which will be explored by the Solar Orbiter and Solar Probe, the ratio of the alpha to proton velocity fluctuation amplitude
 can be an order-of-magnitude larger for
can be an order-of-magnitude larger for
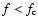 than for
than for
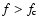 .
Hence one may expect that, if the proton velocity fluctuation spectrum
.
Hence one may expect that, if the proton velocity fluctuation spectrum
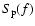 is somehow smooth around
is somehow smooth around 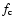 ,
then the alpha one
,
then the alpha one
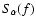 will show an apparent spectral break. Now let us revisit this problem in light of the discussion presented in this paper and see what changes the pressure anisotropies may introduce.
will show an apparent spectral break. Now let us revisit this problem in light of the discussion presented in this paper and see what changes the pressure anisotropies may introduce.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0992fig6.eps}
\end{figure}](/articles/aa/full/2009/04/aa10992-08/Timg255.gif) |
Figure 6:
Radial dependence of the ratio of the alpha to the proton velocity fluctuation amplitudes
 induced by Alfvénic activities in super-Alfvénic portions of the fast solar wind. The dashed curves correspond to the isotropic model, while the hatched areas give the possible range
induced by Alfvénic activities in super-Alfvénic portions of the fast solar wind. The dashed curves correspond to the isotropic model, while the hatched areas give the possible range
 may occupy when the parameters
may occupy when the parameters
 and
and
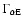 vary in the ranges given in text.
Both the zero-frequency (upper portion) and WKB ( lower) estimates are given.
vary in the ranges given in text.
Both the zero-frequency (upper portion) and WKB ( lower) estimates are given. |
| Open with DEXTER |
Restrict ourselves to either the high-latitude region or the region inside say 100  such that the magnetic field may be seen as radial. Furthermore, suppose that the waves are propagating parallel to the magnetic field in the empirical fast wind profiles detailed in Sect. 3. Figure 6 presents the radial dependence of
such that the magnetic field may be seen as radial. Furthermore, suppose that the waves are propagating parallel to the magnetic field in the empirical fast wind profiles detailed in Sect. 3. Figure 6 presents the radial dependence of
 in the region between 40 and 100
in the region between 40 and 100  for both the zero-frequency (upper part) and WKB (lower part) solutions. For comparison, the dashed curves represent the corresponding results in the isotropic model. To construct Fig. 6, all the possible values of
for both the zero-frequency (upper part) and WKB (lower part) solutions. For comparison, the dashed curves represent the corresponding results in the isotropic model. To construct Fig. 6, all the possible values of
 and
and
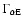 have been examined. As a result, at any radial location the ratio
have been examined. As a result, at any radial location the ratio
 varies from model to model, and the range in which this ratio may occupy is given by the hatched area. The zero-frequency solutions are obtained by solving Eq. (20), while for hydromagnetic WKB Alfvén waves it is well known that
varies from model to model, and the range in which this ratio may occupy is given by the hatched area. The zero-frequency solutions are obtained by solving Eq. (20), while for hydromagnetic WKB Alfvén waves it is well known that
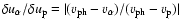 ,
where
,
where
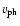 is the wave phase speed and given by (e.g., Barnes & Suffolk 1971; Isenberg 1984)
is the wave phase speed and given by (e.g., Barnes & Suffolk 1971; Isenberg 1984)
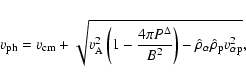
in which
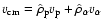 is the speed of center of mass, and
is the speed of center of mass, and
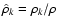 (
(
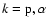 )
defines the fractional ion mass density.
)
defines the fractional ion mass density.
From Fig. 6 one can see that the zero-frequency and WKB solutions are well separated from each other, in the isotropic and anisotropic cases alike. For the isotropic model,
 in the zero-frequency case increases monotonically from 3.79 at 40
in the zero-frequency case increases monotonically from 3.79 at 40  to 4.68 at 100
to 4.68 at 100  .
On the other hand, in the WKB case it decreases first from 0.22 at 40
.
On the other hand, in the WKB case it decreases first from 0.22 at 40  and attains its minimum of 0.083 at 60.3
and attains its minimum of 0.083 at 60.3  and then increases to 0.15 at 100
and then increases to 0.15 at 100  .
The difference in
.
The difference in
 between the zero-frequency and WKB solutions may be slightly smaller in the anisotropic than in the isotropic case for some combinations of
between the zero-frequency and WKB solutions may be slightly smaller in the anisotropic than in the isotropic case for some combinations of
![$[\Gamma_{\rm p E}, \Gamma_{\rm\alpha E}]$](/articles/aa/full/2009/04/aa10992-08/img188.gif) ,
but the difference is still quite significant. From this we can conclude that, with realistic ion temperature anisotropies included, the alpha velocity fluctuation spectrum
,
but the difference is still quite significant. From this we can conclude that, with realistic ion temperature anisotropies included, the alpha velocity fluctuation spectrum
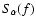 during Alfvénic activities will also show an apparent break near
during Alfvénic activities will also show an apparent break near 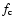 ,
if the proton one
,
if the proton one
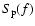 is smooth there.
This break is entirely a linear property, and has nothing to do with the nonlinearities that may also shape the fluctuation spectra.
is smooth there.
This break is entirely a linear property, and has nothing to do with the nonlinearities that may also shape the fluctuation spectra.
6 Summary
This study has been motivated by the apparent lack of an analysis on the angular momentum transport in a multicomponent solar or stellar wind with differentially flowing ions and species temperature anisotropy. Moreover, there has been an outstanding discrepancy between available measurements and models concerning the relative importance of the particle LP and magnetic contribution  to the solar angular momentum loss rate per steradian L. The Helios measurements indicate that for fast (slow) solar wind with
to the solar angular momentum loss rate per steradian L. The Helios measurements indicate that for fast (slow) solar wind with
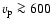 (
( 400)
400)
 ,
LP tends to be negative (positive), with the positive sign denoting the direction of corotation with the Sun.
Furthermore, LP tends to be larger than
,
LP tends to be negative (positive), with the positive sign denoting the direction of corotation with the Sun.
Furthermore, LP tends to be larger than  in the slow wind. The behavior of LP derives from that of individual ion angular momentum fluxes,
in the slow wind. The behavior of LP derives from that of individual ion angular momentum fluxes,  and
and 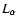 ,
thereby calling for a multifluid approach.
,
thereby calling for a multifluid approach.
Starting with a general set of multifluid transport equations with gyrotropic species pressure tensors, we have derived the equations for both the angular momentum conservation (Eqs. (10) and (20) in Sect. 2), and the energy and linear momentum balance (Eqs. (A.1) to (A.4) in the Appendix). These equations are not restricted to radial outflows in the equatorial plane, instead they are valid for arbitrary axisymmetrical winds that include two major ion species, and therefore are expected to find applications in general outflows from late-type stars. To focus on the problem of angular momentum transport, we refrained from solving the full set of equations governing the meridional dynamics. Rather, we constructed, largely based on the available in situ measurements, the empirical profiles for the meridional magnetic field and flow parameters.
Only the ion temperature anisotropies are considered, i.e., the electron temperature is seen as isotropic. For both the fast and slow solar wind profiles, we solved the angular momentum conservation law (Eqs. (10) and (20)) to examine how the azimuthal speeds of protons
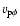 and alpha particles
and alpha particles
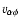 ,
as well as the individual components in the solar angular momentum budget are influenced by the ion temperature anisotropies. To this end, solutions to the isotropic version are obtained for comparison.
,
as well as the individual components in the solar angular momentum budget are influenced by the ion temperature anisotropies. To this end, solutions to the isotropic version are obtained for comparison.
Our main conclusions are:
- 1.
- From the derived equations governing the energy transport, a simple analysis given in the Appendix yields that the adiabatic cooling may be considerably influenced with the introduction of the azimuthal components. Such an influence is understandably more prominent in the low-latitude regions. This means, when modeling the species temperature anisotropy, for a quantitative comparison of model computations to be made with the near-ecliptic measurements such as made by Helios, the spiral magnetic field has to be taken into account.
- 2.
- In agreement with the single-fluid case (Weber 1970; Weber & Davis 1970), incorporating species temperature anisotropy leads to a situation where the total angular momentum loss rate per steradian L is determined by the behavior of the solution to the angular momentum conservation law in the vicinity of the Alfvén point where the combined Alfvénic Mach number
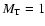 .
However,
.
However,  has to take into account the contribution from both ion species, as defined by Eq. (18).
has to take into account the contribution from both ion species, as defined by Eq. (18).
- 3.
- Relative to the isotropic case, the introduced species temperature anisotropy may enhance or decrease L by up to 10%, and introduce an absolute change of up to
 1.8
1.8
 in individual ion azimuthal speeds in the region between 0.3 and 1 AU. While these changes seem modest, the corresponding changes in the angular momentum fluxes convected by protons
in individual ion azimuthal speeds in the region between 0.3 and 1 AU. While these changes seem modest, the corresponding changes in the angular momentum fluxes convected by protons  or alpha particles
or alpha particles 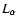 may change substantially. In contrast, the flux associated with magnetic stresses
may change substantially. In contrast, the flux associated with magnetic stresses  hardly varies.
hardly varies.
- 4.
- However, introducing ion temperature anisotropies cannot resolve the discrepancy between in situ measurements and models. For the fast wind solutions, while in extreme cases LP may become negative
 always stays positive. On the other hand, for the slow solar wind solutions examined, LP never exceeds
always stays positive. On the other hand, for the slow solar wind solutions examined, LP never exceeds  even though
even though  may be smaller than the
individual ion contribution. This is because, for both the slow and fast wind solutions,
may be smaller than the
individual ion contribution. This is because, for both the slow and fast wind solutions,  and
and 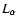 always have opposite signs.
always have opposite signs.
- 5.
- The discussion on the angular momentum transport has some bearing on the ion velocity fluctuation spectra Sk (f) (
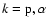 )
during Alfvénic activities in the super-Alfvénic regions, which are likely to be explored by future missions such as Solar Orbiter and Solar Probe. In agreement with Li & Li (2008) where species temperature anisotropies are neglected, an analysis based on the WKB and zero-frequency solutions yields that
)
during Alfvénic activities in the super-Alfvénic regions, which are likely to be explored by future missions such as Solar Orbiter and Solar Probe. In agreement with Li & Li (2008) where species temperature anisotropies are neglected, an analysis based on the WKB and zero-frequency solutions yields that
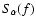 will show an apparent break around some critical frequency
will show an apparent break around some critical frequency 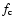 if
if
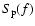 is smooth there. This
is smooth there. This
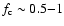
 10-5
10-5
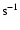 is the well-known frequency that separates the genuinely wave-like fluctuations from quasi-static ones.
is the well-known frequency that separates the genuinely wave-like fluctuations from quasi-static ones.
Acknowledgements
We thank the referee (Dr. Horst Fichtner) for his very helpful comments. This research is supported by an STFC rolling grant to Aberystwyth University.
In Sect. 2, we have demonstrated that the vector equations governing a time-independent multicomponent solar wind with species temperature anisotropy are allowed to be decomposed into a force balance condition across the poloidal magnetic field and a set of transport equations along it. The azimuthal dynamics has been discussed in the text, whereas this Appendix provides some discussion on the poloidal dynamics. In particular, we shall derive the equations governing the poloidal motion vk l of ion species (
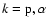 ), and the species temperatures
), and the species temperatures
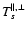 (
(
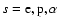 )
in rather general situations.
)
in rather general situations.
Due to the presence of vkN in the l component of the ion momentum Eq. (2),
one may expect that the N-component of Eq. (2) has to be solved. In fact, there is no need to do so because vk N appears only in the difference
vj N-vk N, which may be found from the 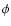 component of Eq. (2). Substituting
vj N-vk N into the l component of Eq. (2) will then eliminate the cumbersome
component of Eq. (2). Substituting
vj N-vk N into the l component of Eq. (2) will then eliminate the cumbersome  and vk N. Note that this technique, first devised by McKenzie et al. (1979), ensures the conservation of not only total momentum but also total energy (see Li & Li 2006). Specifically, the resulting equations for the poloidal dynamics are
and vk N. Note that this technique, first devised by McKenzie et al. (1979), ensures the conservation of not only total momentum but also total energy (see Li & Li 2006). Specifically, the resulting equations for the poloidal dynamics are
where
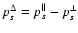 (
(
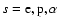 ),
),
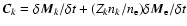 results from Coulomb frictions, and the prime ' represents the derivative with respect to the arclength l. When deriving Eqs. (A.3) and (A.4), we have used the fact that the expression
results from Coulomb frictions, and the prime ' represents the derivative with respect to the arclength l. When deriving Eqs. (A.3) and (A.4), we have used the fact that the expression
may be simplified by expressing 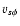 via the alignment condition (10),
the result being
via the alignment condition (10),
the result being
Similarly, one may find that
Now let us compare these equations with those in Isenberg (1984). It is straightforward to show that Eqs. (A.3) and (A.4) are equivalent to Eqs. (A.3) and (A.4) in Isenberg (1984) by specializing to a spherically symmetric solar wind and by noting that
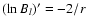 .
On the other hand, using the alignment condition (10) one may find that
.
On the other hand, using the alignment condition (10) one may find that
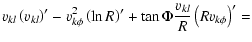 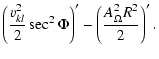 |
|
|
(A.5) |
Again specializing to a spherical solar wind, one then finds that Eq. (A.2) is equivalent to (A.2) in Isenberg (1984). It should be stressed that although working in a frame of reference corotating with the Sun, as did Isenberg (1984), substantially simplifies the algebra, it does not offer the information on the specific form of the spiral angle 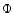 ,
whose functional dependence on the flow speeds has to be assumed a priori. In practice, Isenberg (1984) assumed that the velocity of center of mass
,
whose functional dependence on the flow speeds has to be assumed a priori. In practice, Isenberg (1984) assumed that the velocity of center of mass
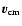 is radial in an inertial frame beyond 10
is radial in an inertial frame beyond 10  ,
which is certainly a good assumption for the present slow-rotating Sun. However, from our discussion on the azimuthal dynamics, there is in general no guarantee that
,
which is certainly a good assumption for the present slow-rotating Sun. However, from our discussion on the azimuthal dynamics, there is in general no guarantee that
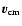 is radial, and the deviation may be substantial for winds that flow from a faster rotating star.
is radial, and the deviation may be substantial for winds that flow from a faster rotating star.
Introducing azimuthal components may influence the ion flow speeds vk l both directly and indirectly. The direct consequence is that azimuthal components may introduce into the reduced meridional momentum Eq. (A.2) an effective force (see the first three terms).
Note that in a corotating frame the magnitude of the ion velocity becomes
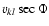 ,
from relation (A.5) one may see that in such a frame all particles move in the same centrifugal potential
,
from relation (A.5) one may see that in such a frame all particles move in the same centrifugal potential
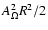 .
Therefore in effect the introduced force tends to reduce the magnitude of the ion speed difference with increasing distance as
.
Therefore in effect the introduced force tends to reduce the magnitude of the ion speed difference with increasing distance as 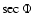 tends to increase.
This effect has been explored in detail in Li & Li (2006) and Li et al. (2007), where it is shown that the influence may play an important part in the force balance for the solar wind. In fact, introducing solar rotation alone is able to reproduce the
tends to increase.
This effect has been explored in detail in Li & Li (2006) and Li et al. (2007), where it is shown that the influence may play an important part in the force balance for the solar wind. In fact, introducing solar rotation alone is able to reproduce the
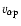 profile measured by Ulysses beyond 2 AU if a proper value of
profile measured by Ulysses beyond 2 AU if a proper value of
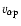 is imposed there. On the other hand, vk l may be altered indirectly by the modified pressure gradient force due to changes in the temperatures, which in turn are caused by the changes in the heat fluxes (the third term in Eqs. (A.3) and (A.4)) and through the adiabatic cooling (the second term). A detailed discussion on the former requires a specific form for the heat flux, which is beyond the scope of the present paper. As a consequence, we shall focus on the latter instead.
is imposed there. On the other hand, vk l may be altered indirectly by the modified pressure gradient force due to changes in the temperatures, which in turn are caused by the changes in the heat fluxes (the third term in Eqs. (A.3) and (A.4)) and through the adiabatic cooling (the second term). A detailed discussion on the former requires a specific form for the heat flux, which is beyond the scope of the present paper. As a consequence, we shall focus on the latter instead.
Neglecting the terms in the second pair of square parentheses, Eqs. (A.3)
and (A.4) give
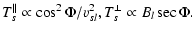 |
|
|
(A.6) |
Note that the relation governing
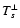 simply reflects the conservation of magnetic moment.
Now that in the region say r>10
simply reflects the conservation of magnetic moment.
Now that in the region say r>10 
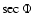 is significant and increases with r,
is significant and increases with r,
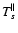 (
(
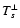 )
may be substantially reduced (enhanced) relative to the case where
)
may be substantially reduced (enhanced) relative to the case where
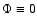 .
This effect is particularly significant in the near-ecliptic region and for the slow solar wind. For instance, restrict ourselves to the equatorial plane and consider the region between say 10
.
This effect is particularly significant in the near-ecliptic region and for the slow solar wind. For instance, restrict ourselves to the equatorial plane and consider the region between say 10  and 1 AU. Suppose vs l remains constant and
and 1 AU. Suppose vs l remains constant and
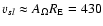 km s-1. Now that roughly speaking
km s-1. Now that roughly speaking
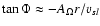 ,
when the spiral field is considered,
,
when the spiral field is considered,
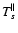 (
(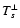 )
at 1 AU is 1/2 (
)
at 1 AU is 1/2 (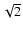 )
times the value for a purely radial magnetic field. This suggests that for making any quantitative comparison of the modeled species temperature anisotropy with the near-ecliptic measurements such as made by Helios, the spiral magnetic field has to be considered.
)
times the value for a purely radial magnetic field. This suggests that for making any quantitative comparison of the modeled species temperature anisotropy with the near-ecliptic measurements such as made by Helios, the spiral magnetic field has to be considered.
For completeness, we note that the force balance condition across the N direction comes from the N component of the total momentum, which reads
where
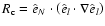 is the signed curvature radius of the poloidal magnetic line of force. Obviously, this force balance condition determines the poloidal magnetic field configuration in response to the electric currents associated with the flow. This equation, combined with the transport equations along the meridional magnetic lines of force, may be solved alternately to find a self-consistent solution to the vector equations by using the approach by Pneuman & Kopp (1971) or Sakurai (1985).
is the signed curvature radius of the poloidal magnetic line of force. Obviously, this force balance condition determines the poloidal magnetic field configuration in response to the electric currents associated with the flow. This equation, combined with the transport equations along the meridional magnetic lines of force, may be solved alternately to find a self-consistent solution to the vector equations by using the approach by Pneuman & Kopp (1971) or Sakurai (1985).
-
Banaszkiewicz, M., Axford, W. I., & McKenzie, J. F.
1998, A&A, 337, 940 [NASA ADS]
(In the text)
-
Barakat, A. R., & Schunk, R. W. 1982, Plasma Phys.,
24, 389 [NASA ADS] [CrossRef]
(In the text)
-
Barnes, A., & Suffolk, G. C. J. 1971, J. Plasma
Phys., 5, 315
- Belcher, J. W., &
MacGregor, K. B. 1976, ApJ, 210, 498 [NASA ADS] [CrossRef]
-
Bouvier, J., Forestini, M., & Allain, S. 1997, A&A, 326,
1023
- Frazin,
R. A., Cranmer, S. R., & Kohl, J. L. 2003, ApJ,
597, 1145 [NASA ADS] [CrossRef]
(In the text)
- Gary,
S. P., McKean, M. E., Winske, D., et al. 1994,
J. Geophys. Res., 99, 5903 [NASA ADS] [CrossRef]
(In the text)
- Heinemann, M., &
Olbert, S. 1980, J. Geophys. Res., 85, 1311 [NASA ADS] [CrossRef]
- Hellinger, P., &
Trávnícek, P. 2006, J. Geophys. Res., 111,
A01107 [CrossRef]
(In the text)
- Hollweg, J. V., &
Isenberg, P. A. 2002, J. Geophys. Res., 107(A7),
1147
(In the text)
- Hu,
Y. Q., & Habbal, S. R. 1999,
J. Geophys. Res., 104, 17045 [CrossRef]
(In the text)
- Isernberg, P. A. 1984,
J. Geophys. Res., 89, 6613 [CrossRef]
(In the text)
- Kohl,
J. L., Noci, G., Antonucci, E., et al. 1998, ApJ, 501,
L127 [NASA ADS] [CrossRef]
(In the text)
- Leer, E.,
& Axford, W. I. 1972, Sol. Phys., 23, 238 [NASA ADS] [CrossRef]
(In the text)
- Li, B., & Li, X.
2006, A&A, 456, 359 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Li, B., & Li, X.
2007, ApJ, 661, 1222 [NASA ADS] [CrossRef]
(In the text)
- Li, B., & Li, X.
2008, ApJ, 682, 667 [NASA ADS] [CrossRef]
(In the text)
- Li, B., Li, X.,
& Labrosse, N. 2006, J. Geophys. Res., 111,
A08106 [CrossRef]
(In the text)
- Li, B., Habbal,
S. R., & Li, X. 2007, ApJ, 661, 593 [NASA ADS] [CrossRef]
(In the text)
-
Marsch, E., & Richter, A. K. 1984,
J. Geophys. Res., 89, 5386 [CrossRef]
(In the text)
- Marsch,
E., Mühlhäuser, K.-H., Rosenbauer, H., Schwenn, R., &
Denskat, K. U. 1981, J. Geophys. Res., 86, 9199 [NASA ADS] [CrossRef]
(In the text)
-
Marsch, E., Mühlhäuser, K.-H., Rosenbauer, H., Schwenn,
R., & Neubauer, F. M. 1982a, J. Geophys. Res.,
87, 35 [NASA ADS] [CrossRef] (M82a)
-
Marsch, E., Mühlhäuser, K.-H., Schwenn, R., et al.
1982b, J. Geophys. Res., 87, 52 [NASA ADS] [CrossRef] (M82b)
-
McComas, D. J., Barraclough, B. L., Funsten, H. O.,
et al. 2000, J. Geophys. Res., 105, 10419 [NASA ADS] [CrossRef]
(Mc00)
(In the text)
-
McKenzie, J. F., Ip, W.-H., & Axford, W. I. 1979,
Ap&SS, 64, 183 [NASA ADS] [CrossRef]
(In the text)
-
Mestel, L., & Spruit, H. C. 1987, MNRAS, 226, 57 [NASA ADS]
- Pizzo,
V., Schwenn, R., Marsch, E., et al. 1983, ApJ, 271, 335 [NASA ADS] [CrossRef]
(In the text)
-
Pneuman, G. W., & Kopp, R. A. 1971, Sol. Phys.,
18, 258 [NASA ADS] [CrossRef]
(In the text)
- Sakurai, T.
1985, A&A, 152, 121
(In the text)
-
Scherer, K., Marsch, E., Schwenn, R., & Rosenbauer, H. 2001,
A&A, 366, 331 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Schwenn, R.
1990, Large-scale structure of the interplanetary medium, in
Physics of the Inner Heliosphere I, Large Scale Phenomena,
ed. R. Schwenn, & E. Marsch (New York:
Springer-Verlag), 99 (Sch90)
- Smith,
E. J., & Balogh, A. 1995, Geophys. Res. Lett.,
22, 3317 [NASA ADS] [CrossRef]
(In the text)
- Weber, E. J.
1970, Sol. Phys., 13, 240 [NASA ADS] [CrossRef]
(In the text)
- Weber, E. J., &
Davis, Jr., L. 1967, ApJ, 148, 217 [NASA ADS] [CrossRef]
- Weber, E. J., &
Davis, Jr., L. 1970, J. Geophys. Res., 75, 2419 [CrossRef]
Copyright ESO 2009
![$\displaystyle \qquad\quad - \frac{1}{n_k m_k}\left[\frac{\delta\vec{M}_k}{\delta t}
+\frac{Z_k n_k}{n_{\rm e}}\frac{\delta\vec{M}_{\rm e}}{\delta t} \right]$](/articles/aa/full/2009/04/aa10992-08/img69.gif)
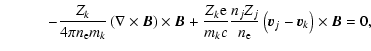
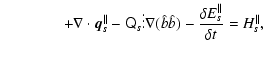
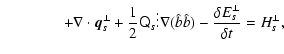
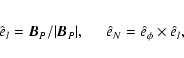
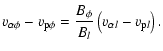
![$\displaystyle %
\nabla\cdot \left[\frac{1}{R}\left(B_\phi \vec{v}_{{\rm e} P} - v_{{\rm e} \phi} \vec{B}_{P}\right)\right] =0.$](/articles/aa/full/2009/04/aa10992-08/img102.gif)
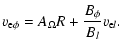
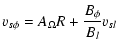
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0992fig1.eps}
\end{figure}](/articles/aa/full/2009/04/aa10992-08/Timg110.gif)
![$\displaystyle %
\frac{1}{R}\left\{\sum_k \rho_k v_{k l} \left(R v_{k \phi}\righ...
... \pi}\left[\left(1-\frac{4\pi P^\Delta}{B^2}\right)R B_\phi\right]'\right\} =0,$](/articles/aa/full/2009/04/aa10992-08/img111.gif)
![$\displaystyle %
R\left[ v_{{\rm p} \phi} + \eta v_{\alpha \phi} -
\frac{B_l B_\...
...rho_{\rm p} v_{{\rm p}l}}\left(1-\frac{4\pi P^\Delta}{B^2}\right)\right] = A_L,$](/articles/aa/full/2009/04/aa10992-08/img115.gif)
![$\displaystyle %
\left[L_k, L_{\rm M}, L_{\rm ani}\right] = R\left(\frac{B_{l{\r...
...k l}v_{k\phi}, \frac{-B_l B_\phi}{4\pi}, \frac{B_l B_\phi P^\Delta}{B^2}\right]$](/articles/aa/full/2009/04/aa10992-08/img123.gif)
![$\displaystyle %
\tan\Phi \left[M_{\rm T}^2 - \left(1-\beta^\Delta\cos^2\Phi\right)\right]
= \epsilon \left[\frac{A_L}{(1+\eta)A_\Omega R^2}-1\right],$](/articles/aa/full/2009/04/aa10992-08/img124.gif)
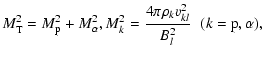
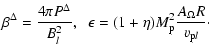
![$\displaystyle c_3 = M_{\rm T}^2-1, c_2 = \epsilon\left[1-\lambda\left(\frac{R_{\rm a}}{R}\right)^2\right],$](/articles/aa/full/2009/04/aa10992-08/img137.gif)
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0992fig2.eps}
\end{figure}](/articles/aa/full/2009/04/aa10992-08/Timg180.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0992fig3.eps}
\end{figure}](/articles/aa/full/2009/04/aa10992-08/Timg232.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0992fig4.eps}
\end{figure}](/articles/aa/full/2009/04/aa10992-08/Timg233.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0992fig5.eps}
\end{figure}](/articles/aa/full/2009/04/aa10992-08/Timg234.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0992fig6.eps}
\end{figure}](/articles/aa/full/2009/04/aa10992-08/Timg255.gif)
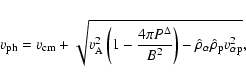
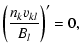
![$\displaystyle \qquad\qquad + \frac{1}{n_s k_{\rm B}}\left[\nabla\cdot \vec{q}_s...
...hat{b}\hat{b})-\frac{\delta E_s^\parallel}{\delta t} - H_s^\parallel\right] =0,$](/articles/aa/full/2009/04/aa10992-08/img271.gif)
![$\displaystyle \qquad\qquad + \frac{1}{n_s k_{\rm B}}\left[\nabla\cdot \vec{q}_s...
...\nabla(\hat{b}\hat{b})-\frac{\delta E_s^\perp}{\delta t} - H_s^\perp\right] =0,$](/articles/aa/full/2009/04/aa10992-08/img273.gif)
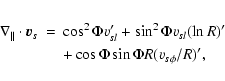
![\begin{eqnarray*}\nabla_\parallel\cdot\vec{v}_s = v_{sl}\left[\ln \left(v_{sl}\sec\Phi\right)\right]'.
\end{eqnarray*}](/articles/aa/full/2009/04/aa10992-08/img278.gif)
![\begin{eqnarray*}\nabla_\perp\cdot\vec{v}_s
= -v_{sl}\left[\ln \left(B_{l}\sec\Phi\right)\right]'.
\end{eqnarray*}](/articles/aa/full/2009/04/aa10992-08/img279.gif)