A&A 494, 11-20 (2009)
DOI: 10.1051/0004-6361:200810903

Formation of young boxy/peanut bulges in ringed barred galaxies

H. Wozniak1 - L. Michel-Dansac2,3


1 - Université de Lyon, 69000 Lyon, France; Université Lyon 1, 69622 Villeurbanne, France; Centre de Recherche Astrophysique de Lyon, Observatoire de Lyon, 9 avenue Charles André, 69561 Saint-Genis Laval Cedex, France; CNRS, UMR 5574; École Normale Supérieure de Lyon, Lyon, France
2 - IATE, CONICET, OAC, Universidad Nacional de Córdoba, Laprida 854, X5000BGR, Córdoba, Argentina
3 - Consejo Nacional de Investigaciones Científicas y Técnicas, Argentina

Received 3 September 2008 / Accepted 15 October 2008

Abstract
Aims. We investigate whether the formation mechanism of boxy and peanut-shaped (B/PS) bulges could depend on the gas content of the galaxy.
Methods. We have performed N-body simulations with and without a gaseous component. In the second case star formation/feedback recipes have also been implemented to create new stellar populations.
Results. As in many previous studies, in our N-body collisionless simulation, the B/PS is due to the classical break in the z mirror symmetry lasting roughly 200 Myr. When a gaseous component and star formation recipes are added to the simulation, the bulge-growing mechanism is quite different. The young stellar population that is born in the thin gaseous disc rapidly populates vertical resonant orbits triggered by the combined effects of the linear horizontal and vertical ILRs. This leads to a B/PS bulge mainly made of stellar material younger than the surrounding population.

The non-linear analysis of the orbital structure shows that the main orbit family responsible for the B/PS is not the same in the two cases. The 2:2:1 orbits prevail in the collisionless simulation whereas additional asymmetrical families contribute to the B/PS if a dissipative component is present and can form new stars. We found that 2:3:1 and 2:5:1 orbits trap a significant fraction of the mass.

A flat ringed discy stellar component also appears simultaneously with the thickening of the young population. It is due to the star formation in a nuclear gaseous disc located in the central kpc, inside the ILR, and accumulated there by the torques exerted by the large-scale bar. Remarkably, it remains flat throughout the simulation although it develops a nuclear bar, leading to a double-barred galaxy.
Conclusions. We predict that two populations of B/PS bulges could exist and even coexist in the same galaxy.

Key words: galaxies: active - galaxies: kinematics and dynamics - galaxies: nuclei - galaxies: Seyfert - galaxies: evolution - galaxies: spiral

1 Introduction

How galactic bulges form is one of the leading questions for the galaxy formation theories. A consensus is begining to emerge (e.g. Athanassoula 2005) that two scenarios of bulge formation compete. The older scenario is the formation by an initial gravitational collapse or, in a more recent scenario by a series of minor mergers in a similar way to massive elliptical galaxies. The second scenario relies on the secular evolution of stellar discs. This led Kormendy & Kennicutt (2004) to make a distinction between ``pseudobulges'' that are ``bulges'' formed through secular evolution, and ``classical'' bulges, those with round smooth isophotes that show no discy structure in the central regions and thus are built up through mergers or a dissipative collapse.

This dichotomy has been slightly refined by Athanassoula (2005) who proposed to further split the pseudobulge category into two classes. The first one contains boxy-peanut shaped bulge (B/PS bulges hereafter) that are due to the vertical orbital structure of stellar bars seen edge-on (Combes et al. 1990; Pfenniger 1984; Pfenniger & Friedli 1991; Combes & Sanders 1981). The frequency of B/PS bulges is high: 45% of all bulges are B/PS, while amongst those the exact shape of the bulge depends mainly on the viewing angle to the bar (Lütticke et al. 2000b,a). The observed incidence of B/PS bulges is however consistent with that expected if they are associated with relatively strong bars. Near infrared observations (Bureau et al. 2006) have also revealed several B/PS features in ``classical'' bulges. As shown by N-body simulations, true peanuts are bars seen side-on, i.e. with the major-axis of the bar roughly perpendicular to the line-of-sight. For less favourable viewing angles, the bulge/bar looks boxy, and if the bar is seen end-on it looks almost spherical. Stronger bars also lead to more prominent peanut shapes, as demonstrated observationally (e.g. Lütticke et al. 2000b) and theoretically (e.g. Bureau & Athanassoula 2005).

According to Athanassoula (2005), ``disk-like'' bulges (DL bulges hereafter) belong to a second class. They are formed by star formation occurring in the gaseous inflow possibly driven by a stellar bar. Bulges formed according to this scenario can have observational properties attributed normally to stellar discs (exponential photometric profiles, blue color, substructures like spiral arms, nuclear bars, circumnuclear rings, etc.). In general, they can contain a measurable amount of gas, as well as a young stellar population sometimes distributed in bright spots. According to their mode of formation, DL bulges should have a much smaller scaleheight than B/PS or classical bulges since the gas distribution is rather flat even in the central galactic region. It is thus very questionable to name these structures ``bulge'' (see discussion by Athanassoula 2005).

From the simulation point of view, it has been considered that DL bulges deserved little attention. However, they did appear under several other names (exponential bulges, nuclear discs, double-bars, bar-within-bar, etc.) in a number of numerical simulations or theoretical works (i.e. Friedli et al. 1996; Shlosman & Begelman 1989; Wozniak & Champavert 2006; Friedli & Martinet 1993; Wozniak et al. 2003; Shlosman et al. 1990). The main difficulty in self-consistently studying the formation mechanism of such bulges or other related central/nuclear morphological features comes from the fact that numerical codes have to include a dissipative component and recipes to mimic star formation and feedback processes, even using very simple rules and/or crude approximations. Apart from some peculiar cases, collisionless N-body codes are thus not able to reproduce DL bulges.

DL bulges could be associated with central velocity dispersion drops (Wozniak et al. 2003) such as those observed by Emsellem et al. (2001) and Márquez et al. (2003). The $\sigma$-drops result from the concentration of new stars toward the centre, and because this population of new stars is newly formed from the low-dispersion gas component, its velocity dispersion is much lower than for the old population. This effect is also amplified by the fact that the gas dispersion also drops toward the centre (and therefore the new stellar component too). This is due to the strong accumulation of gas toward the centre, in a nuclear disk, where dissipation is stronger than elsewhere, and where the gas therefore cools down efficiently. The stellar velocity dispersion could remain low even if the star formation rate is rather low (Wozniak & Champavert 2006), e.g. 1  $M_{\odot}\ \mbox{yr}^{-1}$, that is the same order of magnitude as the typical gaseous mass inflow rate into nuclear rings (Regan et al. 1997). This is additional evidence of a small DL bulge scaleheight.

We decided to investigate the edge-on properties of B/PS and DL bulges. As stated above, this kind of study must perform N-body simulations including gas and star formation recipes. Typical simulations are presented in Sect. 2. In the rest of this paper we mainly discuss the formation mechanisms of both the B/PS and DL bulges and their dynamical properties. In particular, we show that the young stellar population is able to form a B/PS bulge via a slightly different dynamical mechanism than classical B/PS bulge (Sect. 3). The formation of this young B/PS bulge is accompanied by a flat nuclear disc (Sect. 3). This could be interpreted through a linear and non-linear dynamical analysis of the families of resonant orbits (Sect. 5).

It should be stressed that young populations are much brighter for a few 107 yr than old populations, so a DL bulge may also result from the light contrast, and not only from the mass distribution. In accompanying papers we will therefore address the issue of detecting young B/PS bulges predicted by our simulations (Michel-Dansac & Wozniak 2008) and their kinematics (in preparation). For this purpose, we will use photometrically calibrated simulations including the absorption by the dust distribution in the disc.

   
2 Description of the numerical simulations


  \begin{figure} \par\resizebox{18cm}{!}{\includegraphics{0903f1.eps}} \end{figure} Figure 1: Face-on projected mass distribution in the central 10 kpc for t=600, 1000, 1500 and 2000 Myr. The snapshots have been rotated to align the bar with the x-axis. ``young pop.'' means only the population of particles created during the run.
Open with DEXTER


  \begin{figure} \par\resizebox{18cm}{!}{\includegraphics{0903f2.eps}} \end{figure} Figure 2: Left panel: edge-on projected mass distribution in the central 20 $\times $ 6 kpc for t=600, 1000, 1500 and 2000 Myr. The snapshots have been rotated to align the bar with the x-axis. Right panel: only the population of particles created during the run.
Open with DEXTER

For clarity, we will concentrate on a single case extracted from a dozen such simulations of various resolutions and initial setups. The generic simulation, named A sf hereafter, is thus representative of our database. Other examples can be found in Michel-Dansac & Wozniak (2008).

An initial stellar population is set up to reproduce a typical disc galaxy. Positions and velocities for $2.5\times 10^6$ particles are drawn from a superposition of two axisymmetrical Miyamoto & Nagai (1975) discs of mass M1 and M2 (cf. Table 1), of scalelengths 1and 3.5 kpc and a common scaleheight of 0.5 kpc. Initial velocity dispersions are computed solving numerically the Jeans equations according to the Hernquist (1993) method. The method was extended to take account of the presence of a dissipative component when solving for the stellar equation. The initial velocity dispersion was chosen to be anisotropic with $\sigma_r = \sigma_z$ and $\sigma_{\theta}^2 = \sigma_r^2 \kappa^2 / (4\Omega^2)$, where $\sigma_r$, $\sigma_{\theta}$ and $\sigma_z$ are three components of the velocity dispersion along respectively the radial, azimutal and vertical directions and $\kappa$ and $\Omega$ are respectively the radial and angular epicyclic frequencies. The resulting initial Q parameter in the central 500 pc radius increases quickly with radius from 1 to 1.5 and then slowly increases up to 2.3 in the external part of the disc.

The initial disc radius is 30 kpc. The gaseous component of run A sf is represented by 50 000 particles for a total mass of $1.1\times 10^{10}$ $M_{\odot }$ distributed in a 6 kpc scalelength Miyamoto-Nagai disc.

Table 1: List of runs. Masses are in 1011 $M_{\odot }$ units.

A reference run of pure collisionless particles, named B nosf, has been computed to carry out various dynamical comparisons. For this homologous run, M1 and M2 have been proportionally scaled so as to keep the same total mass and spatial distribution as A sf.

The evolution is computed with a particle-mesh N-body code, derived from the original version of the Geneva group (Pfenniger & Friedli 1993; Friedli & Benz 1993), which includes stars, gas and recipes to simulate star formation. The broad outline of the code is the following: the gravitational forces are computed with a particle-mesh method using a 3D log-polar grid with $(N_R, N_\phi, N_Z)=(60,64,312)$ active cells. The smallest radial cell in the central region is 36 pc large and the vertical sampling is 50 pc. The extent of the mesh is 100 kpc in radius and $\pm $7.8 kpc in height. The hydrodynamics equations are solved using the SPH technique. Since we used a polar grid and we need an accurate determination of the forces in the central region, we have improved the pre-computation of self-forces by subdividing each cell in $(n_r, n_\phi, n_z)=(32,6,6)$ subcells. Self-forces are then linearly interpolated before being subtracted from the gravitational forces. The spatial resolution and force accuracy are thus much higher than in any of our previous studies based on the same code (Friedli et al. 1996; Emsellem et al. 2006; Michel-Dansac & Wozniak 2006; Hernandez et al. 2005; Wozniak & Champavert 2006; Wozniak et al. 2003; Michel-Dansac & Wozniak 2004).

The star formation process is based on Toomre's criterion for the radial instability of gaseous discs (cf. Michel-Dansac & Wozniak 2004, for more details). When star formation is active, the radiative cooling of the gas is computed assuming a solar metallicity. In Figs. 1 and 2 we display the face-on and edge-on views of the bar region of A sf for four times which will be used throughout this paper. They have been chosen as being illustrative of the bulge evolution. At the end of the simulation ( $t\approx 3000$ Myr), the total number of particles is roughly $3.2\times 10^{6}$ for the stellar component and 30 000 for the gaseous one. 45% of the gas has been transformed into stellar particles, mainly in the central 10 kpc.

The main effect of a live dark halo (except to flatten the rotation curve of the disc at a large distance) is to permit the exchange of angular momentum with the stellar disc. The rate and the amplitude of these exchanges depend on the velocity dispersion of both the disc and the halo, and on the relative halo mass (e.g. Debattista & Sellwood 2000; Valenzuela & Klypin 2003; Athanassoula 2003). The stellar disc could lose between a few % and 40% of its angular momentum mainly through resonances. Depending on the rate at which the stellar disc losses its angular momentum, the bar grows quite differently. Considering Martinez-Valpuesta et al. (2006) simulations as representative, roughly 2/3 of the angular momentum loses by the bar-unstable part of the stellar disc is absorbed by the halo, the rest going to the outer disc. Most of these exchanges happen during the buckling of the bar. Afterward, the halo absorbs all the angular momentum lost by the disc, leading to a second phase of buckling (Martinez-Valpuesta et al. 2006). The lack of a live dark halo in our simulations thus has the main consequence that we are not able to find any second buckling phase.

However, our simulations are not completely devoid of vertical exchanges since the Miyamoto-Nagai density distribution allows us to build substantially inflated bulges, which is the case with our choice of parameters that leads to an S0-like initial stellar distribution. Thus the evolution of the particles confined near the z=0 plane is also driven by vertical exchange of angular momentum. Moreover, this paper is a first report of the effect of a gaseous component with active star formation on the vertical structure of bars. It is important to be able to disentangle the effect of the dissipative component from that of the halo on the disc evolution. Thus, simulations with a live dark halo, that are still in progress, will be reported elsewhere.

   
3 Central region thickening

In the case of pure N-body simulations, i.e. made of collisionless particles only, whenever a disc galaxy forms a bar, a B/PS bulge develops in a few dynamical times. This process was firstly studied by Combes & Sanders (1981), confirmed by Combes et al. (1990) and Raha et al. (1991), and recently reanalyzed by many authors (Athanassoula 2002; Martinez-Valpuesta et al. 2006; Athanassoula 2003; Athanassoula & Misiriotis 2002; Mihos et al. 1995; Athanassoula 2005, etc.). A stellar bar starts thin and then buckles out of the plane after a short phase of mirror symmetry breaking in the z direction (Pfenniger & Friedli 1991). Thus, initially asymmetrical with respect to the equatorial plane, the bar finally tends towards symmetry (Martinez-Valpuesta et al. 2006). Only a fraction of the whole bar buckles (Athanassoula 2005), so that the outermost part of the bar stays thin and planar.

This is once more what happens for the bar in B nosf (see Fig. 3). Between $t\approx 1400$ and 1600 Myr the vertical thickening starts due to a break in the z mirror symmetry. It is only for t>1600 Myr that the z-distribution becomes more symmetrical.


  \begin{figure} \par\hspace*{10mm}\resizebox{8cm}{!}{\includegraphics{0903f3a.eps... ...\par\hspace*{10mm}\resizebox{8cm}{!}{\includegraphics{0903f3d.eps}} \end{figure} Figure 3: Edge-on projected mass distribution of run B nosf in the central 20 $\times $ 6 kpc for t=600, 1000, 1500 and 2000 Myr.
Open with DEXTER

In the case of A sf  most of the young stellar population lies in a razor-like central disc during the first 450 Myr. This is due to the small vertical scaleheight of the gas distribution that remains thin because of its dissipative nature. It is well-known that such a stellar razor-thin disc is highly unstable (e.g. Merritt & Sellwood 1994). Indeed, 450 Myr after the beginning of the young disc formation, the most central part of the disc starts to thicken out of the equatorial plane. In roughly a bar rotation period, the vertical distribution becomes symmetrically peanut shaped over the central 2 kpc (Fig. 2, right panel, at t=600 Myr), while the young bar is approximately 8 kpc long (Fig. 1). However, at this time, the total mass of the central disc still being low, the thickening process has no detectable effect on the global mass distribution (Fig. 2, left panel).

Afterward, the peanut-shape widens out as the young disc continuously evolves and increases in mass. The thick part of the disc doubles its radial size in less than 1 Gyr. The vertical scaleheight also increases with time leading to a well-developed peanut-shaped bulge for t > 1500 Myr. It is noteworthy that the total mass distribution, hence including both the initial and young population, plainly displays a B/PS bulge. This is mainly due to the mass of the young population that amounts to a significant fraction of the whole mass at that time. Indeed, the B/PS bulge is clearly much less marked if we only display the mass distribution of the initial population (Fig. 4).


  \begin{figure} \par\hspace*{1cm}\resizebox{8cm}{!}{\includegraphics{0903f4a.eps}... ...}\par\hspace*{1cm}\resizebox{8cm}{!}{\includegraphics{0903f4d.eps}} \end{figure} Figure 4: Edge-on projected mass distribution of the initial population in the central 20 $\times $ 6 kpc for t=600, 1000, 1500 and 2000 Myr.
Open with DEXTER

Disentangling the two causes that could be responsible for the increase in boxiness of the initial population is not so obvious. Indeed, as the mass of the young population trapped in the B/PS increases, the gravitational potential deviates more and more from its initial quasi-spherical shape. This leads to a vertical mass redistribution of the initial population since particles can be trapped by orbits associated with vertical resonant families. But the initial disc population could be also unstable towards vertical instabilities (Raha et al. 1991). This is supported by looking at the homologous simulations B nosf that also develop a B/PS bulge (Fig. 3). For B nosf we said above that the growth mechanism is the same as for all other collisionless simulations of cold stellar discs performed so far.

However, a few differences between B nosf and A sf should be noticed:

1.
At the end of the buckling phase, the extent of the boxy region is slightly wider for B nosf than A sf. Moreover, B nosf is much more peanut-shaped than A sf, especially at t=2000 Myr and beyond. In Sect. 5 we attempt to explain this in terms of resonances.
2.
The buckling is clearly asymmetrical for B nosf between t=1400 and 1600 Myr, whereas it remains symmetrical for A sf. If any asymmetry in the mass distribution appears during the evolution, its scaleheight should be less than the vertical resolution of the code (i.e. 50 pc). Indeed, since the z-distribution of the A sf young population remains always symmetrical with respect to the equatorial plane, the potential well created by the young population is also permanently symmetrical. It thus could be more difficult to break the z-symmetry for A sf than for B nosf. This difference supports the interpretation that vertical resonant orbits are populated.
In principle, we cannot exclude the possibility that the thickening of the young population might be asymmetrical because low-order bending modes, those that can give an asymmetrical-shaped mass distribution, can be erased by our 50 pc vertical resolution. Indeed, it has been shown by Merritt & Sellwood (1994) that finite grid effects, especially the vertical mesh resolution, could stabilize the low-order bending modes in the case of a perfectly thin disc. However, the young disc created in all our simulations is always embedded in the initial stellar population which has a much higher scaleheight (initially 500 pc, increasing with time). The vertical distribution of the initial stellar population also remains symmetrical with respect to the equatorial plane (cf. Figs. 3 and 4). Moreover our vertical resolution is much higher than for the Merritt & Sellwood simulations. The vertical oscillating frequencies of particles thus are not dominated by the mesh spacing as is the case for Merritt & Sellwood (1994) simulations.


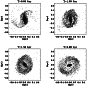   \begin{figure} \resizebox{8cm}{!}{\includegraphics{0903f5.eps}} \end{figure} Figure 5: Face-on gas mass distribution in the central region where the flat nuclear stellar disc made of the young population develops for A sf. The gas particle distribution has not been convolved by the SPH kernel to emphasize the ring structure.
Open with DEXTER

4 Flat nuclear disc

As discussed above, a thin stellar disc cannot remain flat for a long time, such as the A sf initial young central disc. However, for A sf  even if a significant part of the young stellar disc thickens rapidly, there is a small nuclear component which remains flat for a very long time (Fig. 5), i.e. until the end of the simulation ($\approx $3.5 Gyr). This nuclear component is made up of a young stellar population formed in the gaseous disc accumulated in that region because of the torques exerted by the large-scale stellar bar. The formation of this flat nuclear structure is thus concomitant with the thickening of the central part discussed in Sect. 3. After 2 Gyr, the stellar mass amounts to roughly $7.25\times 10^{9}$ $M_{\odot }$ in a cylinder of R = 0.5 kpc and $z \pm 0.5$ kpc. The young population accounts for roughly 34% of the total mass.

The nuclear disc quickly develops a small bar with its own pattern speed, almost 10 times higher than the large-scale bar. The nuclear bar is encircled by a circumnuclear ring (Fig. 5). The nuclear bar appears at $t\approx 575$ Myr and is long-lived, although at the resolution of our simulations (between 36 pc at the centre and 100 pc at 1 kpc), it periodically dissolves in a spiral-like structure. The detailed study of the morphological, dynamical and kinematical properties of the nuclear bar and the circumnuclear ring deserves a dedicated paper and thus will be publish elsewhere (Wozniak 2008). Hereafter we ignore the internal structure of the nuclear disc.

The existence of flattened and rapidly rotating nuclear stellar discs has been predicted by Shlosman & Begelman (1989) and further studied by Shlosman et al. (1990). They showed that such stellar discs could remain flattened for a long time since the two-body relaxation is a slow process. Chung & Bureau (2004) detected such a nuclear disc in roughly 1/3 of their sample of 24 edge-on B/PS galaxies. They have given clear evidence that these discs exhibit a $\sigma$-drop in their centre. They also speculated on the possibility that such discs are formed through gas inflow and subsequent star formation. The whole initial young central disc discussed in Sect. 3 cannot be analogous to the flat disc of Shlosman & Begelman (1989), but its nuclear component obviously has similar properties.

From the kinematical point of view, the nuclear component is undoubtedly associated with the $\sigma$-drop phenomenon. Wozniak et al. (2003) showed that such a young nuclear stellar disc is responsible for the $\sigma$-drop since it is the kinematical signature of stars that have been born from a dynamically cold gaseous component. The presence of the nuclear bar and transient spiral structure in A sf marginally increases the radial velocity dispersion, but the effect on the line-of-sight velocity dispersion remains weak so that a $\sigma$-drop should be visible in double-barred galaxies. A sf thus confirms the potential relationship between nuclear disc and $\sigma$-drop in B/PS bulges as suggested by Chung & Bureau (2004).

The respective sizes of the nuclear disc and peanut-shaped bulge are given in Table 2. The two components enlarge as the galaxy evolves but the ratio of the box over the disc sizes also slightly increases with time. The two phenomena, whose the common initial cause is the presence of a young stellar population formed in the inflowing gaseous material driven by a large-scale bar, seem dynamically distinct. Both morphological structures seem to evolve independently from each other. However, the main driver of the internal dynamics is well-known to be the large-scale bar and the set of resonances associated with its rotation pattern.

Table 2: Rough sizes of the box (from rotation axis to corner) and the central stellar disc (radius in kpc) determined on the mass distribution of the young population alone. The radius of main linear resonances for A sf and B nosf. hILR is the horizontal inner Lindblad resonance, vILR the vertical one and hUHR is the horizontal ultra harmonic resonance.

   
5 Horizontal and vertical resonances

   
5.1 Linear analysis

Numerous authors have tried to correlate the size of morphological structures to the dynamical resonance locations. Circumnuclear and outer rings seem to be correlated with the location of, respectively, the inner Lindblad resonance (ILR) and outer Lindblad resonance (OLR) (cf. Buta & Combes 1996). The ratio of nuclear bar length to that of the large-scale bar could be similar to the ILR to corotation (CR) ratio, the nuclear bar corotation being dynamically coupled to the large-scale bar ILR (e.g. Rautiainen & Salo 1999). However, some other simulations did not show such coupling (e.g. Heller et al. 2001); this matter is still under debate.

To determined the location of the linear CR and ILR dynamic resonances, we computed the circular orbit frequency $\Omega$ and the radial epicyclic frequency $\kappa$ as (Pfenniger 1990):

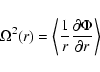\begin{displaymath}\Omega^2(r) = \left\langle \frac{1}{r}\frac{\partial\Phi}{\partial r} \right\rangle \end{displaymath} (1)


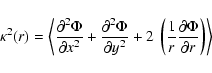\begin{displaymath}\kappa^2(r) = \left\langle \frac{\partial^2\Phi}{\partial x^2... ...rac{1}{r}\frac{\partial\Phi}{\partial r} \right) \right\rangle \end{displaymath} (2)

where $\Phi$ is the gravitational potential and $\langle\cdots\rangle$stands for an azimuthal average.

Strictly speaking, these frequencies predict the oscillation frequencies of the orbits in the axisymmetrical case only. They do not provide any indication of whether families of periodic orbits do follow such oscillations when the bar growth breaks the axisymmetry. However, a number of previous orbital studies (cf. Wozniak & Michel-Dansac 2007; Michel-Dansac & Wozniak 2006, and discussion therein) suggest that the epicyclic approximation could lead to an acceptable estimation of the resonance locations displayed in Table 2, in particular if we are mainly interested in their evolution rather than their accurate absolute position. For instance, using a careful integration of orbits to accurately compute $\Omega$ and $\kappa$, Michel-Dansac & Wozniak (2006) found that the error on $R_{\rm CR}$ remains within 10%. This technique has been used to study a few snaphots when looking for higher order resonances (cf. Sect. 5.2).


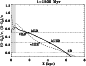  \begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics{0903f6.eps}} \end{figure} Figure 6: Resonance diagram $(\Omega -\Omega _{\rm p})/\kappa $(horizontal resonances, full line) and $(\Omega -\Omega _{\rm p})/\nu $ (vertical resonances, dashed line) at t=1500 Myr. Location of ILR (dot-dash), UHR (triple dot-dash) and CR (dot) are plotted. The shaded box depicts the region occupied by the nuclear disc.
Open with DEXTER

The flat nuclear disc is entirely inside the linear ILR of the large-scale bar, its radius being roughly 0.5 kpc at t=1500 Myr. Indeed, $R_{\rm hILR}$  the horizontal ILR (hILR) radius computed using the linear approximation is $\approx $1.9 kpc from the centre (cf. Fig. 6). The gaseous component which also forms a nuclear disc occupies the same region as the young stellar nuclear disc. During the evolution of the disc, it is well known that the large-scale bar slows down, leading $R_{\rm hILR}$ to increase with time. Hence one could imagine that the size of the nuclear disc increases proportionally to $R_{\rm hILR}$ but in fact its growth saturates after roughly 1.5 Gyr. The nuclear disc does not entirely fill the region encircled by the hILR. Indeed, the radius where $\Omega-\kappa/2$ is maximum is expected to be the limiting dynamical radius. In Fig. 6, the limiting radius is roughly where $(\Omega -\Omega _{\rm p})/\kappa $ is maximum, that is quite close to an $\Omega-\kappa/2$ local maximum.

The combined effects of the horizontal and vertical ILRs cause the planar orbits lying in the equatorial plane to be destabilized (Combes et al. 1990), but the B/PS region extends outside the ILRs. However, as already outlined by Pfenniger & Friedli (1991), in order to observe a well defined boundary in the B/PS it is necessary that families of orbits supporting the shape cease to exist or, at least, become unstable beyond some well-defined height. Pfenniger & Friedli (1991) suggested by default that corotation could be the limiting resonance. However, at t=1500 Myr, the vertical ILR (vILR) is located at $\approx $1.7 kpc, which is very similar to the distance of the corner of the B/PS from the axis of rotation (cf. Table 2) that could be the extent of orbit families associated with the vILR. This obviously suggests that the ILRs, and their associated families of resonant orbits, are responsible for limiting the extent of orbits in the vertical direction. Since it has been shown that the horizontal UHR delineates the bulk of the bar in the equatorial plane (Wozniak & Michel-Dansac 2007; Michel-Dansac & Wozniak 2006), the combined effects of UHR and ILRs play a very important role in shaping the central region of disc galaxies.

At t=1500 Myr (Fig. 6) the location of the hILR is very close to the location of the vILR ( $R_{\rm vILR}$  $\approx 1.7$ kpc at t=1500 Myr). This coincidence has been observed by previous authors (Combes et al. 1990; Pfenniger & Friedli 1991) and it has been suggested that this situation could have some consequences on the local dynamics. As shown in Fig. 7, for A sf the coincidence occurs during all the run, $R_{\rm vILR}$ being always slightly smaller than $R_{\rm hILR}$, although the difference decreases with time. The rapid changes in the nuclear mass distribution due to the gas inflow imply rapid fluctuations of the ILR positions as well, the fluctuation timescale typically being the local dynamical time (less than 50 Myr).


  \begin{figure} \par\resizebox{8.5cm}{!}{\includegraphics{0903f7.eps}} \end{figure} Figure 7: Evolution of horizontal (lines) and vertical (dots) linear ILR radius for run A sf (black thick line and full symbols) and B nosf (dotted lines and opened symbols).
Open with DEXTER

For B nosf, the coincidence arises progressively (cf. Fig. 7). Indeed, during the first 1.6 Gyr there is no vILR. The vILR appears at a radius $R_{\rm vILR}$  $\approx 1.4$ kpc and then increases to coincide with the hILR at $t\approx 2.1$ Gyr. We have said above that the B/PS bulge formation for B nosf follows a different path than for A sf. Indeed, before the vILR appears, the stellar disc buckles out asymmetrically. It is likely only when families of orbits associated with the vILR appear that the mass distribution could be symmetrized with respect to the equatorial plane. This is also the case for A sf although both ILRs appear simultaneously. The thickening of A sf is thus symmetric because ILR resonant families exist from the beginning of the bulge formation.

   
5.2 Non-linear analysis

To be able to discuss the potential effect of higher order resonances, we have computed the orbital frequencies $\Omega$, $\kappa$ and $\nu$of a representative sample of particles for a few selected snapshots. We have applied a variant of the technique of Athanassoula (2003). We have frozen the potential at a given time in the simulation and then computed orbits in the inertial potential to determine the principal frequencies using the technique of Carpintero & Aguilar (1998). We used almost 50 000 particles as initial conditions chosen at random in a limited domain of the phase-space. Indeed, being mainly focused on the resonances inside the bar, we restrict our computation to the particles that a priori reside in the region encircled by the corotation. We a posteriori checked that the ($E_{\rm J}$, r) space ($E_{\rm J}$ being the Jacobi constant) and time-averaged Lindblad diagram ($E_{\rm J}$, ${\bar L_z}$) are well sampled by this choice. To discuss our results we will used the notation of Sellwood & Wilkinson (1993) for closed (periodic) orbits. In this notation, m:n:l implies m radial oscillations in the (x,y) plane and n vertical oscillations in z as the orbit achieves l rotations about the center.

We have selected the snapshot t=2000 Myr for B nosf which is the moment when the B/PS shape is well established and the snapshot t=1500 for A sf. To easily identify periodic orbits that shape the morphology of barred galaxies, we display the distribution of ${\cal K}=(\Omega -\Omega _{\rm p})/\kappa $ and ${\cal N}=(\Omega -\Omega _{\rm p})/\nu $ in Figs. 8 to 9. Families of periodic orbits thus have commensurable ratios ${\cal K} = l/m$ and ${\cal N} = l/n$.


  \begin{figure} \par\includegraphics[width=8.8cm]{0903f8.eps} \end{figure} Figure 8: Distribution of mass as a function of ${\cal K}=(\Omega -\Omega _{\rm p})/\kappa $ ( upper panel) and ${\cal N}=(\Omega -\Omega _{\rm p})/\nu $ ( lower panel) for B nosf at t=2000 Myr. The total mass is normalised to unity. The 2:1:l ( ${\cal K}=0.5$), 3:1:l ( ${\cal K}=0.33$) and 4:1:l ( ${\cal K}=0.25$) resonances are plotted as dotted lines. Multi-periodic orbits (l>1) are superposed on l=1 orbits.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm]{0903f9.eps} \end{figure} Figure 9: As Fig. 8 for A sf at t=1500. The peak at ${\cal K}=0.5$ has been truncated to 0.15 but extends to a value of 0.20.
Open with DEXTER

In these Figures, we have discarded orbits for which the maximal absolute radial extent is less than 1 kpc to avoid contamination by quasi-circular orbits that remain confined in the central nuclear disc. These flat orbits do not participate in shaping the bulge and mostly populate the regions ${\cal K}=1$ and ${\cal N}=0$. On the contrary we did not try to filter out multi-periodic orbits (l>1) so that they are mixed with l=1 orbits.

For the two snapshots, the dominant family of orbits is related to the equatorial 2:n:1 resonance, that is the external hILR ( ${\cal K} = 1/2$) since we have discarded as much as possible resonant families associated with the innermost hILR. However, both the $\cal K$ and the $\cal N$ diagrams are quite different for A sf and B nosf and deserve to be separately discussed, then compared.

For B nosf (Fig. 8), the dominant family is made of 2:2:l orbits ( ${\cal K} = 1/2$ and ${\cal N}=1/2$). These 2:2:1 orbits are known to be responsible for the classical B/PS bulges (Combes et al. 1990; Pfenniger & Friedli 1991) found in collisionless N-body simulations and have thus focused most attention under various names (e.g. $B_{\rm z_1}$ for Pfenniger 1984, z1 for Hasan et al. 1993, x1v3 for Skokos et al. 2002). These orbits dominate the $\cal K$ and $\cal N$ distributions. However, since the mass fraction trapped around the horizontal and the vertical frequencies are different, this suggests that a fraction of the ${\cal K}=0.5$ peak is populated by 2:n:1 orbits with $n \neq 2$.

Several other non-negligible contributions are concentrated around ${\cal K}=0.25$ (4:n:1 orbits related to the UHR), $0.4, \approx 0.6$ and $\approx $0.75. It is much more difficult to uniquely identify the orbit families responsible for these peaks but they mostly contain multi-periodic trapped orbits. For instance we found 5:n:2 orbits that contribute to the ${\cal K}=0.4$ peak.


  \begin{figure} \par\includegraphics[width=9cm]{0903f10.eps} \end{figure} Figure 10: Examples of dominant families of orbits for A sf at t=1500 Myr. From top to bottom, a quasi 2:2:1 orbit and three different instances of 2:3:1 orbits.
Open with DEXTER

For A sf (Fig. 9), the distributions are very different even if the main contribution is still concentrated around ${\cal K}=0.5$ as for B nosf. The fraction of mass (roughly 0.2) trapped for ${\cal K}=0.5$ is however much higher than for B nosf (0.13). The secondary peaks are less prominent than for B nosf and they form a forest of frequencies betwen ${\cal K}=0.1$ and 0.8.

The vertical structure is also very different from the collisionless run. The mass trapped around ${\cal N}=1/3$ (the vertical 3:1 resonance) is slightly greater than for ${\cal N}=1/2$ resonant orbits. ${\cal K} = 1/2$ for these orbits, as for 2:2:1 orbits, so that they must to be classified as 2:3:1 resonant orbits. A few examples are shown in Fig. 10.

The role of this family of orbits has been emphasized by Heller & Shlosman (1996) who demonstrated that it is connected to and amplified by the presence of a massive nuclear ring. Indeed, Heller & Shlosman (1996) showed that the major periodic orbits within the corotation radius are affected by the perturbation of a massive ring. The main family of orbits that sustain a stellar bar (the so-called x1 family in the Contopoulos & Papayannopoulos (1980) notation) becomes vertically unstable for several ranges of Jacobi constant ($E_{\rm J}$) values. In the $E_{\rm J}$ domain where x1coexists with x2 and x3 families (that are respectively stable and unstable elliptical-like orbits perpendicular to the bar and that occupy the region between the two ILRs), two x1 instability strips provoke z and $\dot{z}$ bifurcations to 2:2:1 families (the so-called symmetrical BAN - banana - and asymmetrical ABAN - anti-banana - families) and 2:3:1 families.

Heller & Shlosman (1996) showed that the width of these instability gaps depends on the mass of the ring. As the ring mass is increased, the instability strip responsible for 2:3:1 orbits grows in size and moves toward lower EJ. In some extreme situations where the mass of the ring is very high (e.g. 109 $M_{\odot }$) some instability strips appear for the x2 family.

2:3:1 orbits are symmetrical with respect to the (x,z) plane and antisymmetrical with respect to the (y,z) one (or the converse) unlike 2:2:1 orbits that are either symmetrical or antisymmetrical about both the (x,y) and (y,z) planes. Heller & Shlosman (1996) (their Fig. 7 and 8) and Skokos et al. (2002) (their Fig. 9) display typical members of this family. It has been noted by Skokos et al. (2002) and Patsis et al. (2002) that the 2:3:1 family (called x1v3 in these papers) as well as other families associated with higher order vertical resonances (i.e. 2:4:1, 2:5:1 etc.), could play an important role in shaping small sized B/PS bulges because the z extent remains small whatever the values of $E_{\rm J}$ are. For A sf they appear to be a major contribution to the shape of the young B/PS bulge whereas they are fully absent for B nosf.


  \begin{figure} \par\includegraphics[width=9cm]{0903f11.eps} \end{figure} Figure 11: Examples of other boxy-shaped families of orbits for A sf at t=1500 Myr.
Open with DEXTER

For A sf the main family after 2:2:1 and 2:3:1 is the 2:5:1, visible in Fig. 9 around ${\cal N}=0.2$. As discussed by Patsis et al. (2002) this family is also a strong contributor to the B/PS bulge. But, as for 2:3:1 orbits, they are absent in B nosf. Many other kinds of resonant orbits contribute to the B/PS. In Fig. 11 we display a few examples. Their contribution is mainly concentrated around ${\cal K}\approx 0.2$ and 0.66 whereas ${\cal N}=0.2$.

Even if the families of closed periodic orbits are the backbone of any stellar bar, strictly speaking they occupy a null volume of the phase-space. Only orbits trapped around the stable families are responsible for the shape of the bar. These trapped orbits have fundamental frequencies slightly shifted from those of their parent families so that they are responsible for the broadening of the spectral lines around the commensurable value of $\cal K$ and $\cal N$.

   
6 Conclusions

We have numerically investigated some dynamical properties of edge-on boxy or peanut-shaped (B/PS) and disc-like (DL) (pseudo-)bulges. Our results are summarised as follows:

1.
We are able to confirm that the B/PS in N-body collisionless simulations is due to the classical break in the z mirror symmetry. However, in our numerical simulation that includes a gaseous component and star formation recipes, the bulge-growing mechanism is quite different from the pure N-body case. The young stellar population that is born in a thin gaseous disc rapidly populates vertical resonant orbits triggered by the combined effects of the horizontal and vertical ILRs. This leads to a B/PS bulge mainly made of stellar material younger than the surrounding population. The morphology and extent of young B/PS bulges are significantly different from the classical B/PS bulge. We thus predict that two populations of B/PS bulges could exist and even coexist. They might be distinguished by deep photometric observations or careful stellar population analyses.

2.
In N-body collisionless simulations the main orbit family responsible for the B/PS is the 2:2:1. On the contrary, if a dissipative component is present and can form new stars, additional asymmetrical families contribute to the B/PS. In the case of our simulation, 2:3:1 and 2:5:1 orbits trap a significant fraction of the mass. Their appearance could be linked to the massive circumnuclear ring.

3.
A flat discy stellar component appears simultaneously with the thickening of the young population. It is due to star formation in the nuclear gaseous disc. Remarkably, it remains flat throughout the simulation (3.5 Gyr) although it develops a bar, as predicted by Shlosman & Begelman (1989). This suggests that nuclear bars, embedded in large-scale counterparts, are flat structures. Both the stellar and gas discs are located well inside the ILR, limited by the radius where $(\Omega -\Omega _{\rm p})/\kappa $ is maximum.

Acknowledgements
We warmly thank Luis Aguilar for providing his code to compute orbital frequencies and Daniel Pfenniger for fruitful discussions about the computation of resonances. Our computations were performed on the CRAL 18 node cluster of PCs funded by the INSU ATIP # 2JE014 and several grants from the INSU Programme National Galaxie. LMD acknowledges support from the Universidad Nacional Autónoma de México (UNAM) for part of this work, the University of Lyon, the HORIZON project and the ECOS-Sud program # A07U01, for financial support for his visits during which this paper was submitted.

References

 
Copyright ESO 2009