We study the spatial clustering of 538 X-ray selected AGN in the 2 deg2 XMM-COSMOS field that are spectroscopically identified with
A&A 494, 33-48 (2009)
DOI: 10.1051/0004-6361:200810821
R. Gilli1 - G. Zamorani1 - T. Miyaji2 - J. Silverman3 - M. Brusa4 - V. Mainieri5 - N. Cappelluti4 - E. Daddi6 - C. Porciani3 - L. Pozzetti1 - F. Civano7 - A. Comastri1 - A. Finoguenov4 - F. Fiore8 - M. Salvato9 - C. Vignali10 - G. Hasinger4 - S. Lilly3 - C. Impey11 - J. Trump11 - P. Capak9 - H. McCracken12 - N. Scoville9 - Y. Taniguchi13 - C. M. Carollo3 - T. Contini14 - J.-P. Kneib15 - O. Le Fevre15 - A. Renzini16 - M. Scodeggio17 - S. Bardelli1 - M. Bolzonella1 - A. Bongiorno4 - K. Caputi3 - A. Cimatti10 - G. Coppa10 - O. Cucciati18 - S. de la Torre15 - L. de Ravel15 - P. Franzetti17 - B. Garilli17 - A. Iovino18 - P. Kampczyk3 - C. Knobel3 - K. Kovac3 - F. Lamareille14 - J.-F. Le Borgne14 - V. Le Brun15 - C. Maier3 - M. Mignoli1 - R. Pellò14 - Y. Peng3 - E. Perez Montero14 - E. Ricciardelli16 - M. Tanaka5 - L. Tasca15 - L. Tresse15 - D. Vergani1 - E. Zucca1 - U. Abbas15 - D. Bottini17 - A. Cappi1 - P. Cassata15 - M. Fumana17 - L. Guzzo18 - A. Leauthaud19 - D. Maccagni17 - C. Marinoni20 - P. Memeo17 - B. Meneux4 - P. Oesch3 - R. Scaramella8 - J. Walcher12
1 - INAF - Osservatorio Astronomico di Bologna, Via Ranzani 1, 40127
Bologna, Italy
2 -
Instituto de Astronomía, Universidad Nacional Autónoma de
México, Ensenada, México (mailing address: PO Box 439027, San Ysidro, CA, 92143-9027, USA)
3 -
Institute of Astronomy, Swiss Federal Institute of Technology (ETH
Hönggerberg), 8093, Zürich, Switzerland
4 -
Max-Planck-Institut für extraterrestrische Physik, Postfach 1312,
85741 Garching, Germany
5 -
European Southern Observatory, Karl-Schwarzschild-Strasse 2, Garching
85748, Germany
6 -
Laboratoire AIM, CEA/DSM - CNRS -
Université Paris Diderot, DAPNIA/SAp, Orme des Merisiers, 91191
Gif-sur-Yvette, France
7 -
Harvard-Smithsonian Center for
Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
8 -
INAF - Osservatorio Astronomico di Roma, via di Frascati 33,
00040 Monte Porzio Catone (Roma), Italy
9 -
California Institute of Technology, MC 105-24, 1200 East California
Boulevard, Pasadena, CA 91125, USA
10 -
Dipartimento di Astronomia, Università degli Studi di Bologna,
Via Ranzani 1, 40127 Bologna, Italy
11 -
Steward Observatory, University of Arizona, Tucson, AZ 85721, USA
12 -
Institut d'Astrophysique de Paris, 98 bis Boulevard Arago, 75014
Paris, France
13 -
Research Center for Space and Cosmic Evolution, Ehime
University, Bunkyo-cho 2-5, Matsuyama 790-8577, Japan
14 -
Laboratoire d'Astrophysique de Toulouse-Tarbes, Université de
Toulouse, CNRS, 14 avenue E. Belin, 31400 Toulouse, France
15 -
Laboratoire d'Astrophysique de Marseille, CNRS-Université
de Provence, Traverse du Siphon, BP 8, 13012 Marseille, France
16 -
Dipartimento di Astronomia, Università di
Padova, Vicolo Osservatorio 2, 35122 Padova, Italy
17 -
INAF - Istituto di Astrofisica
Spaziale e Fisica Cosmica, Via Bassini 15, 20133 Milan, Italy
18 -
INAF - Osservatorio Astronomico di Brera, 23807 Merate (LC), Italy
19 -
University of California, Lawrence Berkeley National Laboratory,
1 Cyclotron Rd, Berkeley, CA 94720, USA
20 -
Centre de Physique Théorique, UMR 6207 CNRS-Université de
Provence, Case 907, 13288 Marseille, France
Received 18 August 2008 / Accepted 22 October 2008
Abstract
We study the spatial clustering of 538 X-ray selected AGN in the 2 deg2 XMM-COSMOS field that are spectroscopically identified with
![]() and span the redshift range
z=0.2-3.0. The median
redshift and X-ray luminosity of the sample are z = 0.98 and
and span the redshift range
z=0.2-3.0. The median
redshift and X-ray luminosity of the sample are z = 0.98 and
![]() erg s-1, respectively. A strong
clustering signal is detected at
erg s-1, respectively. A strong
clustering signal is detected at ![]()
![]() level, which is the
most significant measurement obtained to date for clustering of X-ray
selected AGN. By fitting the projected correlation function
level, which is the
most significant measurement obtained to date for clustering of X-ray
selected AGN. By fitting the projected correlation function
![]() with a power law on scales of
with a power law on scales of
![]() Mpc, we derive a
best-fit comoving correlation length of
Mpc, we derive a
best-fit comoving correlation length of
![]() Mpc
and slope of
Mpc
and slope of
![]() (Poissonian errors; bootstrap errors
are about a factor of 2 larger). An excess signal is observed in the
range
(Poissonian errors; bootstrap errors
are about a factor of 2 larger). An excess signal is observed in the
range
![]() Mpc, which is due to a large-scale
structure at
Mpc, which is due to a large-scale
structure at
![]() containing about 40 AGN, a feature which is
evident over many wavelengths in the COSMOS field. When removing the
containing about 40 AGN, a feature which is
evident over many wavelengths in the COSMOS field. When removing the
![]() structure or computing
structure or computing
![]() in a narrower range
around the peak of the redshift distribution (e.g.
z=0.4-1.6), the
correlation length decreases to
in a narrower range
around the peak of the redshift distribution (e.g.
z=0.4-1.6), the
correlation length decreases to
![]() Mpc, which is
consistent with what is observed for bright optical QSOs at the same
redshift.
Mpc, which is
consistent with what is observed for bright optical QSOs at the same
redshift.
We investigate the clustering properties of obscured and unobscured
AGN separately, adopting different definitions for the source
obscuration. For the first time, we are able to provide a significant
measurement for the spatial clustering of obscured AGN at ![]() .
Within the statistical uncertainties, we do not find evidence that AGN
with broad optical lines (BLAGN) cluster differently from AGN without
broad optical lines (non-BLAGN).
Based on these results, which are limited by object statistics,
however, obscured and unobscured AGN are consistent with inhabiting
similar environments.
.
Within the statistical uncertainties, we do not find evidence that AGN
with broad optical lines (BLAGN) cluster differently from AGN without
broad optical lines (non-BLAGN).
Based on these results, which are limited by object statistics,
however, obscured and unobscured AGN are consistent with inhabiting
similar environments.
The evolution of AGN clustering with redshift is also investigated. No significant difference is found between the clustering properties of XMM-COSMOS AGN at redshifts below or above z=1.
The correlation length measured for XMM-COSMOS AGN at ![]() is
similar to that of massive galaxies (stellar mass
is
similar to that of massive galaxies (stellar mass
![]() )
at the same redshift. This suggests
that AGN at
)
at the same redshift. This suggests
that AGN at ![]() are preferentially hosted by massive galaxies,
as observed both in the local and in the distant (
are preferentially hosted by massive galaxies,
as observed both in the local and in the distant (![]() )
Universe. According to a simple clustering evolution scenario, we find
that the relics of AGN are expected to have a correlation length as
large as
)
Universe. According to a simple clustering evolution scenario, we find
that the relics of AGN are expected to have a correlation length as
large as
![]() Mpc by z=0, and hence to be hosted by
local bright (
Mpc by z=0, and hence to be hosted by
local bright (
![]() )
ellipticals.
)
ellipticals.
We make use of dark matter halo catalogs from the Millennium
simulation to determine the typical halo hosting moderately luminous
![]() AGN. We find that XMM-COSMOS AGN live in halos with masses
AGN. We find that XMM-COSMOS AGN live in halos with masses
![]() .
By combining the
number density of XMM-COSMOS AGN to that of the hosting dark matter
halos we estimate the AGN duty cycle and lifetimes. We find lifetimes
approximately of 1 Gyr for AGN at
.
By combining the
number density of XMM-COSMOS AGN to that of the hosting dark matter
halos we estimate the AGN duty cycle and lifetimes. We find lifetimes
approximately of 1 Gyr for AGN at ![]() ,
which are longer than
those estimated for optically bright QSOs at the same redshift. These
longer lifetimes mainly reflect the higher number density of AGN
selected by X-ray samples.
,
which are longer than
those estimated for optically bright QSOs at the same redshift. These
longer lifetimes mainly reflect the higher number density of AGN
selected by X-ray samples.
Key words: galaxies: active - cosmology: large-scale structure of Universe - cosmology: observations - X-rays: galaxies
Several pieces of evidence point towards an intimate correlation between the evolution of galaxies and the accretion and growth of supermassive black holes (SMBHs) at their centers, indicating that most galaxies in the Universe spent a fraction of their lifetimes as active galactic nuclei (AGN). In the local Universe, most galaxy bulges indeed host a supermassive black hole (see e.g. Ferrarese & Ford 2005, for a review), whose mass scales with the bulge mass and stellar velocity dispersion (Ferrarese & Merritt 2000; Gebhart et al. 2000). Furthermore, the growth of SMBHs during active accretion phases, which is traced by the cosmological evolution of the AGN luminosity function (Ueda et al. 2003; Hasinger et al. 2005; La Franca et al. 2005; Silverman et al. 2008a), has been shown to eventually match the mass function of SMBHs in the local Universe (e.g. Marconi et al. 2004; Yu & Tremaine 2002; Shankar et al. 2004).
While the SMBH vs. galaxy co-evolution is now an accepted scenario, the details of this joint evolution are not fully understood yet. Nuclear activity in bright QSOs is thought to be induced by major mergers or close encounters of gas-rich galaxies in the context of hierarchical structure formation (e.g. Kauffmann & Haehnelt 2000; Cavaliere & Vittorini 2002; Hopkins et al. 2006). Alternatively, nuclear activity can be simply related to the physical processes (e.g. star formation) going on in a single galaxy, without being induced by mergers or interactions with neighboring objects (e.g. Granato et al. 2004). Overall, the role played by the environment in triggering both nuclear activity and star formation is still a matter of debate.
Just like local ultraluminous infrared galaxies (Sanders & Mirabel
1996), the population of bright submillimeter sources at ![]() (Chapman et al. 2003) is hosting both star formation and nuclear
activity (Alexander et al. 2005), as a result of galaxy interactions
(Tacconi et al. 2008).
However, the majority of
(Chapman et al. 2003) is hosting both star formation and nuclear
activity (Alexander et al. 2005), as a result of galaxy interactions
(Tacconi et al. 2008).
However, the majority of ![]() AGN selected at faint X-ray fluxes
seem to be hosted by galaxies with a spectral energy distribution
typical of passively evolving objects (Mainieri et al. 2005). The
concurrent growth of black holes and stellar mass has been observed in
IR galaxies at
AGN selected at faint X-ray fluxes
seem to be hosted by galaxies with a spectral energy distribution
typical of passively evolving objects (Mainieri et al. 2005). The
concurrent growth of black holes and stellar mass has been observed in
IR galaxies at ![]() by Daddi et al. (2007), who suggested a
long-lived (>0.2 Gyr) AGN plus starburst phenomenon, unlikely to be
triggered by rapid merger events. In the local galaxies observed by
the Sloan Digital Sky Survey (SDSS, York et al. 2000), nuclear activity
does not appear to be correlated to the presence of close companions,
while star formation does (Li et al. 2008). A common merger origin for
both phenomena cannot be ruled out, however, provided they occur at
different times (see Li et al. 2008).
by Daddi et al. (2007), who suggested a
long-lived (>0.2 Gyr) AGN plus starburst phenomenon, unlikely to be
triggered by rapid merger events. In the local galaxies observed by
the Sloan Digital Sky Survey (SDSS, York et al. 2000), nuclear activity
does not appear to be correlated to the presence of close companions,
while star formation does (Li et al. 2008). A common merger origin for
both phenomena cannot be ruled out, however, provided they occur at
different times (see Li et al. 2008).
The relation between nuclear activity and the environment can be studied via clustering techniques in the context of large-scale structure formation, in which the growth of baryonic structures is supposed to follow the formations of dark matter halos (DMHs).
The comparison between the clustering properties of AGN and those of
DMHs predicted by cold dark matter (CDM) models can be used to
evaluate the typical mass of the DMHs in which AGN form and reside as
a function of cosmic time. The most recent measurements have shown
that bright QSOs in the redshift range z=0-3 reside into DMHs of mass
![]() (Grazian et al. 2004; Porciani et al. 2004; Croom et al. 2005; but see Padmanabhan et al. 2008,
for lower mass estimates at
(Grazian et al. 2004; Porciani et al. 2004; Croom et al. 2005; but see Padmanabhan et al. 2008,
for lower mass estimates at ![]() ).
In addition, the ratio between the AGN space density and the
space density of host DMHs may provide an estimate of the AGN lifetime
(e.g. Martini & Weinberg 2001). Current estimates are largely
uncertain, constraining the AGN lifetime in the range of a few
).
In addition, the ratio between the AGN space density and the
space density of host DMHs may provide an estimate of the AGN lifetime
(e.g. Martini & Weinberg 2001). Current estimates are largely
uncertain, constraining the AGN lifetime in the range of a few ![]() 106-108 yr (Grazian et al. 2004; Porciani et al. 2004). Finally, the comparison between the clustering
properties of different galaxy types and AGN can be used to estimate
AGN hosts and to estimate the descendant and progenitors of
AGN at any given redshifts.
106-108 yr (Grazian et al. 2004; Porciani et al. 2004). Finally, the comparison between the clustering
properties of different galaxy types and AGN can be used to estimate
AGN hosts and to estimate the descendant and progenitors of
AGN at any given redshifts.
AGN clustering has been traditionally studied by means of the
two-point correlation function applied to optically selected QSO
samples (e.g. Shanks et al. 1987; La Franca et al. 1998). The most recent and solid results of these
analyses come from the two largest QSO surveys to date, namely the 2dF
QSO Redshift Survey (2QZ, e.g. Croom et al. 2005), and the
SDSS. The 2QZ is based on a sample of more than 20 000 objects with
redshifts
![]() .
When calculating the
correlation function in real space and approximating it with a
power law
.
When calculating the
correlation function in real space and approximating it with a
power law
![]() ,
the QSO correlation length and
slope were found to be
,
the QSO correlation length and
slope were found to be
![]() Mpc and
Mpc and
![]() at a median redshift of
at a median redshift of
![]() (Da Angela
et al. 2005). Some evidence of a flattening towards smaller
scales was also reported, with
(Da Angela
et al. 2005). Some evidence of a flattening towards smaller
scales was also reported, with
![]() at projected scales below
at projected scales below
![]() Mpc (Da Angela et al. 2005). The clustering
level of 2QZ QSOs is similar to that of early type galaxies at the
same redshift (Coil et al. 2004; Meneux et al. 2006), suggesting they
reside in environments of similar density. A tentative detection of
Mpc (Da Angela et al. 2005). The clustering
level of 2QZ QSOs is similar to that of early type galaxies at the
same redshift (Coil et al. 2004; Meneux et al. 2006), suggesting they
reside in environments of similar density. A tentative detection of
![]() AGN residing preferentially in the same environment of blue
rather than red galaxies has been reported by Coil et al. (2007). The
QSO clustering is observed to be a strong function of redshift (Croom
et al. 2005; Porciani & Norberg 2006), with the correlation length of
luminous QSOs at
AGN residing preferentially in the same environment of blue
rather than red galaxies has been reported by Coil et al. (2007). The
QSO clustering is observed to be a strong function of redshift (Croom
et al. 2005; Porciani & Norberg 2006), with the correlation length of
luminous QSOs at ![]() being as high as
r0=24 h-1 Mpc (Shen
et al. 2007). This suggests that luminous, early QSOs are hosted by
the most massive and rare DMHs and hence form in the highest density
peaks of the dark matter distribution. The evidence of luminosity
dependent clustering is, on the contrary, still marginal (Porciani &
Norberg 2006).
being as high as
r0=24 h-1 Mpc (Shen
et al. 2007). This suggests that luminous, early QSOs are hosted by
the most massive and rare DMHs and hence form in the highest density
peaks of the dark matter distribution. The evidence of luminosity
dependent clustering is, on the contrary, still marginal (Porciani &
Norberg 2006).
The above results are mostly based on AGN selected by means of their
blue optical colors and broad optical lines; i.e., they essentially
refer to unobscured, type 1 AGN. With the notable exception of the
measurement performed by the SDSS on a local sample of narrow-line AGN
(Li et al. 2006), to date there has been no information on the clustering
properties of obscured AGN, which, based on the results from deep
X-ray surveys (Brandt & Hasinger 2005; Tozzi et al. 2006) and X-ray
background synthesis models (e.g. Gilli et al. 2007a),
are found to be a factor of ![]() 4 more numerous than unobscured
ones; i.e., they are the most abundant AGN population in the Universe,
dominating the history of accretion onto SMBHs (e.g. Fabian 1999). If
the unified model strictly applies, i.e. the nuclear obscuration is
just an orientation effect, one should not expect differences in the
clustering properties of obscured and unobscured AGN. However, several
exceptions to the strict unified model are known. Source obscuration
is in many cases related to the gas content and evolutionary stage of
the host galaxy, rather than to a small-scale torus intercepting the
line of sight (Malkan et al. 1998). Models have been proposed in which
the onset of nuclear activity starts embedded in an envelope of gas
and dust, which is later on swept out by the QSO radiation (see
e.g. Hopkins et al. 2006). If this were the case, obscured and
unobscured AGN would be just two subsequent stages along a galaxy
lifetime. The different durations of these two stages and their
relation with the environment may produce different clustering
properties between obscured and unobscured AGN.
4 more numerous than unobscured
ones; i.e., they are the most abundant AGN population in the Universe,
dominating the history of accretion onto SMBHs (e.g. Fabian 1999). If
the unified model strictly applies, i.e. the nuclear obscuration is
just an orientation effect, one should not expect differences in the
clustering properties of obscured and unobscured AGN. However, several
exceptions to the strict unified model are known. Source obscuration
is in many cases related to the gas content and evolutionary stage of
the host galaxy, rather than to a small-scale torus intercepting the
line of sight (Malkan et al. 1998). Models have been proposed in which
the onset of nuclear activity starts embedded in an envelope of gas
and dust, which is later on swept out by the QSO radiation (see
e.g. Hopkins et al. 2006). If this were the case, obscured and
unobscured AGN would be just two subsequent stages along a galaxy
lifetime. The different durations of these two stages and their
relation with the environment may produce different clustering
properties between obscured and unobscured AGN.
One obvious way to obtain samples of obscured AGN is through X-ray observations. Besides reducing the obscuration bias dramatically, especially in the hard 2-10 keV band, X-ray selection also has the advantage of being effective in selecting distant low-luminosity AGN, whose optical light is diluted by the host galaxy emission and therefore missed by color-based optical surveys.
In the past years the limited sample size of X-ray selected AGN
prevented clustering analyses as detailed as for optically selected
objects. In particular, the lack of dedicated optical follow-up
programs of X-ray sources providing large samples with spectroscopic
measurements, has not allowed accurate estimates of the spatial
clustering of X-ray selected AGN, limiting most studies to angular
clustering. Numerous investigations of the two point angular
correlation function of X-ray sources have indeed appeared in the
literature, but the results suffer from rather large
uncertainties. Early attempts to measure the angular clustering of
X-ray selected sources were performed by Vikhlinin et al. (1995) and
Carrera et al. (1998) based on ROSAT pointings. More recent results
based on Chandra and XMM data have been obtained by Basilakos et al. (2004), Gandhi et al. (2006), Puccetti et al. (2006), Miyaji et al. (2007), Carrera et al. (2007), Plionis et al. (2008), and Ueda et al. (2008). In particular, Miyaji et al. (2007) and Gandhi et al. (2006) have computed the angular correlation function over
contiguous areas of a few square degrees (the 2 deg2COSMOS field and the ![]() 4 deg2 XMM-LSS field, respectively),
which should reduce the impact of cosmic variance. In the COSMOS field,
Miyaji et al. (2007) measured a correlation length of about
4 deg2 XMM-LSS field, respectively),
which should reduce the impact of cosmic variance. In the COSMOS field,
Miyaji et al. (2007) measured a correlation length of about
![]() Mpc, while only a loose constraint (
Mpc, while only a loose constraint (
![]() ) Mpc
was obtained in the XMM-LSS by Gandhi et al. (2006). Very recently an
attempt to measure the angular clustering of high-redshift (
) Mpc
was obtained in the XMM-LSS by Gandhi et al. (2006). Very recently an
attempt to measure the angular clustering of high-redshift (![]() ),
X-ray selected AGN has been done by Francke et al. (2008).
),
X-ray selected AGN has been done by Francke et al. (2008).
The few examples of spatial clustering of X-ray selected sources
appeared in the literature are limited by low statistics. Based on a
sample of ![]() 220 QSOs at
220 QSOs at ![]() found in the 80 deg2 ROSAT
North Ecliptic Pole survey (NEP, Gioia et al. 2003), Mullis
et al. (2004) were able to measure a correlation signal to
found in the 80 deg2 ROSAT
North Ecliptic Pole survey (NEP, Gioia et al. 2003), Mullis
et al. (2004) were able to measure a correlation signal to
![]()
![]() level. By fixing the correlation slope to
level. By fixing the correlation slope to
![]() ,
they found a best-fit correlation length of
,
they found a best-fit correlation length of
![]() Mpc. Because of the relatively short
exposures in the NEP survey and the limited ROSAT sensitivity and
bandpass (0.1-2.4 keV), only bright, luminous, unobscured QSOs have been
detected in this sample (median
Mpc. Because of the relatively short
exposures in the NEP survey and the limited ROSAT sensitivity and
bandpass (0.1-2.4 keV), only bright, luminous, unobscured QSOs have been
detected in this sample (median
![]() erg s-1, corresponding to
erg s-1, corresponding to
![]() erg s-1 for a spectral slope of
erg s-1 for a spectral slope of
![]() ). Later, by analyzing data from the Chandra Deep
Field South (CDFS, Rosati et al. 2002) and Chandra Deep
Field North (CDFN, Alexander et al. 2003), Gilli et al. (2005) were able to detect clustering at >
). Later, by analyzing data from the Chandra Deep
Field South (CDFS, Rosati et al. 2002) and Chandra Deep
Field North (CDFN, Alexander et al. 2003), Gilli et al. (2005) were able to detect clustering at >![]() level
for
level
for ![]() AGN with
AGN with
![]() erg s-1.
However, the best-fit correlation length was found to vary by a factor
of
erg s-1.
However, the best-fit correlation length was found to vary by a factor
of ![]() 2 between the two fields (
r0=10 h-1 Mpc in the CDFS,
r0=5 h-1 Mpc in the CDFN), revealing strong cosmic variance
over these small, 0.1 deg2 each, sky areas. Although with limited
significance (
2 between the two fields (
r0=10 h-1 Mpc in the CDFS,
r0=5 h-1 Mpc in the CDFN), revealing strong cosmic variance
over these small, 0.1 deg2 each, sky areas. Although with limited
significance (![]()
![]() ), in the CDFs, it was also possible to
determine the clustering properties of obscured AGN only, which did
not show significant differences with respect to those of unobscured
ones within the uncertainties (Gilli et al. 2005). The most
recent measurement is the one performed in the larger, 0.4 deg2field covered by the CLASXS (Yang et al. 2006). A correlation length
of
), in the CDFs, it was also possible to
determine the clustering properties of obscured AGN only, which did
not show significant differences with respect to those of unobscured
ones within the uncertainties (Gilli et al. 2005). The most
recent measurement is the one performed in the larger, 0.4 deg2field covered by the CLASXS (Yang et al. 2006). A correlation length
of ![]() 5.7 h-1 Mpc was found for X-ray selected AGN at
5.7 h-1 Mpc was found for X-ray selected AGN at ![]() ,
with average luminosity of
,
with average luminosity of
![]() erg s-1.
erg s-1.
A large number of X-ray surveys are ongoing and are expected to provide larger samples of sources over wide sky areas and with different limiting fluxes. They will allow studies of clustering of AGN in different redshift and luminosity regimes. A few examples of such surveys are X-Bootes (Murray et al. 2005), XMM-LSS (Pierre et al. 2007), Extended CDFS (Lehmer et al. 2005), AEGIS (Nandra et al. 2005), and XMM-COSMOS (Hasinger et al. 2007). One of these samples, the XMM survey in the 2 deg2 COSMOS field (XMM-COSMOS), has been specifically designed to study with the best statistics the clustering of X-ray selected AGN. One of the main goals of XMM-COSMOS was indeed to provide the best measurement to date of the correlation function of X-ray selected AGN and to allow a reliable measurement of the correlation function of obscured AGN at z>0 for the first time.
The optical spectroscopic identification of the 1822 pointlike X-ray sources detected by XMM-COSMOS continues. In this paper we present the results based on the first third of the objects. The paper is organized as follows. In Sect. 2 we summarize the X-ray and optical follow-up observations of the XMM-COSMOS sample and present the source catalog used in our analysis. In Sect. 3 we describe the methods of estimating the correlation function of X-ray selected sources. In Sect. 4 several safety checks are performed to validate the adopted techniques. The results of our analysis are presented in Sect. 5. In Sect. 6 the results are discussed and interpreted. The conclusions and prospects for future work are finally presented in Sect. 7.
Throughout this paper, a flat cosmology with
![]() and
and
![]() is assumed (Spergel et al. 2007). For comparison with previous measurements we
refer to correlation lengths and distances in units of h-1 Mpc
comoving, where
is assumed (Spergel et al. 2007). For comparison with previous measurements we
refer to correlation lengths and distances in units of h-1 Mpc
comoving, where
![]() km s-1 Mpc-1. Masses of dark
matter halos are also expressed in units of
km s-1 Mpc-1. Masses of dark
matter halos are also expressed in units of
![]() for
consistency with the Millennium simulation, and AGN and halo space
densities are expressed in units of h3 Mpc-3. AGN luminosities
and lifetimes are calculated using h=0.7.
for
consistency with the Millennium simulation, and AGN and halo space
densities are expressed in units of h3 Mpc-3. AGN luminosities
and lifetimes are calculated using h=0.7.
The XMM-COSMOS survey is part of the COSMOS legacy project (see
Scoville et al. 2007a, for an overview of the survey), an extensive
multiwavelength campaign to observe a
![]() deg equatorial
field centered at
deg equatorial
field centered at
![]() .
A number of
large programs with the major observing facilities have been already
performed or are ongoing, including HST (Scoville et al. 2007b), VLT
(Lilly et al. 2007), SUBARU (Taniguchi et al. 2007), VLA (Schinnerer
et al. 2007), XMM (Hasinger et al. 2007), Chandra (Elvis et al. 2009) Spitzer (Sanders et al. 2007), and GALEX (Zamojski et al. 2007; Schiminovich et al. in preparation).
.
A number of
large programs with the major observing facilities have been already
performed or are ongoing, including HST (Scoville et al. 2007b), VLT
(Lilly et al. 2007), SUBARU (Taniguchi et al. 2007), VLA (Schinnerer
et al. 2007), XMM (Hasinger et al. 2007), Chandra (Elvis et al. 2009) Spitzer (Sanders et al. 2007), and GALEX (Zamojski et al. 2007; Schiminovich et al. in preparation).
XMM-COSMOS is a mosaic made of 53 partially overlapping XMM pointings
that cover the entire 2 deg2 COSMOS field. The XMM observations were
allocated across two announcements of opportunities (AO-4 and AO-5)
and performed in two different passes![]() , for a total of 1.4 Ms exposure time. Each pass was arranged into a regular grid of
, for a total of 1.4 Ms exposure time. Each pass was arranged into a regular grid of ![]() 30 ks pointings separated by 8 arcmin each to cover the full 2 deg2 field. In the second pass the grid pattern was shifted by 1
arcmin with respect to the first pass to ensure maximum uniformity in
the sensitivity over the final mosaic. The limiting fluxes reached in
the regions of maximum exposure are
30 ks pointings separated by 8 arcmin each to cover the full 2 deg2 field. In the second pass the grid pattern was shifted by 1
arcmin with respect to the first pass to ensure maximum uniformity in
the sensitivity over the final mosaic. The limiting fluxes reached in
the regions of maximum exposure are
![]() ,
,
![]() ,
,
![]() erg cm-2 s-1 in the 0.5-2,
2-10, and 5-10 keV, respectively, while the entire 2 deg2 area is
covered down to
erg cm-2 s-1 in the 0.5-2,
2-10, and 5-10 keV, respectively, while the entire 2 deg2 area is
covered down to
![]() ,
,
![]() ,
,
![]() erg cm-2 s-1 in the same bands. In total 1822
pointlike sources have been detected in at least one band down to a
likelihood threshold of 10 (see Cappelluti et al. 2007, for the source
detection process). The final catalog will be presented in a
forthcoming paper (Cappelluti et al. 2009). A number of
results concerning the first pass (0.8 Ms total exposure) have been
published by Cappelluti et al. (2007), Miyaji et al. (2007), and Mainieri
et al. (2007).
erg cm-2 s-1 in the same bands. In total 1822
pointlike sources have been detected in at least one band down to a
likelihood threshold of 10 (see Cappelluti et al. 2007, for the source
detection process). The final catalog will be presented in a
forthcoming paper (Cappelluti et al. 2009). A number of
results concerning the first pass (0.8 Ms total exposure) have been
published by Cappelluti et al. (2007), Miyaji et al. (2007), and Mainieri
et al. (2007).
The optical identification of XMM sources is currently in progress
(see Brusa et al. 2007, for the initial results based on the first 12 XMM pointings). Unique optical and/or infrared counterparts for most
(![]() 88%) of the XMM sources have now been recognized. Thanks to
the Chandra observations in the central COSMOS square deg (Elvis et al. 2009), a number of formerly ambiguous identifications have now
been made secure (Brusa et al. in preparation). The main dedicated
spectroscopic follow-up programs of XMM sources are being conducted
with the IMACS instrument at the 6 m Magellan telescope (Trump et al. 2007) and with VIMOS at the VLT within the zCOSMOS program
(e.g. Lilly et al. 2007; see Fig. 1). A number of
spectroscopic redshifts were also obtained by cross-correlating the
XMM catalog with published spectroscopic catalogs like the SDSS. About
46% of the total spectroscopic sample were obtained with only IMACS
observations, 25% with only zCOSMOS, and another 24% has been
observed in both programs. The remaining 5% were obtained by
cross-correlation with public catalogs. Quality flags were assigned to
the redshifts measured by IMACS and zCOSMOS. We considered here only
the 621 X-ray pointlike sources with highest quality flags, which have
been identified as extragalactic objects. By considering the 150
duplicated redshifts (i.e. those objects observed by both IMACS and
VIMOS) the accuracy in the redshift measurements is verified to be
88%) of the XMM sources have now been recognized. Thanks to
the Chandra observations in the central COSMOS square deg (Elvis et al. 2009), a number of formerly ambiguous identifications have now
been made secure (Brusa et al. in preparation). The main dedicated
spectroscopic follow-up programs of XMM sources are being conducted
with the IMACS instrument at the 6 m Magellan telescope (Trump et al. 2007) and with VIMOS at the VLT within the zCOSMOS program
(e.g. Lilly et al. 2007; see Fig. 1). A number of
spectroscopic redshifts were also obtained by cross-correlating the
XMM catalog with published spectroscopic catalogs like the SDSS. About
46% of the total spectroscopic sample were obtained with only IMACS
observations, 25% with only zCOSMOS, and another 24% has been
observed in both programs. The remaining 5% were obtained by
cross-correlation with public catalogs. Quality flags were assigned to
the redshifts measured by IMACS and zCOSMOS. We considered here only
the 621 X-ray pointlike sources with highest quality flags, which have
been identified as extragalactic objects. By considering the 150
duplicated redshifts (i.e. those objects observed by both IMACS and
VIMOS) the accuracy in the redshift measurements is verified to be
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0821_f1.ps}
\end{figure}](/articles/aa/full/2009/04/aa10821-08/Timg75.gif) |
Figure 1: Distribution on the sky of the 1822 pointlike sources detected by XMM (crosses). Spectroscopically identified objects are shown as filled circles. The area covered by spectroscopic observations is also shown: the large circles show the 16 Magellan IMACS pointings, while the polygon represents the area presently covered by zCOSMOS observations. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0821_f2.ps}
\end{figure}](/articles/aa/full/2009/04/aa10821-08/Timg77.gif) |
Figure 2: Soft X-ray luminosity vs. redshift relation for the spectroscopically identified sources in XMM-COSMOS. Broad line AGN (BLAGN) and non broad line AGN (non-BLAGN) are shown as blue open circles and red filled circles, respectively. Only objects in the redshift range z=0.2-3 (vertical dashed lines) have been considered for the clustering analysis. |
| Open with DEXTER | |
The 0.5-2 keV X-ray luminosity vs. redshift distribution of BLAGN and
non-BLAGN, is shown in Fig. 2. BLAGN are on average observed
at higher redshift and at luminosities above 1042.5 erg s-1,
while non-BLAGN are observed down to very low X-ray luminosities and
may therefore include a significant fraction of normal galaxies. To
exclude from the sample those objects that are not likely to be AGN, we
then considered only those sources at a redshift higher than 0.2. As
shown in Fig. 2, this cut essentially removes most
low-luminosity objects, leaving in the sample only objects with
![]() erg s-1
erg s-1![]() . In
addition we considered for our analysis only objects at redshifts
below 3, since beyond this limit the source density becomes extremely
low and the selection function is very uncertain (see Sect. 3).
. In
addition we considered for our analysis only objects at redshifts
below 3, since beyond this limit the source density becomes extremely
low and the selection function is very uncertain (see Sect. 3).
By exploiting the large multiwavelength database available in
COSMOS, Salvato et al. (2009) are able to estimate a photometric
redshift for ![]()
![]() of the XMM sources. For the remaining 15% of
the sample, the main reason for not attempting a photometric redshift
estimate was the ambiguity in the correct association with the
optical/IR counterpart (see Brusa et al. 2007). This issue, however,
is not expected to introduce any bias related to source
distances. Therefore the redshift distribution estimated using
photometric redshifts should be very close to that of the entire XMM sample. On the contrary, spectroscopic redshifts have been measured
for a minority (
of the XMM sources. For the remaining 15% of
the sample, the main reason for not attempting a photometric redshift
estimate was the ambiguity in the correct association with the
optical/IR counterpart (see Brusa et al. 2007). This issue, however,
is not expected to introduce any bias related to source
distances. Therefore the redshift distribution estimated using
photometric redshifts should be very close to that of the entire XMM sample. On the contrary, spectroscopic redshifts have been measured
for a minority (![]()
![]() )
of the total XMM sample (including 34 stars), making it possible that objects with measured
spectroscopic redshift are not a fair representation (i.e. a random
sampling) of the total AGN population detected by XMM. The I-band
magnitude vs. redshift distribution of the objects with spectroscopic
redshifts and only photometric redshifts is shown in
Fig. 3. Objects only with photometric redshift are on average
optically fainter and at higher redshift than objects with
spectroscopic redshifts. A Kolmogorov-Smirnov test performed on the
redshifts distribution of objects with and without spectroscopic
redshift indicates that they differ at >
)
of the total XMM sample (including 34 stars), making it possible that objects with measured
spectroscopic redshift are not a fair representation (i.e. a random
sampling) of the total AGN population detected by XMM. The I-band
magnitude vs. redshift distribution of the objects with spectroscopic
redshifts and only photometric redshifts is shown in
Fig. 3. Objects only with photometric redshift are on average
optically fainter and at higher redshift than objects with
spectroscopic redshifts. A Kolmogorov-Smirnov test performed on the
redshifts distribution of objects with and without spectroscopic
redshift indicates that they differ at >![]() level; i.e., the
spectroscopic sample is not a fair representation of the entire AGN
population detected by XMM. We therefore impose a magnitude cut at
level; i.e., the
spectroscopic sample is not a fair representation of the entire AGN
population detected by XMM. We therefore impose a magnitude cut at
![]() ,
which excludes only a small fraction (<
,
which excludes only a small fraction (<![]() )
of
spectroscopically identified objects but increases the spectroscopic
completeness to about 60%. The redshift distribution of objects
brighter than
)
of
spectroscopically identified objects but increases the spectroscopic
completeness to about 60%. The redshift distribution of objects
brighter than
![]() with and without spectroscopic redshifts are
statistically indistinguishable. Therefore, we conclude that, for
objects with
with and without spectroscopic redshifts are
statistically indistinguishable. Therefore, we conclude that, for
objects with
![]() ,
the spectroscopic selection does not include
any bias against high-redshift objects.
,
the spectroscopic selection does not include
any bias against high-redshift objects.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0821_f3.ps}
\end{figure}](/articles/aa/full/2009/04/aa10821-08/Timg82.gif) |
Figure 3:
I-band magnitude vs. redshift distribution of the optical
counterparts of XMM sources. Objects with spectroscopic redshift
or only photometric redshift are shown as filled circles or
crosses, respectively. The dashed horizontal line shows the
|
| Open with DEXTER | |
In the following we consider the sample of 538 XMM objects with
![]() and spectroscopic redshift in the range
z=0.2-3.0 as our
reference sample. The average redshift and X-ray luminosity of this
sample are z=0.98 and
and spectroscopic redshift in the range
z=0.2-3.0 as our
reference sample. The average redshift and X-ray luminosity of this
sample are z=0.98 and
![]() erg s-1,
respectively. The redshift distribution of the sample sources is shown
in Fig. 4. A number of redshift structures are observed, the
most prominent of which is at
erg s-1,
respectively. The redshift distribution of the sample sources is shown
in Fig. 4. A number of redshift structures are observed, the
most prominent of which is at
![]() ,
also observed at other
wavelengths in COSMOS (Lilly et al. 2007).
,
also observed at other
wavelengths in COSMOS (Lilly et al. 2007).
The basic statistics commonly used to measure the clustering
properties of galaxies is the two point correlation function ![]() ,
defined as the excess probability over random of finding a pair with
one object in the volume dV1 and the second in the volume dV2,
separated by a distance r (Peebles 1980):
,
defined as the excess probability over random of finding a pair with
one object in the volume dV1 and the second in the volume dV2,
separated by a distance r (Peebles 1980):
![\begin{displaymath}{\rm d}P = n^2[1+\xi(r)]{\rm d}V_1{\rm d}V_2,
\end{displaymath}](/articles/aa/full/2009/04/aa10821-08/img84.gif) |
(1) |
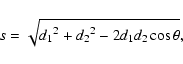 |
(2) |
![\begin{displaymath}d_i = {c\over{H_0}}\int_0^{~z_i}{\rm d}z~\left[\Omega_{\rm m}(1+z)^3+\Omega_{\Lambda}\right]^{-1/2}.
\end{displaymath}](/articles/aa/full/2009/04/aa10821-08/img87.gif) |
(3) |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0821_f4.ps}
\end{figure}](/articles/aa/full/2009/04/aa10821-08/Timg88.gif) |
Figure 4:
Redshift distribution for the 538 X-ray sources in the
reference sample in bins of
|
| Open with DEXTER | |
To overcome these problems one can resort to the so-called projected
correlation function:
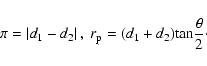 |
(5) |
An integration limit
![]() has to be chosen in Eq. (4) to
maximize the correlation signal. Indeed, one should avoid
has to be chosen in Eq. (4) to
maximize the correlation signal. Indeed, one should avoid
![]() values that are too high, since they would mainly add noise to the
estimate of
values that are too high, since they would mainly add noise to the
estimate of
![]() .
On the other hand, scales that are too small,
comparable to the redshift uncertainties and to the pairwise
velocity dispersion (i.e. the dispersion in the distribution of the
relative velocities of source pairs), should also be avoided since
they would not allow the whole signal to be recovered.
.
On the other hand, scales that are too small,
comparable to the redshift uncertainties and to the pairwise
velocity dispersion (i.e. the dispersion in the distribution of the
relative velocities of source pairs), should also be avoided since
they would not allow the whole signal to be recovered.
The typical uncertainty in the redshift measurements
(
![]() corresponds to comoving scales below
corresponds to comoving scales below
![]() Mpc at all redshifts. The pairwise velocity dispersion measured in the
local Universe (500-600 km s-1; Marzke et al. 1995;
Zehavi et al. 2002) is expected to decrease by
Mpc at all redshifts. The pairwise velocity dispersion measured in the
local Universe (500-600 km s-1; Marzke et al. 1995;
Zehavi et al. 2002) is expected to decrease by ![]()
![]() at
at ![]() (see e.g. the
(see e.g. the ![]() CDM simulations by Kauffmann et al. 1999), thus corresponding to
CDM simulations by Kauffmann et al. 1999), thus corresponding to ![]()
![]() Mpc. To
search for the best integration radius
Mpc. To
search for the best integration radius
![]() ,
we measured
,
we measured
![]() for the XMM-COSMOS reference sample for different
for the XMM-COSMOS reference sample for different
![]() values ranging from 3 to
values ranging from 3 to
![]() Mpc. In Fig. 5 (upper
panel), we show the increase of
Mpc. In Fig. 5 (upper
panel), we show the increase of
![]() with the integration radius
with the integration radius
![]() at those projected scales where most of the clustering
signal is coming from (
at those projected scales where most of the clustering
signal is coming from (
![]() Mpc). The
Mpc). The
![]() values
appear to converge for
values
appear to converge for
![]() Mpc. Similarly,
the amplitude of the spatial correlation function
Mpc. Similarly,
the amplitude of the spatial correlation function
![]() (Fig. 5 bottom panel) or the amplitude of the projected
correlation function
(Fig. 5 bottom panel) or the amplitude of the projected
correlation function
![]() (not shown) is converging
for
(not shown) is converging
for
![]() Mpc
Mpc![]() . The
correlation length r0 and slope
. The
correlation length r0 and slope ![]() are strongly correlated:
when r0 increases,
are strongly correlated:
when r0 increases, ![]() decreases. The correlation length
appears to reach a maximum at
decreases. The correlation length
appears to reach a maximum at
![]() Mpc, while
Mpc, while
![]() is constant in the range
is constant in the range
![]() Mpc. Based on these considerations, we adopt
Mpc. Based on these considerations, we adopt
![]() Mpc in the following analysis, which is the minimum
Mpc in the following analysis, which is the minimum
![]() value
at which the correlation function converges, and returns the
smaller errors on the best-fit correlation parameters
value
at which the correlation function converges, and returns the
smaller errors on the best-fit correlation parameters
![]() and
and
![]() .
We note that with this choice r0 is smaller by
.
We note that with this choice r0 is smaller by ![]()
![]() than the maximum value measured at
than the maximum value measured at
![]() Mpc, but we do not try to correct for this
small bias.
Mpc, but we do not try to correct for this
small bias.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0821_f5.ps}
\end{figure}](/articles/aa/full/2009/04/aa10821-08/Timg117.gif) |
Figure 5:
Upper panel: projected correlation function
|
| Open with DEXTER | |
To measure
![]() we created random samples of sources in our
fields and measured the excess of pairs at separations
we created random samples of sources in our
fields and measured the excess of pairs at separations
![]() with respect to the random distribution. We used the minimum variance
estimator proposed by Landy & Szalay (1993), which is found to
have a nearly Poissonian variance and to outperform other popular
estimators, especially on large scales (e.g., see Kerscher et al. 2000):
with respect to the random distribution. We used the minimum variance
estimator proposed by Landy & Szalay (1993), which is found to
have a nearly Poissonian variance and to outperform other popular
estimators, especially on large scales (e.g., see Kerscher et al. 2000):
![\begin{displaymath}\xi(r_{\rm p}, \pi)=\frac{[DD]-2[DR]+[RR]}{[RR]},
\end{displaymath}](/articles/aa/full/2009/04/aa10821-08/img119.gif) |
(7) |
![\begin{displaymath}[DD]\equiv DD(r_{\rm p}, \pi)\frac{n_r(n_r-1)}{n_d(n_d-1)}
\end{displaymath}](/articles/aa/full/2009/04/aa10821-08/img120.gif) |
(8) |
![\begin{displaymath}[DR]\equiv DR(r_{\rm p}, \pi)\frac{(n_r-1)}{2 n_d}
\end{displaymath}](/articles/aa/full/2009/04/aa10821-08/img121.gif) |
(9) |
![\begin{displaymath}[RR]\equiv RR(r_{\rm p}, \pi),
\end{displaymath}](/articles/aa/full/2009/04/aa10821-08/img122.gif) |
(10) |
Since both the redshift and the coordinate
![]() distributions of the identified sources are potentially affected by
observational biases, special care has to be taken in creating the
sample of random sources. This has been extensively discussed by Gilli
et al. (2005) for the Chandra Msec Fields (see. e.g. their
Sect. 4.2) where similar problems have been encountered. In that paper
we showed that extracting the coordinates of the random sources from
the coordinate ensemble of the real sample and using the observed
redshifts to create a smoothed redshift distribution for the random
sample is a sufficiently accurate procedure. As in Gilli et al. (2005), we assumed a Gaussian smoothing length
distributions of the identified sources are potentially affected by
observational biases, special care has to be taken in creating the
sample of random sources. This has been extensively discussed by Gilli
et al. (2005) for the Chandra Msec Fields (see. e.g. their
Sect. 4.2) where similar problems have been encountered. In that paper
we showed that extracting the coordinates of the random sources from
the coordinate ensemble of the real sample and using the observed
redshifts to create a smoothed redshift distribution for the random
sample is a sufficiently accurate procedure. As in Gilli et al. (2005), we assumed a Gaussian smoothing length
![]() ,
which is a good compromise between scales that are too small,
which would suffer from local density variations, and those that are
too large, which would oversmooth the distribution. We nonetheless
verified that our results do not change significantly when using a
smoothing length in the range
,
which is a good compromise between scales that are too small,
which would suffer from local density variations, and those that are
too large, which would oversmooth the distribution. We nonetheless
verified that our results do not change significantly when using a
smoothing length in the range
![]() .
The smoothed
redshift distribution adopted for our simulations is shown in
Fig. 4. The adopted procedure, if anything, would slightly
reduce the correlation signal, since it removes the effects of angular
clustering. Each random sample is built to contain more than 20 000 objects.
.
The smoothed
redshift distribution adopted for our simulations is shown in
Fig. 4. The adopted procedure, if anything, would slightly
reduce the correlation signal, since it removes the effects of angular
clustering. Each random sample is built to contain more than 20 000 objects.
We binned the source pairs in intervals of
![]() and measured
and measured
![]() in each bin. The resulting datapoints were then
fitted by a power law of the form given in Eq. (6), and the
best-fit parameters
in each bin. The resulting datapoints were then
fitted by a power law of the form given in Eq. (6), and the
best-fit parameters ![]() and r0 were determined via
and r0 were determined via ![]() minimization. Given the small number of pairs that fall into some
bins (especially on the smallest scales), we used the formulae of
Gehrels (1986) to estimate the 68% confidence interval
(i.e.
minimization. Given the small number of pairs that fall into some
bins (especially on the smallest scales), we used the formulae of
Gehrels (1986) to estimate the 68% confidence interval
(i.e. ![]() errorbars in Gaussian statistics).
errorbars in Gaussian statistics).
A possible concern related to the analysis methods presented in the previous section is the random-sample generation. Indeed, placing the random sources at the coordinates of the real sources completely removes the contribution to the signal due to angular clustering. This procedure could therefore underestimate the true correlation length.
We try to quantify this effect by considering a random sample
simulated according to the XMM-COSMOS sensitivity maps (see e.g. Miyaji
et al. 2007; and Cappelluti et al. 2007). Briefly, each simulated
source is extracted from a reference input
![]() ,
placed at random
in the XMM-COSMOS field, and kept in the random sample if its flux is
above the sensitivity map value at that position. It is evident that
this method is producing a random sample that only accounts for the
varying X-ray sensitivity along the COSMOS field, but does not account
for the positional biases related to the optical follow-up
program.
The result of this test is that the measured correlation length
increases by
,
placed at random
in the XMM-COSMOS field, and kept in the random sample if its flux is
above the sensitivity map value at that position. It is evident that
this method is producing a random sample that only accounts for the
varying X-ray sensitivity along the COSMOS field, but does not account
for the positional biases related to the optical follow-up
program.
The result of this test is that the measured correlation length
increases by ![]()
![]() with respect to the former case.
with respect to the former case.
An additional test was performed prompted by the X-ray flux
distribution of objects with spectroscopic redshift being different
from that of the total XMM sample. In particular, the fraction of
objects with spectroscopic redshift Frac is constant (about 70%)
for X-ray fluxes
![]() erg cm-2 s-1, while it decreases towards fainter fluxes, reaching 0.0 at
erg cm-2 s-1, while it decreases towards fainter fluxes, reaching 0.0 at
![]() .
Objects with spectroscopic redshifts
may therefore undersample the regions of maximum X-ray sensitivity, in
which the X-ray source density is higher, producing a more regular
distribution on the sky than the total XMM sample. We therefore
created a new random sample by first placing sources on the field
according to the X-ray sensitivity map as discussed in the previous
paragraph and then keeping only a fraction of them, with a
flux-dependent ``keeping'' probability given by the observed relation
Frac vs. flux described above. When computing the projected
correlation function using this new random sample, we find a result
similar to what was obtained in the previous test, i.e. a
.
Objects with spectroscopic redshifts
may therefore undersample the regions of maximum X-ray sensitivity, in
which the X-ray source density is higher, producing a more regular
distribution on the sky than the total XMM sample. We therefore
created a new random sample by first placing sources on the field
according to the X-ray sensitivity map as discussed in the previous
paragraph and then keeping only a fraction of them, with a
flux-dependent ``keeping'' probability given by the observed relation
Frac vs. flux described above. When computing the projected
correlation function using this new random sample, we find a result
similar to what was obtained in the previous test, i.e. a ![]()
![]() higher r0 value than obtained when placing random objects exactly
at the coordinates of real objects.
higher r0 value than obtained when placing random objects exactly
at the coordinates of real objects.
Again, this new random sample unfortunately also does not fully
account for the positional biases related to the optical follow-up
programs. Indeed, given the very complex optical follow-up that
combines results from different programs, it is impossible for us to
estimate the correct selection function of our sample, but it is
likely that the selection of the masks used for optical spectroscopy,
which cover the COSMOS field unevenly, leaving some patches of the
field poorly covered, while covering other patches rather extensively,
is causing the main positional bias. This can be for instance
appreciated in Fig. 1, in which 3 of the 4 inner circles representing
Magellan IMACS pointings (16 pointings in total) have a higher density
of objects with spectroscopic redshift (cyan dots) than all the
remaining pointings. We therefore believe that the systematic upward
shift of ![]() in r0 that we obtained with these tests is
likely to be an upper limit. Also, we note that, when performing error
analysis considering bootstrap errors (see next paragraph), a
difference of
in r0 that we obtained with these tests is
likely to be an upper limit. Also, we note that, when performing error
analysis considering bootstrap errors (see next paragraph), a
difference of ![]() is within the total error budget. Given this
limited difference, we are confident that our results are not strongly
affected by the method used to generate the random source sample.
is within the total error budget. Given this
limited difference, we are confident that our results are not strongly
affected by the method used to generate the random source sample.
While many of the correlation function estimators used in the
literature have a variance substantially larger than Poisson (because
source pairs in general are not independent, i.e. the same objects
appear in more than one pair), the estimator used here was shown to
have a nearly Poissonian variance (Landy & Szalay 1993). It
has, however, to be noted that the Landy & Szalay (1993)
estimator was originally tested in the approximation of weak
clustering, so that Poisson errorbars may in our case underestimate
the true uncertainties. Bootstrap resampling has often been used to
estimate the uncertainties in the correlation function best-fit
parameters (e.g. Mo et al. 1992), but this technique
may return an overestimate of the real uncertainties (Fisher et al. 1994). We tested bootstrap errors by randomly extracting 100 samples of 538 sources each from our total sample, allowing for
repetitions. The rms in the distribution of the best-fit
correlation lengths and slopes is a factor of ![]() 2.8 and
2.8 and ![]() 2 greater than the Poisson errorbars, respectively. In the following we
simply quote r0 and
2 greater than the Poisson errorbars, respectively. In the following we
simply quote r0 and ![]() ,
together with their
,
together with their ![]() Poisson errors, bearing in mind that the most likely uncertainty is
about a factor of 2 higher.
Poisson errors, bearing in mind that the most likely uncertainty is
about a factor of 2 higher.
![\begin{figure}
\par\mbox{\includegraphics[width=8.2cm,clip]{0821_f6a.ps}\hspace*{4mm}
\includegraphics[width=8.2cm,clip]{0821_f6b.ps} }\end{figure}](/articles/aa/full/2009/04/aa10821-08/Timg134.gif) |
Figure 6:
Left panel: projected correlation function for the
XMM-COSMOS AGN reference sample (538 objects with
z=0.2-3.0 and
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0821_f7.ps}
\end{figure}](/articles/aa/full/2009/04/aa10821-08/Timg139.gif) |
Figure 7:
Projected correlation function for different XMM-COSMOS AGN
subsamples. Upper panel: broad line AGN (open circles) vs.
non-broad line AGN (filled circles). Middle panel: X-ray
unabsorbed (
|
| Open with DEXTER | |
We are repeating our angular auto-correlation function analysis
using the full three-year data (55 pointings instead of the first-year
23 pointings used in Miyaji et al. 2007). We plan to use the accurate
(![]()
![]() )
photometric redshifts presented by Salvato et al. (2009) to calculate the angular correlation function of XMM AGNs
selected by redshift. Preliminary results show
)
photometric redshifts presented by Salvato et al. (2009) to calculate the angular correlation function of XMM AGNs
selected by redshift. Preliminary results show
![]() Mpc for the z>0 sample, which is fully consistent with the
measurement presented in Miyaji et al. (2007), while the correlation
length is reduced to
Mpc for the z>0 sample, which is fully consistent with the
measurement presented in Miyaji et al. (2007), while the correlation
length is reduced to
![]() Mpc (1
Mpc (1![]() errors)
for the sample obtained by excluding objects in the redshift range
z=0.34-0.36. These values are consistent within the errors with
those obtained with the present analysis, despite being systematically
higher. The angular analysis results, however, still vary with the
angular scale range used for fitting, as well as with error estimation
methods. A more detailed discussion of the comparison of the results
presented in this paper with those obtained through the study of the
angular auto-correlation function and cross-correlation function with
galaxies will be presented in a future paper (Miyaji et al., in
prep.).
errors)
for the sample obtained by excluding objects in the redshift range
z=0.34-0.36. These values are consistent within the errors with
those obtained with the present analysis, despite being systematically
higher. The angular analysis results, however, still vary with the
angular scale range used for fitting, as well as with error estimation
methods. A more detailed discussion of the comparison of the results
presented in this paper with those obtained through the study of the
angular auto-correlation function and cross-correlation function with
galaxies will be presented in a future paper (Miyaji et al., in
prep.).
It is interesting to investigate the projected correlation function
for different source subsamples. For each subsample we placed the
sources of the random sample only at the positions of the sources in
that subsample. The projected correlation function was then fitted
both leaving the slope free and fixing it to
![]() ,
the
standard value measured in most galaxy samples, which is also similar
to the slope of 1.88 measured for the total XMM-COSMOS sample. Fixing
the slope allows a more direct comparison between the correlation
lengths of the different subsamples when a two-parameter fit is poorly
constrained.
,
the
standard value measured in most galaxy samples, which is also similar
to the slope of 1.88 measured for the total XMM-COSMOS sample. Fixing
the slope allows a more direct comparison between the correlation
lengths of the different subsamples when a two-parameter fit is poorly
constrained.
We investigated the clustering properties of sources optically
classified as broad line AGN (BLAGN) or non-BLAGN. The class of
non-BLAGN is admittedly a mixed bag, which may include obscured AGN,
weak unobscured AGN, whose optical emission is diluted by the host
galaxy light, and normal galaxies. The cut at z>0.2 (roughly
corresponding to
L0.5-2>1041.5 erg s-1), however, should
guarantee that the non-BLAGN sample is mostly populated by AGN in
which the absence of broad optical lines is solely due to nuclear
obscuration. Therefore, investigating the clustering properties of
BLAGN and non-BLAGN should be a proxy to investigate the clustering
properties of unobscured vs. obscured AGN. For the sample of 305 BLAGN,
we measured a correlation correlation length of
![]() Mpc and a slope of
Mpc and a slope of
![]() ,
while for the 229 non-BLAGN we measured a similar correlation length,
,
while for the 229 non-BLAGN we measured a similar correlation length,
![]() Mpc, and a somewhat flatter slope
Mpc, and a somewhat flatter slope
![]() .
The projected correlation functions of BLAGN
and non-BLAGN AGN are shown in Fig. 7 (upper panel).
It should be noted that a proper comparison between the clustering
properties of BLAGN and non-BLAGN should take possible redshift
effects into account, since BLAGN are generally observed at higher
redshift than non-BLAGN (median z=1.5 vs. z=0.7, see Table 1). In
principle, the correlation length of a given AGN and galaxy population
is expected to change with redshift, being intimately related to the
evolution of the hosting dark matter halos, and one should therefore
compare source populations at the same redshift to establish whether
they reside in the same environment or not. We will return to this in
the discussion.
.
The projected correlation functions of BLAGN
and non-BLAGN AGN are shown in Fig. 7 (upper panel).
It should be noted that a proper comparison between the clustering
properties of BLAGN and non-BLAGN should take possible redshift
effects into account, since BLAGN are generally observed at higher
redshift than non-BLAGN (median z=1.5 vs. z=0.7, see Table 1). In
principle, the correlation length of a given AGN and galaxy population
is expected to change with redshift, being intimately related to the
evolution of the hosting dark matter halos, and one should therefore
compare source populations at the same redshift to establish whether
they reside in the same environment or not. We will return to this in
the discussion.
Table 1: Summary of best-fit clustering parameters.
To investigate the clustering properties of obscured vs. unobscured AGN further, we also considered the column density measurements obtained from the spectral analysis of XMM data. We considered here the measurements performed by Mainieri et al. (2007 and in prep.), who performed X-ray spectral fits for those objects with more than 100 counts in the 0.3-10 keV band and found absorption in excess of the Galactic value in about 25% of their sample (see details in Mainieri et al. 2007). We considered here only objects with more than 200 counts in the 0.3-10 keV band, for which the determination of the column density is more reliable. By matching the Mainieri et al. objects with more than 200 counts with our reference sample, we end up with 290 objects for which a column density has been estimated: 70 of these do show absorption in excess of the galactic value. We note that 21 out of the 190 broad line AGN with measured column density have absorption in excess of the Galactic value, which is consistent with the 10% fraction of X-ray absorbed broad line AGN found in other X-ray selected samples (see e.g. Tozzi et al. 2006; Brusa et al. 2003). A few words of caution should, however, be spent on these sources. First, simulations run on input X-ray unabsorbed spectra show that, especially for sources at high redshift and relatively low photon statistics, the spectral fit may return spurious positive values for the absorption (see e.g. Tozzi et al. 2006). Second, the fraction of X-ray absorbed sources might be related to the significance threshold used to assess the presence of X-ray absorption. In particular, Mainieri et al. consider an X-ray source as absorbed if the addition of a photoelectric cut off in the spectral fit improves it at a level of more than 90% as assessed by an F-test. One would then expect that, in about 7 out of 70 absorbed sources (either BLAGN or non-BLAGN), the measured column density is spurious. At any rate, results do not change significantly if we include those 21 candidate X-ray absorbed BLAGN in the total X-ray absorbed sample or not.
We first verified that the projected correlation function of the 290
objects with X-ray spectroscopy is consistent with that of our full
reference sample and then tried to measure the projected correlation
function for absorbed and unabsorbed sources
separately. Unfortunately, the small number statistics prevent us from
getting a significant clustering signal for the 70 X-ray absorbed AGN,
while for the 220 X-ray unabsorbed objects we found a correlation
length of
![]() ,
somewhat higher than that measured for the
subsample of BLAGN. When restricting the analysis to the redshift
range
z=0.4-1.6, i.e. around the peak of the redshift distribution,
which also excludes the redshift structure at z=0.36, the correlation
length of the X-ray unabsorbed objects decreases to
,
somewhat higher than that measured for the
subsample of BLAGN. When restricting the analysis to the redshift
range
z=0.4-1.6, i.e. around the peak of the redshift distribution,
which also excludes the redshift structure at z=0.36, the correlation
length of the X-ray unabsorbed objects decreases to
![]() ,
consistent with what is measured for the full reference sample in the
same redshift interval.
,
consistent with what is measured for the full reference sample in the
same redshift interval.
To overcome the limitations due to the small size of the sample of
objects with reliable ![]() measurements, we tried to calibrate a
relation between the X-ray column density
measurements, we tried to calibrate a
relation between the X-ray column density ![]() and the hardness ratio
(HR), defined as the difference between the source X-ray photons
detected in the 2-10 keV band and those detected in the 0.5-2 keV
band, normalized to the sum of the photons in the two
bands
and the hardness ratio
(HR), defined as the difference between the source X-ray photons
detected in the 2-10 keV band and those detected in the 0.5-2 keV
band, normalized to the sum of the photons in the two
bands![]() . The distribution of the column
density vs. hardness ratio for objects with more than 200 counts is
shown in Fig. 8 (left panel): most of the objects with
. The distribution of the column
density vs. hardness ratio for objects with more than 200 counts is
shown in Fig. 8 (left panel): most of the objects with
![]() do show absorption in excess of
do show absorption in excess of
![]() ,
therefore we
adopt a rough threshold at
,
therefore we
adopt a rough threshold at
![]() to divide X-ray absorbed from
X-ray unabsorbed AGN (see also Hasinger 2008; and Fig. 11 in Mainieri
et al. 2007). The HR distribution as a function of redshift for the
538 objects in the reference sample is shown in Fig. 8 (right panel). Most BLAGN fall below the
to divide X-ray absorbed from
X-ray unabsorbed AGN (see also Hasinger 2008; and Fig. 11 in Mainieri
et al. 2007). The HR distribution as a function of redshift for the
538 objects in the reference sample is shown in Fig. 8 (right panel). Most BLAGN fall below the
![]() line, while
non-BLAGN AGN do show higher HR values on average. The poorly
populated upper-right corner of the figure, i.e. the high-HR - high-zregion, suffers from obvious selection effects due to i) the bias
against faint (distant and absorbed) magnitude targets in the optical
spectroscopy follow-up (see also Fig. 4 in Brusa et al. 2007) and ii) the K-correction effects that make high-redshift absorbed spectra to
appear softer in the X-ray bandpass (i.e. lower HR values). It is
noted that BLAGN form a sort of horizontal sequence at
line, while
non-BLAGN AGN do show higher HR values on average. The poorly
populated upper-right corner of the figure, i.e. the high-HR - high-zregion, suffers from obvious selection effects due to i) the bias
against faint (distant and absorbed) magnitude targets in the optical
spectroscopy follow-up (see also Fig. 4 in Brusa et al. 2007) and ii) the K-correction effects that make high-redshift absorbed spectra to
appear softer in the X-ray bandpass (i.e. lower HR values). It is
noted that BLAGN form a sort of horizontal sequence at
![]() ,
which is indeed the hardness ratio value expected by a canonical power
law spectrum with photon index
,
which is indeed the hardness ratio value expected by a canonical power
law spectrum with photon index
![]() and no absorption. Since
we consider all objects with
and no absorption. Since
we consider all objects with
![]() as unabsorbed sources, the
adopted cut conservatively accounts for any dispersion in the photon
index distribution of BLAGN. We measured
as unabsorbed sources, the
adopted cut conservatively accounts for any dispersion in the photon
index distribution of BLAGN. We measured
![]() for absorbed and
unabsorbed objects separately. At projected scales below
for absorbed and
unabsorbed objects separately. At projected scales below
![]() Mpc, absorbed and unabsorbed AGN are similarly
correlated, while absorbed AGN appear less correlated on larger
scales. This results in absorbed AGN formally having a lower
correlation length (
Mpc, absorbed and unabsorbed AGN are similarly
correlated, while absorbed AGN appear less correlated on larger
scales. This results in absorbed AGN formally having a lower
correlation length (
![]() vs.
vs.
![]() Mpc) and a
steeper slope (
Mpc) and a
steeper slope (
![]() vs.
vs. ![]() )
than unabsorbed
objects. The projected correlation function for unabsorbed AGN does
not change significantly if we restrict the analysis to the redshift
range 0.2-1.3, i.e. the same range as used for absorbed AGN (see
Table 1). The projected correlation function of unabsorbed and
absorbed AGN in the same
z=0.2-1.3 redshift interval are shown in
Fig. 7 (middle panel). The larger correlation length
measured for unabsorbed objects is essentially due to most objects in
the z=0.36 structure having
)
than unabsorbed
objects. The projected correlation function for unabsorbed AGN does
not change significantly if we restrict the analysis to the redshift
range 0.2-1.3, i.e. the same range as used for absorbed AGN (see
Table 1). The projected correlation function of unabsorbed and
absorbed AGN in the same
z=0.2-1.3 redshift interval are shown in
Fig. 7 (middle panel). The larger correlation length
measured for unabsorbed objects is essentially due to most objects in
the z=0.36 structure having
![]() (see Fig. 8, right
panel). Indeed, when removing this structure, the correlation length
for X-ray unabsorbed AGN decreases to
(see Fig. 8, right
panel). Indeed, when removing this structure, the correlation length
for X-ray unabsorbed AGN decreases to
![]() (see
Fig. 7, middle panel), which, given the large errorbars,
is not significantly different from that of X-ray absorbed objects. To
summarize, from our analysis we cannot claim that X-ray absorbed and
X-ray unabsorbed AGN possess different clustering properties.
(see
Fig. 7, middle panel), which, given the large errorbars,
is not significantly different from that of X-ray absorbed objects. To
summarize, from our analysis we cannot claim that X-ray absorbed and
X-ray unabsorbed AGN possess different clustering properties.
The study of AGN clustering as a function of redshift provides several pieces of information about the formation and evolution of the AGN population.
Because of the limited sample size, we simply split the XMM-COSMOS AGN
sample in two subsamples of objects below and above redshift 1. The
correlation functions of the 276 AGN at z<1 and of the 262 AGN at
z>1 are shown in Fig. 7 (lower panel). The best-fit
correlation parameters for objects at z<1 are found to be
![]() Mpc and
Mpc and
![]() ,
while for objects at
z>1 the best-fit parameters are
,
while for objects at
z>1 the best-fit parameters are
![]() Mpc and
Mpc and
![]() .
When removing the z=0.36 structure, the
correlation length of objects at z<1 decreases to
.
When removing the z=0.36 structure, the
correlation length of objects at z<1 decreases to
![]() Mpc (see Table 1). In Sect. 6.3. we discuss the
correlation lengths of the various XMM-COSMOS redshift subsamples as
compared to those of other optical and X-ray selected samples at
different redshifts.
Mpc (see Table 1). In Sect. 6.3. we discuss the
correlation lengths of the various XMM-COSMOS redshift subsamples as
compared to those of other optical and X-ray selected samples at
different redshifts.
We finally investigated the dependence of the AGN clustering
parameters on the X-ray luminosity, since this may reveal whether
objects shining with different luminosities reside in dark matter
halos with different masses, hence constraining the distribution of
the AGN Eddington ratios (see e.g. Lidz et al. 2006; Marulli et al. 2009, and the discussion in Sect. 6.3). Again, because of the
limited size of the sample, we simply divided it into two almost
equally populated subsamples, the dividing line being at
![]() erg s-1 (corresponding to
erg s-1 (corresponding to
![]() erg s-1 for a typical AGN X-ray spectrum). As
shown in Fig. 2, splitting the sample at this luminosity is
almost equal to splitting the sample at a redshift of
erg s-1 for a typical AGN X-ray spectrum). As
shown in Fig. 2, splitting the sample at this luminosity is
almost equal to splitting the sample at a redshift of ![]() .
Indeed, when computing the clustering parameters of the higher
(lower) luminosity sample, these are very similar to the z>1 (z<1)
sample, and therefore are not reported here.
.
Indeed, when computing the clustering parameters of the higher
(lower) luminosity sample, these are very similar to the z>1 (z<1)
sample, and therefore are not reported here.
The galaxy and AGN census in the ![]() Universe has been recently
enlarged by a number of surveys with different areas and
sensitivities, which allowed investigation of the spatial distribution
of different populations. The comparison between the clustering
properties of AGN and galaxies allows to first approximation to infer
which galaxy population is hosting any given AGN population, under the
simple hypothesis that AGN activity at a given redshift is randomly
sampling the host galaxy population. The comparison between
Universe has been recently
enlarged by a number of surveys with different areas and
sensitivities, which allowed investigation of the spatial distribution
of different populations. The comparison between the clustering
properties of AGN and galaxies allows to first approximation to infer
which galaxy population is hosting any given AGN population, under the
simple hypothesis that AGN activity at a given redshift is randomly
sampling the host galaxy population. The comparison between ![]() AGN samples obtained from surveys with different sensitivities may
also reveal any dependence of AGN clustering on luminosity. As far as
X-ray selected AGN are concerned, a correlation length of
r0=5.7+0.8-1.5 h-1 Mpc has been measured for
AGN samples obtained from surveys with different sensitivities may
also reveal any dependence of AGN clustering on luminosity. As far as
X-ray selected AGN are concerned, a correlation length of
r0=5.7+0.8-1.5 h-1 Mpc has been measured for ![]() 230 objects in the 0.4 deg2 CLASXS survey (Yang et al. 2006). Objects
in the CLASXS have redshift and luminosity distributions very similar
to those of our sample, and therefore they should trace the AGN
population sampled by XMM-COSMOS almost exactly. To check whether the
different techniques used for the clustering analysis may introduce
significant differences, we analyzed the CLASXS sample using the same
techniques as were used in this work finding best-fit clustering
parameters in very good agreement with the Yang et al. (2006)
values. The difference between the r0 values measured in XMM-COSMOS
and in CLASXS full samples (8.6 vs. 5.7 h-1 Mpc, respectively)
therefore appears to be inherent to the two fields considered. While a
prominent redshift spike is observed at z=0.36 in XMM-COSMOS, no such
similar structures are found in the CLASXS field. Indeed, when
removing the structure at z=0.36, the correlation length of
XMM-COSMOS AGN decreases to
230 objects in the 0.4 deg2 CLASXS survey (Yang et al. 2006). Objects
in the CLASXS have redshift and luminosity distributions very similar
to those of our sample, and therefore they should trace the AGN
population sampled by XMM-COSMOS almost exactly. To check whether the
different techniques used for the clustering analysis may introduce
significant differences, we analyzed the CLASXS sample using the same
techniques as were used in this work finding best-fit clustering
parameters in very good agreement with the Yang et al. (2006)
values. The difference between the r0 values measured in XMM-COSMOS
and in CLASXS full samples (8.6 vs. 5.7 h-1 Mpc, respectively)
therefore appears to be inherent to the two fields considered. While a
prominent redshift spike is observed at z=0.36 in XMM-COSMOS, no such
similar structures are found in the CLASXS field. Indeed, when
removing the structure at z=0.36, the correlation length of
XMM-COSMOS AGN decreases to ![]() 6.3 h-1 Mpc, in good agreement
with the value measured in CLASXS. Moreover, when restricting the
analysis to XMM-COSMOS AGN in the redshift range
z=0.4-1.6, the
correlation length (
6.3 h-1 Mpc, in good agreement
with the value measured in CLASXS. Moreover, when restricting the
analysis to XMM-COSMOS AGN in the redshift range
z=0.4-1.6, the
correlation length (![]() 5.2 h-1 Mpc) is very similar to what is
measured in CLASXS. One therefore may wonder about the frequency with
which prominent large-scale structures are sampled in X-ray surveys of
different sky areas, i.e. the effects of cosmic variance. Indeed,
based on simulated galaxy mock catalogs over 2 deg2 fields
(Kitzbichler & White 2006), some evidence exists that the COSMOS
field has some excess of structures with respect to the average.
5.2 h-1 Mpc) is very similar to what is
measured in CLASXS. One therefore may wonder about the frequency with
which prominent large-scale structures are sampled in X-ray surveys of
different sky areas, i.e. the effects of cosmic variance. Indeed,
based on simulated galaxy mock catalogs over 2 deg2 fields
(Kitzbichler & White 2006), some evidence exists that the COSMOS
field has some excess of structures with respect to the average.
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{0821_f8.ps}
\end{figure}](/articles/aa/full/2009/04/aa10821-08/Timg211.gif) |
Figure 8:
Left panel. Column density |
| Open with DEXTER | |
The correlation length of XMM-COSMOS AGN can be compared to that of
different galaxy populations at ![]() .
Coil et al. (2004) find
.
Coil et al. (2004) find
![]() Mpc for emission line galaxies in the DEEP2
survey, while Meneux et al. (2006) find
Mpc for emission line galaxies in the DEEP2
survey, while Meneux et al. (2006) find
![]() Mpc
for star-forming blue galaxies in the Vimos-VLT Deep Survey (VVDS, Le Fevre et al. 2004). The populations of red absorption-line galaxies
in the same surveys have instead larger correlation lengths:
Mpc
for star-forming blue galaxies in the Vimos-VLT Deep Survey (VVDS, Le Fevre et al. 2004). The populations of red absorption-line galaxies
in the same surveys have instead larger correlation lengths:
![]() Mpc for absorption line galaxies in the DEEP2
(Coil et al. 2004) and
Mpc for absorption line galaxies in the DEEP2
(Coil et al. 2004) and
![]() Mpc for red, early type
galaxies in the VVDS (Meneux et al. 2006). Recently, a correlation
length as large as
Mpc for red, early type
galaxies in the VVDS (Meneux et al. 2006). Recently, a correlation
length as large as
![]() Mpc has been measured for
luminous infrared galaxies (LIRG,
Mpc has been measured for
luminous infrared galaxies (LIRG,
![]() )
at
)
at
![]() ,
which are forming stars at high rates (
,
which are forming stars at high rates (
![]() yr-1; see Gilli et al. 2007b). Since at
yr-1; see Gilli et al. 2007b). Since at ![]() star formation
is closely related to galaxy mass (Noeske et al. 2007; Elbaz et al. 2007), even LIRGs, as well as
star formation
is closely related to galaxy mass (Noeske et al. 2007; Elbaz et al. 2007), even LIRGs, as well as ![]() early type galaxies, are
massive objects with stellar mass
early type galaxies, are
massive objects with stellar mass
![]() .
The fact that XMM-COSMOS AGN show similar correlation
length to these systems (see Fig. 9), suggests that, similar
to what is observed at z=0 (Kauffmann et al. 2004) and at
.
The fact that XMM-COSMOS AGN show similar correlation
length to these systems (see Fig. 9), suggests that, similar
to what is observed at z=0 (Kauffmann et al. 2004) and at ![]() (Daddi et al. 2007), at
(Daddi et al. 2007), at ![]() nuclear activity is hosted by
the more massive galaxies (see also Georgakakis et al. 2007). This is
in good agreement with the analysis by Silverman et al. (2008b), who
investigated the occurrence of nuclear activity on a sample of
nuclear activity is hosted by
the more massive galaxies (see also Georgakakis et al. 2007). This is
in good agreement with the analysis by Silverman et al. (2008b), who
investigated the occurrence of nuclear activity on a sample of ![]() 8000 galaxies selected from the zCOSMOS spectroscopic catalog,
finding that the fraction of galaxies hosting an AGN increases towards
large stellar masses at
8000 galaxies selected from the zCOSMOS spectroscopic catalog,
finding that the fraction of galaxies hosting an AGN increases towards
large stellar masses at ![]() .
In particular, most (
.
In particular, most (![]()
![]() )
AGN at
)
AGN at ![]() reside in galaxies with stellar mass
reside in galaxies with stellar mass
![]() ,
in agreement with the conclusions
from our clustering analysis.
,
in agreement with the conclusions
from our clustering analysis.
While on small scales, comparable to the dimensions of dark matter
halos, AGN and galaxy clustering are difficult to predict because of
merging and interactions that can trigger a number of physical
processes, on larger scales (e.g., >![]() Mpc), where
interactions are rare, the AGN correlation function should follow that
of the hosting dark matter halos.
Mpc), where
interactions are rare, the AGN correlation function should follow that
of the hosting dark matter halos.
An interesting consequence is that one can estimate the masses of the
typical halos hosting an AGN population by simply comparing their
clustering level. According to the standard ![]() CDM hierarchical
scenario, dark matter halos of different mass cluster differently,
with the more massive halos more clustered for any given epoch,
and it is straightforward to compute the correlation function for
halos above a given mass threshold. It is worth noting that, since less
massive halos are more abundant, the correlation function of halos
above a given mass threshold is very similar to the clustering of
halos with mass close to that threshold. Also, it is important to note
that, as far as our measurements are concerned, the best-fit clustering
parameters are obtained from datapoints mostly on large scales
(
CDM hierarchical
scenario, dark matter halos of different mass cluster differently,
with the more massive halos more clustered for any given epoch,
and it is straightforward to compute the correlation function for
halos above a given mass threshold. It is worth noting that, since less
massive halos are more abundant, the correlation function of halos
above a given mass threshold is very similar to the clustering of
halos with mass close to that threshold. Also, it is important to note
that, as far as our measurements are concerned, the best-fit clustering
parameters are obtained from datapoints mostly on large scales
(
![]() Mpc; see Fig. 6). Therefore the measured
r0 and
Mpc; see Fig. 6). Therefore the measured
r0 and ![]() values are essentially due to the clustering signal
on large scales, where the AGN correlation function follows that of
the dark matter, allowing a meaningful comparison with the clustering
expected for dark matter halos.
values are essentially due to the clustering signal
on large scales, where the AGN correlation function follows that of
the dark matter, allowing a meaningful comparison with the clustering
expected for dark matter halos.
We considered the dark matter halo catalogs available for the
Millennium simulation![]() (Springel et al. 2005). Halo catalogs are available at different time steps along
the simulation. Here we considered those at
(Springel et al. 2005). Halo catalogs are available at different time steps along
the simulation. Here we considered those at ![]() (parameter stepnum=41 in the simulation). In total there are about
(parameter stepnum=41 in the simulation). In total there are about
![]() halos with mass above
halos with mass above
![]() in a cubic
volume of 500
in a cubic
volume of 500![]() Mpc on a side. We computed the correlation
function and the space density of halos above 7 mass thresholds
ranging from log(
Mpc on a side. We computed the correlation
function and the space density of halos above 7 mass thresholds
ranging from log(
![]() to 13.2 in steps of 0.4. Here we
use as halo mass estimator the simulation parameter m_Crit200,
defined as the mass within the radius where the integrated halo
overdensity is 200 times the critical density of the simulation. The
halo correlation length was estimated by fitting with a power law
the halo correlation functions on scales above
to 13.2 in steps of 0.4. Here we
use as halo mass estimator the simulation parameter m_Crit200,
defined as the mass within the radius where the integrated halo
overdensity is 200 times the critical density of the simulation. The
halo correlation length was estimated by fitting with a power law
the halo correlation functions on scales above
![]() Mpc. The
results are shown in Fig. 9, where it is clear that
more massive halos are more clustered and less numerous.
Mpc. The
results are shown in Fig. 9, where it is clear that
more massive halos are more clustered and less numerous.
We computed the space density of AGN in XMM-COSMOS as expected from
published X-ray luminosity functions (see details in Sect. 6.5) and
compared the r0 and density values of our population with those of
other AGN and galaxy populations at ![]() and with those of dark
matter halos at
and with those of dark
matter halos at ![]() as computed above. We considered the
XMM-COSMOS AGN in the redshift range
z=0.4-1.6, i.e. around the peak
of the selection function and excluding the redshift structure at
z=0.36. The comparison is shown in Fig. 9.
as computed above. We considered the
XMM-COSMOS AGN in the redshift range
z=0.4-1.6, i.e. around the peak
of the selection function and excluding the redshift structure at
z=0.36. The comparison is shown in Fig. 9.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0821_f9.ps}
\end{figure}](/articles/aa/full/2009/04/aa10821-08/Timg231.gif) |
Figure 9:
Space density vs. correlation length for the XMM-COSMOS AGN
compared to that of other AGN and galaxy populations at |
| Open with DEXTER | |
By comparing the halo and the galaxy r0 values, XMM-COSMOS AGN
appear to be hosted by halos with masses ![]()
![]() ,
similar to absorption line galaxies and LIRGs,
which indeed show similar correlation lengths. However, while
absorption line galaxies and LIRGs appear to be more abundant than the
hosting halos (with an average of 2-4 such galaxies per halo),
XMM-COSMOS AGN appear to be a factor of
,
similar to absorption line galaxies and LIRGs,
which indeed show similar correlation lengths. However, while
absorption line galaxies and LIRGs appear to be more abundant than the
hosting halos (with an average of 2-4 such galaxies per halo),
XMM-COSMOS AGN appear to be a factor of ![]() 5 less abundant than
the hosting halos, suggesting that nuclear activity is present in
about
5 less abundant than
the hosting halos, suggesting that nuclear activity is present in
about ![]()
![]() of halos of that mass. Considerations about the
duty cycle and lifetimes of XMM-COSMOS AGN will be presented in
Sect. 6.5.
of halos of that mass. Considerations about the
duty cycle and lifetimes of XMM-COSMOS AGN will be presented in
Sect. 6.5.
To investigate the evolution of the AGN clustering properties with
redshift we combined the results from XMM-COSMOS with recent findings
from other X-ray and optical surveys. When necessary, the results were
corrected to the cosmology adopted here. The values of the correlation
lengths reported in this section were usually calculated by fixing
![]() to 1.8, therefore allowing a consistent comparison. When
different slopes were measured/adopted, we discuss the case and verify
the effects of assuming
to 1.8, therefore allowing a consistent comparison. When
different slopes were measured/adopted, we discuss the case and verify
the effects of assuming
![]() .
Only results from spatial
clustering analysis are considered.
.
Only results from spatial
clustering analysis are considered.
As for the X-ray surveys we considered the results from the ROSAT NEP
survey and from the Chandra Msec fields. In the NEP survey, Mullis et al. (2004) found a correlation length of
![]() Mpc on scales of
Mpc on scales of
![]() Mpc for
source pairs at a median redshift
Mpc for
source pairs at a median redshift
![]() .
In the CDFS and
CDFN, the correlation length measured by Gilli et al. (2005) is
.
In the CDFS and
CDFN, the correlation length measured by Gilli et al. (2005) is
![]() Mpc and
Mpc and
![]() Mpc,
respectively. Although the best-fit slopes in the Chandra Msec fields
are rather flat (
Mpc,
respectively. Although the best-fit slopes in the Chandra Msec fields
are rather flat (
![]() ), the best-fit correlation lengths
increase by only
), the best-fit correlation lengths
increase by only ![]()
![]() if the slope is fixed to 1.8 (Gilli et al. 2005).
if the slope is fixed to 1.8 (Gilli et al. 2005).
As for optically selected AGN, we considered the results of Croom et al. (2005) based on more than 20 000 objects in the final
catalog of the 2dF QSO Redshift Survey (2QZ), where the QSO
correlation length is found to increase significantly from ![]() to
to ![]() ,
and very flat slopes (
,
and very flat slopes (
![]() )
have been
measured. As discussed by Croom et al. (2005), these flat
slopes stem from redshift-space distortions that are relevant when the
correlation function is measured down to small scales in redshift
rather than in real space. The real-space clustering for the total 2QZ sample has instead been measured by Da Angela et al. (2005)
via the projected correlation function. On the same scales as
considered by Croom et al. (2005) and when approximating
)
have been
measured. As discussed by Croom et al. (2005), these flat
slopes stem from redshift-space distortions that are relevant when the
correlation function is measured down to small scales in redshift
rather than in real space. The real-space clustering for the total 2QZ sample has instead been measured by Da Angela et al. (2005)
via the projected correlation function. On the same scales as
considered by Croom et al. (2005) and when approximating
![]() by a single power law, they found that, while the slope of
the total 2QZ sample steepens significantly from
by a single power law, they found that, while the slope of
the total 2QZ sample steepens significantly from
![]() to
to
![]() ,
the correlation length only marginally
decreases by 10% (from
,
the correlation length only marginally
decreases by 10% (from
![]() Mpc to
Mpc to
![]() Mpc). In the following we therefore simply
consider the values as measured by Croom et al. (2005) for
the 2QZ correlation lengths in different redshift bins. These results
are consistent with those obtained by Porciani et al. (2004) using 2dF
QSOs in a narrower redshift range. In the local Universe (
Mpc). In the following we therefore simply
consider the values as measured by Croom et al. (2005) for
the 2QZ correlation lengths in different redshift bins. These results
are consistent with those obtained by Porciani et al. (2004) using 2dF
QSOs in a narrower redshift range. In the local Universe (
![]() ),
the clustering of bright optical QSOs (B<15 mag) has been recently
determined by Grazian et al. (2004) by means of the
Asiago-ESO/RASS QSO survey (AERQS). These authors measured
),
the clustering of bright optical QSOs (B<15 mag) has been recently
determined by Grazian et al. (2004) by means of the
Asiago-ESO/RASS QSO survey (AERQS). These authors measured
![]() Mpc at a median redshift of
Mpc at a median redshift of ![]() on comoving
scales
on comoving
scales
![]() Mpc by fixing the correlation slope to
Mpc by fixing the correlation slope to
![]() .
Given the above considerations for the Chandra Msec
fields and the 2QZ and given the rather large uncertainties we have to
deal with, we consider the value quoted by Grazian et al. (2004) as if
obtained by fixing
.
Given the above considerations for the Chandra Msec
fields and the 2QZ and given the rather large uncertainties we have to
deal with, we consider the value quoted by Grazian et al. (2004) as if
obtained by fixing ![]() to 1.8. All the measurements discussed above
are shown in Fig. 10.
to 1.8. All the measurements discussed above
are shown in Fig. 10.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0821_f10.ps}
\end{figure}](/articles/aa/full/2009/04/aa10821-08/Timg248.gif) |
Figure 10:
Correlation length vs. redshift for XMM-COSMOS AGN compared to
that of other AGN samples. The big blue filled circle refers to the
z=0.4-1.6 XMM-COSMOS sample. Big red filled circles refer to the z<1and z>1 samples. The big open circle refers to the z<1 sample when
excluding the z=0.36 spike. Solid and dotted errorbars correspond to
Poissonian and bootstrap uncertainties, respectively. The filled
square at |
| Open with DEXTER | |
Unfortunately, it is not possible to perform a completely unbiased comparison between the various samples because different redshifts generally sample different luminosities, and AGN clustering may be a function of AGN luminosity if the latter correlates with the mass of the hosting dark halo (e.g. Kauffmann & Haehnelt 2002).
In Fig. 10, sources at z<0.3 and z>2 appear to be the most
clustered ones, and these also correspond to the most luminous AGN. At
z<0.3 the median 0.5-10 keV luminosity of the AGN in the AERQS and
NEP samples is about
![]() (see Mullis et al. 2004;
and Gilli et al. 2005). At z>2 the median absolute B-band
luminosity of the 2QZ QSOs corresponds to a median 0.5-10 keV
luminosity of
(see Mullis et al. 2004;
and Gilli et al. 2005). At z>2 the median absolute B-band
luminosity of the 2QZ QSOs corresponds to a median 0.5-10 keV
luminosity of
![]() (assuming a standard QSO SED, e.g. Elvis
et al. 2009). The less clustered sources are found at
(assuming a standard QSO SED, e.g. Elvis
et al. 2009). The less clustered sources are found at ![]() ,
but these have lower luminosities (
,
but these have lower luminosities (
![]() ). In general, a
clear dependence of clustering amplitude on AGN luminosity has not
been observed yet. On the contrary, the available evidence, if any,
points towards a similar clustering for sources at the same redshift
but with different luminosities. Croom et al. (2005) and
Porciani & Norberg (2006) could not find any significant evidence of
luminosity dependent clustering in the 2QZ. From a cross-correlation
analysis between galaxies and AGN, Adelberger & Steidel (2005)
claim that AGN at
). In general, a
clear dependence of clustering amplitude on AGN luminosity has not
been observed yet. On the contrary, the available evidence, if any,
points towards a similar clustering for sources at the same redshift
but with different luminosities. Croom et al. (2005) and
Porciani & Norberg (2006) could not find any significant evidence of
luminosity dependent clustering in the 2QZ. From a cross-correlation
analysis between galaxies and AGN, Adelberger & Steidel (2005)
claim that AGN at ![]() cluster similarly within a 10 mag
luminosity range. From a theoretical point of view, one would expect
little clustering dependence on the observed AGN luminosity if this is
not directly related to the host halo mass; i.e., if, at any given
redshift, objects that reside in halos within a narrow mass range have
very different luminosities (e.g. Lidz et al. 2006). For instance, even
assuming a dependence of black hole (and host galaxy) mass on the
hosting halo mass, a wide spread in the distribution in the Eddington
ratios would make BH of similar masses radiate at very different
luminosities. Indeed, although the average Eddington ratio of SDSS
QSOs has been shown to increase towards high luminosities, the spread
in the distribution is wide (McLure & Dunlop 2004). Moreover, it has
been recently suggested (Gavignaud et al. 2008) that the dispersion in
the black hole mass-luminosity increases even more for lower AGN
luminosities. Finally, in the local Universe, Constantin & Vogeley
(2006) find that low-luminosity LINERs are more clustered than higher
luminosity Seyfert galaxies, showing that the relation between AGN
luminosity and clustering may even be reversed for low-luminosity AGN
with respect to the expectations based on a monotonically increasing
relation between luminosity and black hole mass. Large statistical
samples, beyond the reach of the data presented in this work, are
needed to firmly establish any dependence of AGN clustering on
luminosity (see e.g. Porciani & Norberg 2006).
cluster similarly within a 10 mag
luminosity range. From a theoretical point of view, one would expect
little clustering dependence on the observed AGN luminosity if this is
not directly related to the host halo mass; i.e., if, at any given
redshift, objects that reside in halos within a narrow mass range have
very different luminosities (e.g. Lidz et al. 2006). For instance, even
assuming a dependence of black hole (and host galaxy) mass on the
hosting halo mass, a wide spread in the distribution in the Eddington
ratios would make BH of similar masses radiate at very different
luminosities. Indeed, although the average Eddington ratio of SDSS
QSOs has been shown to increase towards high luminosities, the spread
in the distribution is wide (McLure & Dunlop 2004). Moreover, it has
been recently suggested (Gavignaud et al. 2008) that the dispersion in
the black hole mass-luminosity increases even more for lower AGN
luminosities. Finally, in the local Universe, Constantin & Vogeley
(2006) find that low-luminosity LINERs are more clustered than higher
luminosity Seyfert galaxies, showing that the relation between AGN
luminosity and clustering may even be reversed for low-luminosity AGN
with respect to the expectations based on a monotonically increasing
relation between luminosity and black hole mass. Large statistical
samples, beyond the reach of the data presented in this work, are
needed to firmly establish any dependence of AGN clustering on
luminosity (see e.g. Porciani & Norberg 2006).
Overall, when removing the redshift structure at z=0.36, the clustering of XMM-COSMOS AGN appears in good agreement with what is measured for optical and X-ray selected AGN at different redshifts. A larger correlation length is instead found for objects at z<1 if the redshift structure is not removed.
To interpret our clustering measurements at different redshifts, we
considered the halo catalogs in the Millennium simulation and computed
their correlation function above different halo mass thresholds and at
different redshifts. We essentially repeated the computation presented
in Sect. 6.2 for halos at
z=0.1, 0.5, 1.0, 1.5, 2.0, and 3.0. The r0vs. redshift curves for halos above different mass thresholds are shown
in Fig. 10. Both our ![]() and z>1 AGN samples seem to be
hosted by halos with mass above
and z>1 AGN samples seem to be
hosted by halos with mass above
![]() .
For
XMM-COSMOS AGN at z<1 the minimum mass of the host halos varies from 12.4 to 12.8 depending on whether the z=0.36 structure is excluded or
included from the computation of r0.
.
For
XMM-COSMOS AGN at z<1 the minimum mass of the host halos varies from 12.4 to 12.8 depending on whether the z=0.36 structure is excluded or
included from the computation of r0.
As shown in the previous sections, under simple assumptions, it is
possible to use the spatial clustering of an extragalactic source
population measured at a given epoch to estimate the typical dark
matter halos in which these objects reside. Furthermore, it is also
possible to estimate their past and future history by following the
halo evolution in the cosmological density field. A useful quantity
for such analyses is the bias factor, defined as
![]() ,
where
,
where
![]() and
and
![]() are the correlation function of the considered AGN or
galaxy population and that of dark matter, respectively. In general
the bias parameter can be a function of scale r, redshift z, and
object mass M. For simplicity we adopt the following definition
here:
are the correlation function of the considered AGN or
galaxy population and that of dark matter, respectively. In general
the bias parameter can be a function of scale r, redshift z, and
object mass M. For simplicity we adopt the following definition
here:
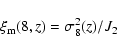 |
(12) |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0821_f11.ps}
\end{figure}](/articles/aa/full/2009/04/aa10821-08/Timg269.gif) |
Figure 11: Expected redshift evolution of the bias and correlation length of different XMM-COSMOS AGN samples according to a conserving scenario. The evolution curves are normalized to the observed datapoints. Blue filled circle: z=0.4-1.6 sample. Red circles: z<1 and z>1 samples. The open circle shows the result for the z<1 sample when the z=0.36 structure is excluded. Solid and dotted errorbars correspond to Poissonian and bootstrap uncertainties, respectively. |
| Open with DEXTER | |
From an observational point of view, the fraction of galaxies in
mergers appears to be a very debated issue. Recent works suggest that
close galaxy pairs (merger candidates) are a strong function of
redshift, evolving as
(1+z)3-4 (Kartaltepe et al. 2007; Kampzyck
et al. 2007). By extrapolating the current estimates, at ![]() about 50% of luminous galaxies are expected to be found in close
pairs/mergers. However, at
about 50% of luminous galaxies are expected to be found in close
pairs/mergers. However, at ![]() the fraction of galaxies in close
pairs is still
the fraction of galaxies in close
pairs is still ![]()
![]() and decreases to
and decreases to ![]()
![]() at
at ![]() .
In the following we will consider the non merging conserving
model as a fairly adequate representation of the bias evolution of
.
In the following we will consider the non merging conserving
model as a fairly adequate representation of the bias evolution of
![]() XMM-COSMOS AGN towards lower redshifts; i.e., it will be used
to estimate the likely descendants of XMM-COSMOS AGN. On the contrary,
since merging is expected to be significant towards higher redshift, we
will not try to estimate their high-z progenitors.
XMM-COSMOS AGN towards lower redshifts; i.e., it will be used
to estimate the likely descendants of XMM-COSMOS AGN. On the contrary,
since merging is expected to be significant towards higher redshift, we
will not try to estimate their high-z progenitors.
In the galaxy conserving model, the bias evolution can be
approximated by
| b(z)=1+[b(0)-1]/D(z) | (13) |
In Fig. 11 we show the evolution of b(z) and r0(z) for
various XMM-COSMOS AGN samples, including the z=0.4-1.6 sample, the
sample at z>1 and the sample at z<1 with or without the structure
at z=0.36. By z=0 the correlation length of XMM-COSMOS AGN should
evolve to
![]() Mpc, which is typical of passive,
early type galaxies in the local Universe (Colless et al. 2001; Zehavi
et al. 2004). The correlation slope of the local early type population
Mpc, which is typical of passive,
early type galaxies in the local Universe (Colless et al. 2001; Zehavi
et al. 2004). The correlation slope of the local early type population
![]() also appears consistent with that of XMM-COSMOS
AGN at
also appears consistent with that of XMM-COSMOS
AGN at ![]() .
In principle, the evolution curves shown in
Fig. 11 can also be used to predict which r0 value a given
XMM-COSMOS subsample should have as a function of redshift, allowing
a proper comparison between measurements obtained at different
redshifts. Indeed, the correlation length of AGN in the z>1 sample
(median
.
In principle, the evolution curves shown in
Fig. 11 can also be used to predict which r0 value a given
XMM-COSMOS subsample should have as a function of redshift, allowing
a proper comparison between measurements obtained at different
redshifts. Indeed, the correlation length of AGN in the z>1 sample
(median ![]() )
is expected to evolve to
)
is expected to evolve to
![]() Mpc
by
Mpc
by ![]() ,
i.e. the median redshift of the z<1 sample, whose
correlation length has been measured as varying between 8.0 and 5.2 h-1 Mpc, depending on the inclusion of the z=0.36structure. Given this uncertainty and the large errorbars in
Fig. 11, it is still difficult to claim that objects at
redshift greater or smaller than 1 are sampling different environments.
,
i.e. the median redshift of the z<1 sample, whose
correlation length has been measured as varying between 8.0 and 5.2 h-1 Mpc, depending on the inclusion of the z=0.36structure. Given this uncertainty and the large errorbars in
Fig. 11, it is still difficult to claim that objects at
redshift greater or smaller than 1 are sampling different environments.
Under simple assumptions it is possible to put limits on the AGN
lifetime at any given redshift. Following Martini & Weinberg
(2001), we assumed that the AGN in our sample reside within
halos above a given mass threshold and that each halo hosts at most
one active AGN at a time. The AGN lifetime tQ can then be estimated
with the following relation:
The definition of halo lifetime is somewhat ambiguous since halos are
continuously accreting matter. Martini & Weinberg (2001)
defined
![]() as the median time interval for a halo of mass M to
be incorporated into a halo of mass 2M and used the extended
Press-Schechter formalism to calculate it. To a first approximation
as the median time interval for a halo of mass M to
be incorporated into a halo of mass 2M and used the extended
Press-Schechter formalism to calculate it. To a first approximation
![]() ,
where tU(z) is the Hubble time at redshift
z. With these approximations Eq. (14) can be rewritten as
,
where tU(z) is the Hubble time at redshift
z. With these approximations Eq. (14) can be rewritten as
Since
![]() is known from the comparison between the halo and the
AGN correlation length, it is straightforward to estimate
is known from the comparison between the halo and the
AGN correlation length, it is straightforward to estimate
![]() from the number of halos with
from the number of halos with
![]() within the Millennium
simulation box. For halos with
within the Millennium
simulation box. For halos with
![]() ,
where XMM-COSMOS AGN at
,
where XMM-COSMOS AGN at ![]() reside, the space
density is
reside, the space
density is
![]() Mpc-3 (see
Fig. 9). For the cosmology adopted here the Hubble time at
z=1 is
Mpc-3 (see
Fig. 9). For the cosmology adopted here the Hubble time at
z=1 is ![]() 6.3 Gyr.
6.3 Gyr.
The comoving space density of XMM-COSMOS AGN has been estimated by
considering literature X-ray luminosity function of AGN selected in
the 2-10 keV band, which should therefore include unobscured, as well
as moderately obscured, objects as the objects populating our
sample. Once accounting for band effects![]() , the median luminosity of our
, the median luminosity of our
![]() sample (
sample (
![]() in the 0.5-10 keV band; see Table 1)
translates into a 2-10 keV luminosity of
in the 0.5-10 keV band; see Table 1)
translates into a 2-10 keV luminosity of
![]() .
At these
luminosities,
.
At these
luminosities, ![]() AGN in the La Franca et al. (2005) XLF have a
space density of
AGN in the La Franca et al. (2005) XLF have a
space density of ![]()
![]() Mpc-3. A similar
value for the AGN density is obtained when using the XLF by Ueda et al. (2003).
Therefore, by considering an AGN density of
Mpc-3. A similar
value for the AGN density is obtained when using the XLF by Ueda et al. (2003).
Therefore, by considering an AGN density of ![]()
![]() Mpc-3 (obtained by rescaling the La Franca et al. space density
by the fraction of objects with
Mpc-3 (obtained by rescaling the La Franca et al. space density
by the fraction of objects with
![]() ,
as is the case for our
selection), a duty cycle
,
as is the case for our
selection), a duty cycle
![]() of 0.18 is obtained, which
translates into an AGN lifetime of
of 0.18 is obtained, which
translates into an AGN lifetime of ![]() 1.1 Gyr.
1.1 Gyr.
This estimated lifetime is more than one order of magnitude longer than
that estimated by Porciani et al. (2004) for bright optical QSOs at
![]() in the 2QZ survey. The difference in the measured lifetime
is essentially due to the difference between the space density of
XMM-COSMOS AGN and 2QZ QSOs at
in the 2QZ survey. The difference in the measured lifetime
is essentially due to the difference between the space density of
XMM-COSMOS AGN and 2QZ QSOs at
![]() Mpc-3, see Table 1 in Porciani et al. 2004). Such a difference is, on the other hand, expected given the
relatively bright limiting magnitude (
Mpc-3, see Table 1 in Porciani et al. 2004). Such a difference is, on the other hand, expected given the
relatively bright limiting magnitude (
![]() )
of the 2QZ sample that, in addition, does not include obscured AGN. The
estimated lifetime for XMM-COSMOS AGN is significantly shorter than
the
)
of the 2QZ sample that, in addition, does not include obscured AGN. The
estimated lifetime for XMM-COSMOS AGN is significantly shorter than
the ![]() 8 Gyr time span between z=1 and z=0. This, in
combination with the estimate that XMM-COSMOS AGN will cluster with
r0=8 h-1 Mpc at z=0, depicts a consistent scenario in which XMM-COSMOS AGN
will switch off by z=0, leaving relic (dormant) supermassive black
holes in local elliptical galaxies.
8 Gyr time span between z=1 and z=0. This, in
combination with the estimate that XMM-COSMOS AGN will cluster with
r0=8 h-1 Mpc at z=0, depicts a consistent scenario in which XMM-COSMOS AGN
will switch off by z=0, leaving relic (dormant) supermassive black
holes in local elliptical galaxies.
We have studied the clustering properties of 538 moderately luminous
AGN at z=0.2-3 in the 2 deg2 COSMOS field, selected in the X-rays
and spectroscopically identified to
![]() .
Our main results can
be summarized as follows:
.
Our main results can
be summarized as follows:
Acknowledgements
This work is based on observations obtained with XMM-Newton, an ESA Science Mission with instruments and contributions directly funded by ESA Member States and the USA (NASA). We gratefully acknowledge the contribution of the entire COSMOS collaboration (http://www.astro.caltech.edu/~cosmos). In Italy, the XMM-COSMOS projects is supported by ASI-INAF and PRIN/MIUR under grants I/023/05/00 and 2006-02-5203. The zCOSMOS ESO Large Program Number 175.A-0839 is acknowledged. R.G. thanks Carlo Nipoti, Federico Marulli, Enzo Branchini, and Lauro Moscardini for stimulating discussions. The referee is acknowledged for providing useful comments. The Millennium Simulation databases used in this paper and the web application providing online access to them were constructed as part of the activities of the German Astrophysical Virtual Observatory.