1 - INAF - Osservatorio Astrofisico di Arcetri, 50125 Firenze, Italy
2 - Dipartimento di Fisica, Università della Calabria, 87036 Rende (CS), Italy
3 - National Solar Observatory, PO Box 62, Sunspot NM, USA

Abstract
Context. The exact nature of the quiet solar chromosphere and especially its temporal variation, are still subjects of intense debate. One of the contentious issues is the possible role of the magnetic field in structuring the quieter solar regions.
Aims. We characterize the dynamics of the quiet inter-network chromosphere by studying the occurrence of acoustic shocks and their relation with the concomitant photospheric structure and dynamics, including small scale magnetic structures.
Methods. We analyze a comprehensive data set that includes high-resolution chromospheric (Ca II 854.2 nm) and photospheric (Fe I 709.0 nm) spectra obtained with the IBIS imaging spectrometer in two quiet-Sun regions. This is complemented by high-resolution sequences of MDI magnetograms of the same targets. From the chromospheric spectra we identify the spatio-temporal occurrence of the acoustic shocks. We compare it with the photospheric dynamics by means of both Fourier and wavelet analysis and study the influence of magnetic structures on the phenomenon.
Results. Mid-chromospheric shocks occur within the general chromospheric dynamics pattern of acoustic waves propagating from the photosphere. In particular, they appear as a response to underlying powerful photospheric motions at periodicities nearing the acoustic cut-off, consistent with 1-D hydrodynamical modeling. However, their spatial distribution within the supergranular cells is highly dependent on the local magnetic topology, both at the network and internetwork scale. We find that large portions of the internetwork regions undergo very few shocks, since they are ``shadowed'' by the horizontal component of the magnetic field. The latter is betrayed by the presence of chromospheric fibrils, observed in the core of the Ca II line as slanted structures with distinct dynamical properties. The shadow mechanism also appears to operate on the very small scales of inter-network magnetic elements, and provides for a very pervasive influence of the magnetic field even in the quietest region analyzed.
Conclusions. The magnetic field might play a larger role in structuring the quiet solar chromosphere than normally assumed. The presence of fibrils highlights a clear disconnection between the photospheric dynamics and the response of the geometrically overlaying chromosphere. As these results hold for a mid-chromospheric indicator such as the Ca II 854.2 line, it is expected that diagnostics formed in higher layers, such as UV lines and continua, will be affected to a greater extent by the presence of magnetic fields, even in quiet regions. This is relevant for the chromospheric models that make use of such diagnostics.

Observations have long shown that the outer solar atmosphere is not in radiative equilibrium, with the net radiative loss of the quiet chromosphere estimated at between $\approx$ 4 kWm^-2 (Vernazza et al. 1981) and 14 kWm^-2 (Anderson & Athay 1989). The identification of the source and exact mechanism of deposition of the energy needed to maintain a stationary situation is often referred to as the problem of chromospheric heating. It has been a vexing problem in solar physics for decades.

In stellar atmospheres, strong density stratification makes it relatively easy for propagating acoustic waves, excited by the turbulent convection, to develop into shocks. Indeed this mechanism was proposed early on as a plausible means to provide the necessary energy input to the solar chromosphere (Schwarzschild 1948; Biermann 1948). Much theoretical and numerical work has since been conducted to assess the viability of the acoustic heating as the basic heating mechanism for nonmagnetic chromospheres of slowly rotating stars (e.g. Ulmschneider & Musielak 2003; Narain & Ulmschneider 1996).

A landmark work on this topic was the 1-D radiative-hydrodynamical modeling of Carlsson & Stein (1995,1997,2002), who derived the chromospheric response to acoustic waves in the absence of magnetic fields. Using an observed photospheric piston, they could reproduce the temporal evolution of the chromospheric Ca II H spectral line over long intervals with remarkable accuracy. In particular, they reproduced the occurrence of the H_2V (K_2V) grains observed in the spectral profile of the resonance H and K lines of Ca II. The grains consist of quasi-periodic brightenings in the violet wings of the lines, with a $\sim$ 150-200 s repetition rate, and they are associated with strong redshifts of the line core position (see Rutten & Uitenbroek 1991, hereafter RU91, and Sect. 3). Carlsson & Stein (1997), hereinafter CS97, show how the grains are due to weak acoustic shocks developing at heights of about 1 Mm in the non magnetic atmosphere, driven primarily by photospheric acoustic waves with periodicities close to the cutoff value of $\sim$ 5.5 mHz. A controversial byproduct of their model is that the intermittent acoustic shocks greatly enhance both the emissivity and the temperature but only locally, without causing a net outward increase in the average chromospheric temperature (Carlsson & Stein 1995). If the CS97 shocks correctly represent the acoustic heating mechanism, the non-magnetic chromosphere would be essentially cold. This is contrary to the common view, derived from semi-empirical static models, of a chromosphere characterized everywhere by a steady temperature rise (Vernazza et al. 1981; Fontenla et al. 2007; Avrett & Loeser 2008). The failure of the CS97 model to reproduce spatially and temporally resolved quiet Sun UV observations obtained with SUMER in chromospheric lines (Carlsson et al. 1997) has further sharpened the controversy.

$\begin{figure} \par\includegraphics[width=16cm,height=7.6cm]{0694f1.eps} \end{figure}$

Figure 1: Top row: data set 1; bottom row: data set 2. The images refer to data acquired around the middle of the observing sequences. Axes are given in arcsec. Panels a), e): broadband continuum at 710 nm. The image in data set 2 has been speckle reconstructed with the technique of Wöger (2006). Panels b), f): co-temporal HR MDI maps, saturated at $\pm$ 500 G. Data set 2 attains to an enhanced, bi-polar network region. Panels c), g): intensity in the red wing of the Ca II 854.2 nm at about 0.1 nm from line core. Bright points clearly correspond to small-scale magnetic features. Panels d), h): line core intensity of Ca II 854.2 nm. Note the large extension of fibrils originating in the magnetic elements.

Open with DEXTER

From the observational point of view, gaining further insight into this issue requires new data that can simultaneously achieve high spatial and temporal resolution, and spectral information with different diagnostics, over extended fields of view (FOV). Most of the debate on this point has been based on (older) spectrographic observations obtained in the Ca II H and K lines, and on UV spectral data obtained by Skylab or, more recently, by SUMER onboard SOHO (Wilhelm et al. 1995). Spectrographic data suffer, however, from a limited FOV in fixed slit observations or from a low cadence when scanning an extended region. In the UV, the limited flux and instrumental response further lower the achievable spatial and temporal resolution, an important limitation if the dynamic picture just described for the chromosphere is the correct one (Wedemeyer-Böhm & Wöger 2008). Historically, imaging with broad-band filters has been used widely, both in the UV and visible range. Such data, however, often mix signals arising from vastly different regions of the solar atmosphere, as well as missing signatures of strong velocities that might shift the lines outside the filter band. For a general review of the issues of chromospheric observations, we refer to Rutten (2007), only adding here that the POLIS spectrograph (Beck et al. 2005) has recently become operational, producing new high quality Ca II H spectra that have been employed in studies of the quiet chromosphere (Rezaei et al. 2008,2007; Beck et al. 2008).

In this paper we use an entirely different type of instrument, the Interferometric BIdimensional Spectrometer (IBIS, Cavallini 2006), to derive novel results about the dynamics of the quiet solar chromosphere and in particular the presence (or absence) of acoustic shocks. IBIS is an imaging spectrometer installed at the Dunn Solar Telescope (DST) of the US National Solar Observatory, and it provides observations that combine high spatial and temporal resolution over an extended two-dimensional FOV, with the full spectral information in both photospheric and chromospheric lines. In this sense, it is an ideal instrument for overcoming many of the observational shortcomings outlined above. We analyze the behavior of the chromospheric Ca II 854.2 nm line that, as shown in Cauzzi et al. (2008) (hereafter Paper I), is one of the most promising diagnostics for high-resolution chromospheric studies. Equally important, the availability of spectral information over a 2-D FOV is crucial for understanding the very dynamic and non-local chromosphere. We further combine the Ca II 854.2 observations with simultaneous and cospatial photospheric data also obtained with IBIS and magnetic data from MDI (Scherrer et al. 1995). This allows us to address the relationships between the chromospheric and photospheric dynamics and the influence of the magnetic field. We analyze two completely analogous data sets obtained on separate days, both times in quiet regions near disk center, and in so doing uncover the fundamental role played by the local magnetic topology.

The paper is organized as follows. In Sect. 2 we describe the observations. Sections 3 and 4 provide evidence that mid-chromospheric acoustic shocks are clearly observed in the Ca II 854.2 nm line, and outline the methods we use to identify them. In Sect. 5 we report on the derived shock properties, both in relation to earlier findings obtained primarily with Ca II K observations, and as new results regarding their spatial distribution. Sections 6 and 7 address the occurrence of the shocks in relation to the magnetic field structure and evolution, and the photospheric dynamics. Finally, in Sects. 8 and 9 we discuss our findings and provide conclusions

2 Observations

The IBIS design and general issues on data reduction have been described in earlier papers (Cavallini 2006; Janssen & Cauzzi 2006; Reardon & Cavallini 2008), so we mention here only the characteristics most relevant to the present work. IBIS is based on two air spaced Fabry Perot Interferometers in a classical mount, and it acquires quasi-monochromatic images in the range 560-860 nm ( ${\it FWHM} = 2$ -4.5 pm). Rapid sequential tuning to different wavelengths allows the spectral sampling of a number of selected lines, providing spectral information over a circular, 80'' diameter FOV. Typically, a spectral line is sampled in 10-30 spectral points, within a total acquisition time of 3-10 s. Data can be obtained at the full resolution of 0.083''/ pixel, or binned to increase the photon flux and reduce the CCD readout time. Coupled with the high-order adaptive optics system of on the DST (Rimmele 2004), IBIS images often attain spatial resolution close to the diffraction limit of the 76-cm telescope.

2.1 The IBIS data sets

The data utilized in this work were acquired in two quiet areas in close proximity to disk center on 2004 May 31 (in the following data set 1) and 2004 June 02 (data set 2). On both days the same acquisition scheme was adopted, sequentially sampling the photospheric Fe I line at 709.0 nm and the chromospheric Ca II 854.2 nm line. The time necessary to scan the lines was, respectively, 4 s and 7 s, while the overall cadence for the full sequence was 19 s (the Fe II 722.4 nm line was also included in the sequence, but not used in this paper). The spatial scale was set to 0.166''/pixel ( $\approx$ 120 km at the solar surface). The photospheric data for set 2 were utilized in Janssen & Cauzzi (2006), while both photospheric and chromospheric data, again for set 2, were analyzed in Vecchio et al. (2007), hereafter V07. The Ca II data for both days has been further described in Paper I.

We analyzed two stretches of 55 mn of continuous observations (175 time steps) obtained in good to excellent seeing conditions on each day. Data set 2 had a better seeing than data set 1. We examined the full spectral profiles, as well as studying parameters extracted from them. In particular, for each spatial position in the FOV we extract by means of spline interpolation both the intensity and the position of the minima of the spectral line profiles. The latter are interpreted in terms of Doppler shift, with the zero position for the velocity scale defined as the spatio-temporal average of the whole dataset over a quiet portion of the FOV (see also discussion in Janssen & Cauzzi 2006, and Paper I).

Figure 1 gives a synopsis of the data around the middle of the observational sequence for both days. The observed FOV is shown at different wavelengths, together with the simultaneous high-resolution (HR) MDI magnetograms. The leftmost column shows the broadband continuum at 710 nm, indicating on both days a mostly quiet scene, with slightly lower contrast in the magnetic regions that delineate the supergranular network. At higher magnification these can be resolved as tiny bright points embedded within the intergranular lanes (especially in the speckle-reconstructed image of data set 2). The second column displays the high-resolution MDI data obtained simultaneously to the IBIS data sets. The network elements are discernible in the two FOVs, but highlight a very different magnetic environment, with a weaker, unipolar network in data set 1 and an enhanced bipolar network for data set 2. The third column shows IBIS images acquired at about 0.1 nm from the core of the Ca II 854.2 nm line. Together with the reversed granulation pattern, these monochromatic images display bright elements with a one-to-one correspondence to magnetic elements (Leenaarts et al. 2006, Paper I). Finally, the fourth column shows the images in the core of the Ca II line, which outline a ``segregated'' picture, with part of the FOV occupied by fibrils originating from even the smallest magnetic elements, and part of it, farthest from the magnetic network, showing an abundance of small bright points surrounded by much darker regions (compare the temporal evolution of this region from Movie 2 in Paper I).

2.2 The magnetic environment

High-resolution MDI magnetograms are available for almost the whole duration of the IBIS observations on both days. They have a spatial scale of 0.6''/pixel, and a cadence of 1 mn. The MDI maps outline a very different magnetic configuration of the two regions (Fig. 1 panels b, f). Coronal images confirm this difference: while at photospheric level both regions could be classified as quiet, EIT Fe XII 19.5 nm images acquired around the time of the IBIS observations clarify that the May 31 region is localized at the edge of an equatorial coronal hole, while the June 2 region corresponds to a decaying coronal bright point (Fig. 2). In neither case did we observe significant variations of the magnetic configuration over the duration of the IBIS observations.

The differences in magnetic topology are already reflected at the chromospheric level, in the morphology shown by the Ca II line core intensities. In set 2 we observe a large number of elongated fibrilar structures, with a complex spatio-temporal evolution and connecting, in many cases, regions of opposite polarity. In contrast, the number and length of fibrils in data set 1 are much lower, suggesting either short loops that close near the network elements or more vertical structures that follow magnetic field lines extending into interplanetary space. To qualitatively assess the 3-D magnetic field configuration, we computed a potential field extrapolation starting from the MDI longitudinal field, assumed as the vertical component of the vector field at a height of about 200 km. The area utilized for the extrapolation is about six times larger than the IBIS FOV. In Fig. 3 we show the resulting magnetic fields, extrapolated up to a height of 2.5 Mm. Representative closed lines within this extended region are drawn in thin red, while field lines that open to more distant regions or the interplanetary space are drawn in thick green. The closed field lines closely resemble the chromospheric morphology: in data set 2 the volume is dominated by field lines connecting opposite polarity network points, spanning large fraction of the FOV, and reaching heights up to about 2 Mm. The quieter data set 1, instead, is characterized by short, and low-lying, closed field lines fanning out from the network points and reaching to nearby internetwork weak magnetic concentrations. The fibrillar structures so prominent in the Ca II core images appear a reliable proxy for the presence of a magnetic canopy (Paper I, V07).

$\begin{figure} \hbox{\hglue 0.4cm \includegraphics[width=4cm,height=4cm]{0694f2a... ...glue -0.05cm \includegraphics[width=4cm,height=4cm]{0694f2b.eps} }\end{figure}$	Figure 2: Full-disk EIT images acquired in Fe XII 19.5 nm on 2004 May 31 ( left) and 2004 June 02 ( right). The cross-hairs indicate the center of the IBIS FOV for each day. The IBIS FOV covers roughly the small coronal bright point intersected by the cross-hair on the right panel.
Open with DEXTER

$\begin{figure} \vbox{ \hbox{\hglue 0.5cm \includegraphics[width=8cm,height=6cm]{... ...lue -3.2cm \includegraphics[width=12cm,height=5cm]{0694f3d.eps} }}\end{figure}$

Figure 3: Representative field lines from the MDI-extrapolated potential magnetic field. Left panels: data set 1. Right panels: data set 2. The thick green lines trace the open field lines, the thin red lines draw field lines closing within the considered area. The white dashed circles delineate the IBIS FOV for each data set. The vertical scale in the bottom panels is the height given in Mm.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=15cm,height=8.7cm,clip]{aa10694f4.eps} \end{figure}$

Figure 4: Ca II 854.2 nm spectral profiles vs. time (given in s), for four positions within the internetwork. Panels a), b) refer to data set 1; panels c), d) to data set 2. The time axis spans the whole duration of the observations. Note the distinctive saw-tooth appearance. The thin white line in panel a) indicates the evolution with time of the line core Doppler shift. Maximum velocities reach 6-7 km s^-1 from average position.

Open with DEXTER

3 Evidence of acoustic shocks in the internetwork

As for the Ca II H and K lines, the formation of Ca II 854.2 nm spans a wide range of atmospheric heights (Paper I). From the far wings in toward the core, the line gradually samples from the low to the high photosphere, while the line core itself is formed in the lower chromosphere. However, as shown by Skartlien et al. (1994) and more recently by Pietarila et al. (2006), the presence of hydrodynamic shocks in the non-magnetic chromosphere determines a wide range of heights for the formation of the line core, spanning from as low as 700 km up to 1300 km. The shocks induce rapid variations in the thermodynamics of the affected atmosphere, resulting in asymmetric Ca II 854.2 spectral profiles (cf. Figs. 3 and 7 of Pietarila et al. 2006).

Figure 4 displays the observed temporal evolution of the IBIS Ca II 854.2 nm spectral profiles for four representative pixels, two for each data set. The pixels were chosen as typical of the internetwork regions of the FOV. As described in Paper I, the sequence of line core images shows a rapidly evolving scene with areas that are seething with small bright features immersed in an otherwise dark background (compare Movie 2 in Paper I). The spectral profiles of Fig. 4 clearly show how this appearance is the result of the line being repeatedly shifted, strongly towards the blue followed by a slower, smaller amplitude drift back toward the red. The pattern is repeated at the dominant chromospheric periodicity of $\approx$ 120-180 s throughout the whole course of the observations. Such strong line shifts are viewed as an enhanced brightness when observed in the narrowband, fixed-wavelength core images. Their spatial coherence determines how the bright features are observed with respect to the background intensity (see Sect. 5).

A nonlinear steepening of the acoustic waves propagating upward from the photosphere at periodicities shorter than the acoustic cut-off period of $\approx$ 180 s is prescribed by the sharp decrease in density and the approximate conservation of wave energy. This is clearly reflected in the spectra of Fig. 4, where we observe both a deviation of the oscillations from a sinusoidal form, and a large amplitude of the excursions. At these periodicities, the typical rms of chromospheric Doppler shifts is around 1 km s^-1, vs. $\sim$ 0.07 km s^-1 of photospheric motions, cf. Reardon et al. (2008). However, many of the line-shift episodes not only display much stronger Doppler amplitudes, on the order of 5-6 km s^-1, but also exhibit a very abrupt change from high redshift to high blueshift, often within a single 19-second temporal step in our sampling. Further, the maximum redshift of the line often coincides with a brightening episode just blueward of the line core, lasting 50-70 s, with enhanced intensities up to 1.5-2 times the average value at this wavelength. They are also associated with an increased intensity in the extended line wings, that progresses in time from the far wings towards the core. For the wavelength range of our observations, this time is less than about 60 s. Clear examples in Fig. 4 occur at t=1850 s in panel a, or at t=1050, 1200 s in panel d.

These features are analogous with those of the Ca II K_2V grains (Cram & Dame 1983; Liu 1974; Cram et al. 1977, RU91), which have been unequivocally identified as due to hydrodynamic shocks in the mid chromosphere (hereafter we will use the terms grains and shocks interchangeably). A clear example of the resemblance between the temporal evolution of the Ca II K and Ca II 854.2 lines in a non-magnetic atmosphere is provided by comparing Fig. 4 with Fig. 2 of Kamio & Kurokawa (2006). All the characteristics previously described for the IBIS data appear very obvious in the latter high-resolution observations (note the different axes of their figure with respect to Fig. 4). The Doppler shifts are clearer in the Ca II 854.2 line, while the bright grains and related wing enhancements are less prominent when compared to the H and K lines. These differences are a consequence of the different formation and wavelengths of the two lines: the Ca II 854.2 line has a much stronger Doppler sensitivity due to its longer wavelength, and the Planck function (to which the emissivity is related) has a much weaker temperature dependence in the near-IR.

To our knowledge, this is the first time that acoustic shocks in the quiet internetwork chromosphere are convincingly (and abundantly) observed in the Ca II 854.2 line, due to both the high spectral and spatial resolution of the IBIS data. Indeed, synthetic profiles calculated with the 1-D hydrodynamical code of CS97 agree well with the features described above (Pietarila, private commun.; Cauzzi et al. 2007). As further evidence, we show in Fig. 5 the development of Ca II 854.2 spectra of two example pixels, at several times during the passing of a shock wave. The profiles in the right panels are representative of a large fraction of internetwork pixels, for which the characteristic shifts and asymmetries of the spectral line are in excellent agreement with the results of the simulations displayed in Fig. 7 of Pietarila et al. (2006). As an interesting case, we also show in the left panels the spectral profiles for a more extreme event, where a strong shock deforms the whole line shape up to the far blue wing.

$\begin{figure} \par\includegraphics[scale=0.7]{0694f5a.eps}\hspace*{8mm} \includegraphics[scale=0.7]{0694f5b.eps} % \end{figure}$	Figure 5: Temporal evolution of the Ca II 854.2 line during a shock, for two internetwork pixels. Intensity is given in arbitrary units. The time indicated in each panel is expressed in s from an arbitrary zero point. The thin vertical line indicates the average position of the line core throughout the full spatio-temporal sample. Note the broadening of the line during the upward phase.
Open with DEXTER

4 Shock identification

We adopt two different methods of using the temporal sequence of the full spectral profiles to locate shocks in our datasets. For clarity of exposition, we briefly describe here only their most relevant characteristics, with further details given in the Appendix. The first method we call the ``velocity'' method. By analyzing the temporal profile of the chromospheric line-of-sight velocity for each spatial position, we identify times of brusque, strong displacements from downward to upward motions. The method utilizes a threshold both in amplitude of the displacement and in the temporal interval in which this displacement occurs, set at a maximum of two time steps of the IBIS sequence (i.e. 38 s). The second method uses the ``proper orthogonal decomposition'' technique (POD, Holmes et al. 1996), which separates a time-series of spectral profiles into multiple orthogonal eigenmodes. These are then ordered in terms of decreasing energy content, i.e. of their contribution to the whole intensity profile. The periodic velocity shifts that produce the sawtooth shape in the temporal sequence of internetwork Ca II 854.2 spectra is clearly identified by the POD in a single antisymmetric eigenmode (see panel b of Fig. A.1), properly modulated by a temporal coefficient. After finding all the spatial positions for which this eigenmode represents the dominant mode, we define the shock occurrence at the times when the positive peak of the fluctuation shifts from the red to the blue side of the line. We apply the same temporal threshold as in the velocity method, but no amplitude threshold.

For both methods we derive a time series of binary ``shock maps'' defining the times of occurrence and spatial distribution of the shocks. An example of the POD results is given in Figs. 6a,e. The results from the two methods are similar. As a general characteristic, the POD identifies weaker shocks occurring more frequently, most notably in the areas filled with fibrils, for which the velocity method essentially finds no shocks (see Sects. 5.1 and 5.3 below). This can be attributed to the absence of a prescribed threshold for the amplitude of the shocks in the POD case. We point out other differences and similarities as we describe other results of the analysis.

5 Shock properties

5.1 Spatial size and occurrence

From the shocks maps defined above, we can derive the size of a shock by measuring the area covered by contiguous pixels possessing values of one. We discarded any shock area covering less than 2 pixels in either direction, imposing an effective lower limit of $0.3 \times 0.3$ arcsec² to their dimension. For both data sets we find average shock extents of 0.4 arcsec² (using the POD method) to 0.8 arcsec². Under the assumption that the shocks are roughly circular, this corresponds to diameters of 0.7 arcsec to 1.0 arcsec. These values can be compared to the typical 1-2 arcsec size of the K_2V grains as reported in the literature (e.g. RU91; Liu 1974; Tritschler et al. 2007), although a number of factors set apart our analysis from the more common intensity threshold approach.

$\begin{figure} \par\includegraphics[width=15.8cm,clip]{0694f6.eps} \end{figure}$

Figure 6: Spatial distribution of properties related to shocks. Top row: data set 1; bottom row: data set 2. Results shown in a) through c), and e) through g) have been derived from the POD analysis. Axes are in arcsec. Panels a), e): binary ``shock maps'' at a time around the middle of the sequence. Panels b), f): cumulative number of shocks within the whole observational sequence. Panels c), g): maps of the shocks' cumulative amplitude over the whole duration of the observations. Panels d), h): spatial distribution of the Fourier power for chromospheric velocity, integrated over frequencies at and slightly above the acoustic cut-off (5.5-8.0 mHz).

Open with DEXTER

The average number of shocks occurring at any time within a given area can also be estimated. To this end, we selected for both data sets a 30'' diameter area roughly covering the center of a supergranulation cell centered at (x,y) = (14,0) for data set 1 and ( (x,y) = (-4,2)) for data set 2 (see Fig. 1). We find an average number of shocks within these areas ranging from 13 (velocity method, data set 2) to 24 (either method, data set 1). The number of K_2V bright grains in a typical supergranulation cell have been reported at between 10 and 20 in ``the best K_2V spectroheliograms'' (RU91). Our average values are only somewhat higher than these previous findings, but we observe large variations in the number of shocks during the course of the observations, mostly correlated to the seeing conditions: during moments of good to excellent seeing, more than 30 shocks can be identified within a single cell.

5.2 Temporal recurrence

We can further analyze the temporal behavior of the shock occurrence by using two methods. The first one, described in the Appendix, shows that the spatial areas where shocks occur in large numbers are dominated by shock periodicities around the three minutes typical of the chromosphere. We also take another approach here by calculating the histograms of the ``waiting times'' for the shocks, defined simply as the interval between one shock and the next. No significant difference is found between the two methods of shock identification.

The results are shown in Fig. 7 where a strong peak around 120-150 s is observed for both data sets, with a sharp decline on shorter time scales and a slower decrease towards longer periods. The data do not show any evidence of shock periodicities below 120 s (i.e. frequencies above 8 mHz), although such periods would be observable with our data. The long tail of the curves at longer periodicities highlights that Ca II 854.2 shocks do not occur in a continuous fashion, but often in separate bursts. At the same time, no obvious values of waiting time between bursts emerge from the curves, although a change in the slope of the distribution appears around 4-5 mn. Assuming this value distinguishes between shocks in the same burst and between different bursts, we find that the average number of shocks per burst is only 1.25, and that the average number of bursts within the whole sequence is around 3.

All of this bears on the total number of shocks observed in each pixel, displayed in panels b), f) of Fig. 6 (using the POD results). From these maps it is clear that most of the internetwork locations only develop shock for a fraction of the observing sequence: only between 25% and 30% of the ``shocking pixels'' display 5 or more shocks during the whole sequence. The maximum number of shocks for any given pixel is around 15 for both data sets and methods, although this is attained only in a very few pixels.

5.3 Spatial pattern

A striking result emerging from panels b) and f) in Fig. 6 is the extreme inhomogeneity of the spatial distribution of the total number of shocks. In particular, large portions of the internetwork clustered around the magnetic elements experience very few shocks, or none at all. The velocity method provides the same spatial patterns, but with even more extended regions displaying very few shocks. In the maps of Fig. 6, more than 20% of the pixels in data set 1, and 30% in data set 2, do not experience any shock throughout the whole course of the observations. These values increase to a surprising 50%, respectively 60%, for areas with a total number of shocks $\le$ 2. These areas are significantly larger than the area occupied by the photospheric magnetic elements, less than 10% in both cases. These results highlight how chromospheric dynamical properties are poorly constrained by the usually adopted photospheric magnetic diagnostics, a fact already noted in Paper I.

We further note that these ``very few shocks'' areas are essentially coincident with the fibrils observed in the Ca II line core images (compare Fig. 6 with Fig. 1), which are again revealed as a crucial player in shaping the chromospheric dynamics (cf. V07 and Paper I). Conversely, the highest number of shocks is recorded in areas well removed from both the photospheric magnetic network and the fibrils. These areas are consolidated in small patches scattered within the internetwork.

$\begin{figure} \par\mbox{\includegraphics[width=4.5cm,clip]{0694f8a.eps} \hspace*{5mm} \includegraphics[width=3.3cm,clip]{0694f8b.eps} } \par \end{figure}$	Figure 8: Scatterplot of the cumulative amplitude of shocks vs. Fourier power of chromospheric velocities, integrated in a band of frequencies just above the acoustic cut-off (5.5-8.0 mHz). Both axes are in arbitrary units. To avoid pixel crowding, the 2-D distribution is represented by contours, in logarithmic levels.
Open with DEXTER

$\begin{figure} \par\includegraphics[scale=0.9]{0694f9a.eps}\hspace*{2mm} \includegraphics[scale=0.9]{0694f9b.eps} \end{figure}$

Figure 9: Cumulative shock maps for data set 1 (panel a)) and 2 (panel b)). Overlaid is the contour of the high resolution MDI magnetic flux, averaged over the course of the IBIS observations. The contour level is set at 8 G. Compare how even minute magnetic structures within the internetwork, probably occurring only for a fraction of the observations, correspond to a decreased number of Ca II shocks. Spatial scale in arcsec.

Open with DEXTER

5.4 Shocks and Fourier velocity power

Panels c and g of Fig. 6 provide the cumulative amplitude of the shocks over the duration of the observations, again derived from the POD analysis (Sect. A.2).

It is interesting to compare the amplitude maps with the distribution of the chromospheric velocity Fourier power, integrated over the 5.5-8.0 mHz range just above the acoustic cut-off frequency. The latter is shown in panels d and h of Fig. 6. As discussed in V07 for a subset of the data utilized here, in such maps all the magnetic elements are surrounded by areas of very low velocity power, corresponding to the ``magnetic shadows'' first introduced by Judge et al. (2001) in an analysis of chromospheric SUMER data. They are also coincident with the fibrillar structures so prominent in Ca II core images and, as clear from Fig. 6, with the chromospheric regions where few shocks occur during the observational sequence.

The scatterplots in Fig. 8 display a clear pixel-by-pixel relationship between the velocity power and the cumulative shock amplitude: a simple linear regression finds a correlation of about 0.65. From these correlations, we surmise that a large fraction of what is commonly identified as the ``3-mn chromospheric oscillations'' signal in Fourier analysis (e.g. Deubner & Fleck 1990; Noyes 1967; Orrall 1966) stems from the presence of shocks, even if they do occur with the intermittent character described above. In practice, the linear Fourier analysis identifies the shock periodicity and provides a measure of the amplitude of the velocity fluctuations at this dominant frequency, even though the physical phenomenon that produces this signal is very nonlinear.

6 Shock occurrence vs. magnetic structures

Numerous observational studies have searched for a connection between the occurrence of K_2V grains and the presence of magnetic structures in the internetwork as evidence for a possible excitation mechanism (see e.g. the Introduction of Lites et al. 1999). The majority of these have concluded that the grains are essentially a hydrodynamical phenomenon, for which magnetism plays a minor role at most. However, there remain some claims about a tight correspondence between the presence of small-scale bipoles in the internetwork and K_2V grains, most recently by Sivaraman et al. (2000). Our comprehensive data sets, combining high-cadence spectral data over extended areas with actual magnetic field measurements, can be used to examine this question.

A coarse inspection of the magnetic maps of Fig. 1 and the cumulative shock maps of Fig. 6 immediately shows that shocks do not occur at the locations of magnetic structures. A closer inspection shows that the shocks apparently avoid even the smallest magnetic elements. In Fig. 9 we show again the cumulative shock maps for both data sets, overlaid with the contours of the time-averaged MDI magnetic maps. While the noise in the average MDI maps is reduced to a level of about 5 G, in Fig. 9 the magnetic contour level is set to 8 G to allow visibility of the weak and/or transient structures (the network elements have an average magnetic flux of 200-300 G). From Fig. 9, one infers that even small magnetic structures impede the development of the shocks, and notes the small ``shadows'' in the shock maps surrounding several tiny internetwork magnetic structures, for example at positions (-30, 10); (-10, -7); (11, 2) in data set 1 or (-14, 27); (12, -33) in data set 2.

A deeper analysis of this issue involves measuring the magnitude of the magnetic field in those areas that undergo shocks. We first selected, in both data sets, the quiet regions where the temporal average of the MDI magnetic flux does not exceed 30 G. We then divided these regions into two parts, one collecting the pixels where several shocks ( $n \ge 5$ ), over the duration of the observations, are observed and the other collecting pixels with a smaller number of shocks ( $1\le n \le 4$ ). Excluding the n = 0 pixels effectively avoids most of the magnetic shadows associated with the network elements (cf. Fig. 6). The magnetic flux distributions obtained from the temporally resolved MDI maps in the two classes of pixels are shown in Fig. 10. The vertical line at 15 G represents the noise level for a single pixel in MDI maps. In both data sets, the distributions for the two classes of pixels start diverging shortly after the noise value, with the pixels undergoing many shocks characterized by noticeably lower values of the magnetic flux.

$\begin{figure} \hbox{ \hglue -1.cm \includegraphics[scale=0.6]{0694f10a.eps}\hglue -2.5cm \includegraphics[scale=0.6]{0694f10b.eps} }\end{figure}$	Figure 10: Distribution of MDI longitudinal magnetic flux measured in points undergoing a large (dotted line) and small (solid) number of shocks, respectively.
Open with DEXTER

The curves diverge at the level of 10^-2 in relative occurrence; i.e., only a small fraction of the pixels displays this effect. Nevertheless, the difference is clear. Combined with the maps in Fig. 9, this shows that the internetwork magnetic fields actually seem to have a negative effect on the development of shocks. Magnetograms with higher sensitivity and spatial resolution than those of MDI might reveal whether there is a critical area or flux value below which this effect no longer holds.

7 Shock occurrence vs. photospheric velocities

We now examine the relationship between the occurrence of shocks and the underlying photospheric dynamics. We do so with both classical Fourier analysis and wavelet analysis on photospheric velocities, which is a more efficient way to take the highly intermittent character of the shocks into account.

7.1 Fourier phase difference spectra

The spatially-averaged Fourier velocity power spectra for these data sets are displayed in Reardon et al. (2008) and Paper I, and are in general very similar to previously published spectra (e.g. Deubner & Fleck 1990). The photospheric curve shows a strong maximum around the classical 5 mn periodicity ( $\nu \sim 3.5$ mHz), while the chromospheric curve for the internetwork shows a flatter maximum from $\sim$ 4.5 to 7 mHz. Here we concentrate instead on the phase relationship between the photospheric and chromospheric velocities as a way to study the propagation of acoustic waves.

$\begin{figure} \par\vbox{ \hbox{ \hglue -1.2cm \includegraphics[width=6.5cm,heig... ...e -2.8cm \includegraphics[width=6.5cm,height=6cm]{0694f11d.eps} }}\end{figure}$

Figure 11: Panels a), b): Fourier spectra of phase differences between the photospheric and chromospheric velocities, for data set 1 and 2, respectively. The diagram has been calculated over the points in the FOV that develop at least 5 shocks throughout the observational sequence. Panels c), d): corresponding coherence spectra (solid line). Dashed lines refer to the coherence measured for an equally populated sample of pixels undergoing less than 5 shocks; dotted lines to the coherence for the case of fibrils.

Open with DEXTER

Panels a and b in Fig. 11 display the phase difference spectra between the Fourier transforms of the chromospheric and photospheric velocities, obtained over the pixels that develop at least 5 shocks throughout the observational sequence. The figure is built by plotting the binned phase difference $\Delta\phi$ weighted by the cross-power amplitude and normalized per temporal frequency bin; for details see Krijger et al. (2001) and references therein. The noisier scatterplot for data set 1 is due to the worse seeing conditions than for data set 2. A positive phase difference describes signals propagating upward in the solar atmosphere, so the scatterplots clearly show the propagation of acoustic waves from photosphere to chromosphere, up to about 10-12 mHz. The bottom panels c, d provide the coherence spectra of the Fourier velocity signal. The coherence is very high around the velocity power peak at 5-6 mHz (see Paper I), and falls below the confidence limit of 0.5 around 8-9 mHz.

If we consider an equal-size sample of pixels characterized by a smaller number of shocks, we essentially obtain the same phase differences (not shown in the figure) and slightly lower coherence values. The same photospheric piston mechanism thus seems at the base of all quiet chromospheric oscillations, regardless of whether other atmospheric properties are conducive to the development of many mid-chromospheric shocks or not. The coherence is instead much smaller if we use an equal sample of pixels belonging to the fibrillar areas, the areas where most pixels do not develop any chromospheric shocks, especially for data set 2. In these atmospheric regions, a direct (vertical) relationship between photospheric and chromospheric dynamics no longer holds.

$\begin{figure} \par\includegraphics[width=12cm,clip]{0694f12.eps} \end{figure}$

Figure 12: Examples of spatio-temporal occurrence of chromospheric shocks (small diamonds) in relation to the photospheric velocity power at periodicities between 120 and 200 s ( left and center panels) and magnetic features from MDI ( right panels). Velocity power contour levels are set to the average value over the whole FOV plus half standard deviation. Top row refers to data set 1; bottom row to data set 2. The temporal axis is shorter than the full IBIS observational sequence as wavelet maps are not reliable in the initial and final temporal samples, and because of the delay applied between photospheric and chromospheric signal. The x-axes coordinates are given in the same units as in the FOV of Figs. 1, 6, 9. Left panels correspond to y= 5, 0 for data sets 1 and 2, and define quiet areas with strong correspondence between photospheric dynamics and shocks' occurrence. Center panels correspond to y= 12, 3 for data sets 1 and 2, and show areas with comparable photospheric dynamics but notably reduced development of shocks. This is due to the presence of small-scale magnetic structures, as outlined by the contours in the right panels. Contours are set at 30 G for the magnetic flux. For data set 1 the MDI sequence ends before the respective IBIS temporal sequence (cf. upper right panel).

Open with DEXTER

The coherence spectra display a curious bump around 7 mHz, most evident in data set 2. Such a feature has already been reported by Deubner & Fleck (1990) in a spectrographic analysis of a quiet region. Like these authors, we find no obvious explanation for the feature. We suspect that it might be related to the ``aureoles'' of enhanced high-frequency power sometimes measured in both photospheric and chromospheric signatures around active regions or strong network elements (see e.g. Krijger et al. 2001, and references therein). The bump is indeed more evident in data set 2, which has stronger magnetic fields and a more ``active region-like'' magnetic configuration than data set 1.

7.2 Photospheric velocity power and shock occurrence

In their analysis of K_2V grain formation, CS97 note that photospheric acoustic waves at or near the cut-off frequency play the most important role for the development of shocks. In particular, they stated that whenever photospheric velocities have significant power around 5 mHz, there will usually be significantly bright grains. To check these statements, we performed a wavelet analysis of the photospheric velocities. We concentrate on the spatio-temporal features showing enhanced power at periodicities between 120 and 200 s (5-8 mHz), taken as higher values than the average over the whole sample (this accounts for about 35% of the total number of pixels). Hereinafter we refer to them as ``areas'', even if they contain a temporal dimension.

Figure 12 shows example that the mechanism outlined by CS97 is most probably at work. In all panels the x-axis represents the spatial dimension along a horizontal cut within a quiet region in the FOV, while the y-axis displays the temporal dimension over the duration of the observations. Top panels refer to instances in data set 1; bottom panels to data set 2. In figure, the occurrence of Ca II 854.2 shocks is represented by small diamonds. Contours outline the areas of enhanced photospheric velocity power (left and center panels), and the presence of magnetic features (right panels). In the left panels, most of the patches of strong photospheric velocity power encompass the areas where shocks are observed, indicating a relationship between these two phenomena. The coincidence in the case of data set 1 is particularly striking, with photospheric contours enclosing the chromospheric shocks for the whole sequence over extended areas. We note that, in order to obtain this coincidence, a delay of about 120 s (6 time steps) has been applied between the photospheric signal and the occurrence of shocks. This is consistent with the idea that the photospheric perturbations propagate upward at the speed of sound over a $\sim$ 700-1000 km height difference.

However, determining whether all areas of enhanced photospheric power indeed give rise to shocks proved a difficult task. As the presence of magnetic fields breaks the direct relationship between the photospheric and chromospheric dynamics, one has to carefully select the areas to scrutinize this phenomenon. The center panels of Fig. 12 provide a clear example of this. The plots were obtained for spatial positions still well removed from the magnetic network, and in them we observe that in several instances, especially for data set 2, areas of enhanced photospheric power do not produce any shocks, contrary to the expectations of the hydrodynamical modeling. The small magnetic structures responsible for this lack of shocks are outlined in the right panels, at a level of $\sim$ 30 G. It is obvious how the shocks generally avoid both the magnetic elements proper, and some surface around them, as for the larger network shadows.

We hence attempted to identify the quietest portions of the FOV for both data sets, by combining the series of MDI maps with the Ca II 854.2 core intensity maps (see also Fig. 14). In both cases we selected a $8'' \times 13''$ area ( $50\times80$ spatial pixels, considered independent) positioned almost at the center of the FOV, which displayed the least magnetic flux in MDI maps and no obvious evidence of fibrils in Ca II core images. For these regions, we find that more than 80% of the areas with enhanced photospheric velocity power contain shocks. Furthermore, the number of shocks measured in each area is directly proportional to the spatio-temporal extent of that area, thus the development of acoustic shocks appears to be continuous as long as photospheric conditions are favorable. As a rough estimate of the influence of magnetic structures, we compare the total number of shocks measured in these quietest portions of the FOV, taken as prototypes for the undisturbed acoustic shocks mechanism, with those measured in the whole supergranular cells defined in Sect. 5.1. We find that the quietest regions produce, per unit area, from almost 2 (data set 1) up to 3 (data set 2) times more shocks than the supergranular cells as a whole.

We have shown that high photospheric velocity power at the cut-off periodicity is certainly responsible for the development of shocks. But do all shocks occur in areas of high power? To answer this question, we show the distribution of the photospheric velocity power for both data sets in Fig. 13. The curves have been calculated for all the pixels undergoing shocks and pixels where shocks are not observed. Again a delay of 120 s has been applied between photospheric and chromospheric signals. The photospheric power is obviously stronger in the former case than in the latter, as expected from the results described above, with an average value 45% higher for data set 1, and 35% for data set 2. By measuring the area enclosed below the curves, we find that over 55% of the shocks in both data sets occur in areas with photospheric power greater than the average value (the latter accounting for 35% of the total pixels, as stated before). This is to be considered a lower limit, as shocks that are part of a common pattern sometimes lie just outside of the areas defined by the photospheric level, as clearly seen in Fig. 12. Thus, a large fraction of shocks is due to enhanced power in the photosphere at periodicities near the cut-off. Possible causes for shocks not accounted for by this mechanism could be the additional contribution from high-frequency waves when waves near the acoustic cutoff frequency are weak (CS97), as well as some instances of non-vertical propagation.

8 Summary and discussion

The temporal sequences of internetwork Ca II 854.2 nm spectra show compelling evidence for abundant acoustic shocks in the mid-chromosphere (Sect. 3). The evolution of spectral characteristics of the Ca II 854.2 line during these events is complely analogous to the more famous Ca II K_2V grains, clearly explained by CS97 as due to weak acoustic shocks in the mid-chromosphere. We have set out to provide a comprehensive view of the occurrence of these shocks, by combining a broad array of complementary diagnostics, including spectral information in both photospheric and chromospheric lines, high spatial resolution over an extended field-of-view, simultaneous high-resolution magnetic maps from MDI, and observations of two different quiet Sun targets with different magnetic topologies for a period of about 1 h each at high cadence. We surmise that such a dataset is rather unique, and so hope to provide insight into the issue.

${\rm Shock~ identification.}$ We identified the spatio-temporal locations of chromospheric shocks by using a velocity criterion on the Ca II 854.2 nm line, namely the abrupt displacement of the profile from red to blue. This approach provides several intrinsic advantages over the more commonly used intensity threshold methods (see e.g. Tritschler et al. 2007, and references therein). Using a velocity determination avoids confusion between brightenings from shocks and those due to transient small-scale magnetic structures within the internetwork. The latter correspond to what has been termed ``magnetic grains'' (RU91) or ``persistent flashers'' (de Wijn et al. 2008; Brandt et al. 1992), and even though as bright as the internetwork grains, they are characterized by longer evolutionary timescales. Analysis of filtergrams in Ca II H and K may confuse the intensity signature from these two different processes. Our shock identification technique also identifies the start time of each shock, assuring that they are counted only once during the temporal sequence, something that can be difficult with threshold methods. Finally, by using the full spectral profile, we reduce the influence of spatially and spectrally scattered light and photometric errors. The velocity method for identifying shock relies on a threshold for the amplitude of the red-to-blue Doppler shift, but while some of the shock parameters did show a dependence on the threshold value (in particular the size, and total number), others, such as the temporal characteristics and spatial distribution, did not.

Shock properties. Many of the properties that we have derived for the Ca II 854.2 shocks are analogous to those reported in the literature for K_2V grains, confirming that the two phenomena represent the same physical process. In particular, we find that the Ca II 854.2 shocks often appear in bursts, with the typical interval between shocks ranging from $\sim$ 2 to 4 mn (peaking around 150 s), and intervals between bursts of 5 mn and longer. This intermittent behavior is a reflection of their essentially stochastic nature (CS97). No obvious periodicity below 120 s is observed.

The shocks are not ubiquitous, whether in space or in time. Only 25 to 30% of the quiet internetwork displays five or more shocks during the $\sim$ 1 h sequences. Assuming that shocks give rise to K_2V emission for about 60-80 s for each event (e.g. Beck et al. 2008), this rate of occurrence translates into a measurable K_2V emission for about 6-10% of the total spatio-temporal sample, in agreement with earlier works (e.g. Steffens et al. 1996; von Uexkuell & Kneer 1995). Recently, using high-resolution Ca II H spectra acquired with POLIS, Beck et al. (2008) claimed that in quiet Sun regions the core of the Ca II H resonance line spends about half of the time in emission. This is probably misleading, as they implicitly assume that shocks occur everywhere and continuously with the typical 3 mn periodicity, an assumption obviously not fulfilled on the Sun.

$\begin{figure} \par\includegraphics[scale=0.47]{0694f13a.eps}\hspace*{4mm} \includegraphics[scale=0.47]{0694f13b.eps} \end{figure}$	Figure 13: Distribution of photospheric velocity power between 120 and 200 s periodicity for positions undergoing shocks (thick curves) and not (thin curves). Panel a) refers to data set 1; panel b) to data set 2. The overall higher power values in data set 2 are due to better seeing conditions.
Open with DEXTER

The average shock size of 0.7''-1.0'' arcsec measured from the Ca II 854.2 data is noticeable smaller than the 1''-2'' arcsec typically reported for K_2V grains. We believe our measurement comes closer to the true size of the shocks due to the higher spatial resolution reached with IBIS than with older works, the limited influence of instrumental scattered light on our measurements, and the reduced scattering in the solar atmosphere for the Ca II 854.2 line with respect to the H and K. A small extension of the shocks explains why earlier spectral observations of the Ca II 854.2 nm in the quiet internetwork, obtained with a 0.6'' pixel size, did not display the clear sawtooth behavior seen in Fig. 4 (cf. Fig. 3 in Deubner & Fleck 1990). The smaller effective size of the Ca II 854.2 shocks, together with the overall better resolution, accounts for the higher rate of occurrence that we measure in a typical supergranular cell (>20 in our case, vs. 10-20 in the ``best spectroheliograms'', cf. RU91).

$\begin{figure} \par\includegraphics[width=12cm,clip]{aa10694f14.eps} \end{figure}$

Figure 14: Maximum ( top row) and minimum ( bottom row) intensity of the Ca II line core throughout the 55 mn sequences. Left: data set 1; right: data set 2. The scale has been set in radiation temperature (K, see text for details). This representation of the data immediately provides a distinction among the three major chromospheric components: the bright network, the acoustic chromosphere where acoustic shocks show up as tiny bright points, and the magnetic chromosphere threaded by slanted fibrils that can appear as either dark or bright.

Open with DEXTER

Spatial distribution and magnetic shadows. An important result of our analysis is the extreme inhomogeneity of the spatial distribution of the shocks (Sect. 5.3). It has long been known that shocks can be relatively rare and widely dispersed in the supergranular cells (e.g. Lites et al. 1994). Indeed we find that up to 50-60% of the FOV display none or very few shocks, even for the case of data set 1 which, since situated at the edge of a coronal hole, arguably has one of the weakest possible magnetic configuration. However, with our data we clearly show that the shocks are concentrated in the internetwork but away from the regions where chromospheric fibrils are present. The local magnetic topology outlined by the fibrils is very different for the two data sets, with many short loops closing back from the network elements to the near internetwork regions in set 1 and longer and more stable fibrils nearly spanning the supergranular cell in set 2 (Fig. 3). This nature of the canopy and the spatial distribution of the shocks is not easily predicted using only photospheric indicators such as the granulation in the continuum or the location of the network magnetic elements.

A second interesting result is that the total amplitude of the shocks over the course of the observations is directly related to the magnitude of the Fourier power of chromospheric velocities with periods around 3 mn (Fig. 8). Thus, the shocks represent a large, if not dominant, contribution to the ``3-mn chromospheric oscillations'' (e.g. Noyes 1967; Orrall 1966), even if they do occur with an intermittent character. Because the shocks are related to large excursions of the spectral line, corresponding to several km s^-1 when parametrized in terms of line-core Doppler shifts, they can contribute a large fraction of the velocity signal around the acoustic cutoff frequency in classical Fourier analysis, even if they do not occur continuously. The two quantities are essentially equivalent, at least in the quiet Sun.

These two results fit in nicely with several pieces of evidence reported in the literature about the so-called ``magnetic shadows'' and allow us to form a coherent explanation of their existence. First introduced by Judge et al. (2001) the shadows are regions of reduced Fourier oscillatory power at the 3-mn periodicity, often observed in low- and mid-chromospheric signatures around (but not coincident with) magnetic network elements. They have been reported in intensity observations of the continuum at 119 nm obtained with SUMER (Judge et al. 2001), and of the continuum at 160 nm obtained with TRACE (Krijger et al. 2001), as well as in Fourier analysis of chromospheric velocities by V07 and Lites et al. (1994).

All these works invoke the presence of horizontal magnetic field lines (the ``canopy'') to somehow disturb the propagation of normal acoustic waves towards the outer solar atmosphere, for example, by means of wave scattering or mode conversion (Judge et al. 2001; McIntosh & Judge 2001; McIntosh et al. 2003). With our data, we prove that the shadows correspond to a strong suppression of the number of acoustic shocks. Furthermore we show that the shadows are tied to the presence of chromospheric fibrils, i.e. to structures with a very distinct physical structure with respect to the surrounding atmosphere. Indeed, we believe they are compared best to the H $\alpha$ mottles and fibrils observed around the magnetic network of the quiet Sun, which can be explained either by elevated structures, such as spicules, or by ``embedded'' ones (see e.g. the discussion in Al et al. 2004). Hence, the upward propagating acoustic waves may be disturbed not so much by the horizontal field itself as by the different stratifications of the atmosphere. This should be taken into account in any discussions in terms of high- or low- plasma $\beta$ (the ratio of kinetic to magnetic pressure) as the main distinguishing factor between an ``acoustically-dominated'' and a `magnetically-dominated' atmosphere. An estimate of $\beta$ that uses the classical, semi-empirical temperature and density values (e.g. from VAL) might not be appropriate in these regions. In the case of elevated structures, it is also possible that the acoustic shocks develop normally in the low chromosphere whenever photospheric conditions are favorable, and the higher-lying fibrils simply act as a mask by hiding the lower layers from view. Some support for this scenario can be gathered in de Wijn et al. (2007), as well as from Movie 2 in Paper I, where the lateral motions of the fibrils at times ``uncover'' the presence of bright grains, especially towards the end of their horizontal extension (see also Fig. 14).

Photospheric drivers. The analysis of Sect. 7.1 clearly shows that the Ca II 854.2 shocks partake of the general chromospheric dynamics, responding to acoustic waves propagating from lower layers. The phase relationships between photospheric and chromospheric velocities in regions undergoing shocks are fully consistent with earlier results obtained for general internetwork areas, proving the propagation of acoustic waves up to 10-12 mHz (Deubner & Fleck 1990). The shocks in this general oscillation pattern must then be triggered by complementary circumstances. By means of a wavelet analysis we find that instances of high photospheric velocity power at periodicities between 120 and 200 s (5-8 mHz) are correlated well with the occurrence of chromospheric shocks. Tellingly, the correlation is maximized when allowing for a delay of $\sim$ 120 s between the photospheric and chromospheric signals, indicating a photospheric perturbations propagating upward at the speed of sound over a $\sim$ 700-1000 km height difference.

The small dimension of the shocks is not completely correlated with the piston's size, and the analysis in Sect. 7.2 shows how areas of coherent photospheric oscillations at the relevant periodicity have lateral sizes of up to several arcsec. However, it is important to note that these areas completely encircle the majority of the pixels that develop shocks (left panels in Fig. 12). All of these results are consistent with the analysis of CS97 that states how the appearance of the bright grains, including their size, is fully determined by powerful waves near or just above the acoustic cutoff frequency interfering with higher frequency waves. The interference pattern that determines the actual size and recurrence of shocks will be contained within, but not necessarily coincident with, the regions of enhanced photospheric velocity at the dominant frequencies.

The strength of photospheric motions is not the only factor shaping the ``quiet'' chromosphere and its dynamics. We find that the presence of magnetic structures profoundly influences what occurs in the lower chromosphere and, in particular, whether the acoustic mechanism outlined above can operate undisturbed. Many areas with suitable photospheric dynamics do not develop shocks (the ``shadows'') and show a decreased coherence between the vertical photospheric and chromospheric velocity signals at all frequencies (panels c and d of Fig. 11). The dynamics of the fibrils present in the shadows' areas probably is more closely related to the oscillatory behavior at their footpoints than to the directly underlaying layers. Interestingly, we note that pixels developing a small number of shocks have a lower coherence than the ones developing many shocks, so we assume that this is related to a mechanism similar to the shadows, just operating on smaller scales. Several hints support this hypothesis, such as: the diffuse appearance of the Ca II line core images (Fig. 1, especially panel d) that might betray short, unresolved fibrils; the correlation between the presence of small, transient magnetic structures observed in the MDI HR maps and the reduction in total shock numbers (Fig. 9); the lack of chromospheric shocks in areas corresponding to enhanced photospheric velocity power patches, if nearby small-scale magnetic structures exist (Sect. 7.2).

${\rm Vertical~ propagation.}$ Throughout this paper, we have searched for correlations between photospheric and chromospheric signal under the assumption of vertical propagation. This is of course a limitation of our analysis and has often been invoked as one of the major problems in the CS97 study of K_2V grains (e.g. Ulmschneider et al. 2005). However, there are several indications that this assumption is not misguided. First, the level of coherence between the photospheric and chromospheric velocities at the dominant frequency of $\sim$ 5 mHz is very high, especially for the quieter data set 1 (Fig. 11). This would not be the case if the propagation were not predominantly vertical. Indeed, we find a much lower coherence value for the case of the chromospheric fibrils, which have an obviously slanted geometry. Second, the wavelet analysis of Sect. 7.2 shows how patches of high photospheric power at the relevant periodicity coincide closely with the appearance of shocks in the chromospheric areas directly above them. As the photospheric patches of high power extend for 1500-3000 km in the horizontal dimension, i.e. at least twice as far as the vertical separation between the regions of formation of the Fe I and Ca II lines, a small deviation from the vertical (say below 30 $^\circ$ ) would also not cause any drastic difference in our results.

The wavelet analysis shows that in some instances chromospheric shocks are measured even in the absence of high photospheric power. These could be obvious candidates for a search for the effects of inclined propagation, so they deserve further investigation. They could also be related to the presence of high-frequency waves or photospheric power just below our cutoff for enhanced power.

Still, it appears that small magnetic structures represent a more important factor in the shaping of the 3-D chromospheric dynamics, reducing the overall number of shocks by large amounts (Sect. 7.2).

${\rm Three~quiet~chromospheres.}$ From our results, we propose that the ``quiet'' lower chromosphere should be considered as comprising at least three components, as somewhat anticipated in Judge et al. (2001) and pointed out in Paper I. These three components are: 1- the purely acoustic chromosphere, where the strong photospheric motions at frequencies near the acoustic cut-off can propagate upwards undisturbed and develop into shocks; 2- the network and internetwork magnetic elements, which open up partially from the photosphere and are heated by a still unexplained mechanism (see Hasan & van Ballegooijen 2008, and references therein); and 3- the inclined fibrils that magnetically connect horizontally separated areas. The fibrils can span as long as a supergranular cell (as in data set 2) or as short as few arcseconds (as in the smallest shadows in Fig. 6 d); in either case, they define chromospheric volumes with very different dynamical properties than the other two components. In particular, they show a reduced chromospheric vertical velocity power at all frequencies (see also Paper I), distinctly longer evolutionary timescales (V07), a lack of vertical coherence between the photospheric and chromospheric signals (Sect. 7.1).

These three components can be immediately identified by using maps of the Ca II 854.2 line core intensity, a reliable indicator of temperature (Cauzzi et al., in preparation). In particular, we show in Fig. 14 the maximum (top row) and minimum (bottom row) values of the line-core intensity, measured for each spatial pixel within the 55 mn observing sequences. In this figure the intensity has been converted to radiation temperature by scaling the average intensity computed over the full spatio-temporal sample to the calibrated atlas intensity of Neckel (1999) and applying the inverse Planck function (the average intensity corresponds to 3800 K). Obviously this definition does not represent the real kinetic temperatures, as the line is not formed in LTE, but it does indicate the magnitude of the variations. In Fig. 14 the acoustic shocks stand out clearly in the maximum intensity maps as bright specks with a quasi-granular appearance (but with smaller dimensions) and temperatures up to 4200 K. At times, especially in data set 2, the shocks can even be discerned amongst the long fibrils, supporting the idea of the latter operating as a switch between the lower chromosphere and the observer. The canopy-free internetwork regions where there are significant numbers of shocks are also the regions of the lowest intensity, and presumably lowest temperature, in the entire sequence, with radiation temperature values as low as 3400 K. The magnetic elements also appear as distinct quasi-granular sources, but larger and brighter than the acoustic shocks, with temperature excursions ranging from a minimum of 4000 to maxima of 4700 K. Finally, the slanted fibrils have a very different morphology and might be better defined as the ``diffuse'' sources in both the maximum and minimum intensity maps. Two things about them are particularly remarkable: they are the component whose intensity (temperature) changes the least between maximum and minimum values, with highest values close to the network points and cooler ends towards the internetwork; and they cover a large fraction of the FOV, even for data set 1. The magnetic influence appears very pervasive over the quiet Sun.

Finally, it would appear that Fig. 14 also offers a definitive statement on about the spatial correspondence between small-scale magnetic structures and K_2V bright points (e.g. Sivaraman et al. 2000). Indeed, many such small magnetic concentrations are visible in the internetwork portion of the FOV in both of our data sets, and they do correspond to enhanced bright ``points'', some of them only 1-2'' wide. However, they also are clearly distinguished from the acoustic grains by the diffuse cocoon around them, made up most probably of unresolved fibrils. They appear just like miniature versions of normal network elements (Krijger et al. 2001). The analysis of Sect. 6 makes it clear that these bright structures do not participate in the typical dynamics of acoustic shocks, making them K_2V bright ``points'', but not K_2V bright grains! Claims to the contrary, such as those of Sivaraman et al. (2000), stem from the limited coverage of the available datasets or the limited number of co-spatial magnetic and K_2V measurements.

9 Conclusions

In our analysis, we reach two main conclusions, both of which are represented in Fig. 14.

The first is that temporally resolved spectra of the Ca II 854.2 nm provide a comprehensive picture of the occurrence of acoustic shocks in the quiet solar atmosphere. We determine that these shocks are a fundamental part of the general chromospheric dynamics, as they essentially make up the bulk of the three-minute oscillations in the middle chromosphere. We find that the shocks occur in direct response (after a 120 s delay) to powerful photospheric oscillations near the acoustic cutoff frequency, with a primarily vertical propagation. No major role is found for waves with periods below 120 s or with a slanted propagation, consistent with the 1-D purely hydrodynamical simulations of Carlsson & Stein (1997). Portions of the quiet chromosphere are then the site of brief episodes when the acoustic shocks dramatically enhance the temperature (Fig. 14a and b) mixed with extended periods of lower temperatures (Fig. 14c and d), as opposed to the steady-state mean temperature rise typically assumed in semi-empirical models (see the discussion in Carlsson 2007; Carlsson & Stein 1995).

The second, more important conclusion is that these acoustic processes are very often significantly disturbed by the presence of a magnetic field, even in the quiet Sun. Both at the network and (surprisingly) at internetwork scales, the signature of acoustic shocks is suppressed both in and around the footpoints of magnetic structures. Hence the distribution of shocks is considerably reduced compared to what would be inferred from the amplitude of the photospheric oscillations alone. The main player in this respect appears to be the magnetic topology and, in particular, the question of whether the field has an open or closed configuration. The areas of modified acoustic behavior coincide with the presence of chromospheric fibrils, betraying an atmosphere that is stratified differently with respect to the classical 1-D view.

These results provide an important hint to the longstanding controversy about why the dynamical model of CS97 fails to predict the ubiquitous emission observed in UV lines (e.g. Carlsson 2007; Avrett & Loeser 2008; Kalkofen 2001; Kalkofen et al. 1999). Our analysis is based on observations in the Ca II 854.2 nm line, a spectral signature formed relatively low in the atmosphere. Our data provide uncontroversial evidence that, even at these heights, the quiet atmosphere is highly structured by pervasive magnetic fields that connect different locations. The presence of fibrils is a clear testimony to these inter-connections. It is then natural to assume that other spectral diagnostics forming in higher, less dense parts of the atmosphere, experience such a magnetic structuring to an even greater extent, much as advocated by Ayres (2002).

Far UV lines and continua are one such diagnostic, and they figure prominently in the derivation of the temperature structure in semi-empirical models, often as spatial and temporal averages (e.g. Avrett & Loeser 2008). It follows that a substantial fraction of the UV flux could originate in magnetic structures, even in the quiet internetwork chromosphere. This could happen either because of the volume filling of the magnetic field at these heights or because of the dominant weight of magnetic-related brightness in the averages. Figure 14 illustrates how magnetic concentrations introduce a brightness component with a different spatial distribution and temporal evolution than for the purely acoustic case. This happens on spatial scales at the limit of the resolution of many modern instruments, including SUMER. Any averaged or marginally resolved observation of the chromospheric flux might then contain a sizable magnetic component, in ways not immediately predictable by using only photospheric indicators. A dominance of the magnetic topology in the quiet upper chromosphere would also explain why UV observations obtained with SUMER have produced so many disparate results. These range from the clear signature of upward propagating acoustic waves reported by Wikstøl et al. (2000) all the way from the photosphere up to the base of the corona, as could happen in the case of a coronal hole, to instances of complete disconnection between the observed lower and upper chromospheric dynamics (Judge et al. 2001,2003), as would be the case for regions with a locally closed magnetic topology. In this scenario, obviously there is no need to reconcile the predictions of CS97, a purely non-magnetic model, with the UV observations, as they pertain to completely different physical regimes.

We thus conclude that the radiative losses in the ``non-magnetic'' (quotes are necessary at this point) solar chromosphere are strongly influenced, and possibly dominated, by processes related to magnetic fields. We note that this same conclusion has been reached by Judge and collaborators (Judge et al. 2003,2004; Judge & Carpenter 1998), in a precise analysis of UV emission lines for both the case of the Sun and other stars with convective envelopes. The presence of fibrils in large fractions of the quiet atmosphere provides a plausible agent for such dominance. On the one hand, they disrupt the normal vertical propagation of acoustic waves from lower layers, strongly reducing the effects of a purely acoustic mechanism in shaping the chromosphere. On the other, they provide the means to transport energy of a magnetic origin, or mediated by the magnetic elements, from the network footpoints towards the center of the supergranular cells. We note that this idea is consistent with several recent works that have called into question whether the photospheric acoustic flux at high frequencies is sufficient to compensate for the chromospheric radiative losses (Fossum & Carlsson 2005,2006) or, even more pertinent, whether different energy sources, such as low- frequencies magneto-acoustic waves or atmospheric gravity waves, might play a more important role (Straus et al. 2008; Jefferies et al. 2006).

Appendix A: Identification of shocks

A.1 The velocity threshold approach

A way to identify acoustic shocks ``events'' is through the sawtooth peaks in the velocity field, defined via the Doppler shift of the line intensity minimum. The small white crosses in Fig. 4 panel a show this parameter for the particular pixel. As apparent from both Figs. 4 and 5, during the upward phases of the shock, the spectral line broadens considerably in the blue wing, probably leading to an underestimate of the actual value of the vertical velocity by using the simple Doppler shift of the minimum. However, such an effect does not seem particularly severe (compare for example Fig. 7 in Pietarila et al. 2006), and the sign of the recovered velocity is always correct.

Following the temporal behavior of the velocity, for each spatial pixel a shock event is then defined to occur at the time when the velocity experiences an abrupt jump from high positive to high negative values (downward to upward motion). As a temporal threshold for this velocity jump, we utilize a maximum interval of two time steps, i.e. a 38 s window. The threshold for the amplitude of the velocity jump is set at a value of 4 km s^-1. This is safely above the rms value of $\sim$ 1 km s^-1 measured for chromospheric velocities at the dominant periodicity, and it allows us to identify the most energetic events. Experiments with lower and higher values of the velocity threshold cause a different number of shock events to be counted, but do not alter the main conclusions about their overall spatio/temporal distribution.

With these two combined criteria we can identify the presence of an acoustic shock at any given time or location within the FOV, and hence derive a temporal series of binary maps defining their spatial distribution, similar to the examples displayed in Figs. 6 a and e. A value of the shock strength can also be defined as the maximum velocity difference between downward and upward velocities during the shock. Given the limitations of the Doppler shift of the intensity minimum, described above, both of these values can be considered as lower limits to the actual distributions.

A.2 The proper orthogonal decomposition approach

As an independent validation of the results obtained through the velocity threshold method, we also attempted a more general approach, based on an analysis of the whole spectral shapes. This approach makes use of the proper orthogonal decomposition (POD) technique, initially developed to study coherent structures in channel flow turbulence and recently applied to various astrophysical problems (Carbone et al. 2002; Vecchio 2006; Lawrence et al. 2004; Rees et al. 2000; Vecchio et al. 2005). As the POD technique is not yet widely known, we describe it in some detail in the following.

A.2.1 The POD method

In the framework of the POD, a spatio-temporal field u(r,t) is decomposed as $\sum_{j=0}^ {\infty}a_j(t)\Psi_j(r)$ . The orthonormal basis functions, $\Psi_j$ , are not given a priori but are obtained from the experiment, and can hence assume the proper functional shape of the phenomenon. The time coefficients a_j(t), computed from the projection of the data on the corresponding basis functions, represent the time evolution of the jth mode associated with that eigenfunction. The modes are then ordered according to a parameter, the ``energy'' content of fluctuations associated with them, quantifying the relative contribution of each mode to the signal reconstruction. The most energetical mode (j=0) is associated to the average contribution to the signal. For more details, we refer to the text by Holmes et al. (1996).

A.2.2 Application of POD to Ca II 854.2 profiles

We apply the POD to analyzing the temporal evolution of the spectral profiles (like those shown in Fig. 4) for each pixel of the FOV separately, considering the (wavelength-dependent) intensity fluctuations around the mean profile. Thus, in our application, the POD decomposition of a wavelength-time spectrum will be

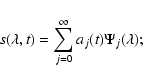
$\begin{figure} { \vbox{ \hbox{ \hglue -2.3cm \includegraphics[width=5.5cm,height... ... \includegraphics[width=5.5cm,height=3.2cm]{0694f15j.eps} }} } \par \end{figure}$

Figure A.1: Example of POD analysis for two pixels from data set 1. Panels a), b), e), f) refer to a pixel displaying a large number of shocks with 3 mn periodicity. a): Eigenfunction of the mode j=0 (average of the signal). b): Eigenfunction describing the shocks' contribution, displaying the typical asymmetric shape. Since the eigenfunctions are orthonormal, their amplitude is arbitrary. e): actual measured spectra. f): contribution to the profiles in e) reconstructed using only the POD mode associated to an eigenfunction like b) (mode 1 in this case). For clarity, only the positive portion of the reconstructed function is displayed. Panels c), d), g), h): as before, but for a pixel where only a few, energetically unimportant shocks are found by the POD analysis (shock mode = 3). Panels i), j): POD temporal coefficients used in the reconstructions of panels f) and h). A 3 mn periodicity is evident in panel i).

Open with DEXTER

$\begin{figure} \par\includegraphics[width=12cm,height=10cm,clip]{0694fA2.eps} \end{figure}$	Figure A.2: Panels a) and b): maps of mode pertaining to the shock eigenfunctions, for data sets 1 and 2. c) and d): maps of dominant periodicity in coefficients a_i(t), for data sets 1 and 2. Spatial axes in arcsec.
Open with DEXTER

Panel e in Fig. A.1 displays, as an example, the actual temporal evolution of the spectrum corresponding to an internetwork pixel in data set 1, where we find evidence of several shocks. Panel a shows the corresponding POD eigenfunction $\Psi_0(\lambda)$ of the mode j=0, i.e. the temporally averaged spectrum. The chromospheric steepening of acoustic oscillations, which eventually will lead to shock development, induce an intensity fluctuation characterized by a well-defined behavior, i.e. a large displacement of the line from the average position, with an asymmetric contribution in the two wings. The POD analysis isolates this behavior in a single mode, whose eigenfunction has the typical shape shown in panel b of Fig. A.1. It is characterized by two opposite lobes of different amplitude, indicating positive and negative contributions to the average profile towards the blue and the red wavelengths. The sign of the time coefficient (to be multiplied to the eigenfunction) selects when the positive contribution is in the red or in the blue parts of the spectrum.

Thus for each pixel the mode associated to the (possible) shock contribution can be identified by looking at the shape of the eigenfunctions, including the lobe asymmetry. Suppose that this is the mode j=i for the spectrum of Fig. A.1 e. The wavelength-time intensity contribution of this mode to the actual spectral evolution can be expressed as $a_i(t)\Psi_i(\lambda)$ , and is shown in panel f of Fig. A.1 (for clarity we have displayed only its positive part). It illustrates how the modifications to the spectral profiles induced by this mode are in general stronger and more extended in the blue wing of the line, as well as the fact that, on average, the variations in the red wing last longer than in the blue wing. The latter property is also present in the simulations of CS97. For this particular pixel, i=1, i.e. the mode characterizing the eigenfunction $\Psi_i(\lambda)$ is the one with the highest ``energy'' content of fluctuations.

A.2.3 Dominant POD modes and periodicities

Obviously, not all the pixels within the FOV have spectra similar to those displayed in panel e of Fig. A.1. Panel g of the same figure provides an illuminating example, showing the temporal evolution of the spectrum for a pixel pertaining to a fibril within the FOV of data set 1. The average spectrum (POD eigenfunction of the mode j=0) is given in panel c, the ``shock-mode'' eigenfunction for j=i is shown in panel d, and the POD reconstruction for this mode is displayed in panel h. For this case, the mode characterizing the eigenfunction $\Psi_i(\lambda)$ is i=3, i.e. with a much lower energy than the example of panel e.

Panels a and b of Fig. A.2 display the spatial distribution, for both data sets, of the mode i defined above. (As said before, modes with i > 3 contain an energy less than 1% and have not been considered.) For the majority of the internetwork pixels i=1, i.e. the ``shock-mode'' is the most energetic component of the intensity fluctuation. However, large portions of the FOV exist, apparently pertaining to the photospheric internetwork but surrounding the magnetic elements quite extensively, for which the relevant eigenfunction corresponds to the mode i = 2. Their typical energy fluctuation content is less than half that pertaining to the pixels with shock-mode i=1. This effect is more prominent in data set 2, in correspondence to a larger extension of the fibrillar structures visible in the line core images.

The coefficients a_j(t) provide the temporal behavior of the different POD modes for each spatial pixel. For example, the coefficients used in the recostructions of Fig. A.1 f and h are plotted in the same figure (panels i and j), and show that for the first case the ``shock'' eigenfunction has a clear periodicity nearing 150 s, while for the second one the temporal coefficient has more erratic behavior. Maps of the dominant periodicities in the a_j(t) coefficients, for each pixel and for the shock-associated j=i POD mode, are reported in panels c and d of Fig. A.2. They have been derived from a Fourier analysis of the coefficients, but the same result is obtained if using a wavelet analysis of the time series, by considering the wave period containing the highest number of wave packets with significant power. In both data sets, for most of the pixels characterized by the i = 1 POD mode, the dominant periodicity is $\sim$ 200 s and slightly shorter (frequencies between 5 and 7 mHz). This is consistent with the typical chromospheric periodicity of $\sim$ 3 mn for acoustic oscillations, deriving from the atmospheric filtering of the photospheric p-modes. The association between i=1 POD mode and this periodicity essentially reflects the strong steepening of the acoustic waves propagating in the chromosphere. We note that the two data sets display differences in this association, with a more fragmented distribution of the short-periodicity areas, and a stronger presence of longer periodicities (4 mHz or less) in data set 2.

We further note that some spatial locations within the magnetic network areas display ``shock-associated'' eigenfunction i=1 as well, but are characterized by longer periodicities (frequency below 4 mHz). They will be considered in more detail in a future paper.

A.2.4 POD shocks

Finally, in order to identify the occurrence of shocks from a pattern such as is displayed in Fig. A.1 f or h, we can simply count the events characterized by a red peak followed by a blue peak, with the jump occurring within the same temporal delay defined before (38 s), without applying any threshold to the amplitude of the events. Rather, an amplitude can be defined as the intensity difference of the two peaks of the mode ( $a_i(t)\Psi_i(\lambda)$ ) on either (temporal) side of the shock. Such a difference is related to the variations induced by the shock over an average profile for the pixel, and is then again a measure of the strength of the event. As in the velocity analysis, repeating this calculation for each pixel we can derive a temporal series of binary maps, displaying the shocks' spatial distribution, as well as maps of their amplitudes. Panels a and e of Fig. 6 show typical ``shocks maps'', for a time around the middle of the temporal sequence.

The solar chromosphere at high resolution with IBIS

II. Acoustic shocks in the quiet internetwork and the role of magnetic fields

1 Introduction

2 Observations

2.1 The IBIS data sets

2.2 The magnetic environment

3 Evidence of acoustic shocks in the internetwork

4 Shock identification

5 Shock properties

5.1 Spatial size and occurrence

5.2 Temporal recurrence

5.3 Spatial pattern

5.4 Shocks and Fourier velocity power

6 Shock occurrence vs. magnetic structures

7 Shock occurrence vs. photospheric velocities

7.1 Fourier phase difference spectra

7.2 Photospheric velocity power and shock occurrence

8 Summary and discussion

9 Conclusions

Appendix A: Identification of shocks

A.1 The velocity threshold approach

A.2 The proper orthogonal decomposition approach

A.2.1 The POD method

A.2.2 Application of POD to Ca II 854.2 profiles

A.2.3 Dominant POD modes and periodicities

A.2.4 POD shocks

References

$\begin{figure} \hbox{ \hglue -0.8cm \par\includegraphics[width=6cm,height=6.5cm]... ...lue -2.2cm \includegraphics[width=6cm,height=6.5cm]{0694f7b.eps} }\end{figure}$	Figure 7: Distribution of waiting times between shocks, for data set 1 (panel a)) and data set 2 (panel b)).
Open with DEXTER