A&A 493, L49-L52 (2009)
DOI: 10.1051/0004-6361:200811082
LETTER TO THE EDITOR
F. Hersant1,2 - V. Wakelam1,2 - A. Dutrey1,2 - S. Guilloteau1,2 - E. Herbst3
1 - Université de Bordeaux, Laboratoire d'Astrophysique de Bordeaux (LAB), France
2 -
CNRS/INSU - UMR 5804, BP 89, 33271 Floirac Cedex, France
3 -
Departments of Physics, Astronomy, and Chemistry, The Ohio State University, Columbus, OH 43210, USA
Received 3 October 2008 / Accepted 9 December 2008
Abstract
Aims. We attempt to understand the presence of gas phase CO below its sublimation temperature in circumstellar disks. We study two promising mechanisms to explain this phenomenon: turbulent mixing and photodesorption.
Methods. We compute the chemical evolution of circumstellar disks including grain surface reactions with and without turbulent mixing and CO photodesorption.
Results. We show that photodesorption significantly enhances the gas phase CO abundance, by extracting CO from the grains when the visual extinction remains below about 5 mag. However, the resulting dependence of column density on radial distance is inconsistent with observations so far. We propose that this inconsistency could be the result of grain growth. On the other hand, the influence of turbulent mixing is not found to be straightforward. The efficiency of turbulent mixing depends upon a variety of parameters, including the disk structure. For the set of parameters we chose, turbulent mixing is not found to have any significant influence on the CO column density.
Key words: stars: circumstellar matter - stars: planetary systems: protoplanetary disks - astrochemistry - turbulence
In circumstellar disks, because of the high densities, carbon monoxide is expected to stick onto grains at
temperatures below about 17 K. However,
millimeter interferometric observations of several circumstellar disks around
T Tauri stars (e.g. DM
Tau, GM Aur, and LkCa15) have revealed that a large amount of CO remains gaseous at temperatures as low
as 10 K (Dartois et al. 2003; Piétu et al. 2007). These authors show that the bulk of CO is at temperatures
below 17 K between 100 and 800 AU from the central star.
Since these disks are much older than the sticking timescale of
CO onto grains (![]() 102 yr), some mechanism must prevent the complete depletion of CO.
102 yr), some mechanism must prevent the complete depletion of CO.
Aikawa & Nomura (2006) proposed that the presence of cold CO in disks can be a consequence of vertical turbulent mixing (See also Fig. 4 of Willacy et al. 2006). Semenov et al. (2006) studied in detail the influence of both vertical and radial mixing on the abundance of cold CO. They found that vertical mixing cannot account for the observed abundance of cold CO, while the situation improves slightly when considering the full 2D mixing (vertical and radial). However, Aikawa (2007) computed analytically the influence of vertical mixing on the abundance of cold CO and concluded that vertical mixing was sufficient to achieve an abundance of CO consistent with that observed by Dartois et al. (2003). The apparent discrepancy with Semenov et al. (2006) can be understood as a consequence of the different efficiencies of grain surface reactions in their studies (Aikawa 2007).
On the other hand, Öberg et al. (2007) measured the photodesorption rate of CO in the laboratory. They found a rate similar to that found for H2O by Westley et al. (1995), about 2 orders of magnitude higher than previously available theoretical estimates (Draine & Salpeter 1979), implying that this non-thermal desorption process was an appealing candidate for explaining the abundance of cold CO in various astrophysical environments. This motivated us to investigate the influence of both vertical mixing and photodesorption on the CO column density in disks, using a parametric model consistent with interferometric observations of circumstellar disks.
In Sect. 2, we describe the physical and chemical model used, while Sect. 3 is devoted to the results of our computations. In Sects. 4 and 5, we discuss our results and present our conclusions.
To consistently compare with the physical structure observed by Piétu et al. (2007),
we use a simple disk model with physical quantities varying as power laws of the radius, similar to the
parametric disk model used by Piétu et al. (2007) to reproduce their interferometric maps. The vertical
temperature distribution is defined to have two layers, one cold layer with a constant temperature of 10 K, and
a warm layer in radiative equilibrium with the central star radiation.
This behavior is typical of disk models (e.g. Aikawa & Nomura 2006; D'Alessio et al. 1999). The precise location of the transition between the two layers varies between models.
We chose this transition
at 2 pressure scale heights, a location similar to that used by Dartois et al. (2003) to fit their data.
The constant mid-plane temperature,
although surprising at first sight, is
consistent both with the temperature observed in 13CO
J=1-0 by Piétu et al. (2007) and the surface
density power exponent of -3/2 observed in the outer parts of most ``undisturbed'' disks (see Dutrey 2008, for a
review). In an ![]() -model (Shakura & Syunyaev 1973), the product of the temperature and the surface density
is indeed assumed to vary as R-3/2. Therefore, a constant mid-plane temperature in an stationary
-model (Shakura & Syunyaev 1973), the product of the temperature and the surface density
is indeed assumed to vary as R-3/2. Therefore, a constant mid-plane temperature in an stationary ![]() -model is the only way
that the surface density decreases as R-3/2. This regions of almost constant temperature
are also found in the more complete disk models developed by D'Alessio et al. (2001,1999).
-model is the only way
that the surface density decreases as R-3/2. This regions of almost constant temperature
are also found in the more complete disk models developed by D'Alessio et al. (2001,1999).
The laws that we use in the present paper are:
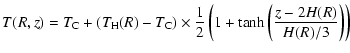 |
(1) | ||
| (2) | |||
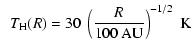 |
(3) | ||
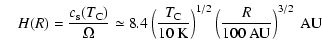 |
(4) | ||
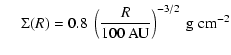 |
(5) |
where ![]() is the isothermal sound speed,
is the isothermal sound speed, ![]() is the Keplerian frequency, and
is the Keplerian frequency, and ![]() is the surface
density. From these laws, the mass density
is the surface
density. From these laws, the mass density ![]() is then computed from the hydrostatic equilibrium.
is then computed from the hydrostatic equilibrium.
The chemical evolution of the disk is computed with a 1D vertical model that takes into account both gas-phase
and grain surface chemistries. This code was adapted from the OSU gas-grain code developed by the
astrochemistry team of Eric Herbst. The formalism of surface chemistry and various processes are described in
Hasegawa et al. (1992) and Garrod et al. (2007). The gas-phase chemical network uses updates from
osu_03_2008![]() . The complete network
(gas and grain) contains 655 species and 6067 reactions. Grains are assumed to be of interstellar type. To
model the CO and H2 UV self-shielding, we use
the approximation from Lee et al. (1996). The code is written in Fortran 90 and uses the DLSODES routine from
the ODEPACK package (Hindmarsh 1983) to solve the differential equations. The initial abundances of our
calculations are taken from the output of a gas-phase calculation of a dark cloud (
. The complete network
(gas and grain) contains 655 species and 6067 reactions. Grains are assumed to be of interstellar type. To
model the CO and H2 UV self-shielding, we use
the approximation from Lee et al. (1996). The code is written in Fortran 90 and uses the DLSODES routine from
the ODEPACK package (Hindmarsh 1983) to solve the differential equations. The initial abundances of our
calculations are taken from the output of a gas-phase calculation of a dark cloud (
![]() cm-3, T=10 K,
cm-3, T=10 K,
![]() )
after
107 yr and our elemental abundances are the EA3 conditions from
Wakelam & Herbst (2008), with an S abundance of
)
after
107 yr and our elemental abundances are the EA3 conditions from
Wakelam & Herbst (2008), with an S abundance of
![]() .
The gas-grain model is then allowed to evolve for 105 yr
with 32 vertical points. A period of 105 yr is the radial mixing timescale at 100 AU, as well as the
evolutionary timescale for the disk structure. Computing for a longer time would in principle require a full
2D (R,z) approach and an evolving disk model.
.
The gas-grain model is then allowed to evolve for 105 yr
with 32 vertical points. A period of 105 yr is the radial mixing timescale at 100 AU, as well as the
evolutionary timescale for the disk structure. Computing for a longer time would in principle require a full
2D (R,z) approach and an evolving disk model.
| (6) | |||
| (7) |
| |
= | (8) | |
| = | (9) |
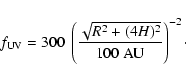 |
(10) |
We compute the vertical turbulent mixing using an ![]() turbulent viscosity (Shakura & Syunyaev 1973), where the
diffusivity
turbulent viscosity (Shakura & Syunyaev 1973), where the
diffusivity ![]() is given by:
is given by:
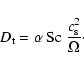 |
(11) |
The resulting equations for the chemical abundances xi are:
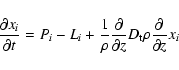 |
(12) |
The vertical mixing and the chemistry are computed using first-order operator splitting, the chemistry being computed before the mixing inside a time step. This induces intrinsic errors, which are controlled by reducing the time step. We adapted the time step so that the splitting errors remain below 5% relative accuracy, by comparing with simulations without operator splitting, which are far more time-consuming.
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm]{1082fig1.ps}
\end{figure}](/articles/aa/full/2009/03/aa11082-08/Timg38.gif) |
Figure 1: Vertical distribution of gaseous CO at 100 AU from the central star, (a) no photodesorption, no diffusion (dotted-dashed line), (b) no photodesorption, diffusion (dashed line), (c) photodesorption, no diffusion (dotted line), (d) photodesorption, diffusion (solid line). Superimposed on the graph are the temperature (thick grey line) and visual extinction (thick dashed grey line) as a function of height above the midplane. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm]{1082fig2.ps}
\end{figure}](/articles/aa/full/2009/03/aa11082-08/Timg39.gif) |
Figure 2: As Fig. 1 but for R=300 AU. |
| Open with DEXTER | |
The vertical distribution of gas phase CO was computed at 100, 200, 300, 400, 500, and 600 AU, for 4 different
models, with or without CO photodesorption and/or vertical mixing.
Figures 1, 2, and 3 show the resulting vertical CO distributions. The ``handle-bar'' shape of the vertical
abundance profile at all radii is the result of CO photodissociation at high altitudes (mostly visible at 300
and 500 AU) and CO freezing onto grains in the dense mid-plane
(below
![]() ). Carbon is locked
in different dominant forms as a function of height:
frozen CO in
the midplane, then frozen CO2, gaseous CO, and finally atomic C in the photodissociated region. The
thickness of each layer depends on the radius (through density, temperature,
and
). Carbon is locked
in different dominant forms as a function of height:
frozen CO in
the midplane, then frozen CO2, gaseous CO, and finally atomic C in the photodissociated region. The
thickness of each layer depends on the radius (through density, temperature,
and ![]() ). In the 100 AU profile (Fig. 1), a dip is visible in the CO distribution without mixing. This dip is the consequence of a
layer of N2H+, which initiates a secondary reaction chain (dominated by grain chemistry) started by:
). In the 100 AU profile (Fig. 1), a dip is visible in the CO distribution without mixing. This dip is the consequence of a
layer of N2H+, which initiates a secondary reaction chain (dominated by grain chemistry) started by:
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm]{1082fig3.ps}
\end{figure}](/articles/aa/full/2009/03/aa11082-08/Timg42.gif) |
Figure 3: As Fig. 1 but for R=500 AU. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm]{1082fig4.ps}
\end{figure}](/articles/aa/full/2009/03/aa11082-08/Timg43.gif) |
Figure 4: Total column density of gaseous CO as a function of the radial distance, (a) no photodesorption, no diffusion (dotted dashed line), (b) no photodesorption, diffusion (dashed line), (c) photodesorption, no diffusion (dotted line), (d) photodesorption, diffusion (solid line). The grey lines are the corresponding cold CO (T < 17 K) column density profiles. |
| Open with DEXTER | |
Photodesorption by primary UV photons is the most important process affecting the abundance of gas-phase CO. When the visual extinction is sufficiently low (below about 5 mag), this desorption mechanism is efficient enough to preserve a significant abundance of CO. For radii larger than 200 AU, the total column density of gas phase CO is increased by an order of magnitude when this process is taken into account. The situation is different at 100 AU. Here, the visual extinction reaches a value of 5 mag at 2 pressure scale heights, and grains receive insufficient primary UV photons to enable efficient photodesorption of CO. The secondary UV photons originating from the interaction of H2 with electrons induced by cosmic rays are then the only photodesorbing photons. They maintain a small fraction of CO in the gas phase but do not influence the total CO column density by more than 10%.
In our simulations, vertical mixing has a small influence on the total column densities of CO. At 100 AU (and 200 AU), as shown in Fig. 4, the presence of a layer of N2H+ appears as a sink of CO (via reaction 13) and the total CO column density is reduced by vertical mixing. This is the reason why the CO abundance below z=2H is lower in the case with diffusion (Fig. 1). The low efficiency of vertical mixing is a consequence of two effects. First, when CO condenses onto grains, grain chemistry transforms it into more refractory species, thereby preventing desorption when it diffuses back to the warm region. The second reason is the consequence of a dilution effect. Due to a temperature transition at 2 pressure scale heights, the warm region represents less than 10% of the total mass. This is obviously a possible bias of our disk model, the influence of vertical mixing being very sensitive to this transition. For a transition deeper inside in the disk, as considered by Aikawa & Nomura (2006) and Aikawa (2007), vertical mixing is far more efficient. Accurate knowledge of the true thermal structure of the disk would be required to obtain a more precise estimate.
Figure 4 shows that photodesorption increases the total CO column density, but also makes the CO column density flatter. Piétu et al. (2007) measured a steep radial profile of CO column density, varying as R-3 or even more steeply, with about 1017 cm-2 at 300 AU. This gradient is steeper than for our models without photodesorption. Quantitative comparisons with observations are however far from being straightforward because they require the generation of CO emission maps and iterations on the physical structure to find the best fit for each chemical setup. Incidentally, the flat CO column density profile is a common feature of disk chemical models. In our case, we would like to raise a few points:
We have shown that CO photodesorption appears to be a good candidate to explain the abundance of cold gas phase CO in circumstellar disks. However, it tends to create a flatter radial profile for the CO column density, in contrast to that observed in disks. Therefore, more work is necessary to solve this problem. Consideration of the photodissociating UV flux and variations in its penetration inside the disk due to grain growth and geometry seem to provide an avenue to improve our modelling of circumstellar disks. Moreover, we have shown that the influence of vertical mixing on the abundance of CO is not straightforward. Rather, the efficiency of vertical mixing depends upon many parameters, including the details of the disk structure (density and temperature) and the level of grain growth, all of which remain uncertain today.
Acknowledgements
F.H. was supported by a CNRS fellowship. F.H. wishes to thank Alan Hindmarsh for useful advice on the use of LSODES. We thank the referee Yuri Aikawa for constructive remarks which helped us to improve the clarity of the paper. F.H., V.W., A.D. and S.G. are financially supported by the French program ``Physique Chimie du Milieu Interstellaire'' (PCMI). E.H. thanks the National Science Foundation (US) for its support of his program in astrochemistry.