A&A 493, 947-958 (2009)
DOI: 10.1051/0004-6361:200810696
V. Sommariva1,2 - G. Piotto2 - M. Rejkuba1 - L. R. Bedin3 - D. C. Heggie4 - R. D. Mathieu5 - S. Villanova6
1 - ESO, Karl-Schwarzschild-Strasse 2, 85748 Garching bei München, Germany
2 - Astronomy Department, Padova University, vic. Osservatorio 2, 35122
Padova, Italy
3 -
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD, USA
4 -
School of Mathematics and Maxwell Institute for Mathematical Sciences, University of Edinburgh, Edinburgh, EH9 3JZ, UK
5 -
Department of Astronomy, University of Wisconsin Madison, WI, 53706, USA
6 -
Grupo de Astronomia, Departamento de Fisica, Universidad de Concepcion, Casilla 160-C, Concepcion, Chile
Received 28 July 2008 / Accepted 2 October 2008
Abstract
Aims. We present a large multi-epoch high resolution spectroscopic investigation searching for binary candidates in the Galactic Globular Cluster (GGC) M4. The aim of our work is the identification of binary candidates, and the determination of the binary fraction and of the binary radial distribution.
Methods. We have obtained 5973 individual spectra of 2469 stars with the multifiber facility FLAMES+GIRAFFE at VLT. Selected stars range from the red giant branch tip to one magnitude below the TO, and cover the entire cluster. Each star has been observed at least twice, with a temporal interval of about three years. For 484 stars we have three epochs. Radial velocities were obtained with the classical cross-correlation technique, using a solar type spectrum as the template.
Results. The average radial velocity of the observed cluster members is 70.29 ![]()
![]() km s-1. The search for variations in radial velocities among the stars with multi-epoch observations yielded 57 binary star candidates. Our radial velocity measurement accuracy allowed us to identify at a
km s-1. The search for variations in radial velocities among the stars with multi-epoch observations yielded 57 binary star candidates. Our radial velocity measurement accuracy allowed us to identify at a ![]() level binaries with radial velocity variations larger than
level binaries with radial velocity variations larger than ![]() 0.3 km s-1 for the target stars with
0.3 km s-1 for the target stars with ![]() ,
and larger than
,
and larger than ![]() 0.5 km s-1 for the targets with
0.5 km s-1 for the targets with ![]() .
We identified 4 binary star candidates out of 97 observed targets inside the core radius, and 53 candidates out of 2372 observed stars outside the core radius. Accounting for the incompleteness affecting our survey, the lower limit for the total binary fraction is f=3.0
.
We identified 4 binary star candidates out of 97 observed targets inside the core radius, and 53 candidates out of 2372 observed stars outside the core radius. Accounting for the incompleteness affecting our survey, the lower limit for the total binary fraction is f=3.0 ![]()
![]() .
The lower limit for the binary fraction in the cluster core is f=5.1
.
The lower limit for the binary fraction in the cluster core is f=5.1 ![]()
![]() ,
while outside the core it decreases to f=3.0
,
while outside the core it decreases to f=3.0 ![]()
![]() .
Similarly, we found f=4.5
.
Similarly, we found f=4.5 ![]()
![]() and f=1.8
and f=1.8 ![]()
![]() for the binary fraction inside and outside the half mass radius.
for the binary fraction inside and outside the half mass radius.
Key words: techniques: spectroscopic - Galaxy: globular clusters: individual: M4 (NGC 6121) - stars: binaries: spectroscopic
The frequency of binary systems is one of the key parameters in dynamical models of star clusters (see review by Hut et al. 1992a,b, and references therein). Through their formation and destruction, binaries play a fundamental role in the dynamical evolution of a globular cluster, especially during the core collapse phase. They can be seen as an efficient heating source that can halt the core collapse (Hut et al. 1992a,b). Additionally, encounters between binary systems and other single or multiple stars can on the one hand disrupt the wider binaries, and on the other lead to the formation of some exotic objects like blue stragglers, millisecond pulsars or X-ray binaries (e.g. Bailyn 1995). There are three basic search techniques for binary systems in a star cluster: (i) photometric study of the so-called secondary sequence in the color-magnitude diagram created by the superposition of two main sequence stars (e.g. Bellazzini et al. 2002; Sollima et al. 2007; Milone et al. 2008); (ii) the study of the light curves of eclipsing binaries (e.g. Yan & Mateo 1994; Albrow et al. 2001; Kaluzny et al. 2008); and (iii) the search for spectroscopic radial velocity variations of the stars at different epochs (e.g. Côté & Fischer 1996; Pryor et al. 1988; Côté et al. 1996). All three methods have some advantages and some limitations. For instance, the photometric study has the advantage of needing only one observational campaign, but it cannot constrain the orbital parameters. On the other hand, the search for eclipsing binaries is sensitive only to systems with periods of less than 10 days (Mateo 1993), and moreover it has some limitations given by the inclination of the systems, and it requires multi-epoch observations. The latter limitation is common to the spectroscopic search for velocity variations. However, this method has important advantages over the last two, because it allow us to determine the orbital period and the eccentricity in an unbiased way. Observational constraints of the period distribution for binary systems are interesting, not only because dynamical processes preferentially eliminate the wider systems (Heggie 1975; Hut 1983), but also because when the period is known it is possible to discriminate between tidal capture and primordial binaries and place some constraints on the system's mass.
Table 1: Previous spectroscopic binary star investigations.
Until now there have been few searches for binary stars in globular clusters through spectroscopic observations of radial velocity variations. In particular, most of the previous work has been limited either to bright red giant branch stars (e.g. M22 observations by Côté et al. 1996), or, due to the relatively low multiplex capabilities of instruments, to a relatively small number of stars per cluster (e.g. Yan & Cohen 1996; Côté & Fischer 1996). A list of all the published spectroscopic binary star investigations is shown in Table 1: the first column gives the name of the globular cluster, the second column the number of stars considered, the third one the number of binary candidates found, and the last one the authors of the search.
The most complete spectroscopic binary-search in M4 is by Côté & Fischer (1996), who analyzed 33 turn-off dwarf stars. Their observations were tuned to search for ultra-hard binaries on the main sequence of the cluster. From the observed variability of two stars, they conclude that
the best-fit binary fraction in this cluster is 15 ![]()
![]() .
We did not find any stars in common with the sample. In this work we analyze several thousand stars in order to estimate
the binary fraction in M4 more accurately.
.
We did not find any stars in common with the sample. In this work we analyze several thousand stars in order to estimate
the binary fraction in M4 more accurately.
The reasons to select M4 as our target are the following. First, it shows no evidence for any central brightness cusp (Trager et al. 1995) indicative of core collapse, despite the fact that the cluster age exceeds its central relaxation time (Harris 1996)
by a factor of approximately 400. Is the lack of evidence of core collapse due to the
presence of a large fraction of binaries? We compare M4 with NGC 6397. NGC 6397 has a mass, relaxation time and Galactic orbit similar to those of M4. Therefore it should be at a similar stage of its evolution, and yet it has a completely different structure with a collapsed core.
Is this due to the lack of primordial binaries? The aim of our investigation is to test this theoretical picture for the first time against observations. This is a fundamental test of our current understanding of the problem, and vital input for future theoretical research. The advent of dedicated machines like the GRAPEs (Hut & Makino 1999), already allows realistic N-body modelling of (open) star clusters with up to 5 ![]() 104 particles (Portegies Zwart et al. 2004). In a few years, with GRAPE-DR, realistic N-body modeling of GC with up to 5
104 particles (Portegies Zwart et al. 2004). In a few years, with GRAPE-DR, realistic N-body modeling of GC with up to 5 ![]() 105 particles (like the estimated original number of stars in M4 and NCG 6397, which makes these two clusters the ideal test cases) will be feasible. At that point, observational inputs, and the comparison of the model with the observed parameters will become of fundamental importance for our understanding of the evolution of the GC, similarly to what happens when we compare stellar evolution models with observed color-magnitude diagrams and luminosity functions.
105 particles (like the estimated original number of stars in M4 and NCG 6397, which makes these two clusters the ideal test cases) will be feasible. At that point, observational inputs, and the comparison of the model with the observed parameters will become of fundamental importance for our understanding of the evolution of the GC, similarly to what happens when we compare stellar evolution models with observed color-magnitude diagrams and luminosity functions.
In order to make realistic models, a number of observational data are needed. Most of them are already available for M4, including mass functions at different radial distances, the proper motion and radial velocity information. This work provides significant improvement to the latter. Only the fundamental information on its binary population is missing. Additional reasons that make M4 our first priority target are that it has an extended (relatively uncrowded) core, making it feasible for search for binaries with a multifiber facility as FLAMES@VLT where the portion of binaries should be highest. Moreover, M4 is the cluster closest to the Sun, which enables us to study the binaries below the turn-off, and these are pristine tracers, as binaries containing giants might be destroyed by internal mass transfer (a prediction that we want to check by observing a few hundred giants). The ultimate goal of the present study is to establish the frequency of binary systems in M4, and to determine their radial distribution within the cluster. These two quantities are intimately linked to the internal dynamics of the cluster. Comparing the current binary frequency in the cluster with the results of dynamical modeling, it is possible to infer important constraints on the primordial binary population.
Heggie & Giersz (2008) recently constructed a dynamical evolutionary model for M4. It is based on a Monte Carlo simulation including an appropriate stellar initial mass function, a primordial binary population, galactic tidal effects, synthetic stellar and binary evolution, relaxation, and three- and four-body interactions. The most surprising discovery from this model was that M4 was found to be a post-collapse cluster sustained by binary burning. The model also provides detailed predictions for the period and spatial distribution of binary systems.
In this paper we will present the results of the spectroscopic search for binary systems in M4. In a forthcoming publication we will make detailed comparisons of our results with the model of Heggie & Giersz (2008).
The organization of this work is as follows: the observations and sample selection are presented in Sect. 2, the data reduction is described in Sect. 3, the radial velocity analysis is carried out in Sect. 4, while the results are presented in Sect. 5. The spatial distribution and the lower limits on the frequency of binaries are discussed in the last section.
In July 2003, we collected a single spectrum for 2684 stars in the GGC M4. The main purpose of this original project (ESO-program 71.D-0205) was the study of the internal velocity dispersion field of M4. In the following, we will refer to these observations as the first epoch (epoch I). For 2469 stars observed in the first epoch we obtained a second spectrum between July and September 2006 (epoch II) under ESO-program 77.D-0182 with the aim of measuring radial velocity variations for those stars in order to identify binary candidates.
In addition to these, for a subsample of 364 stars, mainly in the core of the cluster, we collected a third epoch (epoch III), separated by ![]() 5 weeks from epoch II,
with the intent of detecting short-period binaries.
5 weeks from epoch II,
with the intent of detecting short-period binaries.
All data were obtained with the high resolution spectrograph FLAMES+GIRAFFE at VLT (Pasquini et al. 2000). FLAMES is the Fibre Large Array Multi Element Spectrograph mounted at the Nasmyth A platform of the 8.2 m Kueyen (UT2) telescope, which is part of the Very Large Telescope (VLT) of the European Southern Observatory (ESO) situated on Cerro Paranal. With FLAMES in MEDUSA mode it is possible to observe up to 132 targets at the same time over a field of view of 25 arcmin diameter.
The fibers are accurately placed with the aid of magnetic buttons on a metallic plate (two plates are available at all time: one in place, and the other preparing the buttons for the next pointing). During epoch I twentyfive plates were collected, during epoch II in addition to the same number of plates, three plates with stars placed mainly in the core were taken. These three plates were repeated during epoch III.
The GIRAFFE spectrograph operates at resolutions R= 6000-48 000 across the entire visible range, 360-940 nm. It is equipped with two gratings, high (HR) and low (LR) resolution and with a single 2K ![]() 4K EEV CCD (15
4K EEV CCD (15 ![]() m pixels).
m pixels).
FLAMES is the ideal instrument for this kind of study thanks to the large field of view, the high multiplex capability, the precision in radial velocities and the faint magnitudes that it can reach. For our project the ability to register the radial velocities of stars on a common reference system is a crucial issue. Any unexpected systematic errors between epochs would introduce serious limits to the accuracy of the radial velocity variations that we could see. For this reason during our observations we implemented simultaneous calibrations using the Th-Ar lamp. In total 5973 spectra were collected in three different epochs from the red giant tip to below the Turn-Off (TO). Our sample covers most of the cluster extension, from the inner core out to the cluster outskirts. For 2469 stars we have spectra in two epochs; for a subsample of 484 stars, we have three epochs. For 34 stars we also obtained a fourth epoch. This is due to the fact that together with the 364 stars in the core for which we obtained the third epoch (three repeated plates), we observed an additional 120 stars randomly selected among the targets of epoch II. These repeated stars will provide important cross-checks of the registration of different plates to a common radial velocity system.
Epochs I and II have the purpose of detecting mainly soft-binary candidates with period of up to a few years from the cluster center to its outskirts. Epoch III was taken a few weeks after epoch II with the purpose of identifying hard binaries with period of up to a few weeks inside the cluster core, where binaries are expected to be more numerous because of mass-segregation.
All stars, at all epochs, were selected from our astrometric and photometric catalog (Anderson et al. 2006) with the following criterion: each star at any given magnitude V has no neighbors brighter than a magnitude V+2.5 within an angular distance of 1.2 arcsec (for comparison, the radius of the fibre correspond to only 0.6 arcsec). The catalogue is based on Wide Field Imager (WFI) data from the ESO/MPIA 2.2 m telescope, and has astrometric internal precision of ![]() 7 mas. More recently the photometry has been revised by Momany (private communication). Therefore we decided to use that photometry in the following. The target stars are shown as thick (red) dots in the color-magnitude diagram presented in Fig. 1.
7 mas. More recently the photometry has been revised by Momany (private communication). Therefore we decided to use that photometry in the following. The target stars are shown as thick (red) dots in the color-magnitude diagram presented in Fig. 1.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10696fig1.ps}
\end{figure}](/articles/aa/full/2009/03/aa10696-08/Timg15.gif) |
Figure 1: Small dots show the color-magnitude diagram for all the stars in our astro-photometric catalog. The stars highlighted with thick dots (in red in the electronic version) are the stars for which we have collected spectra. |
| Open with DEXTER | |
Table 2: The fundamental parameters of M4.
All stars were observed with the HR9 setup (514.3-535.6 nm) centered at 525.8 nm. This instrumental configuration offers high resolution (R=25 800) and the best radial velocity accuracy (Royer et al. 2002). This setup covers 200 Å, and a CCD pixel corresponds to 0.05 Å. It provides the best compromise in terms of signal-to-noise ratio (SNR) achievable for red giant stars and the number of spectral lines necessary for accurate Doppler measurements. The stars were grouped in three different subsamples centered at V= 16.5, 17, and 17.5, and their spectra were collected with an exposure time of 1200 s, 1500 s, and 1800 s, respectively, in order to guarantee that each spectrum has a minimum SNR = 10. On the basis of our experience with previous M4 observations and the GIRAFFE pipeline, this is the minimum signal to noise ratio that we need to reach the required radial velocity precision of a few hundreds m/s. Figure 2 shows the positions of the target stars with respect to the cluster center. In our observational strategy we covered all the isolated bright stars in the FLAMES field of view.
Table 3 contains the list of all the plates used for the present work. The first column lists the plate ID (which, according to the ESO file naming convention, contains also the time and date of the exposure start), the second column contains the exposure times, and the third one gives the value of the air mass during the observation. The last column reports the seeing as measured by DIMM, the ESO seeing monitor in Paranal.
Figure 3 displays the value of the signal to noise ratio for all our spectra as a function of the visual magnitude. To estimate the SNR we selected three regions of the spectrum dominated by the continuum, and took average of the three vales of SNR determined with the
IRAF![]() splot task. Inspection of the spectra confirms these values to be consistent with the Poisson noise associated with the object+sky signal. In the figure the asterisks indicate the stars
observed with 1200 s exposures, the squares the stars observed with 1500 s exposures, and the three point stars the stars observed with 1800 s exposure.
splot task. Inspection of the spectra confirms these values to be consistent with the Poisson noise associated with the object+sky signal. In the figure the asterisks indicate the stars
observed with 1200 s exposures, the squares the stars observed with 1500 s exposures, and the three point stars the stars observed with 1800 s exposure.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10696fig2.ps}
\end{figure}](/articles/aa/full/2009/03/aa10696-08/Timg27.gif) |
Figure 2: Spatial distribution of the target stars with respect to the center reported in Table 1. The coordinates are given in arcminutes. Observations from different epochs are shown with different symbols (and colors). The core radius is 0.83, corresponding to 0.53 pc assuming a distance of 1.7 kpc for M4. The white stripes are due to gaps between the CCDs of the WFI at 2.2 m camera where our astrometry comes from. |
| Open with DEXTER | |
Table 3: Summary of the observations. Repeated plates between epoch II and epoch III are marked with an *.
The data reduction was performed using the pipeline developed at Geneva and Paris Observatories (Blecha et al. 2000): the GIRAFFE BaseLine Data Reduction Software (girBLDRS), version 1.13. With it we removed the instrumental signature from the observed data, subtracting the bias and dividing by the normalized flat-field. Flat-field observations were also used to trace the position of all the fibres, and to derive the parameters for the optimal extraction of science exposures. Finally, the wavelength calibration was determined using the day-time Th-Ar lamp exposures.
As we emphasized above, in order to to achieve our scientific goals it is fundamental to register all the radial velocity measurements into a common reference system free - as much as possible - of any systematic error down to ![]() 1 km s-1.
1 km s-1.
Drifts inside the instrument could introduce fiber-to-fiber, plate-to-plate, and epoch-to-epoch systematic errors in the radial velocity measurements. These drifts are due to different conditions of the instrument (for example a variation of the temperature between the night-time calibrations and during the night-time science exposures, or small mechanical shifts caused by earthquakes that occur rather frequently in northern Chile). Such differences would result not only in a different global shift of the velocities derived in the two cases, but also in a fiber-to-fiber difference as a result of a different rotation of the slit geometry.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10696fig3.ps}
\end{figure}](/articles/aa/full/2009/03/aa10696-08/Timg28.gif) |
Figure 3: Estimated signal-to-noise ratio for each of our spectra (see text). Different symbols indicate stars observed with different exposure times. |
| Open with DEXTER | |
In Sect. 4 we will deal with the plate-to-plate and epoch-to epoch systematic errors that can be treated as global shifts. Most of the fiber-to-fiber correction is achieved by adjusting the slit geometry using the day-time Th-Ar exposure closest in time to the science observations. This is done with the wcalslit pipeline task. The remaining fibre-to-fibre drifts are corrected using the five simultaneous Th-Ar fibres that are present in all our scientific frames. We first describe wcalslit and its application, because it has to be done prior to final fibre extraction and wavelength calibration.
The pipeline uses the physical description of the slit geometry and therefore iteratively, using the first guess of the wavelength solution, matches the measured expected positions of the emission Th-Ar lamp lines. However, if there are any drifts in the instrument, the slit geometry needs to be adjusted. The procedure of how to correct the slit geometry and therefore improve the wavelength calibration using only the day-time Th-Ar calibration frames is given at the url http://girbldrs.sourceforge.net/ by the authors of the pipeline. The wcalslit task determines the positions of all the 135 fibres in the Th-Ar day-time lamp frame and compares them with the expected positions in the girSlitGeoMedusa1(2)H9.tfits file which is one of the necessary calibration files of the pipeline. If differences are found, wcalslit updates the table. This task has to be run separately for Medusa1 and Medusa2, i.e. the two plates that are available for FLAMES-Medusa observations.
After adjusting the slit geometry calibration files in this way, we proceeded with the data reduction, by re-extracting the calibration frames: flat-field and wavelength Th-Ar calibration, as well as science exposures. The newly extracted flat-fields were divided, and the newly determined wavelength calibration applied.
FLAMES offers the possibility to observe simultaneously with the on-sky exposure the Th-Ar calibration lamp source through five MEDUSA fibres, which are distributed uniformly over the detector: fibres 1, 32, 63, 94, and 125. These five simultaneous fibres are essential to achieve the optimal wavelength calibration.
Therefore, in order to verify and eliminate any residual wavelength drifts across the 130 fibres, we acquired simultaneous calibration spectra in each of our observations. The unfortunate drawback in having the simultaneous Th-Ar lamps on during the 30 min long exposures is some contamination of the stellar spectra in the fibres located directly next to the simultaneous fibres on the detector. In the subsequent analysis we discarded those spectra, because their velocity measurements had larger errors or, in a few cases of faint stellar spectra, could not be reliably determined.
The current version of girBDLRS corrects the variations of the wavelength solution across the CCD in an automated way. After the fibre extraction and wavelength calibration of all the fibres (including simultaneous calibration fibres) according to the solution obtained using
the reference Th-Ar day-time calibration frame, it computes the shift between the expected and measured position of Th-Ar lines for each of the five simultaneous fibres. For each of the five simultaneous calibration fibres, the average shift is computed and then a linear
regression is fitted to fibre position vs. average shift. Wavelength calibrations for all the fibres are then corrected by applying the computed linear correction. In the second iteration the shifts between the expected and measured average positions of Th-Ar lines of the
simultaneous calibration fibres are typically smaller than 0.001 nm (i.e. ![]() 0.6 km s-1).
0.6 km s-1).
In total we had 56 frames, each with 80-130 spectra, including the sky and the simultaneous calibration fibers. At the end we obtained a total of 5973 stellar spectra. In Fig. 4 we show examples of the spectra that we obtained after the reduction for bright, intermediate and faint stars (V = 12, 14, and 16, respectively).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10696fig4.ps}
\end{figure}](/articles/aa/full/2009/03/aa10696-08/Timg29.gif) |
Figure 4: Extracted spectra for three stars with different magnitudes: in the upper panel for a bright star with V magnitude 12, in the middle panel for an intermediate star with V magnitude 14, and in the bottom panel for a faint star with V magnitude 16. |
| Open with DEXTER | |
We used a cross-correlation technique (Griffin 1967; Tonry & Davis 1979) to measure the radial velocities of all our targets. The cross-correlation of the extracted and wavelength calibrated spectra is included in the girBLDRS pipeline, in the last step, after the correction of the wavelength calibration using the simultaneous calibration fibres.
In the cross-correlation technique the observed spectrum is matched (correlated) with the template. The observed and template spectra should be of a similar spectral type in order to minimize systematic errors due to template missmatch. The template spectrum is shifted in wavelength (velocity) space and the difference with respect to the observation computed until the best fit is found.
The particular implementation of the cross-correlation technique adopted in the girBLDRS is described by Baranne et al. (1996) and Dubath et al. (1990). It uses the numerical mask as the template for cross correlation, in our case based on the solar spectrum from the solar Flux Atlas of Kurucz et al. (1984). For most solar spectral lines the mask provides the lower and upper limits of a wavelength window centered on the line. For any shift in wavelength between the observed spectrum and the numerical mask, the integral of the observed spectrum within the mask windows is calculated. The whole cross-correlation function is then constructed by evaluating the integrals for shifts ranging from a minimum to a maximum selected velocity. More specifically, the template is shifted to a minimum radial velocity and the integral of the observed spectrum passing through the numerical mask evaluated. Then the template is shifted by steps of 0.005 nm (2.8 km s-1) up to the highest chosen radial velocity. The cross-correlation function is computed at each step over the whole velocity domain. In this way, the cross-correlation function is an ``average spectral line'' over all the lines present in the template. It is fitted with a Gaussian, and its peak corresponds to the wavelength (velocity) shift of the object spectrum, and therefore it represents a direct measure of the radial velocity. The girBLDRS pipeline computes the radial velocity for all the stars, including the heliocentric correction. The width of the cross-correlation function depends on the instrumental and object line broadening.
The greater the number of spectral lines in the considered wavelength interval, and the higher the resolution of the spectrum, the higher is the precision of the velocity determination. Therefore, in order to achieve the best possible precision, we have used the HR9 setup of the FLAMES+GIRAFFE spectrograph, because it covers a wavelength region very rich in iron lines, has one of the highest resolutions offered by the instrument, and the highest throughput for the G and K-type stars. For the cross-correlation process we selected a solar template mask (G2), because it corresponds to the average spectral type of our targets, given that we observed red giant branch stars with magnitudes ranging from the tip of the RGB (V=11) to one magnitude below the turn off (V=16.8).
In order to check whether our radial velocities are affected by systematic errors due to template mismatch we performed the following test. First, we plotted all radial velocities as a function of the B-V color and of the V magnitude. Figure 5 shows that there is no evidence of any systematic dependence of the radial velocity either on the magnitude or the B-V color.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10696fig5.ps}
\end{figure}](/articles/aa/full/2009/03/aa10696-08/Timg30.gif) |
Figure 5: Radial velocities as a function of color ( upper panel) and magnitude ( bottom panel) obtained for our individual spectra. Different colors refer to different epochs. The horizontal line indicates the mean radial velocity (value at the top) of all the stars. |
| Open with DEXTER | |
We computed the radial velocities for several plates also using an F0 star template mask. In order to compare the two results, we calculated the radial velocity differences computed by using the two
different templates: we found an average value of 65 ![]() 11 m s-1. We repeated the same test only with the few stars that we observed in the horizontal branch (see Fig. 1), and we found that the mean radial velocity difference computed using the two different templates is
about 80
11 m s-1. We repeated the same test only with the few stars that we observed in the horizontal branch (see Fig. 1), and we found that the mean radial velocity difference computed using the two different templates is
about 80 ![]() 34 m s-1.
34 m s-1.
In this section we describe how we minimized the plate-to-plate and epoch-to-epoch systematic errors (global shifts in the velocity reference frame).
As described in Sects. 3 and 4, within each plate the velocities were computed on the common reference system, which - if there were no systematic errors - should be the same for all the plates, and should coincide with the Solar system barycentric rest-frame.
In order to measure any possible deviations from this, we considered - in each plate - the five simultaneous calibration fibres (described in Sect. 3). In all our plates, these fibres provide Th-Ar calibration-lamp spectra for which we also can measure wavelength shifts.
To test the presence and size of the average radial velocity differences between different plates we first defined a radial velocity system common to all the plates. This was assumed to be the average of the five calibration fiber velocities of the first plate, of the first night, and of the first epoch. In the following we will refer to this plate as the reference-plate. We then calculated the difference of the velocities from the calibration fibres of other plates, with respect to that of the reference-plate.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10696fig6.ps}
\end{figure}](/articles/aa/full/2009/03/aa10696-08/Timg31.gif) |
Figure 6: The average radial velocity differences for the simultaneous calibration fibers between the reference plate and all the other plates (Px) plotted as a function of the Modified Julian day. There is a systematic offset in the radial velocity zero point between the two epochs. |
| Open with DEXTER | |
The result is shown in Fig. 6 where the amount of the global shift in km s-1 is plotted as a function of the Modified Julian day. It appears that within each epoch the velocities of plates are
registered to a common reference system within ![]() 50 m s-1. Going from epoch I to epoch II/epoch III the shifts are larger, of the order of
50 m s-1. Going from epoch I to epoch II/epoch III the shifts are larger, of the order of ![]() 100 m s-1.
100 m s-1.
We then corrected our plate-to-plate and epoch-to-epoch global shifts simply applying to all plates their velocity difference with respect to the reference plate. This put all the velocities from different plates into a common radial velocity system within
![]() 100 m s-1 (not necessarily coincident with the true Solar system barycenter).
100 m s-1 (not necessarily coincident with the true Solar system barycenter).
Figures 7 and 8 show the results of the application of the above procedure. The two figures show the differences in radial velocity for stars with multiple spectra before (Fig. 7) and after (Fig. 8) the application of the correction. In the upper panel, there are the bright stars with (V<15), in the bottom panel, the faint stars with (V>15). In these figures the the thick black line marks the position of the zero, the solid lines represent the mean and the dotted lines the median. After the subtraction of the zero point shifts the mean and the median are close to zero, as expected.
Some systematic trends in our radial velocities are expected. Effects such as
gravitational redshift (![]() 0.5 m s-1 for red dwarf stars) and convective blue shifts (
0.5 m s-1 for red dwarf stars) and convective blue shifts (![]() -0.2-0.3 km s-1 for Red Giants, Madsen et al. 2002) are not affecting differential measurements for the binary search, but they do affect the absolute value of the velocity in the Solar system barycenter rest-frame. We did not attempt any correction for them, since these two effects are pushing in opposite directions, we simply add an average
contribution of 0.3 km s-1 to our uncertainties on the absolute radial velocities.
Moreover, because of the zero point global shifts mentioned in Sect. 4.1, we have an additional systematic error of
-0.2-0.3 km s-1 for Red Giants, Madsen et al. 2002) are not affecting differential measurements for the binary search, but they do affect the absolute value of the velocity in the Solar system barycenter rest-frame. We did not attempt any correction for them, since these two effects are pushing in opposite directions, we simply add an average
contribution of 0.3 km s-1 to our uncertainties on the absolute radial velocities.
Moreover, because of the zero point global shifts mentioned in Sect. 4.1, we have an additional systematic error of ![]() 0.1 km s-1. In conclusion, the resulting average velocity for M4 is:
0.1 km s-1. In conclusion, the resulting average velocity for M4 is:
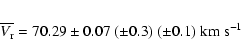
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10696fig7.ps}
\end{figure}](/articles/aa/full/2009/03/aa10696-08/Timg33.gif) |
Figure 7: Histogram of differences of multiple radial velocity measurements used to evaluate the reliability of our calibrations. In this case no corrections have been applied to our measurements. The upper panel shows the bright stars ( V < 15), the bottom panel shows the faint stars ( V > 15). The solids lines are the mean and the dotted lines are the median. The thick black line marks the position of a null difference. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10696fig8.ps}
\end{figure}](/articles/aa/full/2009/03/aa10696-08/Timg34.gif) |
Figure 8: Histogram of differences of multiple radial velocity measurements used to evaluate the reliability of our calibrations. In this case the shift found in the way described in the text has been applied. In the upper panel we show the results for the bright stars ( V < 15), the bottom panel for the faint stars ( V > 15). The solid lines are the mean, and the dotted lines are the median. The thick black line marks the position of a null difference. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10696fig9.ps}
\end{figure}](/articles/aa/full/2009/03/aa10696-08/Timg35.gif) |
Figure 9: Left: color magnitude diagram of the stars in our photometric catalog. Thick dots indicate the target stars for which we have spectra. Right: for five different magnitude intervals, the histogram of the radial velocity distribution. Note that, in order to increase the statistics, the brightest bin covers a wider range in magnitude. |
| Open with DEXTER | |
The left side of Fig. 9 shows the CMD for our target stars. We divided our sample of stars in five bins in V magnitude. The right panel of Fig. 9 shows the histogram of the distribution into radial velocity ![]() of the stars in each bin, and the least
square best fit Gaussian.
of the stars in each bin, and the least
square best fit Gaussian.
The labels in each panel give the values of the average radial velocity (
![]() )
for that bin and its dispersion (
)
for that bin and its dispersion (
![]() ).
).
The weighted mean of the five independent values is
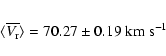
Our measured radial velocity is in good agreement with previous studies. In particular, Peterson et al. (1995) measured the average radial velocity of M4 to be
![]()
![]() 0.6 km s-1 from the radial velocities of 200 giant stars. Côté & Fisher (1996) analyzed 33 turn-off dwarf stars and reported a value of 70.3
0.6 km s-1 from the radial velocities of 200 giant stars. Côté & Fisher (1996) analyzed 33 turn-off dwarf stars and reported a value of 70.3 ![]() 0.7 km s-1.
0.7 km s-1.
In this section we describe the selection of the binary candidates from the measured radial velocity variations.
Our approach, which is adequate for stars with two or more epochs, is based on the comparison of the observed weighted rms velocity for single stars with the average rms for each star at the same magnitude. Stars with rms several times larger than expected are likely to be binary candidates.
The weight wi,j for the i-star, observed in the j-plate used to compute the rms, is provided by the pipeline formal errors
![]() ,
according to the relation:
,
according to the relation:
![]() .
We note that these errors underestimate the true errors, but they contain valuable information on the goodness of the Gaussian fit to the cross-correlation function, which is related to the goodness of the observed spectrum (see Sect. 3). More explicitly, this strategy turns out to be the most robust against false detections caused by a bad
spectrum (which received an almost null weight), i.e. spectra with particularly low SNR, or altered by cosmic ray events. The weighted mean radial velocity for the i-star observed in n plates,labeled as j-plate, with j from 1 to n (with n=2, 3, or 4, depending on the available number of epochs) has been calculated as:
.
We note that these errors underestimate the true errors, but they contain valuable information on the goodness of the Gaussian fit to the cross-correlation function, which is related to the goodness of the observed spectrum (see Sect. 3). More explicitly, this strategy turns out to be the most robust against false detections caused by a bad
spectrum (which received an almost null weight), i.e. spectra with particularly low SNR, or altered by cosmic ray events. The weighted mean radial velocity for the i-star observed in n plates,labeled as j-plate, with j from 1 to n (with n=2, 3, or 4, depending on the available number of epochs) has been calculated as:
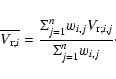
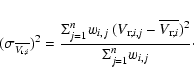
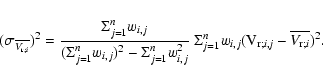
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10696fig10.ps}
\end{figure}](/articles/aa/full/2009/03/aa10696-08/Timg50.gif) |
Figure 10:
The weighted rms as a function of the magnitude is shown for all the
M4 stars that have been observed in at least two epochs. A large rms is likely to be due to an intrinsic variation of the radial velocity. The solid line connecting
|
| Open with DEXTER | |
The present data allow us to identify a the 3![]() level binary candidates with velocity variation greater than
level binary candidates with velocity variation greater than ![]() 0.3 km s-1 for the bright stars (
0.3 km s-1 for the bright stars (![]() ), and velocity variations greater than
), and velocity variations greater than ![]() 0.5 km s-1 for the faint stars (V>15). We found 57 binary candidates. Figure 11 shows the location of the binary candidates in the CMD. With the triangle we shown the binary candidate found also in the photometric binary sample of Milone et al. (2008).
0.5 km s-1 for the faint stars (V>15). We found 57 binary candidates. Figure 11 shows the location of the binary candidates in the CMD. With the triangle we shown the binary candidate found also in the photometric binary sample of Milone et al. (2008).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10696fig11.ps}
\end{figure}](/articles/aa/full/2009/03/aa10696-08/Timg51.gif) |
Figure 11: Location of the binary candidates (large red dots) in the CMD. The triangle (green in the electronic version) indicates a binary candidate found also in the photometric sample (Milone et al. 2008). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10696fig12.ps}
\end{figure}](/articles/aa/full/2009/03/aa10696-08/Timg52.gif) |
Figure 12: Radial distribution of the binary system candidates. The inner circle represents the cluster core. The outer circle indicates the total area of the cluster covered by observations. The dotted circle contains the binaries inside the half mass radius. |
| Open with DEXTER | |
In Table 4 we give the list of the binary system candidates coming from two epochs, three epochs, and in one case with four epoch spectra. For each star, the table gives the radial velocity as measured in the different epochs with the corresponding errors, the coordinates (RA and
Dec) in degrees, the Modified Julian Date of the observations, the number of epochs that each star has been observed, the radial distance from the center in arcmin, and the B and V magnitudes from the calibrated photometric catalogue (Momany, private communication). Figure 12 shows the radial distribution of the binary candidates. The total binary fraction that we found is f=2.3 ![]()
![]() .
The quoted the error is 1-
.
The quoted the error is 1-![]() error. This is significantly smaller than the binary fraction presented by Coté & Fischer (1996), but within the erros it is consistent, since Coté & Fischer quote
error. This is significantly smaller than the binary fraction presented by Coté & Fischer (1996), but within the erros it is consistent, since Coté & Fischer quote ![]()
![]() error. We split our sample in two subsamples on the basis of the magnitude of the star in order to calculate the percentage of the binary system candidates below and above the turn off. We found that the fraction of binaries among stars below the turn off is f=1.9
error. We split our sample in two subsamples on the basis of the magnitude of the star in order to calculate the percentage of the binary system candidates below and above the turn off. We found that the fraction of binaries among stars below the turn off is f=1.9 ![]()
![]() ,
while the fraction above the TO is f=2.7
,
while the fraction above the TO is f=2.7 ![]()
![]() .
We detected a total of 4 candidates out of 97 observed targets inside the core radius, and 53 candidates out of 2372 observed stars outside the core radius. These numbers imply a lower limit for the binary fraction f=4.1
.
We detected a total of 4 candidates out of 97 observed targets inside the core radius, and 53 candidates out of 2372 observed stars outside the core radius. These numbers imply a lower limit for the binary fraction f=4.1 ![]()
![]() inside the cluster core, and f=2.2
inside the cluster core, and f=2.2 ![]()
![]() outside the
core. We also found that that the fraction of binaries inside the half mass radius (
outside the
core. We also found that that the fraction of binaries inside the half mass radius (
![]() pc) is f=3.0
pc) is f=3.0 ![]()
![]() ,
while outside
,
while outside
![]() we have f=1.5
we have f=1.5 ![]()
![]() .
It is worth noticing that the sample that we found represents only spectroscopic binary candidates and not the total population of binary systems: based on Gaussian statistic it is probable that our
sample includes some false detections, and is incomplete. With at least one other epoch we could
confirm the candidates found with this survey, and reach a significantly higher completeness in our estimate of the binary fraction. In order to quantify what we would gain from one additional epoch, and to have an empirical estimate of the completeness of our present search, we analyzed the binary
fraction we obtained from the subsample of stars with three epochs. We calculated how many binary candidates have been detected using three epochs of the data and we compared this number with the
candidates that would be detected using only two epochs. We found that using only two epochs we can identify 8 candidates out of the available 484 targets. We analyzed all the possible
combinations between the epochs, and the results were the same, and therefore robust.
Using all three epochs we found 12 candidates out of the 484 targets. All the 8 candidates from the two epoch observations could be confirmed by adding the third epoch. A third epoch of observations is extremely important: our simple test shows that the binary fraction from two epochs suffers from an incompleteness of at least of 40%.
.
It is worth noticing that the sample that we found represents only spectroscopic binary candidates and not the total population of binary systems: based on Gaussian statistic it is probable that our
sample includes some false detections, and is incomplete. With at least one other epoch we could
confirm the candidates found with this survey, and reach a significantly higher completeness in our estimate of the binary fraction. In order to quantify what we would gain from one additional epoch, and to have an empirical estimate of the completeness of our present search, we analyzed the binary
fraction we obtained from the subsample of stars with three epochs. We calculated how many binary candidates have been detected using three epochs of the data and we compared this number with the
candidates that would be detected using only two epochs. We found that using only two epochs we can identify 8 candidates out of the available 484 targets. We analyzed all the possible
combinations between the epochs, and the results were the same, and therefore robust.
Using all three epochs we found 12 candidates out of the 484 targets. All the 8 candidates from the two epoch observations could be confirmed by adding the third epoch. A third epoch of observations is extremely important: our simple test shows that the binary fraction from two epochs suffers from an incompleteness of at least of 40%.
Table 4: List of the binary system candidates found. The columns are: ID, radial velocity and relative error that comes form the pipeline, the mean of the radial velocity, the weighed error, the Modified Julian Day of observations, number of epochs, coordinates (RA and Dec), distance from the center in arcminutes, V, B magnitude.
Accounting for this incompleteness, and considering the number of targets with two and three epochs observed inside and outside the core, we have that the fraction of binary candidates in the whole sample is f=3.0 ![]()
![]() ,
inside the core becomes f=5.1
,
inside the core becomes f=5.1 ![]()
![]() ,
and f=3.0
,
and f=3.0 ![]()
![]() outside the core. In the same way, we find f=4.5
outside the core. In the same way, we find f=4.5 ![]()
![]() and f=1.8
and f=1.8 ![]()
![]() for the fraction of binaries inside and outside the cluster half mass radius.
for the fraction of binaries inside and outside the cluster half mass radius.
We have obtained 5973 individual spectra of 2469 stars in the Galactic globular cluster M4. Each star has been observed at least twice, in a temporal interval of about three years. For 484 stars we have three epochs. All the data were obtained with the same instrument FLAMES+GIRAFFE at VLT, and with the same set-up. This database represents the largest multi-epoch high resolution spectroscopic sample ever collected in a globular cluster.
The observed stars cover a large range in luminosity, from the red giant branch tip to more than 1 mag below the TO, and cover most of the cluster extension from the inner core to the outskirts.
We cross-correlated all the stellar spectra with the solar template to derive accurate radial velocities. The average radial velocity of the observed stars is 70.29 ![]()
![]() km s-1, where the systematic errors in parenthesis include the effects such as gravitational redshift, convective blue shifts, and the global zero point uncertainty of the radial
velocity. No systematic shift in average velocity is observed as a function of
the stellar magnitude and color.
km s-1, where the systematic errors in parenthesis include the effects such as gravitational redshift, convective blue shifts, and the global zero point uncertainty of the radial
velocity. No systematic shift in average velocity is observed as a function of
the stellar magnitude and color.
The search for variations in radial velocities among the stars with multi-epoch observations yielded 57 binary star candidates. The candidates in the bright sample (![]() )
have
)
have ![]() velocity
variations larger than
velocity
variations larger than ![]() 0.3 km s-1, while the fainter candidates (V>15 mag) have
0.3 km s-1, while the fainter candidates (V>15 mag) have ![]() velocity variations larger than
velocity variations larger than ![]() 0.5 km s-1.
0.5 km s-1.
There are four binary star candidates out of 97 observed targets inside the core radius, and 53 candidates out of 2372 observed stars outside the core radius. We have shown that increasing the stellar coverage from two epochs to three epochs, the number of binary candidates increases by 40%.
Accounting for this incompleteness affecting stars with only two epochs, we have found that the lower limit for the binary fraction is f=3.0 ![]()
![]() ;
the binary fraction in the cluster core is f=5.1
;
the binary fraction in the cluster core is f=5.1 ![]()
![]() ,
which decreases to f=3.0
,
which decreases to f=3.0 ![]()
![]() outside the core.
Similarly, we found f=4.5
outside the core.
Similarly, we found f=4.5 ![]()
![]() and f=1.8
and f=1.8 ![]()
![]() for the binary fraction
inside and outside the half mass radius. As expected from energy equipartition, the binary fraction is higher in the central parts of the cluster.
for the binary fraction
inside and outside the half mass radius. As expected from energy equipartition, the binary fraction is higher in the central parts of the cluster.
In the next paper we will present detailed completeness simulations to accurately constrain the total binary fraction in the cluster as a function of magnitude, period, and other orbital parameters. These will then be used together with the dynamical evolutionary modeling of Heggie & Giersz (2008) to derive the limits for the primordial binary fraction in M4.
This model is specifically tailored to this cluster. It includes all the main processes affecting the distribution of single stars and binaries in 12 Gyr of evolution, i.e. two-, three- and four-body encounters, the galactic tide, and the internal evolution of single and binary stars. It provides satisfactory fits to the surface-brightness profile, velocity dispersion profile and luminosity functions (in two fields) of M4, but the properties of its binary stars are still poorly constrained. We shall examine this model using the same observational constraints (on magnitude, radial distribution and cadence) as in the actual observations ofM4 reported in this paper, in order to test our estimates of the completeness of the observational sample, and to improve our assumptions on the initial abundance and other parameters of the binaries in this cluster.
Acknowledgements
We thank Claudio Melo for his kind advice on the pipeline and Antonino Milone for providing his reults on the photometric binary. We also thank the referee for his helpful comments and suggestions.