A&A 493, 1155-1160 (2009)
DOI: 10.1051/0004-6361:200810294
N. F. Allard1,2 - J. F. Kielkopf3
1 - Observatoire de Paris, GEPI, UMR 8111, CNRS, 61 avenue de l'Observatoire, 75014 Paris, France
2 - Institut d'Astrophysique de Paris, UMR 7095, CNRS, Université Pierre et Marie Curie, 98bis boulevard Arago, 75014 Paris, France
3 - Department of Physics and Astronomy, University of Louisville, Louisville, KY, 40292, USA
Received 30 May 2008 / Accepted 14 October 2008
Abstract
Context. An accurate determination of the line broadening of the Lyman series of atomic hydrogen has been shown to be fundamental to interpretating UV and FUV spectra of DA white dwarfs. Quasi-molecular lines have been detected in the red wing of Lyman-![]() ,
Lyman-
,
Lyman-![]() ,
and Lyman-
,
and Lyman-![]() .
They arise from radiative collisions of excited atomic hydrogen with unexcited neutral hydrogen atoms or protons.
.
They arise from radiative collisions of excited atomic hydrogen with unexcited neutral hydrogen atoms or protons.
Aims. The aim of this paper is twofold. First, we examine the range of validity of the one-perturber approximation widely used to calculate the line wing. Second, we study the relative contributions of the two main transitions contributing to the far wing of the Lyman-![]() line profile according to the effective temperature and perturber density.
line profile according to the effective temperature and perturber density.
Methods. In cool white dwarfs, the perturber density is so high that the one-perturber approximation breaks down and the collisional effects must be treated by using the autocorrelation formalism in order to take into account simultaneous collisions with more than one perturbing atom.
Results. We show that, at the low temperatures of cool white dwarfs, the contribution of the singlet
![]() transition cannot be neglected in the calculation of Lyman-
transition cannot be neglected in the calculation of Lyman-![]() profile perturbed by neutral hydrogen. A comparison with experimental laboratory spectra shows that the effects of multiple H-perturbers appear in the far wing.
profile perturbed by neutral hydrogen. A comparison with experimental laboratory spectra shows that the effects of multiple H-perturbers appear in the far wing.
Conclusions. A reliable determination of the line profiles for the physical conditions of cool white dwarfs requires a unified theory that takes account of both the singlet and triplet transitions contributing to Lyman-![]() using accurate interaction potentials and radiative dipole transition moments. Multiple perturber effects must be considered and the autocorrelation formalism permits calculations for the densities of the atmospheres of cool white dwarfs.
using accurate interaction potentials and radiative dipole transition moments. Multiple perturber effects must be considered and the autocorrelation formalism permits calculations for the densities of the atmospheres of cool white dwarfs.
Key words: stars: white dwarfs - line: profiles - radiation mechanisms: general - stars: atmospheres
In Allard & Kielkopf (1991), we presented calculations
of the dependence on temperature and density of the resonance broadening in
the far wing of the Lyman-![]() line for atmospheres of DA white dwarfs.
We highlighted the importance of the close collisions of many perturbers, which leads to the formation of a series of satellites in the far red wing of Lyman-
line for atmospheres of DA white dwarfs.
We highlighted the importance of the close collisions of many perturbers, which leads to the formation of a series of satellites in the far red wing of Lyman-![]() .
We emphasized that these effects would provide a previously unrecognized source
of opacity for the photosphere of a DA white dwarf when it cools
to below 10 000 K. As a consequence, we concluded the far wing of Lyman-
.
We emphasized that these effects would provide a previously unrecognized source
of opacity for the photosphere of a DA white dwarf when it cools
to below 10 000 K. As a consequence, we concluded the far wing of Lyman-![]() becomes an important consideration when the age of the galactic disk is estimated from the luminosity function of very cool white dwarfs.
becomes an important consideration when the age of the galactic disk is estimated from the luminosity function of very cool white dwarfs.
In Allard et al. (2004), we presented a study of the influence of
temperature on the line wing and satellites of the Lyman-![]() absorption profiles, and compared synthesized absorption spectra
with HST spectra of ZZ Ceti white dwarfs, typically at temperatures from
10 000 to 15 000 K. In this paper, we extend that work to the physical conditions of
very cool white dwarfs with
absorption profiles, and compared synthesized absorption spectra
with HST spectra of ZZ Ceti white dwarfs, typically at temperatures from
10 000 to 15 000 K. In this paper, we extend that work to the physical conditions of
very cool white dwarfs with
![]() below 5000 K.
We restrict our study to the collisional effects due to atomic hydrogen.
below 5000 K.
We restrict our study to the collisional effects due to atomic hydrogen.
It is of considerable interest to determine line profiles in these
extreme physical conditions. A small fraction of the DA white dwarfs are known to have
effective temperatures
![]() K.
Such objects were discussed by Wolff et al. (2002) and Kowalski & Saumon (2006).
K.
Such objects were discussed by Wolff et al. (2002) and Kowalski & Saumon (2006).
![\begin{figure}
\par\includegraphics[width=12cm,clip]{0294fig1.eps}
\end{figure}](/articles/aa/full/2009/03/aa10294-08/Timg22.gif) |
Figure 1:
Correlation diagram for H2 states contributing to Lyman- |
| Open with DEXTER | |
The correlation diagram in Fig. 1 allows us to identify
the molecular transitions that contribute to Lyman-![]() .
Solid and dotted lines are respectively used for singlet and triplet
states. The version shown here corrects one presented in Allard et al. (1994)
in which the labels of the a and h triplet states were interchanged. The correct correlation diagram shown here was used in Allard et al. (1998), and in our subsequent work, but the correction was not clearly explained in that paper.
.
Solid and dotted lines are respectively used for singlet and triplet
states. The version shown here corrects one presented in Allard et al. (1994)
in which the labels of the a and h triplet states were interchanged. The correct correlation diagram shown here was used in Allard et al. (1998), and in our subsequent work, but the correction was not clearly explained in that paper.
In Allard et al. (1999), we developed a new theory
taking into account the dependence on interatomic distance of the transition
probability of allowed and asymptotically forbidden transitions.
Our approach, which introduces the concept of a modulated dipole transition
moment into the calculation of the line shape, allows us to take into account the two asymptotically forbidden transitions (
![]() and
and
![]() )
of quasi-molecular
hydrogen that dissociate into (1s, 2s) atoms. Our results show that they constitute a minor contribution compared with the other transitions.
)
of quasi-molecular
hydrogen that dissociate into (1s, 2s) atoms. Our results show that they constitute a minor contribution compared with the other transitions.
Collisions of neutral H atoms contribute strongly to the red wing of Lyman-![]() through transient singlet states of H2. The
through transient singlet states of H2. The
![]()
![]()
![]() and
and ![]()
![]()
![]() free-free transitions lead to quasi-molecular line satellites corresponding to the Lyman and Werner H2 bands. These satellites were observed in experimental spectra of laser-produced plasma sources, which simulate white dwarf atmospheric conditions in the laboratory (Kielkopf & Allard 1995).
free-free transitions lead to quasi-molecular line satellites corresponding to the Lyman and Werner H2 bands. These satellites were observed in experimental spectra of laser-produced plasma sources, which simulate white dwarf atmospheric conditions in the laboratory (Kielkopf & Allard 1995).
We use the molecular data of
Spielfiedel (2003) and Spielfiedel et al. (2004).
In Fig. 2, we have plotted the potential energies of the 2 transitions that contribute most to the far red wing of the Lyman-![]() :
the triplet transition b
:
the triplet transition b
![]()
![]() a
a
![]() and the singlet
and the singlet
![]() transition.
transition.
In Fig. 3, we have plotted the potential difference
related to the
![]() transition,
together with the modulated dipole moment of this transition for different
temperatures. The corresponding figure for the singlet
transition,
together with the modulated dipole moment of this transition for different
temperatures. The corresponding figure for the singlet
![]() transition is given in Fig. 2 of Allard et al. (2004). The radiative electric dipole transition moment of each component of the line depends on R, and changes during the collision. In Allard et al. (1999), we defined
transition is given in Fig. 2 of Allard et al. (2004). The radiative electric dipole transition moment of each component of the line depends on R, and changes during the collision. In Allard et al. (1999), we defined
![]() as a modulated dipole given by (Allard et al. 1999)
as a modulated dipole given by (Allard et al. 1999)
![\begin{displaymath}D(R)=\tilde{\rm d}_{ee'}[R(t)] =
{\rm d}_{ee'}[R(t)]{\rm e}^{-\frac {V_e [R(t)]}{2kT}},
\end{displaymath}](/articles/aa/full/2009/03/aa10294-08/img33.gif) |
(1) |
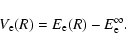 |
(2) |
| (3) |
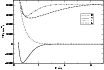 |
Figure 2:
Molecular potentials for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0294fig3.eps}
\end{figure}](/articles/aa/full/2009/03/aa10294-08/Timg38.gif) |
Figure 3:
Variation with temperature in the modulated dipole
and the difference potential of the
|
| Open with DEXTER | |
Many problems in collision-induced, radiative transitions have been solved by using the one-perturber approximation. At very low densities, the binary model for an optically active atom in collision with one perturber is valid for the entire profile, apart from the central part of the line.
Semi-classical and quantum calculations of the wing of Lyman-![]() were first developed by Sando et al. (1969) and Sando & Wormhoudt (1973). The semi-classical methods used by Sando & Wormhoudt (1973) were generalized for applying to entire profiles in the unified Franck-Condon theory of Szudy & Baylis (1975). This method has been used widely for the
analysis of line-broadening experiments (Allard & Kielkopf 1982).
Its simplicity derives from a neglect, in the line wing, of
multiple close collisions. The profiles computed with this approach
provide a unified expression from the line core to the wing.
However, in the satellite region of the line wing the results are only valid when
densities are so low that the probability of close collision of more than two
atoms is negligibly small in comparison to the contributions from binary
collisions. In real systems, multiple perturber collisions cannot be
neglected beyond the satellite except at very low density.
were first developed by Sando et al. (1969) and Sando & Wormhoudt (1973). The semi-classical methods used by Sando & Wormhoudt (1973) were generalized for applying to entire profiles in the unified Franck-Condon theory of Szudy & Baylis (1975). This method has been used widely for the
analysis of line-broadening experiments (Allard & Kielkopf 1982).
Its simplicity derives from a neglect, in the line wing, of
multiple close collisions. The profiles computed with this approach
provide a unified expression from the line core to the wing.
However, in the satellite region of the line wing the results are only valid when
densities are so low that the probability of close collision of more than two
atoms is negligibly small in comparison to the contributions from binary
collisions. In real systems, multiple perturber collisions cannot be
neglected beyond the satellite except at very low density.
An exact methodology for the quantum calculation at high densities,
as encountered in stellar atmospheres or laboratory plasmas, is unknown.
However, the results of their quantum calculation are also reproduced by
a semi-classical approach, and are a successful test of the semi-classical
methods. Fortunately, the semi-classical methods can also be extended
by unified theories of line broadening to permit an inclusion of the effects
of multiple collisions (Allard & Kielkopf 1982). The density expansion
(Royer 1971, 1978) enables the accurate numerical evaluation of the far wing possible for many conditions of astrophysical interest.
Figure 4 shows the total profile that takes into account
the 4 allowed transitions, the
![]() and
and
![]()
![]()
![]() singlet transitions,
and the
b
singlet transitions,
and the
b
![]()
![]() a
a
![]() and
and
![]() triplet transitions. The red wing is dominated by the contribution of multiple-perturber collisions, and the expansion of the autocorrelation function in density must be completed to the fourth order to be comparable
with the result obtained from a unified calculation.
triplet transitions. The red wing is dominated by the contribution of multiple-perturber collisions, and the expansion of the autocorrelation function in density must be completed to the fourth order to be comparable
with the result obtained from a unified calculation.
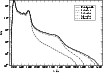 |
Figure 4:
Contribution of the different orders of the expansion to the profile for T=10 000 K and
|
| Open with DEXTER | |
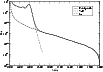 |
Figure 5:
Contribution of the
|
| Open with DEXTER | |
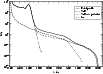 |
Figure 6:
Contribution of the
|
| Open with DEXTER | |
In the following, we restrict our study to the singlet
![]() and triplet
and triplet
![]() transitions, the two transitions
that contribute most to the red wing of the Lyman-
transitions, the two transitions
that contribute most to the red wing of the Lyman-![]() line.
All calculations are completed using the density expansion to the seventh order.
line.
All calculations are completed using the density expansion to the seventh order.
The total profiles shown in the figures are the Fourier transforms of the correlation function given by Eq. (121) of Allard et al. (1999), in which the contributions from different components of the transition enter with their statistical weights. The figures also show the individual components for comparison,
weighted as if they were the only contribution to the profile.
The profiles presented here are applicable to wavelengths between
the Lyman-![]() line and the far infrared.
line and the far infrared.
Figure 5 shows the prominent satellite that arises from the
![]() -B
-B
![]() free-free transition
of a neutral hydrogen atom in the presence of other ground state atoms.
The two-body H(1s)-H(2p) satellite is at approximately 1600 Å.
It arises from the extremum of -20 200 cm-1 in the
free-free transition
of a neutral hydrogen atom in the presence of other ground state atoms.
The two-body H(1s)-H(2p) satellite is at approximately 1600 Å.
It arises from the extremum of -20 200 cm-1 in the
![]() difference potential, when the two atoms are separated by about 2 Å (see Fig. 2 of Allard et al. 2004). The contribution of the
difference potential, when the two atoms are separated by about 2 Å (see Fig. 2 of Allard et al. 2004). The contribution of the
![]() transition is identical to the first order of the expansion shown in Fig. 5. At such a low density (
transition is identical to the first order of the expansion shown in Fig. 5. At such a low density (
![]() atoms cm-3), the one-perturber approximation is valid, and the total profile above 1800 Å is due to the triplet
atoms cm-3), the one-perturber approximation is valid, and the total profile above 1800 Å is due to the triplet
![]() transition.
transition.
When the H density is increased to
![]() atoms cm-3,
Fig. 6 shows that the far wing of the individual profile from the
atoms cm-3,
Fig. 6 shows that the far wing of the individual profile from the
![]() transition above 1800 Å is due to multiple-perturber collisions.
In a simple additive approximation,
a three-body satellite to Lyman-
transition above 1800 Å is due to multiple-perturber collisions.
In a simple additive approximation,
a three-body satellite to Lyman-![]() should result from
an H(2p) atom radiating while it is close to two H(1s) atoms. A difference potential minimum of approximately
should result from
an H(2p) atom radiating while it is close to two H(1s) atoms. A difference potential minimum of approximately
![]() cm-1 is expected in this case. The effect observed in laboratory spectra at 2500 Å discussed below is -45 300 cm-1 from the Lyman-
cm-1 is expected in this case. The effect observed in laboratory spectra at 2500 Å discussed below is -45 300 cm-1 from the Lyman-![]() line center. At
line center. At
![]() atoms cm-3 the total profile above 1800 Å is still primarily due to the
atoms cm-3 the total profile above 1800 Å is still primarily due to the
![]() transition, but the
transition, but the
![]() second satellite begins to contribute to the amplitude of the far wing.
second satellite begins to contribute to the amplitude of the far wing.
When the density is as high as
![]() atoms cm-3 (Fig. 4),
the one-perturber binary approximation is no longer valid.
The amplitude of the first satellite is linear with density until 1021, but for
atoms cm-3 (Fig. 4),
the one-perturber binary approximation is no longer valid.
The amplitude of the first satellite is linear with density until 1021, but for
![]() ,
the amplitude of the first satellite begins to decrease with increasing
density. When this density is reached, the probability of a
collision with two perturbers is higher than the probability of a
collision with only one perturber (see e.g. Allard 1978; Royer 1978). Theoretically, as shown by Royer (1971), the probability of m perturbers in a volume V is shown in Fig. 27 of Allard & Kielkopf (1982). These variations in amplitude of the first and second satellites are well explained using a square well potential, as is shown in the
analysis of Allard (1978) (Fig. 5), and also reported in Allard & Kielkopf (1982)
(Figs. 18 and 19). This dependence on the average number of perturbers in the collision volume is expected on the basis of the Poisson distribution, which indicates the probability of
finding a select number of uncorrelated perturbers in this collision volume.
It was first identified in experimental alkali spectra by Exton & Snow (1978) and by Kielkopf & Allard (1979).
,
the amplitude of the first satellite begins to decrease with increasing
density. When this density is reached, the probability of a
collision with two perturbers is higher than the probability of a
collision with only one perturber (see e.g. Allard 1978; Royer 1978). Theoretically, as shown by Royer (1971), the probability of m perturbers in a volume V is shown in Fig. 27 of Allard & Kielkopf (1982). These variations in amplitude of the first and second satellites are well explained using a square well potential, as is shown in the
analysis of Allard (1978) (Fig. 5), and also reported in Allard & Kielkopf (1982)
(Figs. 18 and 19). This dependence on the average number of perturbers in the collision volume is expected on the basis of the Poisson distribution, which indicates the probability of
finding a select number of uncorrelated perturbers in this collision volume.
It was first identified in experimental alkali spectra by Exton & Snow (1978) and by Kielkopf & Allard (1979).
The appearance of an extended wing shown in Fig. 7 is sensitive to temperature because of the variation in modulated transition dipole moment with temperature. Figure 3 illustrates that there is no contribution from triplets above 1900 Å (-30 000 cm-1) for T=5000 K because the modulated transition dipole moment is too weak.
 |
Figure 7:
Variation of the extension of the individual profile due to the
|
| Open with DEXTER | |
 |
Figure 8:
Contribution of the
|
| Open with DEXTER | |
 |
Figure 9:
Contribution of the
|
| Open with DEXTER | |
Figures 8 and 9 show
how the line profiles vary as the
temperature decreases from T=8000 K to 5000 K. The
![]() and
and
![]() quasi-molecular transitions both contribute and must be included. In Fig. 8, we have compared the total profile,
for which multiple perturber effects are taken into account,
with the total profile for when the
expansion is stopped at first order, which is equivalent to the
one perturber approximation. Due to the weighting, the singlet
quasi-molecular transitions both contribute and must be included. In Fig. 8, we have compared the total profile,
for which multiple perturber effects are taken into account,
with the total profile for when the
expansion is stopped at first order, which is equivalent to the
one perturber approximation. Due to the weighting, the singlet
![]() provides
only 1/3 of the total line far wing strength.
Nevertheless, the contributions of singlet collisions with multiple perturbers
dominate the 1800-3000 Å region. Consequently, the ultraviolet triplet
provides
only 1/3 of the total line far wing strength.
Nevertheless, the contributions of singlet collisions with multiple perturbers
dominate the 1800-3000 Å region. Consequently, the ultraviolet triplet
![]() transition does not, in itself, account for the far red wing of the Lyman-
transition does not, in itself, account for the far red wing of the Lyman-![]() profile broadened by collisions with atomic hydrogen. In their analysis of the missing opacity in cool, dense, white dwarf stars, Kowalski & Saumon (2006) did not include this effect.
profile broadened by collisions with atomic hydrogen. In their analysis of the missing opacity in cool, dense, white dwarf stars, Kowalski & Saumon (2006) did not include this effect.
Satellites in the far wings of Lyman-![]() are seen in
the emission spectra of plasmas produced when a pulsed laser excites an H2 gas target (Kielkopf & Allard 1998). This earlier work on Lyman
are seen in
the emission spectra of plasmas produced when a pulsed laser excites an H2 gas target (Kielkopf & Allard 1998). This earlier work on Lyman![]() was based on experiments for conditions under which only binary collisions were
important in the spectral regions up to 1600 Å that were analyzed.
We have developed techniques to use initial pressures of above 100 atmospheres, yielding
laser-produced plasmas with atomic densities over 1021 atoms cm-3at the temperature of the atmosphere of a white dwarf. A preliminary report
presented by Kielkopf & Allard (2000) described measurements of high density sources that extended from the Lyman-
was based on experiments for conditions under which only binary collisions were
important in the spectral regions up to 1600 Å that were analyzed.
We have developed techniques to use initial pressures of above 100 atmospheres, yielding
laser-produced plasmas with atomic densities over 1021 atoms cm-3at the temperature of the atmosphere of a white dwarf. A preliminary report
presented by Kielkopf & Allard (2000) described measurements of high density sources that extended from the Lyman-![]() wing beyond the 1600 Å satellite, where the effects of more than one perturber acting simultaneously on the radiating atom are expected to appear.
wing beyond the 1600 Å satellite, where the effects of more than one perturber acting simultaneously on the radiating atom are expected to appear.
A dense, hydrogen plasma produced by an energetic pulsed laser emits a continuous spectrum in the infrared, visible, ultraviolet, and vacuum ultraviolet spectral regions. The spectrum is time-dependent, arising in a nominally cylindrical shock propagating outward from the focus of the laser under predictable conditions (Kielkopf 1995, 2000).
For the data shown here, a pulsed Nd:YAG laser (1064 nm, 10 Hz, 300 mJ/pulse)
was focused into a static cell filled with 99.999% pure H2.
The arrangement was similar to that described by Kielkopf & Allard (1998), except that the cell and its windows
were designed to operate at elevated pressures. For spectra below
1850 Å, a 2 mm thick MgF2 window separated the cell from the spectrograph,
and because of window fragility the pressures were limited to 7 atmospheres. Above 1850 Å, a 3 mm thick fluorescence-free fused silica window permitted operation
up to 125 atmospheres. Spectra shown here were recorded with a 0.2 m
aberration-corrected holographic concave grating vacuum monochromator with a spectral resolution of 4 Å. They represent a portion of a comprehensive data set
spanning from 1200 Å in the vacuum ultraviolet to 2.5 ![]() m in the infrared.
Below 1800 Å, a solar blind detector was used to minimize sensitivity to scattered light, but, at longer wavelengths, a sodium salicylate converter and UV-sensitive
photomultiplier provided a nominally flat spectral response up to Balmer-
m in the infrared.
Below 1800 Å, a solar blind detector was used to minimize sensitivity to scattered light, but, at longer wavelengths, a sodium salicylate converter and UV-sensitive
photomultiplier provided a nominally flat spectral response up to Balmer-![]() .
Multichannel photon-counting in 5 ns wide bins recorded the
development of the emission in a single spectral channel
for 5
.
Multichannel photon-counting in 5 ns wide bins recorded the
development of the emission in a single spectral channel
for 5 ![]() s after each laser pulse, and accumulated time-tagged counts were averaged over 400 pulses. The spectral channel was sequentially
stepped, and the acquisition was repeated. Slices in a fixed-width time-window across the spectrum provided snapshots of
the development of the plasma's emission from its fully ionized initial state, a few nanoseconds after plasma production, to a cool, dense atomic gas 5 ms later.
s after each laser pulse, and accumulated time-tagged counts were averaged over 400 pulses. The spectral channel was sequentially
stepped, and the acquisition was repeated. Slices in a fixed-width time-window across the spectrum provided snapshots of
the development of the plasma's emission from its fully ionized initial state, a few nanoseconds after plasma production, to a cool, dense atomic gas 5 ms later.
In addition to
the Lyman-![]() line broadened by neutral atomic collisions discussed here,
there were contributions from collisions of the radiating atom with protons,
from free-free and free-bound transitions of electrons in the
field of protons, from the ionic molecules
H- and H2+, and from the radiative dissociation of neutral H2.
line broadened by neutral atomic collisions discussed here,
there were contributions from collisions of the radiating atom with protons,
from free-free and free-bound transitions of electrons in the
field of protons, from the ionic molecules
H- and H2+, and from the radiative dissociation of neutral H2.
The broadening of Lyman-![]() in proton collisions has been discussed
elsewhere (Kielkopf & Allard 1998).
It is important at wavelengths below 1450 Å in highly ionized hydrogen
plasmas, but there is no significant contribution from these ionic collisions in the
spectral region above 1450 Å during the cooling temporal domain discussed here.
However, we are able to observe that the temperatures of the laser plasmas
measured in this experiment are sufficiently high that there are no bound H2 molecules either. It is a weakly ionized, dense, atomic plasma.
From 1450 Å to 3000 Å, the observable continuum is due entirely to radiative, neutral, atomic collisions associated with the long wavelength ``red'' wing of Lyman-
in proton collisions has been discussed
elsewhere (Kielkopf & Allard 1998).
It is important at wavelengths below 1450 Å in highly ionized hydrogen
plasmas, but there is no significant contribution from these ionic collisions in the
spectral region above 1450 Å during the cooling temporal domain discussed here.
However, we are able to observe that the temperatures of the laser plasmas
measured in this experiment are sufficiently high that there are no bound H2 molecules either. It is a weakly ionized, dense, atomic plasma.
From 1450 Å to 3000 Å, the observable continuum is due entirely to radiative, neutral, atomic collisions associated with the long wavelength ``red'' wing of Lyman-![]() .
.
Above 3000 Å, approaching the Balmer series limit at 3646 Å, the other
contributions noted above become increasingly important. They are well known
and analytical formulations are given by Roberts & Voigt (1971) that may be used to extract a plasma temperature by fitting the continuum in this region. Since the
shock-driven, plasma model predicts a temperature T and density profile in the
plasma, there is a model density ![]() of atomic H corresponding to each
spectroscopic temperature. This density is qualitatively similar to that found in the
plasma region where the n=2 state, the upper state of Lyman-
of atomic H corresponding to each
spectroscopic temperature. This density is qualitatively similar to that found in the
plasma region where the n=2 state, the upper state of Lyman-![]() ,
has
its maximum population. A spectroscopic temperature and density determined in this
way is completely independent of theoretical unified theory modeling of the
Lyman-
,
has
its maximum population. A spectroscopic temperature and density determined in this
way is completely independent of theoretical unified theory modeling of the
Lyman-![]() line-broadening by neutral, atomic hydrogen.
line-broadening by neutral, atomic hydrogen.
Experimental data for initial H2 pressures between 7 and 120 atmospheres were recorded
from 1200 Å in the vacuum ultraviolet to 2.5 ![]() m in the infrared.
Portions of two runs, one for the range 1450-1850 Å and the
other for 1850-3000 Å, are shown in Fig. 10.
For the shorter wavelength data, the spectroscopic diagnostics and
plasma model establish an atomic hydrogen density of
m in the infrared.
Portions of two runs, one for the range 1450-1850 Å and the
other for 1850-3000 Å, are shown in Fig. 10.
For the shorter wavelength data, the spectroscopic diagnostics and
plasma model establish an atomic hydrogen density of
![]() atoms cm-3 and a temperature of
T=4100 K. For the longer wavelength data, acquired for a higher initial density,
the parameters are
atoms cm-3 and a temperature of
T=4100 K. For the longer wavelength data, acquired for a higher initial density,
the parameters are
![]() atoms cm-3 and a temperature of
T=5600 K. The two data sets are scaled so that they match
at the wavelength at which they join. This simple representation allows us to present a qualitative picture of the far wing of the Lyman-
atoms cm-3 and a temperature of
T=5600 K. The two data sets are scaled so that they match
at the wavelength at which they join. This simple representation allows us to present a qualitative picture of the far wing of the Lyman-![]() ,
quasi-molecular continuum emitted by the plasma.
,
quasi-molecular continuum emitted by the plasma.
The prominent 1600 Å satellite
is due to free-free transitions
of atomic H in the 2p state radiating during a collision with
a ground state 1s H atom.
The other weak feature, at 2500 Å, is attributed to
``two-perturber'' collisions in which the atom radiates while two
1s atoms are nearby. Previously, such two-perturber (and higher order)
effects have
been observed in several cases, including by a comprehensive study of
Tl broadened by noble gases and compared to unified theory calculations with
a priori potentials (Kielkopf 1983).
In atomic H, such effects contribute to the opacity far into the red wing
of Lyman-![]() ,
and are thus
important to include in atmosphere models and
synthetic spectra of cool white dwarfs.
The observed spectrum in Fig. 10 is compared to a theoretical spectrum
computed for a density intermediate between that of the two data sets.
The observed profiles are consistent with the
theoretical model although the satellite at 2500 Å appears to have
a different shape than predicted by the additive approximation for
the atomic interaction.
,
and are thus
important to include in atmosphere models and
synthetic spectra of cool white dwarfs.
The observed spectrum in Fig. 10 is compared to a theoretical spectrum
computed for a density intermediate between that of the two data sets.
The observed profiles are consistent with the
theoretical model although the satellite at 2500 Å appears to have
a different shape than predicted by the additive approximation for
the atomic interaction.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{0294fig10.eps}
\end{figure}](/articles/aa/full/2009/03/aa10294-08/Timg55.gif) |
Figure 10:
Comparison of experimental profiles to the theoretical one
calculated for T=4100 K and
|
| Open with DEXTER | |
Previous Lyman-![]() line-profile calculations were completed at low
temperatures and included in atmosphere models by Wolff et al. (2002), and by Kowalski & Saumon (2006).
line-profile calculations were completed at low
temperatures and included in atmosphere models by Wolff et al. (2002), and by Kowalski & Saumon (2006).
Both papers compared synthetic spectra with observed
spectra of BPM4729. Unfortunately, neither paper showed the actual line profiles
that were used, and it is therefore impossible
to compare our work directly with theirs.
However, we note that in Fig. 3 of Wolff et al. (2002), the change in slope of the synthetic spectrum
is certainly due to the second satellite.
Their predicted profile in a pure hydrogen atmosphere does not
agree with observations. Since the transitions and the corresponding potentials used were not specified in the paper, we cannot draw a conclusion about the reason for the discrepancy. Kowalski & Saumon (2006)
were successful in reproducing the spectrum of BPM4729 from the ultraviolet to near IR. They used a line profile calculated in the quasi-static approximation for only the
![]() transition in H-H collisions,
and they also included collisions with H2, but the transitions and symmetries
for the corresponding H3 potentials, which have been taken into account in this work, are not given in the paper. We have seen in our work reported here that the
transition in H-H collisions,
and they also included collisions with H2, but the transitions and symmetries
for the corresponding H3 potentials, which have been taken into account in this work, are not given in the paper. We have seen in our work reported here that the
![]() transition alone is inadequate to account for the spectrum above 1600 Å at elevated atomic hydrogen densities.
transition alone is inadequate to account for the spectrum above 1600 Å at elevated atomic hydrogen densities.
Many-body free-free collisions in dense atomic H have been shown to
perturb the 2p atomic state to the extent that photons are emitted in the ultraviolet, rather than in the vacuum ultraviolet. Extrema in the difference potential-energy surfaces give rise to satellites in the far wing of Lyman-![]() .
The intensity of these satellites depends on the probability of the
collision that produces them, and on the radiative dipole moment of
the transient multi-atom system. The probability increases with
atomic density, and is enhanced by the collision dynamics and
the Boltzmann factor of the excited state. The radiative dipole moment changes significantly in close collisions from its asymptotic value for the unperturbed atom.
.
The intensity of these satellites depends on the probability of the
collision that produces them, and on the radiative dipole moment of
the transient multi-atom system. The probability increases with
atomic density, and is enhanced by the collision dynamics and
the Boltzmann factor of the excited state. The radiative dipole moment changes significantly in close collisions from its asymptotic value for the unperturbed atom.
One such satellite, corresponding to a transition to H(2p)-H(1s)-H(1s),
appears in emission from a laser-produced plasma with an atomic H density
on the order of 1020 atoms cm-3. The observed spectral line
profile is consistent with a unified line-shape theory that includes
contributions from the triplet states. Transitions from the B to the X state for unbound atoms in collision are primarily responsible for the emission between 1500 Å and 3000 Å. Cool, white dwarfs require a special treatment because of the high perturber density involved. Homeier et al. (2007) investigated effects on the Na doublet of the high perturber densities occurring in metal-rich white dwarfs with a helium-dominated atmosphere. The density of neutral, atomic helium
as a perturber of hydrogen Lyman-![]() in two
cool white dwarfs exhibiting strong Na absorption could reach
1022 atoms cm-3. Homeier et al. (2007) demonstrated that successful modeling of spectra at high perturber density requires a unified theory that takes into account multiple perturber effects.
in two
cool white dwarfs exhibiting strong Na absorption could reach
1022 atoms cm-3. Homeier et al. (2007) demonstrated that successful modeling of spectra at high perturber density requires a unified theory that takes into account multiple perturber effects.