A&A 493, 979-1016 (2009)
DOI: 10.1051/0004-6361:200810234
M. B. N. Kouwenhoven1,2 - A. G. A. Brown3 - S. P. Goodwin1 - S. F. Portegies Zwart2,4 - L. Kaper2
1 - Department of Physics and Astronomy, University of Sheffield,
Hicks Building, Hounsfield Road, S3 7RH, Sheffield, UK
2 -
Astronomical Institute ``Anton Pannekoek'',
University of Amsterdam,
Kruislaan 403, 1098 SJ Amsterdam, The Netherlands
3 -
Leiden Observatory, University of Leiden,
PO Box 9513, 2300 RA
Leiden, The Netherlands
4 -
Section Computer Science, University of Amsterdam,
Kruislaan 403, 1098 SJ Amsterdam, The Netherlands
Received 21 May 2008 / Accepted 20 November 2008
Abstract
Knowledge of the binary population in stellar groupings provides important information about the outcome of the star forming process in different environments. Binarity is also a key ingredient in stellar population studies, and is a prerequisite for calibrating the binary evolution channels.
In this paper we present an overview of several commonly used methods of pairing individual stars into binary systems, which we refer to as pairing functions. These pairing functions are frequently used by observers and computational astronomers, either for their mathematical convenience or because they roughly describe the expected outcome of the star forming process. We discuss the consequences of each pairing function for interpreting observations and numerical simulations. The binary fraction and mass ratio distribution generally depend strongly on the selection of the range in primary spectral type in a sample. The mass ratio distribution and binary fraction derived from a binarity survey among a mass-limited sample of targets is thus not representative of the population as a whole.
Neither theory nor observations indicate that random pairing of binary components from the mass distribution, the simplest pairing function, is realistic. It is more likely that companion stars are formed in a disc around a star or that a pre-binary core fragments into two binary components.
The results of our analysis are important for (i) the interpretation of the observed mass ratio distribution and binary fraction for a sample of stars; (ii) a range of possible initial condition algorithms for star cluster simulations; and (iii) how to distinguish between the different star formation scenarios.
Key words: stars: binaries: general - stars: formation - methods: N-body simulations - Galaxy: open clusters and associations: general
Observations and simulations suggest that most stars form in binary systems (e.g. Duquennoy & Mayor 1991; Goodwin & Kroupa 2005; Kouwenhoven et al. 2005,2007b; Goodwin et al. 2007; Mason et al. 1998; Kobulnicky & Fryer 2007), and that a substantial fraction are part of a triple or higher-order system (e.g. Tokovinin & Smekhov 2002; Correia et al. 2006; Tokovinin et al. 2006; Hu et al. 2008). Multiplicity is thus a fundamental property of the star forming process. Detailed knowledge of a young binary population can be employed to study the outcome of star formation, consequently the star formation process itself.
Surveys indicate that the properties of the binary population are a function of the spectral type of the primary star. Practically all O-type stars (Mason et al. 1998) and B/A-type stars (Shatsky & Tokovinin 2002; Kouwenhoven et al. 2007b; Kobulnicky & Fryer 2007) are found in binary or multiple systems. Abt & Levy (1976) report a multiplicity fraction of 55% among F3-G2 stars, and in their CORAVEL spectroscopic study of F7-G9 stars, Duquennoy & Mayor (1991) find a binary fraction of ![]()
![]() .
The binary fraction among M-type stars is
.
The binary fraction among M-type stars is ![]() (Reid & Gizis 1997; Fischer & Marcy 1992; Leinert et al. 1997). For late M-type stars and brown dwarfs the binary fraction decreases to
(Reid & Gizis 1997; Fischer & Marcy 1992; Leinert et al. 1997). For late M-type stars and brown dwarfs the binary fraction decreases to ![]() (e.g., Close et al. 2003; Bouy et al. 2003; Burgasser et al. 2003; Siegler et al. 2005; Joergens 2008; Ahmic et al. 2007; Maxted et al. 2008; Gizis et al. 2003).
(e.g., Close et al. 2003; Bouy et al. 2003; Burgasser et al. 2003; Siegler et al. 2005; Joergens 2008; Ahmic et al. 2007; Maxted et al. 2008; Gizis et al. 2003).
In this paper we discuss in detail several methods of pairing individual stars into binary stars. We refer to the latter algorithms as ``pairing functions''. Several of these have a physical motivation, others are discussed because of their mathematical simplicity. All these pairing functions have in common that they are frequently used in the literature. The main goal of this paper is to explain the consequences of adopting a particular pairing function when doing a numerical simulation, or when interpreting observations. A good understanding of the consequences of each pairing algorithm for the binary population is important for
We study the differences in the various methods of pairing individual stars into binary systems by analysing numerically simulated binary populations. For each binary system, we refer to the most massive component M1 as the primary star, and the least massive component M2 as the companion star. Our adopted definition is purely based on the current mass of the components, i.e., irrespective of their relative luminosity or initial mass. We define the mass ratio as
![]() ,
so that
,
so that
![]() .
The total mass is denoted
.
The total mass is denoted
![]() for a binary system, and
for a binary system, and
![]() for a single star with mass
for a single star with mass ![]() .
In several cases, we construct binary systems from star forming cores of mass M with star forming efficiency
.
In several cases, we construct binary systems from star forming cores of mass M with star forming efficiency ![]() ,
so that the total mass of the resulting objects is
,
so that the total mass of the resulting objects is
![]() .
.
In our simulations each star is given a mass. A subset of the stars is assigned a companion, the other stars remain single stars. The companion is given a mass according to a pairing algorithm. We refer to the algorithm that is used to combine individual stars into binary systems as the pairing function. The pairing function of a binary population may for example be random pairing of both companions from the mass distribution. In the particular case of random pairing, primary and companion are swapped, if necessary, so that the primary is the most massive star.
Depending on which pairing function is used, the mass of the primary star, and in several cases the companion star, is drawn from a mass distribution fM(M). We refer to fM(M) as the generating mass distribution. We denote the resulting mass distributions for primary stars, companion stars, systems, and single stars with
fM1(M),
fM2(M),
![]() ,
and
,
and
![]() ,
respectively. Note that the distributions over primary and companion mass in a stellar grouping are never independent,
,
respectively. Note that the distributions over primary and companion mass in a stellar grouping are never independent,
![]() ,
as by definition
,
as by definition
![]() .
The resulting mass distribution for all single and primary stars is denoted with
fM1,S(M), and the mass distribution for all individual objects (i.e., singles, primaries and companions), is denoted with
.
The resulting mass distribution for all single and primary stars is denoted with
fM1,S(M), and the mass distribution for all individual objects (i.e., singles, primaries and companions), is denoted with
![]() .
The distribution
.
The distribution
![]() that is present immediately after star formation is called the initial mass function (IMF). Note that
that is present immediately after star formation is called the initial mass function (IMF). Note that
![]() is unequal to the generating mass distribution fM(M), except in the random pairing case (see Sect. 6.1).
is unequal to the generating mass distribution fM(M), except in the random pairing case (see Sect. 6.1).
For several pairing functions we generate companions by drawing the mass ratio for a binary from a (generating) mass ratio distribution fq(q)Depending on the additional constraints specific for each pairing function, the resulting overall mass ratio distribution
![]() may or may not be equal to fq(q). The resulting mass ratio distribution may or may not be a function of primary spectral type. We refer to the specific mass ratio distribution for all binaries with a primary of spectral type A or B, for example, with
may or may not be equal to fq(q). The resulting mass ratio distribution may or may not be a function of primary spectral type. We refer to the specific mass ratio distribution for all binaries with a primary of spectral type A or B, for example, with
![]() .
Throughout this paper we will mostly use the expression
fq;M1(q) for the specific mass ratio distribution for an ensemble of binaries with a limited primary mass range.
.
Throughout this paper we will mostly use the expression
fq;M1(q) for the specific mass ratio distribution for an ensemble of binaries with a limited primary mass range.
A common expression to quantify the multiplicity of a stellar population is the multiplicity fraction
![]() (which is often referred to as the binary fraction), defined as
(which is often referred to as the binary fraction), defined as
Each pairing algorithm is provided with a (generating) binary fraction
![]() ,
which describes the fraction of stars that is assigned a preliminary companion star. For most pairing functions this preliminary companion is accepted as such, so that the overall binary fraction
,
which describes the fraction of stars that is assigned a preliminary companion star. For most pairing functions this preliminary companion is accepted as such, so that the overall binary fraction
![]() equal to the generating value
equal to the generating value
![]() .
For several pairing functions, however, additional constraints are set to the properties of the companion. For example, when a pairing function generates a Jupiter-mass companion around a solar-mass star, the ``primary'' is usually considered to be a ``single'' star. For such pairing functions, the resulting overall binary fraction
.
For several pairing functions, however, additional constraints are set to the properties of the companion. For example, when a pairing function generates a Jupiter-mass companion around a solar-mass star, the ``primary'' is usually considered to be a ``single'' star. For such pairing functions, the resulting overall binary fraction
![]() is lower than
is lower than
![]() .
We denote the specific binary fraction for the set of all single stars of spectral type A/B and binary systems with primary spectral type A/B as
.
We denote the specific binary fraction for the set of all single stars of spectral type A/B and binary systems with primary spectral type A/B as
![]() .
.
During our analysis we make several assumptions for reasons of clarity; our models are simplifications of reality. Our results are not limited by these assumptions, and the models can easily be extended. Our main goal is to illustrate the implications of adopting a particular pairing function.
We assume that no triples or higher-order systems are present. Although observations have shown that a significant fraction (![]()
![]() )
of the stars are part of a multiple system (Tokovinin & Smekhov 2002; Eggleton & Tokovinin 2008; Correia et al. 2006; Tokovinin et al. 2006; Hu et al. 2008), the properties of higher-order systems are not well understood. Observational selection effects complicate the derivation of the properties of these systems significantly. Higher-order systems are often ignored in N-body simulations due to computational complications (e.g., van den Berk et al. 2007). A full understanding of star formation, however, ultimately requires a full knowledge of the formation and evolution of higher-order systems.
)
of the stars are part of a multiple system (Tokovinin & Smekhov 2002; Eggleton & Tokovinin 2008; Correia et al. 2006; Tokovinin et al. 2006; Hu et al. 2008), the properties of higher-order systems are not well understood. Observational selection effects complicate the derivation of the properties of these systems significantly. Higher-order systems are often ignored in N-body simulations due to computational complications (e.g., van den Berk et al. 2007). A full understanding of star formation, however, ultimately requires a full knowledge of the formation and evolution of higher-order systems.
In our models the generating binary fraction for the population can be described with a single value
![]() .
For most pairing functions this results in a specific binary fraction
.
For most pairing functions this results in a specific binary fraction
![]() that is independent of primary mass M1. However, in Sect. 6 we describe several cases where, as a result of the pairing properties, the binary fraction is a function of primary mass, even though this dependency is not included explicitly.
that is independent of primary mass M1. However, in Sect. 6 we describe several cases where, as a result of the pairing properties, the binary fraction is a function of primary mass, even though this dependency is not included explicitly.
Selection effects play a major role in the interpretation of binary star observations. A detailed description of the selection effects, such as in Kouwenhoven et al. (2007b), is necessary to derive the pairing function, the mass ratio distribution and the binary fraction from observations. A major bias is generally introduced by studying the binary population in a certain primary mass range; we describe this effect in detail for the different pairing functions. Throughout most of this paper we ignore the other selection effects.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{ps/0234_f1.ps}
\end{figure}](/articles/aa/full/2009/03/aa10234-08/Timg71.gif) |
Figure 1: The cumulative mass distributions ( top) and mass distributions ( bottom) derived by Kroupa (Eq. (2); solid curve) and Salpeter (Eq. (3); dashed curve). The masses at which the slope of the Kroupa mass distribution changes are indicated with the vertical dotted lines. |
| Open with DEXTER | |
Table 1: The distribution of stars over main-sequence spectral type for the Kroupa and Salpeter mass distributions (BD = brown dwarfs).
The mass distribution fM(M) defines the spectrum of masses in a stellar population, and is usually expressed as a single-component power law (Salpeter 1955), a multi-component power law (e.g., Kroupa 2001) or a Gaussian distribution (e.g., Chabrier 2003). In our analysis we consider two mass distributions: the Kroupa mass distribution and the Salpeter mass distribution. The main difference between these is the presence or absence of a turnover in the low-mass regime. The mass distribution derived by Kroupa (2001) is given by
Table 1 lists the fraction of stars of a given spectral type for the Kroupa and Salpeter mass distributions for stars in the mass range
![]() .
For both distributions we list the fraction
.
For both distributions we list the fraction
![]() of objects and the fraction
of objects and the fraction
![]() of the total mass in each mass range. The corresponding probability distributions fM(M) and cumulative distributions
of the total mass in each mass range. The corresponding probability distributions fM(M) and cumulative distributions
![]() are shown in Fig. 1. Most young stellar populations in our Galaxy are described accurately with the Kroupa mass distribution (Bonnell et al. 2007).
are shown in Fig. 1. Most young stellar populations in our Galaxy are described accurately with the Kroupa mass distribution (Bonnell et al. 2007).
In our simulations we draw objects from the mass distribution in the range
![]() ,
i.e., stellar and substellar-mass objects. Objects less massive than
,
i.e., stellar and substellar-mass objects. Objects less massive than
![]() are considered to be planets, and form in a different way than stars or brown dwarfs (see, e.g., Kouwenhoven et al. 2007a; Pollack et al. 1996). The absolute maximum stellar mass is of order
are considered to be planets, and form in a different way than stars or brown dwarfs (see, e.g., Kouwenhoven et al. 2007a; Pollack et al. 1996). The absolute maximum stellar mass is of order
![]() (Zinnecker & Yorke 2007, and references therein). The most massive star in a cluster may well depend on the total mass of the star cluster (Reddish 1978; Vanbeveren 1982; Weidner & Kroupa 2006). Stars more massive than
(Zinnecker & Yorke 2007, and references therein). The most massive star in a cluster may well depend on the total mass of the star cluster (Reddish 1978; Vanbeveren 1982; Weidner & Kroupa 2006). Stars more massive than
![]() ,
however, are extremely rare, are very short-lived, and possibly even form by a different mechanism than most other stars (e.g., Zinnecker & Yorke 2007).
,
however, are extremely rare, are very short-lived, and possibly even form by a different mechanism than most other stars (e.g., Zinnecker & Yorke 2007).
The mass distribution of Kroupa (2001) is for all stars in a population, including single stars, primaries and companions. We note that choosing primaries from an IMF and then choosing secondaries from a mass ratio distribution (Sect. 6.3) will not recover the original IMF. Thus the primary mass distribution function cannot be exactly the same as the desired IMF (see Sect. 7.1; Goodwin et al. 2008; Mal'Kov & Zinnecker 2001). Technically, the mass distribution should therefore not be used to generate, for example, a primary mass distribution. For simplicity, however, we adopt the Kroupa mass distribution as the generating mass distribution for each pairing function. Ideally, one should iteratively determine the generating mass distribution by comparing the outcome of the pairing process with the Kroupa mass distribution. As this is computationally a very expensive exercise, we skip the iteration, and simply adopt the Kroupa mass distribution as the generating mass distribution. For a proper analysis of real observations, one should keep this issue in mind.
The mass ratio distribution describes the distribution over mass ratio q=M2/M1 for a population of binary systems. The mass ratio distribution for binary systems has been studied thoroughly over the last decades (see, e.g., Mazeh et al. 2003; Zinnecker 1984; Halbwachs et al. 2003; Hogeveen 1992a). In this paper we distinguish between three different types of mass ratio distributions. The generating mass ratio distribution is an input distribution that is used by most pairing function algorithms to generate binaries, although some pairing functions (e.g., random pairing) do not require a generating mass ratio distribution. Note that the mass ratio distribution is not the same as the pairing function; the mass ratio distribution is a property of several (not all) pairing functions; see Sect. 6 for details. The overall mass ratio distribution is the mass ratio distribution resulting from the pairing mechanism, for all binaries in the population. The specific mass ratio distribution is that for a sample of stars with primaries in a given mass range. The latter is measured in observations, as a binarity survey is in most cases focused on a particular set of targets with given spectral types.
The (specific) mass ratio distribution is usually obtained by a fit to the observed mass ratio distribution of the sample. The observed distribution is often described with a simple power-law:
Alternatively, to allow for a mass ratio distribution with a peak in the range
![]() ,
we also consider the Gaussian mass ratio distribution:
,
we also consider the Gaussian mass ratio distribution:
For our default model we adopt a (generating) mass ratio distribution of the form fq(q)= 1 with
![]() ,
the flat mass ratio distribution.
,
the flat mass ratio distribution.
We define the pairing function as the algorithm which is used to pair individual stars into binary systems. A well-known pairing function is random pairing from the mass distribution. Others include, for example, a fixed mass ratio distribution. The pairing of binary components in a stellar population results from the combined effect of star formation, stellar evolution, binary evolution, and dynamical interactions. By studying the pairing of binary stars, the contributions of the latter three effects can be evaluated, and an estimate for the primordial binary population can be obtained. This primordial pairing function allows us to constrain the process of star formation.
It is worth considering what pairing we might expect from the actual star formation process, as opposed to the various theoretical constructs we describe in this paper.
Often random pairing has been used to construct binary systems for various models. Random pairing has the obvious advantage that the chosen IMF is, by design, automatically recovered. However, there is no good theoretical reason to suppose that the star formation process would produce a randomly paired distribution. Furthermore, random pairing is ruled out observationally. The observed mass ratio distribution among intermediate mass stars (Shatsky & Tokovinin 2002; Kouwenhoven et al. 2007a,b,2005) and brown dwarfs (Kraus et al. 2008) in the nearby OB association Scorpius-Centaurus have indicated that the binary components are not randomly paired from the mass distribution. The same result is found for the Cygnus OB2 association (Kobulnicky & Fryer 2007), and for F5-K5 stars in the solar neighbourhood (Metchev & Hillenbrand 2008). Random pairing is further excluded by the high prevalence of massive binaries with a mass ratio close to unity, often referred to as the ``twin peak'' in the mass ratio distribution (Lucy 2006; Lucy & Ricco 1979; García & Mermilliod 2001; Pinsonneault & Stanek 2006; Tokovinin 2000; Söderhjelm 2007, see also Sect. 9.1).
Simulations have shown that it is impossible to form significant numbers of
binary systems from an initially single star distribution (Kroupa 1995a),
therefore stars in binary systems must have predominantly formed in binary
systems. Observations of pre-main sequence stars also suggest that they have a higher
multiplicity than field stars (at least for >
![]() ), suggesting that
most stars form in binary (or higher-order) systems (e.g., Goodwin & Kroupa 2005).
It is supposed that a primordial population with a multiplicity of almost 100%
evolves into a field-like binary population through (a) the decay of
higher-order multiple systems (e.g., Goodwin & Kroupa 2005), and (b) the
dynamical destruction of binaries in binary-binary encounters in clusters
(e.g., Kroupa 1995a,c). Thus, the currently observed binary population is a
complex mixture of primordial binaries (i.e. in the same dynamical state as when
they formed), and dynamically evolved binaries (which may have different
characteristics, or even companions to their initial state).
), suggesting that
most stars form in binary (or higher-order) systems (e.g., Goodwin & Kroupa 2005).
It is supposed that a primordial population with a multiplicity of almost 100%
evolves into a field-like binary population through (a) the decay of
higher-order multiple systems (e.g., Goodwin & Kroupa 2005), and (b) the
dynamical destruction of binaries in binary-binary encounters in clusters
(e.g., Kroupa 1995a,c). Thus, the currently observed binary population is a
complex mixture of primordial binaries (i.e. in the same dynamical state as when
they formed), and dynamically evolved binaries (which may have different
characteristics, or even companions to their initial state).
Simulations of binary star formation have comprehensively failed to produce systems that match observations, even when the dynamical evolution of the initial states is accounted for (see Goodwin et al. 2007, and references therein). However, hydrodynamic simulations of star formation suggest that companions usually form by the fragmentation of massive, disc-like circumstellar accretion regions around young stars (see Goodwin et al. 2007, and references therein).
In such a scenario for companion formation it would be expected that the
secondary should have a roughly similar (i.e. within a factor of three or
four) mass to the primary, especially at small separations. A massive enough
region to fragment is only present during the earliest (e.g. class 0/I)
phases of star formation before the star(s) have accreted the majority of
their natal core. Thus, the secondary will be present whilst a large
reservoir of gas is also present around it. In the case of a star that will
eventually grow to be (for example)
![]() the secondary will form
whilst the primary is only
the secondary will form
whilst the primary is only
![]() and several solar masses of
gas are present in the circumstellar environment. A secondary will
presumably form with an initial mass close to the opacity limit for
fragmentation,
and several solar masses of
gas are present in the circumstellar environment. A secondary will
presumably form with an initial mass close to the opacity limit for
fragmentation, ![]()
![]() .
However, it is difficult to imagine
a scenario in which the secondary fails to accrete at least some of the
circumstellar material, especially as the secondary will form with angular
momentum similar to that of the accretion region, and so will be more able
to accrete material (see Goodwin et al. 2007, and references therein; also
Delgado Donate & Clarke 2005). Therefore, the secondary mass is expected to
be a reasonably high fraction of the primary mass. In particular, it
should be difficult for a companion to a B-star to remain at brown dwarf or
M-star mass due to the large amount of material available for accretion.
In particular, we would expect a rough correlation between separation and
mass ratio, with closer companions being generally more massive as is
observed (e.g. Mazeh et al. 1992, for field G-dwarfs).
.
However, it is difficult to imagine
a scenario in which the secondary fails to accrete at least some of the
circumstellar material, especially as the secondary will form with angular
momentum similar to that of the accretion region, and so will be more able
to accrete material (see Goodwin et al. 2007, and references therein; also
Delgado Donate & Clarke 2005). Therefore, the secondary mass is expected to
be a reasonably high fraction of the primary mass. In particular, it
should be difficult for a companion to a B-star to remain at brown dwarf or
M-star mass due to the large amount of material available for accretion.
In particular, we would expect a rough correlation between separation and
mass ratio, with closer companions being generally more massive as is
observed (e.g. Mazeh et al. 1992, for field G-dwarfs).
In addition, dynamical evolution in clusters will act to destroy the most weakly bound systems (i.e. the widest and lowest-mass companions), further biasing the mass ratio distributions away from small-q.
We would therefore argue that random pairing over the full mass range is the last type of pairing that would be expected from the star formation process (see, however, Sect. 6.1.1).
There are many ways to obtain a population of binary systems from a mass distribution fM(M). We analyse the most frequently used algorithms in the sections below. In general, the masses of the members of a stellar grouping are drawn from the mass distribution. A fraction of the stars is assigned a companion star (either from the mass distribution, or using a mass ratio distribution), or the mass is split into a primary and companion star. Four commonly used mechanisms are the following:
The above-mentioned pairing functions (RP, PCRP, and the three variations of PCP and SCP) are described in detail in the subsections below, while their differences are discussed in Sect. 7. Unless stated otherwise, we have adopted a Kroupa generating mass distribution, a flat generating mass ratio distribution (where applicable), and a generating binary fraction
![]() of 100% (see Sect. 8 for a discussion of these assumptions).
The main differences between the (renormalised) resulting mass ratio distributions are show in Fig. 2, where the top panel represents the overall mass ratio distribution. The middle and bottom panels represent the specific mass ratio distributions
fq;M1(q) (the subscript M1 indicates a restricted primary mass range) for binaries with high-mass primaries and low-mass primaries, respectively. Note that the derived mass ratio distribution for a sample of stars does not only depend strongly on the pairing function, but also on the targeted sample of stars.
For the same reason, the (renormalised) companion mass distribution, shown in Fig. 3, depends strongly on the primary mass range. A two-dimensional version of Fig. 2 is shown in Fig. 4. In the sections below we discuss in detail the pairing functions and the above-mentioned figures.
of 100% (see Sect. 8 for a discussion of these assumptions).
The main differences between the (renormalised) resulting mass ratio distributions are show in Fig. 2, where the top panel represents the overall mass ratio distribution. The middle and bottom panels represent the specific mass ratio distributions
fq;M1(q) (the subscript M1 indicates a restricted primary mass range) for binaries with high-mass primaries and low-mass primaries, respectively. Note that the derived mass ratio distribution for a sample of stars does not only depend strongly on the pairing function, but also on the targeted sample of stars.
For the same reason, the (renormalised) companion mass distribution, shown in Fig. 3, depends strongly on the primary mass range. A two-dimensional version of Fig. 2 is shown in Fig. 4. In the sections below we discuss in detail the pairing functions and the above-mentioned figures.
Note that the choices made in this paper do not imply that stellar populations indeed have these properties. It is not known how binary stars are formed, so that no robust predictions of their properties can be made. Different binary formation mechanisms may produce different mass ratio distributions, possibly varying with primary mass, period, or eccentricity (e.g. Krumholz & Thompson 2007; Zinnecker & Yorke 2007; Heggie 1975). In addition, dynamical evolution after the formation process may alter the binary fraction and the mass and mass ratio distributions (e.g., Hills 1975; Heggie 1975), possibly as a function of environment (see, e.g., Kroupa et al. 1999; Reipurth et al. 2007; Köhler et al. 2006; Preibisch et al. 2003; Duchêne et al. 2004; Gaburov et al. 2008, and Sect. 9.2). Other pairing functions suggested in literature include random pairing over a restricted mass range (Kroupa 1995a; Kroupa et al. 2003; Kroupa 1995c; Thies & Kroupa 2007; Kroupa 1995b, see also Sect. 6.1.1), ``special pairing'' (Weidner et al. 2008), ordered pairing (Oh et al, in prep.), pairing resulting from the dissolution of small-N clusters (Clarke 1996b), ``two-step'' pairing (Durisen et al. 2001), binary formation from ring fragmentation (Hubber & Whitworth 2005), and numerous others.
![\begin{figure}
\par\includegraphics[width=16.8cm,clip]{ps/0234_f2.ps}
\end{figure}](/articles/aa/full/2009/03/aa10234-08/Timg118.gif) |
Figure 2:
The (renormalised) mass ratio distributions resulting from the different pairing functions. From top to bottom, the panels show the overall mass ratio distribution (i.e., for all binaries), the mass ratio distribution for binaries with
|
| Open with DEXTER | |
| |
Figure 3:
The (renormalised) companion mass distributions resulting from the different pairing functions, for the models shown in Fig. 2. The curves indicate the distribution for all binaries (dashed curves), for binaries with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{ps/0234_f4.ps}
\end{figure}](/articles/aa/full/2009/03/aa10234-08/Timg121.gif) |
Figure 4:
The distribution of binary systems over primary mass M1 and mass
ratio q for the different pairing functions.
All populations have a Kroupa generating mass distribution, a generating mass ratio distribution of the form fq(q)= 1 (when applicable), and a generating binary fraction
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{ps/0234_f5.ps}
\end{figure}](/articles/aa/full/2009/03/aa10234-08/Timg122.gif) |
Figure 5:
The integration domains for pairing functions RP and PCRP. Left: the integration domain in the (x,y) plane (where x and y are the primary and companion mass, respectively) for the determination of the cumulative distribution of q=y/x. The lower and upper limits on the generating mass distribution are given by c and d, which implies that
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.8cm,clip]{ps/0234_f6.ps}
\end{figure}](/articles/aa/full/2009/03/aa10234-08/Timg126.gif) |
Figure 6:
How does the specific mass ratio distribution
fq;M1(q) resulting from random pairing (RP) depend on the mass distribution and the selected primary mass range? This figure shows the (renormalised) resulting mass ratio distributions for the Kroupa mass distribution ( top panels; Monte Carlo simulations) and the Salpeter mass distribution (bottom panels; analytical calculations) in the mass range
|
| Open with DEXTER | |
| |
Figure 7:
The specific binary fraction
|
| Open with DEXTER | |
In the case of random pairing (RP), the primary and companion mass are both independently drawn from fM(M), and swapped, if necessary, so that the most massive star is the primary. As a result of this swapping, neither the resulting primary mass distribution
fM1(M1), nor the companion mass distribution
fM2(M2), nor the system mass distribution
![]() is equal to the generating mass distribution fM(M); see, e.g., Warner (1961); Mal'Kov & Zinnecker (2001); Tout (1991). On the other hand, the mass distribution of all stars
is equal to the generating mass distribution fM(M); see, e.g., Warner (1961); Mal'Kov & Zinnecker (2001); Tout (1991). On the other hand, the mass distribution of all stars
![]() ,
i.e., all singles, primaries and companions, is equal to fM(M). Mal'Kov & Zinnecker (2001) derived general expressions for the distribution over primary star mass M1, companion star mass M2, and system mass
,
i.e., all singles, primaries and companions, is equal to fM(M). Mal'Kov & Zinnecker (2001) derived general expressions for the distribution over primary star mass M1, companion star mass M2, and system mass
![]() ,
respectively:
,
respectively:
For observational reasons, surveys for binarity are often restricted to a certain range of primary spectral types. To derive the effects of the selection on primary mass, the derivation of fq(q) again proceeds via the cumulative distribution function, which is now given by:
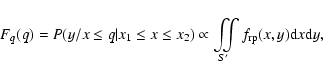 |
(11) |
In the special case where the mass distribution is of the form
![]() with
with
![]() ,
the overall mass ratio distribution is given by
,
the overall mass ratio distribution is given by
For pairing function RP the overall binary fraction
![]() is equal to the generating binary fraction
is equal to the generating binary fraction
![]() .
The specific binary fraction
.
The specific binary fraction
![]() ,
however, depends on the surveyed primary mass range: the larger the primary mass, the higher the specific binary fraction (unless
,
however, depends on the surveyed primary mass range: the larger the primary mass, the higher the specific binary fraction (unless
![]() ).
This can be understood as follows. For random pairing, the mass of the primary stars is drawn from the mass distribution. A fraction
).
This can be understood as follows. For random pairing, the mass of the primary stars is drawn from the mass distribution. A fraction
![]() of the primaries is assigned a companion, and primary and companion are swapped, if necessary, so that the primary is the most massive star. This swapping leads to an increased number of binaries with a high-mass primary, and a decreased number of binaries with a low-mass primary, and hence a mass-dependent binary fraction.
The relation between specific binary fraction and primary mass for random pairing is given by
of the primaries is assigned a companion, and primary and companion are swapped, if necessary, so that the primary is the most massive star. This swapping leads to an increased number of binaries with a high-mass primary, and a decreased number of binaries with a low-mass primary, and hence a mass-dependent binary fraction.
The relation between specific binary fraction and primary mass for random pairing is given by
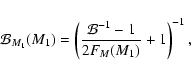 |
(15) |
Restricted random pairing (RRP) is very similar to random pairing (RP) as described in Sect. 6.1, with the difference that the binary components are now drawn from a limited mass range. All properties derived in Sect. 6.1 are thus applicable to the resulting binary sub-population resulting from RRP. However, the nature of RRP implies the presence of one or more other sub-populations that have a formed via another process. The other sub-populations could have alternative pairing function, such as RRP with different lower and upper mass limits, or a completely different pairing function.
Kroupa (1995a,c,b) finds that observations of binary systems are consistent with the population being born with pairing function RRP in the stellar mass range, prior to the effects of pre-main sequence eigenevolution. Further motivated by the difference between the observed mass ratio distribution and semi-major axis distribution of binary systems with a stellar primary and those with a brown dwarf binary (e.g., Close et al. 2003; Bouy et al. 2003; Martín et al. 2003; Burgasser et al. 2003), this implies that the brown dwarf population has formed with a different process (Thies & Kroupa 2008; Kroupa et al. 2003; Thies & Kroupa 2007). Their proposed model with stellar and substellar sub-populations is further supported by the existence of the brown dwarf desert among solar-type stars (see Sect. 9.1).
For primary-constrained random pairing (PCRP), each primary mass M1 is drawn from the mass distribution fM(M) with limits
![]() .
The companion mass M2 is also drawn from the same mass distribution, but with the additional constraint that
.
The companion mass M2 is also drawn from the same mass distribution, but with the additional constraint that
![]() .
The limits on the resulting mass ratio distribution are equivalent to those of random pairing
.
The limits on the resulting mass ratio distribution are equivalent to those of random pairing
![]() .
Writing the primary mass distribution as f(x) and the re-normalised companion mass distribution as f'(y), the expression for the joint probability distribution is
.
Writing the primary mass distribution as f(x) and the re-normalised companion mass distribution as f'(y), the expression for the joint probability distribution is
![]() ,
which is normalised to unity due to the re-normalisation of fy(y).
To derive the overall mass distribution fq one can proceed as for the RP case (see Sect. 6.1). The integration domain S is again as shown in Fig. 5, and
,
which is normalised to unity due to the re-normalisation of fy(y).
To derive the overall mass distribution fq one can proceed as for the RP case (see Sect. 6.1). The integration domain S is again as shown in Fig. 5, and
For a sample with primary masses restricted to the range [x1,x2], Eq. (17) has to be worked out. We will not explicitly show the results here. Most importantly, fq(q) is zero for q<c/x2, and exhibits a peak at
![]() .
The distribution for a sample of binaries with high-mass primaries thus peaks at small q, and the distribution for low-mass binaries peaks at large q. If the primary mass range is narrow (
.
The distribution for a sample of binaries with high-mass primaries thus peaks at small q, and the distribution for low-mass binaries peaks at large q. If the primary mass range is narrow (
![]() ), fq(q) can be approximated with Eq. (14). For a sample of stars with a very narrow primary mass range, the mass ratio distributions resulting from PCRP and RP thus give the same results. Differences between the two pairing functions become larger for realistic primary mass ranges.
), fq(q) can be approximated with Eq. (14). For a sample of stars with a very narrow primary mass range, the mass ratio distributions resulting from PCRP and RP thus give the same results. Differences between the two pairing functions become larger for realistic primary mass ranges.
For pairing function PCRP, the companion mass distribution
fM2(M2) for a set of primaries of identical mass is equal
to the generating mass distribution fM(M) in the mass range
![]() .
The companion mass distribution can thus in
principle be used to derive the properties of the generating mass
distribution. For example, in a set of binaries with a primary mass of
.
The companion mass distribution can thus in
principle be used to derive the properties of the generating mass
distribution. For example, in a set of binaries with a primary mass of
![]() ,
those with mass ratio q<0.08 have brown dwarf
companions. If the observations are of good enough quality to study
the mass ratio distribution below q=0.08, and it is known a priori
that the pairing function is PCRP, the mass ratio distribution can be
used to constrain the slope of the mass distribution in the brown
dwarf regime.
,
those with mass ratio q<0.08 have brown dwarf
companions. If the observations are of good enough quality to study
the mass ratio distribution below q=0.08, and it is known a priori
that the pairing function is PCRP, the mass ratio distribution can be
used to constrain the slope of the mass distribution in the brown
dwarf regime.
The pairing algorithms RP and PCRP appear similar, but their
difference is for example seen in the primary mass distribution. For
RP there is a larger number of binary systems with high-mass
primaries, which can be understood as follows. Suppose a primary mass
M1 of
![]() is drawn from the mass distribution. For PCRP, the
companion mass M2 is always smaller than the primary mass, while
for RP the companion mass can take any value permitted by the mass
distribution (i.e. also M2 > M1, after which the components are
switched). Another difference is that, unlike RP, for PCRP the binary
fraction is independent of primary spectral type:
is drawn from the mass distribution. For PCRP, the
companion mass M2 is always smaller than the primary mass, while
for RP the companion mass can take any value permitted by the mass
distribution (i.e. also M2 > M1, after which the components are
switched). Another difference is that, unlike RP, for PCRP the binary
fraction is independent of primary spectral type:
![]() .
For realistic mass distributions (e.g., Salpeter- or
Kroupa-like), the overall mass ratio distribution
.
For realistic mass distributions (e.g., Salpeter- or
Kroupa-like), the overall mass ratio distribution
![]() of PCRP is
peaked towards large values of q, while that of RP is peaked towards
small values of q. The pairing functions RP and PCRP can be excluded
if more than a
of PCRP is
peaked towards large values of q, while that of RP is peaked towards
small values of q. The pairing functions RP and PCRP can be excluded
if more than a ![]() of the intermediate-mass stars are ``twins'' (
of the intermediate-mass stars are ``twins'' (
![]() ).
).
In models with primary-constrained pairing (PCP), each binary system
is generated by drawing a primary mass M1 from fM(M) in the
range
![]() ,
and a mass ratio q from the generating
distribution hq(q). The companion mass is then calculated from
M2 =
qM1. Due to the nature of this pairing mechanism it is possible that
the resulting companion is of very low mass, for example a planetary
mass if a very small mass ratio is drawn. Below we describe three
variants of pairing function PCP, each of which handles very low mass
companions in a different way: accepting all companions (PCP-I),
rejecting the very low-mass companions (PCP-II), and redrawing the
mass ratio if the companion mass is of very low mass (PCP-III).
,
and a mass ratio q from the generating
distribution hq(q). The companion mass is then calculated from
M2 =
qM1. Due to the nature of this pairing mechanism it is possible that
the resulting companion is of very low mass, for example a planetary
mass if a very small mass ratio is drawn. Below we describe three
variants of pairing function PCP, each of which handles very low mass
companions in a different way: accepting all companions (PCP-I),
rejecting the very low-mass companions (PCP-II), and redrawing the
mass ratio if the companion mass is of very low mass (PCP-III).
PCP-I is the simplest variant of PCP: the primary mass is drawn from fM(M) and the mass ratio from hq(q), and no further constraints are set. As a result, the specific mass ratio distribution
fq;M1(q) and overall mass ratio distribution
![]() are equal to the generating mass ratio distribution hq(q). Additionally, the specific binary fraction
are equal to the generating mass ratio distribution hq(q). Additionally, the specific binary fraction
![]() and overall binary fraction
and overall binary fraction
![]() are equal to the generating binary fraction
are equal to the generating binary fraction
![]() .
.
The companion mass for PCP-I can be arbitrarily small:
![]() .
Several companions may thus have masses significantly lower than the deuterium burning limit (
.
Several companions may thus have masses significantly lower than the deuterium burning limit (![]()
![]() ). Even planetary companions are considered as companion ``stars'' for the pairing function PCP-I. However, if we do include planets, we make the implicit
assumption that the star formation process is scalable down to planetary masses.
This assumption is in contradiction with the theories that suggest that stars and brown dwarfs form by fragmentation (Goodwin et al. 2007; Whitworth et al. 2007), while planets form by
core-accretion (see, e.g., Pollack et al. 1996). This is an important point to keep in mind when using PCP-I, i.e., when adopting a mass ratio distribution that is fully independent of primary spectral type.
). Even planetary companions are considered as companion ``stars'' for the pairing function PCP-I. However, if we do include planets, we make the implicit
assumption that the star formation process is scalable down to planetary masses.
This assumption is in contradiction with the theories that suggest that stars and brown dwarfs form by fragmentation (Goodwin et al. 2007; Whitworth et al. 2007), while planets form by
core-accretion (see, e.g., Pollack et al. 1996). This is an important point to keep in mind when using PCP-I, i.e., when adopting a mass ratio distribution that is fully independent of primary spectral type.
For PCP-II, companions with M2 < c, are rejected, and the corresponding primary stars are classified as single stars. There are two reasons why one may want to consider using PCP-II. First, one may wish to use this prescription if a minimum companion mass is expected from theory, for example the Jeans mass or the opacity limit for fragmentation (e.g., Tohline 1982; Low & Lynden-Bell 1976; Silk 1977b; Hoyle 1953; Rees 1976; Silk 1995; Larson 2005; Silk 1977a; Larson 1992,1969; Masunaga & Inutsuka 2000). The second, more observational approach may be to ``ignore'' the low-mass companions. Although this seems somewhat artificial, this method is often used in practice. Planets are usually not considered as companions (the Sun is a ``single star''), which implies a limit
![]() .
.
Due to the rejection of low-mass companions the overall mass ratio distribution is zero for 0<q<c/d. In the range
![]() ,
the expression for the overall mass ratio distribution is given by:
,
the expression for the overall mass ratio distribution is given by:
The specific binary fraction for a sample of systems with primary mass M1 is given by
As an example, consider a stellar population with
![]() and a generating mass ratio distribution fq(q)=1 and
and a generating mass ratio distribution fq(q)=1 and
![]() ,
systems with B-type primaries and systems with M-type primaries have a resulting specific binary fraction of 99% and 87%, respectively. If we also do not consider brown dwarfs as companions (so
,
systems with B-type primaries and systems with M-type primaries have a resulting specific binary fraction of 99% and 87%, respectively. If we also do not consider brown dwarfs as companions (so
![]() ), then the specific binary fractions are 96% and 51%, respectively.
), then the specific binary fractions are 96% and 51%, respectively.
For PCP-III the primary mass is drawn from fM(M) in the range
![]() ,
and the mass ratio is drawn from hq(q). If the resulting companion star mass is smaller than c, the mass ratio is redrawn from hq(q) until a companion with mass
,
and the mass ratio is drawn from hq(q). If the resulting companion star mass is smaller than c, the mass ratio is redrawn from hq(q) until a companion with mass
![]() is obtained. This is equivalent to renormalising hq(q) in the range
is obtained. This is equivalent to renormalising hq(q) in the range
![]() ,
where
,
where
![]() .
This effectively results in a mass-dependent generating mass ratio distribution h'q(q). The expression for the resulting overall mass ratio distribution
.
This effectively results in a mass-dependent generating mass ratio distribution h'q(q). The expression for the resulting overall mass ratio distribution
![]() are then:
are then:
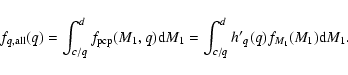 |
(20) |
As a result of the redrawing of the companions for pairing function PCP-III, the resulting overall binary fraction
![]() equals the generating binary fraction
equals the generating binary fraction
![]() ,
and the specific binary fraction
,
and the specific binary fraction
![]() equals
equals
![]() for any primary mass range.
for any primary mass range.
For split-core pairing (SCP) one assumes that the system ``core'' mass ![]() is drawn from a core mass distribution
is drawn from a core mass distribution
![]() with
with
![]() ,
where
,
where ![]() is the star forming efficiency. Split-core pairing is frequently inferred from observations of dense cores in star forming regions, assuming that a fraction of the cores fragment into binaries (see, e.g., Swift & Williams 2008; Goodwin et al. 2008). As a core collapses, it forms one or two stars with a total mass
is the star forming efficiency. Split-core pairing is frequently inferred from observations of dense cores in star forming regions, assuming that a fraction of the cores fragment into binaries (see, e.g., Swift & Williams 2008; Goodwin et al. 2008). As a core collapses, it forms one or two stars with a total mass
![]() .
The resulting minimum and maximum primary masses are thus c and 2d, respectively. The star forming efficiency may be a function of various parameters, for example the mass of the core. For simplicity in our analysis, however, we keep the star forming efficiency fixed to
.
The resulting minimum and maximum primary masses are thus c and 2d, respectively. The star forming efficiency may be a function of various parameters, for example the mass of the core. For simplicity in our analysis, however, we keep the star forming efficiency fixed to
![]() for all values of
for all values of ![]() .
The total mass of each binary is thus
.
The total mass of each binary is thus
![]() .
Note that ``random fragmentation'' (random splitup of a clump into two stellar components) is very different from random pairing of two components from the IMF (see, e.g., Figs. 2 and 3).
.
Note that ``random fragmentation'' (random splitup of a clump into two stellar components) is very different from random pairing of two components from the IMF (see, e.g., Figs. 2 and 3).
For pairing function SCP, the binary total mass is thus drawn from a distribution
![]() .
Note that, although we adopt
.
Note that, although we adopt
![]() in this paper, there is no obvious prerequisite that
in this paper, there is no obvious prerequisite that
![]() should be a standard IMF. The binary is split up according to a mass ratio that is drawn from a generating mass ratio distribution hq(q). Given the core mass
should be a standard IMF. The binary is split up according to a mass ratio that is drawn from a generating mass ratio distribution hq(q). Given the core mass
![]() and the mass ratio q, the primary and companion mass are given by
and the mass ratio q, the primary and companion mass are given by
For pairing function SCP-I, all binary components resulting from the split-up mechanism are accepted, irrespective of their mass. Stars with substellar and planetary companions are thus also considered as ``binary stars''.
Due to the nature of this pairing process, the overall mass ratio distribution is equal to the generating mass ratio distribution. The specific mass ratio distribution, however, is a function of spectral type.
A full derivation of the specific mass ratio distribution is given in Appendix A.4; see also Clarke (1996a). In most cases the primary mass range is contained within the range [2c,d], which corresponds to ``case 7'' in Appendix A.4.
Consider the special case of a single power-law mass distribution
![]() (
(
![]() )
and a uniform mass ratio distribution hq(q)=1. Under these assumptions, the expression for the specific mass ratio distribution is
)
and a uniform mass ratio distribution hq(q)=1. Under these assumptions, the expression for the specific mass ratio distribution is
![]() for
for ![]() ,
if either the primary mass range is contained within the range [2c,d] (case 7), or if x1=x2. Note that this expression is identical to that in Eq. (5). The highest mass binaries thus have on average a small mass ratio, and the lowest mass binaries have on average a large mass ratio. Note that these trends are present, even though the generating mass ratio distribution produces mass ratios in the range
,
if either the primary mass range is contained within the range [2c,d] (case 7), or if x1=x2. Note that this expression is identical to that in Eq. (5). The highest mass binaries thus have on average a small mass ratio, and the lowest mass binaries have on average a large mass ratio. Note that these trends are present, even though the generating mass ratio distribution produces mass ratios in the range ![]() ,
irrespective of the core mass
,
irrespective of the core mass ![]() .
.
Pairing function SCP-I naturally results in a mass-dependent binary fraction:
For SCP-II the companion is rejected if M2 < c, and the primary star becomes single. The resulting primary mass range is then
![]() ,
and the companion mass is in the range
,
and the companion mass is in the range
![]() .
The full derivation for the overall and specific mass ratio distributions is given in Appendix A.4. In most realistic cases the primary mass range [x1,x2] is fully enclosed in the mass range 2c<M1<d (``case 1'').
Unlike SCP-I, the resulting overall mass ratio distribution is unequal to the generating mass ratio distribution, but contains more large-q binaries instead.
.
The full derivation for the overall and specific mass ratio distributions is given in Appendix A.4. In most realistic cases the primary mass range [x1,x2] is fully enclosed in the mass range 2c<M1<d (``case 1'').
Unlike SCP-I, the resulting overall mass ratio distribution is unequal to the generating mass ratio distribution, but contains more large-q binaries instead.
The specific binary fraction
![]() resulting from SCP-II varies with primary mass M1:
resulting from SCP-II varies with primary mass M1:
Figure 7 shows the specific binary fraction
![]() as a function of
as a function of
![]() and hq(q).
The specific binary fraction decreases with decreasing primary mass, as, on average, more low-mass companions are rejected among lower-mass primaries. The majority of the newly formed single stars (due to rejection of low-mass companions) is thus of most low mass. For the very lowest-mass stars, however, the binary fraction increases to unity, as
and hq(q).
The specific binary fraction decreases with decreasing primary mass, as, on average, more low-mass companions are rejected among lower-mass primaries. The majority of the newly formed single stars (due to rejection of low-mass companions) is thus of most low mass. For the very lowest-mass stars, however, the binary fraction increases to unity, as
![]() and
and
![]() for
for
![]() .
The specific binary fraction then rises again to a maximum around M1 = d, and then rapidly drops to zero at
M1 = 2d-c. As a result of the rejection of low-mass companions, the overall binary fraction is always lower than
.
The specific binary fraction then rises again to a maximum around M1 = d, and then rapidly drops to zero at
M1 = 2d-c. As a result of the rejection of low-mass companions, the overall binary fraction is always lower than
![]() .
.
For SCP-III the mass ratio is redrawn when a companion with mass M2<c is produced by the splitting algorithm (similar to PCP-III). This effectively corresponds to a (mass-specific) re-normalised mass ratio distribution h'q(q) in the range
![]() .
The resulting overall mass ratio distribution for SCP-III is given by:
.
The resulting overall mass ratio distribution for SCP-III is given by:
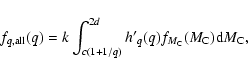 |
(24) |
The overall binary fraction
![]() equals
equals
![]() for SCP-III. The specific binary fraction is given by Eq. (22). Note however, that the primary mass distribution
fM1(M1) resulting from SCP-III is different from that of SCP-III; see Appendix A.4.2 for details.
for SCP-III. The specific binary fraction is given by Eq. (22). Note however, that the primary mass distribution
fM1(M1) resulting from SCP-III is different from that of SCP-III; see Appendix A.4.2 for details.
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{ps/0234_f8.ps}
\end{figure}](/articles/aa/full/2009/03/aa10234-08/Timg216.gif) |
Figure 8:
The mass distributions resulting from the different pairing functions, for the models shown in Fig. 2. From top to bottom, the panels show the primary mass distribution fM1, companion mass distribution fM2, the system mass distribution
|
| Open with DEXTER | |
As discussed in the previous sections, each pairing function results in different properties of the binary population. In this section we provide an overview of the major differences and similarities. In general, each of the properties described below depends on the choice of the pairing function, a generating mass distribution fM(M), a generating mass ratio distribution fq(q), and a generating binary fraction
![]() .
Our example models have a Kroupa generating mass distribution with
.
Our example models have a Kroupa generating mass distribution with
![]() ,
a flat generating mass ratio distribution (if applicable), and a generating binary fraction of 100%. The resulting mass distributions and mass ratio distributions for the different pairing functions are shown in Figs. 2 and 8, respectively.
,
a flat generating mass ratio distribution (if applicable), and a generating binary fraction of 100%. The resulting mass distributions and mass ratio distributions for the different pairing functions are shown in Figs. 2 and 8, respectively.
For pairing functions PCP-I, PCP-III and PCRP the primary mass distribution is identical to fM(M). For pairing function PCP-II, fM1(M) is very similar to fM(M), but it contains less primaries of low mass due to rejection of very low-mass companions (which mostly occurs among low-mass primaries). The latter ``primaries'' are considered as single stars after removal of their companions. For pairing function RP the primary mass distribution is more massive than fM(M) due to swapping of the components that are drawn from fM(M). Pairing functions SCP-I, SCP-II and SCP-III result in smaller average primary masses than fM(M) due to the core splitting.
For all pairing functions the companion mass distribution
fM2(M) is shifted to lower masses with respect to the generating mass distribution fM(M). Pairing functions PCP-III, PCRP and SCP-III result in a large number of low mass companions; the companion mass distribution is sharply peaked at
![]() ;
see Figs. 3 and 8. For a Kroupa generating mass distribution, the other pairing functions show a peak in the companion mass distribution around
;
see Figs. 3 and 8. For a Kroupa generating mass distribution, the other pairing functions show a peak in the companion mass distribution around
![]() .
Pairing functions PCP-I and SCP-I may result in arbitrarily small companion masses, but all other pairing functions have
.
Pairing functions PCP-I and SCP-I may result in arbitrarily small companion masses, but all other pairing functions have
![]() .
All pairing functions have
.
All pairing functions have
![]() .
For each pairing function described in this paper, the companion mass distribution depends strongly on the selected primary mass range (see Fig. 3), but is independent of
.
For each pairing function described in this paper, the companion mass distribution depends strongly on the selected primary mass range (see Fig. 3), but is independent of
![]() .
.
We define the binary system mass distribution
![]() as the distribution of masses
as the distribution of masses
![]() of all binary systems in a population. For pairing function SCP-I the system mass distribution equals the generating mass distribution:
of all binary systems in a population. For pairing function SCP-I the system mass distribution equals the generating mass distribution:
![]() .
For all other pairing functions the expression for the system mass distribution is different from fM(M),
fM1(M) and
fM2(M). For random pairing, for example, the system mass distribution can be described as a convolution (Eq. (9)).
.
For all other pairing functions the expression for the system mass distribution is different from fM(M),
fM1(M) and
fM2(M). For random pairing, for example, the system mass distribution can be described as a convolution (Eq. (9)).
Pairing functions with
![]() result in a population of single stars. For PCP-II and SCP-II, even those with
result in a population of single stars. For PCP-II and SCP-II, even those with
![]() result in single stars. In our analysis we distinguish between the single mass distribution
result in single stars. In our analysis we distinguish between the single mass distribution
![]() and the primary/single mass distribution
fM1,S(M). The latter distribution includes both single stars and primaries and is important for observers. Target lists for binarity surveys are often defined by
fM1,S(M) for a certain mass range, as in practice it is often unknown whether a surveyed star has a companion star.
For most pairing functions the single mass distribution
and the primary/single mass distribution
fM1,S(M). The latter distribution includes both single stars and primaries and is important for observers. Target lists for binarity surveys are often defined by
fM1,S(M) for a certain mass range, as in practice it is often unknown whether a surveyed star has a companion star.
For most pairing functions the single mass distribution
![]() is equal to the generating mass distribution fM(M), and the fraction of single stars among the systems is given by
is equal to the generating mass distribution fM(M), and the fraction of single stars among the systems is given by
![]() ,
where
,
where
![]() is the generating binary fraction. For PCP-II and SCP-II additional single stars are created due to the rejection of very low-mass companions. The generated single stars are mostly of low mass.
Only for pairing functions PCP-I, PCP-II, PCP-III and PCRP, the primary/single star mass distribution
fM1,S(M) is equal to the generating mass distribution fM(M). The primary/single star mass distribution is biased to higher masses for RP, and to lower masses for SCP-I, SCP-II and SCP-III.
is the generating binary fraction. For PCP-II and SCP-II additional single stars are created due to the rejection of very low-mass companions. The generated single stars are mostly of low mass.
Only for pairing functions PCP-I, PCP-II, PCP-III and PCRP, the primary/single star mass distribution
fM1,S(M) is equal to the generating mass distribution fM(M). The primary/single star mass distribution is biased to higher masses for RP, and to lower masses for SCP-I, SCP-II and SCP-III.
The bottom row of Fig. 8 shows the mass distribution
![]() of all stars, including primaries, companions, and single stars. This mass distribution, which includes all stars in the population, is referred to as the mass function of a stellar population. For a zero-age population,
of all stars, including primaries, companions, and single stars. This mass distribution, which includes all stars in the population, is referred to as the mass function of a stellar population. For a zero-age population,
![]() is an initial mass function (IMF), e.g., the Kroupa IMF (Eq. (2)). Only for pairing function RP is the individual star mass distribution
is an initial mass function (IMF), e.g., the Kroupa IMF (Eq. (2)). Only for pairing function RP is the individual star mass distribution
![]() equal to the generating mass distribution fM(M); the other pairing functions result in a distribution
equal to the generating mass distribution fM(M); the other pairing functions result in a distribution
![]() which is biased to lower values with respect to fM(M).
which is biased to lower values with respect to fM(M).
The resulting overall mass ratio distribution
![]() depends on the pairing function. The top panels in Fig. 2 show the significant difference between the overall mass ratio distribution for the different pairing functions. The overall mass ratio distribution
depends on the pairing function. The top panels in Fig. 2 show the significant difference between the overall mass ratio distribution for the different pairing functions. The overall mass ratio distribution
![]() is equal to the generating mass ratio distribution fq(q) for pairing functions PCP-I and SCP-I. For pairing functions PCP-II, PCP-III, SCP-II and SCP-III the overall mass ratio distribution is biased to larger values of q with respect to fq(q). For these pairing functions binaries with very low companion masses, and thus often very low mass ratios, are either rejected or redrawn, resulting in systematically larger values of q. The overall mass ratio distribution of pairing functions RP and PCRP are purely a result of the mass distribution fM(M) and depend strongly on its lower and upper limits.
is equal to the generating mass ratio distribution fq(q) for pairing functions PCP-I and SCP-I. For pairing functions PCP-II, PCP-III, SCP-II and SCP-III the overall mass ratio distribution is biased to larger values of q with respect to fq(q). For these pairing functions binaries with very low companion masses, and thus often very low mass ratios, are either rejected or redrawn, resulting in systematically larger values of q. The overall mass ratio distribution of pairing functions RP and PCRP are purely a result of the mass distribution fM(M) and depend strongly on its lower and upper limits.
Only for pairing function PCP-I is the mass ratio distribution independent of spectral type, and thus equal to the overall and generating mass ratio distributions. For all other pairing functions the specific mass ratio distribution is a function of the primary mass. The middle and bottom panels in Fig. 2 show for each pairing function the specific mass ratio distribution for target samples of different spectral types. For each of these pairing functions, high-mass binaries have on average a lower mass ratio than low-mass binaries. The lowest-mass binaries have a mass ratio distribution peaked to q=1.
Figures 2 and 6 illustrate the strong dependence of the specific mass ratio distribution on the targeted sample in the survey. Figure 4 shows a generalised version of these figures. Each panel shows the two-dimensional distribution f(q,M1) for the different pairing functions. Care should thus be taken when extrapolating the results to the population as a whole. The interpretation of the observations is further complicated by the instrument bias and observational errors, an effect we will discuss in Sect. 9.
An overview of the mass ratio distribution changes is presented in Table 2. The columns show the pairing function, the overall mass ratio distribution, the specific mass ratio distribution for high-mass stars, the specific mass ratio distribution for low-mass stars. The symbols the table indicate whether the mass ratio distribution is equal to (=), almost equal to (![]() ), or biased to low mass ratios (
), or biased to low mass ratios (
![]() )
or large mass ratios (
)
or large mass ratios (![]() ), with respect to hq(q). As the distribution hq(q) is undefined for RP and PCRP, the properties of
fq;M1(q) with respect to
), with respect to hq(q). As the distribution hq(q) is undefined for RP and PCRP, the properties of
fq;M1(q) with respect to
![]() are indicated.
are indicated.
Table 2: The mass ratio distribution resulting from different pairing functions, for different samples, as compared to the generating mass ratio distribution hq(q).
The overall binary fraction
![]() is equal to the generating binary fraction
is equal to the generating binary fraction
![]() for most pairing functions. Only for PCP-II and SCP-II the overall binary fraction is lower than
for most pairing functions. Only for PCP-II and SCP-II the overall binary fraction is lower than
![]() because of the rejection of low-mass companions.
because of the rejection of low-mass companions.
Table 3 provides an overview of the changes in the binary fraction as a function of spectral type and primary mass range. The columns show the pairing function, the overall binary fraction
![]() ,
the specific binary fraction for high-mass stars
,
the specific binary fraction for high-mass stars
![]() and for low-mass stars
and for low-mass stars
![]() .
The last column shows whether the resulting binary fraction is equal to
.
The last column shows whether the resulting binary fraction is equal to
![]() for any primary mass range.
for any primary mass range.
Most pairing functions result in a mass-dependent binary fraction. If the generating binary fraction is lower than 100%, all pairing functions except PCP-I, PCP-III and PCRP result in a specific binary fraction that depends on primary mass (see, e.g., Fig. 7). On the other hand, if
![]() ,
only pairing functions PCP-II and SCP-II result in a varying
,
only pairing functions PCP-II and SCP-II result in a varying
![]() ,
due to the rejection of low-mass companions.
,
due to the rejection of low-mass companions.
For a sample of binaries with high-mass primaries,
![]() is approximately equal to
is approximately equal to
![]() for pairing functions PCP-I, PCP-II, PCP-III and PCRP. For RP, the specific binary fraction for high-mass binaries is higher than
for pairing functions PCP-I, PCP-II, PCP-III and PCRP. For RP, the specific binary fraction for high-mass binaries is higher than
![]() (unless
(unless
![]() ), while for SCP-I, SCP-II and SCP-III the binary fraction for high-mass stars is lower than
), while for SCP-I, SCP-II and SCP-III the binary fraction for high-mass stars is lower than
![]() (unless
(unless
![]() ). For low-mass binaries,
). For low-mass binaries,
![]() is equal to
is equal to
![]() for pairing functions PCP-I, PCP-III, and PCRP. For RP, the specific binary fraction for low-mass stars is only equal to the generating binary fraction if the latter is
for pairing functions PCP-I, PCP-III, and PCRP. For RP, the specific binary fraction for low-mass stars is only equal to the generating binary fraction if the latter is
![]() or
or
![]() ,
and lower in the other cases. For PCP-II the specific binary fraction for low-mass stars is lower than
,
and lower in the other cases. For PCP-II the specific binary fraction for low-mass stars is lower than
![]() .
For SCP-I and SCP-III the binary fraction for low-mass stars is higher than
.
For SCP-I and SCP-III the binary fraction for low-mass stars is higher than
![]() .
For SCP-II the specific binary fraction for low-mass stars may be higher or lower than
.
For SCP-II the specific binary fraction for low-mass stars may be higher or lower than
![]() ,
depending on the properties of fM(M) and fq(q) and the value of
,
depending on the properties of fM(M) and fq(q) and the value of
![]() .
.
Table 3:
The specific binary fraction
![]() as compared to the generating binary fraction
as compared to the generating binary fraction
![]() ,
for different the pairing functions.
,
for different the pairing functions.
Table 4:
Do the properties of a population resulting from a certain pairing function depend on its generating properties? The three generating properties fM(M), fq(q) and
![]() are listed in the top row. For each of the ten quantities listed in the left-most column, we list whether or not they depend on the choice of fM(M), fq(q) and
are listed in the top row. For each of the ten quantities listed in the left-most column, we list whether or not they depend on the choice of fM(M), fq(q) and
![]() .
We indicate dependence and independence with the symbols
.
We indicate dependence and independence with the symbols ![]() and
and ![]() ,
respectively. The results for
fq;M1(q) and
,
respectively. The results for
fq;M1(q) and
![]() are valid only for a population of binaries with identical primary mass M1. The distribution over total system mass
are valid only for a population of binaries with identical primary mass M1. The distribution over total system mass
![]() includes both binary systems and single stars.
includes both binary systems and single stars.
In this section we discuss how the properties of a binary population
depend on the attributes for the pairing functions: the generating
mass distribution fM(M), the generating mass ratio distribution
fq(q), and the generating binary fraction
![]() .
For the most
important properties of a population (with respect to binarity), we
list in Table 4 whether or not they depend on
fM(M), fq(q), or
.
For the most
important properties of a population (with respect to binarity), we
list in Table 4 whether or not they depend on
fM(M), fq(q), or
![]() ,
for each of the eight pairing functions
described in this paper. Note that the system mass distribution
,
for each of the eight pairing functions
described in this paper. Note that the system mass distribution
![]() includes both single stars and binary systems. The specific
mass ratio distribution
fq;M1(q) and specific binary fraction
includes both single stars and binary systems. The specific
mass ratio distribution
fq;M1(q) and specific binary fraction
![]() in Table 4 only refer to samples where all
binaries have identical primary mass M1. For a sample with a finite
primary mass, range, the results for the specific mass ratio
distribution and specific binary fraction are mostly identical to
those of
in Table 4 only refer to samples where all
binaries have identical primary mass M1. For a sample with a finite
primary mass, range, the results for the specific mass ratio
distribution and specific binary fraction are mostly identical to
those of
![]() and
and
![]() ,
respectively. Table 4 also illustrates which
properties of the population can be used to recover fM(M), fq(q),
and
,
respectively. Table 4 also illustrates which
properties of the population can be used to recover fM(M), fq(q),
and
![]() .
For example, for RP, the specific binary fraction
.
For example, for RP, the specific binary fraction
![]() provides information on the generating mass distribution
(e.g., the IMF).
provides information on the generating mass distribution
(e.g., the IMF).
The generating mass distribution. For obvious reasons, all mass
distributions listed in Table 4 depend on
fM(M). The mass ratio distributions for RP and PCRP are defined by,
and depend strongly on the properties of fM(M) and
![]() .
For
PCP-I/II/III,
fq;M1(q) does not depend on fM(M), as both M1 and
q are drawn independently from their generating
distributions. Obtaining the overall mass ratio distribution
.
For
PCP-I/II/III,
fq;M1(q) does not depend on fM(M), as both M1 and
q are drawn independently from their generating
distributions. Obtaining the overall mass ratio distribution
![]() requires integration over the primary mass distribution; as for PCP-II
and PCP-III
fq;M1(q) varies with M1, so does
requires integration over the primary mass distribution; as for PCP-II
and PCP-III
fq;M1(q) varies with M1, so does
![]() .
The overall
binary fraction
.
The overall
binary fraction
![]() is independent of fM(M), except for
PCP-II and SCP-II, for which low-mass companions are rejected. The
specific binary fraction
is independent of fM(M), except for
PCP-II and SCP-II, for which low-mass companions are rejected. The
specific binary fraction
![]() ,
does not depend on fM(M) for
PCRP and PCP-I/II/III due to the independent drawing of M1 and
M2 (or q), while it does vary with fM(M) for SCP-I/II/III as
M1 and q are not drawn independently, and for RP as M1 and
M2 are not drawn independently (due to the swapping of the
components; see Sect. 6.1).
,
does not depend on fM(M) for
PCRP and PCP-I/II/III due to the independent drawing of M1 and
M2 (or q), while it does vary with fM(M) for SCP-I/II/III as
M1 and q are not drawn independently, and for RP as M1 and
M2 are not drawn independently (due to the swapping of the
components; see Sect. 6.1).
The generating mass ratio distribution. The
generating mass ratio distribution fq(q) is undefined for RP and
PCRP. For the other pairing functions, the dependence of
fq;M1(q) and
![]() on fq(q) is obvious. As companion masses are derived from
q, the distributions fM2 and
on fq(q) is obvious. As companion masses are derived from
q, the distributions fM2 and
![]() depend on the choice of
fq(q). Note that that for SCP-II, all parameters vary with fq(q), and
for PCP-II most parameters (except the primary/single mass
distribution) vary with fq(q). The properties of the single stars do
not depend on fq(q), except for PCP-II and SCP-II, where additional
single stars are created due to the rejection of low-mass companions.
depend on the choice of
fq(q). Note that that for SCP-II, all parameters vary with fq(q), and
for PCP-II most parameters (except the primary/single mass
distribution) vary with fq(q). The properties of the single stars do
not depend on fq(q), except for PCP-II and SCP-II, where additional
single stars are created due to the rejection of low-mass companions.
The generating binary fraction. The dependence of
![]() and
and
![]() on the generating binary fraction
on the generating binary fraction
![]() is
trivial. The distributions that do not involve single stars, such as
fM1, fM2,
is
trivial. The distributions that do not involve single stars, such as
fM1, fM2,
![]() and
fq;M1(q), by definition never depend on the choice
of
and
fq;M1(q), by definition never depend on the choice
of
![]() .
The mass distribution of all stars
.
The mass distribution of all stars
![]() (the
``IMF'') depends on the choice of
(the
``IMF'') depends on the choice of
![]() for all pairing functions,
except for RP.
for all pairing functions,
except for RP.
Binarity and multiplicity provide important information about the outcome of the star forming process in different environments (Blaauw 1991,1961). In this paper we explore this issue by making the assumption that binary stars are formed through a simple ``pairing function''. In reality the distribution of stars in fM1,M2(M1,M2) is the result of complex physics involving the collapse of a molecular cloud into stars and stellar systems with discs (which can themselves fragment), followed by dynamical evolution of the protocluster (see Sect. 5). The resulting ``pairing function'' may thus not be describable in terms of the simple probability distributions given in this paper (Sect. 6). However, even if we proceed from our assumption that the pairing of binary stars involves the random selection of a primary mass followed by the secondary (RP, PCRP, PCP-I/II/III) or the random splitting of cores (SCP-I/II/III), the interpretation of the observations is not trivial:
Below we list several properties that have been identified for various binary populations over the last decades. These provide important information on the primordial pairing function, and the formation and evolution of binary populations.
The observed mass-dependent binary fraction.
The observed binary fraction is known to increase with increasing primary spectral type; see, e.g., Bouy et al. (2006); Köhler et al. (2006); Sterzik & Durisen (2004); Lada (2006) for an overview. For early-type (O/B/A) stars the binary fraction approaches 100% (e.g., Shatsky & Tokovinin 2002; Kouwenhoven et al. 2007b; Abt et al. 1990; Mason et al. 1998; Kobulnicky & Fryer 2007). The binary fraction decreases to ![]() for F/G-type stars (Duquennoy & Mayor 1991; Abt & Levy 1976). For M-type stars the binary fraction is
for F/G-type stars (Duquennoy & Mayor 1991; Abt & Levy 1976). For M-type stars the binary fraction is ![]() (Fischer & Marcy 1992; Reid & Gizis 1997; Leinert et al. 1997), and for late M-type stars and brown dwarfs the binary fraction decreases to
(Fischer & Marcy 1992; Reid & Gizis 1997; Leinert et al. 1997), and for late M-type stars and brown dwarfs the binary fraction decreases to ![]() (Bouy et al. 2003; Close et al. 2003; Siegler et al. 2005; Burgasser et al. 2003; Joergens 2008; Maxted et al. 2008; Gizis et al. 2003). Note that this correlation between mass and binary fraction is also predicted by the hydrodynamical/sink particle simulations of Bate (2008).
Assuming that this observational trend is not induced by selection effects, is
inconsistent with pairing functions PCP-I, PCP-III and SCP-I, for
which the binary fraction is independent of primary mass. Furthermore,
observations have ruled out pairing functions RP and PCRP in various
stellar groupings (see Sect. 5). Pairing functions
PCP-II, SCP-II and SCP-III remain options to describe the binary
population, as for these pairing functions the binary fraction increases
with increasing stellar mass, and the average mass ratio decreases
with increasing mass. However, in this paper we merely describe
simplistic (but frequently used) pairing functions. A deeper analysis,
including a study of more complicated pairing functions, combined with
further observations, is necessary for a full description of the
pairing function in the different stellar populations.
(Bouy et al. 2003; Close et al. 2003; Siegler et al. 2005; Burgasser et al. 2003; Joergens 2008; Maxted et al. 2008; Gizis et al. 2003). Note that this correlation between mass and binary fraction is also predicted by the hydrodynamical/sink particle simulations of Bate (2008).
Assuming that this observational trend is not induced by selection effects, is
inconsistent with pairing functions PCP-I, PCP-III and SCP-I, for
which the binary fraction is independent of primary mass. Furthermore,
observations have ruled out pairing functions RP and PCRP in various
stellar groupings (see Sect. 5). Pairing functions
PCP-II, SCP-II and SCP-III remain options to describe the binary
population, as for these pairing functions the binary fraction increases
with increasing stellar mass, and the average mass ratio decreases
with increasing mass. However, in this paper we merely describe
simplistic (but frequently used) pairing functions. A deeper analysis,
including a study of more complicated pairing functions, combined with
further observations, is necessary for a full description of the
pairing function in the different stellar populations.
Twin binaries. Observationally, there is a high prevalence of massive binaries with a mass ratio close to unity, often referred to as the ``twin peak'' in the mass ratio distribution (Lucy 2006; Lucy & Ricco 1979; Pinsonneault & Stanek 2006; Tokovinin 2000; Söderhjelm 2007). High-mass twin binaries are extremely rare for RP and PCRP. For pairing functions PCP and SCP, high-mass twin binaries only occur frequently when this is explicitly put into the generating mass ratio distribution. A high prevalence of low-mass twin binaries, on the other hand, naturally results from all pairing functions except for PCP-I. In general, peaks in the mass ratio distribution can occur for any mass ratio (see, e.g., Fig. 6). The location of the peak depends on the pairing function and the primary mass range, and, if applicable, the mass ratio distribution. In general, the peaks occur at low-q for a sample of high-mass binaries, and at large-q for a sample of low-mass stars. Pairing functions RP and PCRP are thus excluded, while pairing functions PCP and SCP can only result in massive twin binaries if the corresponding generating mass ratio distribution is strongly peaked to q=1.
The brown dwarf desert. The brown dwarf desert is defined as a deficit (not necessarily a total absence) of brown dwarf companions, either relative to the frequency of stellar companions, or relative to the frequency of planetary companions (Grether & Lineweaver 2006; McCarthy & Zuckerman 2004). Theories have been developed that explain the existence of the brown dwarf desert using migration (Armitage & Bonnell 2002) or ejection (Reipurth & Clarke 2001) of brown darfs. The latter scenario ``embryo ejection'' is most popular, and predicts ejectino of brown dwarfs soon after their formation. In this scenario, brown dwarfs could be considered as failed stars. Kouwenhoven et al. (2007a), however, show that the scarcity of brown dwarf companions among intermediate-mass stars can also be explained by an extrapolation of the mass ratio distribution into the brown dwarf regime. Metchev & Hillenbrand (2008) reach a similar conclusion. PCP-I/II/III are thus not excluded by the presence of the brown dwarf desert.
The (initial) mass distribution. The initial or present-day
mass distribution
![]() of a stellar population sets strong
constraints on the star formation process, and is an important feature
of each pairing function. The distribution is often derived after its
members are securely identified
(e.g., Harayama et al. 2008; Preibisch et al. 2002; Stolte et al. 2008; Kroupa 2001). The
measured mass distribution is often the distribution of
single/primary masses
fM1,S(M), as it is not known which
members are single and which are binary, which results in a measured
mass distribution that is biased to higher masses with respect to the
overall mass distribution
of a stellar population sets strong
constraints on the star formation process, and is an important feature
of each pairing function. The distribution is often derived after its
members are securely identified
(e.g., Harayama et al. 2008; Preibisch et al. 2002; Stolte et al. 2008; Kroupa 2001). The
measured mass distribution is often the distribution of
single/primary masses
fM1,S(M), as it is not known which
members are single and which are binary, which results in a measured
mass distribution that is biased to higher masses with respect to the
overall mass distribution
![]() ,
which, if measured just
after star formation, is the IMF. As stellar masses are often derived
from measured luminosities, the presence of unresolved binaries and
crowding may further bias the measured (initial or present-day) mass
distribution to higher masses
(e.g., Maíz Apellániz 2008; Weidner et al. 2008; Vanbeveren 1982).
Over the last decade, considerable effort has been put into studying
possible environmental dependences of the IMF (see, e.g., Elmegreen 2007; Kroupa 2008, for
an overview and examples). The IMF of a
population is presumably a result of the form of the initial core mass
function, and the primordial pairing function (i.e., how these
cores fragment into multiple systems, see Goodwin et al. 2008).
An environmental dependence of the primordial pairing function (e.g.,
mass ratio distribution, binary fraction) implies a different outcome
of the star formation process with environment, it also almost
certainly implies an environmental dependence of the IMF (unless the
core mass function changes in such as way as to mask this change).
,
which, if measured just
after star formation, is the IMF. As stellar masses are often derived
from measured luminosities, the presence of unresolved binaries and
crowding may further bias the measured (initial or present-day) mass
distribution to higher masses
(e.g., Maíz Apellániz 2008; Weidner et al. 2008; Vanbeveren 1982).
Over the last decade, considerable effort has been put into studying
possible environmental dependences of the IMF (see, e.g., Elmegreen 2007; Kroupa 2008, for
an overview and examples). The IMF of a
population is presumably a result of the form of the initial core mass
function, and the primordial pairing function (i.e., how these
cores fragment into multiple systems, see Goodwin et al. 2008).
An environmental dependence of the primordial pairing function (e.g.,
mass ratio distribution, binary fraction) implies a different outcome
of the star formation process with environment, it also almost
certainly implies an environmental dependence of the IMF (unless the
core mass function changes in such as way as to mask this change).
The pairing function, fM(M), fq(q) and
![]() can in principle
be derived from observations of binary systems, provided that the
observations cover a large part of the parameter space
can in principle
be derived from observations of binary systems, provided that the
observations cover a large part of the parameter space ![]() ;
see Sect. 8. A significant
complication, however, is introduced by selection effects, in
particular by detection limits that prevent the detection of faint
companion stars. As an example, a twin peak for high mass binaries
would rule out all of the models presented in this paper if fq(q)is assumed to be flat for PCP and SCP (see
Sect. 9.1). On the other hand, a
twin peak at the low mass end only rules out PCP-I (if the
generating fq(q) is flat). So how should we proceed when interpreting
the observational data? If we assume for the moment that we somehow
know that one of the eight pairing mechanisms discussed in this paper
occurs in Nature, we can advise the following:
;
see Sect. 8. A significant
complication, however, is introduced by selection effects, in
particular by detection limits that prevent the detection of faint
companion stars. As an example, a twin peak for high mass binaries
would rule out all of the models presented in this paper if fq(q)is assumed to be flat for PCP and SCP (see
Sect. 9.1). On the other hand, a
twin peak at the low mass end only rules out PCP-I (if the
generating fq(q) is flat). So how should we proceed when interpreting
the observational data? If we assume for the moment that we somehow
know that one of the eight pairing mechanisms discussed in this paper
occurs in Nature, we can advise the following:
The only practical way of excluding models of binary formation based on observations is to treat the inverse problem with Monte Carlo methods where the observations are predicted from the model and compared to the real observations. In this method selection and observational biases should be included (see, e.g., Kouwenhoven 2006; Kouwenhoven et al. 2007b). Starting from models based on probability distributions for a set of parameters may not be the most useful way of constraining the formation mechanism for binaries as this leaves a lot of freedom. It is more fruitful (but also more difficult) to start from actual physical models of binary formation and see if these are capable of reproducing the observations.
A further complication occurs when one wants to recover the primordial pairing function, i.e., the pairing function that is present just after star formation, as the pairing function of a stellar population evolves over time as a result of several processes. During the first stages of star formation, the newly formed proto-binaries are affected by pre-main sequence eigenevolution (Kroupa 1995a,c,b) due to interaction with the remaining gas in the circumbinary disc. Dynamical interactions can result in ionisation of binaries, the formation of new binary systems, and exchange interactions, and thus alters the pairing function of a stellar population (see, e.g., Kroupa et al. 1999; Reipurth et al. 2007; Preibisch et al. 2003; Köhler et al. 2006; Duchêne et al. 2004; Kroupa et al. 2001). Thie process is enhanced by gravitational focusing (e.g., Gaburov et al. 2008). The pairing function also changes due to stellar evolution, which can change the mass of one or both of the components of a binary system, and in some cases in a merger (e.g., Gaburov et al. 2008; Sills et al. 2002), or in the ejection of one of the components during a supernova event (e.g., Blaauw 1961). The primordial pairing function can be constrained using the technique of inverse dynamical population synthesis (e.g., Kroupa 1995c,b), in which the outcome of N-body simulations is compared with present-day binary population in a Monte Carlo way.
Finally we stress that any interpretation of observations of a binary population in terms of the formation of binaries should start by stating the assumptions one makes in order to restrict the number of solutions to explore. That is, in the context of what class of binary formation mechanisms are the observations interpreted?
Most pairing functions result in a mass ratio distribution that varies with primary spectral type. For this reason one has to be cautious when interpreting the observations of a sample of binaries. Given the observed dataset, what is the pairing function, and what is the generating mass ratio distribution fq(q)? The answer partially depends on the generating mass distribution, which we assume to be the Kroupa mass distribution for now. More importantly, the answer depends on the properties of the surveyed targets. In this example we analyse three cases: a sample where all binaries are studied, a sample of spectral type A/B targets, and a sample of brown dwarf targets. Using Monte-Carlo techniques we determine which pairing function is consistent with an observed flat mass ratio distribution
![]() for each subset, and, if applicable, which generating mass ratio distribution. We assume that the generating mass ratio distribution has the form
for each subset, and, if applicable, which generating mass ratio distribution. We assume that the generating mass ratio distribution has the form
![]() .
We further assume that the observations are complete in the range
.
We further assume that the observations are complete in the range
![]() with
with
![]() ,
and that no binaries with
,
and that no binaries with
![]() are observed due to incompleteness.
are observed due to incompleteness.
Table 5 shows the best-fitting values of ![]() for each pairing function, assuming binaries with q<0.1 cannot be detected. We ignore the other selection effects. The numbers in the three columns represent the most compatible values of
for each pairing function, assuming binaries with q<0.1 cannot be detected. We ignore the other selection effects. The numbers in the three columns represent the most compatible values of ![]() for the overall mass ratio distribution fq(q), and for the specific mass ratio distribution of binaries with A/B primaries and brown dwarf primaries, respectively. For each for the three samples, pairing functions RP and PCRP are excluded with high confidence; these are unable to reproduce the observed flat mass ratio distribution. The best-fitting value for pairing function PCP-I is
for the overall mass ratio distribution fq(q), and for the specific mass ratio distribution of binaries with A/B primaries and brown dwarf primaries, respectively. For each for the three samples, pairing functions RP and PCRP are excluded with high confidence; these are unable to reproduce the observed flat mass ratio distribution. The best-fitting value for pairing function PCP-I is
![]() for all samples. This is not surprising, as for
fq;M1(q)= fq(q) for this pairing function. For PCP-II and PCP-III the derived
for all samples. This is not surprising, as for
fq;M1(q)= fq(q) for this pairing function. For PCP-II and PCP-III the derived ![]() for high-mass stars equals the observed value, but the other two samples contain more binaries with large mass ratios. For pairing functions SCP, the best-fitting intrinsic value of
for high-mass stars equals the observed value, but the other two samples contain more binaries with large mass ratios. For pairing functions SCP, the best-fitting intrinsic value of ![]() is smaller than the observed value of
is smaller than the observed value of ![]() for high-mass binaries, but larger for low-mass binaries. This example illustrates that the inferred intrinsic pairing properties may be significantly different from the observed pairing properties, depending on the pairing function and the selected sample of binaries.
for high-mass binaries, but larger for low-mass binaries. This example illustrates that the inferred intrinsic pairing properties may be significantly different from the observed pairing properties, depending on the pairing function and the selected sample of binaries.
In practice, parameter distributions are often represented with a functional form. Suppose, for example, that we assume that the generating mass ratio distribution has the form
![]() .
If we use this functional form for our model population, and compare simulated observations with the true observations for different values of
.
If we use this functional form for our model population, and compare simulated observations with the true observations for different values of ![]() ,
we will likely find a best-fitting
,
we will likely find a best-fitting ![]() .
This does not necessarily mean that the generating mass ratio distribution has indeed the form
.
This does not necessarily mean that the generating mass ratio distribution has indeed the form
![]() .
In this example we have added another assumption, i.e., that the mass ratio distribution has the form
.
In this example we have added another assumption, i.e., that the mass ratio distribution has the form
![]() .
.
Table 5:
Suppose that a stellar population has an observed mass ratio distribution
![]() for
for
![]() .
What is the pairing function and the generating mass distribution fq(q)? This table lists the exponent
.
What is the pairing function and the generating mass distribution fq(q)? This table lists the exponent ![]() of the generating mass distribution
of the generating mass distribution
![]() that is most compatible with the synthetic observations.
that is most compatible with the synthetic observations.
We have described several methods of pairing individual stars into
binary systems. We refer to these algorithms as pairing
functions. Each pairing function is characterized by a generating
mass distribution fM(M) and a generating binary fraction
![]() ,
and most additionally by a generating mass ratio distribution fq(q). Each
pairing function results in a significantly different binary
population. Depending on the pairing function and the mass range of
the binaries studied, the resulting binary population may or may
not have a mass ratio distribution or binary fraction that is equal
to fq(q) or
,
and most additionally by a generating mass ratio distribution fq(q). Each
pairing function results in a significantly different binary
population. Depending on the pairing function and the mass range of
the binaries studied, the resulting binary population may or may
not have a mass ratio distribution or binary fraction that is equal
to fq(q) or
![]() ,
respectively. The binary fraction and mass ratio
distribution generally depend strongly on the number of substellar objects in
the population, and on the properties of the surveyed sample.
,
respectively. The binary fraction and mass ratio
distribution generally depend strongly on the number of substellar objects in
the population, and on the properties of the surveyed sample.
Eight pairing mechanisms are discussed in detail. For random pairing (RP) both components are randomly drawn from the mass distribution fM(M). For primary-constrained random pairing (PCRP), both components are drawn from fM(M), with the constraint that the companion is less massive than the primary. For primary-constrained pairing (PCP-I, PCP-II, and PCP-III), the primary is drawn from fM(M), and the companion mass is determined using a mass ratio distribution fq(q). For split-core pairing (SCP-I, SCP-II, and SCP-III), the core mass is drawn from fM(M), and the masses of the binary components are determined by the mass ratio fq(q), which splits up the core into two stars. The difference between the variants of pairing functions PCP and SCP lies in the treatment of low-mass companions (see Sect. 6). Seven pairing functions naturally result in a specific mass ratio distribution that depends on primary spectral type, and five naturally result in a mass-dependent binary fraction. Seven out of eight pairing functions always produce a twin peak for low-mass binaries, while none result in a twin peak for high-mass binaries, unless the generating mass ratio distribution is strongly peaked to q=1.
The differences between pairing functions are important for (i) the interpretation of observations; (ii) initial conditions of numerical simulations; and (iii) understanding the outcome of star formation:
Acknowledgements
We would like to thank the referee, Rainer Köhler, for detailed comments and suggestions which helped to improve this paper significantly. We are also thankful to Pavel Kroupa for valuable comments and suggestions. M.K. was supported by PPARC/STFC under grant number PP/D002036/1 and by NWO under project number 614.041.006. M.K. and S.G. acknowledge a Royal Society International Joint Project grant between Sheffield and Bonn. This research was supported by the Netherlands Research School for Astronomy (NOVA) and by the Leids Kerkhoven Bosscha Fonds (LKBF).
In this appendix we discuss for each of the pairing mechanisms described in the
main paper how to calculate the mass ratio distribution function fq(q). The
masses of primary (M1) and secondary (M2) are drawn from the same
generating mass distribution fM(M), or alternatively, the primary is drawn from
fM(M) while
the secondary is drawn from a generating mass ratio distribution. The
generating mass distribution is treated
throughout this appendix as a probability density:
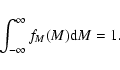 |
(A.2) |
The simplest choice for a pairing function is that of ``random pairing'' (RP). In
this case both component masses are drawn independently from fM(M) and swapped,
if necessary, to ensure that
![]() .
In
this case the joint distribution function
.
In
this case the joint distribution function
![]() for the
component masses is given by:
for the
component masses is given by:
First, general expressions for the mass ratio distributions are derived before
working out specific examples. To derive the mass ratio distribution we follow
the appendix of Piskunov & Mal'Kov (1991) and derive fq(q) from its cumulative
distribution function:
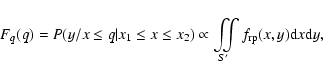 |
(A.7) |
For RP, the overall binary fraction
![]() is equal to the generating binary fraction
is equal to the generating binary fraction
![]() .
The specific binary fraction
.
The specific binary fraction
![]() ,
however, is generally a function of primary mass. For a given primary mass, the number of single stars S(M1) with mass M1 and the number of binary stars B(M1) with primary mass M1 is given by:
,
however, is generally a function of primary mass. For a given primary mass, the number of single stars S(M1) with mass M1 and the number of binary stars B(M1) with primary mass M1 is given by:
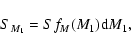 |
(A.9) |
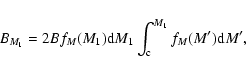 |
(A.10) |
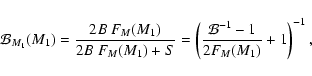 |
(A.11) |
An example of the mass-dependent binary fraction resulting from RP is shown in Fig. 7. Clearly, we have
![]() when S=0, and
when S=0, and
![]() when B=0. Also,
when B=0. Also,
![]() and
and
![]() .
The mass at which the specific binary fraction equals the generating binary fraction can be found by solving
.
The mass at which the specific binary fraction equals the generating binary fraction can be found by solving
![]() ,
which gives
FM(M1) = 0.5. In other words, for pairing function RP the overall binary fraction can be found at the median stellar mass
,
which gives
FM(M1) = 0.5. In other words, for pairing function RP the overall binary fraction can be found at the median stellar mass
![]() .
For higher primary masses,
.
For higher primary masses,
![]() is higher, and for lower primary masses,
is higher, and for lower primary masses,
![]() is lower.
is lower.
From Eqs. (A.5), (A.6), and (A.8)
mass ratio distributions for specific choices of the generating mass
distribution can be derived. The
single power-law defined in Eq. (A.3) is considered here.
Without restrictions on the primary mass range, the cumulative distribution for
q is given by:
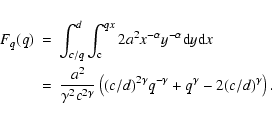
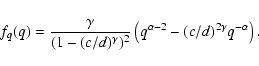 |
(A.12) |
Figure A.1 shows a number of examples of the resulting mass
ratio distributions for different values of c/d and the power-law slope
![]() .
The values for
.
The values for ![]() represent the Salpeter mass distribution (2.35), the
slopes at the lower mass end for the Kroupa (2001) mass distribution (1.3 and 0.3),
and a possible slope at the very low mass end of the mass distribution, where the number of
stars increases with m. The latter value may occur in a multi-part power-law
mass distribution with a real turnover at the low mass end. For
represent the Salpeter mass distribution (2.35), the
slopes at the lower mass end for the Kroupa (2001) mass distribution (1.3 and 0.3),
and a possible slope at the very low mass end of the mass distribution, where the number of
stars increases with m. The latter value may occur in a multi-part power-law
mass distribution with a real turnover at the low mass end. For ![]() the mass distribution decreases
with
the mass distribution decreases
with ![]() and for
and for ![]() it increases with
it increases with ![]() .
However this does
not represent a real turnover in the mass distribution, the number of stars still increases as
the mass goes down as long as
.
However this does
not represent a real turnover in the mass distribution, the number of stars still increases as
the mass goes down as long as ![]() .
Note how the peak in the q distribution changes as the values of
.
Note how the peak in the q distribution changes as the values of ![]() and c/d are changed. For very
small values of c/d one can see from the approximation (A.13)
that fq will be flat for
and c/d are changed. For very
small values of c/d one can see from the approximation (A.13)
that fq will be flat for
![]() and
and
![]() and that it
will peak at small values of q for
and that it
will peak at small values of q for
![]() .
For values of
.
For values of ![]() larger
than 2 the number of low-mass stars is so dominant that large values of q are
favoured (i.e., both M1 and M2 are likely to be small). Conversely, for
larger
than 2 the number of low-mass stars is so dominant that large values of q are
favoured (i.e., both M1 and M2 are likely to be small). Conversely, for
![]() the rise of the number of stars with m again favours large values of
q. For
the rise of the number of stars with m again favours large values of
q. For
![]() the ratio of probabilities to obtain low- or high-mass
stars is such that drawing two equal mass star is unlikely thus favouring small
values of q.
the ratio of probabilities to obtain low- or high-mass
stars is such that drawing two equal mass star is unlikely thus favouring small
values of q.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{ps_app/0234_a1a.eps}\hspac...
...ace*{4mm}
\includegraphics[width=7.7cm,clip]{ps_app/0234_a1d.eps}
\end{figure}](/articles/aa/full/2009/03/aa10234-08/Timg280.gif) |
Figure A.1:
Mass ratio distributions fq(q) for random pairing from the single power-law fM(M). The curves are shown for
|
| Open with DEXTER | |
To find the expression for fq when the primary mass range is restricted
Eq. (A.8) has to be worked out for the single power-law mass distribution.
For
0< q< c/x2 Fq(q)=0, while for
![]() Fq(q) is
given by:
Fq(q) is
given by:
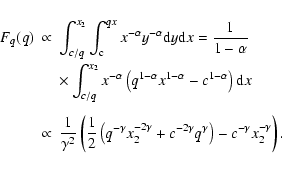
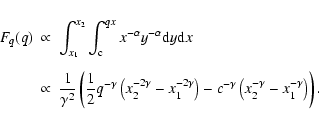
The expression for the specific binary fraction
![]() resulting from random pairing
is listed in Table A.3, and, for the Salpeter generating mass distribution (
resulting from random pairing
is listed in Table A.3, and, for the Salpeter generating mass distribution (
![]() ), shown in Fig. 7.
), shown in Fig. 7.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{ps_app/0234_a2a.eps}\hspac...
...ace*{4mm}
\includegraphics[width=7.7cm,clip]{ps_app/0234_a2d.eps}
\end{figure}](/articles/aa/full/2009/03/aa10234-08/Timg288.gif) |
Figure A.2:
Mass ratio distributions fq(q) for random pairing from a single
power-law fM(M). The solid curve shows the complete mass ratio distribution (for
all binaries in the population). The other curves show what happens to the
observed fq(q) if the primary mass M1 is restricted to
|
| Open with DEXTER | |
In this case (PCRP) the primary and secondary are again drawn independently from
the generating mass distribution, however for the secondary the condition
![]() is
imposed before drawing the secondary mass. That is the probability density
fM2(M2) is re-normalised to the interval [c,M1] (recall that c is
the lower mass limit on the mass distribution).
is
imposed before drawing the secondary mass. That is the probability density
fM2(M2) is re-normalised to the interval [c,M1] (recall that c is
the lower mass limit on the mass distribution).
Writing the re-normalised secondary mass distribution as
f'M2(M2)=f'(y), the expression for the joint probability distribution
![]() is:
is:
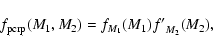 |
(A.17) |
To derive fq one can proceed as for the RP case. The integration domain is as
shown in the left-hand panel of Fig. 5 and the expression for F(q) can be written
as:
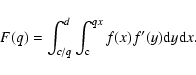 |
(A.18) |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{ps_app/0234_a3a.eps}\hspac...
...ace*{4mm}
\includegraphics[width=7.7cm,clip]{ps_app/0234_a3d.eps}
\end{figure}](/articles/aa/full/2009/03/aa10234-08/Timg293.gif) |
Figure A.3:
Mass ratio distributions fq(q) for PCRP
from a single power-law mass distribution. The curves are shown for
|
| Open with DEXTER | |
For PCRP, the overall binary fraction
![]() equals
equals
![]() ,
and specific binary fraction
,
and specific binary fraction
![]() is equal to the generating binary fraction
is equal to the generating binary fraction
![]() for any mass M1.
for any mass M1.
For the single power-law mass distribution, with lower and upper mass limits c and d, the
joint distribution of x=M1 and y=M2 is:
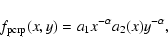 |
(A.20) |
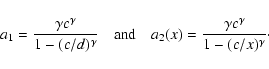 |
(A.21) |
Fq(q) is given by:
![\begin{eqnarray*}F_q(q) & = &\int_{c/q}^d\int_{\rm c}^{qx}\frac{\gamma^2
c^{2\g...
...q^{-\gamma}(c/x)^\gamma - 1}
{(c/x)^\gamma-1}\right]
{\rm d}x.
\end{eqnarray*}](/articles/aa/full/2009/03/aa10234-08/img296.gif)
The resulting expression for fq(q) is:
Figure A.3 shows four examples of the mass ratio distribution for PCRP from a single power-law mass distribution. The curves are for the values of c/d of 0.01, 0.1, 0.3, and 0.5.
For the restricted primary mass range Eq. (A.19) has to be
worked out. For
![]() the expression for Fq is:
the expression for Fq is:
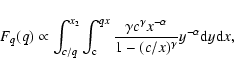
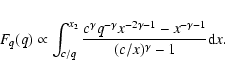
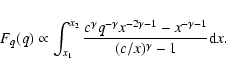
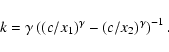 |
(A.25) |
Examples of what happens in the case of PCRP when a
selection is done on primary mass are shown in Fig. A.4.
The behaviour is qualitatively the same as for the
random pairing case.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{ps_app/0234_a4a.eps}\hspac...
...ace*{4mm}
\includegraphics[width=7.7cm,clip]{ps_app/0234_a4d.eps}
\end{figure}](/articles/aa/full/2009/03/aa10234-08/Timg309.gif) |
Figure A.4:
Mass ratio distributions fq(q) for PCRP
from a single power-law mass distribution. The solid curves show the complete mass
ratio distribution (for all binaries in the population). The other curves show
what happens to the observed fq(q) if the primary mass M1 is restricted
to
|
| Open with DEXTER | |
For the pairing mechanism discussed now the assumption is that there is a
physical process which sets the primary mass and the mass ratio of the
binary, rather than setting the masses of primary and secondary. For the primary
constrained pairing mechanism (PCP) the assumption is that M2 is determined
from M1 through the mass ratio q. The probability densities for M1 and
q are specified in this case and they are assumed to be independent. That is:
Again we first derive the general expressions for fq(q) before discussing specific examples.
In this case one always obtains fq(q)=hq(q) because the distributions of qand M1 are independent. Also when restricting the primary mass range the observed mass ratio distribution is equal to the generating distribution.
Here the systems with M2<c are discarded and then:
In this case the generating mass ratio distribution is re-normalised to the
interval [c/M1,1], resulting in a generating distribution h'q(q). The
expressions for fq are then derived as for the PCP-II case:
The following is assumed for hq and
fM1(M1)=f(x) (using x=M1 for
ease of notation):
For the full primary mass range we have from Eq. (A.28):
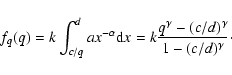 |
(A.34) |
Now the mass ratio distribution is re-normalised to the interval [c/x,1] which
gives:
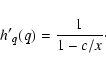 |
(A.39) |
For integer values of ![]() (or
(or ![]() )
special care should be taken. From
the expression above it is clear that
)
special care should be taken. From
the expression above it is clear that ![]() or
or ![]() should be
treated separately. Furthermore the hypergeometric series for
2F1(a,b;c;z)is indeterminate for c=-n where
n=0,1,2,... if neither a nor b is
equal to -m (where m<n and m is a natural number). Here this means that
all cases
should be
treated separately. Furthermore the hypergeometric series for
2F1(a,b;c;z)is indeterminate for c=-n where
n=0,1,2,... if neither a nor b is
equal to -m (where m<n and m is a natural number). Here this means that
all cases
![]() should be treated separately which combined with
the condition
should be treated separately which combined with
the condition
![]() implies that whenever
implies that whenever ![]() (i.e.
(i.e.
![]() )
the expression above will not apply. The case
)
the expression above will not apply. The case ![]() ,
,
![]() ,
is excluded, so the special cases are
,
is excluded, so the special cases are
![]() ,
,
![]() ,
and then the expression for the integrals becomes:
,
and then the expression for the integrals becomes:
For restricted primary mass ranges the results above can be used to evaluate the integrals listed in Eq. (A.43). The normalisation constant k can be obtained from numerical integration of fq(q). Again, if x1=x2 one obtains fq(q)=1/(1-c/x1) for q in the interval [c/x1,1]. Figures A.5 and A.6 show examples of the resulting mass ratio distributions for hq(q)=1 and various single power-law mass distributions for the primaries. The hypergeometric function was calculated using the routine from Press et al. (2007, Sect. 6.13).
Finally, we have listed the expressions for the binary fraction as a function of primary mass in Table A.3.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{ps_app/0234_a5a.eps}\par\vs...
...pace*{2mm}
\includegraphics[width=13cm,clip]{ps_app/0234_a5c.eps}
\end{figure}](/articles/aa/full/2009/03/aa10234-08/Timg359.gif) |
Figure A.5:
Mass ratio distributions fq(q) for PCP-II
and III for a uniform generating mass ratio distribution and primary masses
from the single power-law mass distribution for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{ps_app/0234_a6a.eps}\par\vs...
...pace*{2mm}
\includegraphics[width=13cm,clip]{ps_app/0234_a6c.eps}
\end{figure}](/articles/aa/full/2009/03/aa10234-08/Timg360.gif) |
Figure A.6:
Mass ratio distributions fq(q) for PCP-II
and III for a uniform generating mass ratio distribution and primary masses
from a single power-law mass distribution. The solid curve shows the complete mass ratio
distribution (for all binaries in the population) for c=0.2 and d=2.0. The
other curves show what happens to the observed fq(q) if the primary mass
M1 is restricted to
|
| Open with DEXTER | |
The mechanism of split-core pairing (SCP) works on the assumption that binaries
are formed by the splitting of star-forming cores into two components. The
component masses are specified through their mass ratio. The distribution
function for the core masses ![]() is given by the core
mass function
is given by the core
mass function
![]() and the mass ratio distribution fq(q)is specified independently. The masses of the primary and secondary are then
given by:
and the mass ratio distribution fq(q)is specified independently. The masses of the primary and secondary are then
given by:
The joint probability density
![]() for
for ![]() and q is
written as:
and q is
written as:
We give the general expressions for fq(q) before discussing specific
examples. For ease of notation we use
![]() and
and
![]() .
.
If no selection on primary mass is made one always obtains
fq(q)=hq(q)because the distributions of q and ![]() are independent. Unlike
PCP-I, restricting the primary mass range now does cause changes of the observed
mass ratio distribution with respect to the generating one. Several cases have
to be distinguished on the basis of the value of the primary mass selection
limits x1 and x2 compared to the values of c, d, 2c, and 2d. Note
that x1 and x2 are limits on M1, not
are independent. Unlike
PCP-I, restricting the primary mass range now does cause changes of the observed
mass ratio distribution with respect to the generating one. Several cases have
to be distinguished on the basis of the value of the primary mass selection
limits x1 and x2 compared to the values of c, d, 2c, and 2d. Note
that x1 and x2 are limits on M1, not ![]() .
.
In all cases discussed below a selection
![]() in principle
translates to
in principle
translates to
![]() but the upper and/or lower limits on
x and q used for integrating
but the upper and/or lower limits on
x and q used for integrating
![]() and normalising fq(q) are
different for each case. We introduce the following variables
to distinguish the different cases:
and normalising fq(q) are
different for each case. We introduce the following variables
to distinguish the different cases:
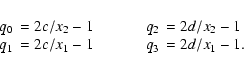
The value of x (core-mass) is restricted to [2c,2d], hence for q<q0 or q>q3 the probability distribution for q vanishes (as these conditions imply M1>x2 or M1<x1, both of which are not allowed). For q<q1 the lower integration limit for x when determining fq is fixed at 2c and for q>q2 the upper limit is fixed at 2d.
Case 1:
![]() In this case the value of q0 is
between 0 and 1 and all other values of qi are larger than 1. This means that
two cases should be distinguished for fq, q<q0 and q>q0, and that the
lower integration limit for x is always fixed at 2c. The expression for
fq is then given by:
In this case the value of q0 is
between 0 and 1 and all other values of qi are larger than 1. This means that
two cases should be distinguished for fq, q<q0 and q>q0, and that the
lower integration limit for x is always fixed at 2c. The expression for
fq is then given by:
Case 2:
![]() This is the same as case 1
except that now q0<0 so that there is only one part to the expression for
fq. The lower integration limit for x is still 2c:
This is the same as case 1
except that now q0<0 so that there is only one part to the expression for
fq. The lower integration limit for x is still 2c:
Case 3:
![]() Now the value of q2 is
in the interval [0,1] which means that for the case q>q2 the upper
integration limit for x is fixed at 2d which leads to a plateau in the
probability density fq:
Now the value of q2 is
in the interval [0,1] which means that for the case q>q2 the upper
integration limit for x is fixed at 2d which leads to a plateau in the
probability density fq:
Case 4:
![]() Now the values of q0 and q1 are in the
interval [0,1] which means that the lower integration limit for x depends on
q. The probability density for q now consists of three parts:
Now the values of q0 and q1 are in the
interval [0,1] which means that the lower integration limit for x depends on
q. The probability density for q now consists of three parts:
Case 5:
![]() The value of q0becomes less than zero and we have:
The value of q0becomes less than zero and we have:
Case 6:
![]() Now the values of q1and q2 are in the interval [0,1]. For q<q1 the lower integration limit
is fixed to 2c and for q>q2 the upper integration limit is fixed to 2d.
In addition it can happen that q1<q2 or
Now the values of q1and q2 are in the interval [0,1]. For q<q1 the lower integration limit
is fixed to 2c and for q>q2 the upper integration limit is fixed to 2d.
In addition it can happen that q1<q2 or
![]() .
The latter case will
cause a plateau of constant probability density fq for
.
The latter case will
cause a plateau of constant probability density fq for
![]() .
So now there are two ``sub-cases''.
.
So now there are two ``sub-cases''.
Case 6a: q1<q2
Case 6b:
![]()
Case 7:
![]() Now the values of q0 and q1 are less
than zero and both q2 and q3 are larger than 1. Hence the probability
density consists of one part only:
Now the values of q0 and q1 are less
than zero and both q2 and q3 are larger than 1. Hence the probability
density consists of one part only:
Case 8:
![]() The value of q2 is
now in [0,1] so fq will consist of two parts:
The value of q2 is
now in [0,1] so fq will consist of two parts:
Case 9:
![]() Now the values of both q2 and q3are in [0,1] and the probability density will vanish if q>q3:
Now the values of both q2 and q3are in [0,1] and the probability density will vanish if q>q3:
The expression for fq is obtained by integrating the joint distribution
![]() over x over the range
over x over the range
![]() and normalising
the resulting expression for fq to 1:
and normalising
the resulting expression for fq to 1:
When the mass range is restricted there are again a number of cases to consider,
depending on the values of x1 and x2. However the situation is less
complicated than for SCP-I. First of all the value of c(1+1/q) is always
larger than 2c for ![]() which means that the value of q1 plays no
role. Secondly the minimum possible value of q is c/x2 and this quantity is
always larger than q0 for
which means that the value of q1 plays no
role. Secondly the minimum possible value of q is c/x2 and this quantity is
always larger than q0 for ![]() (which is mandatory) and therefore also
the value of q0 plays no role. For q<c/x2 fq(q) is always zero. The
values of q2 and q3 do matter as discussed below.
(which is mandatory) and therefore also
the value of q0 plays no role. For q<c/x2 fq(q) is always zero. The
values of q2 and q3 do matter as discussed below.
Case 1:
![]() In this case the integration limits for x,
x1(1+q) and x2(1+q) are guaranteed to be less than 2d. For q<c/x1 the
value of x1(1+q) is less than c(1+1/q) so the lower limit for integral over
x is then fixed at c(1+1/q). The expression for fq(q) becomes:
In this case the integration limits for x,
x1(1+q) and x2(1+q) are guaranteed to be less than 2d. For q<c/x1 the
value of x1(1+q) is less than c(1+1/q) so the lower limit for integral over
x is then fixed at c(1+1/q). The expression for fq(q) becomes:
Case 2:
![]() Now the value of q2 is less
than 1 and for q>q2 the upper limit of the integral over x is fixed at 2d(the value of x2(1+q) being larger than 2d). Now,
Now the value of q2 is less
than 1 and for q>q2 the upper limit of the integral over x is fixed at 2d(the value of x2(1+q) being larger than 2d). Now,
![]() but q2may be larger or smaller than c/x1. So there are two sub-cases:
but q2may be larger or smaller than c/x1. So there are two sub-cases:
Case 2a
![]()
Case 2b
![]()
Case 3: x1>d This is the same as case 2 except that q3<1 which means that fq(q)=0 for q>q3 (this is due to the value of x1(1+q)becoming larger than 2d). There are the same two sub-cases:
Case 3a:
![]()
Case 3b q2>c/x1
Now the generating mass ratio distribution hq is restricted to the range
![]() and re-normalised. The corresponding
distribution is h'q(q) and the expression for fq becomes:
and re-normalised. The corresponding
distribution is h'q(q) and the expression for fq becomes:
When the primary mass range is restricted to
![]() the cases and
expressions for fq(q) are the same as for the SCP-II case, except that
h'q(q) replaces hq(q) everywhere.
the cases and
expressions for fq(q) are the same as for the SCP-II case, except that
h'q(q) replaces hq(q) everywhere.
In order to find the specific binary fraction as a function of primary mass, we first need to find the primary mass distribution
fM1(M1), which can be calculated as:
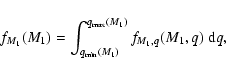 |
(A.69) |
Table A.1: The specific mass ratio distribution fq(q) for pairing function SCP-I, resulting from a power-law generating mass distribution fm(m) and a uniform generating mass ratio distribution hq(q). See Appendix A.4.3 for details.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{ps_app/0234_a7.eps}
\end{figure}](/articles/aa/full/2009/03/aa10234-08/Timg422.gif) |
Figure A.7:
Left: mass ratio distributions fq(q) for split-core pairing I for a
uniform generating mass ratio distribution and core masses from single
power-law mass distribution, where
|
| Open with DEXTER | |
Table A.2:
The specific mass ratio distribution fq(q) for pairing function SCP-II, resulting from a power-law generating mass distribution
![]() and a uniform generating mass ratio distribution hq(q). See Appendix A.4.3 for details.
and a uniform generating mass ratio distribution hq(q). See Appendix A.4.3 for details.
Table A.3:
The specific binary fraction
![]() for the nine pairing functions described in this paper, resulting from a power-law mass distribution fM(M) and a uniform mass ratio distribution hq(q). See Appendices A.1-A.4 for a detailed description, and Fig. 7 for a visualisation.
for the nine pairing functions described in this paper, resulting from a power-law mass distribution fM(M) and a uniform mass ratio distribution hq(q). See Appendices A.1-A.4 for a detailed description, and Fig. 7 for a visualisation.
The number of binary systems with a mass M1 is given by
![]() ,
where N is the total number of systems (singles plus binaries) in the population. The number of single stars with a mass M1 is given by
,
where N is the total number of systems (singles plus binaries) in the population. The number of single stars with a mass M1 is given by
![]() .
The specific binary fraction is thus:
.
The specific binary fraction is thus:
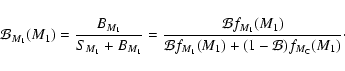 |
(A.71) |
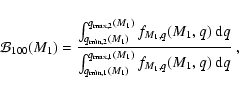 |
(A.76) |
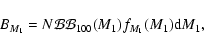 |
(A.77) |
| (A.78) |
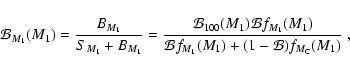 |
(A.79) |
The values for
![]() and
and
![]() for SCP-III are identical to those for SCP-II, and are given by Eqs. (A.74) and (A.75). The expression for the specific binary fraction for SCP-III is the same as in (the one for SCP-I). Note, however, that the primary mass distribution
fM1(M1) is different due to the different limits
for SCP-III are identical to those for SCP-II, and are given by Eqs. (A.74) and (A.75). The expression for the specific binary fraction for SCP-III is the same as in (the one for SCP-I). Note, however, that the primary mass distribution
fM1(M1) is different due to the different limits
![]() and
and
![]() .
The right-hand panel in Fig. 7 shows an example of
.
The right-hand panel in Fig. 7 shows an example of
![]() resulting from SCP-III. The term
resulting from SCP-III. The term
![]() vanishes for
vanishes for
![]() ,
so that
,
so that
![]() in this mass range. A discontinuity appears at M1=2c, beyond which
in this mass range. A discontinuity appears at M1=2c, beyond which
![]() reaches its lowest point, after which it steadily rises until M1=d. Beyond M1=d, the specific binary fraction decreases again to
reaches its lowest point, after which it steadily rises until M1=d. Beyond M1=d, the specific binary fraction decreases again to
![]() at M1=2d, for the same reasons as for SCP-I and SCP-II. The overall binary fraction
at M1=2d, for the same reasons as for SCP-I and SCP-II. The overall binary fraction
![]() is always equal to
is always equal to
![]() for SCP-III.
for SCP-III.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ps_app/0234_a8.ps}
\end{figure}](/articles/aa/full/2009/03/aa10234-08/Timg448.gif) |
Figure A.8: The integration domains for obtaining the primary mass distribution and specific binary fraction for pairing functions SCP-I, SCP-II and SCP-III. The domain S for SCP-I is the parallelogram enclosed by the solid lines. The domain S' for SCP-II and SCP-III is indicated with the shaded region. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{ps_app/0234_a9a.eps}\par\vs...
...pace*{2mm}
\includegraphics[width=13cm,clip]{ps_app/0234_a9c.eps}
\end{figure}](/articles/aa/full/2009/03/aa10234-08/Timg453.gif) |
Figure A.9:
Mass ratio distributions fq(q) for split-core pairing II and III
for a uniform generating mass ratio distribution and core masses from single
power-law mass distribution for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{ps_app/0234_a10.eps}\par
\end{figure}](/articles/aa/full/2009/03/aa10234-08/Timg454.gif) |
Figure A.10:
Mass ratio distributions fq(q) for split-core pairing
II and III for a uniform generating mass ratio distribution and core masses
from a single power-law mass distribution with
|
| Open with DEXTER | |
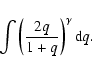 |
(A.82) |
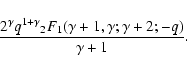 |
(A.83) |
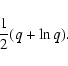 |
(A.84) |
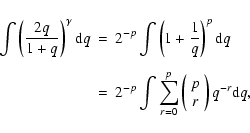
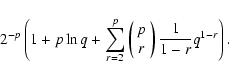 |
(A.85) |
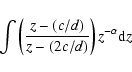 |
(A.88) |
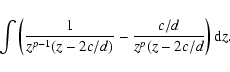 |
(A.91) |