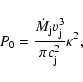A&A 493, 115-118 (2009)
DOI: 10.1051/0004-6361:200810900

Curved Herbig-Haro jets immersed in a stellar wind

A. C. Raga¹ - J. Cantó² - A. Rodríguez-González¹ - A. Esquivel¹

1 - Instituto de Ciencias Nucleares, Universidad Nacional Autónoma de Mexico, Ap. Postal 70-543, 04510 Mexico, Mexico
2 - Instituto de Astronomía, Universidad Nacional Autónoma de Mexico, Ap. Postal 70-468, 04510 Mexico, Mexico

Received 2 September 2008 / Accepted 7 October 2008

Abstract
Context. Several curved Herbig-Haro (HH) jet/counterjet systems have been observed. Some of these systems are the result of a relative motion between the outflow source and the surrounding environment.
Aims. In this paper, we consider the case of an HH jet/counterjet system that is immersed in an isotropic stellar wind. This situation is somewhat different from the previously studied HH jet/plane-parallel side wind interaction, because the isotropic wind is divergent, and has a radially dependent density structure.
Methods. We present an analytic model for a jet/wind interaction that is based on the balance between the ram pressure of the wind and the centrifugal pressure along the curved jet/counterjet path. We consider the case of an isothermal jet.
Results. We find that, if we have a jet and a wind with similar velocities and mass loss rates, the jet/counterjet system only shows a shallow curvature, with a total deflection angle of only a few degrees. However, if we have stronger winds, quite large deflections are produced (e.g., for the interaction of an HH jet with the wind from an O star). The deflection angle depends on neither the separation between the jet and wind sources nor on the ejection direction of the jet/counterjet.

Key words: ISM: kinematics and dynamics - ISM: jets and outflows - ISM: Herbig-Haro objects - stars: winds, outflows

1 Introduction

Cantó & Raga (1995) presented an analytic model of a jet/sidewind interaction, with the idea of modelling the curvature that would result from having an HH jet/counterjet system ejected from a source in relative motion with respect to the surrounding environment. A comparison between the analytic model and a 3D numerical simulation was presented by Lim & Raga (1998). At the time there was no clear application of the model except for the case of HH30, which shows a general curved structure (see López et al. 1995).

A much more convincing example of a curved, molecular jet resulting from a jet/sidewind interaction was later found by Salas et al. (1998). However, the field of HH jet/sidewind interactions came to life with the paper of Bally & Reipurth (2001), who discovered many curved jet/counterjet systems. Several of these objects are in the outskirts of the Orion Nebula, and are outflows from low mass stars interacting with the expanding H II region (see Bally et al. 2006).

These observations gave rise to papers on modelling specific jet/sidewind interaction systems (Masciadri & Raga 2001; Kajdic & Raga 2007). Also, Ciardi et al. (2008) recently described results from laboratory experiments and 3D simulations of jet/sidewind interactions.

In the present paper, we discuss an extension of the analytic model of Cantó & Raga (1995, who studied the interaction of a jet with a plane-parallel sidewind) to the case of an HH jet/counterjet system immersed in an isotropic stellar wind. This model is relevant for the case of an HH jet interacting with a more isotropic wind from an intermediate mass star (a Herbig Ae/Be star) or from a massive star (an O or B star).

The paper is organized as follows. The model is derived in Sect. 2. The solutions obtained for different parameters are shown in Sect. 3. Applications of the models to different jet/wind interaction systems are discussed in Sect. 4. Finally, the results are summarized in Sect. 5.

2 The analytic model

We derive an analytic model for the interaction of a steady jet with an isotropic stellar wind. The model is based on the same assumptions as the one of Cantó & Raga (1995), who modeled a jet interacting with a plane-parallel sidewind.

In order to derive the shape of the jet/counterjet system, one assumes that the ram pressure of the wind (impinging on the side of the jet) is balanced by the centrifugal pressure of the material flowing along the curved jet path. Cantó & Raga (1995) found that the modulus of the jet/counterjet velocity does not depend on position (a result of the fact that the force exerted by the external wind on the jet is always perpendicular to the local jet direction). They also found that the path of the jet/counterjet system remains unchanged if one changes the position of the source along the derived path. This is a direct result of the fact that the centrifugal pressure does not depend on the direction along the jet/counterjet locus in which the flow is moving.

Assuming that the cross section of the jet adopts an equilibrium, isothermal ``plasmon'' shape, Cantó & Raga (1995) derived the relation

$$P_0={{\dot M}_{\rm j} v_{\rm j}^3\over \pi c_{\rm j}^2}\kappa^2,$$ (1)

where P₀ is the pressure of the points on the jet surface on the edge pointing towards the impinging sidewind, ${\dot M}_{\rm j}$ is the mass loss rate, $v_{\rm j}$ the velocity and $c_{\rm j}$ the isothermal sound speed of the jet. The ``curvature'' $\kappa$ can be calculated (see Cantó 1980) as:

$$\kappa={{R^2+2R'^2-RR''}\over {(R^2+R'^2)^{3/2}}},$$ (2)

where $R'={\rm d}R/{\rm d}\theta$ and $R''={\rm d}^2R/{\rm d}\theta^2$. We should note that with this standard definition of $\kappa$, the ``concave'' shape of the jet path shown in Fig. 1 has $\kappa<0$.

We assume that Eq. (1) is still valid in the case of the interaction of a jet with a divergent, isotropic stellar wind. This assumption is valid provided that the width of the jet is much smaller than the separation between the jet and the stellar wind source.

Figure 1: Schematic diagram showing the interaction of an HH jet/counterjet system with an isotropic stellar wind. The position of the jet source is shown with a circle. The stellar wind source is located at the origin of the coordinate system(s). Top frame: the locus of the jet and counterjet is shown with the thick, solid curve. This curve reaches the point of closest approach to the stellar wind source (i.e., the ``stagnation point'' of the curve) on the x-axis of the xy-coordinate system. The locus of the jet/counterjet is given by $R(\theta )$, where R is the spherical radius and $\theta$ the angle with respect to the x-axis. $R(\theta )$ goes to infinity at $\theta =\pm \theta _{\rm m}$. The total deflection of the jet/counterjet path is $\Psi =\pi -2\theta _{\rm m}$. $\beta$is the angle between the radial direction and the normal unit vector ${\hat n}$ to the jet/counterjet path. Bottom frame: two frames of reference (both with the origin on the stellar wind source and with the xy-plane on the plane of the jet/counterjet locus) are used in the analytic model. The xy-frame has the abscissa on the line joining the stellar wind source and the stagnation point (which is at a distance $R_{\rm s}$ from the wind source), and the x'y'-frame has the abscissa on the line joining the wind source and the jet source (which is at a distance D from the wind source). The jet/counterjet system is ejected at an angle $\alpha$, measured counterclockwise from the x' axis. The angle subtended by the jet source, the wind source and the stagnation point is $\theta _{\rm s}$ (the figure shows a configuration with positive $\theta _{\rm s}$).

Open with DEXTER

We now consider the ram pressure $P_{\rm w}$ exerted by the wind on the leading edge of the jet cross section, which is

$$P_{\rm w}=\rho_{\rm w} v_{\rm w}^2\cos^2\beta~,$$ (3)

where $\beta$ is the angle between the radial direction (along $\overline{R}$) and the normal ${\hat n}$ to the curved jet path (see Fig. 1). At the position $R(\theta )$, the wind has a density $\rho_{\rm w}$ and a velocity $v_{\rm w}$.

Assuming a constant velocity, isotropic wind, we have

$$\rho_{\rm w}={{\dot M}_{\rm w}\over 4\pi R^2 v_{\rm w}},$$ (4)

where ${\dot M}_{\rm w}$ is the mass loss rate of the wind. Also, it is straightforward to derive the geometric relation

$$\cos\beta={R\over \sqrt{R^2+R'^2}},$$ (5)

where $R'={\rm d}R/{\rm d}\theta$.

The path of the jet/counterjet system can then be found by setting $P_{\rm w}=P_0$. Combining Eqs. (1-5) we then obtain the differential equation

$$(\epsilon+1)R^2+(2\epsilon+1)R'^2-\epsilon R R''=0,$$ (6)

where the dimensionless parameter $\epsilon$ is given by

$$\epsilon=2\left({{\dot M}_{\rm j}v_{\rm j}\over {\dot M}_{\rm w}v_{\rm w}}\right)^{1/2} {v_{\rm j}\over c_{\rm j}}\cdot$$ (7)

This equation can be integrated two times (with the appropriate boundary conditions) to obtain the solution

$$R={R_{\rm s}\over \cos^\lambda(\theta/\lambda)}~;~~~~~ \lambda\equiv {\epsilon/(1+\epsilon)}\cdot$$ (8)

It is clear that for $\theta=0$, we have $R=R_{\rm s}$, i.e., the radius is equal to the distance between the star and the ``stagnation point'' of maximum approach between the jet/counterjet locus and the stellar wind source (see Fig. 1). For $\theta =\pm \theta _{\rm m}$, we have $R\to \infty$, with

$$\theta_{\rm m}=\lambda{\pi\over 2}\cdot$$ (9)

It is clear that for $\theta\to\pm \theta_{\rm m}$ the path of the jet/counterjet is parallel to the local direction of the stellar wind (i.e., it has a radial direction, see Fig. 1).

Therefore, the total deflection angle of the jet/counterjet path (see Fig. 1) is

$$\Psi=\pi-2\theta_{\rm m}={\pi\over{1+\epsilon}}\cdot$$ (10)

Figure 2: Curves for the jet/counterjet locus for different values of the dimensionless parameter $\epsilon$(see the text). The curves correspond to $\epsilon =0.25$ (most highly curved solution), 0.5, 1.0, 2.0, 4.0, 8.0, 16.0 and 1000 (almost straight solution). The positions are given in units of the distance $R_{\rm s}$ between the wind source and the stagnation point (see Fig. 1). The xy-coordinate system is used (see Fig. 1), so that the wind source is at the origin, and the stagnation point at (x,y)=(1,0).

Open with DEXTER

In Fig. 2 we show the jet/counterjet paths given by Eq. (8) for different values of the dimensionless parameter $\epsilon$(see Eq. (7)). These solutions represent the paths seen in the (x,y) coordinate system which has the x-axis along the direction joining the stellar wind source and the ``stagnation point'' (i.e., the point of maximum approach betwee the jet/counterjet path and the stellar wind source, see Fig. 1). In Fig. 2, the coordinates are given in units of the stagnation distance $R_{\rm s}$.

3 The position of the jet source

In the paths shown (for different values of $\epsilon$) in Fig. 2, one is free to place the jet/counterjet source in any position along the trajectories. In this section, we describe how to choose a solution with an appropriate $\epsilon$ and $R_{\rm s}$ if one has a jet source at a distance D from the stellar wind source, ejecting a jet/counterjet system at an angle $\alpha$ with respect to the direction to the stellar wind source (see Fig. 1).

Figure 3: The jet/counterjet locus for $\epsilon =1$ ( top frame) and for $\epsilon =10$ ( bottom frame). The curves correspond to ejection angles $\alpha =90$ (curve with reflection symmetry on the x'-axis), 75, 60, 45, 30, 15 and $1^\circ$ (see the text). The positions are given in units of the distance D between the wind source and the jet source (see Fig. 1). The x'y'-coordinate system is used (see Fig. 1), so that the wind source is at the origin, and the jet source at (x',y')=(1,0).

Open with DEXTER

Through an inspection of Fig. 1, it is clear that

$$\tan\left({\pi\over 2}-\alpha\right)=\left({R'\over R}\right)_{\theta_{\rm s}},$$ (11)

where $\theta _{\rm s}$ is the angle defined by the jet source and the stagnation point with respect to the position of the stellar wind source. This equation has the solution:

$$\theta_{\rm s}=\lambda\left(\alpha-{\pi\over 2}\right)\cdot$$ (12)

We can now use Eq. (8) to calculate the stagnation stand-off distance $R_{\rm s}$ through the relation $D=R(\theta_{\rm s})$, obtaining the relation

$$R_{\rm s}=D\left[\sin\alpha\right]^\lambda.$$ (13)

The path of the jet/counterjet system in the (x',y') coordinate system can be found by a rotation of Eq. (8) by an angle $\theta _{\rm s}$ (Eq. (12)). That is,

$$R(\theta')={R_{\rm s}\over {\cos^\lambda\left[(\theta'-\theta_{\rm s})/\lambda\right]}}~,$$ (14)

where $\theta'$ is the angle measured from the x'-axis (see Fig. 1). Substituting Eqs. (12-13) in Eq. (14) we then obtain,

$$R(\theta')=D\left[{\sin\alpha\over {\sin\left(\alpha-\theta'/\lambda\right)}} \right]^\lambda\cdot$$ (15)

As expected, Eq. (15) gives R(0)=D, and $R(\theta_{\rm s})= D\sin^\lambda\alpha=R_{\rm s}$. Also, for a jet/counterjet source located at the stagnation point ( $\alpha=\pi/2$) we recover Eq. (8).

In Fig. 3 we present a few examples of this kind of solution. The top panel shows solutions with $\epsilon =1$ and the bottom panel with $\epsilon =10$, for ejection angles $\alpha=1$, 15, 30, 45, 60, 75 and $90^\circ$ (note that the relation between $\epsilon$and $\lambda$ is given by Eq. (8)). It is clear that regardless of the ejection angle, the solutions always have the total deflection angle $\Psi$ given by Eq. (10), which only depends on $\epsilon$.

4 Application to HH jets

4.1 HH jet interacting with an O star wind

Examples of HH jet/O star wind interactions could be the jets from the innermost proplyds in the Orion Nebula (see, e.g. Henney et al. 2002). The brightest star of the Trapezium, $\theta^1$ Ori C, is an O7 V star. For such stars, Sternberg et al. (2003) compute a terminal wind velocity $v_{\rm w}=2250$ km s^-1 and a mass loss rate ${\dot M}_{\rm w}=4.5\times 10^{-7}~M_\odot$ yr^-1. For a typical jet from a low mass star we take $v_{\rm j}=200$ km s^-1and ${\dot M}_{\rm j}=10^{-7}~M_\odot$ yr^-1. Assuming that the jet has an isothermal sound speed $c_{\rm j}\approx 10$ km s^-1, we compute $\epsilon=5.6$ (see Eq. (7)). From Eq. (10) we then derive a total deviation angle $\Psi=27^\circ$ for the curved jet/counterjet locus.

Larger deviations would of course be obtained for lower velocity jets and/or for a wind from a brighter O star. For example, for a jet with $v_{\rm j}=100$ km s^-1and ${\dot M}_{\rm j}=10^{-7}~M_\odot$ yr^-1 interacting with the wind from an O4 V star (with $v_{\rm w}=3250$ km s^-1 and a mass loss rate ${\dot M}_{\rm w}=1.8\times 10^{-6}~M_\odot$ yr^-1, see Sternberg et al. 2003), we obtain $\epsilon=0.83$. Therefore, for this ``weak jet/early O star'' interaction we obtain a total deflection  $\Psi=98^\circ$.

Therefore, we conclude that in an interaction between an HH jet and a wind from an O star one can easily obtain locci for the jet/counterjet systems with substantial deviations from a straight line. The observed total change in position angle of the jet/counterjet path directly gives us the dimensionless parameter $\epsilon$ of the system (see Eqs. (7) and (10)).

4.2 HH jet interacting with a Herbig Ae/Be wind

Examples of interactions between a jet and a Herbig Ae/Be wind could be provided by HH jets in clusters of low/intermediate mass stars. Recently, Rodríguez-González et al. (2008) have modeled the interaction between the winds from a cluster of isotropic stellar wind sources. Carroll et al. (2008) have modeled the interaction of collimated jet/counterjet systems from sources in a cluster of young stars. A real cluster of low and intermediate mass young stars would of course have both relatively isotropic winds (from Herbig Ae/Be stars) and well collimated jets (from lower mass stars). An example of such a system of multiple outflow sources might be the embedded cluster in NGC1333 studied by Walawender et al. (2005) and Jorgensen et al. (2006).

Let us then consider the interaction between a jet (with $v_{\rm j}=200$ km s^-1 and ${\dot M}_{\rm j}=10^{-7}~M_\odot$ yr^-1) and an isotropic wind from a Herbig Ae/Be star, for which we assume $v_{\rm w}=300$ km s^-1 and ${\dot M}_{\rm w}=10^{-6}~M_\odot$ yr^-1 (Finkenzeller & Mundt 1984). For these parameters, we obtain $\epsilon=10.3$, resulting in a total deflection angle $\Psi=16^\circ$. From this, we conclude that an HH jet/counterjet system embedded within a wind from a Herbig Ae/Be star will also show substantial deviations from a straight path.

5 Conclusions

We have derived an analytic model for the interaction of an isothermal jet/counterjet system with an isotropic stellar wind. The model has a full, analytic solution which has interesting properties.

We find that the full deflection angle $\Psi$ of the jet/counterjet locus is only a function of the dimensionless parameter $\epsilon=2M_{\rm j}\sqrt{({\dot M}_{\rm j}v_{\rm j})/({\dot M}_{\rm w}v_{\rm w})}$ (where $M_{\rm j}=v_{\rm j}/c_{\rm j}$ is the jet Mach number, see Eqs. (7) and (10)). $\Psi$ does not depend on the separation D between the jet and wind sources nor on the direction $\alpha$ of the jet/counterjet ejection. However, the distance of maximum approach between the wind source and the jet/counterjet locus (i.e., the ``stagnation distance'' $R_{\rm s}$, see Fig. 1) does depend on $\epsilon$, D and $\alpha$ (see Eq. (13)).

Let us assume that we observe a jet/wind interaction, and that we have the relevant radial velocity and proper motion information necessary to de-project the observed jet/counterjet locus. From the observed source separation D, stagnation distance $R_{\rm s}$ and ejection angle $\alpha$ we can then calculate the dimensionless parameter $\epsilon$ (using Eq. (13)). Alternatively, if the observed jet/counterjet system extends to regions in which it becomes approximately parallel to the direction from the wind source, we can measure the full deflection angle $\Psi$, and use it to derive $\epsilon$ (using Eq. (7)). We could combine the determination of $\epsilon$ with an observationally determined  $M_{\rm j}=v_{\rm j}/c_{\rm j}$ in order to determine the value of the jet to wind momentum rate ration $({\dot M}_{\rm j}v_{\rm j})/({\dot M}_{\rm w}v_{\rm w})$.

We estimate that total deflection angles $\Psi>10^\circ$ should be observed for the interactions between an HH jet and winds from either an O star or from a Herbig Ae/Be star. Therefore, it is to be expected that future observations of such interacting systems should show jet/counterjet systems with substantial curvatures away from the nearby stellar wind sources.

We end by discussing again the limitations of the present model. In our model, we assume that the jet/stellar wind interaction produces a steady flow in which the jet cross section adopts a ``plasmon'' configuration. This plasmon configuration is not solved correctly, as we use the cross section of Cantó & Raga (1995), who derived the shape resulting from the interaction of a plane-parallel sidewind with a jet. We argue that this cross section will still be approximately correct provided that the separation between the jet locus and the stellar wind source is considerably larger than the jet radius. This of course might not be true for some of the jet locci shown in Fig. 3, in which the jets have close encounters with the stellar wind source.

Another possibly incorrect assumption is that we have a steady flow. Ciardi et al. (2008) find that a jet/sidewind interaction leads to instabilities that fragment the jet flow. Even though such effects clearly lie beyond the simple model described in the present paper, from the work of Ciardi et al. (2008) it is clear that the analytic model of Cantó & Raga (1995, calculated with basically the same assumptions as our present model) does produce a reasonable estimate of the jet path obtained from 3D numerical simulations.

Finally, we should mention that the full jet deflection predicted from our models (see Eq. (10)) is in many cases attained only quite far from the stellar wind source. This full deflection therefore could be not reached by actual jet/stellar wind interaction systems. This could be because the jets still have not propagated far enough, or because the stellar wind is confined to a smaller distance from the wind source (due to the presence of a dense, surrounding ISM). Also, at large distances from the wind source, the jet/wind interaction might have different characteristics as the wind becomes a collisionless plasma, resulting in interactions with richer behaviour than can be described with a fluid model.

Acknowledgements

This work was supported by the DGAPA (UNAM) grant IN108207, the CONACyT grants 46828-F and 61547, and by the ``Macroproyecto de Tecnologías para la Universidad de la Información y la Computación'' (Secretaría de Desarrollo Institucional de la UNAM). We thank Andrea Ciardi (the referee) for helpful comments.

References

• Bally, J., & Reipurth, B. 2001, ApJ, 546, 299 [NASA ADS] [CrossRef] (In the text)
• Bally, J., Licht, D., Smith, N., & Walawender, J. 2006, AJ, 131, 473 [NASA ADS] [CrossRef] (In the text)
• Cantó, J. 1980, A&A, 86, 327 [NASA ADS] (In the text)
• Cantó, J., & Raga, A. C. 1995, MNRAS, 277, 1120 [NASA ADS] (In the text)
• Carroll, J. J., Frank, A., Blackman, E. G., Cunningham, J., & Quilen, A. C. 2008 [arXiv:0805.4645] (In the text)
• Ciardi, A., Ampleford, D. J., Lebedev, S. V., & Stehle, C. 2008, ApJ, 678, 968 [NASA ADS] [CrossRef] (In the text)
• Finkenzeller, U., & Mundt, R. 1984, A&A, 55, 109 [NASA ADS] (In the text)
• Henney, W. J., O'Dell, C. R., Meaburn, J., Garrington S. T., & López, J. A. 2002, ApJ, 566, 315 [NASA ADS] [CrossRef] (In the text)
• Jorgensen, J. K., Harvey, P. M., Evans, N. J., II, et al. 2006, ApJ, 645, 1246 [NASA ADS] [CrossRef] (In the text)
• Kajdic, P., & Raga, A. C. 2007, ApJ, 670, 1173 [NASA ADS] [CrossRef] (In the text)
• Lim, A. J., & Raga, A. C. 1998, MNRAS, 298, 871 [NASA ADS] [CrossRef] (In the text)
• López, R., Raga, A. C., Riera, A., Anglada, G., & Estalella, R. 1995, MNRAS, 274, 19 [NASA ADS] (In the text)
• Masciadri, E., & Raga, A. C. 2001, AJ, 121, 408 [NASA ADS] [CrossRef] (In the text)
• Rodríguez-González, A., Esquivel, A., Velázquez, P. F., Raga, A. C., & Melo, V. 2008 [arXiv:0808.1611] (In the text)
• Salas, L., Cruz-González, I., & Porras, A. 1998, ApJ, 500, 853 [NASA ADS] [CrossRef] (In the text)
• Sternberg, A., Hoffman, T. L., & Pauldrach, A. W. A. 2003, ApJ, 599, 1333 [NASA ADS] [CrossRef] (In the text)
• Walawender, J., Bally, J., & Reipurth, B. 2005, ApJ, 129, 2308 [NASA ADS] (In the text)