A&A 493, 325-330 (2009)
DOI: 10.1051/0004-6361:200810343
P. M. Mathews1 - S. B. Lambert2
1 - Department of Theoretical Physics, University of Madras,
Chennai 600025, India
2 - Observatoire de Paris, Département Systèmes
de Référence Temps Espace (SYRTE), CNRS/UMR8630, 75014 Paris, France
Received 7 June 2008 / Accepted 17 October 2008
Abstract
Aims. We aim to compute the rate of increase of the length of day (LOD) due to the axial component of the torque produced by the tide generating potential acting on the tidal redistribution of matter in the oceans and the solid Earth.
Methods. We use an extension of the formalism applied to precession-nutation in a previous work to the problem of length of day variations of an inelastic Earth with a fluid core and oceans. Expressions for the second order axial torque produced by the tesseral and sectorial tide-generating potentials on the tidal increments to the Earth's inertia tensor are derived and used in the axial component of the Euler-Liouville equations to arrive at the rate of increase of the LOD.
Results. The increase in the LOD, produced by the same dissipative mechanisms as in the theoretical work on which the IAU 2000 nutation model is based and in our recent computation of second order effects, is found to be at a rate of 2.35 ms/cy due to the ocean tides, and 0.15 ms/cy due to solid Earth tides, in reasonable agreement with estimates made by other methods.
Key words: reference systems - Earth
The gradual slowing down of the speed of rotation of the Earth
has been going on for hundreds of millions of years, as evidenced by
geological records. For instance, the analysis of sedimentary cyclic
rhythmites of tidal origin has revealed that about 620 Myr ago, the
length of day (LOD) was only 22 h (Williams 2000).
Compilations by Varga et al. (1998) and Denis et al. (2002), of the
estimates by various authors for the LOD over geological time, show that
the LOD increased over the last 0.5 Gyr, at a rate of about
![]() ms per century (ms/cy), wherein the non-tidal
acceleration attributed to the Earth's viscous postglacial
rebound is included.
ms per century (ms/cy), wherein the non-tidal
acceleration attributed to the Earth's viscous postglacial
rebound is included.
The Earth's slowing down is explained as the effect of the axial component of the torque exerted by the tidal potential of the Moon on the density perturbation produced in the Earth by the deformational action of the tidal potential itself. This deformational response is delayed relative to the forcing potential because of the dissipative mechanisms present in the oceans and in the solid Earth; consequently the torque retards the Earth's rotation, and the reciprocal torque on the Moon causes an energy transfer to the Moon, resulting in a gradual increase in the Eath-Moon distance. During a large part of the 20th century, most of the dissipative mechanism in the oceans was thought to occur on shallow sea bottoms (Jeffreys 1929). Tidal dissipation in the deep ocean was considered to be negligible (Lamb 1945). Recent works that take advantage of TOPEX/Poseidon measurements of the ocean surface showed, however, that though most of the friction does occur in the shallow seas, a non-negligible part (up to 30%, according to Egbert & Ray 2001) comes from the deep ocean, generally near areas of rough ocean bottom topography (e.g., the Mid-Atlantic or western Pacific ridges, see Jayne & St. Laurent 2001).
Lengthening of the day can be calculated from the concomitant effect
on the lunar orbit (see, e.g., Williams 1994; Chapront et al. 2002), or
directly estimated from models of ocean and solid Earth tidal responses.
Among various studies, Lambeck (1977) mentions an increase in the length
of day of 2.7 ms/cy that includes a significant non-tidal acceleration of
![]() ms/cy, leaving some 2 ms/cy for the tidal dissipation in both
the oceans and the mantle. Ray et al. (1999) calculated the
lunar and solar torques on the ocean tides using Geosat and
TOPEX/Poseidon altimetry data. They obtained a rate of change of the LOD
of 2.28 ms/cy.
ms/cy, leaving some 2 ms/cy for the tidal dissipation in both
the oceans and the mantle. Ray et al. (1999) calculated the
lunar and solar torques on the ocean tides using Geosat and
TOPEX/Poseidon altimetry data. They obtained a rate of change of the LOD
of 2.28 ms/cy.
In an earlier paper (Lambert & Mathews 2006), a formalism was developed to compute the equatorial components of the second order torque due to external gravitational action on the tidal redistribution of matter in the Earth, and hence to compute the resulting second-order corrections to the nutation. At that time we ignored the equations relating to the third (axial) component of the Earth's rotation vector which govern the variations in the Earth's rotation speed. In the present paper, we extend our previous computations to the axial component, and compute the expressions for the axial torques produced by sectorial and tesseral tidal potentials acting on solid Earth and ocean tidal deformations, and go on to calculate the resultant rate of increase of the LOD. Such an approach differs from that of Ray et al. since we start from more general equations. Moreover, we do not limit our study to ocean tides but include also mantle tides using Earth parameters derived from the IAU 2000 nutation model (Mathews et al. 2002, hereafter referred to as MHB).
The variations in the Earth's rotation rate are governed by the third
component of the vector equation of angular momentum conservation. In a
frame attached to the rotating Earth, it is
| |
= | (2) | |
| = | (3) |
| |
= | C, | (4) |
| = | (5) | ||
| = | (6) |
| (7) |
The third component of
![]() is of the second
order; it is given by
is of the second
order; it is given by
| |
= | m1H2-m2H1 | (8) |
| = | (9) |
| |
= | (10) | |
| = | (11) |
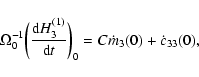 |
(12) |
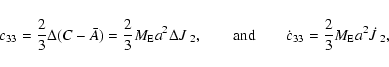 |
(14) |
Thus, knowledge of the constant part of the J2 rate is what is needed in obtaining the first term on the right hand side of Eq. (13).
We note that the contributions from the last two terms in (13), being of the form mimj or cijmk as may be
seen from Eqs. (6) and (9), are expected to be of much smaller
magnitude than the torque ![]() ,
and hence negligible for our purposes.
Nevertheless, if an evaluation of these terms were to be made, one should
keep in mind that the behaviour of the axial rotation of the fluid core
when the Earth is subject to tidal excitations at non-zero frequencies is
quite different from that in a steadily rotating Earth: while the core
rotates along with the mantle (i.e., the differential rotation
,
and hence negligible for our purposes.
Nevertheless, if an evaluation of these terms were to be made, one should
keep in mind that the behaviour of the axial rotation of the fluid core
when the Earth is subject to tidal excitations at non-zero frequencies is
quite different from that in a steadily rotating Earth: while the core
rotates along with the mantle (i.e., the differential rotation
![]() of the core with respect to the mantle is zero) under
steady rotation, the core is virtually decoupled from the mantle and its
axial rotation in space remains unaffected, i.e.,
of the core with respect to the mantle is zero) under
steady rotation, the core is virtually decoupled from the mantle and its
axial rotation in space remains unaffected, i.e.,
![]() ,
for excitation at tidal frequencies. This observation would be of
relevance if the term involving
,
for excitation at tidal frequencies. This observation would be of
relevance if the term involving
![]() in H3(2) were to be
considered. However, as observed above, the last two terms in (13) are too small to be of interest in the present context.
in H3(2) were to be
considered. However, as observed above, the last two terms in (13) are too small to be of interest in the present context.
We go on now to derive expressions for the contributions to the torque
term ![]() in (13) from the action of the tesseral and
sectorial potentials.
in (13) from the action of the tesseral and
sectorial potentials.
In the tesseral case,
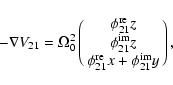 |
(16) |
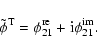 |
(18) |
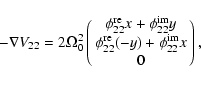 |
(19) |
 |
(21) |
In the above, we have used the fact that only the sectorial deformations
contribute to the difference
c11-c22, which reduces then to
![]() because
because
![]() .
.
The torque ![]() in Eqs. (1) and (13)
is the sum of the expressions (17) and (20).
in Eqs. (1) and (13)
is the sum of the expressions (17) and (20).
The spectral expansions of
![]() and
and
![]() are
as follows:
are
as follows:
Now, the generic terms in the Cartwright & Tayler (1971) spectral
expansions of the tidal potential V21 and V22, at any point within
the Earth at geocentric longitude ![]() and colatitude
and colatitude ![]() ,
are
,
are
![]() and
and
![]() ,
respectively, (with
,
respectively, (with
![]() and
and
![]() ).
Equating these spectral terms to the generic terms in the spectral
expansions obtained by substituting (22) and (23) into the
expressions for V21 and V22 employed in the last section, one
finds the following relations connecting the dimensionless amplitudes
).
Equating these spectral terms to the generic terms in the spectral
expansions obtained by substituting (22) and (23) into the
expressions for V21 and V22 employed in the last section, one
finds the following relations connecting the dimensionless amplitudes
![]() and
and
![]() to the Cartwright & Tayler amplitudes
to the Cartwright & Tayler amplitudes
![]() and
and
![]() ,
respectively:
,
respectively:
| (26) | |||
| (27) |
When these increments are due to the redistribution of matter associated
with the ocean tides and the solid Earth deformations caused by them,
the spectral expansions of
![]() and
and
![]() may be obtained by
combining Eqs. (3) and (2b) of Chapter 6 of the IERS Conventions
2003 with Eq. (13) of the same Chapter. One finds that
may be obtained by
combining Eqs. (3) and (2b) of Chapter 6 of the IERS Conventions
2003 with Eq. (13) of the same Chapter. One finds that
Ocean tide contributions to the axial torques (17) and
(20) make up the major part of these torques, so we consider
these contributions first. Each of the two expressions is a sum
of two mutually complex conjugate parts, and each part is a product of
two functions of time. One function represents the tidal
deformation itself, and the other represents the external tidal
excitation (or potential). The spectral frequencies present in the two
functions are labelled by ![]() and
and ![]() ,
respectively.
On using the expansions (22) and (28), one can see
that
,
respectively.
On using the expansions (22) and (28), one can see
that
Is the sign of the torque generated by each tidal component negative,
as one would expect? In looking at this question, we note from (24) that
![]() is
is
![]() times a
positive constant, and hence that the first term in (33) will be
negative provided that
times a
positive constant, and hence that the first term in (33) will be
negative provided that
![]() is positive. On
the other hand, (25) shows that
is positive. On
the other hand, (25) shows that
![]() is a positive
constant times
is a positive
constant times
![]() and hence a negative contribution will
arise from the second term too if
and hence a negative contribution will
arise from the second term too if
![]() is
positive. An examination of the Cartwright & Tayler tables for the
is
positive. An examination of the Cartwright & Tayler tables for the
![]() and the CSR4 tables for the ocean tide heights
and the CSR4 tables for the ocean tide heights
![]() and
and
![]() shows that both the above
conditions on the signs are satisfied. Therefore our physical expectation
is indeed borne out.
shows that both the above
conditions on the signs are satisfied. Therefore our physical expectation
is indeed borne out.
Consider next the contribution to ![]() from anelastic dissipation
in the solid Earth tides. It is most convenient to incorporate this
effect into the integral (17) by expressing the solid Earth
parts
from anelastic dissipation
in the solid Earth tides. It is most convenient to incorporate this
effect into the integral (17) by expressing the solid Earth
parts
![]() and
and
![]() of
of
![]() and
and
![]() in terms of the relevant compliances
in terms of the relevant compliances ![]() and
and ![]() (see, for
instance, Sasao et al. 1980):
(see, for
instance, Sasao et al. 1980):
For excitations at the semidiurnal frequencies of the sectorial potential,
the value of ![]() is slightly different (
is slightly different (
![]() ),
partly because of the difference in the anelasticity contribution
between the semidiurnal and diurnal frequencies and partly because the
ellipticity of the Earth increments
),
partly because of the difference in the anelasticity contribution
between the semidiurnal and diurnal frequencies and partly because the
ellipticity of the Earth increments ![]() by slightly different
amounts in the different frequency bands.
by slightly different
amounts in the different frequency bands.
Contributions from solid Earth and ocean tides to the increments of
inertia appearing in the torque expressions (17) and (20) have been evaluated. They were obtained from the
solution of the dynamical equations for the rotation of an inelastic Earth with
a fluid core, as explained in Sect. 4 of Lambert & Mathews (2006).
The ocean tide heights have been taken from the CSR4 tables (which are an
extension of the CSR3 release, see Eanes & Bettadpur 1996). The CSR4 tables do
not provide error estimates on the tidal heights. However, Ray et al.
mention an error of roughly 1% on the height of the M2 tidal constituent
of the EGM96S model (Lemoine et al. 1998). Moreover, one should address the
uncertainty in the value of ![]() .
This value is available from two sources.
First, from calculations for the relevant frequency band
(semi-diurnal, diurnal, and low-frequency) using Earth models like PREM
(Dziewonski & Anderson 1981) based on seismological data. The
uncertainties in the Earth models are generally believed to be around
1%, leading to the same uncertainty in the Love number k2 to which
the compliance
.
This value is available from two sources.
First, from calculations for the relevant frequency band
(semi-diurnal, diurnal, and low-frequency) using Earth models like PREM
(Dziewonski & Anderson 1981) based on seismological data. The
uncertainties in the Earth models are generally believed to be around
1%, leading to the same uncertainty in the Love number k2 to which
the compliance ![]() is essentially equivalent. Second, estimations
from the fit of nutation theory results to VLBI data: the MHB estimate
for
is essentially equivalent. Second, estimations
from the fit of nutation theory results to VLBI data: the MHB estimate
for ![]() comes with an uncertainty of about 0.3%. To be
conservative, we will take 1% as a safe estimate of the error.
comes with an uncertainty of about 0.3%. To be
conservative, we will take 1% as a safe estimate of the error.
From Eq. (13), one gets the angular acceleration
![]() ,
in units of
,
in units of
![]() /cy2, which
can be turned into an equivalent LOD rate (in units of ms/cy) following
/cy2, which
can be turned into an equivalent LOD rate (in units of ms/cy) following
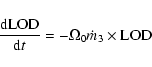 |
(36) |
The secular variations of the length of day produced by sectorial and
tesseral tidal potentials are reported in Table 1. Ray et
al., using various oceanic models released between 1991 and 1998, found a
value of 2.28 ms/cy for the ocean contribution including the atmospheric
tides. Adding the contribution of -0.1 ms/cy from the atmosphere
(equivalent to 55
![]() /cy2 in the rotation rate) to the
oceanic contribution of 2.35 ms/cy, we get the approximate value of
2.25 ms/cy which differs from that of Ray et al. by less than
0.03 ms/cy. The contribution due to solid Earth tides is smaller by a
factor of 20, which represents about 6% of the total. The contribution
of the oceans and the solid Earth tides leads to 2.50 ms/cy. The full
contribution of the mantle, the oceans and the atmosphere amounts to
2.40 ms/cy. Finally, adding -0.55 ms/cy due to the non-tidal acceleration
(Yoder et al. 1983), the total rate of change in the LOD amounts to 1.85 ms/cy.
All these values have a standard error of 1 ms/cy.
/cy2 in the rotation rate) to the
oceanic contribution of 2.35 ms/cy, we get the approximate value of
2.25 ms/cy which differs from that of Ray et al. by less than
0.03 ms/cy. The contribution due to solid Earth tides is smaller by a
factor of 20, which represents about 6% of the total. The contribution
of the oceans and the solid Earth tides leads to 2.50 ms/cy. The full
contribution of the mantle, the oceans and the atmosphere amounts to
2.40 ms/cy. Finally, adding -0.55 ms/cy due to the non-tidal acceleration
(Yoder et al. 1983), the total rate of change in the LOD amounts to 1.85 ms/cy.
All these values have a standard error of 1 ms/cy.
In addition to secular variation of the LOD, periodic variations
arise too from the interaction of the solid Earth and ocean tides with the
tesseral and sectorial potentials. They remain below the current
observational accuracy of the length of day. The largest contributions
have amplitudes of 0.35 ![]() s at the 18.6-year period and 0.24
s at the 18.6-year period and 0.24 ![]() s
at a semi-annual period.
s
at a semi-annual period.
In closing, we wish to note that the result obtained in this work for the tidally induced rate of increase of LOD as well as that for the obliquity rate calculated in an earlier work (Lambert & Mathews 2008), both based on the same theoretical formulation and the same dissipative mechanisms as were employed in the MHB nutation theory (Mathews et al. 2002), are close to the results of other reliable calculations that have appeared in the recent literature like Ray et al. (1999).
Table 1:
Contribution to the angular acceleration
![]() and to
the LOD rate from the action of tidal potentials on ocean and
solid Earth tides.
and to
the LOD rate from the action of tidal potentials on ocean and
solid Earth tides.