A&A 493, 89-105 (2009)
DOI: 10.1051/0004-6361:200810324
M. Emprechtinger1 - P. Caselli2 - N. H. Volgenau1,![]() - J. Stutzki1 - M. C. Wiedner1
- J. Stutzki1 - M. C. Wiedner1
1 - Universität zu Köln,
Zülpicher Str. 77, 50937 Cologne, Germany
2 -
School of Physics and Astronomy, University of Leeds, Leeds LS2 9JT, UK
Received 4 June 2008 / Accepted 16 September 2008
Abstract
Context. Deuterated ions, especially H2D+ and N2D+, are abundant in cold (![]()
![]() ), dense (
), dense (![]()
![]() )
regions, in which CO is frozen out onto dust grains. In such environments, the N2D+/N2H+ ratio can exceed the elemental abundance ratio of D/H by a factor of
)
regions, in which CO is frozen out onto dust grains. In such environments, the N2D+/N2H+ ratio can exceed the elemental abundance ratio of D/H by a factor of ![]() 104.
104.
Aims. We use deuterium fractionation to investigate the evolutionary state of Class 0 protostars. In particular, we expect the N2D+/N2H+ ratio to decrease as temperature (a sign of the evolution of the protostar) increases.
Methods. We observed N2H+ 1-0, N2D+ 1-0, 2-1 and 3-2, C18O 1-0 and HCO+ 3-2 in a sample of 20 Class 0 and borderline Class 0/I protostars. We determined the deuteration fraction and searched for correlations between the N2D+/N2H+ ratio and well-established evolutionary tracers, such as
![]() and the CO depletion factor. In addition, we compared the observational result with a chemical model.
and the CO depletion factor. In addition, we compared the observational result with a chemical model.
Results. In our protostellar sample, the N2H+ 1-0 optical depths are significantly lower than those found in prestellar cores, but the N2H+ column densities are comparable, which can be explained by the higher temperature and larger line width in protostellar cores. The deuterium fractionation of N2H+ in protostellar cores is also similar to that in prestellar cores. We found a clear correlation between the N2D+/N2H+ ratio and evolutionary tracers. As expected, the coolest, i.e. the youngest, objects show the largest deuterium fractionation. Furthermore, we find that sources with a high N2D+/N2H+ ratio show clear indications of infall (e.g.
![]() ). With decreasing deuterium fraction, the infall signature disappears and
). With decreasing deuterium fraction, the infall signature disappears and ![]() tends to be positive for the most evolved objects. The deuterium fractionation of other molecules deviates clearly from that of N2H+. The DCO+/HCO+ ratio stays low at all evolutionary stages, whereas the NH2D/NH3 ratio is >0.15 even in the most evolved objects.
tends to be positive for the most evolved objects. The deuterium fractionation of other molecules deviates clearly from that of N2H+. The DCO+/HCO+ ratio stays low at all evolutionary stages, whereas the NH2D/NH3 ratio is >0.15 even in the most evolved objects.
Conclusions. The N2D+/N2H+ ratio is known to trace the evolution of prestellar cores. We show that this ratio can be used to trace core evolution even after star formation. Protostars with an N2D+/N2H+ ratio above 0.15 are in a stage shortly after the beginning of collapse. Later on, deuterium fractionation decreases until it reaches a value of ![]() 0.03 at the Class 0/I borderline.
0.03 at the Class 0/I borderline.
Key words: ISM: clouds - ISM: evolution - ISM: molecules - stars: formation
Early attempts to describe an evolutionary sequence of protostars classified them according to their near- and mid-infrared spectra. Lada & Wilking (1984) divided a sample of protostellar sources in the ![]() Ophiuchi cloud into three classes (Class I to III with progressive evolutionary stage). André et al. (1993) introduced the Class 0 stage. The strong submillimetre emission of Class 0 objects relative to their bolometric luminosity suggests that the mass of the circumstellar envelope is higher than the mass of the central star. Class 0 objects are the youngest among the protostars. In subsequent years, more sensitive indicators for protostar evolution were established, such as the bolometric temperature (Myers & Ladd 1993), the
Ophiuchi cloud into three classes (Class I to III with progressive evolutionary stage). André et al. (1993) introduced the Class 0 stage. The strong submillimetre emission of Class 0 objects relative to their bolometric luminosity suggests that the mass of the circumstellar envelope is higher than the mass of the central star. Class 0 objects are the youngest among the protostars. In subsequent years, more sensitive indicators for protostar evolution were established, such as the bolometric temperature (Myers & Ladd 1993), the
![]() /
/
![]() ratio (André et al. 1993) and the correlation between the bolometric luminosity and the distance normalised 1.3 mm flux (Saraceno et al. 1996). All these evolutionary indicators are based on the change of the spectral energy distribution (SED) of the protostar. As it heats up, an increasing fraction of the radiation is emitted at shorter wavelengths, leading to an increase in
ratio (André et al. 1993) and the correlation between the bolometric luminosity and the distance normalised 1.3 mm flux (Saraceno et al. 1996). All these evolutionary indicators are based on the change of the spectral energy distribution (SED) of the protostar. As it heats up, an increasing fraction of the radiation is emitted at shorter wavelengths, leading to an increase in
![]() and
and
![]() with time.
with time.
Several theoretical models connect physical properties of the protostars with the time since gravitational collapse (e.g. Smith 1998; Myers et al. 1998). However, although the evolutionary stages determined by different models is the same (i.e. the time sequence is the same), the absolute ages vary significantly. The absolute age for Class 0/I borderline objects, for example, varies between 104 and a few times 105 years (Froebrich 2005). In this paper, we show that it is possible to use the deuterium fractionation of N2H+ as an evolutionary tracer.
The chemistry of cold (
![]() ), dense (
), dense (
![]() )
environments in space is peculiar. Common molecular tracers, such as CO and CS, appear reduced in abundance because they freeze out onto dust grains (e.g. Willacy et al. 1998; Caselli et al. 1999; Kramer et al. 1999; Bergin et al. 2002; Redman et al. 2002; Tafalla et al. 2002, 2004). By comparison, molecules such as N2H+ and NH3 suffer less from depletion. The persistence of nitrogen-bearing species likely stems from the fact that N2, the progenitor of these species, remains in the gas phase longer than CO, despite laboratory measurements finding that the binding energy, as well as the sticking coefficient of N2 and CO on dust, are quite similar (Öberg et al. 2005; Bisschop et al. 2006). Recent theoretical work suggests that the resistance of nitrogen-bearing species to depletion may come from a significant fraction of interstellar nitrogen being in atomic (N) rather than molecular (N2) form (Maret et al. 2006; Flower et al. 2006). Atomic nitrogen has a lower binding energy than molecular nitrogen and CO.
)
environments in space is peculiar. Common molecular tracers, such as CO and CS, appear reduced in abundance because they freeze out onto dust grains (e.g. Willacy et al. 1998; Caselli et al. 1999; Kramer et al. 1999; Bergin et al. 2002; Redman et al. 2002; Tafalla et al. 2002, 2004). By comparison, molecules such as N2H+ and NH3 suffer less from depletion. The persistence of nitrogen-bearing species likely stems from the fact that N2, the progenitor of these species, remains in the gas phase longer than CO, despite laboratory measurements finding that the binding energy, as well as the sticking coefficient of N2 and CO on dust, are quite similar (Öberg et al. 2005; Bisschop et al. 2006). Recent theoretical work suggests that the resistance of nitrogen-bearing species to depletion may come from a significant fraction of interstellar nitrogen being in atomic (N) rather than molecular (N2) form (Maret et al. 2006; Flower et al. 2006). Atomic nitrogen has a lower binding energy than molecular nitrogen and CO.
One consequence of the low temperatures and freeze-out of CO in pre- and protostellar cores is that the abundance of deuterated molecules is greatly enhanced. In such regions, column density ratios for N2D+/N2H+ of 0.24 (Caselli et al. 2002b), D2CO/H2CO ![]() 0.01-0.1 (Bacmann et al. 2003), NH2D/NH3 up to 0.33 (Hatchell 2003), and DCO+/HCO+ in the order of 0.01 (Jørgensen et al. 2004) are found. These ratios are three to four orders of magnitudes over the average ISM D/H ratio of
0.01-0.1 (Bacmann et al. 2003), NH2D/NH3 up to 0.33 (Hatchell 2003), and DCO+/HCO+ in the order of 0.01 (Jørgensen et al. 2004) are found. These ratios are three to four orders of magnitudes over the average ISM D/H ratio of
![]() (Oliveira et al. 2003). Models show that the abundance of H2D+, a fundamental molecule in deuterium chemistry, rises steeply as temperature decreases (e.g. Flower et al. 2004; Roberts & Millar 2000). Consequently, the deuterium fractionation of many other molecules also increases (Millar et al. 2000).
(Oliveira et al. 2003). Models show that the abundance of H2D+, a fundamental molecule in deuterium chemistry, rises steeply as temperature decreases (e.g. Flower et al. 2004; Roberts & Millar 2000). Consequently, the deuterium fractionation of many other molecules also increases (Millar et al. 2000).
In a recent study, Crapsi et al. (2005) investigated the N2D+/N2H+ ratio in 31 low-mass starless cores and finds ratios in the range of a few percent to 0.44. They also find a tight correlation between the N2D+/N2H+ ratio and the CO depletion factor; the ratio is greater where CO is depleted. Furthermore, they attempted to find correlations between the N2D+/N2H+ ratio and various chemical and dynamical evolutionary indicators (e.g. core density, molecular column density, line width, and line asymmetry). Although the dependencies on particular indicators are not always clear, they identified a recognisable trend. The N2D+/N2H+ ratio was generally found to increase as a cloud core evolves towards the moment of protostellar collapse. Another result of their work is that the trends seen in the subsample of Taurus cores were more homogeneous than trends in the total sample. This homogeneity led them to speculate that a core's external environment plays an important role in its evolution. In this work we follow the trend of the N2D+/N2H+ ratio to the subsequent, early protostellar stages.
One recent study that also sought to determine the behaviour of deuterated molecules in protostellar environments is from Roberts & Millar (2007). They determine the N2D+/N2H+ ratio in five low-mass
protostellar cores, using the University of Arizona 12 m telescope (HPBW of 70'' for N2H+ 1-0). Furthermore they measured the D2CO/H2CO and the HDCO/H2CO ratio in these cores. The HDCO/H2CO ratio was similar in most cores (![]() 0.06), with the exception of the object with the highest N2D+/N2H+ ratio, where HDCO/H2CO was lowest. For four sources, the N2D+/N2H+ ratio appeared anti-correlated with the D2CO/H2CO ratio. Only in L 1527 were both N2D+ and D2CO abundances anomalously low. They did not find a correlation between deuterium fractionation and bolometric temperature for any of the observed molecules. However, due to the small number of protostars, this work cannot rule out any trend of the deuterium fractionation in protostellar cores.
0.06), with the exception of the object with the highest N2D+/N2H+ ratio, where HDCO/H2CO was lowest. For four sources, the N2D+/N2H+ ratio appeared anti-correlated with the D2CO/H2CO ratio. Only in L 1527 were both N2D+ and D2CO abundances anomalously low. They did not find a correlation between deuterium fractionation and bolometric temperature for any of the observed molecules. However, due to the small number of protostars, this work cannot rule out any trend of the deuterium fractionation in protostellar cores.
We observed 20 Class 0 protostars in N2H+ and N2D+, using the IRAM 30 m telescope (HPBW of 27'' for N2H+ 1-0, see Sect. 2).
The goal of our study is to investigate the trend in deuterium fractionation after the moment of star formation. Spectra and line parameters are presented in Sect. 3. We expect that the N2D+/N2H+ ratio (determined in Sect. 4.1) should decrease during protostellar evolution due to the internal heating of the core. As the core environment warms up, H2D+ and its more highly deuterated isotopologues are destroyed. Consequently, all other deuterated molecules formed by reactions with H2D+ (such as N2D+) are destroyed as well. In Sect. 4.2- 4.4, the N2D+/N2H+ ratio is compared with evolutionary indicators, namely dust temperature, CO depletion factor, and
![]() /F1.3. Possible correlations with kinematical parameters of the gas are investigated in Sect. 4.5. In addition, we compare the N2D+/N2H+ ratio with the deuterium fractionation of other molecules (Sect. 4.6). Finally, we compare our results with the predictions of a simple chemical model (Sect. 5).
/F1.3. Possible correlations with kinematical parameters of the gas are investigated in Sect. 4.5. In addition, we compare the N2D+/N2H+ ratio with the deuterium fractionation of other molecules (Sect. 4.6). Finally, we compare our results with the predictions of a simple chemical model (Sect. 5).
Our survey includes 20 Class 0 protostellar cores. Table 1 lists the objects, their coordinates, and their estimated distances. The sources were selected in terms of being a) well known (i.e. many complementary data can be found in the literature) and b) representing a range of stages of Class 0 sources, from very young objects (e.g. HH 211, which is one of the youngest protostars according to Froebrich 2005) to borderline objects (Class 0/1), such as L1455 A1 (Froebrich 2005) and Barnard 5 IRS 1 (Velusamy & Langer 1998).
For one object, L 1527, the classification is ambiguous. The continuum data denote it as a Class 0 object, but an embedded source is detected at a wavelength <![]() m (Froebrich 2005), indicating that this protostar is already more evolved. Therefore, this source is also classified as a Class 0/I borderline object.
Most of the objects (13) are located in the Perseus molecular cloud, and all are at a distance closer than 500 pc. For the sources located in Perseus, we assumed a distances of 220 pc (Cernis 1990). Other authors (e.g. Herbig & Jones 1983) give distances greater than 300 pc. Eleven objects belong to a sample of sources catalogued by Froebrich (2005), and for 17 sources, kinetic gas temperatures are known from NH3 observations (Jijina et al. 1999). However, the NH3 observations vary in spatial resolution between 40'' and 80''. To avoid systematic errors, introduced by the different beam sizes, we use these
kinetic temperatures here only to estimate the gas temperature.
m (Froebrich 2005), indicating that this protostar is already more evolved. Therefore, this source is also classified as a Class 0/I borderline object.
Most of the objects (13) are located in the Perseus molecular cloud, and all are at a distance closer than 500 pc. For the sources located in Perseus, we assumed a distances of 220 pc (Cernis 1990). Other authors (e.g. Herbig & Jones 1983) give distances greater than 300 pc. Eleven objects belong to a sample of sources catalogued by Froebrich (2005), and for 17 sources, kinetic gas temperatures are known from NH3 observations (Jijina et al. 1999). However, the NH3 observations vary in spatial resolution between 40'' and 80''. To avoid systematic errors, introduced by the different beam sizes, we use these
kinetic temperatures here only to estimate the gas temperature.
Table 1: Class 0 objects observed for the survey.
The observations were carried out in January 2006 using the IRAM-30 m telescope. In Table 2, the molecular line transitions, their frequencies, and their corresponding half-power beam widths (HPBW) are given. Two different receiver set-ups were used. The first set-up used frequency switching to observe C18O 1-0, N2D+ 2-1, N2D+ 3-2, and HCO+ 3-2 simultaneously. The offsets were 10 (C18O 1-0), 15 (N2D+ 2-1), 25 (N2D+ 3-2), and 28 (HCO+ 3-2) MHz, respectively. The second set-up used an external local oscillator to observe the N2D+ 1-0 line. In this mode, frequency switching was not available, so position switching was used instead. The N2D+ 1-0 line was observed simultaneously with the N2H+ 1-0 and N2D+ 3-2 lines. As a back end, the VESPA autocorrelator was used, which was adjusted to a resolution of about 0.05 km s-1 at each frequency.
Table 2: Observed emission lines.
During observations, the atmospheric ![]() (225 GHz) was about 0.25, which is a typical opacity for winter weather conditions at the IRAM site. The corresponding system temperatures were between 150 K (N2H+ 1-0) and 800 K (HCO+ 3-2).
Pointing was checked every two hours, and the pointing accuracy was better than 3''. Antenna temperatures and main beam temperatures are related by the main beam efficiency,
(225 GHz) was about 0.25, which is a typical opacity for winter weather conditions at the IRAM site. The corresponding system temperatures were between 150 K (N2H+ 1-0) and 800 K (HCO+ 3-2).
Pointing was checked every two hours, and the pointing accuracy was better than 3''. Antenna temperatures and main beam temperatures are related by the main beam efficiency,
![]() ,
which is between 0.8 and 0.42, depending on the observing frequency
,
which is between 0.8 and 0.42, depending on the observing frequency![]() .
.
The results of the N2H+ and N2D+ observations are summarised in Table 3. Figure 1 shows the three N2D+ transitions observed toward HH 211, one of the few sources (total of 6, see Table 3) where all lines are detected. The N2H+ 1-0, N2D+ 2-1, C18O 1-0, and HCO+ 3-2 spectra of all 20 sources are displayed in Fig. 2.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0324fig1.eps}
\end{figure}](/articles/aa/full/2009/01/aa10324-08/Timg22.gif) |
Figure 1: Spectra of N2D+ 1-0, N2D+ 2-1, and N2D+ 3-2 toward HH 211, one of the youngest sources in our sample. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{0324fig2.eps}
\end{figure}](/articles/aa/full/2009/01/aa10324-08/Timg23.gif) |
Figure 2: Spectra of N2H+ 1-0, N2D+ 2-1, C18O 1-0, and HCO+ 3-2 ( from left to right) of all 20 protostars of our sample. To be able to plot all spectra in one plot, we divided the intensities of HCO+ by three. |
| Open with DEXTER | |
Table 3: Line parameters of the N2H+ and N2D+ lines.
The N2H+ 1-0 line was detected in all sources of our sample. The total optical depth was determined by fitting all hyperfine components of the line using the ``METHOD HFS'' of the CLASS program![]() . The relative intensities of the hyperfine components given by Womack et al. (1992) were assumed. With the exception of Per 6, the line optical depths could be determined with at least 3.5
. The relative intensities of the hyperfine components given by Womack et al. (1992) were assumed. With the exception of Per 6, the line optical depths could be determined with at least 3.5![]() in all objects (see Table 3).
in all objects (see Table 3).
![]() was estimated using the equation
was estimated using the equation
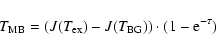
The N2H+ 1-0 line widths found in our protostellar sample are significantly larger than the ones in prestellar cores. The average line width for our sample is 0.61 km s-1, whereas Crapsi et al. (2005) find an average line width of 0.26 km s-1. The line widths reported by Roberts & Millar (2007) are slightly broader than ours (0.85 km s-1), but this difference might be due to the lower spatial resolution of their observations. This suggests that nonthermal motions are not only concentrated nearby the protostar, but also that they pervade the whole associated envelope, increasing outward as commonly found in molecular cloud cores (e.g. Fuller & Myers 1992).
N2D+ was observed in three different transitions (J=1-0, J=2-1 and J=3-2). All three lines were detected in six objects. The ground-state transition, N2D+ 1-0, was detected in only seven sources, but the S/N of four of these is too low to obtain a reliable ![]() from hyperfine component fitting. Only in L 1448 IRS 3 and Barnard 1-b is the line strong enough, and the HFS method yielded
from hyperfine component fitting. Only in L 1448 IRS 3 and Barnard 1-b is the line strong enough, and the HFS method yielded
![]() ,
respectively. The reason for the rarity of N2D+ 1-0 detections is that the Einstein-A coefficient, i.e. the transition probability, increases with
,
respectively. The reason for the rarity of N2D+ 1-0 detections is that the Einstein-A coefficient, i.e. the transition probability, increases with ![]() J3, and thus the A-coefficient for the J=1-0 line is ten times lower than the A-coefficient of the J=2-1 line. Furthermore, the relatively low energies (
J3, and thus the A-coefficient for the J=1-0 line is ten times lower than the A-coefficient of the J=2-1 line. Furthermore, the relatively low energies (
![]() K) and the higher degeneracies of higher rotational states lead to an efficient population of those states under conditions present in protostellar cores (
K) and the higher degeneracies of higher rotational states lead to an efficient population of those states under conditions present in protostellar cores (
![]() cm-3, T=10-20 K).
cm-3, T=10-20 K).
The 2-1 line is the most frequently detected N2D+ line. Only two objects, Per 6 and L 1527, do not show emission in J=2-1. These two objects also show no emission in the other N2D+ lines. In most cases, the J=2-1 lines are optically thin, so that ![]() can be determined by fitting the hyperfine components in only five cases.
can be determined by fitting the hyperfine components in only five cases.
The N2D+ 3-2 line is detected in 15 out of the 20 cores. Because the satellite lines get weaker with increasing J, and due to the higher noise-level of most of these data, it was not possible to derive reliable optical depths.
The integrated intensities of the N2H+ 1-0 lines from the cores in our sample are comparable to the intensities found in prestellar cores (Crapsi et al. 2005), but the optical depths in the protostellar cores are typically lower by a factor of three. The integrated intensity and optical depth of N2D+ 2-1 are approximately the same in pre- and protostellar cores, but N2D+ 3-2 is significantly stronger in the latter (![]() 0.3 K km s-1 and
0.3 K km s-1 and ![]() 1.42 K km s-1, respectively).
1.42 K km s-1, respectively).
The C18O 1-0 and HCO+ 3-2 lines were detected in all 20 sources of our sample. The line parameters are listed in Table 4. The line profile of C18O, which is assumed to be optically thin, looks roughly Gaussian. The only two exceptions are L 1455 A1 and IRAS 03282, which show more complex line shapes, indicating that these sources may contain several velocity components. The C18O line width (FWHM) is quite narrow, typically <1 km s-1. Such narrow line widths indicate that the bulk of the molecular gas is cold, and turbulence is low. The column densities we calculated for C18O (see below), indicate that the C18 1-0 line is optically thin in these objects.
The line shape of HCO+ 3-2 deviates clearly from a Gaussian profile. Double-peaked profiles appear in 12 objects, with minima at the position of the optically thin C18O emission, a clear indication of self-absorption. Asymmetries in the line shape indicate a systematic velocity pattern, which is probably caused by infall motions.
Gregersen et al. (2000) observed several young protostars in HCO+ 3-2 using the Caltech Submillimeter Observatory (CSO). They found line shapes that show similar asymmetries to those we detect (see Sect. 4.5), but the intensities of the lines they observed are significantly lower. This discrepancy is most likely caused by the larger beam size (32.5'') of the CSO at 268 GHz. For three sources common to the Gregersen et al. (2000) study and ours, we determined beam filling factors based on the HCO+ 3-2 lines. We used a CSO beam efficiency of 69.8% at 269 GHz to convert their ![]() to
to
![]() .
Assuming that HCO+ 3-2 is emitted from a small region at the centre of the core, as suggested by our models (see Sect. 5.4), we estimated the size of this region by comparing the
.
Assuming that HCO+ 3-2 is emitted from a small region at the centre of the core, as suggested by our models (see Sect. 5.4), we estimated the size of this region by comparing the
![]() ratio to the ratio of the beam size of the two observations. The derived filling factors for the CSO observations were between 0.26 and 0.36, yielding a diameter of the warm nucleus of approximately 4000 AU. Contributions of the error beams to the IRAM observations have been neglected here, but because of the small size of the HCO+ emitting region means their contribution is <
ratio to the ratio of the beam size of the two observations. The derived filling factors for the CSO observations were between 0.26 and 0.36, yielding a diameter of the warm nucleus of approximately 4000 AU. Contributions of the error beams to the IRAM observations have been neglected here, but because of the small size of the HCO+ emitting region means their contribution is <![]() .
.
Table 4: Observational parameters of the C18O and HCO+ lines.
In this section, we calculate the N2D+/N2H+ ratios and correlate them with physical parameters of the protostars that might influence deuterium fractionation. Some of these parameters, such as dust temperature and bolometric luminosity, can be used to quantify the evolutionary stage of the protostar. Each parameter will be discussed in individual subsections.
To derive the deuterium enhancement, one calculates the ratio of the column densities of a hydrogen-bearing species and its deuterated isotopologue. Many common C-bearing molecules (e.g. HCO+ and H2CO) suffer from depletion in cold and dense environments (see Tafalla et al. 2006), and thus the deuterated species trace slightly warmer regions of the core, where the parent molecules are not depleted. To properly determine the deuterium fractionation of an entire core, one has to observe molecules that are less affected by depletion, such as N2H+ and NH3. Another benefit of observing N-bearing molecules is that their emission lines split into hyperfine components due to the non-zero nuclear spin of nitrogen, enabling optical depths to be measured.
To determine molecular column densities, we used the N2H+ 1-0 and N2D+ 2-1 lines. We chose these lines for three reasons. First, N2D+ 2-1 is detected in most of the sources. Second, the 2-1 transition of N2D+ is observed with the highest S/N. Third, the ratio of the N2D+ 2-1/N2H+ 1-0 lines permits a direct comparison with previous studies (Crapsi et al. 2005; Fontani et al. 2006).
The column densities were derived (Table 5) by assuming a constant excitation temperature, as determined in Sect. 3 (CTEX-method, for details see the appendix of Caselli et al. 2002b). The excitation temperature of N2H+ can be determined in all objects but Per 6 (Table 3), where the N2H+ line is optically thin. For Per 6, we assumed an excitation temperature of 8 K, which is the mean excitation temperature of the sample.
The situation is different for N2D+, since the N2D+ 2-1 line is optically thin in most objects. In the few sources where ![]() could be determined, the excitation temperatures of N2H+ and N2D+ were approximately the same. In all cases where the excitation temperature of N2D+ was unknown, we assumed that it was the same as for N2H+. The estimated errors on the column densities are approximately 15% and 20% for N2H+ and N2D+, respectively. As expected, the N2D+/N2H+ ratios vary significantly from object to object (Table 5). The extreme values are <0.029 for Per 6 and 0.27 for HH 211. For most objects, the ratio is below 0.1.
could be determined, the excitation temperatures of N2H+ and N2D+ were approximately the same. In all cases where the excitation temperature of N2D+ was unknown, we assumed that it was the same as for N2H+. The estimated errors on the column densities are approximately 15% and 20% for N2H+ and N2D+, respectively. As expected, the N2D+/N2H+ ratios vary significantly from object to object (Table 5). The extreme values are <0.029 for Per 6 and 0.27 for HH 211. For most objects, the ratio is below 0.1.
Determining Tex and the column densities as described above, we implicitly assume a unity beam-filling factor for the N2H+ and N2D+ observations. Because dark cloud cores are typically larger than the beam size of our observations (e.g. Caselli et al. 2002a) and because the kinetic temperature of these cores is only ![]() 1.5 times, the excitation temperature of N2H+ indicates that the filling factor is indeed close to one, and certainly >0.67. Using the lower limit for the filling factor would lower the N2H+ column density by 40% and the N2D+ column density by 55%. Therefore, the derived N2D+/N2H+ ratios could be up to 25% lower. The general trend, however, remains and will be discussed in the next section.
1.5 times, the excitation temperature of N2H+ indicates that the filling factor is indeed close to one, and certainly >0.67. Using the lower limit for the filling factor would lower the N2H+ column density by 40% and the N2D+ column density by 55%. Therefore, the derived N2D+/N2H+ ratios could be up to 25% lower. The general trend, however, remains and will be discussed in the next section.
The N2D+ column density was also calculated using the (3-2) line, where detected, following the same procedure as described above. In 13 out of 15 objects, the values for the column density agree within the range of error. In L 1448 IRS3 and L 1157, the column densities determined using N2D+ 3-2 are a factor of two higher than those determined using the 2-1 line. However, because of the lower S/N of the N2D+ 3-2 line, the column densities determined using the J=2-1 transition are more reliable.
Table 5: N2H+ and N2D+ column densities.
The N2H+ and N2D+ column densities derived here are comparable to those found by Crapsi et al. (2005) for prestellar cores (
![]() and
and
![]() for N2H+ and N2D+, respectively).This result is somewhat unexpected, because the optical depth of N2H+ is about three times lower in protostars than in prestellar cores. However, the higher excitation temperatures and broader line widths of N2H+ in protostellar envelopes (over-)compensate for the lower optical depth.
The range of values for the N2D+/N2H+ ratio is also similar. The average ratio in our sample of Class 0 protostars is 0.097, and 20% of the objects have a ratio greater than 0.15. For starless cores, the average ratio is 0.106, and 18% of the sources have ratios above 0.15. However, the N2D+/N2H+ ratio in both protostellar and prestellar cores is significantly larger than the ratio in high mass star-forming regions (always less than 0.02, Fontani et al. 2006), although values as high as 0.1 have been measured with interferometric observations (Fontani et al. 2008).
for N2H+ and N2D+, respectively).This result is somewhat unexpected, because the optical depth of N2H+ is about three times lower in protostars than in prestellar cores. However, the higher excitation temperatures and broader line widths of N2H+ in protostellar envelopes (over-)compensate for the lower optical depth.
The range of values for the N2D+/N2H+ ratio is also similar. The average ratio in our sample of Class 0 protostars is 0.097, and 20% of the objects have a ratio greater than 0.15. For starless cores, the average ratio is 0.106, and 18% of the sources have ratios above 0.15. However, the N2D+/N2H+ ratio in both protostellar and prestellar cores is significantly larger than the ratio in high mass star-forming regions (always less than 0.02, Fontani et al. 2006), although values as high as 0.1 have been measured with interferometric observations (Fontani et al. 2008).
Table 6: Continuum observations and derived properties (dust temperature, C18O column density, CO depletion factor) for sources in our survey.
For three objects in our sample, L 1448 C, HH 211, and L 1527, N2D+/N2H+ was also determined by Roberts & Millar (2007). In general, they find somewhat higher N2D+/N2H+ ratios than we do. In L 1448 C, their ratio is
![]() times greater. In HH 211, their ratio is
times greater. In HH 211, their ratio is
![]() times greater. For L 1527, we report an upper limit of 0.034, whereas Roberts & Millar found a ratio of 0.06. That Roberts & Millar (2007) found similar N2D+/N2H+ ratios at much lower spatial resolution indicates that the deuterium fractionation occurs, as expected, in the cold, extended envelope of the protostellar core. If deuterium fractionation occurred only in the central region, one would expect beam dilution to yield lower N2D+/N2H+ at lower resolutions.
times greater. For L 1527, we report an upper limit of 0.034, whereas Roberts & Millar found a ratio of 0.06. That Roberts & Millar (2007) found similar N2D+/N2H+ ratios at much lower spatial resolution indicates that the deuterium fractionation occurs, as expected, in the cold, extended envelope of the protostellar core. If deuterium fractionation occurred only in the central region, one would expect beam dilution to yield lower N2D+/N2H+ at lower resolutions.
We also estimated the volume densities of the cores. Because the N2D+ lines show only a single velocity component, we used the ratios of the integrated intensities of these lines instead of the
![]() ratios. Thus we obtained a higher S/N. Further we assumed an isothermal cloud with a kinetic temperature determined from NH3 observations (Table 3). The volume density was estimated by fitting the N2D+ J=3-2/J=2-1 ratio, using a radiative transfer code (Pagani 2007, see Sect. 5.2). We derived values between
ratios. Thus we obtained a higher S/N. Further we assumed an isothermal cloud with a kinetic temperature determined from NH3 observations (Table 3). The volume density was estimated by fitting the N2D+ J=3-2/J=2-1 ratio, using a radiative transfer code (Pagani 2007, see Sect. 5.2). We derived values between
![]() cm-3 and
cm-3 and
![]() .
Only IRAS 03282 shows a lower density (
.
Only IRAS 03282 shows a lower density (
![]() ).
However, temperature and density decline with distance from the protostar, so lower spatial resolution observations trace lower average temperatures, densities, and (assuming spherical symmetry) lower column densities. Therefore, the N2D+ 3-2 lines trace, on average, warmer and denser gas than do the N2D+ 2-1 lines, and the densities obtained from the ratios are upper limits. For six sources, we also determined densities using the N2D+ J=2-1/J=1-0 ratios. We were not able to find a density that would reproduce all three lines simultaneously. The density values derived from the J=2-1/J=1-0 line ratio are about a factor 10 lower than those determined from the J=3-2/J=2-1 ratio. This difference again most likely arises because of the lower spatial resolution of the lower frequency observations.
).
However, temperature and density decline with distance from the protostar, so lower spatial resolution observations trace lower average temperatures, densities, and (assuming spherical symmetry) lower column densities. Therefore, the N2D+ 3-2 lines trace, on average, warmer and denser gas than do the N2D+ 2-1 lines, and the densities obtained from the ratios are upper limits. For six sources, we also determined densities using the N2D+ J=2-1/J=1-0 ratios. We were not able to find a density that would reproduce all three lines simultaneously. The density values derived from the J=2-1/J=1-0 line ratio are about a factor 10 lower than those determined from the J=3-2/J=2-1 ratio. This difference again most likely arises because of the lower spatial resolution of the lower frequency observations.
In general,
![]() is expected to rise as a protostar evolves, but there is no exact model of dust temperature as a function of time. As a result, connecting dust temperature to specific protostellar ages depends on which model is used (see Froebrich 2005, and references therein).
is expected to rise as a protostar evolves, but there is no exact model of dust temperature as a function of time. As a result, connecting dust temperature to specific protostellar ages depends on which model is used (see Froebrich 2005, and references therein).
All of our sources, with the exceptions of Per 4 S and SMM 5, have infrared counterparts identified in the IRAS point source or faint source catalogues. In addition, millimetre and submillimetre continuum data are available for many of the sources (see Table 6).
We fitted these data to derive values for dust temperature (
![]() )
and emissivity (
)
and emissivity (![]() )
using Eq. (1) from Kramer et al. (2003):
)
using Eq. (1) from Kramer et al. (2003):
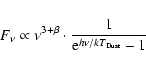
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0324fig3.eps}
\end{figure}](/articles/aa/full/2009/01/aa10324-08/Timg186.gif) |
Figure 3:
Deuterium fractionation (N2D+/N2H+ column density ratio) versus dust temperature. The highest N2D+/N2H+ ratios are seen at the lowest temperatures. As
|
| Open with DEXTER | |
The dust temperatures derived from fitting the continuum data range from approximately 20 K up to 50 K (see Table 6). These temperatures are clearly higher than the excitation temperatures of N2H+ and the kinetic gas temperatures (Table 3). The difference is likely due to the dust emission from warmer regions being stronger than from cold dust, and thus the obtained average temperature is higher than the gas temperature traced by N2H+.
In Fig. 3, the N2D+/N2H+ column density ratio is plotted versus the dust temperature. All objects with N2D+/N2H+ ratio >0.15 have
![]() K. At higher dust temperatures, the deuterium fractionation declines, reaching an average value of approximately 0.05 at 30 K.
K. At higher dust temperatures, the deuterium fractionation declines, reaching an average value of approximately 0.05 at 30 K.
Because CO is one of the main destroyers of H3+ and its deuterated isotopologues, the progenitors of N2D+, the N2D+/N2H+ ratio should be sensitive to CO depletion (e.g. Dalgarno & Lepp 1984; Roberts & Millar 2000).
The CO depletion factor, ![]() ,
is defined as
,
is defined as
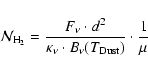
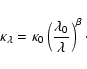
To compare the ![]() mm continuum data with our C18O 1-0 observations, we have to estimate the continuum flux density within a 22'' beam. That the angular diameters of the protostellar envelopes are always greater than the beam is an important issue in this conversion. To compare data taken with different beam sizes, we follow the method of Terebey et al. (1993). They showed that the flux of a dark cloud with a density distribution
mm continuum data with our C18O 1-0 observations, we have to estimate the continuum flux density within a 22'' beam. That the angular diameters of the protostellar envelopes are always greater than the beam is an important issue in this conversion. To compare data taken with different beam sizes, we follow the method of Terebey et al. (1993). They showed that the flux of a dark cloud with a density distribution
![]() and a temperature distribution T=r-q can be described by
and a temperature distribution T=r-q can be described by
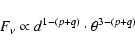
We determined the C18O column density by using the CTEX-method and by assuming that C18O emission is optically thin.
Since the critical density of C18O is 60 times lower than that for N2H+, we expect that
![]() will be higher than
will be higher than
![]() and comparable to the kinetic gas temperature or even slightly higher, due to freeze-out of CO in the cold parts of the cloud. Since the beam sizes of the NH3 observations that were used to derive
and comparable to the kinetic gas temperature or even slightly higher, due to freeze-out of CO in the cold parts of the cloud. Since the beam sizes of the NH3 observations that were used to derive
![]() vary between 40'' and 88'', we adopted a constant excitation temperature of 15 K for all sources. This assumption introduces some error (<15%) in the estimation of the depletion factor. The total number of C18O molecules is then calculated from
vary between 40'' and 88'', we adopted a constant excitation temperature of 15 K for all sources. This assumption introduces some error (<15%) in the estimation of the depletion factor. The total number of C18O molecules is then calculated from
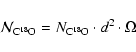
The derived depletion factors lie between 1 and 4 (Table 6). A value below 1 is found toward Barnard 5 IRS 1, and this may be an indication that the C18O canonical abundance is larger in this source. Indeed, the 13CO abundances measured toward Barnard 5 by Pineda et al. (2008) are a factor of two larger than those measured by Frerking et al. (1982) toward Taurus. (The CO abundance variations of about a factor of 2 are well known in star-forming regions, e.g. Lacy et al. 1994.) However, given that CO abundance measurements are not individually available for all the sources, the C18O canonical abundance has been kept the same for the whole sample.
In the central panel of Fig. 4, we show the correlation between CO freeze-out and deuterium fractionation in our sample of protostars. In the top panel, we show the same correlation but for low-mass prestellar cores (Crapsi et al. 2005), and the correlation for massive prestellar cores in the bottom panel (Fontani et al. 2006).
The correlation determined from our sample looks very similar to the correlation found for low-mass prestellar cores. For small depletion factors (![]() (CO)<3), the deuterium fractionation is low as well (<0.1). For depletion factors greater than three, the N2D+/N2H+ ratio rises quickly until it reaches 0.25. The only difference between the protostellar and prestellar cores is that, in the prestellar cores, the deuterium fractionation stays low until the depletion factor is
(CO)<3), the deuterium fractionation is low as well (<0.1). For depletion factors greater than three, the N2D+/N2H+ ratio rises quickly until it reaches 0.25. The only difference between the protostellar and prestellar cores is that, in the prestellar cores, the deuterium fractionation stays low until the depletion factor is ![]() 10. This behaviour reflects the fact that CO is highly depleted in the centre of prestellar cores, whereas it is not depleted in the centres of Class 0 sources. In high-mass prestellar cores, there is no dependence of the deuterium fractionation on
10. This behaviour reflects the fact that CO is highly depleted in the centre of prestellar cores, whereas it is not depleted in the centres of Class 0 sources. In high-mass prestellar cores, there is no dependence of the deuterium fractionation on ![]() (CO). Since the high-mass prestellar cores in the Fontani et al. (2006) sample are at greater distances (a few kpc), these observations might be affected by non-depleted, non-deuterated gas along the line of sight.
(CO). Since the high-mass prestellar cores in the Fontani et al. (2006) sample are at greater distances (a few kpc), these observations might be affected by non-depleted, non-deuterated gas along the line of sight.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0324fig4.eps}
\end{figure}](/articles/aa/full/2009/01/aa10324-08/Timg208.gif) |
Figure 4:
N2D+/N2H+ column density ratio versus CO depletion factor for prestellar cores ( upper panel, Crapsi et al. 2005), Class 0 protostars ( middle panel, this work) and massive prestellar cores ( lower panel, Fontani et al. 2006). The protostellar objects marked with triangles are located in the Perseus cloud. Among the Perseus objects, |
| Open with DEXTER | |
The sources that are not located in the Perseus cloud show lower deuterium fractionation than Perseus sources with the same CO depletion factor. One explanation for this difference is that the Perseus sources are embedded in a dense environment (
![]() ,
Kwon et al. 2006), whereas many of the other cores are isolated. Since CO is not expected to be frozen out in the embedding material, the CO depletion factors of the Perseus cores could be underestimated.
However, systematic errors arising from the different spatial resolutions and different wavelengths of the continuum observations cannot be ruled out. The Perseus cores were observed at
,
Kwon et al. 2006), whereas many of the other cores are isolated. Since CO is not expected to be frozen out in the embedding material, the CO depletion factors of the Perseus cores could be underestimated.
However, systematic errors arising from the different spatial resolutions and different wavelengths of the continuum observations cannot be ruled out. The Perseus cores were observed at ![]() m with a resolution of 31'' (Enoch 2006), and the other cores were observed at
m with a resolution of 31'' (Enoch 2006), and the other cores were observed at ![]() m with a resolution of 40'' (Shirley et al. 2000).
The Perseus source that does not appear to agree with the correlation is L 1448 IRS 3. It has a CO depletion factor of 4.4 but a low deuterium fractionation (0.081). This source is known to consist of multiple cores with several strong outflows (e.g. Volgenau et al. 2006; Looney et al. 2000), but it is not clear how this activity can decrease the deuterium fractionation while maintaining a large amount of CO freeze-out.
m with a resolution of 40'' (Shirley et al. 2000).
The Perseus source that does not appear to agree with the correlation is L 1448 IRS 3. It has a CO depletion factor of 4.4 but a low deuterium fractionation (0.081). This source is known to consist of multiple cores with several strong outflows (e.g. Volgenau et al. 2006; Looney et al. 2000), but it is not clear how this activity can decrease the deuterium fractionation while maintaining a large amount of CO freeze-out.
The correlation among the subsample of Perseus sources is quite good, whereas the non-Perseus sources do not show this functional dependence. We made a least-squares fit of the Perseus data to the equation
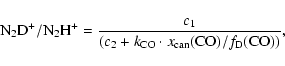
The errors in the depletion factor are around 20 %. These errors do not include the uncertainties in the excitation temperatures, dust temperatures and ![]() 's, which are the main sources of systematic errors in this analysis. A different
's, which are the main sources of systematic errors in this analysis. A different ![]() value, however, would just rescale
value, however, would just rescale ![]() ,
but it would not change the correlation itself. Such a rescaling would also be the effect of a different dust temperature, because
,
but it would not change the correlation itself. Such a rescaling would also be the effect of a different dust temperature, because ![]() (CO) was determined from continuum measurements around 1 mm, which is a wavelength clearly in the Rayleigh-Jeans regime.
Rejecting the assumption of a constant average excitation temperature in all objects would change the correlation significantly.
(CO) was determined from continuum measurements around 1 mm, which is a wavelength clearly in the Rayleigh-Jeans regime.
Rejecting the assumption of a constant average excitation temperature in all objects would change the correlation significantly.
If
![]() is lower than 15 K, we underestimate the depletion factor, and we overestimate it if
is lower than 15 K, we underestimate the depletion factor, and we overestimate it if
![]() is greater than 15 K. But, if we assume that
is greater than 15 K. But, if we assume that
![]() (C18O) is related to the dust temperature, i.e. objects with higher
(C18O) is related to the dust temperature, i.e. objects with higher
![]() also have higher C18O excitation temperatures. Taking the correlation between the N2D+/N2H+ ratio found in the previous section into account, the high deuterium fractionation cores would may have higher
also have higher C18O excitation temperatures. Taking the correlation between the N2D+/N2H+ ratio found in the previous section into account, the high deuterium fractionation cores would may have higher ![]() (CO) values, and the low deuterium fractionation cores would have lower ones. Therefore the correlation would spread out fuorther along the depletion factor axis.
(CO) values, and the low deuterium fractionation cores would have lower ones. Therefore the correlation would spread out fuorther along the depletion factor axis.
The SED of a young stellar object changes as the central protostar heats up the surrounding gas and dust. Several measures have been developed to determine how far a protostar has evolved, including the bolometric temperature (Myers & Ladd 1993), the ratio of the submillimetre to bolometric luminosity (André et al. 1993), and the correlation between luminosity (L) and visual extinction (![]() )
(Adams 1990). Another measure of the evolution of a protostar, developed by Saraceno et al. (1996), is the ratio of
)
(Adams 1990). Another measure of the evolution of a protostar, developed by Saraceno et al. (1996), is the ratio of
![]() to
F1.3D0, the distance-normalised flux at 1.3 mm. As the protostar warms up,
to
F1.3D0, the distance-normalised flux at 1.3 mm. As the protostar warms up,
![]() should rise quickly, whereas
F1.3D0, which is a measure of the envelope mass and less dependent on the temperature, should stay constant or decrease slightly. Hence, the ratio
should rise quickly, whereas
F1.3D0, which is a measure of the envelope mass and less dependent on the temperature, should stay constant or decrease slightly. Hence, the ratio
![]() increases as the protostar evolves.
increases as the protostar evolves.
To determine
F1.3D0 values, we use fluxes at
![]() mm (5 sources), 1.1 mm (4 sources), and 850
mm (5 sources), 1.1 mm (4 sources), and 850 ![]() (2 sources). The continuum fluxes at 1.1 mm and 850
(2 sources). The continuum fluxes at 1.1 mm and 850 ![]() m were corrected using, as before,
m were corrected using, as before, ![]() (or, in the case of Barnard 5 IRS 1,
(or, in the case of Barnard 5 IRS 1, ![]() ). For the distance normalisation and the conversion of the different beam sizes, we used the equation from Terebey et al. (1993) described in the previous section, i.e.,
). For the distance normalisation and the conversion of the different beam sizes, we used the equation from Terebey et al. (1993) described in the previous section, i.e.,
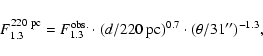
Table 7: Bolometric luminosity and distance-normalised flux of Class 0 protostars in our sample.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0324fig5.eps}
\end{figure}](/articles/aa/full/2009/01/aa10324-08/Timg227.gif) |
Figure 5:
N2D+/N2H+ versus
|
| Open with DEXTER | |
The correlation between
![]() and N2D+/N2H+ is shown in Fig. 5. The objects with the highest deuterium fractionation (>0.15) (IRAS 03282, Barnard 1-B and HH 211) all have low
and N2D+/N2H+ is shown in Fig. 5. The objects with the highest deuterium fractionation (>0.15) (IRAS 03282, Barnard 1-B and HH 211) all have low
![]() ratios and are presumably less-evolved protostars. As the
ratios and are presumably less-evolved protostars. As the
![]() ratio increases, the deuterium fractionation drops quickly. If one considers just the Perseus cores, then the fall-off of the deuterium fractionation is less steep. The
ratio increases, the deuterium fractionation drops quickly. If one considers just the Perseus cores, then the fall-off of the deuterium fractionation is less steep. The
![]() ratios may be lower in the non-Perseus sources because systematic errors in normalisation (see Sect. 4.3) lead to overestimates of the continuum fluxes.
L 1455 A1 has by far the highest
ratios may be lower in the non-Perseus sources because systematic errors in normalisation (see Sect. 4.3) lead to overestimates of the continuum fluxes.
L 1455 A1 has by far the highest
![]() ratio, and by this measure should be the most evolved protostar in the figure. The assertion that L1455 A1 is more evolved than other protostars is reinforced by the relatively low CO depletion factor and high dust temperature. L 1527 is a notable outlier in the sample. Its
ratio, and by this measure should be the most evolved protostar in the figure. The assertion that L1455 A1 is more evolved than other protostars is reinforced by the relatively low CO depletion factor and high dust temperature. L 1527 is a notable outlier in the sample. Its
![]() ratio is one of the lowest in our sample (5.0), but it has an N2D+/N2H+ ratio <0.034 (more discussion on this source is presented in 4.7).
ratio is one of the lowest in our sample (5.0), but it has an N2D+/N2H+ ratio <0.034 (more discussion on this source is presented in 4.7).
So far, we have correlated the N2D+/N2H+ ratios with physical parameters, which are all related to temperature, and thus to the evolutionary stage of the protostar. In this section, we investigate the relation of deuterium fractionation to parameters linked to the kinematics of the gas. Infall, for example, heats up the gas and is expected to influence the gas-phase chemistry.
First, we compare the N2D+/N2H+ ratios with the N2D+ 2-1 line widths (Table 3). Processes such as thermal broadening, turbulent motions, and systematic motions, e.g. infall, all contribute to the full width at half maximum (FWHM) of optically thin emission lines. Thermal broadening plays a relatively minor role, since the thermal line width (FWHM) of N2D+ at 10 K is only 0.12 km s-1 (0.17 km s-1 at 20 K).
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0324fig6.eps}
\end{figure}](/articles/aa/full/2009/01/aa10324-08/Timg228.gif) |
Figure 6: FWHM of N2D+ 2-1 versus N2D+/N2H+. Triangles are Perseus cores. |
| Open with DEXTER | |
In Fig. 6, the N2D+/N2H+ column density ratio is plotted versus the FWHM of N2D+ (2-1). Most of the protostars with high N2D+/N2H+ ratios have narrow N2D+ lines. The two exceptions are Barnard 1-B (
![]() km s-1) and L 1448 C (
km s-1) and L 1448 C (
![]() km s-1), which show the broadest N2D+ lines in the sample. However, all Perseus sources with
km s-1), which show the broadest N2D+ lines in the sample. However, all Perseus sources with
![]() km s-1, including Barnard 1-B and L 1448 C, have multiple embedded sources (Volgenau 2004; Matthews & Wilson 2002). The relative velocity differences between the individual protostars leads to additional line broadening.
km s-1, including Barnard 1-B and L 1448 C, have multiple embedded sources (Volgenau 2004; Matthews & Wilson 2002). The relative velocity differences between the individual protostars leads to additional line broadening.
To be able to trace only the systematic motion of the gas, e.g. infall motion, we used the asymmetry parameter ![]() ,
which was defined by Mardones et al. (1997) as
,
which was defined by Mardones et al. (1997) as
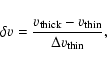
Table 8: Velocities of C18O and HCO+ lines and asymmetry parameters.
In our sample, we find eight sources with a clear indication of infall (i.e.
![]() )
and seven sources with redshifted, optically thick lines (i.e.
)
and seven sources with redshifted, optically thick lines (i.e.
![]() ). For five sources, there is no clear indication of systematic motion (
). For five sources, there is no clear indication of systematic motion (
![]() ). Like previous studies by Mardones et al. (1997) and Gregersen et al. (2000), we find more blueshifted than redshifted objects. The blue excess is defined by Mardones et al. (1997) as
). Like previous studies by Mardones et al. (1997) and Gregersen et al. (2000), we find more blueshifted than redshifted objects. The blue excess is defined by Mardones et al. (1997) as
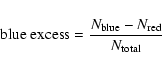
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0324fig7.eps}
\end{figure}](/articles/aa/full/2009/01/aa10324-08/Timg246.gif) |
Figure 7:
Asymmetry parameter |
| Open with DEXTER | |
![]() and, less clearly, R/B are correlated with the deuterium fractionation, and only Per 5 and, once again L 1527, which is a peculiar source (see Sect. 4.7), do not follow the general trend and indicate strong infall motion. The higher the N2D+/N2H+ ratio, the more blueshifted the optically thick emission lines. Such a result was somehow expected, since outflow activity rises with the evolution of the protostar (Richer et al. 2000). The results are also in good agreement with the results of Mardones et al. (1997). Using observations of CS, C34S and H2CO lines, they found that the blue excess of Class 0 protostars is clearly enhanced compared to Class I objects.
However, using observations of HCO+, H13CO+ and N2H+ lines, Gregersen et al. (2000) did not find such trend. They speculate that infall asymmetry disappears later in HCO+. Because our sample contains no true Class I objects, we cannot directly compare their results with ours.
and, less clearly, R/B are correlated with the deuterium fractionation, and only Per 5 and, once again L 1527, which is a peculiar source (see Sect. 4.7), do not follow the general trend and indicate strong infall motion. The higher the N2D+/N2H+ ratio, the more blueshifted the optically thick emission lines. Such a result was somehow expected, since outflow activity rises with the evolution of the protostar (Richer et al. 2000). The results are also in good agreement with the results of Mardones et al. (1997). Using observations of CS, C34S and H2CO lines, they found that the blue excess of Class 0 protostars is clearly enhanced compared to Class I objects.
However, using observations of HCO+, H13CO+ and N2H+ lines, Gregersen et al. (2000) did not find such trend. They speculate that infall asymmetry disappears later in HCO+. Because our sample contains no true Class I objects, we cannot directly compare their results with ours.
We also calculated ![]() using the C18O 1-0 transition as the optically thin line. Contrary to N2H+, which traces the cold, CO depleted envelope, C18O traces the already warmed up central part of the protostar. Thus it traces the region, where the HCO+ 3-2 line comes from, too. But due to the lower critical density of the C18O 1-0 transition, the low-density outskirts of the protostellar envelope might contribute significantly to the C18O emission, which possibly dilute any correlation. Qualitatively, the correlation between
using the C18O 1-0 transition as the optically thin line. Contrary to N2H+, which traces the cold, CO depleted envelope, C18O traces the already warmed up central part of the protostar. Thus it traces the region, where the HCO+ 3-2 line comes from, too. But due to the lower critical density of the C18O 1-0 transition, the low-density outskirts of the protostellar envelope might contribute significantly to the C18O emission, which possibly dilute any correlation. Qualitatively, the correlation between ![]() and the deuterium fractionation looks similar, no matter which optically thin line is used. However, for objects with an N2D+/N2H+ ratio above 0.75,
and the deuterium fractionation looks similar, no matter which optically thin line is used. However, for objects with an N2D+/N2H+ ratio above 0.75, ![]() determined with C18O yields less blue-shifted values. A reason for this difference might be that in these objects, which also show the highest CO depletion factors, the contributions from the environmental material to the C18O emission is expected to be biggest. The bigger contribution of the environmental material is also indicated by the fact that for objects with
determined with C18O yields less blue-shifted values. A reason for this difference might be that in these objects, which also show the highest CO depletion factors, the contributions from the environmental material to the C18O emission is expected to be biggest. The bigger contribution of the environmental material is also indicated by the fact that for objects with
![]() lower than -0.5,
lower than -0.5,
![]() is on average 2.4 times larger than
is on average 2.4 times larger than
![]() ,
whereas for the remaining sources
,
whereas for the remaining sources
![]() is only 1.6 times larger. More turbulent material appears to surround infalling protostellar envelopes.
is only 1.6 times larger. More turbulent material appears to surround infalling protostellar envelopes.
The deuterium fractionation of N2H+ reflects the present time temperature and density better than most other molecules, since it does not significantly deplete (see e.g. Caselli et al. 2002b; Bergin et al. 2002; Schnee et al. 2007), and the chemical reactions for N2D+ formation and destruction are quite fast and simple. Memories of cold phases in the past of the dark cloud core are therefore not expected in the observed N2D+/N2H+ ratio. In this section, we compare the N2D+/N2H+ ratio with the NH2D/NH3 (Hatchell 2003), DCO+/HCO+ ratios (Jørgensen et al. 2004) and the deuterium fractionation of H2CO and CH3OH (Parise et al. 2006) for the sources in our sample where these data are available (Table 9).
Table 9: Deuterium fractionation of several molecular species.
The deuterium fractionation of HCO+ is significantly lower than the fractionation of N2H+ in all objects but one (L 1527).
This difference can be explained by CO, the parent species of HCO+, also being the main destroyer of H2D+ and thus the DCO+/HCO+ ratio traces only those regions where the deuterium fractionation in N2H+ is expected to be lower.
Furthermore, Jørgensen et al. (2004) determine the DCO+/HCO+ ratio using the DCO+ J=3-2 line, which has a critical density of
![]() cm-3. Therefore these DCO+ observations mostly trace the inner, high density part, which might already be warmed up by the embedded protostellar core, thus lowering the DCO+/HCO+ ratio.
The situation with NH3 is different. Like N2H+, NH3 is formed from N2 and does not seem to freeze out (Tafalla et al. 2002). Thus, N2D+ and NH2D emission should originate from the same region. As a consequence, the deuterium fractionation of N2H+ and NH3 should be comparable.
cm-3. Therefore these DCO+ observations mostly trace the inner, high density part, which might already be warmed up by the embedded protostellar core, thus lowering the DCO+/HCO+ ratio.
The situation with NH3 is different. Like N2H+, NH3 is formed from N2 and does not seem to freeze out (Tafalla et al. 2002). Thus, N2D+ and NH2D emission should originate from the same region. As a consequence, the deuterium fractionation of N2H+ and NH3 should be comparable.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0324fig8.eps}
\end{figure}](/articles/aa/full/2009/01/aa10324-08/Timg256.gif) |
Figure 8: Deuterium fractionation of NH3 (red triangles) and N2H+ (black circles) versus dust temperature. |
| Open with DEXTER | |
As shown in Fig. 8, the coldest objects, i.e. the youngest objects in our sample (HH 211 & IRAS 03282), have a deuterium fractionation of NH3 indeed comparable to the fractionation of N2H+. But the warmer the dust gets, the more the ratios diverge. The NH2D/NH3 ratio is about 0.2 at
![]() K, where the N2D+/N2H+ ratio is five times lower.
The differing trends in the two ratios can be explained as follows. Both N2D+ and NH2D are formed directly or indirectly via H2D+ or its multiply deuterated forms, i.e., the formation mechanism is only effective in cold, CO-depleted environments. In regions where CO desorbs from the dust due to the warming up of the protostar, N2D+ and N2H+ disappear quickly from the gas phase, because these species are directly destroyed by CO, forming HCO+ and DCO+, respectively. Thus, with increasing temperature, the N2D+/N2H+ ratio traces material at larger and lager radii (i.e. at lower and lower densities). But deuterium fractionation is related to the density, because of the lower degree of CO depletion at lower densities (see Sect. 5.4 and Fig. 11). In contrast to N2H+ and N2D+, which are pure gas-phase species, ammonia is also found on dust grain mantles, most likely formed by grain-surface reactions (Boogert et al. 2008). The solid NH3, which desorbs from the dust grains as soon as the environmental material warms up, likely has a large deuterium fractionation due to the fossil record of grain surface chemistry and gas phase depletion at low temperatures (e.g. Aikawa et al. 2008). Thus, the observed NH2D/NH3 ratio declines more slowly than the deuterium fractionation of pure gas phase species.
K, where the N2D+/N2H+ ratio is five times lower.
The differing trends in the two ratios can be explained as follows. Both N2D+ and NH2D are formed directly or indirectly via H2D+ or its multiply deuterated forms, i.e., the formation mechanism is only effective in cold, CO-depleted environments. In regions where CO desorbs from the dust due to the warming up of the protostar, N2D+ and N2H+ disappear quickly from the gas phase, because these species are directly destroyed by CO, forming HCO+ and DCO+, respectively. Thus, with increasing temperature, the N2D+/N2H+ ratio traces material at larger and lager radii (i.e. at lower and lower densities). But deuterium fractionation is related to the density, because of the lower degree of CO depletion at lower densities (see Sect. 5.4 and Fig. 11). In contrast to N2H+ and N2D+, which are pure gas-phase species, ammonia is also found on dust grain mantles, most likely formed by grain-surface reactions (Boogert et al. 2008). The solid NH3, which desorbs from the dust grains as soon as the environmental material warms up, likely has a large deuterium fractionation due to the fossil record of grain surface chemistry and gas phase depletion at low temperatures (e.g. Aikawa et al. 2008). Thus, the observed NH2D/NH3 ratio declines more slowly than the deuterium fractionation of pure gas phase species.
Deuterated formaldehyde (HDCO and D2CO) are very abundant, too. The HDCO/H2CO ratio, as well as the D2CO/H2CO ratio, are close to 0.1 (Parise et al. 2006). In their work, Parise et al. also determined the deuterium fractionation of methanol, which even exceeds the deuterium fractionation of formaldehyde (e.g.
![]() ). For both molecules, no obvious correlation between the deuterium fractionation and the core evolutionary stage could be found. Because mainly grain surface chemistry is involved in the deuteration of methanol and formaldehyde, the observed deuterium fractionation is probably a memory of the previous, prestellar phase (Ceccarelli et al. 2001), a similar (although more extreme) case to the one found for ammonia.
). For both molecules, no obvious correlation between the deuterium fractionation and the core evolutionary stage could be found. Because mainly grain surface chemistry is involved in the deuteration of methanol and formaldehyde, the observed deuterium fractionation is probably a memory of the previous, prestellar phase (Ceccarelli et al. 2001), a similar (although more extreme) case to the one found for ammonia.
The youngest objects in our sample are Barnard 1-B, IRAS 03282 and HH 211. All three evolutionary tracers indicate those sources are among the youngest. The depletion factor, ![]() (CO), indicates that L1448 IRS3 and L 1157 are young objects, too, but their
(CO), indicates that L1448 IRS3 and L 1157 are young objects, too, but their
![]() suggest that these sources are, instead, more evolved. A possible solution to this discrepancy lies in acknowledging several assumptions we made in determining the CO depletion factor (e.g. in converting the beam sizes of the continuum and the C18O observations). Although, overall, these assumptions seem to be justified, they might not be valid for all sources, and thus the
suggest that these sources are, instead, more evolved. A possible solution to this discrepancy lies in acknowledging several assumptions we made in determining the CO depletion factor (e.g. in converting the beam sizes of the continuum and the C18O observations). Although, overall, these assumptions seem to be justified, they might not be valid for all sources, and thus the ![]() (CO) values may be less accurate. The three protostars we identified as the youngest also have the highest N2D+/N2H+ ratios (0.18, 0.22, and 0.27 in Barnard 1-B, IRAS 03282, and HH 211, respectively). By this measure, Per 4 S, with a deuterium fractionation of 0.177, should also be very young, but no complementary data are available to confirm this.
(CO) values may be less accurate. The three protostars we identified as the youngest also have the highest N2D+/N2H+ ratios (0.18, 0.22, and 0.27 in Barnard 1-B, IRAS 03282, and HH 211, respectively). By this measure, Per 4 S, with a deuterium fractionation of 0.177, should also be very young, but no complementary data are available to confirm this.
The objects at a moderate evolutionary stage are those with a deuterium fractionation around 0.1 (L 1448 IRS 3, PER 4 N, PER 5). The exception is L 1448 C (N2D+/N2H+ = 0.10), which seems to be more evolved than the others. However, among these intermediately-evolved sources, there are also some with deuterium fractionations of ![]() 0.05 (L 723, B 335, L 1448 IRS 2). For SMM 5 (N2D+/N2H
+ = 0.079), we are unable to determine the evolutionary stage independently, but, because of its N2D+/N2H+ ratio, we think that it belongs to the group of intermediately-evolved objects. The N2D+/N2H+ ratios of the most evolved protostars are, with the exception of L 1448 C (0.10),
0.05 (L 723, B 335, L 1448 IRS 2). For SMM 5 (N2D+/N2H
+ = 0.079), we are unable to determine the evolutionary stage independently, but, because of its N2D+/N2H+ ratio, we think that it belongs to the group of intermediately-evolved objects. The N2D+/N2H+ ratios of the most evolved protostars are, with the exception of L 1448 C (0.10), ![]() 0.05.
0.05.
L 1527 is a special case. The T
![]() (27 K) and especially the
(27 K) and especially the
![]() ratio (5.0) suggest that it is a younger object, but its low N2D+/N2H+ ratio and the fact that an embedded source is detected at wavelengths <
ratio (5.0) suggest that it is a younger object, but its low N2D+/N2H+ ratio and the fact that an embedded source is detected at wavelengths <![]() m indicates that this source is more evolved (Froebrich 2005). Chemical models, which reproduce the observed abundance of long-chain unsaturated hydrocarbons and cyanopolyynes, indicate a more evolved evolutionary stage of L 1527 as well (Hassel et a. 2008). From infrared observations, Tobin et al. (2008) conclude that L 1527 contains a massive protostellar disc, which is seen edge-on. Therefore L 1527 might be a more evolved object than indicated by continuum observations, due to the large obscuration of the central object. Hence, the N2D+/N2H+ ratio seems to be even more reliable than continuum measurements at identifying the youngest protostellar objects.
m indicates that this source is more evolved (Froebrich 2005). Chemical models, which reproduce the observed abundance of long-chain unsaturated hydrocarbons and cyanopolyynes, indicate a more evolved evolutionary stage of L 1527 as well (Hassel et a. 2008). From infrared observations, Tobin et al. (2008) conclude that L 1527 contains a massive protostellar disc, which is seen edge-on. Therefore L 1527 might be a more evolved object than indicated by continuum observations, due to the large obscuration of the central object. Hence, the N2D+/N2H+ ratio seems to be even more reliable than continuum measurements at identifying the youngest protostellar objects.
In conclusion, the N2D+/N2H+ ratio can be used to clearly identify the youngest objects among the Class 0 sources. For more evolved objects, the correlation of evolutionary stage and N2D+/N2H+ ratio is not so clear, but an overall decrease in deuteration with evolutionary stage can be seen.
To explain the results discussed in the previous section, we examined a model of a ``typical'' Class 0 object rather than a specific source. First, we describe the physical properties, e.g. the temperature and density profiles, of the model. Subsequently, we calculate the abundances of the important species and apply a radiative transfer code to simulate the observations.
The density structure of the model is that of a singular isothermal sphere (Shu 1977):
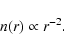
The total envelope mass is assumed to be close to a few solar masses. However, since the model results depend strongly on the density, the total mass varies for different models (see below).
For the temperature profile, we use a power law with an index of -0.4, which is the exponent for optically thin emission from protostellar envelopes, as found by Looney et al. (2003). They also show that, with a density powerlaw index of 2, the radial temperature distribution can significantly deviate from the power-law at radii smaller than 100-200 AU. However, given that we used an inner boundary of 100 AU for the envelope, such deviations do not noticeably influence our model.
To avoid very low temperatures on the outskirts of the envelope, we assume a temperature profile like the one found in prestellar cores (Crapsi et al. 2007):
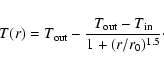
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0324fig9.eps}
\end{figure}](/articles/aa/full/2009/01/aa10324-08/Timg269.gif) |
Figure 9:
Density (dashed line) and temperature (solid lines) profiles of the protostellar core models. The four temperature profiles represent models that yield values for
|
| Open with DEXTER | |
Using this cloud structure, we calculate the continuum flux at 60 ![]() ,
100
,
100 ![]() ,
850
,
850 ![]() ,
and 1.2 mm from the formula:
,
and 1.2 mm from the formula:
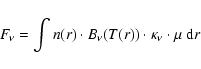
The chemical code used in this study is similar to the one originally described by Caselli et al. (2002b), but updated following Caselli et al. (2008). We assume a spherically symmetric cloud, and follow the time-dependent freeze-out of CO and N2, as well as thermal and non-thermal desorption due to cosmic-ray impulsive heating, neglecting dynamical effects. All the deuterated forms of H3+ are included in the model, and the abundances of the ionic species, such as HCO+, N2H+, and their deuterated couterparts, are given by the steady-state chemical equations using the instantaneous abundaces of the neutral species (see Caselli et al. 2002b, for details). The rate coefficients are adopted from the UMIST database for astrochemistry, available at http://www.udfa.net. For the proton-deuteron exchange reaction (such as H3+ + HD
![]() H2D+ + H2), we use both ``standard rates'' (e.g. as used in Roberts et al. 2004; Ceccarelli & Dominik 2005) as well as the rates more recently measured by Gerlich et al. (2002), which appear to better fit our data (see below). No atomic oxygen is included in the code, given the large uncertainties in its abundance in cold and dense regions (e.g. Bergin & Snell 2002; see also discussion in Sect. 3.2.3 of Caselli et al. 2002b). The cosmic-ray ionization rate is fixed at
H2D+ + H2), we use both ``standard rates'' (e.g. as used in Roberts et al. 2004; Ceccarelli & Dominik 2005) as well as the rates more recently measured by Gerlich et al. (2002), which appear to better fit our data (see below). No atomic oxygen is included in the code, given the large uncertainties in its abundance in cold and dense regions (e.g. Bergin & Snell 2002; see also discussion in Sect. 3.2.3 of Caselli et al. 2002b). The cosmic-ray ionization rate is fixed at
![]() s-1, the average value measured toward high-mass star forming regions by van der Tak & van Dishoeck (2000). The CO and N2 binding energies are assumed to be 1100 K and 982.3 K, respectively, following the prescriptions of Öberg et al. (2005) and Schnee et al. (2007) (see their Sect. 6.2). The model is run for 106 yr, an average age for a dense core. After 106 years, the abundances of the various molecules nearly reache chemical equilibrium, and thus the exact evolution time is not a critical parameter (see Sect. 5.5 for discussion).
s-1, the average value measured toward high-mass star forming regions by van der Tak & van Dishoeck (2000). The CO and N2 binding energies are assumed to be 1100 K and 982.3 K, respectively, following the prescriptions of Öberg et al. (2005) and Schnee et al. (2007) (see their Sect. 6.2). The model is run for 106 yr, an average age for a dense core. After 106 years, the abundances of the various molecules nearly reache chemical equilibrium, and thus the exact evolution time is not a critical parameter (see Sect. 5.5 for discussion).
The results from the chemical model are used as input parameters for a radiative transfer model, a non-LTE Monte-Carlo code developed by Pagani et al. (2007). This code, which is developed from the Bernes code (Bernes 1979), calculates the 1D radiative transfer of both N2H+ and N2D+ and includes line overlap of the hyperfine transitions. Furthermore, recently published collisional coefficients between individual hyperfine levels have been implement (Daniel et al. 2005). For the convolution with the beam, we assumed a Gaussian beam shape with HPBW as listed in Table 2. The distance to the cloud is set to 220 pc, i.e. the distance of the Perseus cloud. From the spectra that we obtained from the Monte-Carlo-code, we determined the N2D+/N2H+ ratio using the CTEX procedure, just as we did for the observed spectra (see Sect. 4.1). Hence, the comparison between the model and the observations is consistent, because possible systematic errors, introduced by the assumption of a constant excitation temperature, are taken into account.
We computed the N2D+/N2H+ ratios for four models with fitted dust temperatures of 20 K, 27 K, 35 K and 45 K, respectively. The deuterium fractionation in these models ranges from 0.23 at 20 K to 0.03 at 45 K. These values fit the observations very well. We derived an H2 density at a radius of 100 AU of
![]() cm-3, which corresponds to a total envelope mass of 4.6
cm-3, which corresponds to a total envelope mass of 4.6 ![]() .
The modelled correlation between the deuterium fractionation and the CO depletion factor (
.
The modelled correlation between the deuterium fractionation and the CO depletion factor (![]() (CO)) fits the observations quite well, too, but in the cooler objects (
(CO)) fits the observations quite well, too, but in the cooler objects (
![]() K), the modelled CO freeze-out is very sensitive to the temperature. Thus, a marginal temperature variation leads to a significant change of the CO depletion factor, and therefore the quality of the fit depends strongly on the model used.
In Fig. 10, a comparison of the models with the observations of the Perseus sources is shown. Results from the models are also listed in Table 10.
The best agreement with observations is found when using the reaction rates measured by Gerlich et al. (2002) for the proton-deuteron exchange reaction. Using the ``standard rates'', we could only fit the observed N2D+/N2H+ ratios by increasing the total envelope mass to 25
K), the modelled CO freeze-out is very sensitive to the temperature. Thus, a marginal temperature variation leads to a significant change of the CO depletion factor, and therefore the quality of the fit depends strongly on the model used.
In Fig. 10, a comparison of the models with the observations of the Perseus sources is shown. Results from the models are also listed in Table 10.
The best agreement with observations is found when using the reaction rates measured by Gerlich et al. (2002) for the proton-deuteron exchange reaction. Using the ``standard rates'', we could only fit the observed N2D+/N2H+ ratios by increasing the total envelope mass to 25 ![]() ,
a value that is clearly higher than expected for low-mass protostars.
,
a value that is clearly higher than expected for low-mass protostars.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0324fi10.eps}
\end{figure}](/articles/aa/full/2009/01/aa10324-08/Timg278.gif) |
Figure 10:
Upper panel: N2D+/N2H+ ratio versus dust temperature. Lower panel: N2D+/N2H+ ratio and the CO depletion factor |
| Open with DEXTER | |
To check that the assumption of a constant excitation temperature does not give a significantly different result from the T-0.4 profile, we calculated beam-averaged column densities from the model abundance profiles as well. The N2D+/N2H+ ratios determined from the beam-averaged column densities are the same as before, to within 20%. The estimated error of the observed N2D+/N2H+ ratio is also approximately ![]() ,
so the fit is good, independently of the method used.
The trend of a decreasing deuterium fraction with increasing
,
so the fit is good, independently of the method used.
The trend of a decreasing deuterium fraction with increasing
![]() is true for both the ratio determined by the CTEX method and the ratio of the beam-averaged column density.
is true for both the ratio determined by the CTEX method and the ratio of the beam-averaged column density.
Table 10: Model results.
The N2D+ J=3-2/J=2-1 intensity ratios of the models range from 0.44 to 1.10, which is comparable to the observed ratios. For the J=2-1/J=1-0 ratios, the models give values that are a factor of two higher than what is observed. However, these ratios are very sensitive to temperature, density, and abundance variations. Taking the simplicity of our model into account, we consider these values to agree with the observations.
Besides N2D+ and N2H+, the abundances of HCO+ and DCO+ were also calculated by the chemical model. The DCO+/HCO+ ratio is significantly lower than the N2D+/N2H+ ratio and ranges from 0.02 to 0.08 in the models with dust temperatures of 45 K and 21 K, respectively. The HCO+ and DCO+ column densities are averaged over a 21'' beam, and thus comparable to the observations conducted by Jørgensen et al. (2004). The values for the DCO+/HCO+ ratio reported by them are between 0.004 and 0.048 and thus a little lower than the modelled ratios (see Tables 10 and 9).
The temperature gradient, caused by the heating of the central object, leads to strong variations in the abundances of many molecules and molecular ions. The more immediate cause of these variations is the freeze-out of CO, which occurs at a temperature of ![]() 20 K. The absence of CO in the gas phase has a big influence on the abundance of many other species, since many molecular ions, e.g. N2H+, are partially destroyed by reactions with CO. In addition, the deuterium fractionation is enhanced in regions where CO is depleted (see Sect. 1). Therefore, the protostellar envelope can be roughly divided into three zones (Fig. 11). In the inner zone, the temperature has increased above
20 K. The absence of CO in the gas phase has a big influence on the abundance of many other species, since many molecular ions, e.g. N2H+, are partially destroyed by reactions with CO. In addition, the deuterium fractionation is enhanced in regions where CO is depleted (see Sect. 1). Therefore, the protostellar envelope can be roughly divided into three zones (Fig. 11). In the inner zone, the temperature has increased above ![]() 20 K, CO evaporates from the grains and, consequently, the abundance of N2H+ as well as the deuterium fractionation, are relatively low in this region. As soon as the temperature drops below the critical value of
20 K, CO evaporates from the grains and, consequently, the abundance of N2H+ as well as the deuterium fractionation, are relatively low in this region. As soon as the temperature drops below the critical value of ![]() 20 K, the CO abundance drops drastically. At the same time, the N2H+ abundance rises by 1-2 orders of magnitude. The N2D+/N2H+ ratio rises as well, but its maximum is at a larger radius than the CO abundance minimum. This is because the temperature at the minimum of the CO abundance is
20 K, the CO abundance drops drastically. At the same time, the N2H+ abundance rises by 1-2 orders of magnitude. The N2D+/N2H+ ratio rises as well, but its maximum is at a larger radius than the CO abundance minimum. This is because the temperature at the minimum of the CO abundance is ![]() 20 K, where the destruction of H2D+ via the reaction
20 K, where the destruction of H2D+ via the reaction
![]() is not neglible.
At even larger radii, the degree of CO depletion decreases as the gas density decreases, which causes the N2H+ abundance to stay more or less constant, and the deuterium fractionation to drop again.
is not neglible.
At even larger radii, the degree of CO depletion decreases as the gas density decreases, which causes the N2H+ abundance to stay more or less constant, and the deuterium fractionation to drop again.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0324fi11.eps}
\end{figure}](/articles/aa/full/2009/01/aa10324-08/Timg282.gif) |
Figure 11: The relative abundance of CO ( upper panel), N2H+ ( middle panel), and the N2D+/N2H+ ratio are shown as a function of radius. It can be clearly seen that the radius at which CO starts to deplete shifts outwards with increasing temperature, as does the peak of the deuterium fractionation. |
| Open with DEXTER | |
During the Class 0 phase, the temperature of the central object increases, as does the temperature of the envelope. Consequently, the radius at which CO freezes out onto dust grains shifts farther outwards, and the fraction of the cloud in which the abundance of deuterated molecules is enhanced gets smaller with time. Furthermore, the mean density of the deuterium fractionated gas decreases, thus the mean local N2D+/N2H+ ratio declines as well. This leads to the decrease in the N2D+/N2H+ column density ratio, which we observe in our sample.
The reason for the different ratios of the deuterated and non-deuterated forms of HCO+ and N2H+ is that the deuterium fractionation is strongest in places where CO, a progenitor of HCO+ and DCO+, is mostly depleted. Thus, in contrast to N2H+, HCO+ is also relatively strong in the warm and dense inner part of the envelope, and the ratio of the column densities of DCO+ and HCO+ is significantly lower than the N2D+/N2H+ ratio. This can be seen in Fig. 12, in which the abundance of the molecules and molecular ions are shown as a function of radius.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0324fi12.eps} \end{figure}](/articles/aa/full/2009/01/aa10324-08/Timg283.gif) |
Figure 12:
The abundances of CO, H3+, H2D+, HCO+, DCO+, N2H+, and N2D+ relative to H2 are shown as a function of radius. The thick lines show the abundance profile of the protonated species. The thin lines show their singly-deuterated counterparts. These profiles apply to the model with
|
| Open with DEXTER | |
The radial abundance profiles we found with our static model are in good agreement with the results of Lee et al. (2005), who calculated a self-consistent dynamical and chemical model of the entire star forming process. In their model, the deuterated species are not calculated, but the abundance profiles of CO, N2H+ and HCO+ at a time ![]() 105 yr after the collapse starts are similar to the profiles we found (see their Fig. 11). This similarity indicates that the assumption of a chemical equilibrium is valid at least for the simple species.
In a more recent paper, Aikawa et al. (2008) get somewhat shorter timescales for the protostellar evolution:
105 yr after the collapse starts are similar to the profiles we found (see their Fig. 11). This similarity indicates that the assumption of a chemical equilibrium is valid at least for the simple species.
In a more recent paper, Aikawa et al. (2008) get somewhat shorter timescales for the protostellar evolution:
![]() years after the beginning of the collapse, the CO desorption radius is
years after the beginning of the collapse, the CO desorption radius is ![]() 2000 AU, which is comparable to the results of our 45 K model. But even for these shorter time scales, the assumption of chemical equilibrium is still valid (see next section).
2000 AU, which is comparable to the results of our 45 K model. But even for these shorter time scales, the assumption of chemical equilibrium is still valid (see next section).
The evolution times of the models are the least constrained values. The estimated ages of Class 0 protostars range from ![]() 104 to a few times 105 years after the collapse has started (Froebrich 2005). The ages vary by a factor of 10 depending on which model is used. However, the crucial time for the deuterium chemistry is the time since the CO started to freeze out, because the freeze-out of CO is the slowest reaction in the network. Thus, the entire prestellar phase has to be taken into account. After a time of 106 years, the abundances have already reached equilibrium. Reducing the time to 105 years changes the N2D+/N2H+ ratio only marginally. The difference between the ratios after 106 years and 105 years is less than 0.01. In models with a evolution time of 104 years, the abundances are no longer in equilibrium. In the coldest protostar (20 K), the deuterium fractionation is already high (0.26), but for the warmer objects, the N2D+/N2H+ ratio is a factor
104 to a few times 105 years after the collapse has started (Froebrich 2005). The ages vary by a factor of 10 depending on which model is used. However, the crucial time for the deuterium chemistry is the time since the CO started to freeze out, because the freeze-out of CO is the slowest reaction in the network. Thus, the entire prestellar phase has to be taken into account. After a time of 106 years, the abundances have already reached equilibrium. Reducing the time to 105 years changes the N2D+/N2H+ ratio only marginally. The difference between the ratios after 106 years and 105 years is less than 0.01. In models with a evolution time of 104 years, the abundances are no longer in equilibrium. In the coldest protostar (20 K), the deuterium fractionation is already high (0.26), but for the warmer objects, the N2D+/N2H+ ratio is a factor ![]() 2 lower than in chemical equilibrium. Although already quite low, these values still agree with the observations. Evolution times longer than 107 years do not change the results, because equilibrium has already been reached.
2 lower than in chemical equilibrium. Although already quite low, these values still agree with the observations. Evolution times longer than 107 years do not change the results, because equilibrium has already been reached.
Another important parameter is the cosmic-ray ionisation rate. In our model, we used
![]() (van der Tak & van Dishoeck 2000). A
(van der Tak & van Dishoeck 2000). A ![]() of
of
![]() increases the N2H+ abundance by a factor of 1.5, but the deuterium fractionation is lowered by 40%. A cosmic-ray ionisation rate of
increases the N2H+ abundance by a factor of 1.5, but the deuterium fractionation is lowered by 40%. A cosmic-ray ionisation rate of
![]() increases the N2D+/N2H+ ratio by 30%.
increases the N2D+/N2H+ ratio by 30%.
The central density of the core, hence the envelope mass, has a similar effect on the deuterium fractionation as ![]() .
In our models, we varied the density to match the observed N2D+/N2H+ ratio best. The only constraint we put on the central density is that the resulting envelope mass should be a few solar masses. For our best-fit model, we derive an envelope mass of 4.6
.
In our models, we varied the density to match the observed N2D+/N2H+ ratio best. The only constraint we put on the central density is that the resulting envelope mass should be a few solar masses. For our best-fit model, we derive an envelope mass of 4.6 ![]() .
Decreasing the density by a factor of a half, the deuterium fractionation decreases by 40%. With a density twice as high as our best-fit model, the N2D+/N2H+ increases by a factor of 1.2.
.
Decreasing the density by a factor of a half, the deuterium fractionation decreases by 40%. With a density twice as high as our best-fit model, the N2D+/N2H+ increases by a factor of 1.2.
The last crucial parameter we investigated is the binding energy of CO and N2 on dust grains. In our model, we used binding energies of 1100 K and 982.3 K for CO and N2, respectively, which are the binding energies on mixed CO-H2O ice. We also calculated the models using the values for ![]() on pure CO ice (855 and 790 for CO and N2, respectively, Öberg et al. 2005). With these values, the resulting N2D+/N2H+ ratios drop to <0.04 for all four temperatures.
on pure CO ice (855 and 790 for CO and N2, respectively, Öberg et al. 2005). With these values, the resulting N2D+/N2H+ ratios drop to <0.04 for all four temperatures.
We observed 20 Class 0 protostars in N2H+ 1-0, N2D+ 1-0, 2-1 and 3-2, C18O 1-0 and HCO+ 3-2. The integrated intensities of the N2H+ 1-0 lines in our sample are comparable to those found in prestellar cores (Crapsi et al. 2005). The optical depths are typically 67% lower in the Class 0 sources, but because the excitation temperature is 2-3 K higher and the line width is about 2.5 time larger, the N2H+ column densities (![]()
![]() )
are also comparable. The presence of a protostar also affects the kinematics of the cores. The N2H+ lines are significantly wider in Class 0 sources than in prestellar cores (on average, 0.61 km s-1 and 0.26 km s-1, respectively). A comparison of our HCO+ observations with observations conducted with a
)
are also comparable. The presence of a protostar also affects the kinematics of the cores. The N2H+ lines are significantly wider in Class 0 sources than in prestellar cores (on average, 0.61 km s-1 and 0.26 km s-1, respectively). A comparison of our HCO+ observations with observations conducted with a ![]() three times larger beam (Gregersen et al. 2000) leads us to the conclusion that HCO+ 3-2 stems mainly from a compact region of about 4000 AU in size.
three times larger beam (Gregersen et al. 2000) leads us to the conclusion that HCO+ 3-2 stems mainly from a compact region of about 4000 AU in size.
The dependence of the N2D+/N2H+ ratio on dust temperature, CO depletion factor, and the
![]() /
/
![]() ratio clearly indicates a close relation between deuterium fractionation and evolutionary stage of a Class 0 protostar. For the subsample of sources in the Perseus cloud, the correlation is striking. This migh indicate the influence of the environment on the deuterium fractionation.
ratio clearly indicates a close relation between deuterium fractionation and evolutionary stage of a Class 0 protostar. For the subsample of sources in the Perseus cloud, the correlation is striking. This migh indicate the influence of the environment on the deuterium fractionation.
The correlation of the deuterium fractionation and the CO depletion factor looks qualitatively like the one found in prestellar cores (Crapsi et al. 2005). However, whereas in prestellar cores, the N2D+/N2H+ ratio stays low until
![]() ,
in protostars, the ratio starts to rise at
,
in protostars, the ratio starts to rise at
![]() .
This difference occurs because CO is highly depleted at the centre of prestellar cores, but not at the centre of protostellar cores.
.
This difference occurs because CO is highly depleted at the centre of prestellar cores, but not at the centre of protostellar cores.
There is a weak correlation of N2D+ line width with N2D+/N2H+ ratio, but line broadening by multiple sources makes this conclusion suspect. A clear correlation with other kinematical tracers, especially with ![]() ,
is found. Sources with a high N2D+/N2H+ ratio clearly show infall motion (
,
is found. Sources with a high N2D+/N2H+ ratio clearly show infall motion (
![]() ). The lower the deuterium fractionation gets, the more
). The lower the deuterium fractionation gets, the more ![]() increases. This might reflect the outflow activity increasing with evolutionary stage (Richer et al. 2000).
increases. This might reflect the outflow activity increasing with evolutionary stage (Richer et al. 2000).
A model with a power-law density and temperature profile reproduces the correlation between the N2D+/N2H+ ratio and both
![]() and the CO depletion factor very well.
In these models, the protostellar envelopes are chemically stratified. The inner part is too warm for CO to freeze out, so that the N2H+ abundance and the deuterium fractionation are low. At radii where the temperature drops below
and the CO depletion factor very well.
In these models, the protostellar envelopes are chemically stratified. The inner part is too warm for CO to freeze out, so that the N2H+ abundance and the deuterium fractionation are low. At radii where the temperature drops below ![]() 20 K, CO is mostly depleted and the N2D+/N2H+ ratio increases by several orders of magnitude. At even larger radii, the lower density decreases the degree of CO depletion, and thus the N2D+/N2H+ ratio also decreases.
20 K, CO is mostly depleted and the N2D+/N2H+ ratio increases by several orders of magnitude. At even larger radii, the lower density decreases the degree of CO depletion, and thus the N2D+/N2H+ ratio also decreases.
The results of this work, in combination with the results of Crapsi et al. (2005), show that the deuterium fractionation is highest at the moment of collapse. The primary use of the deuterium fractionation of N2H+ is to identify very young protostellar objects, because the decline of the N2D+/N2H+ ratio is rather steep.
Comparisons of N2H+ fractionation with the deuterium fractionation of HCO+ and NH3 show clear differences, which are due either to the influence of freeze-out on dust grains, differences in chemical reactions, or both. The low DCO+/HCO+ ratio observed by Jørgensen et al. (2004) is a prediction of our model. In young, i.e., cool objects, the NH2D/NH3 ratio, observed by Hatchell (2003) is comparable to the deuterium fractionation of N2H+. As the temperature increases, the N2D+/N2H+ ratio falls off much faster than the NH2D/NH3 ratio, which stays above 0.15 in all observed objects. This could be due to desorption of deuterium enhanced ammonia from the dust grains.
Acknowledgements
We would like thank the IRAM 30m staff for their assistance during the observations. Furthermore, we gratefully thank L. Pagani for providing us with the Monte-Carlo code. M. Emprechtinger, N. H. Volgenau, and M. C. Wiedner are member of the Nachwuchsgruppe of the Sonderforschungsbereich 494, which is funded by the Deutsche Forschungsgemeinschaft (DFG).