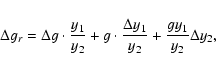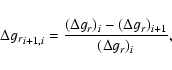A&A 493, 267-282 (2009)
DOI: 10.1051/0004-6361:200809852
A frequency approach to identifying asteroid families
II. Families interacting with nonlinear secular
resonances and low-order mean-motion resonances
V. Carruba1 -
T. A. Michtchenko2
1 - IPD, UNIVAP, São José dos Campos, SP, 12244-000, Brazil
2 -
IAG, Universidade de São Paulo, São Paulo, 05508-900, Brazil
Received 26 March 2008 / Accepted 18 September 2008
Abstract
Aims. In an earlier paper we introduced a new method for determining asteroid families where families were identified in the proper frequency domain (n,g,g+s) (where n is the mean-motion, and g and s are the secular frequencies of the longitude of pericenter and nodes, respectively), rather than in the proper element domain
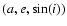 (semi-major axis, eccentricity, and inclination). Here we improve our techniques for reliably identifying members of families that interact with nonlinear secular resonances of argument other than g or g+s and for asteroids near or in mean-motion resonant configurations.
(semi-major axis, eccentricity, and inclination). Here we improve our techniques for reliably identifying members of families that interact with nonlinear secular resonances of argument other than g or g+s and for asteroids near or in mean-motion resonant configurations.
Methods. We introduce several new distance metrics in the frequency space optimal for determining the diffusion in secular resonances of argument 2g-s, 3g-s, g-s, s, and 2s. We also regularize the dependence of the g frequency as a function of the n frequency (Vesta family) or of the eccentricity e (Hansa family).
Results. Our new approaches allow us to recognize as family members objects that were lost with previous methods, while keeping the advantages of the Carruba & Michtchenko (2007, A&A, 475, 1145) approach. More important, an analysis in the frequency domain permits a deeper understanding of the dynamical evolution of asteroid families not always obtainable with an analysis in the proper element domain.
Key words: minor planets, asteroids - celestial mechanics
1 Introduction
In Carruba & Michtchenko (2007) we proposed an alternative approach to the classical Hierarchical Clustering Method (CHCM hereafter) to identifying asteroid families (Zappalà
et al. 1990): rather than looking for clusters in the proper elements
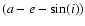 space (semi-major axis, eccentricity and inclination), we searched for families in the
space of proper frequencies (n,g,g+s) (where n is the asteroid mean-motion and g and s are the asteroid secular frequencies of the pericenter and node, respectively).
space (semi-major axis, eccentricity and inclination), we searched for families in the
space of proper frequencies (n,g,g+s) (where n is the asteroid mean-motion and g and s are the asteroid secular frequencies of the pericenter and node, respectively).
The advantages of this approach were numerous, among these: i) secular resonances are more easily identified in the (n,g,g+s) plane, where they are separable, in contrast with the complicated three-dimensional structure that such resonances have in the
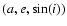 space; ii) the hierarchical clustering method in the frequency domain (FHCM, hereafter) is a very efficient way to identify family members that diffused because of the interplay of the Yarkovsky and YORP effects
and nonlinear secular resonances; and iii) our analysis showed that asteroids families
are also bound by secular resonances such as the z2 resonance for the Eunomia family, and a harmonic of the z1 resonance (the
(s-s6)+(g-g6-2g5+2g7) resonance) for the
Koronis family.
space; ii) the hierarchical clustering method in the frequency domain (FHCM, hereafter) is a very efficient way to identify family members that diffused because of the interplay of the Yarkovsky and YORP effects
and nonlinear secular resonances; and iii) our analysis showed that asteroids families
are also bound by secular resonances such as the z2 resonance for the Eunomia family, and a harmonic of the z1 resonance (the
(s-s6)+(g-g6-2g5+2g7) resonance) for the
Koronis family.
The Carruba & Michtchenko (2007) approach had however some limitations: i) the (n.g,g+s) domain was ideal for studying families interacting with resonances involving the g or the g+s frequencies, but was not the most efficient space to display the effect of resonances involving other combination of frequencies, such as the
k(g-g6)+(s-s6) resonances (zk in the notation of Milani & Knezevic 1994) for k > 1, the
g-g6-s-s6 resonance, or resonances of node of argument s or 2s, and ii) the frequency of the pericenter precession g may not follow a linear trend as a function of n near low-order mean-motion resonances or may be negative
(or retrograde) for asteroid locked in mean-motion resonant configuration.
In this work we extend our investigation of families in the frequency domain to these cases. In the first part of the article we investigate the case of families interacting with nonlinear secular resonances of arguments other than g and g+s. For this purpose, we introduce new appropiate
representative planes and distance metrics that are more efficient to study the process of diffusion in such resonances. Our results show that these new metrics are in general up to 77% more efficient than either the classical approach or the ``standard'' metric in the (n,g,g+s) domain in identifying asteroids that diffused in such secular resonances as family members.
In the second part of our article we study the region near low-order mean-motion resonances, which is quite interesting from a dynamical point of view. Because of the steep behavior of the g frequencies many nonlinear secular resonances overlap in the region. Understanding how to connect fugitives to their original dynamical family in this region could therefore
be a quite interesting and important task. For this purpose we introduce a regularization procedure that allows us to extend families in regions where the behavior of the g frequency
is not linear as a function of n. Our method allows us to identify as family members objects that drifted in the
g+g5-2g6 and
2g+g5-3g6 and that were not recognizable with other approaches.
Finally, we consider the case of resonant asteroids, characterized by a retrograde frequency of pericenter precession g, such as the Hildas and some of the members of the Hansa family.
Our results show that it is possible to extend the family determination method in the
frequency space to regions that were not covered by the Carruba & Michtchenko (2007) approach, while preserving all the advantages of this method. We will start by introducing numerical tools that will be useful to classify the nonlinear secular resonance that we are studying and to quantify the efficiency of our methods in identifying as family members objects that drifted in non linear secular resonances.
2 Families interacting with nonlinear secular resonances of arguments other than g + s
In this section we will discuss the case of families interacting with nonlinear secular resonances of argument other than g+s. Secular resonances involve commensurabilities between the
secular frequencies of precession of the pericenter g or of the node s of the asteroid and of the planets. Linear secular resonances are direct equalities between the frequency of the asteroid and that of the planet. Very strong linear resonances of order 2 are the pericenter
resonances
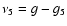 ,
,
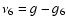 ,
and
,
and
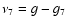 ,
and the node resonances
,
and the node resonances
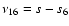 ,
,
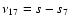 (Williams & Faulkner 1981; Milani & Knezevic 1994). Nonlinear secular resonances are commensurabilities of secular frequencies of higher order. The most accurate way to represent these resonances is in term of combinations of the linear resonances, so that the
2(g-g6)+s-s6 resonant argument (or z2, in the notation
of Milani & Knezevic 1994) becomes
(Williams & Faulkner 1981; Milani & Knezevic 1994). Nonlinear secular resonances are commensurabilities of secular frequencies of higher order. The most accurate way to represent these resonances is in term of combinations of the linear resonances, so that the
2(g-g6)+s-s6 resonant argument (or z2, in the notation
of Milani & Knezevic 1994) becomes
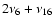 ,
or that
2g+g5-3g6 becomes
,
or that
2g+g5-3g6 becomes
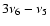 (Michtchenko et al. 2008). Expressed in these terms, it becomes
clearer why some resonances such as the z2 have a stronger dynamical effect than other resonances of the same order that are higher order combination of the linear secular resonances.
In this paper, however, we are interested in identifying families in the space of proper frequencies, and for this purpose it is easier to classify families in terms of the g and s frequencies. We will therefore still first give the name of the resonance as a function
of g and s, and then provide the classification in terms of the linear resonances.
(Michtchenko et al. 2008). Expressed in these terms, it becomes
clearer why some resonances such as the z2 have a stronger dynamical effect than other resonances of the same order that are higher order combination of the linear secular resonances.
In this paper, however, we are interested in identifying families in the space of proper frequencies, and for this purpose it is easier to classify families in terms of the g and s frequencies. We will therefore still first give the name of the resonance as a function
of g and s, and then provide the classification in terms of the linear resonances.
For the purpose of family identification, as in Carruba & Michtchenko (2007), we used a catalog of 172 043 synthetic proper elements and frequencies obtained numerically and publically available at the AstDys site, accessed on May 25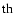 2008. Families in the domain of proper elements are obtained with the standard metric of Zappalà et al. (1990, 1995), while families in the domain of proper frequencies were mostly obtained with the standard metric in the (n,g,g+s) domain (Carruba & Michtchenko 2007, Eq. (3)). To obtain families interacting with resonances of argument other than g+s we introduced a series of alternative distance metric in the
(n,g,2g+s),
(n,g,3g+s), (n,g,g-s), (n,g,s), (n,g,2s) domains.
2008. Families in the domain of proper elements are obtained with the standard metric of Zappalà et al. (1990, 1995), while families in the domain of proper frequencies were mostly obtained with the standard metric in the (n,g,g+s) domain (Carruba & Michtchenko 2007, Eq. (3)). To obtain families interacting with resonances of argument other than g+s we introduced a series of alternative distance metric in the
(n,g,2g+s),
(n,g,3g+s), (n,g,g-s), (n,g,s), (n,g,2s) domains.
To compare the efficiency with which the new distance metrics connect objects in the nonlinear secular resonances with respect to the previous methods we introduce the following procedure.
- 1.
- We delimit a local background around the asteroid families under study. Morbidelli et al. (2003) define the local background limits via these equations:
where the minimal and maximal values of i, q (pericenter distance), and a refer to the observed extreme values of the asteroid families. Table 3
reports the values of a, e, and 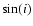 for the families that we studied in this paper. We defined the minimal and maximal value of e as the extreme values in the sample obtained with
Eqs. (1)-(3).
for the families that we studied in this paper. We defined the minimal and maximal value of e as the extreme values in the sample obtained with
Eqs. (1)-(3).
- 2.
- We computed the number of objects in the local background currently inside the resonance of interest. We define the efficiency of our metrics in connecting these object to the family
as the fraction of family members inside the resonance compared to the total number of object in the resonance in the local background.
We will discuss the efficiency of the new distance metrics in more detail in each of the next subsections. Here we just want to clarify that, by efficiency of our distance metrics,
we just intend the ability of the new metrics to connect objects inside secular resonances
to the asteroid family under study. As discussed in the first paper, the potential membership in a family of the asteroid so identified needs to be confirmed by an analysis of its size, and spectral type. Also the actual possibility of migration on timescales comparable to the estimated age of the family needs to be tested via numerical integration.
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{9852fi1a.eps}\hspace*{2.8c...
...ps}\hspace*{2.8cm}
\includegraphics[width=6.3cm,clip]{9852fi1d.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg24.gif) |
Figure 1:
A (g,2g+s) projection of the classical Erigone family (green
circles and of the family obtained with the ``standard'' frequency metric (red crosses, panel A)), and the
(n,g,2g+s) metric of Eq. (4) (red crosses, panel B)). Panels C) and D) display an
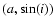 projection of the same families, superimposed to a color and contour plot of the projection of the same families, superimposed to a color and contour plot of the 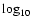 of asteroid number in the local background per unit bin.
of asteroid number in the local background per unit bin. |
| Open with DEXTER |
Finally, previous works (Zappalà et al. 1990, 1995) displayed (a,e),
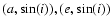 ,
projections of asteroids in the local background of asteroid families. The number of asteroids in these projections furnished information on the local density
of asteroids, and, indirectly, on the local dynamics (regions dynamically unstable because of the effect of mean-motion or secular resonances appeared locally deprieved of asteroids). The number of objects with known proper elements has however improved dramatically since the 90's, and directly plotting the position of asteroids in the local background may result in figures visually saturated. To overcome this problem and to quantitatively determine the local density of asteroids
in the local background we computed the number of asteroids in grids of proper elements and frequencies. Following the approach of Michtchenko et al. (2008), we used steps of 0.008 AU in a, 0.008 in e, and 0.008 in
,
projections of asteroids in the local background of asteroid families. The number of asteroids in these projections furnished information on the local density
of asteroids, and, indirectly, on the local dynamics (regions dynamically unstable because of the effect of mean-motion or secular resonances appeared locally deprieved of asteroids). The number of objects with known proper elements has however improved dramatically since the 90's, and directly plotting the position of asteroids in the local background may result in figures visually saturated. To overcome this problem and to quantitatively determine the local density of asteroids
in the local background we computed the number of asteroids in grids of proper elements and frequencies. Following the approach of Michtchenko et al. (2008), we used steps of 0.008 AU in a, 0.008 in e, and 0.008 in 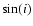 .
To eliminate the problems associated with projecting three-dimensional structure in 2D planes, binning and other effects that may introduce distortions in the density maps we also applied a median filter (Carruba et al. 2004, Appendix 1) to the density maps so obtained. The procedure was repeated until the percentage difference between the number of asteroids before and after the application of the median filter was less than 5%.
We then plotted the color plot of the
.
To eliminate the problems associated with projecting three-dimensional structure in 2D planes, binning and other effects that may introduce distortions in the density maps we also applied a median filter (Carruba et al. 2004, Appendix 1) to the density maps so obtained. The procedure was repeated until the percentage difference between the number of asteroids before and after the application of the median filter was less than 5%.
We then plotted the color plot of the 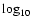 of the number of asteroids per unit bin in
the interval (0, 2.5) in each of the figures where we projected the asteroid families.
We believe that this method allow us to keep the benefits of the old projection method of Zappalà et al. (1995), but extended for the much more numerous database of proper elements currently available.
of the number of asteroids per unit bin in
the interval (0, 2.5) in each of the figures where we projected the asteroid families.
We believe that this method allow us to keep the benefits of the old projection method of Zappalà et al. (1995), but extended for the much more numerous database of proper elements currently available.
Having introduced these tools, we start our discussion by considering families interacting with resonances of argument 2g+s (z2-resonances).
2.1 2g + s resonances
The series of the zk (or
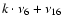 ,
where k is a small integer) resonances and its interaction with the Yarkovsky and YORP effects has been the subject of several recent
studies (Vokrouhlický et al. 2006a,b,c; Carruba et al. 2005, 2007, among others). In Carruba & Michtechenko (2007) we concentrated our attention on the z1 resonance (and its harmonics involving the g7 frequency), of argument g+s. Here we extend our work by analyzing families that interact with the z2 and z3 (see next section) resonance. The z2 and z3 resonances are found in regions near the powerful linear resonance
,
where k is a small integer) resonances and its interaction with the Yarkovsky and YORP effects has been the subject of several recent
studies (Vokrouhlický et al. 2006a,b,c; Carruba et al. 2005, 2007, among others). In Carruba & Michtechenko (2007) we concentrated our attention on the z1 resonance (and its harmonics involving the g7 frequency), of argument g+s. Here we extend our work by analyzing families that interact with the z2 and z3 (see next section) resonance. The z2 and z3 resonances are found in regions near the powerful linear resonance 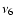 .
In particular, the higher the value of k, the nearer in proper element and frequency domain the resonance is to the
.
In particular, the higher the value of k, the nearer in proper element and frequency domain the resonance is to the 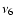 .
For k > 3 the zk resonances overlap with the
.
For k > 3 the zk resonances overlap with the 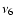 ,
and have no significant dynamical effect of their own (Michtchenko et al. 2008), that is why we do not consider z4 and higher order resonances in this work.
,
and have no significant dynamical effect of their own (Michtchenko et al. 2008), that is why we do not consider z4 and higher order resonances in this work.
Since the work of Milani & Knezevic (1994) it is known that the old Flora family (current Baptistina and Belgica families, and other clumps in the region, Mothé-Diniz et al. 2005) strongly interacts with the z2, and marginally interacts with the z3 resonances. The former Flora family was therefore a very good candidate for an analysis in the frequency domain for what concerns these two resonances. Unfortunately, the region of Flora is characterized by a very high density of asteroids and secular resonances (Michtchenko et al. 2008), which makes an analysis of families in the frequency domain quite difficult (we will return on this subject in Sect. 2.4). Families found in the frequency domain in this region may very quickly converge with the local background, providing very little dynamical information.
To avoid the problems associated with the Flora region we turned our attention to another family strongly interacting with the z2 secular resonance, (163) Erigone. This family has been the subject of a recent study of Vokrouhlický et al. (2006a). Based on results of Monte Carlo simulation of the Yarkovsky and YORP diffusion of family members in semimajor axis,
Vokrouhlický et al. (2006a) estimated the age of the family in 240 Myr, with a 40% uncertainty. The central region of the family is crossed by the z2 resonance, and its right border in the
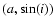 plane is defined by the
4J:-2S:-1A three-body resonance.
plane is defined by the
4J:-2S:-1A three-body resonance.
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{9852fi2a.eps}\hspace*{2.8c...
...ps}\hspace*{2.8cm}
\includegraphics[width=6.3cm,clip]{9852fi2d.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg28.gif) |
Figure 2:
A (g,3g+s) projection of the classical Elektra clump (green
circles and of the family obtained with the ``standard'' frequency metric (red crosses, panel A)), and the
(n,g,3g+s) metric of Eq. (5) (red crosses, panel B)). Panels C) and D) display an
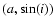 projection of the same families, superimposed
to a color and contour plot of the projection of the same families, superimposed
to a color and contour plot of the 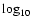 of asteroid number in the local background per unit bin.
of asteroid number in the local background per unit bin. |
| Open with DEXTER |
We determined the family using the CHCM and found that at a cutoff of 68 m/s (for larger values the family expands beyond the
4J:-2S:-1A resonance) 5.0% of its members (33 bodies out of 658 members) are inside the resonance. To best represent asteroids that drifted in the z2 resonance, we introduce a (g,2g+s) representative plane and we determined the family in the frequency space with a metric of the form:
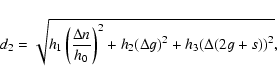 |
(4) |
(where h0 is a normalization factor of dimension 1 degree/'',
h1 = h2 = h3 = 1; 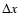 ,
with
x = n, g, 2g+s, represents the difference in x between two neighboring asteroids). We
determined the family in frequency space with the FHCM and with the metric of
Eq. (4), and found that the family is best defined at a cutoff of 0.181''/yr and 0.176''/yr, respectively. Figure 1 displays the (g,2g+s) projection of the two families (panels A and B). The thicker horizontal line shows the location
of the z2 resonance. Panels C and D of Fig. 1 display an
,
with
x = n, g, 2g+s, represents the difference in x between two neighboring asteroids). We
determined the family in frequency space with the FHCM and with the metric of
Eq. (4), and found that the family is best defined at a cutoff of 0.181''/yr and 0.176''/yr, respectively. Figure 1 displays the (g,2g+s) projection of the two families (panels A and B). The thicker horizontal line shows the location
of the z2 resonance. Panels C and D of Fig. 1 display an
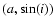 projection of the two families, superimposed with a color plot of the
projection of the two families, superimposed with a color plot of the 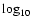 of the number of asteroids per unit bin in the local background, filtered five times with the
median filter of Sect. 2. The thick blue line displays the location of the center of the z2 resonance in the
of the number of asteroids per unit bin in the local background, filtered five times with the
median filter of Sect. 2. The thick blue line displays the location of the center of the z2 resonance in the
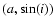 plane calculated with the analytical approach
of Milani & Knezevic (1994), in the
plane calculated with the analytical approach
of Milani & Knezevic (1994), in the
 interval covered by the family
local background and for the mean value of eccentricity of the Erigone family (see Carruba et al. 2005, for a discussion of the limits of this approach, that it is used here only for illustrative purposes). In the local background of the classical Erigone family 2192 objects are currently inside the z2 resonance. This large number of objects is caused by the fact that the local background
of Erigone include the high density region of the former Flora family. Of these objects, 49 (2.2%
of the total) were identified as family members by the standard metric, while 73 (3.3% of the total, 50% more than the metric in the (n,g,g+s) domain) were identified by the
2g+s metric of Eq. (4).
interval covered by the family
local background and for the mean value of eccentricity of the Erigone family (see Carruba et al. 2005, for a discussion of the limits of this approach, that it is used here only for illustrative purposes). In the local background of the classical Erigone family 2192 objects are currently inside the z2 resonance. This large number of objects is caused by the fact that the local background
of Erigone include the high density region of the former Flora family. Of these objects, 49 (2.2%
of the total) were identified as family members by the standard metric, while 73 (3.3% of the total, 50% more than the metric in the (n,g,g+s) domain) were identified by the
2g+s metric of Eq. (4).
![\begin{figure}
\par\includegraphics[width=6.2cm,clip]{9852fi3a.eps}\hspace*{2.8c...
...ps}\hspace*{2.8cm}
\includegraphics[width=6.2cm,clip]{9852fi3d.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg32.gif) |
Figure 3:
A (g,g-s) projection of the classical Phocaea family (green
circles and of the family obtained with the ``standard'' frequency metric (red crosses, panel A)), and the (n,g,g-s) metric of Eq. (6) (red crosses, panel B)). Panels C) and D) display an
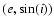 projection of the same families, superimposed
to a color and contour plot of the projection of the same families, superimposed
to a color and contour plot of the 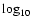 of asteroid number in the local background per unit bin.
of asteroid number in the local background per unit bin. |
| Open with DEXTER |
Note how both the frequency and classical families interact with the pericenter resonance
of argument
2g-3g6+g5 (
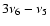 in the notation of Michtchenko et al. 2008, approximately located at a = 2.345 AU), and its harmonics involving the g7 frequency.
The metric in the (n,g,g+s) domain more efficiently identifies objects that drifted in the
4J:-2S:-1A resonance (for a discussion of the mechanism with which such metric identifies objects drifting in mean-motion resonance see Sect. 3.1), but the metric in the
(n,g,2g+s) domain identifies more than 50% more objects that drifted in the z2 secular resonance and depleted the central region of the Erigone family. We believe that the interplay of the Yarkovsky and YORP effect with the z2 resonance could explain part of the lower density of objects observed in the central region of the Erigone family.
in the notation of Michtchenko et al. 2008, approximately located at a = 2.345 AU), and its harmonics involving the g7 frequency.
The metric in the (n,g,g+s) domain more efficiently identifies objects that drifted in the
4J:-2S:-1A resonance (for a discussion of the mechanism with which such metric identifies objects drifting in mean-motion resonance see Sect. 3.1), but the metric in the
(n,g,2g+s) domain identifies more than 50% more objects that drifted in the z2 secular resonance and depleted the central region of the Erigone family. We believe that the interplay of the Yarkovsky and YORP effect with the z2 resonance could explain part of the lower density of objects observed in the central region of the Erigone family.
We summarized the results that we obtained in this section in Table 4.
In view of its higher efficiency, we believe that the metric of Eq. (4) could be an useful tool to study the diffusion of family members in the z2 secular resonance.
2.2 3g + s resonances
The z3 secular resonance occurs in regions very close in the proper element and frequency domains to the 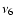 .
Apart from clumps in the former Flora family region, which are quite difficult to
analyze for reasons discussed in Sect. 2.1, we found a clump that is characterized by its interaction with the z3 resonance: (130) Elektra. We determined the clump and found that it is best defined at a cutoff of 233 m/s. We then introduce a distance metric most apt to find neighbors inside the z3 resonance, which has the form:
.
Apart from clumps in the former Flora family region, which are quite difficult to
analyze for reasons discussed in Sect. 2.1, we found a clump that is characterized by its interaction with the z3 resonance: (130) Elektra. We determined the clump and found that it is best defined at a cutoff of 233 m/s. We then introduce a distance metric most apt to find neighbors inside the z3 resonance, which has the form:
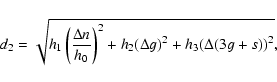 |
(5) |
(where
h1 = h2 = h3 = 1). With the FHCM the clump was defined at a cutoff of 0.1365''/yr, while with the distance metric of Eq. (5) the clump was found with a cutoff of 1.22''/yr. Figure 2 displays the (g,3g+s) projection of the two families, with the ticker horizontal line showing the location of the z3 resonance (note that (130) Elektra itself is currently inside the resonance). Other lines display the location of nonlinear secular resonance up to order eight (we plotted resonances up to this order to be consistent with the order of the z3 resonance). Panels C and D of Fig. 2
display an
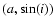 projection of the two frequency families, superimposed with a color plot of the
projection of the two frequency families, superimposed with a color plot of the 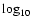 of the number of asteroids per unit bin in the local background, filtered twice with the median filter. Since the Elektra clump is in a region with much lower density of asteroids than the other families that we are studying (with the exception of the Phocaea family), here we use a smaller range of values for the
of the number of asteroids per unit bin in the local background, filtered twice with the median filter. Since the Elektra clump is in a region with much lower density of asteroids than the other families that we are studying (with the exception of the Phocaea family), here we use a smaller range of values for the 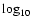 of the number of asteroids per unit bin ([0, 1.5] with respect to the [0, 2.5] range used in the other cases). The thick blue line displays the location of the z3 resonance in the
of the number of asteroids per unit bin ([0, 1.5] with respect to the [0, 2.5] range used in the other cases). The thick blue line displays the location of the z3 resonance in the
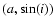 plane computed with the same method of Sect. 2.1. Note how the clump obtained with the metric of Eq. (5) follows the center of the z3 resonance (the location of the resonance center displayed in the figure is approximated and subject to the limitation of the analytical approach of Milani & Knezevic 1994 near the
plane computed with the same method of Sect. 2.1. Note how the clump obtained with the metric of Eq. (5) follows the center of the z3 resonance (the location of the resonance center displayed in the figure is approximated and subject to the limitation of the analytical approach of Milani & Knezevic 1994 near the 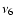 resonance; Carruba et al. 2005). In the local background of the Elektra clump 1755 objects are currently inside the z3 resonance. Of these, 39 (2.2%) were idenitified with the CHCM, 85 (4.8%) with the FHCM, and 137 (7.8%) with the distance metric of Eq. (5). Results are summarized in Table 4. In view of this results, we believe that the the distance metric of Eq. (5) could be an useful tool to study diffusion of family members in the z3 secular resonance.
resonance; Carruba et al. 2005). In the local background of the Elektra clump 1755 objects are currently inside the z3 resonance. Of these, 39 (2.2%) were idenitified with the CHCM, 85 (4.8%) with the FHCM, and 137 (7.8%) with the distance metric of Eq. (5). Results are summarized in Table 4. In view of this results, we believe that the the distance metric of Eq. (5) could be an useful tool to study diffusion of family members in the z3 secular resonance.
2.3 g - s resonances
The Phocaea asteroid family is a group of asteroids with a semi-major axis less than that of the 3:1 mean-motion resonance with Jupiter, a large inclination and a quite large eccentricity. It is also characterized by its interaction with the
g-s-g6+s6 resonance, or
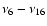 (Knezevic & Milani 2003). We determined the family using the CHCM, and found
that at a cutoff of 134 m/s (for larger values of the cutoff the family merges with other families
in the region such as Wood & Krylov (Gil-Hutton 2006), 16.4% of its members (96 bodies of 584 members) are inside the resonance. In view of its strong interaction with a g-s secular resonance, we thought that the Phocaea family could be best represented in a (g,g-s) plane, and determined it in the frequency space with a metric of the form:
(Knezevic & Milani 2003). We determined the family using the CHCM, and found
that at a cutoff of 134 m/s (for larger values of the cutoff the family merges with other families
in the region such as Wood & Krylov (Gil-Hutton 2006), 16.4% of its members (96 bodies of 584 members) are inside the resonance. In view of its strong interaction with a g-s secular resonance, we thought that the Phocaea family could be best represented in a (g,g-s) plane, and determined it in the frequency space with a metric of the form:
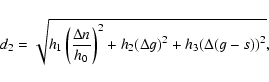 |
(6) |
(where
h1 = h2 = h3 = 1) rather than with the ``standard frequency metric'' of Carruba
& Michtchenko (2007). To test this hypothesis, we determined the family in the frequency space with both approaches. We found that the Phocaea family is best defined at a cutoff of 0.52''/yr with the standard frequency metric, and at 0.595''/yr with the metric of Eq. (6). Figure 3 displays the (g,g-s) projection of the two families (panels A and B, respectively). The thicker horizontal line shows the location of the
g-s+g6-s6 resonance, while the other horizontal lines display harmonics of the same resonance involving combinations of the g5 and g7 frequencies. For reference, an
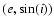 projection of the two family is also displayed in Fig. 3, panels C and D,
superimposed with contour and color plot of the
projection of the two family is also displayed in Fig. 3, panels C and D,
superimposed with contour and color plot of the 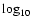 of the number of asteroids per unit bin in the local background, filtered twice with the median filter. As for the case of the Elektra clump, here we use the smaller [0, 1.5] range for the values of the
of the number of asteroids per unit bin in the local background, filtered twice with the median filter. As for the case of the Elektra clump, here we use the smaller [0, 1.5] range for the values of the 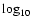 of the number of asteroids per unit bin in the local background. The blue line displays the location of the center of the
of the number of asteroids per unit bin in the local background. The blue line displays the location of the center of the
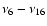 resonance computed with the analytical approach of Milani & Knezevic (1994). Note how the Phocaea family is surrounded by regions with very
little density of asteroids or none. The lack of bodies around the Phocaea family region is caused by the presence of the strong
7J::-2A mean-motion resonance with Jupiter, and by the
resonance computed with the analytical approach of Milani & Knezevic (1994). Note how the Phocaea family is surrounded by regions with very
little density of asteroids or none. The lack of bodies around the Phocaea family region is caused by the presence of the strong
7J::-2A mean-motion resonance with Jupiter, and by the 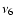 ,
,
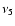 ,
and
,
and
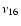 secular resonances (Knezevic & Milani 2003).
secular resonances (Knezevic & Milani 2003).
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{9852fi4a.eps}\hspace*{2.8c...
...ps}\hspace*{2.8cm}
\includegraphics[width=6.3cm,clip]{9852fi4d.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg38.gif) |
Figure 4:
The number of Baptistina members (in blue, left ordinate) and the differential number of family members (in green, right ordinate) as a function of the cutoffs, for the family found with the metric of proper elements (panel A)), the metric in the (n,g,g+s) space (panel B)), the metric of proper elements and frequencies (panel C)), and the metric in the (n,g,s) domain. |
| Open with DEXTER |
In the local background of the classical Phocaea family 279 objects are currently inside the
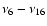 resonance. Of these 96 (34.4% of the total) were identified as family members by the standard frequency metric, while 133 (47.7% of the total) were identified
by the g-s metric of Eq. (6). Note how the standard metric obtained the same number of objects in the g-s resonance than the classical approach, while the metric of Eq. (6) connected 38.5% more objects than both other methods.
We summarized these results in Table 4. In view of this, we believe that the metric of Eq. (6) could be considered a useful tool to study diffusion in g-s secular resonances.
resonance. Of these 96 (34.4% of the total) were identified as family members by the standard frequency metric, while 133 (47.7% of the total) were identified
by the g-s metric of Eq. (6). Note how the standard metric obtained the same number of objects in the g-s resonance than the classical approach, while the metric of Eq. (6) connected 38.5% more objects than both other methods.
We summarized these results in Table 4. In view of this, we believe that the metric of Eq. (6) could be considered a useful tool to study diffusion in g-s secular resonances.
2.4 s resonances
The Baptistina family has been the subject of a recent study by Bottke et al. (2007) where the authors suggested that the Chixculub impactor that produced the Cretaceous/Tertiary (K/T) mass extinction event 65 Myr ago could have been a past member of the family that interacted
with the
7J:-2A mean-motion resonance with Jupiter.
From the point of view of family determination, the Baptistina family is also a very interesting one. The Baptistina family is in the proximity of the powerful 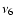 secular resonance and
it is crossed by the
secular resonance and
it is crossed by the
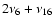 (or z2, as in the notation of Milani & Knezevic 1994
(or z2, as in the notation of Milani & Knezevic 1994![[*]](/icons/foot_motif.gif) ) secular resonance, which would make this family an ideal candidate for the use of the metric of Eq. (4). Unfortunately this
family is in the region of the former Flora family which is characterized by a quite large density of asteroids and a by a dense web of secular and mean-motion resonances, many involving martian
frequencies (Michtchenko et al. 2008), that make an analysis in the frequency domain quite difficult. Our analysis of the Baptistina family and other clumps formerly associated with the Flora family such as (219) Thusnelda, (650) Amalasuntha, (883) Matterania, and others with the FCHM and the metrics of Eqs. (4) and (5) display a typical behavior: the families connect to a few objects for small values of the frequency cutoff and then rapidly merge with the local background.
) secular resonance, which would make this family an ideal candidate for the use of the metric of Eq. (4). Unfortunately this
family is in the region of the former Flora family which is characterized by a quite large density of asteroids and a by a dense web of secular and mean-motion resonances, many involving martian
frequencies (Michtchenko et al. 2008), that make an analysis in the frequency domain quite difficult. Our analysis of the Baptistina family and other clumps formerly associated with the Flora family such as (219) Thusnelda, (650) Amalasuntha, (883) Matterania, and others with the FCHM and the metrics of Eqs. (4) and (5) display a typical behavior: the families connect to a few objects for small values of the frequency cutoff and then rapidly merge with the local background.
An example of this is given in Fig. 4 for the Baptistina family. If we determine the Baptistina family with the classical approach, it is defined for a velocity cutoff of 52 m/s (for larger values of the cutoff the families merges with other known clumps in the region), and the family has 973 members (Fig. 4, panel A, the left ordinate display the number of family members and the right ordinate the differencial number
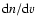 as a function of the cutoff). Note that the family rapidly increases in sizes for slightly larger values of the cutoff, and merges with the local background for a cutoff of 64 m/s. This problem is more dramatic if we use the frequency approach of Carruba & Michtchenko (2007): for a cutoff of less than 0.120''/yr the family has only 30 members, while it merges with the local background for larger values of the cutoff (Fig. 4, panel B).
as a function of the cutoff). Note that the family rapidly increases in sizes for slightly larger values of the cutoff, and merges with the local background for a cutoff of 64 m/s. This problem is more dramatic if we use the frequency approach of Carruba & Michtchenko (2007): for a cutoff of less than 0.120''/yr the family has only 30 members, while it merges with the local background for larger values of the cutoff (Fig. 4, panel B).
Quite simply, it is not possible to obtain significant information about the dynamical evolution of the Baptistina family by using the FHCM. A natural question that arises is why the family can be determined in the proper element, but not in the frequency domain. To answer this question we study the dynamics in the region of the family. The Baptistina family is crossed by the
7J:-2A mean-motion resonance with Jupiter. For values of proper a smaller than that of the resonance, there is a region with a relatively high density of asteroids, all at relatively low distances in the (g+s) dimension and having lower values of 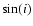 than those of the classical Baptistina
family members. For values of the frequency cutoff lower than 0.120''/yr the family in the frequency domain is confined to right side of the
7J:-2A in the
than those of the classical Baptistina
family members. For values of the frequency cutoff lower than 0.120''/yr the family in the frequency domain is confined to right side of the
7J:-2A in the
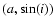 plane. As soon as the frequency cutoff is increased, the family passes the barrier in frequency space presented by the
7J:-2A resonances and rapidly merge with the conspicuous population of low-inclination
objects, jumping to 11 741 family members.
plane. As soon as the frequency cutoff is increased, the family passes the barrier in frequency space presented by the
7J:-2A resonances and rapidly merge with the conspicuous population of low-inclination
objects, jumping to 11 741 family members.
To further confirm this hypothesis, we performed the following numerical experiment: we computed the average value of distances in the g, s and (g+s) spaces between each member of the Baptistina classical family and its neighbor in a radius of 150 m/s in the space of proper elements.
In Fig. 5 we plotted the results as a function of the proper n of family members. As can be seen in the figure, changes in proper g and s follow a U-shaped curve with respect to the n-frequency (the actual dependence is inverse for the s frequency with respect to the g frequency, in the figure we plotted the absolute values of changes), while changes in the g+s are very flat, with the exception of the region near the
7J:-2A resonances where they diverge. This may explain why the Baptistina family in the (n,g,g+s) frequency space was not well-determined. Since distances in the (g+s) space are very weakly dependent on n, and a significant increase in the cutoff is needed to pass the
7J:-2A frequency barrier, small changes in the cutoff after the barrier is passed lead to connect to the vast numbers of objects at low-i, as observed. Similar problems are observed not only for Baptistina, but also for other families and clumps in the region of the former Flora family, such as Thusnelda, Amalasuntha, and Matterania, among others.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9852fig5.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg40.gif) |
Figure 5:
The average values of changes in proper g, s, (g+s)for asteroids to within 150 m/s of the central body, as a function of the body's n, for the members of the classical Baptistina family. Vertical lines display the position of the
7J:-2A mean-motion resonance with Jupiter. |
| Open with DEXTER |
While the FHCM is not very useful in this part of the belt, significant dynamical information can still be obtained using different approaches. One possibility is to use the metric of proper elements and frequencies introduced in Carruba & Michtchenko (2007), Eq. (11). Figure 4, panel C, displays the number of family members obtained with this method as a function of the velocity cutoff. This method allows us to cross the barrier represented by the
7J:-2A mean-motion resonance without creating giant families, but at the cost of partially losing information on family members that migrated in local secular resonances because of the Yarkovsky and YORP effects. Another possible approach could be to use a different metric in frequency space. Rather than to look in the (n,g,g+s) space, we look for the Baptistina family in the (n,g,s) domain. Distances in s as a function of n are less flat than distances in g+s; families obtained in the (n,g,s) domain should therefore be more numerous as a function of the frequency cutoff than families obtained in the (n,g,g+s) domain. We therefore introduce
a metric of the form:
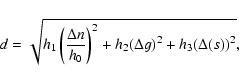 |
(7) |
where
h1 = h2 = h3 = 1. We used this metric for determining the Baptistina family and we found that the family is well defined by a cutoff of 0.113''/yr, and contains 1597 family members at this cutoff (Fig. 4, panel D). Larger values of the cutoff results in families that conglomerate vast populations of low-i asteroids, and the family itself coalesces with the background for a cutoff of 0.127''/yr.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{9852fi6a.eps}\hspace*{1.5cm}
\includegraphics[width=7.2cm,clip]{9852fi6b.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg42.gif) |
Figure 6:
A (g,|s|) projection of the classical Baptistina family (green circles) and of the family obtained with the (n,g,s) metric of Eq. (7) (red crosses, panel A)). Panel B) displays an
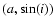 projection of the same families, superimposed to a color and contour plot of the projection of the same families, superimposed to a color and contour plot of the 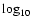 of the asteroid number in the local background per unit bin.
of the asteroid number in the local background per unit bin. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{9852fi7a.eps}\hspace*{2.8c...
...ps}\hspace*{2.8cm}
\includegraphics[width=6.5cm,clip]{9852fi7d.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg43.gif) |
Figure 7:
A (g,2s) projection of the classical Vesta family (green
circles and of the family obtained with the ``standard'' frequency metric (red crosses, panel A)), and the (n,g,2s) metric of Eq. (8) (red crosses, panel B)). Panels C) and D) display an
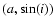 projection of the same families, superimposed
to a color and contour plot of the projection of the same families, superimposed
to a color and contour plot of the 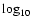 of asteroid number in the local background per unit bin.
of asteroid number in the local background per unit bin. |
| Open with DEXTER |
In Fig. 6 we show a (g,|s|) (panel A, we use the absolute value of s for illustrative purposes) and
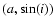 (panel B) projections of the Baptistina family obtained with CHCM and the distance metric of Eq. (7). Superimposed to the the
(panel B) projections of the Baptistina family obtained with CHCM and the distance metric of Eq. (7). Superimposed to the the
 projection there is a color plot of the
projection there is a color plot of the 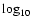 of the number of asteroids
per unit bin in the local background, filtered three times with the median filter. While for the value of the cutoff that was used we were not able to cross the
7J:-2A barrier, the method offered some considerable advantage. In particular, we identified tails of asteroids that possibly
drifted in local node secular resonances (involving martian frequencies) such as the
of the number of asteroids
per unit bin in the local background, filtered three times with the median filter. While for the value of the cutoff that was used we were not able to cross the
7J:-2A barrier, the method offered some considerable advantage. In particular, we identified tails of asteroids that possibly
drifted in local node secular resonances (involving martian frequencies) such as the
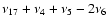 (
(s-s7) -g5 +2g6-g4) resonance and harmonics involving the g7 frequency. The thick blue line in Fig. 6, panel B, displays the location of this resonance in the
(
(s-s7) -g5 +2g6-g4) resonance and harmonics involving the g7 frequency. The thick blue line in Fig. 6, panel B, displays the location of this resonance in the
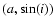 plane computed with the same method of
Sect. 2.1.
plane computed with the same method of
Sect. 2.1.
In the local background of the classical Baptistina family 3130 objects are currently inside the
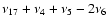 .
Of these, the CHCM identified 36 objects (1.2%) as family members, while the (n,g,s) metric of Eq. (7) identified 163 objects (5.2%). Results are summarized in Table 4. We believe that, considering the limitations imposed by the high density of asteroids and secular resonances in the former Flora family region, the metric of Eq. (7) was able to provide significant dynamical information on former Baptistina family members.
.
Of these, the CHCM identified 36 objects (1.2%) as family members, while the (n,g,s) metric of Eq. (7) identified 163 objects (5.2%). Results are summarized in Table 4. We believe that, considering the limitations imposed by the high density of asteroids and secular resonances in the former Flora family region, the metric of Eq. (7) was able to provide significant dynamical information on former Baptistina family members.
2.5 2s resonances
The Vesta family has been the subject of several recent studies (Carruba et al. 2005, 2007; Carruba & Michtchenko 2007; Nesvorný et al. 2008). From a mineralogical point of view, the Vesta family is interesting because most of its members (including (4) Vesta itself) present a V-type spectrum, which is characterized by a moderately steep red slope shortwards of 0.7 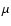 m and a deep
absorption band longwards of 0.75
m and a deep
absorption band longwards of 0.75 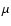 m. This kind of spectra is associated with a basaltic composition (Bus 2002; Duffard et al. 2004). From the point of view of family identification in frequency space the Vesta family is also a very interesting one. In this section we will concentrate on its interaction with a resonance of argument 2s, the
2s-3s6+s7 (
m. This kind of spectra is associated with a basaltic composition (Bus 2002; Duffard et al. 2004). From the point of view of family identification in frequency space the Vesta family is also a very interesting one. In this section we will concentrate on its interaction with a resonance of argument 2s, the
2s-3s6+s7 (
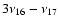 in the Michtchenko et al. 2008, notation). In Sect. 3.1 we will treat the effect that the proximity of the 3J:1A resonance has on the
values of the g frequencies.
in the Michtchenko et al. 2008, notation). In Sect. 3.1 we will treat the effect that the proximity of the 3J:1A resonance has on the
values of the g frequencies.
We start by analyzing the family with the CHCM. The family coalesces with the local background at a cutoff of 68 m/s, so we decided to use a cutoff in the proper element space of 62 m/s (the difference with the cutoff used in Carruba & Michtchenko 2007 is caused by the larger number of asteroids currently available in the synthetic proper element database). Since in this section we are interested in analyzing how the family interacts with the
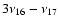 resonance, we represent the Vesta family in the (g,2s) and introduced a new distance metric
of the form:
resonance, we represent the Vesta family in the (g,2s) and introduced a new distance metric
of the form:
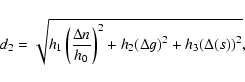 |
(8) |
(where
h1 = h2 = 1, h3 = 2). We determined the Vesta with the FHCM and the new distance metric. We found that the family is best defined at a cutoff of 0.115''/yr (again, the difference with the value of Carruba & Michtchenko 2007 is caused by the larger number of asteroids in the proper element database since the publication of that paper) in the (n.g,g+s) domain, and of 150''/yr in the (n,g,2s) domain. Figure 7 displays the (g,2s) projection of the two families (panels A and B, respectively). The thicker horizontal line shows the location of the
 resonance. The diverging behavior of the values of g for
resonance. The diverging behavior of the values of g for
 is caused by the perturbation of the g values induced by the proximity of the 3J:1A resonance. Techniques to study diffusion of asteroids in this regions will be discussed in Sect. 3.1. Panels C and D displays an
is caused by the perturbation of the g values induced by the proximity of the 3J:1A resonance. Techniques to study diffusion of asteroids in this regions will be discussed in Sect. 3.1. Panels C and D displays an
 projection of the two families, superimposed with color plot of the
projection of the two families, superimposed with color plot of the 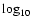 of the number of asteroids per unit bin in the local background, filtered three times with the median filter. The blue line displays the location of the
of the number of asteroids per unit bin in the local background, filtered three times with the median filter. The blue line displays the location of the
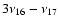 resonance computed with the analytical approach of Milani & Knezevic (1994).
resonance computed with the analytical approach of Milani & Knezevic (1994).
As can be seen in Fig. 7, panel D, the new distance metric was able to identify more objects that diffused from the Vesta family in the
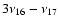 resonance than the other two approaches. In particular, in the local background of the Vesta family we found 1106 asteroids inside the
resonance than the other two approaches. In particular, in the local background of the Vesta family we found 1106 asteroids inside the
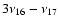 resonance. Of these, 143 (12.9% of the total) were identified with the classical approach, 145 (13.1%) were identified by the FHCM, and 251 (22.7%) by the distance metric of Eq. (8) (we summarize these results in Table 4). We believe therefore that the distance metric of Eq. (8) could be an useful tool to study diffusion of family members in 2s resonances.
resonance. Of these, 143 (12.9% of the total) were identified with the classical approach, 145 (13.1%) were identified by the FHCM, and 251 (22.7%) by the distance metric of Eq. (8) (we summarize these results in Table 4). We believe therefore that the distance metric of Eq. (8) could be an useful tool to study diffusion of family members in 2s resonances.
3 Families interacting with low-order mean-motion resonances
In the previous section we discussed the case of families interacting with nonlinear secular resonances, and we introduced new techniques to study the diffusion of family members in resonances of arguments other than g and g+s. In this section we focus our attention on families interacting with low-order mean-motion resonances such as the
2J:-1A,
3J:-1A, and
3J:-2A. Such resonances can affect asteroidal frequencies in two ways: i) the frequency of pericenter precession g of asteroids near the resonant border may not follow a linear trend as a function of n, as is the case for some of the members of the Vesta family; and ii) it may be negative (retrograde precession) for asteroids locked in resonant configuration, as for the Hildas
in the
3J:-2A and some members of the Hansa family which may be currently locked in the apocentric tail of the 3J:1A mean-motion resonance.
In this section we will study the problem of diffusion into secular resonances in regions affected by low-order mean-motion resonances. For this purpose, we will introduce new techniques
for regulazing the behavior of the g frequency as a function of n (Vesta family) and e (Hansa family). We will start with the case of the Vesta family.
3.1 Families close to the border of low-order mean-motion resonances:
the case of the Vesta family
The proximity of asteroids families to low-order mean-motion resonances may generate difficulties to the process of identifying asteroid families in the frequency domain. To study in more depth this
phenomenon we turn our attention to the Vesta family, whose determination is affected by two of the most typical problems in asteroid family identification. The Vesta family is crossed by the 1:2 mean-motion resonance with Mars (M1:2A hereafter) and its right border in proper a is quite close to the
3J:-1A resonance with Jupiter.
The M1:2A resonance results in a barrier in frequency space that does not allow to connect asteroids in opposite sides of the resonance until a critical value of the cutoff is reached.
Asteroids are connected to the family only for values of the frequency cutoff larger than 0.10''/yr, but lower than the critical value of 0.12''/yr, for which the family coalesces into the local background. In this case a value of the cutoff large enough to connect the family
beyond the M1:2A resonance but lower than the critical one existed. In other cases however, this might not be the case and mean-motion resonances may appear to act as a barrier for asteroid families found either in the frequency or in the element space.
Another effect of mean-motion resonances on family determination is that they significantly
spreads the observed dynamical family in the proper e and 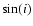 space. Figure 8
displays the behavior of the proper g (panel A) and g+s (panel B) frequencies as a function of n in the region of the 1/2 mean motion resonance with Mars (black dots). As can be seen in the figure, the procedure that generates synthetic proper elements gives values of proper n (or, equivalently, of proper a) located at the center of libration of the mean-motion resonance. As a consequence, objects inside the resonance all have very close values of proper a and n, and the differences
space. Figure 8
displays the behavior of the proper g (panel A) and g+s (panel B) frequencies as a function of n in the region of the 1/2 mean motion resonance with Mars (black dots). As can be seen in the figure, the procedure that generates synthetic proper elements gives values of proper n (or, equivalently, of proper a) located at the center of libration of the mean-motion resonance. As a consequence, objects inside the resonance all have very close values of proper a and n, and the differences 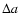 and
and 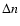 between two neighbors are limited. Asteroids are identified as family members in the frequency domain via the distance metric:
between two neighbors are limited. Asteroids are identified as family members in the frequency domain via the distance metric:
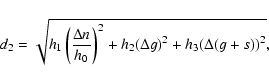 |
(9) |
where h0 is a normalization factor of dimension 1 degree/'', and the simplest choice for the
hi (i=1, 2, 3) weights is to take them all equal to 1 (Carruba & Michtchenko 2007). For the same value of the cutoff d2, therefore asteroids in the resonance can be neighbors in the frequency space for larger changes in proper g and g+s. That is the reason why our metric was able to connect to family objects with significant differences in proper e and 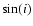 with
respect to the classical Vesta family (Fig. 15, panel B, Carruba & Michtchenko 2007)
with
respect to the classical Vesta family (Fig. 15, panel B, Carruba & Michtchenko 2007)![[*]](/icons/foot_motif.gif) : objects that are neighbors in the frequency domain may be relatively more distant in the proper element space, and viceversa. In particular, in the local background of the Vesta family there are 466 objects inside the M1:2A. Of these, 13 (2.8%) where identified as family members by the CHCM, while 23 (4.9%) where identified by the FHCM. The FHCM was 43.4% more efficient in connecting asteroids to the Vesta family than the CHCM.
: objects that are neighbors in the frequency domain may be relatively more distant in the proper element space, and viceversa. In particular, in the local background of the Vesta family there are 466 objects inside the M1:2A. Of these, 13 (2.8%) where identified as family members by the CHCM, while 23 (4.9%) where identified by the FHCM. The FHCM was 43.4% more efficient in connecting asteroids to the Vesta family than the CHCM.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9852fi8a.eps}\hspace*{1.5cm}
\includegraphics[width=7.5cm,clip]{9852fi8b.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg53.gif) |
Figure 8:
The dependence of proper g and proper g+s versus the proper n in the region of the M1:2A mean-motion resonance. The vertical lines display the borders of the M1:2A resonance. |
| Open with DEXTER |
The effect of the
3J:-1A mean-motion resonance with Jupiter on our method of asteroid family identification is subtler. As discussed in Carruba & Michtchenko (2007) the perturbing effect of the
3J:-1A mean-motion resonance on the g frequency does not allow us to connect asteroids in the proximity of this resonance to the rest of the dynamical family. This is shown in Fig. 9, panel A, where the green circles represent members of the classical
Vesta family, the red crosses members of the family obtained with the frequency method (Carruba & Michtchenko 2007), and the black dots all the asteroids having proper e and 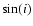 between the minimum and maximum values of the Vesta family. The horizontal green lines display the location of the strongest pericenter resonances in the region, and the vertical lines show the location of the
3J:-1A and M1:2A mean-motion resonances border.
between the minimum and maximum values of the Vesta family. The horizontal green lines display the location of the strongest pericenter resonances in the region, and the vertical lines show the location of the
3J:-1A and M1:2A mean-motion resonances border.
As can be seen in the figure, as soon as the g frequency starts to diverge from a linear behavior (this occurs roughly for n < 93.0 degrees/yr) the frequency metric is no longer able to connect
asteroids in the region with the rest of the dynamical family. A possible solution of this problem is to artificially extend the linear behavior of the g frequency as a function of n from the regular region to the perturbed region at n < 93.0 degrees/yr, so that asteroids in the proximity of the
3J:-1A resonance have assigned the value of the g frequency they should have had if the
3J:-1A resonance were not in the region. In this paper we call this procedure ``regularization''![[*]](/icons/foot_motif.gif) .
.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9852fi9a.eps}\hspace*{1.5cm}
\includegraphics[width=7.5cm,clip]{9852fi9b.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg54.gif) |
Figure 9:
Left panel: the behavior of proper g versus n in the region of the Vesta family. Black dots displays the (n,g) values of objects in the local background, as defined in Sect. 3.1, green circles refers to members of the classical family, and red crosses to members of the frequency family. Right panel: the regularized values of g as a function of n (red crosses), for s larger in the
interval [-45.00, -47.64]''/yr. |
| Open with DEXTER |
For this purpose, we selected asteroids in the synthetic proper element database in
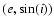 box near Vesta, defined by the maximum and minimum values of e and
box near Vesta, defined by the maximum and minimum values of e and 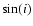 of members of the classical family plus or minus 0.01, and in the n interval between 91.4 degrees/yr (to avoid to include asteroids inside the
3J:-1A) and 96.5 degrees/yr (to avoid the perturbing effect of the
4J:-2S:-1A three-body resonance, which is just outside the range of n values
shown in Fig. 9). Asteroids in this range are shown as black dots in
Fig. 9, panel A. In order to regularize the behavior of asteroids with n < 93 degrees/yr (548 objects were found in this region in the
of members of the classical family plus or minus 0.01, and in the n interval between 91.4 degrees/yr (to avoid to include asteroids inside the
3J:-1A) and 96.5 degrees/yr (to avoid the perturbing effect of the
4J:-2S:-1A three-body resonance, which is just outside the range of n values
shown in Fig. 9). Asteroids in this range are shown as black dots in
Fig. 9, panel A. In order to regularize the behavior of asteroids with n < 93 degrees/yr (548 objects were found in this region in the
 box, in a range of s values between -47.64 and -42.89''/yr) we divided the asteroids in the Vesta family region in two samples characterized by values of s smaller than -45.0''/yr and larger than this value. This was done so as to have a sample of asteroids in both the perturbed and regular regions, such that the behavior of the perturbed asteroids could be simulated by the behavior of the regular ones in the same range of s values. We choose to use two intervals in order to have a
statistically significant number of members (#>100)
box, in a range of s values between -47.64 and -42.89''/yr) we divided the asteroids in the Vesta family region in two samples characterized by values of s smaller than -45.0''/yr and larger than this value. This was done so as to have a sample of asteroids in both the perturbed and regular regions, such that the behavior of the perturbed asteroids could be simulated by the behavior of the regular ones in the same range of s values. We choose to use two intervals in order to have a
statistically significant number of members (#>100)![[*]](/icons/foot_motif.gif) . Once the two set of asteroids were obtained, we first best-fitted
a line to the regular members in each s-interval, and a third-order polynomial curve in n for the g values of the corresponding asteroids in the perturbed region (higher order
polynomial were tried to simulate the perturbed region without significantly improving the accuracy of the fit; see the Appendix for an analysis of the errors on g caused by this procedure).
The values of the g frequencies of the asteroids in the perturbed region were finally regularized
by using the equation:
. Once the two set of asteroids were obtained, we first best-fitted
a line to the regular members in each s-interval, and a third-order polynomial curve in n for the g values of the corresponding asteroids in the perturbed region (higher order
polynomial were tried to simulate the perturbed region without significantly improving the accuracy of the fit; see the Appendix for an analysis of the errors on g caused by this procedure).
The values of the g frequencies of the asteroids in the perturbed region were finally regularized
by using the equation:
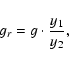 |
(10) |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{9852f10a.eps}\hspace*{2cm}
\includegraphics[width=7cm,clip]{9852f10b.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg56.gif) |
Figure 10:
An
 of the Vesta frequency family (red crosses, panel A)), of the regularized Vesta frequency family (red crosses, panel B)), and of the family obtained with the CHCM (green circles), in the region of the 3:1 mean-motion resonance. The thick blue lines display the location of the
of the Vesta frequency family (red crosses, panel A)), of the regularized Vesta frequency family (red crosses, panel B)), and of the family obtained with the CHCM (green circles), in the region of the 3:1 mean-motion resonance. The thick blue lines display the location of the
 and
and
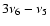 secular resonances obtained with the analytical approach of Milani & Knezevic (1994). secular resonances obtained with the analytical approach of Milani & Knezevic (1994). |
| Open with DEXTER |
where gr is the regularized value of the g frequency,
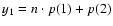 ,
with p(i) (i=1,2) the linear and angular coefficient of the line that best-fit the regular asteroids, and n the asteroid mean-motion, and
,
with p(i) (i=1,2) the linear and angular coefficient of the line that best-fit the regular asteroids, and n the asteroid mean-motion, and
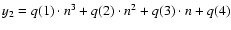 ,
where the q(i) (i=1,...,4) are the coefficient of the third-order polynomial that best-fit the g frequency in the perturbed domain. Values of the p and q coefficients for the two ranges of s values that we used are given in Table 1. The factor g/y2 that multiplies the right side of Eq. (10) is a factor
that quantifies how well the g value of the frequency is represented by the third-order polynomial that models the nonlinear regime of g in the (n,g) plane. This factor is equal to 1 for
a perfect fit, is less than 1 for g < y2 and more than 1 for g > y2.
,
where the q(i) (i=1,...,4) are the coefficient of the third-order polynomial that best-fit the g frequency in the perturbed domain. Values of the p and q coefficients for the two ranges of s values that we used are given in Table 1. The factor g/y2 that multiplies the right side of Eq. (10) is a factor
that quantifies how well the g value of the frequency is represented by the third-order polynomial that models the nonlinear regime of g in the (n,g) plane. This factor is equal to 1 for
a perfect fit, is less than 1 for g < y2 and more than 1 for g > y2.
Table 1:
Numerical values of the coefficients used to regularize g as a function of n for the Vesta family (s-intervals between -42.89 and -45.00''/yr, and between -45.00 and -47.64''/yr).
The right panel of Fig. 9 displays the results of this procedure for the asteroids in the region of the Vesta family with s in the interval
[-45.00,-47.64]''/yr
(results are similar for asteroids with s in the interval
[-42.89,-45.00]''/yr,
and are not shown for concisiness). The black dots display the real values of g, the inclined blue line is the line that best-fit asteroids in the regular region, and the magenta line is the third-order polynomial that best-fit the asteroid in the perturbed region. The red crosses are the regularized values of g. Note how they follow the line of extended linear behavior,
with a spreadth caused by the g/y2 factor in Eq. (10).
We replaced the regularized values of g in the catalog of asteroid synthetic proper elements and we used FHCM on this modified set of elements to re-obtain the Vesta family. For a cutoff of 0.120''/yr the family coalesced with the local background, so we chose to work with a cutoff of 0.119''/yr. With this cutoff we found 8413 members of the Vesta family. Figure 10 displays an
 projection of a part of the Vesta frequency family (red crosses, panel A), and of the regularized Vesta frequency family (red crosses, panel B) in the region near the
3J:-1A resonance (a > 2.38 AU). Superimposed we show a color plot of the
projection of a part of the Vesta frequency family (red crosses, panel A), and of the regularized Vesta frequency family (red crosses, panel B) in the region near the
3J:-1A resonance (a > 2.38 AU). Superimposed we show a color plot of the 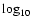 of the number of asteroid per unit bin in the local background of the Vesta family.
The reader may also want to compare this figure with Fig. 15 in Carruba & Michtchenko (2007). With the new method we were able not only to retrieve most of the asteroids that were identified as family members with the CHCM, but also to identify tails of asteroids that drifted in some of the local three-body (such as the
9J:-7S:-2A) and secular (such as the
of the number of asteroid per unit bin in the local background of the Vesta family.
The reader may also want to compare this figure with Fig. 15 in Carruba & Michtchenko (2007). With the new method we were able not only to retrieve most of the asteroids that were identified as family members with the CHCM, but also to identify tails of asteroids that drifted in some of the local three-body (such as the
9J:-7S:-2A) and secular (such as the
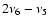 (
g+g5-2g6) and
(
g+g5-2g6) and
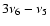 (
2g+g5-3g6)) resonances, not identified as family members by the classical method. In particular, we identified 2265 objects in the
(
2g+g5-3g6)) resonances, not identified as family members by the classical method. In particular, we identified 2265 objects in the
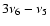 resonance in the local background of the Vesta family. Of these, 83 (3.6% of the total) were identified by the CHCM, 44 (1.9%) by the FHCM, and 130 (5.7%) were identified by the regularized FHCM described in this section (note how in this case, because of the proximity of the
3J:-1A resonance and its effect on the g frequency, the CHCM identified more resonant objects than the unregularized FHCM). The advantages of this method are more evident for what concern the
resonance in the local background of the Vesta family. Of these, 83 (3.6% of the total) were identified by the CHCM, 44 (1.9%) by the FHCM, and 130 (5.7%) were identified by the regularized FHCM described in this section (note how in this case, because of the proximity of the
3J:-1A resonance and its effect on the g frequency, the CHCM identified more resonant objects than the unregularized FHCM). The advantages of this method are more evident for what concern the
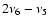 resonance. There are 2839 objects inside this resonance in the local background. Here the CHCM and the FHCM identified none, while the regularized FHCM
identified 5 objects (0.2%). By regularizing the values of g, we were able to retrieve 37% more objects that drifted in the
g+g5-2g6) than with the CHCM, and we extended the Vesta family almost up to the border of the
3J:-1A resonance.
resonance. There are 2839 objects inside this resonance in the local background. Here the CHCM and the FHCM identified none, while the regularized FHCM
identified 5 objects (0.2%). By regularizing the values of g, we were able to retrieve 37% more objects that drifted in the
g+g5-2g6) than with the CHCM, and we extended the Vesta family almost up to the border of the
3J:-1A resonance.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{9852f11a.eps}\hspace*{1.5cm}
\includegraphics[width=7.2cm,clip]{9852f11b.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg64.gif) |
Figure 11:
Proper pericenter precession frequency g versus proper eccentricity for all asteroids in the main belt (panel A)) and for the region of the Hansa family (panel B)). |
| Open with DEXTER |
The procedure that we described in this section presents one disadvantage and several advantages. The disadvantage relates to the procedure itself, which is not easily generalizable. Each family in the proximity of mean-motion resonance presents a different situation and may need an ad hoc approach for the procedure of regularization of the g frequency as a function of n (but we believe that the procedure that we outlined here may serve as a basis for the study of other,
similar cases). The advantages of this approach, however, in our opinion more than compensate for the disadvantages. Apart for the tails of asteroids that drifted in local mean-motion and secular
resonances, that were not recognized as family members by the CHCM, the regularized FHCM that we introduce in this section provides a deeper understanding of the local dynamics, (i.e., the perturbing effect of the
3J:-1A resonance on the g frequency, the consequent overlapping
of g resonances, etc.) which is not furnished by the CHCM. We believe that this alone is a very important benefit of this method, which we will discuss in more detail in the next sections.
3.2 Asteroid in resonant configurations with retrograde
perihelion motion: the Hilda and Hansa families
Another effect that mean-motion resonances have on the precession frequency of the pericenter of asteroids happens for asteroids in resonant configurations. It is well known (Schubart 1988, 2007) that asteroids locked in the
3J:-2A mean-motion resonance with Jupiter (the so-called ``Hildas''). Recently Broz & Vokrouhlický (2008) identified two collisional families, one associated with (153) Hilda, and one associated with (1911) Schubart, among
the population of resonant asteroids. In this paper for convenience we will refer to the whole population of resonant asteroids as ``Hildas'') are characterized by retrograde precession
frequency of the pericenter (negative values of g). Since the precession frequency is higher for objects at low-eccentricities, an useful plane to show the dependence of g on e is the (e,g) plane. As can be seen in Fig. 11, panel A, there is a tail of asteroids
at negative g whose precession frequency values are higher for smaller values of e. No Hilda is currently observed at an eccentricity smaller than 0.07.
While the case of the Hildas was well known, we found that this was not the only population of objects characterized by retrograde values of g. The Hansa family is a family at quite high inclination, quite low eccentricities, near the right side of the
3J:-1A mean-motion
resonance with Jupiter. As can be seen in Fig. 11, panel B, members of the Hansa
family with
e < 0.0179 are also characterized by negative values of the pericenter precession frequencies. We believe this behavior can be explained if we consider the possibility that these
objects could currently be inside the apocentrice tail of the
3J:-1A resonance.
Apocentric and pericentric orbits have been studied in the planar circular restricted three-body problem by Tsiganis et al. (2000) for the case of the 12J:7A resonance, and by Ferraz-Mello et al. (1998), that used a spatial asymmetric expansion of the disturbing function that included the effect of the Great Inequality of Jupiter's longitude for the case of the
2J:-1A resonance. Both these studies were conducted in the planar approximation,
so that their results should be extrapolated to the case of a high-inclined family such as Hansa with a lot of caution. What it is generally observed is that in the planar circular restricted
three-body problem (Sun-Jupiter-Asteroid) the family of nearly circular periodic resonant asteroidal orbits bifurcates at higher energies into a pericenter and apocenter branches, at lower and higher values of semimajor axis a, respectively (Tsiganis et al. 2000, Fig. 1). Basically, in the case of the
3J:-1A resonance, we would expect apocentric orbits to be circulating orbits
of high energy whose equinoctial resonant elements
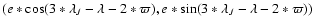 (where
(where
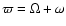 and
and
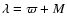 )
would be characterized by the interaction with the saddle point at (0,0). Contrary to normal circulating orbits, apocentric orbits would pass through the origin of the equinoctial orbital plane, while librating orbits would librate in one of the two libration islands of the
3J:-1A resonance.
)
would be characterized by the interaction with the saddle point at (0,0). Contrary to normal circulating orbits, apocentric orbits would pass through the origin of the equinoctial orbital plane, while librating orbits would librate in one of the two libration islands of the
3J:-1A resonance.
We believe that a similar mechanism may be at play in this case, and that the Hansa family as found in Gil-Hutton (2006) using the CHCM may be actually made of two distinct components: one at
e > 0.0179 that corresponds to most of the classical dynamical family and one at lower e, that is made up of objects currently in the apocentric tail of
3J:-1A resonance with Jupiter.
To confirm this hyphothesis we perfomed a 20 000 yr integration of asteroids in both components of the Hansa family with Swift_whm.f, the integrator in the SWIFT package that uses the symplecting mapping of Wisdom & Holman (1991). We included all planets except Mercury and used a time-step of 20 days. Figure 12 displays the time series of the equinoctial resonant elements Fourier filtered so as to eliminate all frequencies with period lower than 1000 yr (Carruba et al. 2005) of two members of the Hansa family, an object in the high-e component ((40971) 1999 TY264, panel A), and an asteroid in the low-e component
((20517) Judycrystal, panel B). As can be seen in the figure, (20517) Judycrystal seems to display the behavior expected in a object in apocentric orbit, which could explain the retrograde values of its pericenter precession frequency. A similar behavior was observed in other
objects in the low-e component of the Hansa family.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9852f13a.eps}\hspace*{1.5cm}
\includegraphics[width=7.5cm,clip]{9852f13b.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg69.gif) |
Figure 13:
An (a,e) (panel A)) and (e,g) (panel B)) projections of
members of the Hansa family (green circles) found in proper element space and members of the family found in the frequency space (red crosses). The black dots show the locations of
background asteroids in the region. |
| Open with DEXTER |
For what concern this paper, we believe that the study of the Hilda-type asteroid families goes beyond the purposes of this work, first because the proper elements of asteroids in the
3J:-2A mean-motion resonant configuration with Jupiter should more appropiately be obtained with analytical
methods such in Miloni et al. (2005), or with ad hoc numerical procedure as in Schubart (1988), rather than with the general Knezevic & Milani (2003) general numerical approach (we also refer the reader to Schubart 2007; and to Broz & Vokrouhlický 2008, for a more recent treatment of Hilda-type orbits).
The Hansa family has so far received much less attention. In the next section we will concentrate on the two components of the Hansa family, the low-e objects possibly in the apocentric tail of the
3J:-1A resonance with Jupiter and the others, at higher eccentricity, and discuss how the tecniques for family determination discussed in Sect. 3.1 can be extended to the case of this family.
3.2.1 The Hansa family
As discussed in the previous subsection, it is quite likely that the Hansa family as found by Gil-Hutton (2006) may be actually made of two well distinct components: a low-eccentricity component of asteroids possibly in apocentric 3J:1A resonant orbits, and an high-eccentricity
component of asteroids not in resonant configuration. Understanding the true nature of the Hansa family is actually a very interesting field of research on its own. Here, however, we are mostly interested in introducing new techniques to determinying asteroid families. For this purpose, and as a numerical experiments, here we applied the regularization technique seen for the case of the Vesta family to the case of the Hansa family, but in the (e,g) space rather than in the (n,g) space.
Figure 13 (right panel) displays how the values of g depend on e for
asteroids in the region of the Hansa family![[*]](/icons/foot_motif.gif) . Note how for eccentricities of less than 0.0179 (vertical line) values of g significantly drop. Inevitably, this behavior of the g frequency creates problems to identifying the Hansa family in the frequency domain.
. Note how for eccentricities of less than 0.0179 (vertical line) values of g significantly drop. Inevitably, this behavior of the g frequency creates problems to identifying the Hansa family in the frequency domain.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9852f14a.eps}\hspace*{1.5cm}
\includegraphics[width=7.5cm,clip]{9852f14b.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg70.gif) |
Figure 14:
An (a,e) (panel A)) and an (e,g) (panel B)) projections of the regularized Hansa family members (red crosses), superimposed to asteroids in the Hansa family region (black dots). The green circles are members of the classical family. |
| Open with DEXTER |
Since (480) Hansa itself is characterized by a significant high value of g, to identify the family in frequency space we used the lowest numbered object in the linear regime, (4880) Tovstorogov. We used a cutoff value in the frequency domain of 0.57''/yr (for larger values the family merged with the local background) and of 146 m/s in the proper element space. Projections of the two families in the (a,e) space plane, supermiposed with asteroids in
the region of the Hansa family (black dots), are shown in Fig. 13, panel A. The horizontal (left panel) and vertical (right panel) lines display the limit value of e (0.0179) for which g drops. Note how objects with high absolute values of g and low e are recognized as
family members by the classical approach, but not by the frequency method.
To try to overcome this problem we regularized the behavior of the g-frequency of asteroids at low eccentricities. For this purpose we employed a procedure similar to the one used for the
Vesta family. We substituted the values of g with the regularized values gr given by:
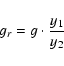 |
(11) |
where gr is the regularized value of the g frequency,
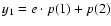 ,
with
p(i) (i=1,2) the linear and angular coefficient of the line that best-fit the regular asteroids, and n the asteroid mean-motion, and
,
with
p(i) (i=1,2) the linear and angular coefficient of the line that best-fit the regular asteroids, and n the asteroid mean-motion, and
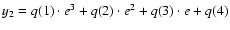 ,
where the q(i)
(i=1,...,4) are the coefficient of the third-order polynomial that best-fit the g frequency in the perturbed domain. Values of the p and q coefficients for the two ranges of s values that we used are given in
Table 2. Figure 14, right panel, displays the location
of the regularized values of gr with respect to e (green circles). The blue line is the line that best fit the data in the regular region, while the magenta line is the third-order polynomial that best-fit the data in the perturbed region. We applied this procedure to the asteroids
in the local background having a value of g smaller than the minimum of those observed
for the family in frequency space, and computed the new family for this modified set of proper frequencies. The family coalesced with the local background for a cutoff of 1.13''/yr,
so we decided to work with a cutoff of 1.12''/yr.
,
where the q(i)
(i=1,...,4) are the coefficient of the third-order polynomial that best-fit the g frequency in the perturbed domain. Values of the p and q coefficients for the two ranges of s values that we used are given in
Table 2. Figure 14, right panel, displays the location
of the regularized values of gr with respect to e (green circles). The blue line is the line that best fit the data in the regular region, while the magenta line is the third-order polynomial that best-fit the data in the perturbed region. We applied this procedure to the asteroids
in the local background having a value of g smaller than the minimum of those observed
for the family in frequency space, and computed the new family for this modified set of proper frequencies. The family coalesced with the local background for a cutoff of 1.13''/yr,
so we decided to work with a cutoff of 1.12''/yr.
Table 2:
Numerical values of the coefficients used to regularize g as a function of e for the Hansa family.
The left panel of Fig. 14 shows an (a,e) projection of the regularized
family (red asterisks), superimposed with the classical family. As can be seen in the figure, our method allows us to recognize as family members objects at very low-eccentricities that were
lost otherwise, and also to connect object not recognized as members by other methods, such as the objects in the region centered at a = 2.58 AU and e =0.03. We therefore believe that this procedure may therefore permit to overcome the problem presented by the perturbed behavior of the
g frequency for apocentric 3J:1A resonant orbits.
4 Discussions
In this work we analyzed the cases of asteroid families interacting with secular resonances of argument other than g or g+s, or with low-order mean-motion resonances. Following the approach of Carruba & Michtchenko (2007), we obtained asteroid families in the proper frequency domain (n,g,g+s) and in other domains most apt to describe the particular resonance that we were studying, and introduced techniques to ``regularize'' the behavior of the g frequency near mean-motion resonances. In particular, we did the following:
- We introduced several new representative planes and distance metrics for studying the case of diffusion of family members in resonances of argument other than g and g+s, such
as the z2, z3,
 ,
,
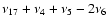 ,
and
,
and
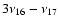 .
Our new approaches (results are summarized in Table 4; the first column reports the family name and the second column the resonance argument, in the Michtchenko et al. 2008, notation) allows us to more efficiently track diffusion in such resonances by a 50% factor with respect to either families found in the proper element space or with the ``standard distance metric'' in frequency space of Carruba & Michtchenko (2007).
.
Our new approaches (results are summarized in Table 4; the first column reports the family name and the second column the resonance argument, in the Michtchenko et al. 2008, notation) allows us to more efficiently track diffusion in such resonances by a 50% factor with respect to either families found in the proper element space or with the ``standard distance metric'' in frequency space of Carruba & Michtchenko (2007).
- We inquired why our method allows us to identify as family members objects currently inside mean-motion resonances that drifted far from the center of the family, as for objects inside the 1:2 resonance with Mars near the Vesta family.
- Introduced a new techniques to regularize the behavior of the g frequency as a function of the n frequency that allowed us to connect to the Vesta family objects near the left border of the 3:1 mean-motion resonance with Jupiter.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9852f15a.eps}\hspace*{1.5cm}
\includegraphics[width=7.5cm,clip]{9852f15b.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg74.gif) |
Figure 15:
Panel A):
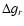 values obtained with Eq. (12) as a function of n for asteroids in the
3J:-1A perturbed region (n<93.0)
near the Vesta family for a third-order approximation of the g(n) values in the region.
Panel B): a plot of the relative changes of the errors in gr between different order
approximation of g(n).
values obtained with Eq. (12) as a function of n for asteroids in the
3J:-1A perturbed region (n<93.0)
near the Vesta family for a third-order approximation of the g(n) values in the region.
Panel B): a plot of the relative changes of the errors in gr between different order
approximation of g(n). |
| Open with DEXTER |
- Investigated the case of families characterized by a retrograde behavior of the g frequency, such as some members of the Hansa family and all the Hildas, and introduced a technique to regularize the behavior of the g frequency as a function of the eccentricity e.
Based on our experience, we believe that the cases we treated in this article should be fairly representative. Other possible resonant combinations, such as resonance of arguments g+2s, g-2s, 3s etc. have a minor effect on the stability of asteroid proper elements according to Milani & Knezevic (1994) and were not treated in this paper. Approaches for treating such resonances can be easily derived from the examples that we provided in this paper. By regularizing the behavior
of the g frequency as a function of n and e and introducing new distance metrics we were able to extend families in regions that were not accessible with the Carruba & Michtchenko (2007) approach, while keeping all the advantages of the recently published method (i.e., identifying objects that drifted in secular resonances due to the Yarkovsky and YORP effects as family
members, simplicity in representing secular resonances etc.). More important, an analysis of asteroid families in the frequency domain may provide insight on the dynamical evolution of its members, in a way not always possible with the classical analysis in the proper element space. Examples of this include the evolution of members of the Erigone family in the z2 resonance, the effect of the
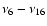 resonance on the Phocaea family, and the role that the apocentric tail of the 3J:1A may have had in shaping the dynamics of 24.4% of the members of the Hansa family. The deeper understanding of the dynamics near asteroid families provided by an analysis
in the frequency domain is, in our opinion, the most important new result of this work.
resonance on the Phocaea family, and the role that the apocentric tail of the 3J:1A may have had in shaping the dynamics of 24.4% of the members of the Hansa family. The deeper understanding of the dynamics near asteroid families provided by an analysis
in the frequency domain is, in our opinion, the most important new result of this work.
Table 3:
The limits in the
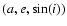 domain of the local background for the families studied in this paper.
domain of the local background for the families studied in this paper.
Table 4:
Percentage of resonant asteroids in the local background identified as family members by the classical method (CHCM), the ``standard'' frequency method (FHCM), and the new distance metrics
introduced in this article (AHCM).
Acknowledgements
We thank the referee, David Vokrouhlický, for his comments and suggestions that helped to improve the original version of the paper. This work has been supported by the São Paulo State Science Foundation - FAPESP (grant 06/50005-5), and the Brazilian National Research Council - CNPq. The authors gratefully acknowledge the support of the Computation Center of the University of São Paulo (LCCA-USP), of the Astronomy Department of the IAG/USP, and of the Physics and
Astronomy department of the IPD/UNIVAP for the use of their facilities.
Appendix A: Estimates of the errorson the regularized values of g
In Sect. 3.1 we introduced a technique to regularize the behavior of the g frequency as a function of n in the region near the
3J:-1A resonance, where g(n) was approximated with a third-order polynomial. Here we try to quantify the errors on gr caused by the application of Eq. (10) on the values of g and n of asteroids near the
3J:-1A. For this purpose we make two assumptions:
- We use the RMS values of the g frequencies available at the AstDyS site as estimates of the errors on g.
- We neglect errors on n
The second assumption is in our opinion justified by the fact that rms values of n in the region of the Vesta family are a factor
10-4-10-2 smaller than the rms of g. With these assumptions, we use Eq. (10) on a set of
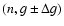 to obtain values
of the regularized frequency gr. Errors on gr can be obtained using the standard propagation of errors formula, i.e.,
to obtain values
of the regularized frequency gr. Errors on gr can be obtained using the standard propagation of errors formula, i.e.,
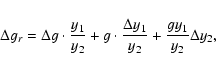 |
(12) |
where 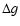 is the rms value of g,
is the rms value of g,
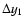 is obtained using:
is obtained using:
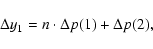 |
(13) |
(where
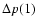 and
and
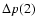 are obtained using least-square formulas for the errors on the linear and angular coefficient of a line (Press et al. 1992); and
are obtained using least-square formulas for the errors on the linear and angular coefficient of a line (Press et al. 1992); and
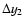 is obtained numerically using a MATLAB routine (polyval.m) that uses the Cholesky factor of the Vandermonde matrix to obtain error estimates of the fitted gr-values (Press et al. 1992).
is obtained numerically using a MATLAB routine (polyval.m) that uses the Cholesky factor of the Vandermonde matrix to obtain error estimates of the fitted gr-values (Press et al. 1992).
Figure 15, panel A, displays
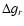 values obtained with Eq. (12) as a function of n for asteroids in the
3J:-1A perturbed region (n<93.0)
near the Vesta family for a third-order approximation of the g(n) values in the region. We computed the errors also for a second, fourth, and fifth approximation of g(n). Figure 15, panel B, is a semi-log plot of the relative changes of the errors in gr between different order approximation of g(n), defined as
values obtained with Eq. (12) as a function of n for asteroids in the
3J:-1A perturbed region (n<93.0)
near the Vesta family for a third-order approximation of the g(n) values in the region. We computed the errors also for a second, fourth, and fifth approximation of g(n). Figure 15, panel B, is a semi-log plot of the relative changes of the errors in gr between different order approximation of g(n), defined as
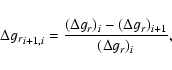 |
(14) |
with i=2-4. As can be seen in the Fig. 15, panel A, errors on gr are in a range between 0.3 and 1.6''/yr. Figure 15, panel B, shows that taking a third-order approximation improved the quality of our fit with respect to a third-order one by an average value of 14%. Using a fourth-order approximation would improve the value of the error by just 4%, and going to fifth-order would grant another 1%. The values of the q(i) coefficients for a fourth-order approximation are however rather large, and produce larger round-off errors in
the estimate of the gr values obtained with Eq. (10). In view of these considerations, we decided to adopt a third-order approximation of g(n) in this work.
- Bottke, W. F.,
Vokrouhlický, D., & Nesvorný, D. 2007, Nature, 449,
48 [NASA ADS] [CrossRef]
(In the text)
- Bowell, E., Muinonen,
K., & Wasserman, L. H. 1994, Asteroid, Comets and Meteorids
III, ed. A. Milani, M. di Martino, & A. Cellino (Dordrecht:
Kluwer), 477
- Broz, M., &
Vokrouhlický, D. 2008, MNRAS, in press
(In the text)
- Bus, J. S., &
Binzel, R. P. 2002a, Icarus, 158, 106 [NASA ADS] [CrossRef]
- Bus, J. S., &
Binzel, R. P. 2002b, Icarus, 158, 146 [NASA ADS] [CrossRef]
- Carruba, V., &
Michtchenko, T. 2007, A&A, 475, 1145 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Carruba, V., Burns, J.
A., Bottke, W., & Nesvorný, D. 2003, Icarus, 162, 308 [NASA ADS] [CrossRef]
- Carruba, V.,
Nesvorný, D., Burns, J. A., Cuk, M., & Tsiganis, K. 2004,
AJ, 128, 1899 [NASA ADS] [CrossRef]
(In the text)
- Carruba, V.,
Michtchenko, T., Roig, F., Ferraz-Mello, S., & Nesvorný,
D. 2005, A&A, 441, 819 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Carruba, V., Roig,
F., Michtchenko, T., Ferraz-Mello, S., & Nesvorný, D.
2007, A&A, 465, 315 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Duffard, R., Lazzaro,
D., Licandro, J., et al. 2004, Icarus, 171, 120 [NASA ADS] [CrossRef]
(In the text)
- Ferraz-Mello, S.,
Michtchenko, T. A., & Roig, F. 1998, AJ, 116, 1491 [NASA ADS] [CrossRef]
(In the text)
- Gil-Hutton, R. 2006,
Icarus, 183, 93 [NASA ADS] [CrossRef]
(In the text)
- Guillens, S. A., Vieira
Martins, R., & Gomes, R. S. 2002, AJ, 124, 2322 [NASA ADS] [CrossRef]
- Knezevic, Z., &
Milani, A. 2000, Celest. Mech. Dyn. Astron., 78, 17 [NASA ADS] [CrossRef]
- Knezevic, Z., &
Milani, A. 2003, A&A, 403, 1165 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Lazzaro, D., Angeli, C.
A., Carvano, J. M., et al. 2004, Icarus, 172, 179 [NASA ADS] [CrossRef]
- McCord, T. B., Adams,
J. B., & Johnson, T. V. 1970, Science, 168, 1445 [NASA ADS] [CrossRef]
- Michtchenko, T. A.,
& Ferraz-Mello, S. 2002, Icarus, 149, 357 [NASA ADS]
- Michtchenko, T. A.,
Carruba, V., & Lazzaro, D. 2008, MNRAS, submitted
(In the text)
- Milani, A., &
Knezevic, Z. 1994, Icarus, 107, 219 [NASA ADS] [CrossRef]
(In the text)
- Milani, A., &
Knezevic, Z. 2003, A&A, 403, 1165 [NASA ADS] [CrossRef] [EDP Sciences]
- Miloni, O.,
Ferraz-Mello, S., & Beaugé, C. 2005, CeMDA, 92, 89 [NASA ADS]
(In the text)
- Morbidelli, A., &
Vokrouhlický, D. 2003, Icarus, 163, 120 [NASA ADS] [CrossRef]
- Morbidelli, A.,
Nesvorný, D., Bottke, W. F., et al. 2003, Icarus, 162,
328 [NASA ADS] [CrossRef]
(In the text)
- Nesvorný, F.,
Roig, B., Gladman, D., et al. 2008, Icarus, 183, 85 [NASA ADS]
(In the text)
- Press, W. H.,
Vetterling, W. T., Teukolsky, S. A., & Flannery, B. P. 1992,
Numerical Recipes in Fortran 77 (Cambridge University Press)
(In the text)
- Sidlichovsky, M.,
& Nesvorný, D. 1997, Cel. Mech. Dyn. Astron., 65, 137 [NASA ADS] [CrossRef]
- Schubart, J. 1998, Cel.
Mech. Dyn. Astron., 43, 309
- Schubart, J. 2007,
Icarus, 188, 189 [NASA ADS] [CrossRef]
(In the text)
- Tsiganis, K.,
Varvoglis, H., & Hadjidemetriou, J. D. 2000, Icarus, 146,
240 [NASA ADS] [CrossRef]
(In the text)
- Vokrouhlický,
D., Broz, M., Bottke, W. F., Nesvorný, D., & Morbidelli,
A. 2006a, Icarus, 181, 118 [NASA ADS]
(In the text)
- Vokrouhlický,
D., Broz, M., Morbidelli, A., et al. 2006b, Icarus, 182, 92 [NASA ADS] [CrossRef]
- Vokrouhlický,
D., Broz, M., Bottke, W. F., Nesvorný, D., & Morbidelli,
A. 2006c, Icarus, 183, 349 [NASA ADS] [CrossRef]
- Williams, J. G., &
Faulkner, J. 1981, Icarus, 46, 390 [NASA ADS] [CrossRef]
(In the text)
- Wisdom, J., &
Holman, M. 1991, AJ, 102, 1528 [NASA ADS] [CrossRef]
(In the text)
- Zappalà, V.,
Cellino, A., Farinella, P., & Knezevic, Z. 1990, AJ, 100,
2030 [NASA ADS] [CrossRef]
(In the text)
- Zappalà, V.,
Bendjoya, Ph., Cellino, A., Farinella, P., & Froeschlè, C.
1995, Icarus, 116, 291 [NASA ADS] [CrossRef]
(In the text)
- Zellner, B., Tholen, D.
J., & Tedesco, E. F. 1985, Icarus, 61, 355 [NASA ADS] [CrossRef]
Copyright ESO 2009
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{9852fi1a.eps}\hspace*{2.8c...
...ps}\hspace*{2.8cm}
\includegraphics[width=6.3cm,clip]{9852fi1d.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg24.gif)
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{9852fi2a.eps}\hspace*{2.8c...
...ps}\hspace*{2.8cm}
\includegraphics[width=6.3cm,clip]{9852fi2d.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg28.gif)
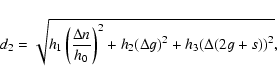
![\begin{figure}
\par\includegraphics[width=6.2cm,clip]{9852fi3a.eps}\hspace*{2.8c...
...ps}\hspace*{2.8cm}
\includegraphics[width=6.2cm,clip]{9852fi3d.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg32.gif)
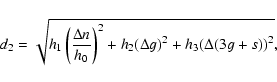
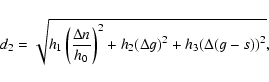
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{9852fi4a.eps}\hspace*{2.8c...
...ps}\hspace*{2.8cm}
\includegraphics[width=6.3cm,clip]{9852fi4d.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg38.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9852fig5.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg40.gif)
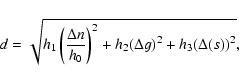
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{9852fi6a.eps}\hspace*{1.5cm}
\includegraphics[width=7.2cm,clip]{9852fi6b.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg42.gif)
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{9852fi7a.eps}\hspace*{2.8c...
...ps}\hspace*{2.8cm}
\includegraphics[width=6.5cm,clip]{9852fi7d.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg43.gif)
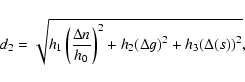
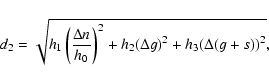
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9852fi8a.eps}\hspace*{1.5cm}
\includegraphics[width=7.5cm,clip]{9852fi8b.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg53.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9852fi9a.eps}\hspace*{1.5cm}
\includegraphics[width=7.5cm,clip]{9852fi9b.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg54.gif)
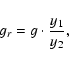
![\begin{figure}
\par\includegraphics[width=7cm,clip]{9852f10a.eps}\hspace*{2cm}
\includegraphics[width=7cm,clip]{9852f10b.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg56.gif)
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{9852f11a.eps}\hspace*{1.5cm}
\includegraphics[width=7.2cm,clip]{9852f11b.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg64.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9852f12a.eps}\hspace*{1.5cm}
\includegraphics[width=7.5cm,clip]{9852f12b.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg68.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9852f13a.eps}\hspace*{1.5cm}
\includegraphics[width=7.5cm,clip]{9852f13b.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg69.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9852f14a.eps}\hspace*{1.5cm}
\includegraphics[width=7.5cm,clip]{9852f14b.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg70.gif)
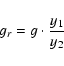
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9852f15a.eps}\hspace*{1.5cm}
\includegraphics[width=7.5cm,clip]{9852f15b.eps}
\end{figure}](/articles/aa/full/2009/01/aa09852-08/Timg74.gif)