A&A 477, 165-172 (2008)
DOI: 10.1051/0004-6361:20078525
A. E. Piskunov1,2,3 - E. Schilbach1 - N. V. Kharchenko1,3,4 - S. Röser1 - R.-D. Scholz3
1 - Astronomisches Rechen-Institut, Mönchhofstraße 12-14, 69120 Heidelberg, Germany
2 -
Institute of Astronomy of the Russian Acad. Sci., 48 Pyatnitskaya
Str., 109017 Moscow, Russia
3 -
Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
4 -
Main Astronomical Observatory, 27 Academica Zabolotnogo Str., 03680 Kiev, Ukraine
Received 22 August 2007 / Accepted 9 October 2007
Abstract
Context. In a previous paper we obtained King's parameters for 236 of 650 Galactic open clusters identified in the ASCC-2.5.
Aims. Estimating tidal radii by use of observable parameters available for all clusters. Bias-free results are required.
Methods. We use methods of stellar statistics and develop a semi-empirical model of open clusters.
Results. We check two effects impacting the determination of tidal radii from a fitting of King's profiles to the observed density distribution, i.e., ellipticity of open clusters and a bias depending on distances. Though a typical cluster has an elliptical form, the effect is rather weak to produce a prominent bias in the resulting tidal radii. In contrast, a distance dependent bias is not negligible and can cause a systematic underestimation of tidal radii computed with ASCC-2.5 data by a factor of two for the most distant clusters of our sample. This finding is used to correct the original results for 236 clusters and to extend the system of tidal radii and masses to all 650 clusters. We found that the semi-major axis of the projected distribution of cluster members on the sky is a parameter suited to estimate tidal radii of open clusters of our sample. No systematic differences are found between measured and calibrated tidal radii. From the comparison with mass estimates based on star counts and on the assumption of the Salpeter IMF, empirical evidence is obtained for an evolution of cluster mass functions starting in young clusters.
Conclusions. The set of homogeneous parameters available for all clusters of our sample is extended by tidal radius and mass. Within 850 pc where our sample is complete, the distributions of tidal radii and masses peak at
![]() pc and
pc and
![]() ,
respectively. In young open clusters, the mass distributions show differences to the Salpeter IMF, and this discrepancy increases with cluster age.
,
respectively. In young open clusters, the mass distributions show differences to the Salpeter IMF, and this discrepancy increases with cluster age.
Key words: Galaxy: open clusters and associations: general - solar neighborhood - Galaxy: stellar content
Our current project aims at studying the properties of the local population of Galactic open clusters. The basic sample consists of 641 open clusters and 9 compact associations identified in the all-sky compiled catalogue ASCC-2.5 (Kharchenko 2001). For each cluster, we determined membership (Kharchenko et al. 2004) and derived a homogeneous set of cluster parameters (Kharchenko et al. 2005a,b). The sample is found to be complete up to a distance of about 850 pc from the Sun (Piskunov et al. 2006). This completeness limit corresponds to a distance modulus (V-MV) of about 10-10.5 (Schilbach et al. 2006) in the case of our cluster sample. In our latest paper of this series (Piskunov et al. 2007, hereafter called Paper I), we present tidal radii and masses of 236 open clusters from this sample. The tidal radii are determined from fitting three-parametric King's profiles to the observed integrated density distribution. Compared to a few open clusters with tidal parameters already available, the number looks very high. However, this subsample can not be used for a statistical study of the population of open clusters, mainly, due to its incompleteness. In this paper we try to fill this gap by constructing a consistent set of tidal parameters for the complete sample.
In an ideal case, all 650 clusters should be passing through the "King's profile fitting pipeline'' which we developed in Paper I. Nevertheless, due to the low quality of density profiles of the remaining clusters, this is not possible, and we had to look for another approach. The idea is to use the 236 clusters as standards to find a relation between tidal radius and an observable parameter available for all clusters. This approach assumes that standard parameters are free of biases as much as possible.
The paper has the following structure. In Sect. 2 we briefly describe the input data and the basic terminology widely used in the present work. In Sect. 3 we consider possible biases which may be inherent in our determination of tidal radii. Section 4 is devoted to building up the homogeneous system of tidal radii and masses for the complete cluster sample. In Sect. 5 we describe the properties of this sample of tidal parameters and compare tidal masses with counted masses available from the literature. In Sect. 6 we summarize the results.
In this paper we use the results of the previous work based on the study of 650 nearby open clusters identified in the ASCC-2.5. For a better understanding, we briefly describe the most relevant aspects and designations widely used in the following sections.
In each cluster, membership determination is carried out in an iterative process
that takes into account spatial (projected density profile), photometric (color
magnitude diagram, CMD), and proper motion (vector point diagram, VPD)
distributions of stars within a cluster area. As a result, we obtain new
coordinates of the cluster centre, the cluster size, location of the cluster's
main sequence (MS) in the CMD, and the mean proper motion of the cluster. The
data are used to derive the distance of the cluster, reddening, and age
(Kharchenko et al. 2005a,b). At the end of the iterations, each star gets
membership probabilities
![]() and
and ![]() of its belonging to the cluster
which are calculated from the location of the star in the CMD and VPD relative
to the cluster MS and the mean proper motion, respectively
(see Kharchenko et al. 2004). Stars deviating from the reference values, both in CMD
and VPD, by less than one rms error are considered to be the most probable
members, and we call them
of its belonging to the cluster
which are calculated from the location of the star in the CMD and VPD relative
to the cluster MS and the mean proper motion, respectively
(see Kharchenko et al. 2004). Stars deviating from the reference values, both in CMD
and VPD, by less than one rms error are considered to be the most probable
members, and we call them ![]() -members. Those deviating by less than two
rms errors are called
-members. Those deviating by less than two
rms errors are called ![]() -members, by less than three rms errors -
-members, by less than three rms errors -
![]() -members. For convenience, we call all stars in the cluster area
"
-members. For convenience, we call all stars in the cluster area
"![]() ''-members. Consequently, the
''-members. Consequently, the ![]() -members form a subsample of
the
-members form a subsample of
the ![]() -members that are, in turn, a subsample of the
-members that are, in turn, a subsample of the ![]() -members,
and so on. Depending on the desired application, which may require either a
cleaner or more complete selection of cluster members, the suitable subsample is
chosen, e.g. all cluster parameters were determined using data on
-members,
and so on. Depending on the desired application, which may require either a
cleaner or more complete selection of cluster members, the suitable subsample is
chosen, e.g. all cluster parameters were determined using data on
![]() -members. The results are included in the catalogue of open cluster
data (COCD) and its extension (Kharchenko et al. 2005a,b).
-members. The results are included in the catalogue of open cluster
data (COCD) and its extension (Kharchenko et al. 2005a,b).
The cluster size was evaluated by analyzing the projected density profiles of
stars in the wider neighbourhood of the cluster centre. In accordance with the
general rule, the apparent cluster radius r2 is the maximum angular distance
from the cluster centre where ![]() -members could be still found. Since
for each cluster the distance from the Sun was determined, the radius r2 can be
easily expressed in linear units (pc). This
parameter is obtained for all 650 clusters (for more details on structural
properties of open clusters see Schilbach et al. 2006).
In contrast, the tidal radius is derived from the fitting of
King (1962) density profiles to the observed integrated density distribution
for 236 clusters of the sample (Paper I).
Assuming that the obtained King parameters
are related to the limiting radii of open clusters, we compute tidal masses for
236 clusters. In order to stress their empirical origin, we call these
parameters, hereafter, measured tidal radii
-members could be still found. Since
for each cluster the distance from the Sun was determined, the radius r2 can be
easily expressed in linear units (pc). This
parameter is obtained for all 650 clusters (for more details on structural
properties of open clusters see Schilbach et al. 2006).
In contrast, the tidal radius is derived from the fitting of
King (1962) density profiles to the observed integrated density distribution
for 236 clusters of the sample (Paper I).
Assuming that the obtained King parameters
are related to the limiting radii of open clusters, we compute tidal masses for
236 clusters. In order to stress their empirical origin, we call these
parameters, hereafter, measured tidal radii
![]() ,
and measured tidal masses
,
and measured tidal masses
![]() .
.
For the majority of 236 clusters, we obtained several sets of King's
parameters, depending on the membership group used. In this case, the solution
with the best goodness-of-fit is chosen. However, comparing
the tidal radii computed with different membership groups, we found
small but systematic differences in the solutions (see Table 1 in Paper I). On
average, the solutions based on samples with less certain membership provide
slightly smaller tidal radii. This effect can probably be explained by a less
reliable estimation of the background in the solutions with ![]() -,
-,
![]() -, and "
-, and "![]() ''-groups than with the
''-groups than with the ![]() -sample.
-sample.
In order to obtain all the tidal radii in the system of ![]() -members, we
compare
-members, we
compare ![]() -,
-, ![]() -, and "
-, and "![]() ''-solutions with the
corresponding tidal radius based on the
''-solutions with the
corresponding tidal radius based on the ![]() -sample, for each membership
group separately. We consider only those clusters for which we
obtained at least two
sets of King's parameters that are larger than their rms errors, i.e. from
the membership group under test and from the
-sample, for each membership
group separately. We consider only those clusters for which we
obtained at least two
sets of King's parameters that are larger than their rms errors, i.e. from
the membership group under test and from the ![]() -sample. The corresponding
relations are fitted by regression lines and are shown in Fig. 1.
The results are used in Sect. 4 to convert the tidal radii obtained from the
solutions with
-sample. The corresponding
relations are fitted by regression lines and are shown in Fig. 1.
The results are used in Sect. 4 to convert the tidal radii obtained from the
solutions with ![]() -,
-, ![]() -, and "
-, and "![]() ''-membership groups into
the system defined by the
''-membership groups into
the system defined by the ![]() -members.
-members.
There are several reasons forcing a cluster to get a non-spherical shape, e.g., the galactic tidal field (Wielen 1985,1974), differential rotation of the Galaxy, encounters with giant molecular clouds (Gieles et al. 2006). Nevertheless, it is still unclear whether an ellipsoidal form can be assumed to be one of the general properties of open clusters. In the past, indications of a flattening were obtained only for a small number of selected clusters. Raboud & Mermilliod (1998b,a) and Adams et al. (2002,2001) found evidence of flattening in the Pleiades and in Preasepe. Their results support the predictions of Wielen's model that explains the ellipsoidal form of clusters by tidal coupling with the Galaxy. On the contrary, flattening found in the Hyades (Oort 1979) deviates from theoretical expectations. Recently, Chen et al. (2004) determined the ellipticity of 31 open clusters, residing in the Galactic anticentre direction, from stellar counts in the 2MASS. Since they do not publish orientations of ellipses in space, a comparison of their data with theoretical predictions is not possible.
| |
Figure 1:
Relations between the tidal radii computed with |
| Open with DEXTER | |
As the information on the ellipticity of open clusters is rather uncertain, we
determined King's parameters in Paper I assuming spherical symmetry in the
projected distribution of cluster stars. Since we used integrated density
profiles in the fitting routine, a possible bias due to a cluster flattening
would be diminished. Indeed, in the outer cluster regions which are important
for the tidal radius determination, the number of stars does not change, either
when counted within a circle of radius R or within an ellipse with semi-major
axis R. In the inner area of a cluster, a circle contains somewhat more stars
than the corresponding ellipse. This would have a consequence for the
determination of the core radius ![]() but should not impact the results on the
tidal radius
but should not impact the results on the
tidal radius
![]() .
On the other hand, the theoretical predictions propose a
spherical form of cluster cores. Therefore, our approach should not lead to
serious biases.
.
On the other hand, the theoretical predictions propose a
spherical form of cluster cores. Therefore, our approach should not lead to
serious biases.
![\begin{figure}
\par\includegraphics[angle=270,width=8.6cm,clip]{8525_f02.eps}\end{figure}](/articles/aa/full/2008/49/aa8525-07/Timg28.gif) |
Figure 2:
Ellipticities of open clusters of our sample. Upper panels:
distributions of ellipticities e, of their rms errors
|
| Open with DEXTER | |
Using information on the membership of stars in the cluster areas, we determined
ellipticities for clusters of our sample (Kharchenko et al. 2007). The ellipticity eis defined as
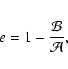
In Fig. 2 (the upper panels) we give the distribution of
ellipticities for clusters having at least 20 most probable members (i.e.,
![]() -members). We conclude that the majority of these clusters have
ellipticities smaller than 0.25, with an average of
-members). We conclude that the majority of these clusters have
ellipticities smaller than 0.25, with an average of
![]() and a
standard deviation of
and a
standard deviation of
![]() .
About 20% of clusters show a
significant flattening (
.
About 20% of clusters show a
significant flattening (
![]() ), whereas for about 40%, the
ellipticities do not significantly differ from zero (
), whereas for about 40%, the
ellipticities do not significantly differ from zero (
![]() ). For
clusters with tidal parameters determined in Paper I, the distribution of their
ellipticities, rms errors, and relative errors have similar properties.
). For
clusters with tidal parameters determined in Paper I, the distribution of their
ellipticities, rms errors, and relative errors have similar properties.
Strictly speaking, we should, however, consider the derived values of
![]() to
be lower limits of the tidal radii. Provided that a cluster has a form of a
three-axial ellipsoid, we observe a projection rather than the real size of a
cluster. The degree of possible discrepancy depends on the axis relation of the
ellipsoid as well as on the orientations of the axes with respect to the line of
sight to the cluster. According to Wielen (1985), due to the tidal coupling
with the Milky Way, equipotential surfaces for an open cluster can be described
by a three-axial ellipsoid. The orthogonal axes are related as 2:1.4:1, with the
major axis directed towards the Galactic centre, the second axis oriented in the
direction of Galactic rotation, and the third axis perpendicular to the
Galactic plane. Provided that open clusters have this elongated form, we would
underestimate the real tidal radii by a factor f of 1.4 at most, for clusters
located in the Galactic plane at
to
be lower limits of the tidal radii. Provided that a cluster has a form of a
three-axial ellipsoid, we observe a projection rather than the real size of a
cluster. The degree of possible discrepancy depends on the axis relation of the
ellipsoid as well as on the orientations of the axes with respect to the line of
sight to the cluster. According to Wielen (1985), due to the tidal coupling
with the Milky Way, equipotential surfaces for an open cluster can be described
by a three-axial ellipsoid. The orthogonal axes are related as 2:1.4:1, with the
major axis directed towards the Galactic centre, the second axis oriented in the
direction of Galactic rotation, and the third axis perpendicular to the
Galactic plane. Provided that open clusters have this elongated form, we would
underestimate the real tidal radii by a factor f of 1.4 at most, for clusters
located in the Galactic plane at
![]() ,
,
![]() .
For all other
clusters, the factor should be smaller and depends on the aspect angle
.
For all other
clusters, the factor should be smaller and depends on the aspect angle ![]() between the line of sight to the cluster (i.e. the Solarcentric vector) and its
Galactocentric vector. Also, the projection of these ellipsoids on the sky must show a
flattening depending on
between the line of sight to the cluster (i.e. the Solarcentric vector) and its
Galactocentric vector. Also, the projection of these ellipsoids on the sky must show a
flattening depending on ![]() .
In Fig. 2 (bottom panel) we
compare the observed distribution of ellipticities with the theoretical
predictions based on Wielen (1985). For convenience we introduce an angle
.
In Fig. 2 (bottom panel) we
compare the observed distribution of ellipticities with the theoretical
predictions based on Wielen (1985). For convenience we introduce an angle
![]() ,
so
,
so
![]() at
at
![]() ,
and
,
and
![]() at
at
![]() .
Although several clusters have flattenings
which coincide with the theoretical expectations, their distribution does not
show a trend with
.
Although several clusters have flattenings
which coincide with the theoretical expectations, their distribution does not
show a trend with ![]() .
In general, the observed ellipticities are smaller
than the predictions, and they are spread randomly around
.
In general, the observed ellipticities are smaller
than the predictions, and they are spread randomly around
![]() .
We conclude that the majority of our clusters do not have a form
of a three-axial ellipsoid, but are similar to oblate spheres with
comparable axes towards the Galactic centre and along the Galactic rotation.
Their real shape is probably defined by an interaction of different effects.
This can result from a differential rotation of the Galaxy that would increase
the second axis of the ellipsoids. Formally, open clusters with axis relations
of 1.25:1.25:1 would show an ellipticity of 0.2 independent of
.
We conclude that the majority of our clusters do not have a form
of a three-axial ellipsoid, but are similar to oblate spheres with
comparable axes towards the Galactic centre and along the Galactic rotation.
Their real shape is probably defined by an interaction of different effects.
This can result from a differential rotation of the Galaxy that would increase
the second axis of the ellipsoids. Formally, open clusters with axis relations
of 1.25:1.25:1 would show an ellipticity of 0.2 independent of ![]() .
In the
case of oblate spheres, the adopted method should not underestimate the tidal
radii, since, even in a projection, we always see the largest axis. Therefore,
we do not intend to correct our results for an ellipticity effect.
.
In the
case of oblate spheres, the adopted method should not underestimate the tidal
radii, since, even in a projection, we always see the largest axis. Therefore,
we do not intend to correct our results for an ellipticity effect.
Since our cluster sample is based on a magnitude limited survey (i.e. the ASCC-2.5 catalogue), one expects a different apparent structure of clusters located at different distances from the Sun due to a continuous loss of absolutely faint members in more remote clusters. This change of the apparent structure of a cluster with increasing distance can occur due to mass segregation i.e., due to a different concentration of members of different masses with respect to the cluster centre. In this context, "different input conditions'' can cause a systematic bias in the resulting King parameters as a function of distances.
To estimate a possible distance dependent bias in the tidal radii determined, we carry out simulations based on a semi-empirical model of clusters of our sample. Starting from the original positions of a given cluster, we move, step by step, the cluster away (or move the observer away). At each step, its apparent structure changes since the cluster "shrinks'', loses faint members, and its remaining members become fainter. In accordance with the standard rules of the pipeline that we applied in Paper I to determine tidal radii for our clusters, we build an apparent density profile of the "moved-away'' cluster, fit the profile by the King model and compare the resulting tidal radius with the original finding.
To take into account both the spatial and magnitude effects if a
cluster is moved away, we developed a model based on stellar counts ![]() in
radial and magnitude bins of
in
radial and magnitude bins of
![]() and
and
![]() mag,
respectively. In fact, these counts present the apparent luminosity functions
mag,
respectively. In fact, these counts present the apparent luminosity functions ![]() in radial circles.
in radial circles.
For each cluster, the model considers two components: the "background'', and
the "cluster'' populations. The background consists of field stars projected on
the cluster area, the proper motions and photometry of which are compatible with
those of the real cluster members. Such stars can occur even among the
most probable cluster members. The density profile ![]() of the background
is computed in angular bins of r at the original position of the cluster and
in the same way as that described in Paper I. In our model we assume that the
background remains unchanged during the simulation, i.e. it does not depend
on how far we move away a cluster.
of the background
is computed in angular bins of r at the original position of the cluster and
in the same way as that described in Paper I. In our model we assume that the
background remains unchanged during the simulation, i.e. it does not depend
on how far we move away a cluster.
The cluster component is obtained from counts ![]() inside the cluster
area
inside the cluster
area
![]() where r2 is the observed radius of the cluster. The
corresponding luminosity functions
where r2 is the observed radius of the cluster. The
corresponding luminosity functions ![]() are corrected for the background
using a background luminosity function
are corrected for the background
using a background luminosity function
![]() constructed for the given
cluster. Finally, the resulting luminosity functions in angular bins are
converted to a linear scale in accordance with the distance of the cluster.
constructed for the given
cluster. Finally, the resulting luminosity functions in angular bins are
converted to a linear scale in accordance with the distance of the cluster.
In the simulation, each cluster is moved away with steps of
![]() .
At each step, magnitude bins dropping below the ASCC-2.5 limiting magnitude
(
.
At each step, magnitude bins dropping below the ASCC-2.5 limiting magnitude
(
![]() )
are excluded from further consideration, and a new density
profile of the remaining cluster members is constructed from
)
are excluded from further consideration, and a new density
profile of the remaining cluster members is constructed from ![]() integrated over the current magnitude range. Moving a cluster away makes it suffer from additional
interstellar extinction. Interstellar extinction AV was computed following Parenago's law
integrated over the current magnitude range. Moving a cluster away makes it suffer from additional
interstellar extinction. Interstellar extinction AV was computed following Parenago's law
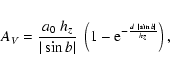
For 56 clusters of our sample, the model calculations were successful in at
least 5 consecutive steps, i.e. these clusters could be moved away, totally, by
more than
![]() .
Their original distance moduli range from
(V-MV)=4.7 to
(V-MV)=13. The results of the simulations for these clusters
are used to derive a correction to
.
Their original distance moduli range from
(V-MV)=4.7 to
(V-MV)=13. The results of the simulations for these clusters
are used to derive a correction to
![]() for a distance dependent bias.
for a distance dependent bias.
In Fig. 3 we show density profiles of the Pleiades as would be
measured in the ASCC-2.5 at two different distances of the cluster; at its real
distance of 130 pc and at a distance of 530 pc from the Sun (
![]() mag). This cluster is selected for illustrating the simulations since it has
high quality membership, a long Main Sequence observed in the ASCC-2.5, and shows
significant mass segregation (see Schilbach et al. 2006), i.e. the effect which may
cause a distance dependent bias in the determination of the tidal radius. Moved
to 530 pc, the Pleiades would have only about half of the members contained in
the ASCC-2.5, and its apparent radius would be decreased by about a factor of four,
from 6 deg to 1.5 deg. The distribution of members appears to be more
concentrated and sharper against the background. Though the accuracy of the
tidal radius derived by the pipeline is lower with increasing distance due to
poorer statistics, the changing of the conditions has only a small influence on
its value (see Fig. 3, panel b). Nevertheless, for the majority
of the 56 clusters the modelled tidal radii are decreasing with larger distances
(e.g., see Fig. 3, panel d), though a few clusters obtain formally
a positive gradient.
mag). This cluster is selected for illustrating the simulations since it has
high quality membership, a long Main Sequence observed in the ASCC-2.5, and shows
significant mass segregation (see Schilbach et al. 2006), i.e. the effect which may
cause a distance dependent bias in the determination of the tidal radius. Moved
to 530 pc, the Pleiades would have only about half of the members contained in
the ASCC-2.5, and its apparent radius would be decreased by about a factor of four,
from 6 deg to 1.5 deg. The distribution of members appears to be more
concentrated and sharper against the background. Though the accuracy of the
tidal radius derived by the pipeline is lower with increasing distance due to
poorer statistics, the changing of the conditions has only a small influence on
its value (see Fig. 3, panel b). Nevertheless, for the majority
of the 56 clusters the modelled tidal radii are decreasing with larger distances
(e.g., see Fig. 3, panel d), though a few clusters obtain formally
a positive gradient.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{8525_f03.eps}\end{figure}](/articles/aa/full/2008/49/aa8525-07/Timg57.gif) |
Figure 3:
Illustration of the performance of the simulation model. Panel a):
density profiles of the Pleiades apparent in the ASCC-2.5 at their original
distance of 130 pc (filled histogram), and if they were moved to 530 pc
(hatched histogram) from the Sun. r is the angular distance from the cluster
centre. Panels b), c): relative variation of the tidal radius determined by
the standard pipeline with increasing distance modulus; Panel b) - for
|
| Open with DEXTER | |
In order to quantify this effect, we consider a relative variation of the tidal
radius
![]() where
where
![]() is the tidal radius of a given cluster at its original distance, and
is the tidal radius of a given cluster at its original distance, and
![]() is its modelled value at a step i. For
each cluster, an unweighted linear fitting of
is its modelled value at a step i. For
each cluster, an unweighted linear fitting of ![]() is carried out as a function of (V-MV).
The slope b of the resulting regression line gives the average relative
variation of the tidal radius per step of
is carried out as a function of (V-MV).
The slope b of the resulting regression line gives the average relative
variation of the tidal radius per step of
![]() .
Since the use
of "apparent distance modulus'' already takes into account a value for AV, the
derived slope does not depend on the adopted details of the interstellar
extinction. The distribution of b for all 56 clusters is shown in Fig. 3, panel (d). We conclude that our model calculations indicate a small but significant
distant dependent bias in the determination of tidal radii, with an average
slope of
.
Since the use
of "apparent distance modulus'' already takes into account a value for AV, the
derived slope does not depend on the adopted details of the interstellar
extinction. The distribution of b for all 56 clusters is shown in Fig. 3, panel (d). We conclude that our model calculations indicate a small but significant
distant dependent bias in the determination of tidal radii, with an average
slope of
![]()
![]() 0.006 mag-1. We checked whether the slope b computed from the model showed a dependence on cluster age, on a parameter s introduced in Schilbach et al. (2006) as an indicator of mass segregation, on the relation of the number of cluster members to background and on other parameters. A correlation was found only between b and (V-MV). In other words, if clusters are "moved away'' the pipeline underestimates their tidal radii, and the degree of
the underestimation is larger for remote clusters than for nearby ones.
0.006 mag-1. We checked whether the slope b computed from the model showed a dependence on cluster age, on a parameter s introduced in Schilbach et al. (2006) as an indicator of mass segregation, on the relation of the number of cluster members to background and on other parameters. A correlation was found only between b and (V-MV). In other words, if clusters are "moved away'' the pipeline underestimates their tidal radii, and the degree of
the underestimation is larger for remote clusters than for nearby ones.
| |
Figure 4:
Distance dependent bias in tidal radii. Panel a): slopes of
|
| Open with DEXTER | |
In Fig. 4a we show the distribution of model slopes b versus
original distance modulus. Since individual data points b have relatively
large rms errors, and their scattering is relatively large, too, we apply a
Lee filter (a standard statistical filtering routine of the IDL library) which is
recommended for retrieving a systematic trend in "noisy'' data. The
distribution of smoothed points can be well approximated by a linear polynom
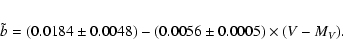
The coefficient ![]() is used in Sect. 4 to correct the previous tidal radii
for the distant depending bias estimated here.
is used in Sect. 4 to correct the previous tidal radii
for the distant depending bias estimated here.
Tidal parameters were determined by a direct fitting of the King model to the
observed density distribution of cluster members (see Paper I) for 236 (36%) of
our clusters. In order to obtain a more significant basis for a further
analysis of the cluster population, an estimation of cluster masses is desirable
for the remaining 414 clusters. Therefore, we searched for a calibration that
can be used to derive cluster tidal radii from observed parameters available for
each cluster. As possible candidates, one can consider the linear radius r2or the semi-major axis ![]() (see Sect. 3.2) since they both describe the
structure of a cluster, though in different way.
(see Sect. 3.2) since they both describe the
structure of a cluster, though in different way.
Being a second-order moment, ![]() is related to the internal density
distribution of cluster members within a cluster, whereas r2 is
defined as a maximum apparent distance of cluster members from the cluster
centre. From this aspect, r2 is more consistent with a tidal radius.
On the other hand, from a statistical point of view,
is related to the internal density
distribution of cluster members within a cluster, whereas r2 is
defined as a maximum apparent distance of cluster members from the cluster
centre. From this aspect, r2 is more consistent with a tidal radius.
On the other hand, from a statistical point of view, ![]() is
a more robust estimate than r2 since it is based on information
on all cluster members. As this property is an important factor for the determination of
tidal masses of clusters, we decided to make the calibration rely upon
is
a more robust estimate than r2 since it is based on information
on all cluster members. As this property is an important factor for the determination of
tidal masses of clusters, we decided to make the calibration rely upon ![]() .
For a better agreement between the systems of tidal
radii
.
For a better agreement between the systems of tidal
radii
![]() and of second-order moments
and of second-order moments ![]() ,
we include a term
depending on the surface density of cluster members in the reduction
polynomial. The best least-squares fit of
,
we include a term
depending on the surface density of cluster members in the reduction
polynomial. The best least-squares fit of ![]() to
to
![]() is achieved with the relation
is achieved with the relation
| |
Figure 5: Differences between measured and calibrated tidal radii via distance modul ( left) and age ( right) of 236 open clusters of our sample. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{8525_f06.eps}\end{figure}](/articles/aa/full/2008/49/aa8525-07/Timg73.gif) |
Figure 6: Schema of construction of the uniform scale of tidal radii. |
| Open with DEXTER | |
The complete scheme of data reduction is shown in Fig. 6. We
start with 236 clusters having tidal parameters
![]() determined directly from
the fitting of three-parametric King's profiles to the observed integrated
density distribution of cluster members. For clusters with tidal radii based on
the solutions with
determined directly from
the fitting of three-parametric King's profiles to the observed integrated
density distribution of cluster members. For clusters with tidal radii based on
the solutions with ![]() -,
-, ![]() -, or "
-, or "![]() ''-membership groups,
we apply the relations derived in Sect. 3.1 and convert them into the system
defined by
''-membership groups,
we apply the relations derived in Sect. 3.1 and convert them into the system
defined by ![]() -members. The resulting
-members. The resulting
![]() of 236 clusters
are used to find a relation between tidal radius and semi-major axis
of 236 clusters
are used to find a relation between tidal radius and semi-major axis ![]() which is also, obtained from the distribution of
which is also, obtained from the distribution of ![]() -members. Then, this
relation is used to estimate calibrated tidal radii
-members. Then, this
relation is used to estimate calibrated tidal radii
![]() for all clusters of
our sample. In the next step, we correct
for all clusters of
our sample. In the next step, we correct
![]() and
and
![]() for the distance dependent bias as found in Sect. 3.3. Finally, according to
King (1962), the resulting tidal radii
for the distance dependent bias as found in Sect. 3.3. Finally, according to
King (1962), the resulting tidal radii ![]() are used to compute tidal masses
are used to compute tidal masses ![]() for each of the 650 clusters from
for each of the 650 clusters from
The tidal radii and masses for the clusters of our sample are listed in a table
that is available in electronic form only, and can be retrieved from the CDS.
For each of the 650 open clusters we give, among other relevant data, the tidal
radius and the corresponding mass computed from the semi-major axis ![]() as
described above (i.e. calibrated parameters). For 236 clusters, the table also
contains the tidal radii and masses based on the direct fitting of the King
model (i.e. measured parameters). The measured parameters should have a higher
priority if the reader is interested in studying individual clusters. For
stellar statistical investigations, however, calibrated parameters are better
suited since they are more homogeneous and available for a larger sample that is
complete up to a distance of about 850 pc from the Sun (see Piskunov et al. 2006).
All (measured and calibrated) tidal parameters are corrected for the
distance dependent bias. The median precision of the tidal radii is about 2 pc, and the median of their relative errors is 0.22.
as
described above (i.e. calibrated parameters). For 236 clusters, the table also
contains the tidal radii and masses based on the direct fitting of the King
model (i.e. measured parameters). The measured parameters should have a higher
priority if the reader is interested in studying individual clusters. For
stellar statistical investigations, however, calibrated parameters are better
suited since they are more homogeneous and available for a larger sample that is
complete up to a distance of about 850 pc from the Sun (see Piskunov et al. 2006).
All (measured and calibrated) tidal parameters are corrected for the
distance dependent bias. The median precision of the tidal radii is about 2 pc, and the median of their relative errors is 0.22.
![\begin{figure}
\par\includegraphics[angle=270,width=6cm,clip]{8525_f07.eps}\end{figure}](/articles/aa/full/2008/49/aa8525-07/Timg76.gif) |
Figure 7: Distributions of tidal radii. The upper panel shows the measured radii for 236 clusters. In the lower panel the distribution of calibrated radii is given for all 650 clusters of our sample. The open histograms correspond to uncorrected radii, the filled/hatched ones are for radii corrected for biases. |
| Open with DEXTER | |
In Fig. 7 we compare measured (upper panels) and calibrated
(bottom panels) tidal radii before and after the correction for a distance
depending bias (open and filled histograms, respectively). As expected, the
corrected radii are, on average, larger, but the shape of their distributions
remains the same as before the corrections. Also, the distributions of measured
and calibrated tidal radii do not differ significantly. Although the sample of
calibrated radii has a larger proportion of small clusters (![]() < 8 pc), their
distribution fits naturally to the distribution of measured tidal radii, and it
does not show any features that would suggest some biases.
< 8 pc), their
distribution fits naturally to the distribution of measured tidal radii, and it
does not show any features that would suggest some biases.
We come to a similar conclusion if we consider the distribution of the
corresponding tidal masses in Fig. 8: the distribution of
calibrated masses (open histogram, lower panel) suits well the distribution of
measured tidal masses (open histogram, upper panel). As expected, the subsample
with measured data includes a larger fraction of the clusters at distances less than 850
pc from the Sun where our cluster sample was found to be complete. A typical
cluster without measured but with calibrated mass is either located at a larger
distance, or it is nearby but is a poorly populated cluster like NGC 7058,
King 6, Mamajek 1. The wing of the mass distribution at
![]() consists
exclusively of associations.
consists
exclusively of associations.
![\begin{figure}
\par\includegraphics[angle=270,width=6cm,clip]{8525_f08.eps}\end{figure}](/articles/aa/full/2008/49/aa8525-07/Timg78.gif) |
Figure 8: Distributions of tidal masses of open clusters. The upper panel shows masses calculated from measured radii for 236 clusters. The lower panel displays the masses calculated from calibrated radii of all 650 clusters of our sample. The open histograms correspond to total distributions, the filled/hatched ones are distributions of corresponding clusters residing in the area where our sample is complete. |
| Open with DEXTER | |
In Paper I we compared our original results on tidal masses with independent determinations based on stellar counts taken from the literature. We found some discrepancies that could not be explained conclusively. Now, after correcting our preliminary results for different systematic effects, it makes sense to repeat the comparison.
We consider masses of galactic open clusters given in Tadross et al. (2002),
Danilov & Seleznev (1994), and Lamers et al. (2005). Tadross et al. (2002) derived cluster masses ![]() for
160 clusters from direct counts of cluster members on CCD frames. Their results
are based on published data taken from different sources. Using original
observations, Danilov & Seleznev (1994) determined masses
for
160 clusters from direct counts of cluster members on CCD frames. Their results
are based on published data taken from different sources. Using original
observations, Danilov & Seleznev (1994) determined masses ![]() for 103 compact, distant (>1 kpc)
clusters by counting stars in cluster areas. Where necessary, the Salpeter
IMF was applied to extrapolate the counts to the limiting magnitude B=16.
Lamers et al. (2005) used data of the COCD to get a normalization of the Salpeter IMF. The masses
for 103 compact, distant (>1 kpc)
clusters by counting stars in cluster areas. Where necessary, the Salpeter
IMF was applied to extrapolate the counts to the limiting magnitude B=16.
Lamers et al. (2005) used data of the COCD to get a normalization of the Salpeter IMF. The masses ![]() were derived for about 380 clusters by extrapolation of
the normalized Salpeter IMF to low mass stars down to
were derived for about 380 clusters by extrapolation of
the normalized Salpeter IMF to low mass stars down to
![]() .
In
Paper I we found that our preliminary results on tidal masses are comparable
with
.
In
Paper I we found that our preliminary results on tidal masses are comparable
with ![]() and
and ![]() but are considerably lower than
but are considerably lower than ![]() .
Since
.
Since ![]() and
and
![]() were expected to be smaller tidal masses, we did not exclude the
possibility that our results were underestimated. On the other hand, the lower
limit of mass integration was chosen arbitrarily in Lamers et al. (2005), and this
(according to Lamers 2007) could cause a mass overestimation by a factor of
two or three. As the masses in Lamers et al. (2005) and Paper I are based on the same
data on membership and cluster parameters taken from Kharchenko et al. (2004) and
Kharchenko et al. (2005a) but use different methods of mass determination, the disagreement
calls for a clear explanation. This was one of the main reasons for us to consider
possible biases in our tidal parameters more carefully.
were expected to be smaller tidal masses, we did not exclude the
possibility that our results were underestimated. On the other hand, the lower
limit of mass integration was chosen arbitrarily in Lamers et al. (2005), and this
(according to Lamers 2007) could cause a mass overestimation by a factor of
two or three. As the masses in Lamers et al. (2005) and Paper I are based on the same
data on membership and cluster parameters taken from Kharchenko et al. (2004) and
Kharchenko et al. (2005a) but use different methods of mass determination, the disagreement
calls for a clear explanation. This was one of the main reasons for us to consider
possible biases in our tidal parameters more carefully.
In Fig. 9 we compare the cluster masses quoted above with tidal
masses computed from the corrected tidal radii. As expected, ![]() and
and ![]() are, on average, smaller than the tidal masses. The trend in
Fig. 9a can be attributed to the data of Danilov & Seleznev (1994), and it
can be explained by a constant limit of apparent magnitudes used for star counts
in all clusters independent of their distance from the Sun.
are, on average, smaller than the tidal masses. The trend in
Fig. 9a can be attributed to the data of Danilov & Seleznev (1994), and it
can be explained by a constant limit of apparent magnitudes used for star counts
in all clusters independent of their distance from the Sun.
On average, the differences between our tidal masses and ![]() have decreased
compared to Paper I, though they are still too large to be explained by random
uncertainties of the methods. According to Fig. 9e, one can
separate three groups of clusters: clusters at
(V-MV)<7.5 with
have decreased
compared to Paper I, though they are still too large to be explained by random
uncertainties of the methods. According to Fig. 9e, one can
separate three groups of clusters: clusters at
(V-MV)<7.5 with ![]() smaller
by a factor of 2.5 than the corresponding tidal masses, clusters at
7.5<(V-MV)<12 where
smaller
by a factor of 2.5 than the corresponding tidal masses, clusters at
7.5<(V-MV)<12 where ![]() are, on average, three times larger than tidal
masses, and clusters at
(V-MV)>12 where both mass estimates are in reasonable
agreement (except two associations with
13<(V-MV)<14). We believe that the
disagreement in masses of nearby clusters has a different nature than the mass
disagreement of more distant clusters.
are, on average, three times larger than tidal
masses, and clusters at
(V-MV)>12 where both mass estimates are in reasonable
agreement (except two associations with
13<(V-MV)<14). We believe that the
disagreement in masses of nearby clusters has a different nature than the mass
disagreement of more distant clusters.
![\begin{figure}
\par\includegraphics[angle=270,width=8.6cm,clip]{8525_f09.eps}\end{figure}](/articles/aa/full/2008/49/aa8525-07/Timg80.gif) |
Figure 9:
Comparison of measured tidal masses |
| Open with DEXTER | |
For nearby clusters, the discrepancy can be explained by a low normalization factor used by Lamers et al. (2005) for the construction of cluster IMFs. This bias may arise from a dependence of the completeness limit of the ASCC-2.5 on (B-V) of the stars. On average, the ASCC-2.5 is complete to V=11.5 for A or F stars. For later spectral classes, the completeness limit becomes brighter than V=11.5. Therefore, in a cluster area with a given nearby cluster, the ASCC-2.5 may contain field stars down to V=11.5 but the faint (i.e., red) cluster members in the flatter part of the cluster main sequence would be missing. If a normalization is computed for the whole magnitude range down to V=11.5 but with an incomplete sample of cluster members at the faint end, the corresponding factor will be too low. In more distant clusters, ASCC-2.5 contains only members in the steeper part of the main sequence, i.e., cluster stars with smaller (B-V). Therefore, the completeness limit of the ASCC-2.5 corresponds to the completeness limit of cluster members, and the normalization factors for the IMFs become correct for remote clusters.
For clusters at
(V-MV)> 7.5, the reason for the disagreement between ![]() and tidal masses is completely different. As we have shown in Schilbach et al. (2006),
our sample contains clusters of different ages at
(V-MV)<10.5, and with
increasing distance the sample becomes more and more "young'' since, at large
distances, the ASCC-2.5 contains only blue luminous stars which are only present in
young clusters. This is a natural consequence of each magnitude-limited survey
used for cluster identification. The systematic effect apparent in
Fig. 9e can, therefore, be better understood if we consider the
relation
and tidal masses is completely different. As we have shown in Schilbach et al. (2006),
our sample contains clusters of different ages at
(V-MV)<10.5, and with
increasing distance the sample becomes more and more "young'' since, at large
distances, the ASCC-2.5 contains only blue luminous stars which are only present in
young clusters. This is a natural consequence of each magnitude-limited survey
used for cluster identification. The systematic effect apparent in
Fig. 9e can, therefore, be better understood if we consider the
relation
![]() as a function of cluster age (Fig. 9f). The
cluster population within 1 kpc from the Sun includes a large portion of
clusters with typical ages of several hundred Myrs (Piskunov et al. 2006). In
such clusters, due to a loss of members (preferentially of small masses) during
the dynamical evolution (e.g. Baumgardt & Makino 2003), the mass spectra of cluster
members differ from the initial mass functions. Assuming the Salpeter IMF for
these clusters, one would, therefore, overestimate cluster masses. This can
explain the increasing difference between
as a function of cluster age (Fig. 9f). The
cluster population within 1 kpc from the Sun includes a large portion of
clusters with typical ages of several hundred Myrs (Piskunov et al. 2006). In
such clusters, due to a loss of members (preferentially of small masses) during
the dynamical evolution (e.g. Baumgardt & Makino 2003), the mass spectra of cluster
members differ from the initial mass functions. Assuming the Salpeter IMF for
these clusters, one would, therefore, overestimate cluster masses. This can
explain the increasing difference between ![]() and tidal masses with increasing
age of clusters. Note that nearby clusters follow the same general trend in
Fig. 9f like the more distant clusters.
and tidal masses with increasing
age of clusters. Note that nearby clusters follow the same general trend in
Fig. 9f like the more distant clusters.
This conclusion has statistical support in Fig. 10 where we
compare calibrated tidal masses with data of Lamers et al. (2005). We exclude
associations and nearby clusters at (V-MV) < 7.5 from the consideration.
Since calibrated tidal masses are available for all clusters, the number of data
points is, however, about twice as large as in Fig. 9f. We
conclude that both mass estimates are in reasonable agreement for the youngest
clusters where dynamical evolution had no time to change the IMF significantly.
For clusters with ages
![]() (a typical scale for two body
encounters), the ratio
(a typical scale for two body
encounters), the ratio
![]() does not change much but is significantly
larger than 1. This can indicate that, already in relatively young clusters, the
actual mass function differs from the Salpeter IMF. For clusters of larger ages
the ratio
does not change much but is significantly
larger than 1. This can indicate that, already in relatively young clusters, the
actual mass function differs from the Salpeter IMF. For clusters of larger ages
the ratio
![]() steadily increases with time and reaches a factor of 10 for
the oldest clusters. We interpret the systematic trend in
Fig. 10 as indirect evidence from observations of an
evolution of MFs in open clusters.
steadily increases with time and reaches a factor of 10 for
the oldest clusters. We interpret the systematic trend in
Fig. 10 as indirect evidence from observations of an
evolution of MFs in open clusters.
![\begin{figure}
\par\includegraphics[angle=270,width=6.45cm,clip]{8525_f10.eps}\end{figure}](/articles/aa/full/2008/49/aa8525-07/Timg85.gif) |
Figure 10:
Same as Fig. 9f but for calibrated tidal masses |
| Open with DEXTER | |
Although being a basic parameter in studies of cluster evolution, the mass of an
open cluster can not be derived directly from the present day observations.
Indirect methods require, however, a number of assumptions that can cause
different biases in the resulting mass estimates. In Paper I we presented mass
estimates of 236 clusters derived via tidal radii. The tidal radii were
obtained from a three-parameter fit of King's profiles to the density
distribution of cluster members projected on the sky. This method assumes
systems with spherical density distributions whereas open clusters can have
elliptical shape and a preferential orientation of their main axes in the
Galaxy. In this case one should expect a systematic underestimation of tidal
radii, depending on the location of clusters with respect to the Sun and to the
centre of the Galaxy. Though a typical open cluster shows an ellipticity
(for details see Kharchenko et al. 2007), no significant trend is found depending on the
aspect angle of clusters. Therefore, we assume that the orientation of open
clusters is rather random. Moreover, the average ellipticity is relatively small
(
![]()
![]() 0.10) in order to produce a prominent bias in the
determination of tidal radii. We cannot claim that for individual
clusters the ellipticity would not have an impact on the results, however this will
not affect the general conclusions based on statistical studies on the cluster
population.
0.10) in order to produce a prominent bias in the
determination of tidal radii. We cannot claim that for individual
clusters the ellipticity would not have an impact on the results, however this will
not affect the general conclusions based on statistical studies on the cluster
population.
Another possible bias in the resulting tidal radii may arise from the relative
bright magnitude limit of the ASCC-2.5 that was used to identify the clusters, to
determine the membership and to construct the density profiles in cluster areas.
Beyond 300 pc from the Sun, the ASCC-2.5 practically does not include dwarfs later
than G0. This fact can introduce discrepancies in the determination of
tidal radii by the method applied. The question is whether possible discrepancies
are of systematic or random nature. Taking into account apparent luminosity functions of
cluster members and field stars in each cluster area, we constructed a
semi-empirical model of clusters found in the ASCC-2.5. "Moving'' a cluster away
from the Sun, we applied the standard pipeline for the determination of tidal
radii. We found that, on average, the pipeline produces smaller tidal radii with
increasing distance of the clusters: for nearby clusters the correction factor
is almost 1 but it becomes about 1.7 for clusters at
(V-MV)=13. As the
simulations are limited to clusters with
![]() ,
for more distant
clusters the correction factor is the result of an extrapolation reaching
a value of about 2 for the most distant cluster of our sample at
,
for more distant
clusters the correction factor is the result of an extrapolation reaching
a value of about 2 for the most distant cluster of our sample at
![]() .
.
Unfortunately, the subsample of 236 clusters with tidal radii derived from the King model is neither representative nor complete to a given distance from the Sun. Therefore, the other main goal of this work was to find a parameter available for all clusters of the sample to estimate the cluster tidal radii. Among different candidates we chose the semi-major axis of the projected distribution of cluster members within the cluster area. The relation between tidal radii and the semi-major axis of 236 clusters was then used to compute calibrated tidal radii for all 650 clusters. We did not find systematic differences between measured and calibrated tidal radii as a function of cluster distance or age. Again, for individual clusters the relation may not be perfect but using reliable information on cluster membership, it provides a confident basis for statistical studies of the properties of the local cluster population.
After the correction for a distance depending bias, measured and calibrated
tidal radii were used to derive tidal masses for the clusters. As expected,
tidal masses are, on average, larger than masses obtained exclusively from star
counts by Danilov & Seleznev (1994) and Tadross et al. (2002). On the other hand, we find systematic
differences between tidal masses and mass estimates by Lamers et al. (2005) who used
COCD data on star counts and the Salpeter IMF extrapolated down to
![]() .
The discrepancy is small for young clusters and increases
considerably with cluster age. We believe that the systematics can be reduced if
the mass estimates by Lamers et al. (2005) would consider a change of the mass function
of a cluster during its dynamical evolution. This assumption can be verified
by comparison with virial masses of open clusters that are based on another
independent method of mass estimate. A corresponding project is underway
(Gieles 2007).
.
The discrepancy is small for young clusters and increases
considerably with cluster age. We believe that the systematics can be reduced if
the mass estimates by Lamers et al. (2005) would consider a change of the mass function
of a cluster during its dynamical evolution. This assumption can be verified
by comparison with virial masses of open clusters that are based on another
independent method of mass estimate. A corresponding project is underway
(Gieles 2007).
Acknowledgements
We acknowledge the anonymous referee for his/her comments, which enabled us to improve the clarity of the paper. This study was supported by DFG grant 436 RUS 113/757/0-2, and RFBR grant 06-02-16379.