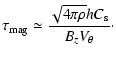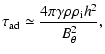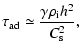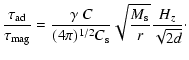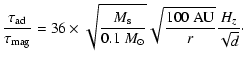A&A 477, 25-34 (2008)
DOI: 10.1051/0004-6361:20078310
Magnetic processes in a collapsing dense core
II. Fragmentation. Is there a fragmentation crisis?
P. Hennebelle1 - R. Teyssier2
1 - Laboratoire de radioastronomie millimétrique, UMR 8112 du
CNRS,
École normale supérieure et Observatoire de Paris,
24 rue Lhomond, 75231 Paris Cedex 05, France
2 - Service d'Astrophysique, CEA/DSM/DAPNIA/SAp, Centres d'Études de Saclay,
91191 Gif-sur-Yvette Cedex, France
Received 18 July 2007 / Accepted 17 September 2007
Abstract
Context. A large fraction of stars are found in binary systems. It is therefore important for our understanding of the star formation process, to investigate the fragmentation of dense molecular cores.
Aims. We study the influence of the magnetic field, ideally coupled to the gas, on the fragmentation in multiple systems of collapsing cores.
Methods. We present high resolution numerical simulations performed with the RAMSES MHD code starting with a uniform sphere in solid body rotation and a uniform magnetic field parallel to the rotation axis. We pay particular attention to the strength of the magnetic field and interpret the results using the analysis presented in a companion paper.
Results. The results depend much on the amplitude, A, of the perturbations seeded initially. For a low amplitude, A=0.1, we find that for values of the mass-to-flux over critical mass-to-flux ratio,  ,
as high as
,
as high as 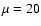 ,
the centrifugally supported disk which fragments in the hydrodynamical case is stabilized and remains axisymmetric. Detailed investigations reveal that this is due to the rapid growth of the toroidal magnetic field induced by the differential motions within the disk. For values of
,
the centrifugally supported disk which fragments in the hydrodynamical case is stabilized and remains axisymmetric. Detailed investigations reveal that this is due to the rapid growth of the toroidal magnetic field induced by the differential motions within the disk. For values of  smaller than
smaller than  5, corresponding to higher magnetic intensities, there is no centrifugally supported disk because of magnetic braking. When the amplitude of the perturbation is equal to A=0.5, each initial peak develops independently and the core fragments for a large range of
5, corresponding to higher magnetic intensities, there is no centrifugally supported disk because of magnetic braking. When the amplitude of the perturbation is equal to A=0.5, each initial peak develops independently and the core fragments for a large range of  .
Only for values of
.
Only for values of  close to 1 is the magnetic field able to prevent the fragmentation.
close to 1 is the magnetic field able to prevent the fragmentation.
Conclusions. Since a large fraction of stars are binaries, the results of low magnetic intensities preventing the fragmentation in the case of weak perturbations is problematic. We discuss three possible mechanisms which could lead to the formation of binary systems, namely the presence of high amplitude fluctuations in the core initially, ambipolar diffusion and fragmentation during the second collapse.
Key words: magnetohydrodynamics (MHD) - instabilities - ISM:
kinematics and dynamics - ISM: structure - ISM: clouds
Understanding the fragmentation of collapsing prestellar dense core, is of great importance
to our understanding of the star formation process. In particular, determining the
number of fragments, their masses and their orbital characteristics are fundamental
and rather challenging problems. A significant fraction of stars are
found in binary or multiple systems (Duquenoy & Mayor 1991; although see Lada 2006).
Many studies have investigated this issue in the context of hydrodynamical calculations
(e.g. Miyama 1992; Boss 1993; Bonnell 1994; Truelove et al. 1998; Bate & Burkert 1997;
Bodenheimer et al. 2000; Matsumoto & Hanawa 2003; Hennebelle et al. 2004; Goodwin et al. 2004;
Banerjee et al. 2004).
Although detailed conclusions appear to be very sensitive to the
initial conditions (i.e. core shape, thermal, rotational and turbulent energy
as well as to the equations of state), some trends can nevertheless be inferred.
It is widely accepted that, under realistic initial conditions, a collapsing dense core
fragments into a few objects, the exact number depending on the specific conditions. Therefore,
fragmentation of a rotating collapsing dense core appears to be the most widely accepted
mechanism to explain the formation of multiple systems. Indeed, it is today the only
viable mechanism since other possibilities such as fission of a rotating protostar or
capture of a companion fail in realistic conditions to produce a large fraction of
binaries (Bodenheimer et al. 2000).
Due to the difficulty of the problem and despite its importance, the question of the role
of the magnetic field in this process has remained little addressed.
With the recent progress achieved in numerical techniques as well as increasing
computing power, several studies have investigated this issue.
Hosking & Whitworth (2003) using an SPH two fluid code conclude that magnetically
subcritical cores do not fragment. Machida et al. (2005) using a nested grid code performed an
extensive number of calculations varying the initial core rotation and magnetic field.
They find that fragmentation is possible if the rotation is sufficiently large and the magnetic
field strength sufficiently small.
Fragmentation of a collapsing magnetized cloud using adaptive mesh refinement techniques have also
been studied by Ziegler (2005), Banerjee & Pudritz (2006) and Fromang et al. (2006) which all find that
the magnetic field has a strong influence.
Price & Bate (2007), using magnetized SPH techniques
which insure the nullity of the divergence of the magnetic field, find that
with large initial perturbations, even for large values of the magnetic strength,
fragmentation is possible.
In all these studies, it has been found that the magnetic field has a strong
impact on the fragmentation of the collapsing dense core.
In this paper, we further study the fragmentation of collapsing cores, focusing mainly
on the influence of the magnetic field strength and the amplitude of the initial perturbation.
Using the analysis developed
in the companion paper by Hennebelle & Fromang (2008, hereafter Paper I),
we try to understand, when possible quantitatively, the physical reasons for the
numerical results.
As in Paper I, we consider initially a uniform density cloud
in solid body rotation,
threaded by a uniform magnetic field. At this stage, we restrict the problem to the case
where the magnetic field and rotation axis are aligned. We note that Price & Bate (2007) have
investigated the influence of initially perpendicular rotation axis and magnetic field.
More realistic initial conditions, including a non uniform density field, turbulent velocity field
and rotation axis non aligned with the magnetic field, will be considered in future studies.
In particular, we determine the lowest
value of  ,
the mass-to-flux over critical mass-to-flux ratio for which fragmentation
is suppressed. It turns out that the results depend strongly on the
amplitude of the initial perturbation.
,
the mass-to-flux over critical mass-to-flux ratio for which fragmentation
is suppressed. It turns out that the results depend strongly on the
amplitude of the initial perturbation.
The paper is organized as follow. In the second section, we consider the same initial
conditions as used in Paper I, namely a spherical uniform one solar mass dense core.
The thermal over gravitational energy of the core is equal to  0.37 and the rotation over gravitational energy is 0.045.
Note that such rotations are typical of (perhaps slightly larger than) values observed in dense cores (Goodman et al. 1993).
The initial density is about
0.37 and the rotation over gravitational energy is 0.045.
Note that such rotations are typical of (perhaps slightly larger than) values observed in dense cores (Goodman et al. 1993).
The initial density is about 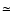
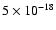 g cm-3and the cloud radius
g cm-3and the cloud radius
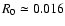 pc. The freefall time is thus of the order of
pc. The freefall time is thus of the order of
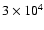 years.
We use a barotropic equation of state:
years.
We use a barotropic equation of state:
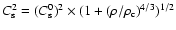 ,
where
,
where
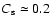 km s-1 is the sound speed and
km s-1 is the sound speed and
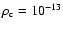 g cm-3.
This set of cloud parameters is known to
give rise to a disk that unambiguously fragments in the pure hydrodynamics case. The only difference to Paper I is that
an m=2 perturbation of amplitude A=0.1 in the density field,
g cm-3.
This set of cloud parameters is known to
give rise to a disk that unambiguously fragments in the pure hydrodynamics case. The only difference to Paper I is that
an m=2 perturbation of amplitude A=0.1 in the density field,
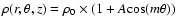 ,
as well as in the Bz field,
is added. In the third section, we further discuss the physical interpretation of the results
obtained in our simulations and we estimate analytically the critical value of
,
as well as in the Bz field,
is added. In the third section, we further discuss the physical interpretation of the results
obtained in our simulations and we estimate analytically the critical value of  for
which it is expected that the magnetic field stabilizes the disk.
In the fourth section, we consider initial density perturbations of amplitude 0.5 and show that in this
case, fragmentation can be obtained for a much wider range of
for
which it is expected that the magnetic field stabilizes the disk.
In the fourth section, we consider initial density perturbations of amplitude 0.5 and show that in this
case, fragmentation can be obtained for a much wider range of  .
The fifth section provides a discussion of possible mechanisms leading to disk fragmentation and the
formation of binaries, even in the presence of magnetic fields.
The sixth section concludes the paper.
.
The fifth section provides a discussion of possible mechanisms leading to disk fragmentation and the
formation of binaries, even in the presence of magnetic fields.
The sixth section concludes the paper.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{8310fig01.ps}\par\vspace*{2m...
....ps}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{8310fig03.ps}\end{figure}](/articles/aa/full/2008/49/aa8310-07/Timg17.gif) |
Figure 1:
Equatorial density and velocity field for mass-to-flux over critical
mass-to-flux ratio 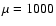 and perturbation amplitude A=0.1.
The size of the figure corresponds to about one ten of the cloud initial radius.
In physical units, this is about 300 AU. The freefall time is about
and perturbation amplitude A=0.1.
The size of the figure corresponds to about one ten of the cloud initial radius.
In physical units, this is about 300 AU. The freefall time is about
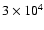 years. years. |
| Open with DEXTER |
We investigate fragmentation in the case where the amplitude of the perturbations
is initially A=0.1. In this case it is found that without rotation no fragmentation
occurs. Therefore, we call this type of fragmentation,
rotationally driven fragmentation.
We next consider various values of the magnetic mass-to-flux over critical mass-to-flux ratio,
namely 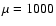 (quasi hydrodynamical case),
(quasi hydrodynamical case), 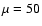 ,
20, 5, 2 and 1.25. Recalling that
,
20, 5, 2 and 1.25. Recalling that
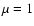 corresponds to the case of a cloud supported by the magnetic field, the
last value corresponds to a strongly magnetized supercritical cloud.
corresponds to the case of a cloud supported by the magnetic field, the
last value corresponds to a strongly magnetized supercritical cloud.
In the following, we display the inner part of the collapsing cloud. The
size of each plot is about 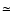 R0/10. This corresponds to a physical size of
R0/10. This corresponds to a physical size of
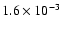 pc or about
pc or about 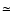 300 AU.
300 AU.
We present the hydrodynamic case (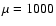 ).
Figure 1 shows three snapshots.
Equatorial density and velocity field are displayed.
The first snapshot is taken shortly after the formation
of the first Larson core. A rotationally supported structure has formed and
since it is very unstable, a strong spiral pattern develops. This is very
similar to the results obtained by other authors (e.g. Matsumoto & Hanawa 2003;
Hennebelle et al. 2004; Goodwin et al. 2004). The next snapshot shows that
the central bar-like structure fragments into two objects whereas the spiral
pattern keeps growing and expanding due to further accretion of mass and momentum.
The last snapshot shows that the centrifugally supported structure continues
fragmenting and that 5 fragments have developed. Altogether, this is very
similar to the results reported by many authors investigating the fragmentation
of hydrodynamical rotating cores. We note that in spite of the strongly non-linear
evolution, the result remains remarkably symmetric due to proper resolution of
the Jeans length (10 numerical cells per Jeans length) despite the use of the Roe solver
known to be weakly diffusive.
).
Figure 1 shows three snapshots.
Equatorial density and velocity field are displayed.
The first snapshot is taken shortly after the formation
of the first Larson core. A rotationally supported structure has formed and
since it is very unstable, a strong spiral pattern develops. This is very
similar to the results obtained by other authors (e.g. Matsumoto & Hanawa 2003;
Hennebelle et al. 2004; Goodwin et al. 2004). The next snapshot shows that
the central bar-like structure fragments into two objects whereas the spiral
pattern keeps growing and expanding due to further accretion of mass and momentum.
The last snapshot shows that the centrifugally supported structure continues
fragmenting and that 5 fragments have developed. Altogether, this is very
similar to the results reported by many authors investigating the fragmentation
of hydrodynamical rotating cores. We note that in spite of the strongly non-linear
evolution, the result remains remarkably symmetric due to proper resolution of
the Jeans length (10 numerical cells per Jeans length) despite the use of the Roe solver
known to be weakly diffusive.
We present results for the weak field cases, 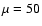 and
and 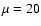 .
Figure 2 shows results for
.
Figure 2 shows results for 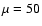 .
Due to the difference in the
initial magnetic strengths, it is not possible to compare the simulations at
exactly the same times.
The first snapshot shows a spiral pattern which is similar to the
one seen in the previous
case. A difference however, is that the central bar-like structure appears to be
much shorter. This is likely due to the central magnetic field which is strongly
amplified by the rapid twisting of field lines. As a result, the cloud first fragments
into three fragments instead of two. This is due to the fact that since the central
bar-like structure does not fragment in two objects as in the previous case, more material
and angular momentum is available in its vicinity to produce one object on each side.
The next snapshot shows that a symmetry breaking occurs due to one of the two
satellites having merged with the central more massive fragment. The structure in the
outer part (
x>0.03 R0) is still quite symmetric. Further fragments are forming in
the outer part of the spiral pattern at
.
Due to the difference in the
initial magnetic strengths, it is not possible to compare the simulations at
exactly the same times.
The first snapshot shows a spiral pattern which is similar to the
one seen in the previous
case. A difference however, is that the central bar-like structure appears to be
much shorter. This is likely due to the central magnetic field which is strongly
amplified by the rapid twisting of field lines. As a result, the cloud first fragments
into three fragments instead of two. This is due to the fact that since the central
bar-like structure does not fragment in two objects as in the previous case, more material
and angular momentum is available in its vicinity to produce one object on each side.
The next snapshot shows that a symmetry breaking occurs due to one of the two
satellites having merged with the central more massive fragment. The structure in the
outer part (
x>0.03 R0) is still quite symmetric. Further fragments are forming in
the outer part of the spiral pattern at
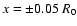 .
.
From these results, one concludes that even for values of  as
large as 50, the magnetic field has a significant impact on the
evolution of the centrifugally supported inner structure, particularly on
its fragmentation. This is due to the strong amplification of the
toroidal and radial magnetic field generated by the differential
motions in the collapsing core and in the centrifugally supported
structure (see Paper I and the following sections).
as
large as 50, the magnetic field has a significant impact on the
evolution of the centrifugally supported inner structure, particularly on
its fragmentation. This is due to the strong amplification of the
toroidal and radial magnetic field generated by the differential
motions in the collapsing core and in the centrifugally supported
structure (see Paper I and the following sections).
Figure 3 shows three snapshots for 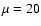 .
The first snapshot shows a weak spiral pattern in the inner part.
The second and third panels shows that the centrifugally supported structure grows
as in the previous cases but it remains much more uniform and the spiral
pattern is much less pronounced.
As shown in
Paper I, the angular momentum profile is similar to the hydrodynamical case since the
magnetic braking is very weak during the collapse phase.
Therefore, the difference to the case
.
The first snapshot shows a weak spiral pattern in the inner part.
The second and third panels shows that the centrifugally supported structure grows
as in the previous cases but it remains much more uniform and the spiral
pattern is much less pronounced.
As shown in
Paper I, the angular momentum profile is similar to the hydrodynamical case since the
magnetic braking is very weak during the collapse phase.
Therefore, the difference to the case 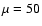 ,
is not less
angular momentum but rather a stronger magnetic field.
Indeed, with a magnetic toroidal component,
the velocity of the fast MHD waves, which can be loosely seen as an
effective sound speed, is:
,
is not less
angular momentum but rather a stronger magnetic field.
Indeed, with a magnetic toroidal component,
the velocity of the fast MHD waves, which can be loosely seen as an
effective sound speed, is:
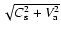 where
where
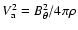 (see Sect. 3). Therefore, the disk is stabilized
against gravitational fragmentation.
As a result, no fragmentation is obtained, only one central star forms and
grows by accretion. We stress that the value of the magnetic field
corresponding to
(see Sect. 3). Therefore, the disk is stabilized
against gravitational fragmentation.
As a result, no fragmentation is obtained, only one central star forms and
grows by accretion. We stress that the value of the magnetic field
corresponding to 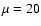 is very modest, far below the
values inferred from observations which indicates that
is very modest, far below the
values inferred from observations which indicates that 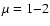 (Crutcher 1999).
(Crutcher 1999).
Finally, to explore whether the suppression of the fragmentation depends on
initial conditions, such as the values of 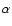 and
and 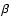 (the ratios
of thermal and rotational to gravitational energies), we have performed runs
with different
(the ratios
of thermal and rotational to gravitational energies), we have performed runs
with different 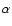 and
and 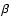 values.
First, we explore the influence of stronger and weaker rotation choosing
values.
First, we explore the influence of stronger and weaker rotation choosing 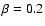 and
and
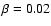 respectively, keeping the value of
respectively, keeping the value of 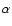 constant.
The behaviour of these runs is very similar to the one with
constant.
The behaviour of these runs is very similar to the one with
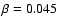 presented here. A large disk forms but it remains well axisymmetric and does not fragment.
We have also explored the effect of a lower thermal energy, taking
presented here. A large disk forms but it remains well axisymmetric and does not fragment.
We have also explored the effect of a lower thermal energy, taking
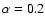 and keeping
and keeping
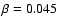 .
The disk is slightly more axisymmetric than in the case
.
The disk is slightly more axisymmetric than in the case
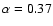 but does not fragment either.
but does not fragment either.
We conclude that, for small initial density perturbations, a magnetized dense core
ideally coupled to the magnetic field and having 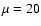 does not fragment
for a large range of initial conditions.
does not fragment
for a large range of initial conditions.
We compare our results with the study of Machida et al. (2005) although it is
not straightforward because their initial
conditions consist of a filament and therefore are different from ours.
Also they used different definitions to quantify the
amount of rotation and magnetic energies in their simulations. Comparison with their Fig. 10 is
worthwhile nevertheless. Their parameter 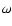 turns out to be equal to
turns out to be equal to
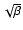 .
However, their initial state has a peak density of about 104 cm-3 which is less
dense than ours by a factor of roughly 100. Since the ratio of rotational over gravitational energies increases during
the collapse, we can say that our
.
However, their initial state has a peak density of about 104 cm-3 which is less
dense than ours by a factor of roughly 100. Since the ratio of rotational over gravitational energies increases during
the collapse, we can say that our
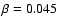 correspond to
correspond to
 in Machida et al.
study (for a homologous contraction
in Machida et al.
study (for a homologous contraction
 ,
this would indicate that
,
this would indicate that
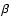 should be divided by roughly
should be divided by roughly 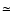 4-5 to be compared with
the Machida et al.'s results).
For values of
4-5 to be compared with
the Machida et al.'s results).
For values of
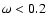 ,
they found that for
,
they found that for
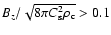 ,
they have no fragmentation.
Comparing this value with our parameters is again not straightforward but
,
they have no fragmentation.
Comparing this value with our parameters is again not straightforward but
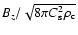 is about
is about
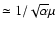 .
For
.
For
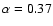 and
and 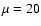 ,
,
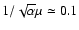 .
Therefore, our results broadly agree with the results of Machida et al. (2005).
.
Therefore, our results broadly agree with the results of Machida et al. (2005).
Comparison with the study of Price & Bate (2007) is not possible at this stage, since they use
a barotropic equation of state which becomes adiabatic at 10-14 g cm-3. Thus, even the hydrodynamical
calculations they present do not fragment when the perturbation is weak (their Fig. 3).
We present results for the intermediate magnetized cases, namely
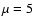 and
and 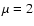 .
Figure 4 shows two snapshots for
.
Figure 4 shows two snapshots for
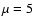 .
As shown in Paper I, no centrifugally supported structure
forms, instead a magnetized pseudo-disk develops.
Pseudo-disks arise when disk-like structures form, say
oblate ellipsoids, which are not supported by rotation and are produced by
the magnetic field. According to the analysis presented
in Paper I, the angular momentum is lower for these values of
.
As shown in Paper I, no centrifugally supported structure
forms, instead a magnetized pseudo-disk develops.
Pseudo-disks arise when disk-like structures form, say
oblate ellipsoids, which are not supported by rotation and are produced by
the magnetic field. According to the analysis presented
in Paper I, the angular momentum is lower for these values of  primarily because the collapse occurs first along the
field lines. Thus, the material within the pseudo-disk and central object
was initially located along the pole and has less angular momentum.
Some magnetic braking also occurs, reducing the angular
momentum further. As a consequence, no centrifugally supported disk is
observed and no fragmentation occurs.
primarily because the collapse occurs first along the
field lines. Thus, the material within the pseudo-disk and central object
was initially located along the pole and has less angular momentum.
Some magnetic braking also occurs, reducing the angular
momentum further. As a consequence, no centrifugally supported disk is
observed and no fragmentation occurs.
Figure 5 shows two snapshots for 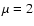 .
The first panel shows that a filamentary structure has developed after
t=1.51 freefall times. We believe that this filament is due to the non-linear
evolution of the initial m=2 perturbation. The reason why it has a shape
different to the previous case is that since the cloud is more supported by the
magnetic field, the collapse lasts 30
.
The first panel shows that a filamentary structure has developed after
t=1.51 freefall times. We believe that this filament is due to the non-linear
evolution of the initial m=2 perturbation. The reason why it has a shape
different to the previous case is that since the cloud is more supported by the
magnetic field, the collapse lasts 30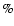 longer. Therefore the perturbation
has more time to develop and to become non-linear. Indeed, if no perturbation is
included initially, an axisymmetric pseudo-disk develops.
longer. Therefore the perturbation
has more time to develop and to become non-linear. Indeed, if no perturbation is
included initially, an axisymmetric pseudo-disk develops.
We now consider the case of a very magnetized supercritical core having
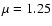 .
As expected the collapsing time is now longer and roughly
equal to two freefall times.
As revealed by the two panels of Fig. 6, the
collapsing dense core remains almost axisymmetric in spite of the
initial m=2 density perturbations. This is due to the strong magnetic support
which prevents the development of the perturbation. Indeed, since the cloud is nearly
supported by the magnetic field, the magnetic Jeans Mass is just slightly smaller
than the cloud mass. Therefore, each peak of the m=2 density perturbation is
gravitationally stable. Moreover, unlike the thermal support, the magnetic support
does not decrease during the collapse since the ratio of magnetic over gravitational
energy stays roughly constant. Therefore the magnetic Jeans mass stays roughly
constant, unlike the thermal Jeans mass.
.
As expected the collapsing time is now longer and roughly
equal to two freefall times.
As revealed by the two panels of Fig. 6, the
collapsing dense core remains almost axisymmetric in spite of the
initial m=2 density perturbations. This is due to the strong magnetic support
which prevents the development of the perturbation. Indeed, since the cloud is nearly
supported by the magnetic field, the magnetic Jeans Mass is just slightly smaller
than the cloud mass. Therefore, each peak of the m=2 density perturbation is
gravitationally stable. Moreover, unlike the thermal support, the magnetic support
does not decrease during the collapse since the ratio of magnetic over gravitational
energy stays roughly constant. Therefore the magnetic Jeans mass stays roughly
constant, unlike the thermal Jeans mass.
3 Physical interpretation
One of the important conclusions reached in the previous section is that
fragmentation can be suppressed even for large values of  ,
i.e. weak
magnetic fields.
Here we discuss the physical reason for the disk stabilization
arising at low magnetic strength. We stress that
since the angular momentum is nearly identical for
,
i.e. weak
magnetic fields.
Here we discuss the physical reason for the disk stabilization
arising at low magnetic strength. We stress that
since the angular momentum is nearly identical for 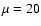 to
the hydrodynamical case (see Paper I), the reason for this
stabilization is not magnetic braking.
to
the hydrodynamical case (see Paper I), the reason for this
stabilization is not magnetic braking.
The influence of the magnetic field on the stability of a
self-gravitating disk was first investigated by Lynden-Bell
(1966) for a uniform rotation. The dispersion relation he obtained
(see his Eq. (1)) entails an effective sound speed
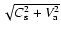 showing that the magnetic pressure term has a stabilizing
influence. However, there is also a destabilizing contribution due to the magnetic
tension term. As a result, such configurations are unstable.
showing that the magnetic pressure term has a stabilizing
influence. However, there is also a destabilizing contribution due to the magnetic
tension term. As a result, such configurations are unstable.
Elmegreen (1987) and Gammie (1996) both consider the influence of
the magnetic field on the stability of a differentially rotating
system. In that case, the shear drives the growth of a
toroidal magnetic component which stabilizes the disk.
They both conclude that whereas in the absence of shear the magnetic
field is strongly destabilizing, it has a stabilizing influence when
significant shear is present. More precisely, Gammie (1996) computed the response
of the disk to nonaxisymmetric perturbations for various value of Q, the
Toomre parameter. He shows that the response is much weaker when a
substantial magnetic field is present and
concludes that the stabilizing effect of the field
becomes significant once the magnetic pressure is comparable to the gas
pressure. This is qualitatively in good agreement with our results. In particular, we see
that the disk in the case 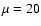 remains much more axisymmetric than
in the case
remains much more axisymmetric than
in the case 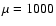 and
and 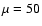 .
.
In order to quantitatively verify that this mechanism is responsible for the disk stabilization,
we have computed the Alfvén speed associated with the azimuthal component of the magnetic field,
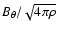 ,
within the disk
at various times corresponding to the period during which fragmentation takes place.
Since both
,
within the disk
at various times corresponding to the period during which fragmentation takes place.
Since both 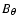 and
and 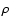 vary, we have integrated at all radii along the z-axis
through the disk.
As explained in Paper I, as soon as the azimuthal component of the magnetic field exceeds the
ram pressure of infalling material, a magnetic tower builds up and the disk starts expanding along
the pole. In this case, the disk boundaries are not clearly defined.
We adopt here a density threshold to define the disk and stop the integration when
vary, we have integrated at all radii along the z-axis
through the disk.
As explained in Paper I, as soon as the azimuthal component of the magnetic field exceeds the
ram pressure of infalling material, a magnetic tower builds up and the disk starts expanding along
the pole. In this case, the disk boundaries are not clearly defined.
We adopt here a density threshold to define the disk and stop the integration when
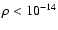 g cm-3.
We calculate
g cm-3.
We calculate
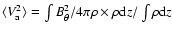 ,
which allows us to estimate
,
which allows us to estimate
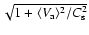 within the disk.
Figure 7 shows
within the disk.
Figure 7 shows
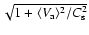 for
for 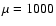 ,
50 and 20. As can be seen, for the case
,
50 and 20. As can be seen, for the case 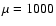 ,
the quantity
,
the quantity
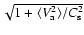 remains smaller than 1.2 at all the
times displayed.
Figure 1 shows that by this time, fragmentation has already occurred.
The second and third panel of Fig. 7 show that
remains smaller than 1.2 at all the
times displayed.
Figure 1 shows that by this time, fragmentation has already occurred.
The second and third panel of Fig. 7 show that
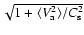 grows
much more rapidly for smaller
grows
much more rapidly for smaller  reaching values greater than 2. The growth is
more rapid for
reaching values greater than 2. The growth is
more rapid for 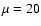 than it is for
than it is for 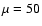 .
We conclude that the growth of the toroidal
component induced by the differential rotation is mainly responsible
for disk stabilization.
.
We conclude that the growth of the toroidal
component induced by the differential rotation is mainly responsible
for disk stabilization.
For simplicity, the works mentioned above have restricted the analysis to a
thin disk. However, the expansion of the magnetic tower
triggered by the growth of the toroidal magnetic field
removes some material from the disk and therefore
reduces the disk surface density. This makes the disk even less prone to fragmentation.
This effect, which is not taken into account in the thin disk analysis,
certainly contributes to further stabilize the centrifugally supported structure against
fragmentation. Indeed, the mass of the disk and the mass within the tower, are roughly
comparable.
We estimate analytically
the value of  at which one expects to find a significant influence
of the magnetic field on the fragmentation. Following Gammie (1996), we
will consider that a strong stabilizing influence is achieved when the
Alfvén speed associated with the toroidal component is comparable to the sound speed.
at which one expects to find a significant influence
of the magnetic field on the fragmentation. Following Gammie (1996), we
will consider that a strong stabilizing influence is achieved when the
Alfvén speed associated with the toroidal component is comparable to the sound speed.
The principle of the analysis is as follow: we compute the growth rate
of the toroidal component inside the centrifugally supported
structure, so that we can estimate the time,
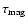 ,
needed for the Alfvén speed to become comparable to the sound speed.
We then compute the dynamical time of the disk,
,
needed for the Alfvén speed to become comparable to the sound speed.
We then compute the dynamical time of the disk,
 ,
over which fragmentation will occur. The critical value of
,
over which fragmentation will occur. The critical value of  ,
below which fragmentation is quenched, is obtained when
,
below which fragmentation is quenched, is obtained when
 is equal to
is equal to
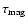 .
.
The growth time of the toroidal magnetic component within the disk has two
contributions. First the twisting of the radial component due to differential
rotation proportional to
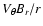 and second the wrapping of the vertical magnetic
component due to the vertical gradient of Bz proportional to
and second the wrapping of the vertical magnetic
component due to the vertical gradient of Bz proportional to
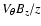 ,
where z is the disk height. The divergence constraint
shows that
,
where z is the disk height. The divergence constraint
shows that
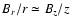 ,
indicating that the 2 contributions are comparable.
,
indicating that the 2 contributions are comparable.
Thus, the growth of 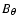 can be estimated by writing
can be estimated by writing
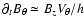 where h is the disk
height. Since we are interested in computing the growth of the
magnetic field from initially small values, we neglect the influence
of the magnetic tower on the disk vertical expansion and write:
where h is the disk
height. Since we are interested in computing the growth of the
magnetic field from initially small values, we neglect the influence
of the magnetic tower on the disk vertical expansion and write:
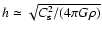 .
With Eq. (1) of Paper I, we obtain
.
With Eq. (1) of Paper I, we obtain
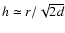 ,
where d is the ratio of the density over
singular isothermal density.
,
where d is the ratio of the density over
singular isothermal density.
If we assume that the disk is roughly Keplerian, we get
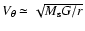 ,
,
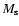 being the mass of
the star and the disk.
Taking the expression of Bz stated by Eqs. (1) of Paper I, we obtain:
being the mass of
the star and the disk.
Taking the expression of Bz stated by Eqs. (1) of Paper I, we obtain:
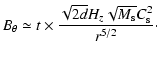 |
|
|
(1) |
The value of
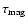 ,
is obtained by requiring
,
is obtained by requiring
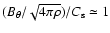 .
Using the expression of density stated by Eq. (1) of Paper I, we obtain:
.
Using the expression of density stated by Eq. (1) of Paper I, we obtain:
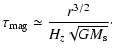 |
|
|
(2) |
The dynamical time of the disk, i.e. the time relevant for fragmentation, is the
rotation time:
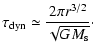 |
|
|
(3) |
Therefore, we obtain:
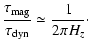 |
|
|
(4) |
To compute the value of Hz, one can use Table 1 of Paper I, but it
is more convenient to express the result in terms of the initial cloud
parameters, namely  and
and 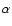 .
The latter is the ratio of
thermal over gravitational energy and is given by
.
The latter is the ratio of
thermal over gravitational energy and is given by
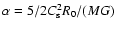 .
From Eq. (4) of Paper I, the value of Hz is
given by
.
From Eq. (4) of Paper I, the value of Hz is
given by
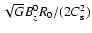 ,
whereas from the definition
of
,
whereas from the definition
of  ,
Bz0 can be written as
,
Bz0 can be written as
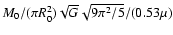
![[*]](/icons/foot_motif.gif) . Gathering the different
expressions, we get:
. Gathering the different
expressions, we get:
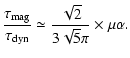 |
|
|
(5) |
We can deduce the critical value of 
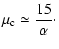 |
|
|
(6) |
Note that this value has not been derived using a rigorous analysis. It is therefore approximate and should be valid within a factor of a few.
For
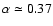 ,
we obtain
,
we obtain
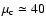 .
This
analytical estimate is therefore in reasonable agreement with our
numerical simulation, since for
.
This
analytical estimate is therefore in reasonable agreement with our
numerical simulation, since for 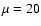 ,
fragmentation is suppressed.
In this case, the toroidal
magnetic pressure becomes comparable to the sound speed in about half
a rotation period. Since typically fragmentation occurs over a few
rotation period, such a fast growth time appears to be sufficient to
prevent the disk from fragmenting.
On the other hand for
,
fragmentation is suppressed.
In this case, the toroidal
magnetic pressure becomes comparable to the sound speed in about half
a rotation period. Since typically fragmentation occurs over a few
rotation period, such a fast growth time appears to be sufficient to
prevent the disk from fragmenting.
On the other hand for 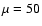 the disk
fragments, confirming that this case is slightly above the critical value.
the disk
fragments, confirming that this case is slightly above the critical value.
For 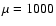 ,
one has
,
one has
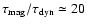 .
Therefore in such a case, the growth of the toroidal
component is too slow to significantly influence the disk evolution.
.
Therefore in such a case, the growth of the toroidal
component is too slow to significantly influence the disk evolution.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{8310fig19.ps}\par\vspace*{2m...
...ps}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{8310fig21.ps}\end{figure}](/articles/aa/full/2008/49/aa8310-07/Timg76.gif) |
Figure 8:
Same as Fig. 1 for 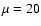 and A=0.5.
The figure corresponds to a length of
and A=0.5.
The figure corresponds to a length of 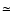 1200 AU,
four times bigger than the length displayed in Fig. 1. 1200 AU,
four times bigger than the length displayed in Fig. 1. |
| Open with DEXTER |
In this section, we investigate the effect of a density fluctuation
having a larger initial amplitude, A=0.5. In that case the cloud is
more prone to fragmentation because the perturbations develop quickly.
Such strong perturbations can be due either to initial conditions
or to strong external triggering.
Although in this section we keep the same amount of rotation as
in the previous section, we also performed simulations with the same initial
conditions but with no rotation and found similar results during the early phase
of fragmentation to the case with rotation.
This indicates that with such strong perturbations, the initial cloud
fragmentation is purely thermal and independent of the rotation. We refer
to this situation as thermal fragmentation.
We present results for weak and intermediate values of magnetic strengths,
namely 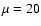 and
and 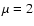 .
Figure 8 shows results for
.
Figure 8 shows results for 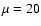 .
The first panel shows that
a filamentary structure develops in which two protostars have formed. The two
protostars are well separated by roughly
.
The first panel shows that
a filamentary structure develops in which two protostars have formed. The two
protostars are well separated by roughly 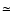
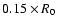 as opposed to
as opposed to
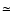
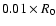 in the case of weaker perturbations.
As explained previously, the fragmentation in this case has a purely thermal
origin and is simply
due to the development of the initial perturbations
(in the case of weak perturbations, rotationally driven
fragmentation does not strongly depend on the perturbation amplitude).
The second panel shows that the two fragments are approaching each other falling along
the filament. The final panel shows that the two fragments have merged and that
a protostellar disk forms. However,
the second collapse is not treated in the simulation, thus only the
first Larson core is considered. Therefore the merging should be considered with
great care. Careful thermodynamic treatment of the first Larson core is required.
Indeed the
first core is known to have a short life time of roughly 103 years. Therefore since
the timeshift between the first and second panel is larger than 104 years, it is
expected that second collapse would have already occurred by the time the two
fragments approach each other. Since stars have very small radii, it is unlikely that
the binary will merge.
Therefore the final product could be a binary rather
than a single protostar.
in the case of weaker perturbations.
As explained previously, the fragmentation in this case has a purely thermal
origin and is simply
due to the development of the initial perturbations
(in the case of weak perturbations, rotationally driven
fragmentation does not strongly depend on the perturbation amplitude).
The second panel shows that the two fragments are approaching each other falling along
the filament. The final panel shows that the two fragments have merged and that
a protostellar disk forms. However,
the second collapse is not treated in the simulation, thus only the
first Larson core is considered. Therefore the merging should be considered with
great care. Careful thermodynamic treatment of the first Larson core is required.
Indeed the
first core is known to have a short life time of roughly 103 years. Therefore since
the timeshift between the first and second panel is larger than 104 years, it is
expected that second collapse would have already occurred by the time the two
fragments approach each other. Since stars have very small radii, it is unlikely that
the binary will merge.
Therefore the final product could be a binary rather
than a single protostar.
Figure 9 shows results for 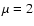 .
Both panels show that
two fragments develop in a similar way as for
.
Both panels show that
two fragments develop in a similar way as for 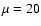 .
Unfortunately,
the relative strong value of the magnetic intensity makes the time steps much
shorter than in the previous case and it becomes computationally expensive to follow the long range evolution.
However, it seems likely that a similar evolution is expected leading to the merging and
the two first cores.
.
Unfortunately,
the relative strong value of the magnetic intensity makes the time steps much
shorter than in the previous case and it becomes computationally expensive to follow the long range evolution.
However, it seems likely that a similar evolution is expected leading to the merging and
the two first cores.
Figure 10 shows results for 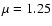 and A=0.5.
As revealed by the first panel, the m=2 density perturbation has
only weakly developed and only two shallow density maxima are visible.
The second panel shows a single object in the centre surrounded by
a pseudo-disk. Since the timeshift between the two panels is about 0.015 freefall time (
and A=0.5.
As revealed by the first panel, the m=2 density perturbation has
only weakly developed and only two shallow density maxima are visible.
The second panel shows a single object in the centre surrounded by
a pseudo-disk. Since the timeshift between the two panels is about 0.015 freefall time (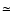
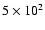 years) there is not sufficient time
for the second collapse to arise. It seems plausible that in this
particular case, a single star will form.
years) there is not sufficient time
for the second collapse to arise. It seems plausible that in this
particular case, a single star will form.
Therefore, it appears that a nearly critically
magnetized dense core, ideally coupled to the magnetic field, is
difficult to fragment into a few objects even if relatively large fluctuations
are initially present. This conclusion is in
good agreement with the conclusion reached by Hosking & Whitworth (2004),
that a magnetically subcritical cloud, which collapses after
sufficient magnetic flux has been lost because of ambipolar diffusion,
does not fragment.
We conclude that, with large amplitude density fluctuations, a collapsing dense
core fragments over a large range of initial conditions as long as it is not
too strongly magnetized. The fragments are due to each initial seed collapsing
individually. The question of the survival of the fragments should however be
carefully investigated. We note that Price & Bate (2007)
reach very similar conclusions. They also propose that in some cases,
such as when the magnetic field is perpendicular to the initial rotation axis, the magnetic field
may help the fragments to survive.
Since there is no question that a significant fraction of stars are binaries, the
efficient stabilization of the disk and the suppression of fragmentation even for
modest field amplitudes may constitute a severe difficulty. We have no answer
to this apparent conundrum but we discuss three possible mechanisms that
may induce the fragmentation
of a dense core and the formation of binaries. We also suggest various observational
tests that could discriminate between these scenarios.
We start with the possibility of having initial sufficiently large fluctuations.
As demonstrated in this paper and in Price & Bate (2007), fragmentation
is possible in such a situation. The question is then how likely are large
initial perturbations?
Observationally the question is not easy to address.
It is nevertheless known that the dense cores
usually are not very uniform and that typically sonic velocity dispersion is observed.
This is broadly compatible with the presence of density perturbations although perhaps not
as large as 50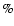 .
On the other hand, cores with a high aspect ratio are observed. If some
of them are elongated, i.e. prolate objects, this may be equivalent to a substantial m=2perturbation.
Indeed, simulations of quiescent cores
having transonic turbulence present significant
fluctuations (Goodwin et al. 2004). It seems however difficult at this stage to infer
quantitatively whether the perturbations generated by this weak turbulence are sufficient
to produce multiple systems.
.
On the other hand, cores with a high aspect ratio are observed. If some
of them are elongated, i.e. prolate objects, this may be equivalent to a substantial m=2perturbation.
Indeed, simulations of quiescent cores
having transonic turbulence present significant
fluctuations (Goodwin et al. 2004). It seems however difficult at this stage to infer
quantitatively whether the perturbations generated by this weak turbulence are sufficient
to produce multiple systems.
Another possibility is that the collapse may be induced by an external agent such as
a supernova remnant or protostellar jet. These are likely to generate
large perturbations. Indeed, all simulations considering clouds evolving far from equilibrium
(Bate et al. 2003; Ballesteros-Paredes et al. 2003; Hennebelle et al. 2006; Peretto et al. 2007)
do find dense cores with initially strong perturbations.
Future works should specify under what conditions
such initial fluctuations are likely to be produced. This may depend on the physical properties
of the molecular clouds in which the dense core is embedded. For example, the answer could be different
in the Taurus molecular cloud in which star formation is relatively quiescent and in the Orion
molecular cloud where star formation is more active.
We stress that this mechanism constitutes a change of paradigm with respect to
the standard hydrodynamical scenario (corresponding to Fig. 1).
Indeed, with this mechanism the fragmentation appears to be the result
of perturbations seeded at large scales rather than an intrinsic properties of the collapsing dense core.
An important prediction of this model is that
the binary should not necessarily be located in the equatorial plane of the core since the initial
perturbations likely should be randomly distributed.
In the present calculations, perfect coupling between gas and magnetic field is assumed.
The loss of flux due to ambipolar diffusion could therefore help to reduce
the magnetic intensity.
The ratio of the ambipolar diffusion time,
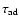 ,
and the freefall time,
,
and the freefall time,
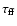 ,
has been computed by Shu et al. (1987). When the magnetic field is just sufficient to compensate for gravity,
they obtain
,
has been computed by Shu et al. (1987). When the magnetic field is just sufficient to compensate for gravity,
they obtain
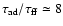 ,
indicating that the ambipolar diffusion time is
larger than the freefall time. When the magnetic field is weaker, the ambipolar time increases
further. Therefore, it appears unlikely that the magnetic field could be removed from the envelope of
a supercritical collapsing core.
,
indicating that the ambipolar diffusion time is
larger than the freefall time. When the magnetic field is weaker, the ambipolar time increases
further. Therefore, it appears unlikely that the magnetic field could be removed from the envelope of
a supercritical collapsing core.
However, the possibility remains that ambipolar diffusion could occur in the disk allowing
the toroidal magnetic field to be diffused out. To investigate this issue, we estimate
the ratio of ambipolar diffusion time in the disk along the vertical direction and the
growth time of the toroidal magnetic field given by Eq. (2).
Here we write it as
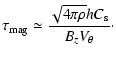 |
|
|
(7) |
The ambipolar diffusion time of the toroidal component along the
vertical direction is:
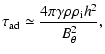 |
|
|
(8) |
where
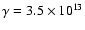 cm3 g-1 s-1 is the drag coefficient
and
cm3 g-1 s-1 is the drag coefficient
and
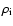 the density of ions.
Since we are interested in the value of
the density of ions.
Since we are interested in the value of 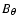 such that
such that
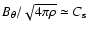 ,
the ambipolar diffusion time becomes:
,
the ambipolar diffusion time becomes:
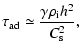 |
|
|
(9) |
following Shu et al. (1987), we write
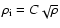 where
where
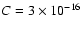 cm-3/2 g1/2.
With
cm-3/2 g1/2.
With
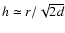 ,
,
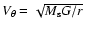 and
and
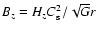 ,
we obtain
,
we obtain
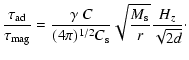 |
|
|
(10) |
Thus, we obtain
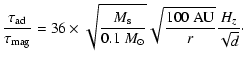 |
|
|
(11) |
For 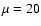 ,
,
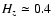 .
From Fig. 2 of Paper I,
.
From Fig. 2 of Paper I,
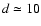 .
Thus, the ambipolar diffusion time is longer than the growth
time of the toroidal component. It is therefore likely that ambipolar
diffusion will not change the picture significantly except if stiffer field variations
than the one calculated above are present.
In this case, ambipolar diffusion could help clouds with low
.
Thus, the ambipolar diffusion time is longer than the growth
time of the toroidal component. It is therefore likely that ambipolar
diffusion will not change the picture significantly except if stiffer field variations
than the one calculated above are present.
In this case, ambipolar diffusion could help clouds with low  to fragment more easily.
We do not expect it however, to shift very significantly
the value of
to fragment more easily.
We do not expect it however, to shift very significantly
the value of  for which fragmentation occurs. Since Hz is proportional
to
for which fragmentation occurs. Since Hz is proportional
to 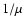 ,
,
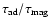 increases rapidly when
increases rapidly when  decreases.
decreases.
Fragmentation during the second collapse has been investigated by Bonnell & Bate (1994)
with the prospect of exploring whether the formation of close binary systems could be possible.
They conclude that fragmentation is indeed possible but that the binaries have to accrete most
of their mass since they are initially very small.
On the other hand, Machida et al. (2007) recently explored magnetized second collapse
taking into account the large Ohmic dissipation (we note that this is not rigorously Ohmic dissipation) that is predicted to occur in the first Larson core by various models
(e.g. Nakano et al. 2002). As a result, most of the magnetic flux is lost making fragmentation easier.
It therefore appears possible that fragmentation could occur during this phase, possibly
driven by rotation. In this case, the binary should gain sufficient angular momentum from the accretion
to increase the separation between the two stars (see e.g. Goodwin et al. 2004).
Interestingly, Banerjee & Pudritz (2006) report the formation of a very close binary in their second collapse
calculations despite the ideal MHD assumption.
The prediction of this model is that the binaries should be in the equatorial plane since the
orbital angular momentum of the binary is due to the angular momentum of the accreting gas.
Also the separation between the 2 stars should increase with time implying that closer binaries
should be observed on average in younger cores.
Note that this mechanism could possibly
work even if the magnetic field is initially very strong in the core.
In order to test each of these scenarios, high resolution observations
would be necessary. In this respect, ALMA will certainly be a very powerful tool,
as demonstrated by the synthetic observations performed by André et al. (2007) using the
present calculations.
We have studied the fragmentation of a collapsing
magnetized molecular dense core by performing a set of numerical
simulations. We interpret the results together with the analysis performed
in the companion paper in which we investigate the accretion and ejection
processes that take place in the simulations.
With our choice of initial conditions,
and for perturbations of low amplitude, unmagnetized cores do
fragment, while magnetized cores having values of  as large as 20
do not fragment. Based on an analytic estimate,
we suggest that for cores having
as large as 20
do not fragment. Based on an analytic estimate,
we suggest that for cores having  larger
than
larger
than 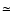
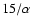 ,
the growth rate of the toroidal component is
too slow to stabilize the disk.
We stress that the suppression of fragmentation in this range of
parameter, is not due to magnetic
braking but to the rapid growth of the toroidal component of the
magnetic field induced by the differential rotation within the
disk. The Alfvén speed associated with this toroidal component adds up
to the sound speed of the disk and stabilize it.
,
the growth rate of the toroidal component is
too slow to stabilize the disk.
We stress that the suppression of fragmentation in this range of
parameter, is not due to magnetic
braking but to the rapid growth of the toroidal component of the
magnetic field induced by the differential rotation within the
disk. The Alfvén speed associated with this toroidal component adds up
to the sound speed of the disk and stabilize it.
For values of  smaller than 5, no big centrifugal disk forms because
first the collapse occurs mainly along the field lines bringing less angular momentum,
and second, magnetic braking removes angular momentum. This makes
these cores even less prone to fragment.
smaller than 5, no big centrifugal disk forms because
first the collapse occurs mainly along the field lines bringing less angular momentum,
and second, magnetic braking removes angular momentum. This makes
these cores even less prone to fragment.
The situation is different if large amplitude perturbations are initially seeded. In this case,
each perturbation develops independently even without rotation. Since the strong field
amplification is primarily due to differential motions in the disk, the
magnetic field is unable to suppress fragmentation except if the core is almost
critical, i.e. the field is initially very strong.
The following evolution of these fragments requires a careful treatment of the thermodynamics
of the first Larson core. It is indeed likely that if the second collapse has not occurred
by the time these fragments approach each other, they will merge. On the other hand, if the
protostars have already formed, the binary system is likely to survive.
For dense cores having rotation and magnetic strength typical of values inferred from observations,
we find that fragmentation is suppressed by the magnetic field if the initial density perturbations
are too small. This constitutes a severe problem, since there is no question that a significant
fraction of stars are binaries.
In view of this, we discuss the likelihood of having sufficient perturbations within the cores
initially as well as the impact of ambipolar diffusion and the possibility of fragmentation during
the second collapse phase. We speculate that the first may depend on the physical characteristic of the
molecular cloud in which the dense core is embedded whereas the latter should berelatively independent
of the large scales and could work even if the magnetic field is initially very strong.
Acknowledgements
Some of the simulations
presented in this paper were performed at the IDRIS supercomputing center and on the CEMAG
computing facility supported by the French Ministry of Research and Education
through a Chaire d'excellence awarded to Steven Balbus.
We thank Sébastien Fromang, Doug Johnstone and Philippe André for a critical reading of the manuscript.
We thank Frank Shu, the referee, for helpful comments.
P.H. thanks Masahiro Machida for related discussions.
- André, P.,
Hennebelle, P., & Peretto, N. 2007, Ap&SS, ed. R. Bachiller
et al. (special issue ALMA), in press
(In the text)
-
Ballesteros-Paredes, J., Klessen, R., & Vazquez-Semadeni, E.
2003, Ap, 592, 188 [CrossRef]
(In the text)
- Banerjee,
R., & Pudritz, R. 2006, Ap, 641, 949 [CrossRef]
(In the text)
- Banerjee,
R., Pudritz, R., & Holmes, L. 2004, MNRAS, 355, 248 [NASA ADS] [CrossRef]
(In the text)
- Bate, M., &
Burkert, A. 1997, MNRAS, 288, 1060 [NASA ADS]
(In the text)
- Bate, M., Bonnell,
I., & Bromm, V. 2003, MNRAS, 339, 577 [NASA ADS] [CrossRef]
(In the text)
-
Bodenheimer, P., Burkert, A., Klein, R., & Boss, A. 2000, in
Protostars and Planets IV, ed. V. Mannings, A. P. Boss, & S. S.
Russell (Tucson: Univ. of Arizona Press), 675
(In the text)
- Bonnell, I.
1994, MNRAS, 269, 837 [NASA ADS]
(In the text)
- Bonnell,
I., & Bate, M. 1994, MNRAS, 271, 999 [NASA ADS]
(In the text)
- Boss, A. 1993, Ap,
410, 157 [CrossRef]
(In the text)
- Crutcher,
R. 1999, Ap, 520, 706 [CrossRef]
(In the text)
- Duquenoy,
A., & Mayor, M. 1991, A&A 248, 485
(In the text)
-
Elmegreen, B. 1987, Ap, 312, 626 [CrossRef]
(In the text)
- Fromang, S.,
Hennebelle, P., & Teyssier, R. 2006, A&A, 457, 371 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Gammie, C.
1996, Ap, 462, 725 [CrossRef]
(In the text)
- Goodman, A.,
Benson, P., Fuller, G., & Myers, P. 1993, Ap, 406, 528 [CrossRef]
(In the text)
- Goodwin, S.,
Whitworth, A., & Ward-Thompson, D. 2004, A&A, 423, 169 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
Hennebelle, P., & Fromang, S. 2008, A&A, 477, 9 [NASA ADS] [CrossRef] [EDP Sciences] (Paper
I)
(In the text)
-
Hennebelle, P., Whitworth, A., Aha, S.-H., & Goodwin, S. 2004,
MNRAS, 340, 870 [NASA ADS] [CrossRef]
(In the text)
-
Hennebelle, P., Whitworth, A., & Goodwin, S. 2006, A&A,
451, 141 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Hosking, G.,
& Whitworth, A. 2004, MNRAS, 347, 994 [NASA ADS] [CrossRef]
(In the text)
- Lada, C. 2006, ApJ,
640, L63 [NASA ADS] [CrossRef]
(In the text)
- Lynden-Bell, D.
1966, Observatory, 86, 57 [NASA ADS]
(In the text)
- Machida, M.,
Matsumoto, T., Hanawa, T., & Tomisaka, K. 2005, MNRAS, 362,
382 [NASA ADS] [CrossRef]
(In the text)
- Machida, M.,
Inutsuka, S.-i., & Matsumoto, T. 2007, ApJ, submitted
[arXiv:astro-ph/07052073]
(In the text)
-
Matsumoto, T., & Hanawa, T. 2003, ApJ, 595, 913 [NASA ADS] [CrossRef]
(In the text)
- Miyama, S.
1992, PASJ, 44, 193 [NASA ADS]
(In the text)
- Nakano, T.,
Nishi, R., & Umebayashi, T. 2002, ApJ, 573, 199 [NASA ADS] [CrossRef]
(In the text)
- Peretto, N.,
Hennebelle, P., & André, P. 2007, A&A, 464, 983 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Price, D., &
Bate, M. 2007, MNRAS, 377, 77 [NASA ADS] [CrossRef]
(In the text)
- Shu, F., Adams, F.,
& Lizano, S. 1987, ARA&A, 25, 23 [NASA ADS] [CrossRef]
(In the text)
- Teyssier,
R. 2002, A&A, 385, 337 [NASA ADS] [CrossRef] [EDP Sciences]
- Truelove,
J., Klein, R., McKee, C., et al. 1998, ApJ, 495, 821 [NASA ADS] [CrossRef]
(In the text)
- Ziegler, U.
2005, A&A, 435, 385 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
Copyright ESO 2007
![\begin{figure}
\par\includegraphics[width=7cm,clip]{8310fig01.ps}\par\vspace*{2m...
....ps}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{8310fig03.ps}\end{figure}](/articles/aa/full/2008/49/aa8310-07/Timg17.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{8310fig04.ps}\par\vspace*{2m...
....ps}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{8310fig06.ps}\end{figure}](/articles/aa/full/2008/49/aa8310-07/Timg21.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{8310fig07.ps}\par\vspace*{2m...
...ps}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{8310fig09.ps}\end{figure}](/articles/aa/full/2008/49/aa8310-07/Timg22.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{8310fig10.ps}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{8310fig11.ps}\end{figure}](/articles/aa/full/2008/49/aa8310-07/Timg23.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{8310fig12.ps}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{8310fig13.ps}\end{figure}](/articles/aa/full/2008/49/aa8310-07/Timg43.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{8310fig14.ps}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{8310fig15.ps}\end{figure}](/articles/aa/full/2008/49/aa8310-07/Timg44.gif)
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{8310fig16.ps}\par\vspace*{...
...s}\par\vspace*{2mm}
\includegraphics[width=6.7cm,clip]{8310fig18.ps}\end{figure}](/articles/aa/full/2008/49/aa8310-07/Timg45.gif)
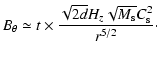
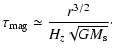
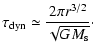
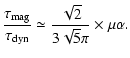
![\begin{figure}
\par\includegraphics[width=7cm,clip]{8310fig19.ps}\par\vspace*{2m...
...ps}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{8310fig21.ps}\end{figure}](/articles/aa/full/2008/49/aa8310-07/Timg76.gif)
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{8310fig22.ps}\par\vspace*{2mm}
\includegraphics[width=7.2cm,clip]{8310fig23.ps}\end{figure}](/articles/aa/full/2008/49/aa8310-07/Timg77.gif)
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{8310fig24.ps}\par\vspace*{2mm}
\includegraphics[width=7.2cm,clip]{8310fig25.ps}\end{figure}](/articles/aa/full/2008/49/aa8310-07/Timg78.gif)