A&A 492, 787-803 (2008)
DOI: 10.1051/0004-6361:200810678
The secrets of T Pyxidis
II. A recurrent nova that will not become a SN Ia
P. Selvelli1 - A. Cassatella2 - R. Gilmozzi3 - R. González-Riestra4
1 - INAF - Osservatorio Astronomico di Trieste, via Tiepolo 11, Trieste, 34143 Trieste,
Italy
2 - INAF-IFSI, via del Fosso del Cavaliere 100, 00133 Roma, Italy, and Dipartimento di Fisica,
Universita' Roma Tre, 00146 Roma, Italy
3 - European Southern Observatory, Karl-Schwarzschild-Str 2, 85748 Garching bei München,
Germany
4 - XMM-Newton Science Operations Centre, ESAC, PO Box 78, 28691 Villanueva de la Cañada, Madrid, Spain
Received 25 July 2008 / Accepted 1 October 2008
Abstract
Aims. We compare the observed and theoretical parameters for the quiescent and outburst phases of the recurring nova T Pyx.
Methods. IUE data were used to derive the disk luminosity and the mass accretion rate, and to exclude the presence of quasi-steady burning at the WD surface. XMM-NEWTON data were used to verify this conclusion.
Results. By various methods, we obtained
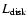
 70
70 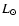 and
and 
 1.1
1.1  10
10
 yr-1. These values were about twice as high in the pre-1966-outburst epoch. This allowed the first direct estimate of the total mass accreted before outburst,
yr-1. These values were about twice as high in the pre-1966-outburst epoch. This allowed the first direct estimate of the total mass accreted before outburst,
 =
=
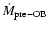
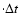 ,
and its comparison with the critical ignition mass
,
and its comparison with the critical ignition mass
 .
We found
.
We found
 and
and
 to be in perfect agreement (with a value close to 5
to be in perfect agreement (with a value close to 5  10
10
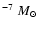 )
for M1
)
for M1  1.37
1.37  ,
which provides a confirmation of the thermonuclear runaway theory. The comparison of the observed parameters of the eruption phase, with the corresponding values in the grid of models by Yaron and collaborators, provides satisfactory agreement for values of M1 close to 1.35
,
which provides a confirmation of the thermonuclear runaway theory. The comparison of the observed parameters of the eruption phase, with the corresponding values in the grid of models by Yaron and collaborators, provides satisfactory agreement for values of M1 close to 1.35  and log
and log  between -8.0 and -7.0, but the observed value of the decay time t3 is higher than expected. The long duration of the optically thick phase during the recorded outbursts of T Pyx, a spectroscopic behavior typical of classical novae, and the persistence of P Cyg profiles, constrains the ejected mass
between -8.0 and -7.0, but the observed value of the decay time t3 is higher than expected. The long duration of the optically thick phase during the recorded outbursts of T Pyx, a spectroscopic behavior typical of classical novae, and the persistence of P Cyg profiles, constrains the ejected mass
 to within 10-5-10
to within 10-5-10
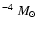 .
Therefore, T Pyx ejects far more material than it has accreted, and the mass of the white dwarf will not increase to the Chandrasekhar limit as generally believed in recurrent novae. A detailed study based on the UV data excludes the possibility that T Pyx belongs to the class of the supersoft X-ray sources, as has been postulated. XMM-NEWTON observations have revealed a weak, hard source and confirmed this interpretation.
.
Therefore, T Pyx ejects far more material than it has accreted, and the mass of the white dwarf will not increase to the Chandrasekhar limit as generally believed in recurrent novae. A detailed study based on the UV data excludes the possibility that T Pyx belongs to the class of the supersoft X-ray sources, as has been postulated. XMM-NEWTON observations have revealed a weak, hard source and confirmed this interpretation.
Key words: stars: novae, cataclysmic variables - stars: supernovae: general - X-rays:
binaries - ultraviolet: general
Classical novae (CNe) are semi-detached binary systems in which a white dwarf (WD) primary star accretes hydrogen-rich matter, by means of an accretion disk, from a companion star which fills its Roche lobe. The ``classical nova'' outburst is a thermonuclear runaway (TNR) process on
the surface of a white dwarf that is produced when, due to the gradual accumulation of hydrogen-rich material on its surface, the pressure at the bottom of the accreted layer, which is partially or fully degenerate, becomes sufficiently high (P 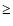 1018-1020 dyn cm-2) for
nuclear ignition of hydrogen to begin. The critical mass for ignition
1018-1020 dyn cm-2) for
nuclear ignition of hydrogen to begin. The critical mass for ignition
 depends
primarily on the mass of the white dwarf as
depends
primarily on the mass of the white dwarf as

 M1-7/3, although more
detailed models show that the ignition mass also depends on both the mass accretion rate
M1-7/3, although more
detailed models show that the ignition mass also depends on both the mass accretion rate  and the core WD temperature (Prialnik & Kovetz 1995; Townsley & Bildsten 2004; Yaron et al. 2005; see also Sect. 8).
and the core WD temperature (Prialnik & Kovetz 1995; Townsley & Bildsten 2004; Yaron et al. 2005; see also Sect. 8).
Recurrent novae (RNe) are a subclass of classical novae characterized by outbursts with recurrence time of the order of decades. We refer to Webbink et al. (hereinafter WLTO, 1987) as the seminal paper on the nature of recurrent novae and to Warner (1995), Hachisu & Kato (2001), and Shore (2008) for further considerations of this topic. Solid theoretical considerations indicate that a model of a recurrent outburst requires a high accretion rate  (10-8-10
(10-8-10
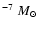 )
onto a WD of mass close to the Chandrasekhar mass limit (Starrfield 1985; WLTO 1987; Livio 1994). However, nova models (Prialnik & Kovetz 1995; Yaron et al. 2005; see also Sect. 8) appear to evade these strict requirements and allow the occurrence of recurrent outbursts also in a (slightly) less massive WD. The ejecta of RNe are expected to be less massive than those of CNe. This is because on the surface of the massive WD expected in
a RN, the critical conditions for ignition are reached with a far less massive envelope. Studies of the ejecta of RNe indicate a mass between 10-6-10
)
onto a WD of mass close to the Chandrasekhar mass limit (Starrfield 1985; WLTO 1987; Livio 1994). However, nova models (Prialnik & Kovetz 1995; Yaron et al. 2005; see also Sect. 8) appear to evade these strict requirements and allow the occurrence of recurrent outbursts also in a (slightly) less massive WD. The ejecta of RNe are expected to be less massive than those of CNe. This is because on the surface of the massive WD expected in
a RN, the critical conditions for ignition are reached with a far less massive envelope. Studies of the ejecta of RNe indicate a mass between 10-6-10
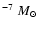 ,
instead of the 10-4-10
,
instead of the 10-4-10
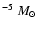 observed in ``classical'' novae (Gehrz et al. 1998; Hernanz & Jose 1998; Starrfield 1999).
observed in ``classical'' novae (Gehrz et al. 1998; Hernanz & Jose 1998; Starrfield 1999).
RNe represent a convenient laboratory to compare the predictions of the TNR theory with the observations. From the observed  and the observed duration of the inter-outburst
interval, in principle, one can obtain a direct estimate of the total mass accreted (
and the observed duration of the inter-outburst
interval, in principle, one can obtain a direct estimate of the total mass accreted (
 )
between two successive outbursts. This quantity can be compared with both the (theoretical) critical ignition mass
)
between two successive outbursts. This quantity can be compared with both the (theoretical) critical ignition mass
 and the mass of the ejected shell
and the mass of the ejected shell
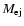 ,
which can be estimated by spectroscopic methods (and, in principle, by photometric methods if dP/P
can be accurately measured, Livio 1991). A similar comparison cannot be made in the case of CNe because the amount of mass accreted prior to outburst is badly determined due to their long inter-outburst interval.
,
which can be estimated by spectroscopic methods (and, in principle, by photometric methods if dP/P
can be accurately measured, Livio 1991). A similar comparison cannot be made in the case of CNe because the amount of mass accreted prior to outburst is badly determined due to their long inter-outburst interval.
Observations of RNe in quiescence and outburst can also be used to determine the secular balance between the total accreted mass
 and that ejected in the explosive phase
and that ejected in the explosive phase
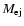 ,
and therefore to investigate the possible role of RNe as progenitors of SN Ia. The ejecta of RNe have an almost ``solar'' chemical composition and are not enriched in ``heavy'' elements, such as
carbon, oxygen and neon. This has been taken as an indication that the massive white dwarf in RNe is not eroded, will gain mass after each cycle of accretion and ejection, and will eventually explode as a type Ia supernova (Hachisu & Kato 2002).
,
and therefore to investigate the possible role of RNe as progenitors of SN Ia. The ejecta of RNe have an almost ``solar'' chemical composition and are not enriched in ``heavy'' elements, such as
carbon, oxygen and neon. This has been taken as an indication that the massive white dwarf in RNe is not eroded, will gain mass after each cycle of accretion and ejection, and will eventually explode as a type Ia supernova (Hachisu & Kato 2002).
In Gilmozzi & Selvelli (2007, hereinafter Paper I), we studied the UV spectrum of T Pyx in detail and our main conclusion was that the spectral energy distribution (SED) is dominated by
an accretion disk in the UV+opt+IR ranges, with a distribution that, after correction for
reddening EB-V = 0.25, is described by a power law
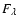 = 4.28
= 4.28  10-6
10-6 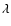 -2.33 erg cm-2 s-1 Å-1, while the continuum in the UV range can also be well represented by a single blackbody of T
-2.33 erg cm-2 s-1 Å-1, while the continuum in the UV range can also be well represented by a single blackbody of T  34 000 K. The observed UV continuum distribution of T Pyx has remained remarkably constant in both slope and intensity during 16 years of IUE observations.
34 000 K. The observed UV continuum distribution of T Pyx has remained remarkably constant in both slope and intensity during 16 years of IUE observations.
In the present study, we use this basic result from the IUE data and other considerations, to constrain the relevant parameters of the system and to attempt to understand the elusive nature of its outbursts. The five recorded outbursts of T Pyx occurred in 1890, 1902, 1920, 1944, and 1966, with a mean recurrence time of 19  5.3 yrs (WLTO). All outbursts were similar in photometric behavior and characterized by a decay time t3
5.3 yrs (WLTO). All outbursts were similar in photometric behavior and characterized by a decay time t3  90
90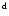 ,
a speed class that is
substantially slower than in other RNe. We divide the paper into several self-contained sections.
,
a speed class that is
substantially slower than in other RNe. We divide the paper into several self-contained sections.
In Sect. 2, we discuss the problem of distance, which we determine to be 3500  500 pc. In
Sect. 3, we analyze the mass function of the system. Using observational data and other
considerations, we obtain
500 pc. In
Sect. 3, we analyze the mass function of the system. Using observational data and other
considerations, we obtain
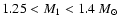 ,
,
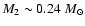 ,
or
,
or
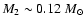 (depending on the as yet uncertain period), and i =25
(depending on the as yet uncertain period), and i =25  5 degrees. In Sect. 4, we derive the absolute magnitude at minimum Mv = 2.53
5 degrees. In Sect. 4, we derive the absolute magnitude at minimum Mv = 2.53  0.23. In Sect. 5, we calculate the bolometric disk luminosity
0.23. In Sect. 5, we calculate the bolometric disk luminosity
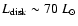 .
.
In Sect. 6 we use various methods to determine the mass accretion rate. The value depends on
 ,
and is
,
and is
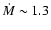

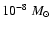 yr-1 for
yr-1 for
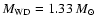 .
In Sect. 7, we derive the accretion rate before the 1966 outburst, and find that it is about twice the value measured with IUE. In Sect. 8, we compare the accreted mass before the last outburst as determined from the
.
In Sect. 7, we derive the accretion rate before the 1966 outburst, and find that it is about twice the value measured with IUE. In Sect. 8, we compare the accreted mass before the last outburst as determined from the  derived in Sect. 7,
derived in Sect. 7,
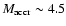

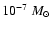 ,
with theoretical calculations of the ignition mass. We find good agreement
(including the inter-outburst interval) for
,
with theoretical calculations of the ignition mass. We find good agreement
(including the inter-outburst interval) for
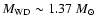 .
In Sect. 9, we compare
the observations of T Pyx with the theoretical models of Yaron et al. (2005), finding good agreement for all parameters with the exception of t3.
.
In Sect. 9, we compare
the observations of T Pyx with the theoretical models of Yaron et al. (2005), finding good agreement for all parameters with the exception of t3.
In Sect. 10, we reanalyze the historical data of the outbursts and reach the inescapable conclusion that the mass ejected in the explosion is
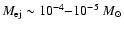 ,
about a factor 100 higher than the accreted mass. This discrepancy is discussed in detail in Sect. 11, and leads to the conclusion that the WD loses mass during the ourbursts. In Sect. 12, we revisit
the parameters of the extended nebula around T Pyx, and demonstrate why the nebula cannot be
used to derive information about the mass ejected during outburst. Section 13 discusses the
mass balance and infers that T Pyx is not destined to become a SN Ia as often postulated for recurrent novae. Far from increasing its mass towards the Chandrasekhar limit, the WD in
T Pyx is being eroded.
,
about a factor 100 higher than the accreted mass. This discrepancy is discussed in detail in Sect. 11, and leads to the conclusion that the WD loses mass during the ourbursts. In Sect. 12, we revisit
the parameters of the extended nebula around T Pyx, and demonstrate why the nebula cannot be
used to derive information about the mass ejected during outburst. Section 13 discusses the
mass balance and infers that T Pyx is not destined to become a SN Ia as often postulated for recurrent novae. Far from increasing its mass towards the Chandrasekhar limit, the WD in
T Pyx is being eroded.
In Sect. 14, we discuss the hypothesis that the WD in T Pyx is undergoing steady nuclear burning
on its surface, and show that it is incompatible with both historical and UV observations. In Sect. 15, we report about XMM observations confirming our analysis by directly disproving the hypothesis.
In Sect. 16, we discuss the recurrence time, and predict that the long awaited next outburst will occur around A.D. 2025. Section 17 reports our conclusions.
An accurate knowledge of distance is fundamental to the determination of the disk luminosity
 (and Mv), the mass accretion rate
(and Mv), the mass accretion rate  ,
and the mass of the
observed nebula surrounding the system
,
and the mass of the
observed nebula surrounding the system
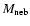 (not to be confused with the mass ejected during outburst,
(not to be confused with the mass ejected during outburst,
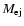 ).
).
In this section, we revisit the problem of determining the distance to T Pyx. We adopt a new accurate determination of the reddening, EB-V = 0.25  0.02, which is based on the depth of the
0.02, which is based on the depth of the 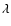 2175 Å interstellar absorption feature (see Paper I).
2175 Å interstellar absorption feature (see Paper I).
An estimate of the absolute magnitude at maximum
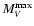 can be obtained from the optical decay time t2 or t3 by extending to a recurrent nova such as T Pyx, the applicability of the Maximum Magnitude versus Rate of Decline (MMRD) relations obtained using data of classical novae.
can be obtained from the optical decay time t2 or t3 by extending to a recurrent nova such as T Pyx, the applicability of the Maximum Magnitude versus Rate of Decline (MMRD) relations obtained using data of classical novae.
This is justified by the fact that it is clearly established that the same kind of physical process for the outburst is involved i.e. a TNR on an accreting WD. The suggestion that recurrent novae in M 31 are fainter than predicted by the MMRD curve (Della Valle & Livio 1998), applies only to the RNe subset that, unlike T Pyx, displays a short t3. The long t3 of T Pyx, the spectral behavior during outburst and the quantity of mass ejected (see Sect. 10) indicate that the same mechanism is operating as in CNe.
The optical decay time of T Pyx is well determined (Mayall 1967; Chincarini & Rosino 1969; Duerbeck 1987,b; WLTO 1987; Warner 1995) with t2  62
62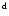 and t3
and t3  92
92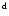 .
From these values, we derived four different estimates for
.
From these values, we derived four different estimates for
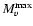 (-7.01, -6.75, -7.00, -6.64) using the S-shaped MMRD relation of Della Valle & Livio (1995), and the two linear and the one S-shaped relations of Downes & Duerbeck (2000), respectively.
(-7.01, -6.75, -7.00, -6.64) using the S-shaped MMRD relation of Della Valle & Livio (1995), and the two linear and the one S-shaped relations of Downes & Duerbeck (2000), respectively.
An additional estimate of the distance can be obtained by assuming that T Pyx, as a moderately fast nova, radiated at near-Eddington luminosity at maximum. This provides
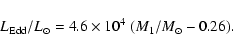 |
(1) |
For a massive white dwarf (M1  1.35
1.35  ), this corresponds to
), this corresponds to
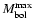
 -6.98. Close to the epoch of maximum light the observed color index showed oscillations about an average value of (B-V) = 0.35 (Eggen et al. 1967; Eggen 1968), or, after correction for reddening,
-6.98. Close to the epoch of maximum light the observed color index showed oscillations about an average value of (B-V) = 0.35 (Eggen et al. 1967; Eggen 1968), or, after correction for reddening,
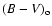
 0.10. Van den Bergh & Younger (1987) found that novae at maximum light have
0.10. Van den Bergh & Younger (1987) found that novae at maximum light have
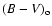 = +0.23
= +0.23  0.06, while Warner (1976) reported that the intrinsic color of novae close to maximum is
0.06, while Warner (1976) reported that the intrinsic color of novae close to maximum is
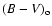
 0.0. The intermediate value for T Pyx was
0.0. The intermediate value for T Pyx was
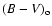
 0.10, which is indicative of a temperature lower than 10 000 K and suggests that, close to maximum light, the nova radiated mostly in the optical. Since the bolometric correction is quite small in this case (BC
0.10, which is indicative of a temperature lower than 10 000 K and suggests that, close to maximum light, the nova radiated mostly in the optical. Since the bolometric correction is quite small in this case (BC  -0.20), it follows that
-0.20), it follows that
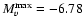 ,
which is quite close to the values obtained above from the four MMRD relations.
,
which is quite close to the values obtained above from the four MMRD relations.
The mean value of the five estimates for
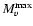 is -6.83, with a median value -6.79 and a formal standard deviation
is -6.83, with a median value -6.79 and a formal standard deviation 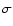 = 0.16. The five estimates are intermediate between the value (-6.4) reported by Payne-Gaposchkin (1957), Catchpole (1968), and Warner (1995) and the single value (-7.47) given by Duerbeck (1981).
= 0.16. The five estimates are intermediate between the value (-6.4) reported by Payne-Gaposchkin (1957), Catchpole (1968), and Warner (1995) and the single value (-7.47) given by Duerbeck (1981).
Adopting
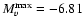 ,
AV=3.15
,
AV=3.15  E(B-V) = 0.79 and
E(B-V) = 0.79 and
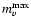
 6.7 (Catchpole 1968; Warner 1995; Chincarini & Rosino 1969), one obtains a distance d = 10
(1+(m-M-A)/5)
6.7 (Catchpole 1968; Warner 1995; Chincarini & Rosino 1969), one obtains a distance d = 10
(1+(m-M-A)/5)  3500 pc. The uncertainties in the individual parameters (0.16 for
3500 pc. The uncertainties in the individual parameters (0.16 for
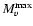 ,
0.1 for
,
0.1 for
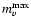 ,
0.06 for AV) correspond to an uncertainty of about 330 pc in the distance, i.e. to a relative uncertainty of the order of 10 percent.
,
0.06 for AV) correspond to an uncertainty of about 330 pc in the distance, i.e. to a relative uncertainty of the order of 10 percent.
A further estimate of the distance can be obtained by comparing the dereddened flux of T Pyx at 1600 Å with the accretion disk models by Wade & Hubeny (1998). As mentioned in Paper I, the most appropriate descriptions of the shape and depth of the lines (models ee and jj at low
inclination angles) correspond to high values of white-dwarf mass and accretion rate, although they provide a continuum that is too steep. In any case, these high M1, high  models, (we have extrapolated
models, (we have extrapolated  to values as high as log
to values as high as log  = -7.5) clearly show that the ratio
= -7.5) clearly show that the ratio
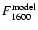 /
/
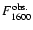 is about 1000. Applying a scaling of a
factor of
is about 1000. Applying a scaling of a
factor of  (1000)0.5 = 31.5 to the model distance (100 pc) would reconcile these
two values. The derived value of
(1000)0.5 = 31.5 to the model distance (100 pc) would reconcile these
two values. The derived value of  3150 pc is in fair agreement with the assumed distance of 3500 pc.
3150 pc is in fair agreement with the assumed distance of 3500 pc.
We recall that a range of distances to T Pyx can be found in the literature. Catchpole (1969) derived a lower limit of 1050 pc from the equivalent width of the CaII K line (EW  400 mÅ) and the EW-distance relationship derived by Beals & Oke (1953) for stars close to the Galactic plane. The EW measurement of Catchpole is however quite uncertain because of possible contamination by emission lines and the low quality of the spectra (the CaII K line falls close to the edge of the spectrum and only two spectra were of sufficient signal in that region).
400 mÅ) and the EW-distance relationship derived by Beals & Oke (1953) for stars close to the Galactic plane. The EW measurement of Catchpole is however quite uncertain because of possible contamination by emission lines and the low quality of the spectra (the CaII K line falls close to the edge of the spectrum and only two spectra were of sufficient signal in that region).
Catchpole (1969), using the two spectra of the highest signal-to-noise-ratio found
that the K line of calcium corresponds to radial velocity of +20 km s-1. According to Catchpole (1969), this velocity agrees well with that of material travelling with the Galactic rotation in the direction of T Pyx; since this direction is, however, close to a node of the rotation curve, the Beals & Oke (1953) method cannot be used to determine the distance.
Warner (1976), used the calibration given by Munch (1968) for stars close to a node in the Galactic rotation curve, and indicated that a star with a measurement of 0.4 Å for the K line should be at least at a distance of 2 kpc.
In a study of the IS Ca II K line towards O- and B-type stars in the Galactic disk, Hunter et al. (2006), presented a new calibration of the the total column density of Ca II K versus distance. In a plot of
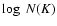 versus
versus 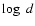 ,
the estimated distance of 3500 pc (
,
the estimated distance of 3500 pc (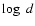 = 3.545) would correspond to
= 3.545) would correspond to 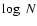 (CaII)
(CaII)  13.0. The EW of the K line measured by Catchpole (1969) corresponds to a column density of 4.9
13.0. The EW of the K line measured by Catchpole (1969) corresponds to a column density of 4.9  1012(
1012(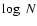 = 12.69), which would correspond to a distance of 2200 pc. However, this value of column density is a lower limit, because the medium is not optically thin in the K line, and a yet higher value of distance is expected.
= 12.69), which would correspond to a distance of 2200 pc. However, this value of column density is a lower limit, because the medium is not optically thin in the K line, and a yet higher value of distance is expected.
By applying T Pyx theoretical predictions for light curves of CVs in outburst, Kato (1990) estimated a distance close to 4000 pc, by comparing the observed magnitude at outburst with the theoretical absolute magnitude prediction at outburst.
In the following, we assume a distance of d=3500  350 pc. A discussion of the
critical role played by distance in the interpretation of the nature of T Pyx is given in Sect. 11.1.
350 pc. A discussion of the
critical role played by distance in the interpretation of the nature of T Pyx is given in Sect. 11.1.
We aim to determine both the disk luminosity and the mass accretion rate of T Pyx. This requires
prior knowledge of the system inclination angle i and the mass of the primary M1. In the disk geometry, the inclination angle is critical to the estimate of the disk luminosity, while M1 and R1 (a function of M1) are key parameters in the correlation between  and
and
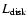 .
For most CVs, the determination of these and other parameters (M2,
.
For most CVs, the determination of these and other parameters (M2,
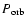 ,
2K) entering the mass function:
,
2K) entering the mass function:
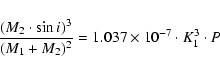 |
(2) |
is a difficult task, and accurate solutions have been obtained only for a few eclipsing systems.
For T Pyx, the situation, ``prima facie'', does not appear encouraging because no system
parameter (not even the orbital period) have been accurately measured. Therefore, one has
to start from a restricted range of values corresponding to the most accurately known
parameters in the mass function equation, based on theoretical or semi-empirical considerations, and derive the corresponding range of allowed solutions for the unknown relevant parameters.
There have been several attempts to measure the orbital period of T Pyx, although, disappointingly, they have resulted in a wide range of values (see Paper I); this is a clear indication that there is no definite photometric clock associated with the system.
Patterson et al. (1998) detected a stable photometric wave at Ph = 1
 829
829  0
0
 002 (a value close to that of the ``most probable'' photometric period Ph = 1
002 (a value close to that of the ``most probable'' photometric period Ph = 1
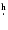 828 of Schaefer et al. 1992), although this interpretation is inconsistent with the presence of another signal at 2
828 of Schaefer et al. 1992), although this interpretation is inconsistent with the presence of another signal at 2
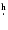 635.
635.
The only spectroscopic determination of the period is that by Vogt et al. (1990), who, in a preliminary study based on a large number (101) of spectra of limited resolution ( 3 Å), reported a spectroscopic period of Ph
3 Å), reported a spectroscopic period of Ph  3
3
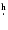 439, without quoting uncertainties.
This spectroscopic period is almost twice the photometric value determined by
Szkody & Feinswog (1988) in the infrared. In other CVs, this behavior is generally interpreted as evidence of ellipsoidal variations in the companion, in a system observed at a
high inclination angle. This is not the case for T Pyx because, as convincingly shown in Paper I, the companion does not contribute to the J light curve, unless the distance is less than 200 pc.
439, without quoting uncertainties.
This spectroscopic period is almost twice the photometric value determined by
Szkody & Feinswog (1988) in the infrared. In other CVs, this behavior is generally interpreted as evidence of ellipsoidal variations in the companion, in a system observed at a
high inclination angle. This is not the case for T Pyx because, as convincingly shown in Paper I, the companion does not contribute to the J light curve, unless the distance is less than 200 pc.
In the following, we consider system solutions for both Ph = 1
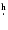 829 (photometric, Patterson et al. 1998) and Ph = 3
829 (photometric, Patterson et al. 1998) and Ph = 3
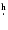 439 (spectroscopic, Vogt et al. 1990). The inclusion of the spectroscopic period could be criticized since it is the result of a preliminary analysis that has not been confirmed by subsequent studies. However, given the complex photometric period
structure and in the absence of a definite physical interpretation of the stable
signal with Ph = 1
439 (spectroscopic, Vogt et al. 1990). The inclusion of the spectroscopic period could be criticized since it is the result of a preliminary analysis that has not been confirmed by subsequent studies. However, given the complex photometric period
structure and in the absence of a definite physical interpretation of the stable
signal with Ph = 1
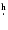 829 (that could even arise from the rotation of a magnetic white dwarf), we believe that the spectroscopic results should be considered, since, in any case, they have not been
challenged by similar studies.
829 (that could even arise from the rotation of a magnetic white dwarf), we believe that the spectroscopic results should be considered, since, in any case, they have not been
challenged by similar studies.
Vogt et al. (1990) found that the projected orbital velocity K1 of the primary, derived
from an analysis of radial velocities of the emission lines, is approximately
24  5 km s-1. Taking into account the limited resolution and the large number of
spectra, this value is probably an upper limit. We assume that this value of K1 is representative of the primary star radial velocity (independently of the period being considered), although we are aware of the problems encountered in associating radial velocity changes with the motion of the WD.
5 km s-1. Taking into account the limited resolution and the large number of
spectra, this value is probably an upper limit. We assume that this value of K1 is representative of the primary star radial velocity (independently of the period being considered), although we are aware of the problems encountered in associating radial velocity changes with the motion of the WD.
Both theoretical considerations and observational determinations (although limited) indicate that the WD masses in classical nova systems are about 1.0  ,
i.e. higher than inferred from the standard field WD mass distribution (Ritter et al. 1991). Theoretical models of
recurrent novae require an even more massive white dwarf (WLTO, Shara 1989; Livio 1994). Therefore, in the following, we allow the mass of the primary, M1, to vary between 1.25 and 1.4
,
i.e. higher than inferred from the standard field WD mass distribution (Ritter et al. 1991). Theoretical models of
recurrent novae require an even more massive white dwarf (WLTO, Shara 1989; Livio 1994). Therefore, in the following, we allow the mass of the primary, M1, to vary between 1.25 and 1.4  .
.
In the absence of any direct information about the secondary (the accretion disk is the dominant luminosity source from the UV to the infrared, Paper I), we can estimate its mass M2 on the basis of the commonly accepted assumptions that: a) the secondary fills its Roche lobe; b) its radius R2 is determined by the Roche geometry; and c) the secondary star obeys a mass-radius relation valid for low mass main sequence stars. In this standard description, the radius of the secondary is well approximated by the equivalent radius 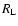 of the Roche lobe itself, i.e. R2
of the Roche lobe itself, i.e. R2 
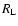 and the spherical volume of the secondary is assumed to equal the volume of its Roche lobe. The equivalent volume radii of the Roche lobe are given in tabular form by several authors (Plavec & Kratochvil 1964; Kopal 1972; Eggleton 1983; Mochnacky 1984). For our purposes, it is convenient however to use the analytical approximation by Paczinsky (1971), which is valid for M2/M1
and the spherical volume of the secondary is assumed to equal the volume of its Roche lobe. The equivalent volume radii of the Roche lobe are given in tabular form by several authors (Plavec & Kratochvil 1964; Kopal 1972; Eggleton 1983; Mochnacky 1984). For our purposes, it is convenient however to use the analytical approximation by Paczinsky (1971), which is valid for M2/M1 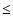 0.8:
0.8:
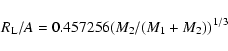 |
(3) |
where we have introduced a new value for the constant (instead of 0.46224) because it yields results that differ by less than 1% from those tabulated by Eggleton (1983) and Mochnacky (1984).
By combining Eq. (3) with Kepler's third law:
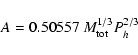 |
(4) |
one obtains an approximate relation between P, M2, and R2 (
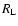 ):
):
|
Ph = 8.997 R23/2 M2-1/2.
|
(5) |
In the crude assumption M2  R2, this provides an approximate relation: M2 = 0.111 Ph by which a rough estimate of the mass of the secondary can be obtained if the orbital period is known. In general, however, the R-M relation for the low MS stars is described more accurately by a relation of the form:
R2, this provides an approximate relation: M2 = 0.111 Ph by which a rough estimate of the mass of the secondary can be obtained if the orbital period is known. In general, however, the R-M relation for the low MS stars is described more accurately by a relation of the form:
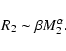 |
(6) |
By combining Eqs. (5) and (6), we derive a more general relation between M2 and Ph:
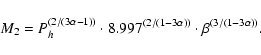 |
(7) |
Values for the parameters  and
and  of the low mass main-sequence stars
were derived from observational data and theoretical considerations. In particular,
Warner (1995) assumed that R2 =
M213/15 (which provides an approximate fit to
the data set by Webbink 1990) and derived M=0.065
of the low mass main-sequence stars
were derived from observational data and theoretical considerations. In particular,
Warner (1995) assumed that R2 =
M213/15 (which provides an approximate fit to
the data set by Webbink 1990) and derived M=0.065  P1.25, while Smith & Dhillon (1998) found a constitutive relation R2 = 0.91
M20.75 and derived M=0.038
P1.25, while Smith & Dhillon (1998) found a constitutive relation R2 = 0.91
M20.75 and derived M=0.038  P1.58.
P1.58.
Patterson et al. (2005) derived an empirical mass-radius sequence for CV secondaries based on masses and radii measured primarily for the superhumping CVs. They found that R2 = 0.62  M20.61 for P shorter than 2.3 h, and R2 = 0.92
M20.61 for P shorter than 2.3 h, and R2 = 0.92  M20.71 for P longer than 2.5 h, and derived M2 = 0.032
M20.71 for P longer than 2.5 h, and derived M2 = 0.032  P2.38 (P
P2.38 (P 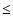 2.3) and M2 = 0.026
2.3) and M2 = 0.026  P1.78 (P
P1.78 (P 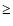 2.5). We inserted the
2.5). We inserted the 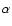 and
and 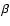 values of Patterson et al. (2005) in Eq. (7) and obtained slightly different results, that is, M2 = 0.02823 P2.41 (short P) and M2 = 0.02554 P1.77 (long P).
values of Patterson et al. (2005) in Eq. (7) and obtained slightly different results, that is, M2 = 0.02823 P2.41 (short P) and M2 = 0.02554 P1.77 (long P).
Table 1:
M2 for Ph = 1.829 and Ph = 3.439 from various M2-P relations or different 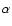 and
and 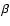 values in the literature (see text).
values in the literature (see text).
Knigge (2006) obtained an independent M2-R2 relation by revisiting and updating the mass-radius relationship for CV secondaries determined by Patterson et al. (2005). We have fitted with a
power-law the data contained in his Table 3 and derived M2-P relations for short P and long P systems. The relations are
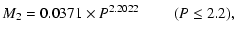 |
|
|
(8) |
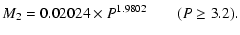 |
|
|
|
Table 1 provides the M2 values obtained by these various methods, for Ph = 1
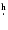 829 (photometric) and Ph = 3
829 (photometric) and Ph = 3
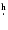 439 (spectroscopic).
439 (spectroscopic).
In the following, we therefore study the system solutions for M2 = 0.12  0.02
0.02  and M2 = 0.24
and M2 = 0.24  0.02
0.02  ,
separately. The corresponding spectral types are in the range M3V-M5V (Kirkpatrick et al. 1991; Legget 1992).
,
separately. The corresponding spectral types are in the range M3V-M5V (Kirkpatrick et al. 1991; Legget 1992).
The above derived range of allowed values for the system parameters (M1: 1.25-1.4  ,
M2 = 0.12
,
M2 = 0.12  (for Ph = 1
(for Ph = 1
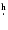 829), M2 = 0.24
829), M2 = 0.24  (for Ph = 3
(for Ph = 3
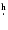 439), K1: 24
439), K1: 24  5 km s-1) can be inserted into Eq. (2) to find the corresponding range
of solutions for the system inclination, which is considered to be a free parameter.
5 km s-1) can be inserted into Eq. (2) to find the corresponding range
of solutions for the system inclination, which is considered to be a free parameter.
Table 2 clearly shows that, given the observational and theoretical constrains for P, K1, M1, and M2, the solutions for the inclination i are in the range between 20 and 30 degrees,
a value close to 25 degrees being the most likely value. In particular, for M1 
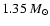 ,
(see also the following) the solutions for i do not change significantly, and for Ph = 1
,
(see also the following) the solutions for i do not change significantly, and for Ph = 1
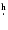 829 (M2 = 0.12
829 (M2 = 0.12  )
and Ph = 3
)
and Ph = 3
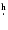 439 (M2 = 0.24
439 (M2 = 0.24  )
are close to 30 and 20 degrees, respectively (see also Fig. 1).
)
are close to 30 and 20 degrees, respectively (see also Fig. 1).
Patterson et al. (1998) suggested that T Pyx is being observed at low system inclination, i.e. i  10
10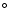 -20
-20 ,
due to the low amplitude of the orbital signal. Shabbaz et al. (1997) estimated the binary inclination i of T Pyx by measuring the separation of the H
,
due to the low amplitude of the orbital signal. Shabbaz et al. (1997) estimated the binary inclination i of T Pyx by measuring the separation of the H emission-line peaks, and obtained a lower limit of
emission-line peaks, and obtained a lower limit of  6
6 .
A low system inclination is also consistent with the small value of the radial velocity,
the sharpness of the emission lines in the optical (Warner 1995), and the steepness of the UV and optical continua (Paper I). However, the presence of radial velocity variations (Vogt et al. 1990), and the modulations in the photometric variations preclude an i value close to zero.
.
A low system inclination is also consistent with the small value of the radial velocity,
the sharpness of the emission lines in the optical (Warner 1995), and the steepness of the UV and optical continua (Paper I). However, the presence of radial velocity variations (Vogt et al. 1990), and the modulations in the photometric variations preclude an i value close to zero.
Table 2:
The system inclination for M1 = 1.25-1.40  and K1 = 24
and K1 = 24  5 km s-1 for the cases (1) Ph = 1
5 km s-1 for the cases (1) Ph = 1
 829, M2 = 0.12; and (2) Ph = 3
829, M2 = 0.12; and (2) Ph = 3
 439, M2 = 0.24.
439, M2 = 0.24.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{0678fig1}
\end{figure}](/articles/aa/full/2008/48/aa10678-08/Timg71.gif) |
Figure 1:
The
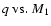 plane for Ph = 3 plane for Ph = 3
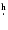 439 and Ph = 1 439 and Ph = 1
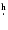 829.
The lines of constant inclination refer to K1=19 km s-1 (solid) and K1=29 km s-1 (dashed), spanning the error range in the value of K1. The values of i are indicated.
The error bars represent the ranges in M1 and M2 discussed in the text. 829.
The lines of constant inclination refer to K1=19 km s-1 (solid) and K1=29 km s-1 (dashed), spanning the error range in the value of K1. The values of i are indicated.
The error bars represent the ranges in M1 and M2 discussed in the text. |
| Open with DEXTER |
It should therefore be noted that, in spite of the large uncertainties in the observational data, the adoption of plausible theoretical assumptions and some semi-empirical constraints has enabled a quite restricted range for the values of the system inclination to be defined. In the
following we will assume i=25  5 degrees for the system inclination angle.
5 degrees for the system inclination angle.
During the quiescent phase after the 1967 outburst, the average optical magnitude of T Pyx is mv = 15.3  0.05 (Warner 1995; Duerbeck 1987,b; Schaefer 1992); for d = 3500
0.05 (Warner 1995; Duerbeck 1987,b; Schaefer 1992); for d = 3500  350 pc and AV = 0.79
350 pc and AV = 0.79  0.06, we obtain an (observed) absolute magnitude at minimum
0.06, we obtain an (observed) absolute magnitude at minimum
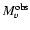 = 1.79
= 1.79  0.21 (Warner 1995, defined this to be the apparent absolute magnitude since the observed flux in quiescence depends on the inclination angle).
0.21 (Warner 1995, defined this to be the apparent absolute magnitude since the observed flux in quiescence depends on the inclination angle).
Assuming that the visual radiation originates in a non-irradiated disk (Paper I), we correct the apparent absolute magnitude
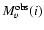 for the inclination angle of the disk (see Warner 1987, 1995) by a term
for the inclination angle of the disk (see Warner 1987, 1995) by a term
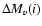 to obtain the ``standard'' or ``reference'' absolute magnitude:
to obtain the ``standard'' or ``reference'' absolute magnitude:
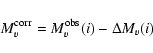 |
(9) |
where
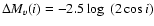 according to WLTO (1987), or
according to WLTO (1987), or
![$\Delta M_v(i)= - 2.5\log~[(1+1.5\cos i)\cos i]$](/articles/aa/full/2008/48/aa10678-08/img77.gif) according to Paczynski & Schvarzenberg-Czerny (1980).
according to Paczynski & Schvarzenberg-Czerny (1980).
For
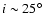 ,
one obtains a correction of
,
one obtains a correction of
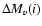
 0.74
0.74  0.06,
by averaging these two relations, and
0.06,
by averaging these two relations, and
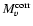 = +2.53
= +2.53  0.22 for the absolute
magnitude, averaged over all aspect angles. This value is about 1.4 mag brighter than the mean absolute magnitude of nova remnants in the same speed class (see Fig. 2.20 and Table 4.6 of Warner 1995). It is also about 2.0 mag brighter than the mean absolute magnitude of novae at
minimum, as obtained from the values given in Table 6 of Downes & Duerbeck (2000).
0.22 for the absolute
magnitude, averaged over all aspect angles. This value is about 1.4 mag brighter than the mean absolute magnitude of nova remnants in the same speed class (see Fig. 2.20 and Table 4.6 of Warner 1995). It is also about 2.0 mag brighter than the mean absolute magnitude of novae at
minimum, as obtained from the values given in Table 6 of Downes & Duerbeck (2000).
The T Pyx remnant is therefore one of the brightest nova remnants, its absolute magnitude
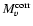 = +2.53 being close to that of the ex-nova HR Del, whose corrected value,
= +2.53 being close to that of the ex-nova HR Del, whose corrected value,
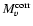 = 2.30, implies that it is a quite luminous object (see also Paper I).
= 2.30, implies that it is a quite luminous object (see also Paper I).
As shown in Paper I, the integrated UV continuum flux of T Pyx in the wavelength range 1180-3230 Å, after correction for reddening, is 1.94  10-10 erg cm-2 s-1. For d = 3500
10-10 erg cm-2 s-1. For d = 3500  350 pc, the corresponding integrated luminosity of the UV continuum is:
350 pc, the corresponding integrated luminosity of the UV continuum is:
where the 20 percent is caused by the 10 percent uncertainty in the distance. Most old novae have
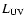 in the range 1-20
in the range 1-20 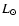 ,
with V 841 Oph at
,
with V 841 Oph at 
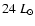 (Gilmozzi et al. 1994), and V603 Aql and RR Pic at
(Gilmozzi et al. 1994), and V603 Aql and RR Pic at 
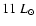 and
and 
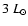 ,
respectively (Selvelli 2004). Therefore, T Pyx is also quite bright in the UV and, again, is challenged
only by HR Del that has
,
respectively (Selvelli 2004). Therefore, T Pyx is also quite bright in the UV and, again, is challenged
only by HR Del that has
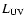 = 56
= 56 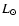 (Selvelli & Friedjung 2002).
(Selvelli & Friedjung 2002).
In the following, we assume that the observed UV and optical luminosity arise from an accretion disk heated by viscous dissipation of gravitational energy. This agrees with the behavior of
similar objects, like old novae and nova-like stars. This assumption is also strongly supported by the fact that the continuum energy distribution in the UV range is well reproduced (Paper I) by a power-law with spectral index 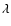 -2.33, as predicted by theoretical optically thick accretion disk models radiating as a sum of blackbodies.
-2.33, as predicted by theoretical optically thick accretion disk models radiating as a sum of blackbodies.
The bolometric disk luminosity
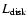 can be estimated from the observed UV and optical luminosity, where the bulk of the continuum radiation is emitted, after correction for the inclination and the unseen luminosity in both the infrared and at
can be estimated from the observed UV and optical luminosity, where the bulk of the continuum radiation is emitted, after correction for the inclination and the unseen luminosity in both the infrared and at 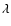
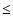 1200 Å. The radiation emitted at wavelengths shorter than Ly
1200 Å. The radiation emitted at wavelengths shorter than Ly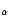 is strongly absorbed and the energy is redistributed to longer wavelengths (Nofar et al. 1992; Wade & Hubeny 1998).
is strongly absorbed and the energy is redistributed to longer wavelengths (Nofar et al. 1992; Wade & Hubeny 1998).
The integration (from 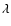
 1000 Å to the IR) of the power-law distribution which represents the observed UV and optical continuum of T Pyx, corresponds to a flux of about 3.6
1000 Å to the IR) of the power-law distribution which represents the observed UV and optical continuum of T Pyx, corresponds to a flux of about 3.6  10-10 erg cm-2 s-1, which corresponds to a bolometric luminosity of 5.24
10-10 erg cm-2 s-1, which corresponds to a bolometric luminosity of 5.24  1035 erg s-1
1035 erg s-1  136.5
136.5 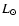 .
This value refers to the adopted inclination of about 25 degrees. After correction to the ``standard'' inclination of about 57 degrees and by considering an average limb-darkening factor similar to that in the optical, we
obtain an angle (4
.
This value refers to the adopted inclination of about 25 degrees. After correction to the ``standard'' inclination of about 57 degrees and by considering an average limb-darkening factor similar to that in the optical, we
obtain an angle (4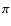 )
averaged bolometric disk luminosity (hereinafter
)
averaged bolometric disk luminosity (hereinafter
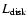 )
of about 70
)
of about 70  15
15 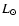 ,
where the relative uncertainty (21 percent) derives from the combination of the uncertainties in the distance and the inclination. We consider this to be the reference disk luminosity for the ``recent'', post-1967-outburst epoch. We note that the Wade & Hubeny (1998) models indicate (their Fig. 8) that in the UV region close to 1200 A (where the effect is larger) the limb-darkening correction, from i of about 25 degrees to i of about 60 degrees, corresponds to a flux reduction of about 30 percent (this is limb darkening alone, and the geometric projection factor cos i is not included).
,
where the relative uncertainty (21 percent) derives from the combination of the uncertainties in the distance and the inclination. We consider this to be the reference disk luminosity for the ``recent'', post-1967-outburst epoch. We note that the Wade & Hubeny (1998) models indicate (their Fig. 8) that in the UV region close to 1200 A (where the effect is larger) the limb-darkening correction, from i of about 25 degrees to i of about 60 degrees, corresponds to a flux reduction of about 30 percent (this is limb darkening alone, and the geometric projection factor cos i is not included).
A rough estimate of the 4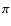 averaged bolometric disk luminosity can also be obtained from
averaged bolometric disk luminosity can also be obtained from
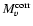 = +2.53. Adopting an average disk temperature of about 28 000 K (the UV continuum indicates
= +2.53. Adopting an average disk temperature of about 28 000 K (the UV continuum indicates  34 000 K, although this is too hot to match the optical fluxes), the corresponding bolometric correction is
34 000 K, although this is too hot to match the optical fluxes), the corresponding bolometric correction is
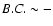 2.7, and
2.7, and
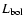
 92.9
92.9 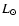 ,
in fair agreement with the previous estimate. In this comparison, we
neglected the effects of temperature stratification in the accretion disk.
,
in fair agreement with the previous estimate. In this comparison, we
neglected the effects of temperature stratification in the accretion disk.
One could in principle estimate the mass accretion rate  by comparing the observed spectral distribution with that of proper accretion disk models. This approach is not viable in our case for the following reasons: a) the spectral index of model disks that consist of blackbodies is hardly sensitive to the mass accretion rate
by comparing the observed spectral distribution with that of proper accretion disk models. This approach is not viable in our case for the following reasons: a) the spectral index of model disks that consist of blackbodies is hardly sensitive to the mass accretion rate  ;
b) most models providing
;
b) most models providing  as a
function of the continuum slope do not include the case of a massive WD with high accretion rates; c) disk models depend on a large number of parameters, so that model fitting does not generally provide unique results.
as a
function of the continuum slope do not include the case of a massive WD with high accretion rates; c) disk models depend on a large number of parameters, so that model fitting does not generally provide unique results.
Alternatively, if, as in our case, one can make the reasonable assumption that the disk is heated by viscous dissipation of gravitational energy, the mass accretion rate  can be
obtained from the relation:
can be
obtained from the relation:
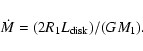 |
(10) |
With this method,  is not model dependent but the knowledge of
is not model dependent but the knowledge of
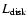 and M1 is required.
and M1 is required.
Numerically,  can be represented by:
can be represented by:
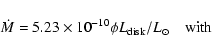 |
(11) |
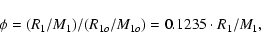 |
(12) |
where R1 is the WD radius in 10
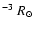 ,
,
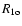 = 8.10
= 8.10  10
10
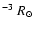 is the radius of a WD of mass M1 = 1.0
is the radius of a WD of mass M1 = 1.0  ,
and M1 is in solar masses.
,
and M1 is in solar masses.
We obtained average values for R1 as a function of M1 from various WD radius-mass relations in the literature (Hamada & Salpeter 1961; Nauenberg 1972; Anderson 1988; Politano et al. 1990; Livio 1994). By fitting a quadratic function to these average values, for M1 in the range 1.0 to 1.4  ,
we found that:
,
we found that:
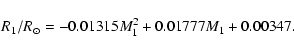 |
(13) |
The upper curve in Fig. 2 is a plot of the standard R1  M1-1/3 relation, which is generally valid for M1
M1-1/3 relation, which is generally valid for M1 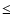 1.0
1.0  ,
while the lower curve represents the quadratic fit to the average values for M1 in the range 1.0 to 1.4
,
while the lower curve represents the quadratic fit to the average values for M1 in the range 1.0 to 1.4  ,
with a relative
uncertainty of
,
with a relative
uncertainty of
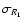 /R1 = 0.07.
/R1 = 0.07.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{0678fig2}
\end{figure}](/articles/aa/full/2008/48/aa10678-08/Timg96.gif) |
Figure 2:
The lower curve represents a quadratic fit to the average values of the WD radius as a function of M1 derived from various WD radius-mass relations in the literature (dots). The upper curve is the standard R1  M1-1/3 relation.
M1-1/3 relation. |
| Open with DEXTER |
Columns 2-4 in Table 3 indicate R1, 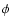 ,
and
,
and  for M1 in the range 1.00-1.4
for M1 in the range 1.00-1.4  .
We note that
.
We note that 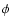 = 1.00 for M1 = 1.0
= 1.00 for M1 = 1.0  ,
and decreases to
about 0.23 for M1 = 1.4
,
and decreases to
about 0.23 for M1 = 1.4  .
The accretion rate
.
The accretion rate  in Table 3 is calculated for the (present) luminosity
in Table 3 is calculated for the (present) luminosity
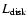
 70
70 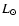 ,
derived from UV data. In the case of a massive WD, the mass accretion rate is close to 1.1
,
derived from UV data. In the case of a massive WD, the mass accretion rate is close to 1.1  0.3
0.3  10
10
 yr-1. The uncertainty in
yr-1. The uncertainty in  is of the order of 23 percent and derives from the uncertainties in the distance, the correction for the inclination, and
the value of R1.
is of the order of 23 percent and derives from the uncertainties in the distance, the correction for the inclination, and
the value of R1.
Table 3:
M1, R1, the factor 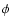 = (R1/M1)/(R1o/M1o), the post-1967 mass accretion rate
= (R1/M1)/(R1o/M1o), the post-1967 mass accretion rate  (for
(for
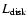 = 70
= 70 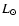 ), the ignition mass, and the recurrence time
), the ignition mass, and the recurrence time 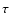 =
=
 /
/ (see Sect. 8).
(see Sect. 8).
An independent confirmation of these values for the mass accretion rate can be obtained from the mass accretion rate versus boundary layer luminosity (
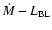 ) relation given in Table 2 of Patterson & Raymond (1985), if one assumes that
) relation given in Table 2 of Patterson & Raymond (1985), if one assumes that
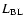

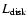 .
Their Table 2 indicates that (for M1 = 1.0) a mass accretion rate
.
Their Table 2 indicates that (for M1 = 1.0) a mass accretion rate  of 1.6
of 1.6  10
10
 yr-1, close to that derived above, would correspond to a luminosity
of 1.3
yr-1, close to that derived above, would correspond to a luminosity
of 1.3  1035 erg s-1. With the same
1035 erg s-1. With the same  ,
a larger luminosity is expected by extrapolation to M1 values close to 1.3
,
a larger luminosity is expected by extrapolation to M1 values close to 1.3  ,
in close agreement with the value found for
,
in close agreement with the value found for
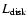 (2.70
(2.70  1035 erg s-1).
1035 erg s-1).
The
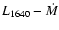 relation reported in the same Table 2 does not, however, provide
a consistent result. The average (de-reddened) flux on earth in the HeII 1640 line is 6.32
relation reported in the same Table 2 does not, however, provide
a consistent result. The average (de-reddened) flux on earth in the HeII 1640 line is 6.32  10-13 erg cm-2 s-1 (Paper I) and the corresponding luminosity for d=3500 pc is 9.3
10-13 erg cm-2 s-1 (Paper I) and the corresponding luminosity for d=3500 pc is 9.3  1032 erg s-1. Table 2 of Patterson & Raymond (1985) indicates instead a L1640 = 1.2
1032 erg s-1. Table 2 of Patterson & Raymond (1985) indicates instead a L1640 = 1.2  1032 erg s-1 for
1032 erg s-1 for  = 1018 g s-1 = 1.587
= 1018 g s-1 = 1.587  10
10
 yr-1, M1 = 1, and extrapolation to higher M1 values does not appear to be able of reproducing the observed HeII luminosity. In T Pyx there is probably a nebular contribution to L1640 that is added to that produced by the BL. It should also be emphasized that the HeII 1640 emission line exhibits significant changes, while the UV continuum remains constant in intensity and slope (see Paper I). This behavior casts doubts about the
suitability of the
yr-1, M1 = 1, and extrapolation to higher M1 values does not appear to be able of reproducing the observed HeII luminosity. In T Pyx there is probably a nebular contribution to L1640 that is added to that produced by the BL. It should also be emphasized that the HeII 1640 emission line exhibits significant changes, while the UV continuum remains constant in intensity and slope (see Paper I). This behavior casts doubts about the
suitability of the
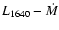 method for the specific case of T Pyx.
method for the specific case of T Pyx.
Another estimate of  can be obtained by direct application of the
can be obtained by direct application of the
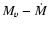 relations reported in the literature. WLTO (1987) derived a relation between the absolute optical
magnitude and the accretion rate for the ``reference'' disk model (Warner 1987), after
correction for the disk inclination:
relations reported in the literature. WLTO (1987) derived a relation between the absolute optical
magnitude and the accretion rate for the ``reference'' disk model (Warner 1987), after
correction for the disk inclination:
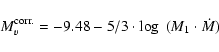 |
(14) |
where M1 is in solar masses and  is in solar masses per year. In the case of T Pyx,
for M1 in the range 1.25-1.4
is in solar masses per year. In the case of T Pyx,
for M1 in the range 1.25-1.4  ,
one obtains values of
,
one obtains values of  close to 5.0
close to 5.0  10
10
 yr-1. It should be noted, however, that in the
yr-1. It should be noted, however, that in the
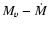 relation given by WLTO there is no explicit dependence on R1, which strongly
depends on M1, especially for massive WDs. If
relation given by WLTO there is no explicit dependence on R1, which strongly
depends on M1, especially for massive WDs. If  is corrected for the factor
is corrected for the factor
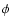 = (R1/M1)/(R1o/M1o) one obtains that
= (R1/M1)/(R1o/M1o) one obtains that  (1.25) = 3.50
(1.25) = 3.50  10
10
 yr-1 and
yr-1 and  (1.40) = 1.60
(1.40) = 1.60  10
10
 yr-1. If
one instead adopts the Paczynski & Schvarzenberg-Czerny (1980) correction for i, the corresponding
yr-1. If
one instead adopts the Paczynski & Schvarzenberg-Czerny (1980) correction for i, the corresponding  values are 2.85
values are 2.85  10
10
 yr-1 and 1.22
yr-1 and 1.22  10
10
 yr-1 respectively.
yr-1 respectively.
Lipkin et al. (2001) improved the
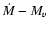 relations presented by Retter & Leibowitz (1998) and Retter & Naylor (2000) and derived the new relation
relations presented by Retter & Leibowitz (1998) and Retter & Naylor (2000) and derived the new relation
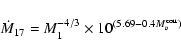 |
(15) |
where
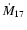 is the mass transfer rate in 1017 g s-1 and
is the mass transfer rate in 1017 g s-1 and
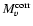 is
the inclination-corrected absolute magnitude of the disk. The factor
M1-4/3 comes from the factor R1/M1 in the assumption, generally valid for WDs with M
is
the inclination-corrected absolute magnitude of the disk. The factor
M1-4/3 comes from the factor R1/M1 in the assumption, generally valid for WDs with M 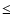 1
1  ,
that
MR3 = const. However, this R1-M1 relation (polytropes) is not applicable if the WD is
massive because in this case R1 decreases with a far steeper slope as M1 increases (see Sect. 6 and Fig. 2). The adoption of the standard R1
,
that
MR3 = const. However, this R1-M1 relation (polytropes) is not applicable if the WD is
massive because in this case R1 decreases with a far steeper slope as M1 increases (see Sect. 6 and Fig. 2). The adoption of the standard R1  M1-1/3 relation for massive WD has the effect of overestimating R1 and in turn overestimating
M1-1/3 relation for massive WD has the effect of overestimating R1 and in turn overestimating  .
This is especially true for M1
.
This is especially true for M1  1.4, for which the difference between the R1 values estimated from the R1
1.4, for which the difference between the R1 values estimated from the R1  M1-1/3 relation and the more general R1-M1 relations (Hamada & Salpeter 1961; Nauenberg 1972; Anderson 1988; Politano et al. 1990; Livio 1994) reaches its maximum value (Fig. 2).
M1-1/3 relation and the more general R1-M1 relations (Hamada & Salpeter 1961; Nauenberg 1972; Anderson 1988; Politano et al. 1990; Livio 1994) reaches its maximum value (Fig. 2).
The Lipkin et al. (2001) formula corrected for the proper R1/M1 ratio in massive white dwarfs according to the 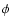 factors of Table 3, provides values of
factors of Table 3, provides values of  = 1.38
= 1.38  10-8 and 0.59
10-8 and 0.59  10-8 for white dwarfs with M1 = 1.25
10-8 for white dwarfs with M1 = 1.25  and M1 = 1.40
and M1 = 1.40  ,
respectively. These values are about one half of the corresponding values obtained from the WLTO formula. It should be noted, however, that, in the derivation of
Lipkin et al. (2001) formula there is the assumption that Lv/
,
respectively. These values are about one half of the corresponding values obtained from the WLTO formula. It should be noted, however, that, in the derivation of
Lipkin et al. (2001) formula there is the assumption that Lv/
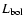
 0.14. In the case of T Pyx, this Lv/
0.14. In the case of T Pyx, this Lv/
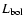 ratio is lower by a factor of about two and therefore the
ratio is lower by a factor of about two and therefore the  derived using their formula is underestimated by a similar amount. In conclusion, the various methods provide quite consistent results and we can confidently assume that the mass accretion rate derived from ``recent'' UV and optical data is 1.86
derived using their formula is underestimated by a similar amount. In conclusion, the various methods provide quite consistent results and we can confidently assume that the mass accretion rate derived from ``recent'' UV and optical data is 1.86  0.4
0.4  10
10
 yr-1 for M1 = 1.25, and 0.84
yr-1 for M1 = 1.25, and 0.84  0.2
0.2  10
10
 yr-1 for M1 = 1.40
yr-1 for M1 = 1.40  .
For an intermediate value of M1 = 1.33
.
For an intermediate value of M1 = 1.33  we obtain that
we obtain that 
 1.3
1.3  10
10
 yr-1.
yr-1.
Table 4 summarizes the adopted values of the basic parameters and their estimated errors.
Table 4:
The basic quantities.
Schaefer (2005) published a large collection of quiescent B-magnitudes for the recurrent novae T Pyx and U Sco using information from archival plates, from the literature, and from his own
collection of CCD magnitudes. The photometric data of T Pyx start in 1890 and therefore cover all of the known inter-outburst intervals.
According to these data, during the inter-outburst phase in the years 1945-1966, T Pyx was a factor of 2 brighter in the B band than during the present quiescent phase after the 1967 outburst. Since no significant changes in the (B-V) color index were found during both of these quiescence phases, one can safely deduce that in 1945-1966 T Pyx was a factor of 2 brighter also in terms of visual and bolometric flux. Using the WLTO and the Lipkin et al. (2001) relations, one finds that the mass accretion rate in epochs pre-1966-outburst, hereinafter
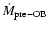 ,
was about twice the values of
,
was about twice the values of  for post 1967, obtained in the previous section.
for post 1967, obtained in the previous section.
Therefore, we estimate that the mass accretion rate
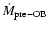 during the last
pre-outburst interval (1945-1966) was between 1.68
during the last
pre-outburst interval (1945-1966) was between 1.68  0.4
0.4  10
10
 yr-1 and 3.72
yr-1 and 3.72  0.8
0.8  10
10
 yr-1, for M1 = 1.25 and M1 = 1.40 respectively.
yr-1, for M1 = 1.25 and M1 = 1.40 respectively.
These are the values that are compared in Sects. 8 and 9 with the theoretical models of nova. The post-1967 accretion values (Table 3) are considered in Sect. 16 in the context of the ``missing'' outburst and the next expected outburst.
A nova outburst occurs when, due to the gradual accumulation of H-rich material on the surface of the white dwarf, the pressure at the bottom of the accreted layer becomes sufficiently high for nuclear ignition of H to begin (Shara 1981; Fujimoto 1982; MacDonald 1983). Since the radius R1 of the white dwarf varies approximately as
M1-1/3 for M1  1.0
1.0  ,
the critical pressure for ignition
,
the critical pressure for ignition
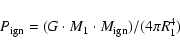 |
(16) |
corresponds to a critical ignition mass
 that decreases approximately as
M1-7/3,
while, for more massive WDs
that decreases approximately as
M1-7/3,
while, for more massive WDs
 ,
decreases with a steeper slope (see Table 3 and Fig. 2). In any case, massive white dwarfs need to accrete a small amount of mass to reach the critical conditions.
,
decreases with a steeper slope (see Table 3 and Fig. 2). In any case, massive white dwarfs need to accrete a small amount of mass to reach the critical conditions.
For a given M1 value, the critical ignition mass has been calculated by various authors and the
reported values (for a given M1) differ from each other mostly in the choice of the critical pressure at the base of the accreted envelope, which varies between 2.0  1019 and 6.0
1019 and 6.0  1019 dynes cm-2 (see Gehrz et al. 1998; Starrfield et al. 1998a,b,c; Livio & Truran 1992; Hernanz & José 1998; Truran 1998). These studies indicate that a lower limit to
1019 dynes cm-2 (see Gehrz et al. 1998; Starrfield et al. 1998a,b,c; Livio & Truran 1992; Hernanz & José 1998; Truran 1998). These studies indicate that a lower limit to
 (for a massive white dwarf with M1 close to 1.4
(for a massive white dwarf with M1 close to 1.4  )
is in the range 2.0-4.0
)
is in the range 2.0-4.0  10-6
10-6  .
However, as first pointed out by MacDonald (1983) and in more detail by Shara (1989) and Prialnik & Kovetz (1995), the behavior of a CN eruption
and in particular the critical mass depends (apart from the WD mass) also on the mass accretion rate (since the WD is heated by accretion) and the temperature of the isothermal white dwarf core.
.
However, as first pointed out by MacDonald (1983) and in more detail by Shara (1989) and Prialnik & Kovetz (1995), the behavior of a CN eruption
and in particular the critical mass depends (apart from the WD mass) also on the mass accretion rate (since the WD is heated by accretion) and the temperature of the isothermal white dwarf core.
Townsley & Bildsten (2004) confirmed that the earlier prescriptions for ignition, based on the simple scaling

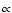 R4 M1-1 for a unique
R4 M1-1 for a unique
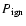 ,
are inadequate
and that a system of a given M1 mass can have value of
,
are inadequate
and that a system of a given M1 mass can have value of
 that varies by a
factor of 10 for different
that varies by a
factor of 10 for different  .
At the high
.
At the high  values typical of most CVs,
the critical pressure can decrease to values as low as 3
values typical of most CVs,
the critical pressure can decrease to values as low as 3  1018 dyn cm-2, and the critical mass decreases accordingly. Thus, in a massive white dwarf accreting at significantly high rates, one expects a value for
1018 dyn cm-2, and the critical mass decreases accordingly. Thus, in a massive white dwarf accreting at significantly high rates, one expects a value for
 as low as 2-4
as low as 2-4  10
10
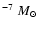 .
.
The critical envelope mass
 as a function of M1 and
as a function of M1 and  can be numerically approximated to be:
can be numerically approximated to be:
(Kahabka & van Den Heuvel 2006) where M1 is in  and
and  is in
is in  yr-1.
yr-1.
Table 5 indicates (for various M1 and hence R1 values)
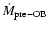 ,
the theoretical
,
the theoretical
 ,
the accreted mass
,
the accreted mass
 =
= 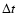
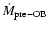 ,
where
,
where 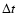 = 22 yrs is the pre-1966 inter-outburst interval, and
= 22 yrs is the pre-1966 inter-outburst interval, and 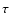 =
=
 /
/
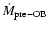 ,
that is, the expected recurrence time in years. The mass accretion rate and
,
that is, the expected recurrence time in years. The mass accretion rate and
 were calculated using the quadratic fit for R1 as a function of M1for massive white dwarfs derived in Sect. 6 (see also Table 3), and not the approximation R1
were calculated using the quadratic fit for R1 as a function of M1for massive white dwarfs derived in Sect. 6 (see also Table 3), and not the approximation R1  M1 -1/3. Table 5 clearly shows that, after allowances for errors in the estimate of
M1 -1/3. Table 5 clearly shows that, after allowances for errors in the estimate of
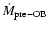 ,
the expected recurrence time
,
the expected recurrence time 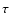 =
=
 /
/
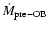 is close to the observed value (22 yr) for M1
is close to the observed value (22 yr) for M1  1.36-1.38
1.36-1.38  corresponding to
corresponding to
 and
and
 in the range 3.0 to 6.0
in the range 3.0 to 6.0  10-7
10-7  .
.
This agrees with the estimate of Kato (1990) that the white dwarf mass for T Pyx is between 1.3 and 1.4  ,
while in a subsequent paper Kato & Hachisu (1991) assumed M1 = 1.33
,
while in a subsequent paper Kato & Hachisu (1991) assumed M1 = 1.33  .
.
We confirmed the results for
 using the approximate relation for the ignition mass as a function of M1 and
using the approximate relation for the ignition mass as a function of M1 and  given by Kolb et al. (2001):
given by Kolb et al. (2001):
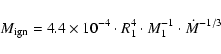 |
(18) |
(where
 and M1 are in
and M1 are in  ,
R1 is in 109 cm, and
,
R1 is in 109 cm, and  is in 10
is in 10
 yr-1) and obtained
yr-1) and obtained
 = 2.72
= 2.72  10
10
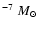 .
A similar result is also obtained by graphical interpolation in Fig. 5 of Kahabka & Van Den Heuvel (1997), which for M1
.
A similar result is also obtained by graphical interpolation in Fig. 5 of Kahabka & Van Den Heuvel (1997), which for M1  1.37 and
1.37 and 
 2
2  10
10
 yr-1 provides an ignition mass close to 3.0
yr-1 provides an ignition mass close to 3.0  10
10
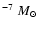 (we note, however, that these parameters fall within a region in which only weak flashes are expected). In addition, we derived
(we note, however, that these parameters fall within a region in which only weak flashes are expected). In addition, we derived
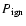 as a function of
as a function of  and the WD temperature from Fig. 3 of Yaron et al. (2005), and found that
and the WD temperature from Fig. 3 of Yaron et al. (2005), and found that
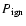
 4.8
4.8  1018 for
1018 for  = 2
= 2  10
10
 yr-1 (we note that in this regime there is a weak dependence on the WD temperature). The insertion of this value of
yr-1 (we note that in this regime there is a weak dependence on the WD temperature). The insertion of this value of
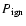 in Eq. (16) gives
in Eq. (16) gives
 = 3.8
= 3.8  10
10
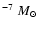 .
.
The consistency of all these results confirms that in the case of T Pyx the ignition mass was close to 4.5  10
10
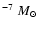 .
.
Table 5:
M1, the estimated pre-1967-outburst accretion rate
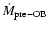 (for
(for
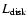 = 140
= 140 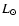 ), the theoretical ignition mass
), the theoretical ignition mass
 ,
the accreted mass
,
the accreted mass
 = 22
= 22 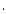
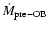 and the expected recurrence time
and the expected recurrence time 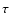 =
=
 /
/
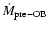 .
.
In the recurrent nova T Pyx, the theoretical ignition mass and observed accreted mass
are in excellent agreement for a massive WD, which provides new, independent support of the TNR theory. Theoretical expectations have received only limited confirmation because studies of the system parameters (in U Sco, T Cr B) have provided contradictory results.
The realization that three basic and independent parameters, the white dwarf mass M1, the temperature of its isothermal core 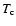 ,
and the mass transfer rate
,
and the mass transfer rate  ,
control the behavior of a CN eruption, and the improvements in computer power and codes, has enabled
an increase in sophistication in simulating a nova outburst. Prialnik & Kovetz (1995) presented an extended grid of multicycle nova evolution models that have been extensively used by researchers. Each observed nova characteristic (e.g. peak luminosity, recurrence time, duration of the high luminosity phase, outburst amplitude, mass of ejecta, average outflow velocity, etc.) can be reproduced by a particular combinations of values of M1,
,
control the behavior of a CN eruption, and the improvements in computer power and codes, has enabled
an increase in sophistication in simulating a nova outburst. Prialnik & Kovetz (1995) presented an extended grid of multicycle nova evolution models that have been extensively used by researchers. Each observed nova characteristic (e.g. peak luminosity, recurrence time, duration of the high luminosity phase, outburst amplitude, mass of ejecta, average outflow velocity, etc.) can be reproduced by a particular combinations of values of M1, 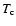 ,
and
,
and  .
Following this earlier study, Yaron et al. (2005) extended and refined the resolution in the grid of models, including a considerable number of new parameter combinations. The full grid covers the
entire range of observed characteristics, even those of peculiar objects.
.
Following this earlier study, Yaron et al. (2005) extended and refined the resolution in the grid of models, including a considerable number of new parameter combinations. The full grid covers the
entire range of observed characteristics, even those of peculiar objects.
By matching the observed characteristics of a particular nova with its theoretical counterpart, it is therefore possible to derive information about the mass and temperature of the white dwarf and its average accretion rate. Therefore, the grids in Tables 2 and 3 of Yaron et al.
(2005) can be used to determine a set of fundamental parameters that provides the
closest agreement with the observed data.
In the case of T Pyx, a comparison of the observed parameters for the eruption phase (the recurrence time 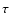 ,
the outburst amplitude A, the decay rate t3, the expansion velocity
,
the outburst amplitude A, the decay rate t3, the expansion velocity
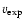 )
with the corresponding values in the grid clearly indicates that the closest agreement corresponds
to values that are intermediate in between 1.25 and 1.40 for M1, and -8.0 and -7.0 for log
)
with the corresponding values in the grid clearly indicates that the closest agreement corresponds
to values that are intermediate in between 1.25 and 1.40 for M1, and -8.0 and -7.0 for log  ;
at these high
;
at these high  values, the effects of the core temperature
values, the effects of the core temperature 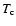 are minor. Since a denser grid is not available, we calculated intermediate values by graphical and non-linear interpolation in the published values. A satisfactory agreement with the observed data comes from a model (model A) with M1 = 1.36 and log
are minor. Since a denser grid is not available, we calculated intermediate values by graphical and non-linear interpolation in the published values. A satisfactory agreement with the observed data comes from a model (model A) with M1 = 1.36 and log  = 7.5 (
= 7.5 ( = 3.2
= 3.2  10-8), which provides:
10-8), which provides: 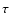
 20,
20,
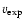
 -1200, A
-1200, A  7.6, t3
7.6, t3  13, and
13, and

 5.0
5.0  10-7. Following our interpolation of the data, Yaron (2007) kindly provided us with results obtained by execution of the code for other intermediate models, that is, WD masses between 1.30 and 1.33, log
10-7. Following our interpolation of the data, Yaron (2007) kindly provided us with results obtained by execution of the code for other intermediate models, that is, WD masses between 1.30 and 1.33, log  between -7
and -8, and different WD temperatures. The closest agreement with the observed values originates in a model with M1 = 1.33, T1 = 107, log
between -7
and -8, and different WD temperatures. The closest agreement with the observed values originates in a model with M1 = 1.33, T1 = 107, log  = -7.3 (model B), although the model with M1 = 1.30, T1 = 107, and log
= -7.3 (model B), although the model with M1 = 1.30, T1 = 107, and log  = -7.15 (model C) is also acceptable.
In Table 6, we also include, as an illustration, a model directly obtained from the published Tables 2 and 3, for M1 = 1.4
= -7.15 (model C) is also acceptable.
In Table 6, we also include, as an illustration, a model directly obtained from the published Tables 2 and 3, for M1 = 1.4  and
and  = 1.0
= 1.0  10-8 (model D).
10-8 (model D).
The value for
 (about 7
(about 7  10-7
10-7  )
that corresponds to the model of Yaron et al. (2005) with M1 = 1.33 and log
)
that corresponds to the model of Yaron et al. (2005) with M1 = 1.33 and log
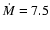 ,
is close to that (
,
is close to that ( 6.0
6.0  10
10
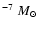 )
estimated by the observed average
)
estimated by the observed average
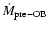 (about 3.0
(about 3.0  10
10
 yr-1) and the observed inter-outburst recurrence time of 22 yrs.
yr-1) and the observed inter-outburst recurrence time of 22 yrs.
Table 6:
A comparison between Yaron et al. (2005) grids and observations.
For T Pyx, the values of two of the independent, theoretical parameters (M1 and  )
have
been already constrained to within a limited range by theoretical considerations (M1) or inferred by direct observations (
)
have
been already constrained to within a limited range by theoretical considerations (M1) or inferred by direct observations ( ). Since the model grids require similar values for M1 and
). Since the model grids require similar values for M1 and  ,
the results appear to be consistent. An additional fine tuning of the model data could certainly improve the fit but the overall agreement between models and observations can be considered satisfactory: an important parameter such as the recurrence time is reproduced quite well and for the other basic quantities the discrepancy is not large.
,
the results appear to be consistent. An additional fine tuning of the model data could certainly improve the fit but the overall agreement between models and observations can be considered satisfactory: an important parameter such as the recurrence time is reproduced quite well and for the other basic quantities the discrepancy is not large.
A parameter that deserves special comment is t3. It is not explicitly listed in the theoretical grid but can be associated to
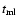 ,
and was included by Yaron (2007) in specific calculations. The observed t3 value is about three times longer than the expected value. Models with such long t3 would correspond to higher
,
and was included by Yaron (2007) in specific calculations. The observed t3 value is about three times longer than the expected value. Models with such long t3 would correspond to higher
 and therefore
to far more massive ejecta. Models with a longer t3 (i.e. Model-C in Table 6) would be of too low
and therefore
to far more massive ejecta. Models with a longer t3 (i.e. Model-C in Table 6) would be of too low
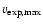 and too high
and too high
 .
.
In Sect. 10.2 we demonstrate that the spectroscopic observations acquired during the last outburst in 1966 indicate the ejection of a more massive shell than that expected from the simple estimate based on the quiescence
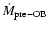 and a times interval
and a times interval 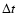 of 22 years.
of 22 years.
Contini & Prialnik (1997) presented evolutionary calculations of TNRs on the surface of an accreting WD that simulates the observed outburst characteristics of T Pyx and found that
the model that reproduces the observed characteristics of T Pyx most accurately is obtained for an
accretion rate of 10
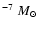 yr-1 onto a 1.25
yr-1 onto a 1.25  WD; the (theoretical)
mass ejected in a single outburst is expected to be close to 1.6
WD; the (theoretical)
mass ejected in a single outburst is expected to be close to 1.6  10
10
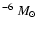 .
They also modeled the nebular spectrum and found that the theoretical fluxes agree with
those derived from observations (Williams 1982) if a distance of
.
They also modeled the nebular spectrum and found that the theoretical fluxes agree with
those derived from observations (Williams 1982) if a distance of  2 kpc is assumed. However, our detailed study of the T Pyx luminosity and mass accretion rate suggested an
2 kpc is assumed. However, our detailed study of the T Pyx luminosity and mass accretion rate suggested an
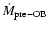 value close to 3.7
value close to 3.7  10
10
 yr-1, onto a 1.25
yr-1, onto a 1.25  WD for d
WD for d  3.5 kpc. If d
3.5 kpc. If d  2.0 kpc, this would imply that
2.0 kpc, this would imply that 
 1.2
1.2  10-8, a factor of 10 lower than assumed by Contini & Prialnik (1997). We note that a distance as large as about 7.0 kpc is required to derive a luminosity correspomding to
10-8, a factor of 10 lower than assumed by Contini & Prialnik (1997). We note that a distance as large as about 7.0 kpc is required to derive a luminosity correspomding to 
 10-7. See Sect. 11.1 for additional considerations of the distance.
10-7. See Sect. 11.1 for additional considerations of the distance.
The five recorded outbursts of T Pyx occurred in 1890, 1902, 1920, 1944, and 1966, with a mean recurrence time of 19  5.3 yrs (see WLTO, 1987). A common feature of these outbursts was the far longer optical decline time (t3 = 90
5.3 yrs (see WLTO, 1987). A common feature of these outbursts was the far longer optical decline time (t3 = 90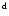 )
compared with that of other recurrent novae, which, with the exception of CI Aql (t3 = 33 d) and IM Nor (t3 = 50 d), are generally much faster, with t3 of the order of days.
)
compared with that of other recurrent novae, which, with the exception of CI Aql (t3 = 33 d) and IM Nor (t3 = 50 d), are generally much faster, with t3 of the order of days.
The well studied outburst of Dec. 1966 exhibited a sharp initial rise to a shoulder (pre-maximum halt on Dec. 10, 1966) in V of about 7.9, a near flat maximum close to V = 7.5 (which lasted about 30 days), a sharp peak at V=6.8 on Jan. 9, 1967, and a slow decline with t3  90
90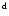 .
The first spectroscopic observations were obtained by Catchpole (1969), 12.6 days after the initial halt. The spectrum was characterized by sharp P Cyg features in the hydrogen lines and by other weak emission lines. The presence of the absorption features endured until March 5, 1967, and since then they became quite ``diffuse''. Catchpole (1969), apart from the value of 850 km s-1 at some epochs, reported outflow velocities of the order of -2000 km s-1 for both absorption and emission (permitted and forbidden) components.
.
The first spectroscopic observations were obtained by Catchpole (1969), 12.6 days after the initial halt. The spectrum was characterized by sharp P Cyg features in the hydrogen lines and by other weak emission lines. The presence of the absorption features endured until March 5, 1967, and since then they became quite ``diffuse''. Catchpole (1969), apart from the value of 850 km s-1 at some epochs, reported outflow velocities of the order of -2000 km s-1 for both absorption and emission (permitted and forbidden) components.
There is an observational gap of about 40 days in the spectra obtained by Catchpole, which was fortunately covered in part (from 09 Jan. 1967 to 16 Feb. 1967) by the spectroscopic data by Chincarini & Rosino (1969). They described the absorption system in the Balmer lines (up to H12) as being particularly sharp and strong and noted an increase in the expansion velocity
from -1535 km s-1 on Jan. 31, 1967, to -1760 km s-1 on Feb. 2, 1967 and -1820 km s-1 on Feb. 6, 1967. According to Chincarini & Rosino (1969), the mean radial velocity during the period Jan. 31-Feb. 6 determined from all measurable absorption lines was -1810  40 km s-1.
40 km s-1.
Outflow velocities of the order of 1500-2200 km s-1 were also observed in previous outbursts. Adams & Joy (1920) reported the presence of ``dark'' components of radial velocity up to -2100 km s-1 a few days after maximum. Joy (1945) observed expansion velocities of 1700 km s-1 in forbidden emission lines in spectra taken some
months after outburst. Similar values were also found by Herbig (1945) and
reported by Payne-Gaposchkin (1957).
The ``principal absorption system'' is generally associated with the bulk of the mass ejected
during outburst, and for most novae has a velocity close to that of the ``nebular system'' as determined from the width of the nebular emission lines (Payne-Gaposchkin 1957; Mc Laughlin 1956; Pottasch 1959). The
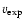 value reported by Joy (1945) referred to observations during the nebular phase, three-four months after outburst. That the emission lines in the nebular spectrum showed velocities of the same order as those deduced from the absorption lines of the principal spectrum is an indication of near constant expansion.
value reported by Joy (1945) referred to observations during the nebular phase, three-four months after outburst. That the emission lines in the nebular spectrum showed velocities of the same order as those deduced from the absorption lines of the principal spectrum is an indication of near constant expansion.
We note that in the literature on T Pyx little attention has been paid to the fact that for almost three months after the initial halt T Pyx showed a strong continuum with the presence of emission and absorption lines of similar strength. The persistence for almost three months (about t3) of displaced absorption components in the H (and FeII) lines, which are observable by
combining the spectroscopic observations of Catchpole (1969) and Chincarini & Rosino (1969) for the 1966 outburst, indicates an optically thick phase of similar duration.
In this respect, we recall that, before the outburst of 1966-1967, Mc Laughlin (1965) noted that T Pyx was exceptional among RNe since its photometric and spectroscopic behavior
closely resembled that of a typical nova both close to maximum (where it remained for several weeks to within about a magnitude) and in the nebular stage.
The similarity between the spectroscopic and photometric characteristics of the
outbursts of T Pyx and those of CNe, which allegedly eject about
10-4-10
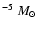 ,
suggests in itself that during outburst T Pyx expelled a shell of comparable mass.
,
suggests in itself that during outburst T Pyx expelled a shell of comparable mass.
Classical novae undergo an optically thick phase during which they resemble each other, a fact that can be explained by the same mechanism (i.e. flux redistribution) producing the spectrophotometric
light curve (Shore 1998, 2008). To achieve flux redistribution, the material must reach column densities of the order of 1023-1024 cm-2, which corresponds to masses of about 10-4-10
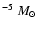 .
.
An optically thick stage also characterized the outbursts of T Pyx, as can be directly inferred from the lengthy period of time during which the optical magnitude was close to its maximum value, with t3  90
90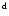 ,
and from the presence of absorption lines of HI and FeII, which lasted for at least 80 days.
,
and from the presence of absorption lines of HI and FeII, which lasted for at least 80 days.
From the duration of the optically thick phase (associated to t2) and the observed
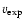 ,
using simple assumptions, we can estimate the mass of the shell ejected during outburst. The outer radius of the shell can be estimated from the observed expansion velocity (
,
using simple assumptions, we can estimate the mass of the shell ejected during outburst. The outer radius of the shell can be estimated from the observed expansion velocity (
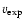
 1500 km s-1) and the time elapsed from outburst, assuming continuous ejection. This assumption is justified by the persistence of displaced absorption components with similar equivalent widths. The shell radius is:
1500 km s-1) and the time elapsed from outburst, assuming continuous ejection. This assumption is justified by the persistence of displaced absorption components with similar equivalent widths. The shell radius is:
The corresponding shell volume is V  1.84
1.84  1045 cm3. These values are
conservative because the terminal velocity was probably higher. To reproduce the optically thick stage recognized from the presence and persistence of the absorption lines, the
column density must be of the order of 1023 cm-2. Therefore, the average density in the shell must be close to 108-109 cm-3, (we note that the density should scale as R-3). This density value agrees with the spectroscopic behavior and the presence of permitted emission lines only. If we assume that the ejecta are homogeneous and consist of
ionized hydrogen, the mass might be estimated as
1045 cm3. These values are
conservative because the terminal velocity was probably higher. To reproduce the optically thick stage recognized from the presence and persistence of the absorption lines, the
column density must be of the order of 1023 cm-2. Therefore, the average density in the shell must be close to 108-109 cm-3, (we note that the density should scale as R-3). This density value agrees with the spectroscopic behavior and the presence of permitted emission lines only. If we assume that the ejecta are homogeneous and consist of
ionized hydrogen, the mass might be estimated as
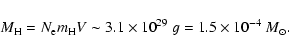 |
(19) |
This value is probably an upper limit because of the assumptions of continuous ejection and homogeneous shell.
In an alternative approach, following Williams (1994), one can estimate the hydrogen column density produced by an expanding shell of mass 1.0  10
10
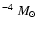 :
:
![\begin{displaymath}%
N_{\rm H}\cdot R = 3.0 \times 10^{52}\cdot R^{-2}\quad [{\rm cm}^{-2}].
\end{displaymath}](/articles/aa/full/2008/48/aa10678-08/img125.gif) |
(20) |
For T Pyx at day 60 (=t2), we find that R2 = 5.8  1029 [cm2], and
1029 [cm2], and 
 R
R  5.2
5.2  1022 [cm-2]. A mass of the ejecta higher than 10-4 is therefore required to produce an optically thick stage until day 60.
1022 [cm-2]. A mass of the ejecta higher than 10-4 is therefore required to produce an optically thick stage until day 60.
It is well established that in novae, the mass of the ejected envelope is directly correlated with the optical decay time t2 or t3 (Livio 1994). Therefore, an independent estimate of the ejected shell mass can be derived from the relation:
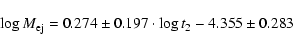 |
(21) |
(Della Valle et al. 2002). Even after considering the large uncertainties in this
relationship, a t2 = 62 implies a mass for the envelope
implies a mass for the envelope
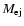
 10
10
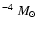 ,
which is similar to the mass ejected by classical novae.
,
which is similar to the mass ejected by classical novae.
The data leading to Eq. (21) suffer from a large scatter. We suspect that the ejecta expansion velocity plays also an important role and should be included in the relation.
Shore (2002, 2008) suggested an approximate scaling relation for the optically thick stage:
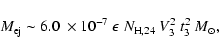 |
(22) |
where V3 is the outflow velocity in 103 km s-1, and 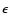 is the filling factor that, for this stage, can be assumed to be of the order of 0.1. For t3 = 90, f=0.1,
is the filling factor that, for this stage, can be assumed to be of the order of 0.1. For t3 = 90, f=0.1,
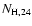 = 0.1-1.0, and V3 = 1.5, the derived values for
= 0.1-1.0, and V3 = 1.5, the derived values for
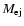 are in the range 1.5
are in the range 1.5  10-4-1.5
10-4-1.5  10
10
 .
.
Finally, the ejected mass can be estimated using the following scaling law from Cassatella et al. (2005), which depends on the approximate assumption that the filling factor in novae ejecta is the same as in V1668 Cyg:
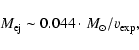 |
(23) |
where
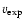 is in km s-1 and the constant is set to the values of
the ejected mass and the expansion velocity of V1668 Cyg (Stickland et al. 1981). Using
is in km s-1 and the constant is set to the values of
the ejected mass and the expansion velocity of V1668 Cyg (Stickland et al. 1981). Using
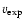 = 1500 km s-1, one finds that for T Pyx,
= 1500 km s-1, one finds that for T Pyx,
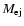
 2.93
2.93  10
10
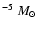 .
.
We recall that Kato & Hachisu (1991), from their models of steady-state winds for a nova with M1 = 1.33 X=0.5 and Z=0.02 and the observed t3, suggested the ejection of a massive
envelope with
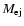 of about 10
of about 10
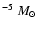 in a single outburst.
in a single outburst.
All the previous results agree with the considerations of Shore (1998), who
pointed out that, for a typical ejection velocity of about -2000 km s-1, a
nova with an optical decline time longer than a week must eject
a mass higher than 10
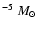 .
.
We also recall the fact that in classical novae close to maximum, the Balmer lines develop P-Cygni profiles, which is a clear indication that a significant amount of material was ejected during the outburst (Starrfield 1993).
Therefore, all quantitative methods and the qualitative consideration of the photometric and spectral behavior of T Pyx during the outbursts indicate the presence of a massive envelope with
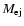
 10-4-10
10-4-10
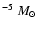 .
.
The ejection of a massive shell during the early (optically thick) outburst phase contrast significantly with the results of the UV + optical observations during quiescence and the theoretical requirements for
 ,
which imply a
,
which imply a
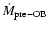
 2.2
2.2  10-8 and a total mass for the accreted shell
10-8 and a total mass for the accreted shell
 of about
of about  5.0
5.0  10
10
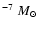 (see Sect. 8). It is also in contrast with the
conclusions of Sect. 9 that indicated that the closest agreement between the grid models and the observed properties of the system during outburst and Q corresponds to a model with
(see Sect. 8). It is also in contrast with the
conclusions of Sect. 9 that indicated that the closest agreement between the grid models and the observed properties of the system during outburst and Q corresponds to a model with 
 3.0
3.0  10
10
 yr-1 and
yr-1 and

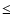 1.3
1.3  10
10
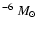 (Table 6). During outburst, T Pyx has apparently ejected far more material than it has
accreted.
(Table 6). During outburst, T Pyx has apparently ejected far more material than it has
accreted.
Studies of classical novae containing a massive WD indicated that these objects eject apparently more material than theoretically predicted (Starrfield et al. 1998a,b; Vanlandingham et al. 1996; Shore 1998). These authors emphasized the significant discrepancy between
the observed mass of the ejecta and the predicted critical mass of accreted nova envelopes for massive WDs (
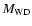
 1.25
1.25  ), the mass of the observed shell being one order of magnitude (or more) higher than that predicted by the models.
), the mass of the observed shell being one order of magnitude (or more) higher than that predicted by the models.
For these CNe one could attribute the discrepancy to some inadequacy in the TNR models or in the methods to determine the nebular mass. In the case of T Pyx, the situation, however, differs because there is a serious mismatch between the shell mass indicated by the optical
observations during outburst (
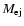
 10-4-10-5
10-4-10-5  )
and that determined by the UV and optical observations during quiescence (which give
)
and that determined by the UV and optical observations during quiescence (which give
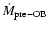
 2.2
2.2  10
10
 yr-1 and therefore
yr-1 and therefore


 = 5.0
= 5.0  10
10
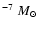 ). Therefore, the mass ejected during outburst is about a factor of 100 higher than both the theoretical ignition mass
). Therefore, the mass ejected during outburst is about a factor of 100 higher than both the theoretical ignition mass
 and the total mass accreted before outburst,
and the total mass accreted before outburst,
 .
.
We note that using the post 1966 value of  instead of that inferred for the pre-outburst interval would produce an even larger discrepancy.
instead of that inferred for the pre-outburst interval would produce an even larger discrepancy.
Although
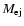 does not depend on distance,
does not depend on distance,
 does (due to its dependence on both
does (due to its dependence on both
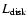 and
and
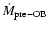 ), and therefore the mismatch between
), and therefore the mismatch between
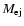 and
and
 depends crucially on the assumed distance. The uncertainty in the
adopted distance was found in Sect. 2 to be of the order of 10 percent. However, we note, that even the adoption of an unlikely distance of, say, 10 000 pc (at about 20
depends crucially on the assumed distance. The uncertainty in the
adopted distance was found in Sect. 2 to be of the order of 10 percent. However, we note, that even the adoption of an unlikely distance of, say, 10 000 pc (at about 20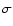 from the estimated
value) would only partially alleviate this inconsistency, and at the expense of an uncomfortably high mass accretion rate, well within the range for the onset of steady burning. This would imply
characteristic temperatures and luminosities that are not observed (see also Sect. 14 for a further
discussion). A larger distance would also necessarily imply that T Pyx was super-Eddington at maximum, a circumstance that appears unlikely due to its slow photometric and
spectroscopic developments during outburst.
from the estimated
value) would only partially alleviate this inconsistency, and at the expense of an uncomfortably high mass accretion rate, well within the range for the onset of steady burning. This would imply
characteristic temperatures and luminosities that are not observed (see also Sect. 14 for a further
discussion). A larger distance would also necessarily imply that T Pyx was super-Eddington at maximum, a circumstance that appears unlikely due to its slow photometric and
spectroscopic developments during outburst.
A lower distance would correspond to a lower values of
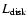 ,
and hence
,
and hence
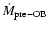 and
and
 ,
to values that are theoretically incompatible with the
occurrence of outbursts with an average interval of 22 years. It would also exacerbate
the discrepancy between the low value of
,
to values that are theoretically incompatible with the
occurrence of outbursts with an average interval of 22 years. It would also exacerbate
the discrepancy between the low value of
 obtained from
the UV observations (and the models) and the apparently high mass of the ejecta, as inferred from the behavior during outburst. Therefore, there is not much leeway to invoke a
different distance to explain the discordance.
obtained from
the UV observations (and the models) and the apparently high mass of the ejecta, as inferred from the behavior during outburst. Therefore, there is not much leeway to invoke a
different distance to explain the discordance.
The nebula surrounding T Pyx has been the target of several spectroscopic and imaging observations. Duerbeck & Seitter (1979) first reported the presence of a strong nebulosity
around T Pyx, with radius r  5'', whose origin was tentatively attributed to the 1966 outburst and whose strength was described as unusual. By the assumption of an outburst expansion velocity of -900 km s-1, a low distance (
5'', whose origin was tentatively attributed to the 1966 outburst and whose strength was described as unusual. By the assumption of an outburst expansion velocity of -900 km s-1, a low distance ( 600 pcs) was derived.
600 pcs) was derived.
Williams (1982) obtained spectral scans of the northern portion of the nebula of T Pyx. The spectrum was similar to that of as a typical PN, probably photoionized by radiation from the hot remnant, and lacked the strong CNO enhancements characteristic of the ejecta of classical
novae.
Comparing images acquired in 1979.0 and 1982.9, Seitter (1987) found that the
nebula did not increase in size during that time interval.
Shara et al. (1989) from deep narrowband CCD images confirmed the faint, extended
H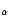 + NII halo (twice as large as the inner nebula), first reported by Duerbeck (1987,b). A smooth, small [OIII] nebula with r
+ NII halo (twice as large as the inner nebula), first reported by Duerbeck (1987,b). A smooth, small [OIII] nebula with r  2'' was also found. Shara et al. (1989) also compared the relative sizes of the main nebula with r
2'' was also found. Shara et al. (1989) also compared the relative sizes of the main nebula with r  5'' in 1985 and in 1979 but failed as well to find any detectable expansion during the 6 year interval, confirming the finding of
Seitter (1987). High resolution imagery data from HST was obtained by Shara et al. (1997). The nebula was resolved into more than two thousand individual knots, and a comparison between
images taken at four epochs indicated that these individual knots retained a
similar pattern, without any evidence of expansion. These data confirm the apparent stationarity in the 10'' diameter nebula suggested by previous observations. Shara et al. (1997) found an upper limit of 40
5'' in 1985 and in 1979 but failed as well to find any detectable expansion during the 6 year interval, confirming the finding of
Seitter (1987). High resolution imagery data from HST was obtained by Shara et al. (1997). The nebula was resolved into more than two thousand individual knots, and a comparison between
images taken at four epochs indicated that these individual knots retained a
similar pattern, without any evidence of expansion. These data confirm the apparent stationarity in the 10'' diameter nebula suggested by previous observations. Shara et al. (1997) found an upper limit of 40 (1500/d) (km s-1) for the expansion velocity of the knots. They also detected nine distinct peaks in the brightness distribution, an indication that a
multiple nebula model was required.
(1500/d) (km s-1) for the expansion velocity of the knots. They also detected nine distinct peaks in the brightness distribution, an indication that a
multiple nebula model was required.
Many studies, disappointingly inconclusive, addressed the problem of the mass of
the nebula. In this respect, it should be noted that large uncertainties are generally associated with estimates of the mass of novae ejecta, since the mass estimate depends critically on
quantities that are not reliably measured, e.g.: distance, electron density, ionization structure in the nebula, geometry, and filling factor. Therefore, it is unsurprising that a range of masses
for the nebula of T Pyx has been proposed in the literature.
From the nebular H intensity measured by Williams (1982), WLTO (1987)
obtained a lower limit to
intensity measured by Williams (1982), WLTO (1987)
obtained a lower limit to
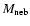 of 10
of 10
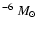 ,
while Shara (1989),
using the H
,
while Shara (1989),
using the H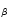 intensity with the requirement
intensity with the requirement 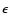
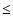 1 for the filling
factor derived an upper limit of 1.0
1 for the filling
factor derived an upper limit of 1.0  10
10
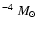 .
From the intensity of the H
.
From the intensity of the H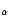 and [NII] lines, Seitter (1987) found a mass close to 8.0
and [NII] lines, Seitter (1987) found a mass close to 8.0  10
10
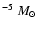 .
From the H
.
From the H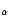 flux and considerations based on HST imagery, Shara et al. (1997) obtained 1.3
flux and considerations based on HST imagery, Shara et al. (1997) obtained 1.3  10
10
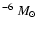 to be the most reliable estimate for the nebula mass (with an
assumed distance of 1500 pc), the electron density being, allegedly, the main uncertainty factor.
to be the most reliable estimate for the nebula mass (with an
assumed distance of 1500 pc), the electron density being, allegedly, the main uncertainty factor.
We add one more estimate for the mass of the nebula, based on the H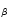 flux obtained by Williams (1982) scaled to the entire nebula, after correction for the new reddening and distance. We obtain:
flux obtained by Williams (1982) scaled to the entire nebula, after correction for the new reddening and distance. We obtain:
with a relative error of about 25 percent, arising from the uncertainties in the distance and the flux. By combining the two common relations:
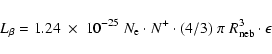 |
(24) |
and
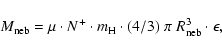 |
(25) |
(where 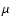 = 1.4 is the mean atomic weight and
= 1.4 is the mean atomic weight and 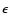 is the filling factor), one finds that the mass of the nebula (independent of
is the filling factor), one finds that the mass of the nebula (independent of  and
and
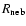 ) is
) is
 |
(26) |
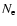 is inaccurately determined because, as noted by Williams (1982),
the spectrum is too poor in number of lines to constrain the physical parameters of the nebula accurately. However, from the presence of a quite strong emission feature near 3722 Å, attributable to [OII] 3726.1 and 3728.8 one can estimate that the nebula density is less
than 3.0
is inaccurately determined because, as noted by Williams (1982),
the spectrum is too poor in number of lines to constrain the physical parameters of the nebula accurately. However, from the presence of a quite strong emission feature near 3722 Å, attributable to [OII] 3726.1 and 3728.8 one can estimate that the nebula density is less
than 3.0  103 cm-3, since these two forbidden lines have critical density log
103 cm-3, since these two forbidden lines have critical density log
 = 3.5 and 2.8, respectively. If we assume that
= 3.5 and 2.8, respectively. If we assume that 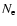
 103 cm-3, a value also adopted by Shara et al. (1997) from other considerations, we find that
103 cm-3, a value also adopted by Shara et al. (1997) from other considerations, we find that
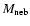
 5.84
5.84  10
10
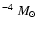 .
.
A value of this order for the total mass of the nebula, which has apparently increased from the contribution of several successive outbursts, agrees with the ejection during
outburst of a massive shell ( 10
10
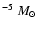 )
as suggested in Sect. 10.2.
)
as suggested in Sect. 10.2.
The fact that the nebula of T Pyx is still clearly observed despite its large distance seems hardly compatible with a mass of 10
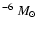 derived in previous studies. In the most well
studied CNe, which on average are closer in distance than T Pyx, the ejected nebula has, at best, a similar strength and/or is barely evident a few years after outburst. We think that the peculiar strength of the nebula of T Pyx may be explained by the fact that most of the gas ejected in
successive outbursts has accumulated into a nearly stationary envelope that is strongly
irradiated by a more than average luminous UV central source.
derived in previous studies. In the most well
studied CNe, which on average are closer in distance than T Pyx, the ejected nebula has, at best, a similar strength and/or is barely evident a few years after outburst. We think that the peculiar strength of the nebula of T Pyx may be explained by the fact that most of the gas ejected in
successive outbursts has accumulated into a nearly stationary envelope that is strongly
irradiated by a more than average luminous UV central source.
Alternatively, one can guess that the observed nebula of T Pyx was produced in a peculiar event and is not associated with the recorded and/or previous outbursts. Its apparent stationarity and the lack of changes over a timescale of about fifteen years (Shara et al. 1997) supports this
interpretation. Williams (1982) noted that the spectrum of the nebula around T Pyx is almost similar to typical planetary nebula, of approximately solar composition.
We emphasize that the optically thick shell discussed in Sects. 10.1 and 10.2 was observed only
spectroscopically during the outburst phases, and that there is no definite, direct link with the extended nebula. Simple calculations indicate that, if d=3500 pc, the angular radius
of the shell, after ten years of constant expansion at 1500 km s-1, would be less than 1''.
If the radius of the nebula
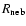 is known, from the observed angular radius r (
is known, from the observed angular radius r ( 10'') and the distance, one can obtain the filling factor
10'') and the distance, one can obtain the filling factor  with the help of Eq. (24). After insertion of the values for
with the help of Eq. (24). After insertion of the values for  = 6.22
= 6.22  1031 erg s-1,
1031 erg s-1,
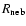
 5.2
5.2  1017 cm, and
1017 cm, and 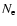
 1.1 N+, one obtains that
1.1 N+, one obtains that
Therefore, for 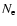
 103 cm-3,
103 cm-3, 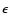 is close to 10-3. A filling factor of
is close to 10-3. A filling factor of  10-3 can be obtained independently from the relation of Harrison &
Stringfellow (1994):
10-3 can be obtained independently from the relation of Harrison &
Stringfellow (1994):
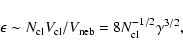 |
(27) |
where  is the fraction of the spherical nebula intercepted by the clumps. From the figures of Shara et al. (1997), we estimate that
is the fraction of the spherical nebula intercepted by the clumps. From the figures of Shara et al. (1997), we estimate that 
 0.05 and, if the number of clumps
0.05 and, if the number of clumps
 is
is  2000 (Shara et al. 1997), we find that
2000 (Shara et al. 1997), we find that 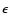
 2
2  10-3. We note that the filling factors estimated for the ejecta of other novae have a wide range of values, from 4
10-3. We note that the filling factors estimated for the ejecta of other novae have a wide range of values, from 4  10-1 (Vanlandingham et al. 1999, for nova LMC 1990 No. 1), to
10-6 Saizar & Ferland (1994) for nova QU Vul. Williams et al. (1981) found an intermediate value,
10-1 (Vanlandingham et al. 1999, for nova LMC 1990 No. 1), to
10-6 Saizar & Ferland (1994) for nova QU Vul. Williams et al. (1981) found an intermediate value, 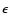
 2
2  10-3 for the recurrent nova U Sco. Mason et al. (2005) found
10-3 for the recurrent nova U Sco. Mason et al. (2005) found 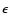
 10-4-10-1 for nova SMC 2001 and nova LMC 2002, and Balman & Oegelman (1999) estimated
10-4-10-1 for nova SMC 2001 and nova LMC 2002, and Balman & Oegelman (1999) estimated 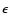
 5
5  10-3-3
10-3-3  10-1 for the shell of GK Per. Mason et al. (2005) have suggested
10-1 for the shell of GK Per. Mason et al. (2005) have suggested 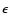
 10-5-10-2 for T Pyx.
10-5-10-2 for T Pyx.
It is accepted that type Ia supernovae represent the complete thermonuclear disruption of mass-accreting white dwarfs that reach the Chandrasekhar limit by accretion (Nomoto et al. 1984; Woosley & Weaver 1986). Within this general framework, there exist single degenerate models (Whelan & Iben 1973) in which a WD accretes from a non-degenerate companion, and double degenerate models (e.g. Iben & Tutukov 1984) that involve the merger between two WDs. Hachisu (2002, 2003) and Hachisu & Kato (2001, 2002) proposed a unified picture of binary evolution to SNe Ia in which recurrent novae could be understood to be part of the
evolutionary stages of supersoft X-ray sources and symbiotic channels to SNe Ia.
The mass M1 must be close to the Chandrasekhar limit before a recurrent nova can become a SN Ia, and the WD must also increase in the long term, after many cycles of accretion and ejection
(Starrfield et al. 1985). However, in the case of T Pyx, even if M1 were close to the
limit, which is not clearly established since M1 appears to be close to 1.37  ,
the
results of the previous sections indicate that the mass balance situation is unclear:
,
the
results of the previous sections indicate that the mass balance situation is unclear:
On the one hand, the photometric and spectroscopic behavior close to outburst, as mentioned in Sect. 10.2, appear to be consistent with the ejection of a rather massive shell, while the UV data and theoretical models (at the specific M1 and  values) indicate that the ignition mass is low (
values) indicate that the ignition mass is low ( 5.0
5.0  10
10
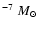 ). This indicates that during outburst the WD ejects more material than it accumulates and that a secular decrease in the mass of the white dwarf is expected. Therefore, evolution to become a SNIa appears to be excluded.
). This indicates that during outburst the WD ejects more material than it accumulates and that a secular decrease in the mass of the white dwarf is expected. Therefore, evolution to become a SNIa appears to be excluded.
On the other hand, the ejection of a more-massive-than-accreted shell is apparently in contrast with the observational evidence that the chemical composition of the T Pyx nebula is close to solar (Williams 1982). This appears to exclude any erosion of the white dwarf and implies that the white dwarf does not lose mass after cycles of accretion and ejection. However, this presupposes that the chemical composition of the observed nebula is representative of that of a single shell ejected during outburst.
It is unclear whether these substantial discrepancies originates in flaws in the theoretical assumptions or the interpretation of the observations. They certainly highlight the need
for accurate values of the most critical parameters of this recurrent nova, i.e. the mass
and chemical composition of the shell ejected during outburst.
In any case, the behavior of T Pyx raises several doubts about the common assumption that in recurrent novae far less material is ejected during the outburst than is accreted by the white dwarf, and therefore that its mass increases toward the Chandrasekhar limit (Starrfield 2002). In assessing whether recurrent novae could be progenitors of type Ia supernovae, we note that Hachisu & Kato (2001), discovered that, among six recurrent novae, only T Pyx is offset significantly from the region occupied in an a orbital period - donor mass plane (their Fig. 3) by the progenitors of SNe Ia.
To explain the alleged extremely blue color of T Pyx in quiescence, WLTO (1987) proposed that nuclear burning continues even during its Q state, consistent with the slow outburst development,
which suggests that the accreted envelope was only weakly degenerate at the onset of TNR.
Patterson et al. (1998) attributed the luminosity of T Pyx (and V Sagittae) to quasi-steady thermonuclear burning and suggested the object to be included in the class of the supersoft X-ray sources.
However, the color of T Pyx
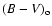 = -0.26 used in these studies is based on a significant overcorrection for the reddening, assumed to be EB-V = 0.36, instead of the correct
value EB-V = 0.25 (see Paper I and earlier communications, e.g. Gilmozzi et al. 1998). It is unfortunate that both the value
= -0.26 used in these studies is based on a significant overcorrection for the reddening, assumed to be EB-V = 0.36, instead of the correct
value EB-V = 0.25 (see Paper I and earlier communications, e.g. Gilmozzi et al. 1998). It is unfortunate that both the value
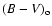 = -0.26 of Patterson et al. (1998) and the statement about the ``extremely blue color'' of T Pyx was adopted widely in the
literature (see for example Anupama 2002; Parthasaraty et al. 2007). We note, incidentally, that in the same paper Patterson et al. (1998) assumed too high a reddening correction (EB-V = 0.33) for V Sge; the IUE data suggest, instead a value close to 0.23. We recall that for T Pyx the observed (B-V) is about 0.14
= -0.26 of Patterson et al. (1998) and the statement about the ``extremely blue color'' of T Pyx was adopted widely in the
literature (see for example Anupama 2002; Parthasaraty et al. 2007). We note, incidentally, that in the same paper Patterson et al. (1998) assumed too high a reddening correction (EB-V = 0.33) for V Sge; the IUE data suggest, instead a value close to 0.23. We recall that for T Pyx the observed (B-V) is about 0.14  0.04 (WLTO 1987; Bruch & Engel 1994; Downes et al. 1997; Schaefer 2005; see also Table 7). This would imply that
0.04 (WLTO 1987; Bruch & Engel 1994; Downes et al. 1997; Schaefer 2005; see also Table 7). This would imply that
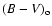
 -0.11, close to the value
-0.11, close to the value
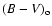 = -0.06 given by Szkody (1994).
= -0.06 given by Szkody (1994).
Patterson et al. (1998) assumed that Mv = 1.3 and after a significant bolometric correction (based on the assumption of an extremely hot source being present, a consequence of the overestimate of the reddening), derived a quiescent bolometric luminosity higher than 1036 erg s-1, which considered to be a true lower limit. This encouraged them to invoke nuclear burning on the surface of the WD as the main power source, considering the disturbingly
high  (
( 10
10
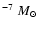 yr-1) required in the case of pure accretion power.
yr-1) required in the case of pure accretion power.
However, the IUE and the optical data do not appear to be reproduced by the model depicted by Patterson et al. (1998), since the following observational evidence contradicts with their conclusions:
- 1.
- One of the main results of Paper I was that the de-reddened UVOIR continuum of T Pyx is reproduced well by a single power-law
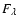
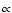
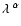 with
a slope
with
a slope
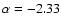 ,
representative of a steady accretion disk. Alternatively, as shown in Paper 1, the UV continuum can be well fitted by a blackbody of temperature 34 000 K. There is no way to reconcile these firm observational results with the presence of a supersoft source of
typical T
,
representative of a steady accretion disk. Alternatively, as shown in Paper 1, the UV continuum can be well fitted by a blackbody of temperature 34 000 K. There is no way to reconcile these firm observational results with the presence of a supersoft source of
typical T  3.0
3.0  105 K, since its expected slope in the UV region (
105 K, since its expected slope in the UV region (
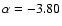 )
would be inconsistent with the UV observations.
)
would be inconsistent with the UV observations.
- 2.
- As shown in Sect. 5, the IUE observations in 1980-1996 and the optical and IR photometric data indicate that
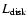 = 2.7
= 2.7  1035 erg s-1, which corresponds to emission mainly in the directly observed UV range. Therefore, in the absence of any direct or indirect evidence of a hot source, it is unlikely that
1035 erg s-1, which corresponds to emission mainly in the directly observed UV range. Therefore, in the absence of any direct or indirect evidence of a hot source, it is unlikely that
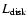 is higher than 1036 erg s-1.
is higher than 1036 erg s-1.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{0678fig3}
\end{figure}](/articles/aa/full/2008/48/aa10678-08/Timg150.gif) |
Figure 3:
Comparison between the reddening-corrected SWP spectra of the supersoft source V Sge (continuous line) and of T Pyx (dashed line). The continuum of T Pyx has been scaled to that of V Sge (multiplied by a factor 40). Note the prominence of the high ionization lines of NV 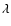 1240, CIV 1240, CIV 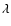 1550, HeII 1550, HeII 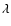 1640, and NIV 1640, and NIV 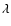 1719 in V Sge, in contrast with their moderate intensity or absence in T Pyx. 1719 in V Sge, in contrast with their moderate intensity or absence in T Pyx. |
| Open with DEXTER |
- 3.
- Under steady-state hydrogen-burning conditions, the accretion rate

 can be estimated to be:
can be estimated to be:
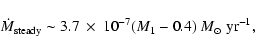 |
(28) |
(Hachisu & Kato (2001), which is valid for hydrogen content X=0.7. In the case of T Pyx, one calculates 

 3.2
3.2  10
10
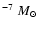 yr-1. This
value is almost a factor of 30 higher than the value of
yr-1. This
value is almost a factor of 30 higher than the value of 
 1.1
1.1  10
10
 yr-1 obtained from the IUE data for the post outburst phase.
yr-1 obtained from the IUE data for the post outburst phase.
- 4.
- After correction for inclination, the apparent absolute magnitude of Mv = 1.79 corresponds to a 4-
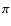 averaged absolute magnitude of
averaged absolute magnitude of
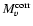 = 2.53, to be compared with the average value
= 2.53, to be compared with the average value
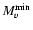
 4.0 for ex-novae (Warner 1995). This implies that T Pyx is more luminous than other ex-novae, as mentioned in Sect. 4, but is not ``extremely bright''. We can explain why T Pyx is brighter than other novae in terms of repeated nova eruptions and heating of the primary, which triggers irradiation of the secondary and produces a
higher than average
4.0 for ex-novae (Warner 1995). This implies that T Pyx is more luminous than other ex-novae, as mentioned in Sect. 4, but is not ``extremely bright''. We can explain why T Pyx is brighter than other novae in terms of repeated nova eruptions and heating of the primary, which triggers irradiation of the secondary and produces a
higher than average  .
.
- 5.
- The emission line spectrum of T Pyx is not that of an high excitation object: NV
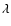 1240 is nearly absent, HeII
1240 is nearly absent, HeII 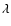 1640 is weaker than CIV
1640 is weaker than CIV 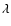 1550 and barely present in several spectra, the OIV lines close to
1550 and barely present in several spectra, the OIV lines close to 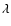 1405 are absent. A comparison
between the IUE spectra of T Pyx and V Sge (Fig. 3) clearly shows remarkable differences and a much lower excitation character in T Pyx. From an inspection of IUE spectra of several CVs, we also found that the spectrum of T Pyx is similar to that of the old novae V533 Her and V603 Aql
and to some spectra of the intermediate polar TV Col. The old nova RR Pic definitely
shows higher excitation than T Pyx, with far stronger NV and HeII emissions.
1405 are absent. A comparison
between the IUE spectra of T Pyx and V Sge (Fig. 3) clearly shows remarkable differences and a much lower excitation character in T Pyx. From an inspection of IUE spectra of several CVs, we also found that the spectrum of T Pyx is similar to that of the old novae V533 Her and V603 Aql
and to some spectra of the intermediate polar TV Col. The old nova RR Pic definitely
shows higher excitation than T Pyx, with far stronger NV and HeII emissions.
Other findings considerations also exclude the H-burning-bloated-WD hypothesis:
- 1.
- The complexity of the optical photometric behavior in T Pyx (Shaefer et al. 1992; Patterson et al. 1998) is difficult to explain if the bulk of the luminosity originates in a spherically symmetric radiation source associated with H-burning on top of a bloated white dwarf.
- 2.
- If the majority of the gas undergoes steady burning, it would be difficult to understand how the remainder that accumulates in the degenerate envelope could burn explosively every 20 years.
- 3.
- The outburst amplitude of T Pyx,
 8.0 mag, is close to that found for classical
novae of similar t3 and similar system inclination (Warner 1995, 2008). If, as assumed by Patterson et al. (1998), the luminosity during quiescence is greater than 1036 erg s-1 then, with an outburst amplitude of about 8 magnitudes, the luminosity would reach 1040 erg s-1, implying that T Pyx is an object intermediate between a nova and a SN Ia.
8.0 mag, is close to that found for classical
novae of similar t3 and similar system inclination (Warner 1995, 2008). If, as assumed by Patterson et al. (1998), the luminosity during quiescence is greater than 1036 erg s-1 then, with an outburst amplitude of about 8 magnitudes, the luminosity would reach 1040 erg s-1, implying that T Pyx is an object intermediate between a nova and a SN Ia.
To support the hypothesis of steady nuclear burning Patterson et al. (1998) considered all CVs of comparable
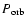 and deduced that the
and deduced that the  in T Pyx was a factor of 5000 higher than in other CVs of similar
in T Pyx was a factor of 5000 higher than in other CVs of similar
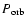 .
One should compare T Pyx with objects that are similar, that is, with recent novae. After outburst, the nova system remains in an excited state and
.
One should compare T Pyx with objects that are similar, that is, with recent novae. After outburst, the nova system remains in an excited state and  increases due to the irradiation of the secondary. Patterson et al. (1998) correctly excluded from their Fig. 14 all old novae within 30 yr of the outburst because of
their systematically too high luminosity levels. Adopting the same line of reasoning, T Pyx should also have been excluded. In this respect, we note that the
increases due to the irradiation of the secondary. Patterson et al. (1998) correctly excluded from their Fig. 14 all old novae within 30 yr of the outburst because of
their systematically too high luminosity levels. Adopting the same line of reasoning, T Pyx should also have been excluded. In this respect, we note that the  of T Pyx is only slightly higher than that observed in recent ex-novae (e.g. RR Pic, V841Oph, HR Del, etc.) (Selvelli 2004).
of T Pyx is only slightly higher than that observed in recent ex-novae (e.g. RR Pic, V841Oph, HR Del, etc.) (Selvelli 2004).
Table 7:
XMM observations compared with IUE fluxes and ground based photometry.
Based on the conclusions of Patterson et al. (1998) of an the extremely high luminosity (
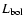 far higher than 1036 erg s-1), Knigge et al. (2000) investigated in detail the evolution of the T Pyx system and proposed that the system is a wind-driven supersoft X-ray source. In this scenario, a strong, radiation-induced wind is excited from the secondary star, and
increases the rate of binary evolution, causing the system to destroy itself either by evaporation of the secondary star or in a type Ia SN if the WD reaches the Chandrasekhar limit. Knigge et al. (2000) therefore proposed that either the primary, the secondary, or both stars may be committing assisted stellar suicide
far higher than 1036 erg s-1), Knigge et al. (2000) investigated in detail the evolution of the T Pyx system and proposed that the system is a wind-driven supersoft X-ray source. In this scenario, a strong, radiation-induced wind is excited from the secondary star, and
increases the rate of binary evolution, causing the system to destroy itself either by evaporation of the secondary star or in a type Ia SN if the WD reaches the Chandrasekhar limit. Knigge et al. (2000) therefore proposed that either the primary, the secondary, or both stars may be committing assisted stellar suicide
This scenario is, admittedly, highly speculative, and depends crucially on the unsubstantiated assumption that both the temperature and luminosity of T Pyx are extremely high. The IUE and optical data are instead consistent with a more conventional scenario of accretion power, as in other CVs, and we confidently predict that, fortunately, any form of suicide in the near future is extremely unlikely.
Finally, we note that Greiner et al. (2003) did not find T Pyx to be a supersoft X-ray source, and that T Pyx does not appear in NASA's HEASARC tool (a master compilation of EUV and X-ray databases).
While this work was close to completion, the data for X-ray observations of T Pyx by XMM became publicly available. This prompted us to perform a preliminary analysis of the data to verify
the presence or absence of a supersoft source.
T Pyx was observed by XMM-Newton on November 10, 2006. All the three EPIC cameras were operated in Full Frame mode with the Medium filter. The total useful exposure time after filtering for high
radiation periods was 22.1 ks. Optical Monitor data were taken simultaneously with the X-ray
observations. The values (see Table 7) are consistent with the values given in Paper I (IUE and optical observations) and confirm the stability of the SED with time. The reduction of the XMM EPIC data was carried out with SAS version 7.1, using standard methods. T Pyx was detected as a faint source that had an observed EPIC-pn count-rate of 8.5  10-3 cts s-1 and
emission over the complete range 0.2-8 keV.
10-3 cts s-1 and
emission over the complete range 0.2-8 keV.
Figure 4 shows the XMM-Newton EPIC-pn spectrum of T Pyx compared to a blackbody of 2.4  105 K and a luminosity of 1.0
105 K and a luminosity of 1.0  1037 erg s-1. The blackbody spectrum was simulated assuming an exposure time of 20 ks, similar to that of the data, with two assumptions: a distance of 3500 pc and a reddening EB-V = 0.25 (as in this paper), and a distance of 3000 pc and a reddening of 0.4 (as assumed by Knigge et al. 2000). The presence of a supersoft component with a temperature of 2.4
1037 erg s-1. The blackbody spectrum was simulated assuming an exposure time of 20 ks, similar to that of the data, with two assumptions: a distance of 3500 pc and a reddening EB-V = 0.25 (as in this paper), and a distance of 3000 pc and a reddening of 0.4 (as assumed by Knigge et al. 2000). The presence of a supersoft component with a temperature of 2.4  105 K and a luminosity of 1.0
105 K and a luminosity of 1.0  1037 erg s-1, whose existence was postulated by both Patterson et al. (1998) and Knigge et al. (2000), can be definitely excluded. Such a bright component would be easily visible at soft energies (i.e. below 0.5 keV), and this is not the case. Any supersoft emission, if present, would be several
orders of magnitude fainter than expected.
1037 erg s-1, whose existence was postulated by both Patterson et al. (1998) and Knigge et al. (2000), can be definitely excluded. Such a bright component would be easily visible at soft energies (i.e. below 0.5 keV), and this is not the case. Any supersoft emission, if present, would be several
orders of magnitude fainter than expected.
The data are compatible with the presence of a relatively hard source of low luminosity, but their low statistical quality (227 counts in the range 0.2-8. keV) does not allows us to perform a reliable fit. We also note that extrapolation of the observed IUE spectrum (power-law) into the X-ray range would result in an unrealistically high flux, several orders of magnitude higher than observed. The existence of such a high flux was already excluded in Paper I on the basis of the intensity of the HeII 1640 Å line.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{0678fig4}
\end{figure}](/articles/aa/full/2008/48/aa10678-08/Timg155.gif) |
Figure 4:
The XMM-Newton EPIC-pn spectrum of T Pyx ( bottom) compared with the
simulations of a 20 ks exposure of a blackbody of 2.4  105 K and a luminosity of 1
105 K and a luminosity of 1  1037 erg s-1 computed with two assumptions: a distance of 3500 pc and a reddening EB-V = 0.25 (values assumed in this paper, dots), and a distance of 3000 pc and
a reddening of 0.4 (values assumed by Knigge et al. 2000, continuous line). The three spectra shown here have been re-binned to 20 counts per bin.
1037 erg s-1 computed with two assumptions: a distance of 3500 pc and a reddening EB-V = 0.25 (values assumed in this paper, dots), and a distance of 3000 pc and
a reddening of 0.4 (values assumed by Knigge et al. 2000, continuous line). The three spectra shown here have been re-binned to 20 counts per bin. |
| Open with DEXTER |
We therefore ask from which process or in which source the observed X-ray emission originates?
In a CV (nova or quiescent nova) X-rays may be produced by at least three different mechanisms or regions (see Kuulkers et al. 2006; Krautter 2008):
- 1.
- Thermal emission from the hot white dwarf nova remnant in the late outburst phases. The nova becomes a strong X-ray emitter with a soft SED.
- 2.
- Emission from the inner accretion disk (BL) or the accretion columns (in magnetic CVs). One expects to observe a typical X-ray emission of CVs in quiescence, with a thermal bremsstrahlung spectrum.
- 3.
- Shocks in the circumstellar medium surrounding the nova system where the expanding nova shell and/or a nova wind interact with each other or with pre-existing CS material. The expected hard X-ray spectrum originates from thermal bremsstrahlung with
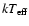 temperatures 0.2-15 keV, and with
temperatures 0.2-15 keV, and with 
 1033-1034 erg s-1 (O'Brien et al. 1994).
1033-1034 erg s-1 (O'Brien et al. 1994).
- 4.
- The corona of an active dwarf M star companion.
In T Pyx, as already mentioned, the XMM data would exclude case 1. corresponding to a strong
SSS source. Case 2 can also be ruled out because, for a CV accreting at the quite high rates of T Pyx, the BL is optically thick and one would expect to observe (see Patterson &
Raymond 1985) only soft X-ray emission with luminosity comparable to the disk luminosity,
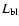

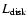
 2.7
2.7  1035 erg s-1. For case 4, we note that a high level of coronal heating at values of
1035 erg s-1. For case 4, we note that a high level of coronal heating at values of  /
/
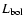
 10-3 persists for the active dMe stars, and the emission was detected in surveys of nearby stars (see Giampapa & Fleming 2002), although any detection would be impossible at the
distance of T Pyx.
10-3 persists for the active dMe stars, and the emission was detected in surveys of nearby stars (see Giampapa & Fleming 2002), although any detection would be impossible at the
distance of T Pyx.
We suggest that the most likely origin of the observed hard X-ray emission is from shocks within the circumstellar envelope. We note that in GK Per, Balman et al. (2006) detected hard X-ray emission by direct imaging with Chandra. The total X-ray spectrum of the nebula consists of two thermal prominent components of emission. GK Per has a large amount of CS material, which is most likely a residual of a planetary nebula phase, and the shell remnant shows a clumpy structure similar to that observed in T Pyx by Shara et al. (1997) with HST. We recall that the studies by Orio et al. (2001) by Orio (2004) of the X-ray emission from classical and recurrent novae
demonstrated that emission from shocked ejecta is expected to last about two years, but
may last for up to a century, if, for example, there is pre-existing circumstellar material (as in the case of GK Per). Hernanz & Sala (2007) reported on X-ray observations of V4633 Sgr
performed with XMM-Newton between 2.6 and 3.5 yr after outburst. The X-ray spectrum is
dominated by thermal plasma emission, which most probably originated in the shock heated ejecta.
Unfortunately, the limited spatial resolution of the available XMM data do not enable any
spatially-resolved study to be completed, because the pixel size is about 4 arcsec
compared with the optical radius of the nebula which is about 5 arcsec.
Also the XMM observations, excluding the possibilities of continuous burning and the supersoft source scenario (a massive white dwarf accreting at high rates), appear to exclude T Pyx becoming a
SN Ia by means of the supersoft X-ray source channel described by Hachisu (2002, 2003).
As reported in Paper I, we started an observing program in 1986 with IUE to monitor T Pyx prior to (and during) the expected next outburst that was supposed to occur in the late eighties of
the last millennium. Unfortunately, the star successfully managed to postpone the
long-awaited outburst, and at the present time (2008) has surpassed by eighteen years the longest inter-outburst interval so far recorded (24 yrs).
As mentioned in Sect. 7, Schaefer (2005) published the results of a study of the inter-outburst interval in the recurrent novae T Pyx and U Sco. From an analysis of the available data, he found that the two novae are relatively bright during short inter-eruption intervals and dim
during long intervals, suggesting that the product of the inter-eruption interval times the average bolometrically corrected flux is a constant. Therefore, in the case of T Pyx, the lack of the post-1967 outburst is explained by a lower luminosity and therefore a lower  .
From the decline in the observed quiescent B magnitude in the time intervals before and after the
1966 outburst, Schaefer (2005) also predicted that the next outburst of T Pyx will occur around 2052.
.
From the decline in the observed quiescent B magnitude in the time intervals before and after the
1966 outburst, Schaefer (2005) also predicted that the next outburst of T Pyx will occur around 2052.
With the help of considerations in Sect. 8 and the data in Tables 3 and 5, we can further investigate this prediction. The recurrence time can be estimated from the (theoretical)
 and the observed mass accretion rate.
and the observed mass accretion rate.
 depends mainly on M1and
depends mainly on M1and  ,
while
,
while  ,
for a given
,
for a given
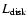 ,
is a function also of
M1 and R1, which, in turn, is a function of M1. Tables 3 and 5 list
,
is a function also of
M1 and R1, which, in turn, is a function of M1. Tables 3 and 5 list
 ,
,
 ,
and the recurrence time
,
and the recurrence time 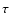 =
=
 /
/ (years) for various M1 values. Table 5 (pre-1967
(years) for various M1 values. Table 5 (pre-1967  values) clearly shows that the observed inter-outburst interval (22 years) corresponds to M1 values
values) clearly shows that the observed inter-outburst interval (22 years) corresponds to M1 values  1.36-1.38
1.36-1.38  .
Table 3, which contains post 1967-outburst
.
Table 3, which contains post 1967-outburst  values indicates that the observed interval, which, so far, is longer than 42 years, corresponds to M1
values indicates that the observed interval, which, so far, is longer than 42 years, corresponds to M1 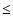 1.38
1.38  .
The most likely value of M1 is therefore close to 1.37
.
The most likely value of M1 is therefore close to 1.37  .
.
We note that a reduction by a factor two in the mass accretion rate corresponds to an increase in the expected recurrence time 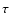 by a larger factor because, for a given M1,
by a larger factor because, for a given M1,
 increases as
increases as  decreases. For the relevant values of T Pyx, the decrease by a
factor of 2 in
decreases. For the relevant values of T Pyx, the decrease by a
factor of 2 in  is accompanied by an increase by a factor of about 50 percent in
is accompanied by an increase by a factor of about 50 percent in
 .
For the next outburst, therefore one expects an increase in the inter-outburst interval
.
For the next outburst, therefore one expects an increase in the inter-outburst interval 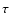 by a factor of approximately 3.0, to values near 60 years (see Table 3).
Our prediction for the next outburst date is therefore around A.D. 2025. With this
new date, contrasted with that of Schaefer (A.D. 2052), we (or at least some of us) feel a bit more confident about the chance of personally testing this prediction.
by a factor of approximately 3.0, to values near 60 years (see Table 3).
Our prediction for the next outburst date is therefore around A.D. 2025. With this
new date, contrasted with that of Schaefer (A.D. 2052), we (or at least some of us) feel a bit more confident about the chance of personally testing this prediction.
However, given the uncertainties in  and
and
 ,
the possibility of a more imminent outburst cannot be ruled out. In this case, X-ray and other observations during the first outburst stages will be of paramount importance in determining the mass ejected in a single event.
,
the possibility of a more imminent outburst cannot be ruled out. In this case, X-ray and other observations during the first outburst stages will be of paramount importance in determining the mass ejected in a single event.
We have accurately determined, from UV and other observations, the accretion disk luminosity of T Pyx during both the pre- and post-1966 inter-outburst phases. For M1  1.37
1.37  ,
we have found that
,
we have found that
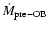
 2.2
2.2  10
10
 yr-1.
By combining the measured accretion rate with the duration of the inter-outburst phase
(
yr-1.
By combining the measured accretion rate with the duration of the inter-outburst phase
( = 22 yrs), the total accreted mass is inferred to be
= 22 yrs), the total accreted mass is inferred to be
 =
=
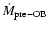
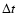
 5.2
5.2  10
10
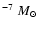 .
This value is in
excellent agreement with the theoretical ignition mass (
.
This value is in
excellent agreement with the theoretical ignition mass (
 )
)  5.0
5.0  10
10
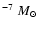 expected for a massive white dwarf accreting at the quoted rate. Therefore, both the time interval between the last two outburst and the absence of the awaited post-1967 outburst (due to the lower
expected for a massive white dwarf accreting at the quoted rate. Therefore, both the time interval between the last two outburst and the absence of the awaited post-1967 outburst (due to the lower  in the post-1967 time interval) are explained in a
self-consistent way.
in the post-1967 time interval) are explained in a
self-consistent way.
This is the first reliable determination of the mass accreted prior to a nova outburst,
 ,
owing to the dominance of the accretion disk luminosity over that of the secondary star at UV, optical and IR wavelengths, as well as good observational coverage during the
inter-outburst phases. Unfortunately,
,
owing to the dominance of the accretion disk luminosity over that of the secondary star at UV, optical and IR wavelengths, as well as good observational coverage during the
inter-outburst phases. Unfortunately,
 cannot be confidently determined in
other cases, such as classical novae, because of their long inter-outburst interval, nor in other recurrent novae, due to the faintness of the source, the lack of systematic UV observations, or the dominance of light from the giant companion over that from the accretion disk.
cannot be confidently determined in
other cases, such as classical novae, because of their long inter-outburst interval, nor in other recurrent novae, due to the faintness of the source, the lack of systematic UV observations, or the dominance of light from the giant companion over that from the accretion disk.
In T Pyx, the consistency between the observed
 and the theoretical
and the theoretical
 supports the good quality of the observations and the reliability of the models and
represents a new, direct confirmation of the validity of the TNR theory, which associates a massive white dwarf with the recurrent nova phenomenon. A detailed comparison of the observed parameters with the theoretical grids of Yaron et al. (2005) indicates that the closest
agreement is obtained with a models of a rather massive white dwarf (M1
supports the good quality of the observations and the reliability of the models and
represents a new, direct confirmation of the validity of the TNR theory, which associates a massive white dwarf with the recurrent nova phenomenon. A detailed comparison of the observed parameters with the theoretical grids of Yaron et al. (2005) indicates that the closest
agreement is obtained with a models of a rather massive white dwarf (M1  1.25-1.40
1.25-1.40  )
that accretes at high
)
that accretes at high  rates (
rates (
 10-8-10-7
10-8-10-7  yr-1). However, no combination of the theoretical parameters can reproduce the observed values reliably, t3 being the most difficult parameter to describe.
yr-1). However, no combination of the theoretical parameters can reproduce the observed values reliably, t3 being the most difficult parameter to describe.
The literature data of the spectroscopic and photometric evolution during the outbursts of T Pyx clearly indicate the occurrence of an optically thick phase that lasted about three months. This implies an ejected mass of
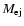
 10
10
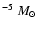 or higher, i.e. much
higher than the mass of the accreted shell
or higher, i.e. much
higher than the mass of the accreted shell

 5.2
5.2  10
10
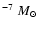 ,
inferred from UV and other observations during quiescence. Therefore, T Pyx ejected far more material than it has accreted.
,
inferred from UV and other observations during quiescence. Therefore, T Pyx ejected far more material than it has accreted.
There is no way to reconcile this discrepancy given the small uncertainty in the value of  ;
even if allowance is made for an uncertainty of a factor two, one obtains an upper limit to
;
even if allowance is made for an uncertainty of a factor two, one obtains an upper limit to
 that is smaller by a factor of at least ten than the theoretical value of
that is smaller by a factor of at least ten than the theoretical value of
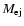 .
Only for accretion rates higher than 4
.
Only for accretion rates higher than 4  10
10
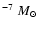 yr-1 would the accreted mass
yr-1 would the accreted mass
 be comparable with the estimated ejected mass
be comparable with the estimated ejected mass
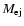 .
However, these high rates would correspond to the steady-burning regime, while our detailed discussion of Sect. 14 definitely excluded this possibility. Further confirmation of our considerations can be found in the the very recent results of XMM observations that exclude
the presence of a super-soft-source in T Pyx.
.
However, these high rates would correspond to the steady-burning regime, while our detailed discussion of Sect. 14 definitely excluded this possibility. Further confirmation of our considerations can be found in the the very recent results of XMM observations that exclude
the presence of a super-soft-source in T Pyx.
The important point is that far more material appears to have been ejected during the last outburst of T Pyx than has been accreted by the white dwarf. This raises several doubts about the common assumption that the white dwarf in recurrent novae increases in mass toward
the Chandrasekhar limit, and about the possible role of RNe as progenitors of SNIa. We note that Della Valle & Livio (1996), based on statistical considerations on the frequency of occurrence of RNe in M 31 and LMC, deduced that RNe are not a major class of progenitors of type Ia
supernovae. The behavior of T Pyx represents observational confirmation of this conclusion.
Further confirmation for other RNe is required, and this highlights the crucial need for accurate determinations of the most critical parameters of RNe, i.e. the mass accretion rate,
and the mass and chemical composition of the shell ejected in a single outburst.
In the case of T Pyx, at present, useful information can be obtained from highly spatially resolved spectrophotometry of the nebula that resolves its innermost part (associated with the last eruption), whose apparent radius should be by now larger than 1''. At the same
time, spatially resolved observations of the outer portions of the nebula will
shed light on its poorly known chemical composition and on its complex velocity structure.
Acknowledgements
We gratefully acknowledge the valuable conversations about the elusive nature of this recurrent nova that we have had with many colleagues in the last fifteen years, while waiting for its allegedly imminent outburst. In roughly chronological order we wish to thank in particular
M. Livio, D. Prialnik, M. Shara, J. A. De Freitas-Pacheco, M. Contini, S. Shore, R. E. Williams, M. Friedjung, O. Yaron, J. Danziger, and M. Della Valle.
- Adams, W. S., &
Joy, A. H. 1920, Pop. Astr., 28, 514
(In the text)
- Anderson, N. 1988, ApJ,
325, 266 [NASA ADS] [CrossRef]
(In the text)
- Anupama, G. C. 2002,
Classical Nova Explosions, AIP Conf. Proc., 637, 32
(In the text)
- Balman, S. 2006, Adv.
Space Res., 38, 2840 [NASA ADS] [CrossRef]
- Balman, S., &
Oumlgelman, H. B. 1999, ApJ, 518, L111 [NASA ADS] [CrossRef]
(In the text)
- Beals, C. S., &
Oke, J. B. 1953, MNRAS, 113, 530 [NASA ADS]
(In the text)
- Bruch, A., & Engel,
A. 1994, A&AS, 104, 79 [NASA ADS]
(In the text)
- Cassatella, A.,
Altamore, A., & González-Riestra, R. 2005, A&A, 439,
205 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Catchpole, R. M. 1969,
MNRAS, 142, 119 [NASA ADS]
(In the text)
- Chincarini, G., &
Rosino, L. 1969, IAU Coll.: Non-Periodic Phenomena in Variable
Stars, 261 [NASA ADS]
(In the text)
- Contini, M., &
Prialnik, D. 1997, ApJ, 475, 803 [NASA ADS] [CrossRef]
(In the text)
- Della Valle, M., &
Livio, M. 1995, ApJ, 452, 704 [NASA ADS] [CrossRef]
(In the text)
- Della Valle, M., &
Livio, M. 1996, ApJ, 473, 240 [NASA ADS] [CrossRef]
(In the text)
- Della Valle, M., &
Livio, M. 1998, ApJ, 506, 818 [NASA ADS] [CrossRef]
(In the text)
- Della Valle, M.,
Pasquini, L., Daou, D., & Williams, R. E. 2002, A&A, 390,
155 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Downes, R. A., &
Duerbeck, H. W. 2000, AJ, 120, 2007 [NASA ADS] [CrossRef]
(In the text)
- Downes, R., Webbink, R.
F., & Shara, M. M. 1997, PASP, 109, 345 [NASA ADS] [CrossRef]
(In the text)
- Duerbeck, H. W. 1981,
PASP, 93, 552 [CrossRef]
(In the text)
- Duerbeck, H. W.
1987a, Space Sci. Rev., 45, 1 [NASA ADS]
(In the text)
- Duerbeck, H. W.
1987b, The Messenger, 50, 8 [NASA ADS]
- Duerbeck, H. W., &
Seitter, W. C. 1979, The Messenger, 17, 1 [NASA ADS]
(In the text)
- Eggen, O. J. 1968,
QJRAS, 9, 329
(In the text)
- Eggen, O. J.,
Mathewson, D. S., & Serkowski, K. 1967, Nature, 213, 1216 [NASA ADS] [CrossRef]
(In the text)
- Eggleton, P. P. 1983,
ApJ, 268, 368 [NASA ADS] [CrossRef]
(In the text)
- Fujimoto, M. Y. 1982,
ApJ, 257, 752 [NASA ADS] [CrossRef]
(In the text)
- Gehrz, R. D., Truran,
J. W., Williams, R. E., & Starrfield, S. 1998, PASP, 110,
3 [NASA ADS] [CrossRef]
(In the text)
- Giampapa, M. S., &
Fleming, T. A. 2002, Stellar Coronae in the Chandra and XMM-NEWTON
Era, ASP Conf. Ser., 277, 247
(In the text)
- Gilmozzi, R., &
Selvelli, P. 2007, A&A, 461, 593 [NASA ADS] [CrossRef] [EDP Sciences] (Paper I)
(In the text)
- Gilmozzi, R., Selvelli,
P. L., & Cassatella, A. 1994, Mem. Soc. Astron. Ital., 65,
199 [NASA ADS]
(In the text)
- Gilmozzi, R., Selvelli,
P., & Cassatella, A. 1998, Ultraviolet Astrophysics Beyond the
IUE Final Archive, 413, 415 [NASA ADS]
(In the text)
- Greiner, J., Orio, M.,
& Schartel, N. 2003, A&A, 405, 703 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Hachisu, I. 2002, The
Physics of Cataclysmic Variables and Related Objects, ASP Conf.
Ser., 261, 605
(In the text)
- Hachisu, I. 2003,
Symbiotic Stars Probing Stellar Evolution, ASP Conf. Ser., 303,
261
(In the text)
- Hachisu, I., &
Kato, M. 2001, ApJ, 558, 323 [NASA ADS] [CrossRef]
(In the text)
- Hachisu, I., &
Kato, M. 2002, Classical Nova Explosions, AIP, 637, 284
(In the text)
- Hachisu, I., Kato, M.,
& Nomoto, K. 1999, ApJ, 522, 487 [NASA ADS] [CrossRef]
- Hamada, T., &
Salpeter, E. E. 1961, ApJ, 134, 683 [NASA ADS] [CrossRef]
(In the text)
- Harrison, T. E., &
Stringfellow, G. S. 1994, ApJ, 437, 827 [NASA ADS] [CrossRef]
(In the text)
- Herbig, G. H. 1945,
PASP, 57, 168 [NASA ADS] [CrossRef]
(In the text)
- Hernanz, M., &
José, J. 1998, Wild Stars in the Old West, ASP Conf. Ser.,
137, 368
(In the text)
- Hernanz, M., &
Sala, G. 2007, ApJ, 664, 467 [NASA ADS] [CrossRef]
(In the text)
- Hunter, I., Smoker, J.
V., Keenan, F. P., et al. 2006, MNRAS, 367, 1478 [NASA ADS] [CrossRef]
(In the text)
- Iben, I., Jr., &
Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef]
(In the text)
- Joy, A. H. 1945, PASP,
57, 171 [NASA ADS] [CrossRef]
(In the text)
- Kahabka, P., & van
den Heuvel, E. P. J. 1997, ARA&A, 35, 69 [NASA ADS] [CrossRef]
(In the text)
- Kahabka, P., & van
den Heuvel, E. P. J. 2006, Compact stellar X-ray sources, Cambridge
Astrophys. Ser., 461
(In the text)
- Kato, M. 1990, ApJ,
362, L17 [NASA ADS] [CrossRef]
(In the text)
- Kato, M., &
Hachisu, I. 1991, ApJ, 373, 620 [NASA ADS] [CrossRef]
(In the text)
- Kirkpatrick, J. D.,
Henry, T. J., & McCarthy, D. W., Jr. 1991, ApJS, 77, 417 [NASA ADS] [CrossRef]
(In the text)
- Knigge, C. 2006, MNRAS,
373, 484 [NASA ADS] [CrossRef]
(In the text)
- Knigge, C., King, A.
R., & Patterson, J. 2000, A&A, 364, L75 [NASA ADS]
(In the text)
- Kolb, U., Rappaport,
S., Schenker, K., & Howell, S. 2001, ApJ, 563, 958 [NASA ADS] [CrossRef]
(In the text)
- Kopal, Z. 1972, Adv.
Astron. Astrophys., 9, 1 [NASA ADS]
(In the text)
- Krautter, J. 2008, in
Classical Novae, 2nd Ed., ed. M. F. Bode, & A. Evans
(Cambridge: Cambridge University Press), Cambridge Astrophys. Ser.,
43, 232
(In the text)
- Kuulkers, E., Norton,
A., Schwope, A., & Warner, B. 2006, Compact stellar X-ray
sources, 421 [NASA ADS]
(In the text)
- Leggett, S. K. 1992,
ApJS, 82, 351 [NASA ADS] [CrossRef]
(In the text)
- Lipkin, Y., Leibowitz,
E. M., Retter, A., & Shemmer, O. 2001, MNRAS, 328, 1169 [NASA ADS] [CrossRef]
(In the text)
- Livio, M. 1991, ApJ,
369, L5 [NASA ADS] [CrossRef]
(In the text)
- Livio, M. 1994,
Saas-Fee Advanced Course 22: Interacting Binaries, 135 [NASA ADS]
(In the text)
- Livio, M., &
Truran, J. W. 1992, ApJ, 389, 695 [NASA ADS] [CrossRef]
(In the text)
- MacDonald, J. 1983,
ApJ, 267, 732 [NASA ADS] [CrossRef]
(In the text)
- Mason, E., Della Valle,
M., Gilmozzi, R., Lo Curto, G., & Williams, R. E. 2005,
A&A, 435, 1031 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Mayall, M. W. 1967,
JRASC, 61, 349 [NASA ADS]
(In the text)
- McLaughlin, D. B. 1956,
Vistas in astronomy, 2 (Pergamon Press), 1477
(In the text)
- McLaughlin, D. B. 1965,
in Stellar Structure - Stars and Stellar Systems (Chicago Univ.
Press), 600
(In the text)
- Mochnacki, S. W. 1984,
ApJS, 55, 551 [NASA ADS] [CrossRef]
(In the text)
- Münch, G. 1968,
Stars and Stellar Systems, 7, 365
(In the text)
- Nauenberg, M. 1972,
ApJ, 175, 417 [NASA ADS] [CrossRef]
(In the text)
- Nofar, I., Shaviv, G.,
& Wehrse, R. 1992, Cataclysmic Variable Stars, 29, 65 [NASA ADS]
(In the text)
- Nomoto, K., Thielemann,
F.-K., & Yokoi, K. 1984, ApJ, 286, 644 [NASA ADS] [CrossRef]
(In the text)
- O'Brien, T. J., Lloyd,
H. M., & Bode, M. F. 1994, MNRAS, 271, 155 [NASA ADS]
(In the text)
- Orio, M. 2004, Rev.
Mex. Astron. Astrofis. Conf. Ser., 20, 182 [NASA ADS]
(In the text)
- Orio, M., Covington,
J., & Oegelman, H. 2001, A&A, 373, 542 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Orio, M.,
Tepedelenlioglu, E., Starrfield, S., Woodward, C. E., & Della
Valle, M. 2005, ApJ, 620, 938 [NASA ADS] [CrossRef]
- Paczynski, B. 1971,
ARA&A, 9, 183 [NASA ADS] [CrossRef]
- Paczynski, B., &
Schwarzenberg-Czerny, A. 1980, Acta Astron., 30, 127 [NASA ADS]
(In the text)
- Parthasarathy, M.,
Branch, D., Jeffery, D. J., & Baron, E. 2007, New Astron. Rev.,
51, 524 [NASA ADS] [CrossRef]
(In the text)
- Patterson, J., &
Raymond, J. C. 1985, ApJ, 292, 550 [NASA ADS] [CrossRef]
(In the text)
- Patterson, J., Kemp,
J., Shambrook, A., et al. 1998, PASP, 110, 380 [NASA ADS] [CrossRef]
(In the text)
- Patterson, J., Kemp,
J., Harvey, D. A., et al. 2005, PASP, 117, 1204 [NASA ADS] [CrossRef]
(In the text)
- Payne-Gaposchkin, C.
1957, in The Galactic Novae (North Holland), 23
(In the text)
- Plavec, M., &
Kratochvil, P. 1964, Bulletin of the Astronomical Institutes of
Czechoslovakia, 15, 165 [NASA ADS]
(In the text)
- Politano, M., Livio,
M., Truran, J. W., & Webbink, R. F. 1990, IAU Colloq., 122,
Physics of Classical Novae, 369, 386
(In the text)
- Pottasch, S. 1959, Ann.
Astrophys., 22, 297 [NASA ADS]
(In the text)
- Prialnik, D., &
Kovetz, A. 1995, ApJ, 445, 789 [NASA ADS] [CrossRef]
(In the text)
- Retter, A., &
Leibowitz, E. M. 1998, MNRAS, 296, L37 [NASA ADS] [CrossRef]
(In the text)
- Retter, A., &
Naylor, T. 2000, MNRAS, 319, 510 [NASA ADS] [CrossRef]
(In the text)
- Ritter, H., Politano,
M., Livio, M., & Webbink, R. F. 1991, ApJ, 376, 177 [NASA ADS] [CrossRef]
(In the text)
- Saizar, P., &
Ferland, G. J. 1994, ApJ, 425, 755 [NASA ADS] [CrossRef]
(In the text)
- Schaefer, B. E. 2005,
ApJ, 621, L53 [NASA ADS] [CrossRef]
(In the text)
- Schaefer, B. E.,
Landolt, A. U., Vogt, N., et al. 1992, ApJS, 81, 321 [NASA ADS] [CrossRef]
(In the text)
- Seitter, W. C. 1987, RS
Ophiuchi and the Recurrent Nova Phenomenon (VNU Science Press),
63 [NASA ADS]
(In the text)
- Selvelli, P. 2004,
Baltic Astron., 13, 93 [NASA ADS]
(In the text)
- Selvelli, P., &
Friedjung, M. 2003, A&A, 401, 297 [NASA ADS] [CrossRef] [EDP Sciences]
- Shahbaz, T., Livio, M.,
Southwell, K. A., & Charles, P. A. 1997, ApJ, 484, L59 [NASA ADS] [CrossRef]
- Shara, M. M. 1981, ApJ,
243, 926 [NASA ADS] [CrossRef]
(In the text)
- Shara, M. M. 1989,
PASP, 101, 5 [NASA ADS] [CrossRef]
(In the text)
- Shara, M. M., Moffat,
A. F. J., Williams, R. E., & Cohen, J. G. 1989, ApJ, 337,
720 [NASA ADS] [CrossRef]
(In the text)
- Shara, M. M., Zurek, D.
R., Williams, R. E., et al. 1997, AJ, 114, 258 [NASA ADS] [CrossRef]
(In the text)
- Shore, S. N. 2002,
Classical Nova Explosions, AIP Conf. Proc., 637, 175
(In the text)
- Shore, S. N. 2008,
Classical Novae, 2nd Ed., ed. M. F. Bode, & A. Evans (Cambridge
University Press), Cambridge Astrophys. Ser., 43, 194
(In the text)
- Shore, S. N., &
Starrfield, S. 1998, Stellar Evolution, Stellar Explosions and
Galactic Chemical Evolution, 413
- Smith, D. A., &
Dhillon, V. S. 1998, MNRAS, 301, 767 [NASA ADS] [CrossRef]
(In the text)
- Starrfield, S. 1993,
Astrophys. Space Sci. Libr., 177, 209 [NASA ADS]
(In the text)
- Starrfield, S. 1999,
Phys. Rep., 311, 371 [NASA ADS] [CrossRef]
(In the text)
- Starrfield, S. 2002,
Classical Nova Explosions, AIP, 637, 89
(In the text)
- Starrfield, S., Sparks,
W. M., & Truran, J. W. 1985, ApJ, 291, 136 [NASA ADS] [CrossRef]
(In the text)
- Starrfield, S.,
Vanlandingham, K., Schwarz, G., Hauschildt, P. H., & Shore, S.
N. 1998a, Stellar Evolution, Stellar Explosions and Galactic
Chemical Evolution, 433
(In the text)
- Starrfield, S.,
Truran, J. W., Wiescher, M. C., & Sparks, W. M. 1998b, MNRAS,
296, 502 [NASA ADS] [CrossRef]
- Starrfield, S.,
Truran, J. W., Sparks, W. M., et al. 1998c, Wild Stars in the Old
West, ASP Conf., 137, 352
- Stickland, D. J.,
Penn, C. J., Seaton, M. J., Snijders, M. A. J., & Storey, P. J.
1981, MNRAS, 197, 107 [NASA ADS]
(In the text)
- Szkody, P. 1994, AJ,
108, 639 [NASA ADS] [CrossRef]
(In the text)
- Szkody, P., &
Feinswog, L. 1988, ApJ, 334, 422 [NASA ADS] [CrossRef]
(In the text)
- Townsley, D. M., &
Bildsten, L. 2004, ApJ, 600, 390 [NASA ADS] [CrossRef]
(In the text)
- Truran, J. W. 1998,
Stellar Evolution, Stellar Explosions and Galactic Chemical
Evolution, 425
(In the text)
- van den Bergh, S.,
& Younger, P. F. 1987, A&AS, 70, 125 [NASA ADS]
(In the text)
- Vanlandingham, K. M.,
Starrfield, S., Wagner, R. M., Shore, S. N., & Sonneborn, G.
1996, MNRAS, 282, 563 [NASA ADS]
(In the text)
- Vanlandingham, K. M.,
Starrfield, S., Shore, S. N., & Sonneborn, G. 1999, MNRAS, 308,
577 [NASA ADS] [CrossRef]
(In the text)
- Vogt, N., Barrera, L.
H., Barwig, H., & Mantel, K.-H. 1990, Accretion-Powered Compact
Binaries, 391 [NASA ADS]
(In the text)
- Wade, R. A., &
Hubeny, I. 1998, ApJ, 509, 350 [NASA ADS] [CrossRef]
(In the text)
- Warner, B. 1976,
Structure and Evolution of Close Binary Systems, IAU Symp., 73,
85
(In the text)
- Warner, B. 1986, MNRAS,
222, 11 [NASA ADS]
- Warner, B. 1987, MNRAS,
227, 23 [NASA ADS]
(In the text)
- Warner, B. 1995,
Cataclysmic Variable Stars (Cambridge University Press), Cambridge
Astrophys. Ser.
(In the text)
- Warner, B. 2008, in
Classical Novae, 2nd Ed., ed. M. F. Bode, & A. Evans (Cambridge
University Press), Cambridge Astrophys. Ser., 43, 16
(In the text)
- Webbink, R. F. 1990,
Accretion-Powered Compact Binaries, 177 [NASA ADS]
(In the text)
- Webbink, R. F., Livio,
M., Truran, J. W., & Orio, M. 1987, ApJ, 314, 653 [NASA ADS] [CrossRef] (WLTO,
1987)
(In the text)
- Whelan, J., & Iben,
I. J. 1973, ApJ, 186, 1007 [NASA ADS] [CrossRef]
(In the text)
- Williams, R. E. 1982,
ApJ, 261, 170 [NASA ADS] [CrossRef]
(In the text)
- Williams, R. E. 1994,
ApJ, 426, 279 [NASA ADS] [CrossRef]
(In the text)
- Williams, R. E.,
Sparks, W. M., Gallagher, J. S., et al. 1981, ApJ, 251, 221 [NASA ADS] [CrossRef]
(In the text)
- Woosley, S. E., &
Weaver, T. A. 1986, ARA&A, 24, 205 [NASA ADS] [CrossRef]
(In the text)
- Yaron, O. 2007, private
communication
(In the text)
- Yaron, O., Prialnik,
D., Shara, M. M., & Kovetz, A. 2005, ApJ, 623, 398 [NASA ADS] [CrossRef]
(In the text)
Copyright ESO 2008
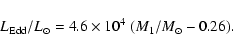
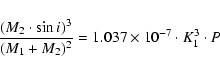
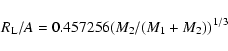
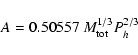
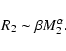
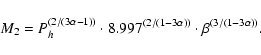
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{0678fig1}
\end{figure}](/articles/aa/full/2008/48/aa10678-08/Timg71.gif)
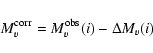
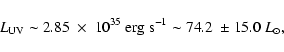
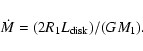
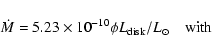
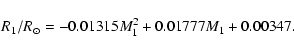
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{0678fig2}
\end{figure}](/articles/aa/full/2008/48/aa10678-08/Timg96.gif)
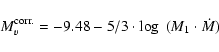
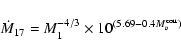
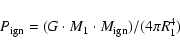
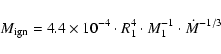
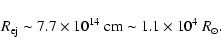
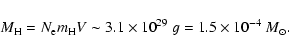
![\begin{displaymath}%
N_{\rm H}\cdot R = 3.0 \times 10^{52}\cdot R^{-2}\quad [{\rm cm}^{-2}].
\end{displaymath}](/articles/aa/full/2008/48/aa10678-08/img125.gif)
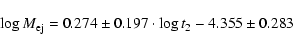
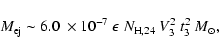
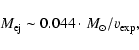
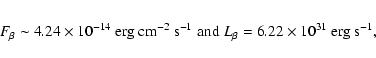
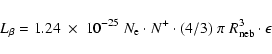
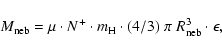
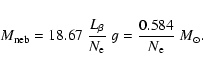
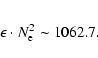
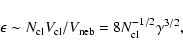
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{0678fig3}
\end{figure}](/articles/aa/full/2008/48/aa10678-08/Timg150.gif)
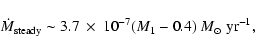
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{0678fig4}
\end{figure}](/articles/aa/full/2008/48/aa10678-08/Timg155.gif)