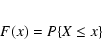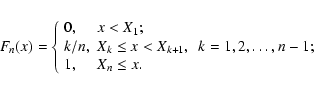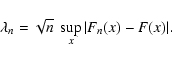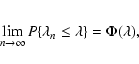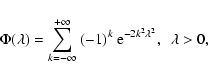A&A 492, L33-L34 (2008)
DOI: 10.1051/0004-6361:200811188
LETTER TO THE EDITOR
Kolmogorov stochasticity parameter measuring the randomness in the cosmic microwave background
V. G. Gurzadyan1 - A. A. Kocharyan1,2
1 - Yerevan Physics Institute and Yerevan State University, Yerevan,
Armenia
2 - School of Mathematical Sciences, Monash University, Clayton, Australia
Received 20 October 2008 / Accepted 4 November 2008
Abstract
The Kolmogorov stochasticity parameter (KSP) is applied to quantify the degree of randomness (stochasticity) in the temperature maps of the Cosmic Microwave Background radiation maps. It is shown that the KSP for the WMAP5 maps is about twice as high as that of the simulated maps for the concordance  CDM cosmological model, implying that a randomizing effect exists that has not been taken into account by the model. As was revealed earlier, underdense regions in the large scale matter distributions, i.e. the voids, possess hyperbolic and, hence, randomizing properties. The degree of randomness for the Cold Spot appears to be about twice as high as the average of the mean temperature level spots in the sky, which supports the void nature of the Cold Spot. Kolmogorov's parameter then acts as a quantitative tracer of the voids by means of the CMB.
CDM cosmological model, implying that a randomizing effect exists that has not been taken into account by the model. As was revealed earlier, underdense regions in the large scale matter distributions, i.e. the voids, possess hyperbolic and, hence, randomizing properties. The degree of randomness for the Cold Spot appears to be about twice as high as the average of the mean temperature level spots in the sky, which supports the void nature of the Cold Spot. Kolmogorov's parameter then acts as a quantitative tracer of the voids by means of the CMB.
Key words: cosmology: cosmic microwave background
The statistic introduced by Kolmogorov in 1933 (Kolmogorov 1933) is based on a stochasticity parameter of a given sequence of real numbers. This measurement of stochasiticity is applied successfully to measure the objective randomness degree of finite sequences due to dynamical systems or in number theory (Arnold 2008).
We apply the Kolmogorov stochasticity parameter (KSP) in a physical problem of cosmological interest, namely, a study of the properties of the Cosmic Microwave Background (CMB) radiation, which is one of the basic sources of information of the early Universe and its present structure. Previous studies have included non-Gaussianities reported for the CMB properties, such as the multipole alignments, hemisphere anomalies, temperature-independent ellipticity of the excursion sets, large-scale symmetry (see Eriksen et al. 2007; Copi et al. 2007; Gurzadyan & Torres 1997; Gurzadyan et al. 2005, 2007, 2008). Among the signals with low probability at Gaussian fluctuations is a region in the southern sky known as the Cold Spot (Vielva et al. 2004; Cruz et al. 2005).
The present study concerns the CMB non-Gaussianities and also the voids, i.e. underdense regions in the large scale matter distribution. The idea is as follows. On the one hand, the voids are one of the discussed phenomena associated with the CMB, particularly that are responsible for the nature of the Cold Spot anomaly, see Inoue et al. (2007), Cardwell & Stebbins (2008), Uzan et al. (2008), and Das & Spergel (2008). On the other hand, the voids can act as hyperbolic lenses (Gurzadyan & Kocharyan 2008a,b) as demonstrated for a Friedmann-Robertson-Walker universe with perturbations of the metric. A similar conclusion on the voids acting as divergent lenses is drawn in (Das & Spergel 2008). According to the theory of dynamical systems, the hyperbolicity of the geodesic flows, Anosov flows particularly known in this relation, implies the decay of the time correlation functions and a loss of information on the initial conditions (Arnold 1989).
If the voids are hyperbolicity regions, they are therefore able to randomize the distribution of the null geodesics and, hence, the temperature distribution in the CMB maps. The line-of-sight distribution of the voids must be of particular importance in the degree of randomization. If this were due to a void, the Cold Spot would be an illustrative case.
To reveal this effect of randomization, we estimated the KSP both for the CMB temperature map and the map simulated for the power-spectrum-defined parameters of the  CDM concordance model. We then estimated the KSP for both the Cold Spot and threshold temperature regions of the same size in the observed temperature map. Both the randomization and ellipticity of the CMB maps therefore represent observational tracers of the hyperbolicity.
CDM concordance model. We then estimated the KSP for both the Cold Spot and threshold temperature regions of the same size in the observed temperature map. Both the randomization and ellipticity of the CMB maps therefore represent observational tracers of the hyperbolicity.
Let
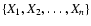 be n independent values of the same real-valued random variable X ordered in an increasing manner
be n independent values of the same real-valued random variable X ordered in an increasing manner
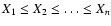 and let
and let
be a cumulative distribution function (CDF) of X. Their empirical distribution function Fn(x) is defined by the relations
Kolmogorov's stochasticity parameter 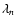 has the following form (Kolmogorov 1933; Arnold 2008)
has the following form (Kolmogorov 1933; Arnold 2008)
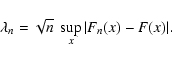 |
(1) |
Kolmogorov proved in Kolmogorov (1933) that for any continuous CDF F
where  ,
,
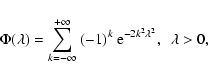 |
(2) |
the convergence is uniform, and 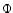 (Kolmogorov's distribution) is independent on F.
KSP is evaluated to measure the objective stochasticity degree of datasets (Arnold 2008). It is straightforward to observe that the inequalities
(Kolmogorov's distribution) is independent on F.
KSP is evaluated to measure the objective stochasticity degree of datasets (Arnold 2008). It is straightforward to observe that the inequalities
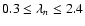 can be considered as practically certain (Kolmogorov 1933).
can be considered as practically certain (Kolmogorov 1933).
The temperature maps of the CMB are sequences of numbers indicating the temperature assigned to the pixels in certain coordinate representation, commonly in HEALPix (Gorski et al. 2005).
For the analysis, we used the latest, 5-year data obtained by the Wilkinson Microwave Anisotropy Probe (WMAP) at 94 GHz (3.2 mm, W-band). This band has the best resolution of all bands and is the least contaminated by the Galactic synchrotron radiation.
The Cold Spot region is defined to be an area of 3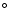 radius centred on l = 208
radius centred on l = 208
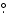 7, b = -55
7, b = -55
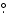 6, which corresponds to a string of temperature values of 2155 pixels that vary within the interval
6, which corresponds to a string of temperature values of 2155 pixels that vary within the interval
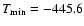 and
and
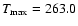 (in
(in 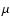 K).
K).
The KSP was calculated for 150 similar regions of size of the Cold Spot but neither cold or hot, i.e. with
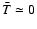 ,
randomly distributed over the sky, excluding, as usual, the Galactic disk region
,
randomly distributed over the sky, excluding, as usual, the Galactic disk region
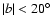 .
The KSP parameter was also estimated for 150 simulated regions of the same size and condition. The simulations were performed with a standard scheme using the HEALPix package (synfast), superimposing the noise of WMAP with its FWHM beam smoothing (see e.g. Gurzadyan et al. 2005, 2007, 2008).
.
The KSP parameter was also estimated for 150 simulated regions of the same size and condition. The simulations were performed with a standard scheme using the HEALPix package (synfast), superimposing the noise of WMAP with its FWHM beam smoothing (see e.g. Gurzadyan et al. 2005, 2007, 2008).
Table 1:
Mean values and variances for
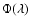 .
.
For each dataset k, we assumed that F(x) was the CDF for Gaussian distribution, calculated
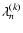 in Eq. (1), estimated
in Eq. (1), estimated
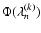 in Eq. (2), and finally obtain the mean probability
in Eq. (2), and finally obtain the mean probability 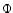 .
.
The mean values and variances derived for the observed WMAP's map, the simulated map, and the Cold Spot are given in the table.
To be able to trace the role of the dust, KSP for the Cold Spot was also estimated for the WMAP's foreground reduced maps at W, Q, and V bands.
We have demonstrated that the real CMB sky is random with twice as high degrees as a simulated one, i.e. there is an additional randomizing effect that is not included in the cosmological model. The Cold Spot is also about twice as random as similar size regions across the sky. If this was due to the randomizing effect of the hyperbolic voids, it would in particular support the void nature of the Cold Spot. Kolmogorov's parameter may then be used as a tool for probing the voids of the Universe by means of properties of the CMB. Thus, this study should be considered as a preliminary step to be followed with detailed analysis of the regions of different degree of randomness in CMB maps.
The application of Kolmogorov's parameter that we have presented here justifies its further use in physical problems, since it appears calculable and insightful.
Acknowledgements
We are thankful to the referee for valuable comments and to A. Kashin for discussions and help.
- Arnold, V. I. 1989,
Mathematical Methods of Classical Mechanics (Springer-Verlag)
(In the text)
- Arnold, V. 2008,
Nonlinearity, 21, T109 [NASA ADS] [CrossRef]
(In the text)
- Caldwell, R. R., &
Stebbins, A. 2008, Phys. Rev. Lett., 100, 191302 [NASA ADS] [CrossRef]
(In the text)
- Copi, C. J., Huterer, D.,
Schwarz, D. J., & Starkman, G. D. 2007, Phys. Rev. D, 75,
023507 [NASA ADS] [CrossRef]
(In the text)
- Cruz, M.,
Martinez-Gonzalez, E., Vielva, P., & Cayon, L. 2005, MNRAS,
356, 29 [NASA ADS] [CrossRef]
(In the text)
- Das, S., & Spergel, D. N.
2008 [arXiv:0809.4704]
(In the text)
- Eriksen, H. K., Banday, A. J.,
Górski, K. M., Hansen, F. K., & Lilje, P. B. 2007, ApJ,
660, L81 [NASA ADS] [CrossRef]
(In the text)
- Górski, K. M., Hivon, E.,
Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef],
http://healpix.jpl.nasa.gov
(In the text)
- Gurzadyan, V. G., & Torres,
S. 1997, A&A, 321, 19 [NASA ADS]
(In the text)
- Gurzadyan, V. G., &
Kocharyan, A. A. 2008a, [arXiv:0805.4279]
(In the text)
- Gurzadyan, V. G., &
Kocharyan, A. A. 2008b, [arXiv:0807.1239]
- Gurzadyan, V. G., de Bernardis,
P., de Troia, G., et al. 2005, Mod. Phys. Lett., A20, 893
(In the text)
- Gurzadyan, V. G., Bianco, C.
L., Kashin, A. L., Kuloghlian, H., & Yegorian, G. 2007, Phys.
Lett. A, 363, 121 [NASA ADS] [CrossRef]
(In the text)
- Gurzadyan, V. G., Starobinsky,
A. A., Ghahramanyan, T., et al. 2008, A&A, 490, 929 [CrossRef] [EDP Sciences]
(In the text)
- Inoue, K. T., &
Silk, J. 2007, ApJ, 664, 650 [NASA ADS] [CrossRef]
(In the text)
- Kolmogorov, A. N. 1933, G. Ist.
Ital. Attuari, 4, 83
(In the text)
- Uzan, J.-P., Clarkson, C.,
& Ellis, G. F. R. 2008, Phys. Rev. Lett., 100, 191303 [NASA ADS] [CrossRef]
(In the text)
- Vielva, P.,
Martinez-Gonzalez, E., Barreiro, R. B., et al. 2004, ApJ, 609,
22 [NASA ADS] [CrossRef]
(In the text)
Copyright ESO 2008