A&A 492, L29-L32 (2008)
DOI: 10.1051/0004-6361:200811022
LETTER TO THE EDITOR
On the combination of ACE data with numerical simulations to determine the initial characteristics of a CME
E. Chané1,2 -
S. Poedts1 -
B. van der Holst1,3
1 - Centrum voor Plasma-Astrofysica, K.U. Leuven, Celestijnenlaan 200B, 3001 Leuven, Belgium
2 -
Institut für Geophysik und Meteorologie, Universität zu Köln, Cologne, Germany
3 -
Center for Space Environment Modeling, University of Michigan, Ann Arbor, MI 48109-2143, USA
Received 23 September 2008 / Accepted 4 November 2008
Abstract
Aims. Our goal is to combine the Advanced Composition Explorer (ACE) data with numerical simulations to determine the initial characteristics of the halo coronal mass ejection (CME), which was observed on April 4, 2000.
Methods. The evolution of a CME from the Sun to 1 AU is simulated in the framework of 2.5 D (axi-symmetric) ideal Magnetohydrodynamics (MHD). The initial parameters of the CME model are adjusted to reproduce the ACE data as accurately as possible. The initial parameters leading to the best fit are then assumed to be the most plausible initial parameters of the CME event.
Results. Once the ACE data and the transit time were successfully reproduced, we concluded that, at 1.5 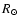 ,
the CME had a maximal magnetic field strength of
,
the CME had a maximal magnetic field strength of
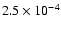 T and a total mass of
T and a total mass of
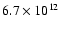 kg, and the CME linear speed up to 30
kg, and the CME linear speed up to 30  was 1524 km s-1.
was 1524 km s-1.
Key words: Sun: coronal mass ejections (CMEs) -
magnetohydrodynamics (MHD)
In situ measurements obtained by spacecrafts located at the Sun-Earth Lagrangian
point L1 (ACE and SOHO) are fundamental for forecasting magnetic storms on Earth.
The polarity of the solar wind, for instance, is known to be a key parameter
in predicting magnetic storms.
Due to the proximity between L1 and the Earth (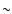
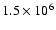 km),
a solar wind perturbation (e.g. a coronal mass ejection) typically needs
one hour to travel from L1 to the Earth.
Consequently, magnetic storm forecasts based on L1 measurements can ideally be made
only a couple of hours in advance.
On the other hand, solar wind perturbations usually need about three days to travel
from the Sun to the Earth.
As a result, using observations of the Sun to reproduce in situ measurements
obtained at L1 would enable earlier magnetic storm forecasts.
km),
a solar wind perturbation (e.g. a coronal mass ejection) typically needs
one hour to travel from L1 to the Earth.
Consequently, magnetic storm forecasts based on L1 measurements can ideally be made
only a couple of hours in advance.
On the other hand, solar wind perturbations usually need about three days to travel
from the Sun to the Earth.
As a result, using observations of the Sun to reproduce in situ measurements
obtained at L1 would enable earlier magnetic storm forecasts.
The Wang-Sheeley-Arge model, developed by Wang & Sheeley (1990,1991)
and improved by Arge & Pizzo (2000), is an empirical model that uses the photospheric
magnetic field data to predict the solar wind speed and the interplanetary magnetic field (IMF) polarity at L1.
Even though this model yields some realistic results, it does not take CMEs into account,
and important parameters, such as the magnitude of the magnetic field components, cannot be predicted.
The empirical shock arrival (ESA) model developed by Gopalswamy et al. (2001)
can be used to predict the time of arrival of CMEs at L1. It assumes a constant
acceleration for the CME, which only depends on the initial CME velocity.
The time of arrival is then directly related to the initial velocity.
The ESA model does not predict the solar wind characteristics at L1, but only
forecasts the time of arrival of a CME.
A promising alternative for predicting the in situ data at L1 could be numerical simulations.
This task is especially difficult for simulations including CMEs, since the CME characteristics close to the Sun
(magnetic field topology, density, etc.) are poorly known.
Consequently, the development of a new method for determining these characteristics is very important for space weather.
In our preceding studies, numerical simulations were used to understand the evolution of CMEs.
Jacobs et al. (2005), for instance, investigated the influence of the background solar wind on numerical simulations
of the evolution of CMEs by means of a 2.5 D (axi-symmetric) MHD model.
The influence of the initial magnetic polarity of the CME flux rope was later studied by Chané et al. (2005).
In these two papers, it was shown that the background wind and the initial magnetic polarity strongly
influence the shape, the size, the speed, and the trajectory of CMEs.
Because the computational domain of these two studies was limited to
30 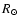 ,
comparisons with
in situ data (e.g. ACE, SOHO) were not possible.
The computational domain was therefore extended up to 1 AU in Chané et al. (2006).
Unfortunately, due to the unrealistically high density of the solar wind model used in this paper,
reproductions of the in situ data obtained by ACE were difficult and yielded unsatisfactory results.
,
comparisons with
in situ data (e.g. ACE, SOHO) were not possible.
The computational domain was therefore extended up to 1 AU in Chané et al. (2006).
Unfortunately, due to the unrealistically high density of the solar wind model used in this paper,
reproductions of the in situ data obtained by ACE were difficult and yielded unsatisfactory results.
In the present letter, an improved solar wind model, displaying a more realistic density profile, is used
to reproduce the in situ data obtained by the ACE spacecraft after the halo
CME event of 2000 April 4.
This is done simply by adjusting the CME initial parameters (density, magnetic field strength, velocity)
in the numerical simulation model to yield the best possible fit with the ACE data.
The initial parameters leading to the best fit are then assumed to be the most
plausible initial parameters.
Hence, the information at 1 AU is used to
derive the characteristics of the CME when it was still close to the Sun.
![\begin{figure}
\par\includegraphics[angle=90,width=7.4cm,clip]{1022fig1.eps}
\end{figure}](/articles/aa/full/2008/47/aa11022-08/Timg6.gif) |
Figure 1:
The solar wind model. The colour-coding represents the logarithm of the plasma density;
the magnetic field lines are drawn in black;
the black arrows represent the radial velocity;
the size of the arrows is proportional to the velocity magnitude. |
| Open with DEXTER |
The numerical simulations discussed in the present letter
were performed using the versatile advection code (VAC) (Tóth 1996)
with the so-called TVDLF finite volume shock-capturing scheme on a two-dimensional 589 536 cell mesh.
The inner and the outer boundaries are located at 1 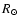 and 1 AU, respectively.
and 1 AU, respectively.
The solar wind model used in the present study is an improvement over our previous wind model (cf. Jacobs et al. 2005) and is based on a wind model developed by Groth et al. (2000).
This model represents the solar wind during the solar minimum and includes an artificial heating/cooling source term in the momentum equation.
This source term produces the right ratio of velocities at the poles and in the equatorial plane.
In this new version of our model, the density at the inner boundary (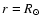 )
is decreased
by a factor of two at the equator and by a factor of six at the pole in order to fit the observations (Gallagher et al. 1999).
This density profile at the inner (
)
is decreased
by a factor of two at the equator and by a factor of six at the pole in order to fit the observations (Gallagher et al. 1999).
This density profile at the inner (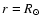 )
boundary is given by
)
boundary is given by
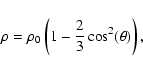 |
(1) |
where 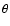 represents the colatitude and where
represents the colatitude and where 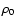 ,
the number density at the equator,
is equal to
,
the number density at the equator,
is equal to
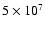 cm-3.
cm-3.
Figure 1 displays the density, velocity vectors, and magnetic field lines of our
solar wind model up to 15 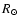 .
This model succeeds in reproducing the fast solar wind at the poles and the observed sharp
density gradients between open and closed magnetic regions.
Figure 2 shows the density, radial velocity, magnetic field, and temperature profiles
of the wind model at 1 AU on top of the in situ measurements obtained by the Ulysses spacecraft.
This figure indicates that the background solar wind agrees both qualitatively and quantitatively
with Ulysses solar minimum observations.
.
This model succeeds in reproducing the fast solar wind at the poles and the observed sharp
density gradients between open and closed magnetic regions.
Figure 2 shows the density, radial velocity, magnetic field, and temperature profiles
of the wind model at 1 AU on top of the in situ measurements obtained by the Ulysses spacecraft.
This figure indicates that the background solar wind agrees both qualitatively and quantitatively
with Ulysses solar minimum observations.
![\begin{figure}
\par\includegraphics[angle=90,width=8.4cm,clip]{1022fig2.eps}
\end{figure}](/articles/aa/full/2008/47/aa11022-08/Timg12.gif) |
Figure 2:
Comparison between Ulysses data (blue dots) and our wind model at 1 AU (black curves).
The Ulysses data were measured between November 1, 1994 and August 1, 1995 when the
spacecraft was situated between 1.34 and 2.03 AU from the Sun. |
| Open with DEXTER |
For the CME, a simple,
easily understandable model is chosen.
In this model, a high-density, high-pressure flux rope
is superposed on the background solar wind with an initial prescribed radial velocity.
The density and radial velocity profile of the initial perturbation are defined as follows (in local coordinates):
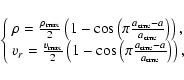 |
(2) |
where
 is the radius of the flux rope,
a denotes the distance from the centre of the flux rope,
and
is the radius of the flux rope,
a denotes the distance from the centre of the flux rope,
and
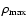 and
and
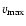 are the maximum density
and the maximum radial velocity added on top of the background solar wind, respectively.
are the maximum density
and the maximum radial velocity added on top of the background solar wind, respectively.
The initial magnetic field is defined as
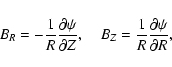 |
(3) |
where
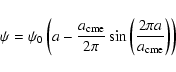 |
(4) |
is the poloidal magnetic flux function.
Several CME initiation models have already been proposed in the literature, e.g.
the flux cancellation (Amari et al. 2000; van Ballegooijen & Martens 1989) or emergence model (Dubey et al. 2006; Chen & Shibata 2000),
the footpoints shearing model (Jacobs et al. 2006; Low 1977; Mikic et al. 1988),
and the breakout model (van der Holst et al. 2007; Antiochos 1998).
However, since there is no general consensus yet on the triggering mechanism,
we instead assume that the CME has already been initiated.
The early evolution of the CME is approximated by our flux rope model.
The centre of the CME is initially placed at 1.5 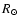 from the centre of the Sun.
The radius of the initial CME,
from the centre of the Sun.
The radius of the initial CME,
 ,
is 0.3
,
is 0.3 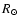 .
.
![\begin{figure}
\par\includegraphics[trim=0mm 0mm 0mm 0mm,clip,width=7.8cm,angle=90]{1022fig3.eps}
\end{figure}](/articles/aa/full/2008/47/aa11022-08/Timg19.gif) |
Figure 3:
Overview of the initial parameters of the 24 simulations performed
during the parameter study. |
| Open with DEXTER |
On April 4, 2000 a full halo CME event was observed by LASCO and EIT.
At 1632 UT, after a data gap of 90 minutes, the CME was observed for the first time in the C2 frame.
Unfortunately, the leading edge of the CME was already beyond the C2 field of view (further than 6 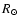 ).
The plane-of-sky speed of the CME was reported to be 1188 km s-1.
Two days later, this CME arrived on Earth and a strong shock was measured by ACE on April 6 at 1604 UT.
This CME produced the second strongest magnetic storm in the year 2000
(Dst value of -228 nT). This was the strongest magnetic storm since November 1991
and one of the seven largest magnetic storms in the history of Dst measurements
(Jadav et al. 2005).
The day-side magnetopause, which was at 11
).
The plane-of-sky speed of the CME was reported to be 1188 km s-1.
Two days later, this CME arrived on Earth and a strong shock was measured by ACE on April 6 at 1604 UT.
This CME produced the second strongest magnetic storm in the year 2000
(Dst value of -228 nT). This was the strongest magnetic storm since November 1991
and one of the seven largest magnetic storms in the history of Dst measurements
(Jadav et al. 2005).
The day-side magnetopause, which was at 11 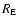 before the arrival of the shock, was compressed inside the
geostationary orbit for more than six hours and was located at only 5.5
before the arrival of the shock, was compressed inside the
geostationary orbit for more than six hours and was located at only 5.5 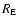 at 2351 UT (Huttunen et al. 2002).
In addition, aurorae were observed in the mid-Atlantic states of the United States, in central Japan, and
in central Europe (Ruohoniemi et al. 2001; Huttunen et al. 2002).
at 2351 UT (Huttunen et al. 2002).
In addition, aurorae were observed in the mid-Atlantic states of the United States, in central Japan, and
in central Europe (Ruohoniemi et al. 2001; Huttunen et al. 2002).
A simulation of this CME event was performed using our 2.5 D (axi-symmetric) simple CME model and the measured and simulated signals
at 1 AU were compared. We assumed that at 1530 UT, the CME was perfectly circular and
located at 1.5 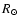 from the centre of the Sun in the equatorial plane, with a radius of 0.3
from the centre of the Sun in the equatorial plane, with a radius of 0.3 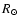 .
Three parameters of our 2.5 D CME model (average initial speed, total mass and magnetic field) were adjusted
to reproduce the ACE spacecraft data as close by as possible.
To obtain a good fit, 24 simulations were performed.
An overview of the parameter study can be seen in Fig. 3.
The average initial speed (
.
Three parameters of our 2.5 D CME model (average initial speed, total mass and magnetic field) were adjusted
to reproduce the ACE spacecraft data as close by as possible.
To obtain a good fit, 24 simulations were performed.
An overview of the parameter study can be seen in Fig. 3.
The average initial speed (
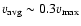 )
was modified between 300 km s-1 and 2230 km s-1;
the total mass between
)
was modified between 300 km s-1 and 2230 km s-1;
the total mass between
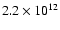 kg and
kg and
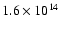 kg;
the initial magnetic field between
kg;
the initial magnetic field between
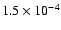 T and 10-3 T.
The ``average initial speed'' refers to the average speed superimposed on the solar wind at the beginning
of the simulation by means of Eq. (2).
Notice that this velocity does not have the same meaning as the velocity derived from the LASCO observations.
T and 10-3 T.
The ``average initial speed'' refers to the average speed superimposed on the solar wind at the beginning
of the simulation by means of Eq. (2).
Notice that this velocity does not have the same meaning as the velocity derived from the LASCO observations.
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{1022fig4.eps}
\end{figure}](/articles/aa/full/2008/47/aa11022-08/Timg25.gif) |
Figure 4:
Comparison between the in situ data obtained by the ACE spacecraft
(red curves) and our simulation (blue curves) as a function of time
(expressed in hour since the start of the simulation). |
| Open with DEXTER |
The results of our best attempt to fit the ACE data are shown
in Fig. 4. As can be seen on this figure, in spite of the simple CME model used,
our simulation successfully reproduces
the in situ measurements: the general shape of the curves is similar,
the plasma density displays realistic values, and the transit time is reproduced successfully.
The leading shock, characterised by a sharp jump in the density and velocity
curves, arrives only 1.5 h too early in the simulation. In addition, the plasma speed inside the CME
is about 15% higher in the simulation than in the observations.
While the plateaux of the density curves are similar in both cases
(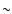 20 cm-3), the following density peak is 2.7 times too high in the simulation.
The magnetic cloud arrives three hours too late in the simulation and is also slightly smaller than
the observed magnetic cloud. The magnitude of the magnetic field peak is 25% higher in the
simulation, but the typical reversal of the magnetic field is clearly present.
The discrepancy between the simulated and observed density in the magnetic cloud may stem from the real CME not
exactly propagating in the direction of the Earth. As a matter of fact, the event observed
by LASCO was brightest and most structured over the West limb. In other words, the Earth was probably hit only
by the flank of the CME and not by its frontal part. Unfortunately, this feature cannot be
reproduced by means of axi-symmetric, 2.5 D simulations.
Due to CPU time constraints, the parameter study was limited and could probably be improved
by extending the parameter scans and the amount of scanned parameters.
20 cm-3), the following density peak is 2.7 times too high in the simulation.
The magnetic cloud arrives three hours too late in the simulation and is also slightly smaller than
the observed magnetic cloud. The magnitude of the magnetic field peak is 25% higher in the
simulation, but the typical reversal of the magnetic field is clearly present.
The discrepancy between the simulated and observed density in the magnetic cloud may stem from the real CME not
exactly propagating in the direction of the Earth. As a matter of fact, the event observed
by LASCO was brightest and most structured over the West limb. In other words, the Earth was probably hit only
by the flank of the CME and not by its frontal part. Unfortunately, this feature cannot be
reproduced by means of axi-symmetric, 2.5 D simulations.
Due to CPU time constraints, the parameter study was limited and could probably be improved
by extending the parameter scans and the amount of scanned parameters.
In spite of its shortcomings, our simulation is, to our knowledge, the best attempt ever made to fit
the in situ data at 1 AU.
Even though comparisons between simulations and observations at 1 AU can be found in the literature
(for example Wu et al. 2007; Lugaz et al. 2007; Odstrcil et al. 2005; Tóth et al. 2007), none of them matches the data correctly.
![\begin{figure}
\par {\hspace*{8mm}\includegraphics[width=7.7cm]{1022fig5.eps}\hs...
...vspace*{3mm}
\includegraphics[width=8.7cm,angle=90]{1022fig6.eps}
\end{figure}](/articles/aa/full/2008/47/aa11022-08/Timg26.gif) |
Figure 5:
Height-time plot of the leading edge of the CME. Top: observations; Bottom: simulation. |
| Open with DEXTER |
The initial parameters used to obtain these results are:
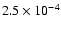 T
for the initial maximal magnetic field,
T
for the initial maximal magnetic field,
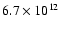 kg for the total mass,
and 1490 km s-1 for the average initial velocity.
As already mentioned, this velocity does not reflect the original velocity of the leading edge of the CME but is
the average velocity superimposed on the wind at the beginning of the simulation.
Either way, the velocity of the leading edge can be deduced from the height-time plot presented in Fig. 5.
Using a simple linear fit, a speed of 1524 km s-1 is found.
The same method was used by the LASCO team to find a plane-of-sky speed of
1188 km s-1.
Since the plane-of-sky speed is measured in a plane perpendicular to the Sun-Earth line,
the difference of 30% between the simulated and observed velocity could be caused by projection effects.
It is important to understand that, in 2.5 D axi-symmetric simulations, the CME is initially a torus
with a plasma density equally distributed in the longitudinal direction (around the Sun). As a result, comparing the mass of the CME determined
with our method and the real mass of the CME is not straightforward.
However, Jacobs et al. (2007) have shown that 2.5 D and 3 D CME simulations give very similar results if the initial
total momentum of the CME is the same.
In other words, we are confident that our new method can be used to determine the total mass of a CME, although it uses 2.5 D axi-symmetric simulations.
Nevertheless, since the density measured by ACE is not perfectly reproduced for this particular CME ejecta (the density peak is 2.7 times too high),
the total mass determined is this study (
kg for the total mass,
and 1490 km s-1 for the average initial velocity.
As already mentioned, this velocity does not reflect the original velocity of the leading edge of the CME but is
the average velocity superimposed on the wind at the beginning of the simulation.
Either way, the velocity of the leading edge can be deduced from the height-time plot presented in Fig. 5.
Using a simple linear fit, a speed of 1524 km s-1 is found.
The same method was used by the LASCO team to find a plane-of-sky speed of
1188 km s-1.
Since the plane-of-sky speed is measured in a plane perpendicular to the Sun-Earth line,
the difference of 30% between the simulated and observed velocity could be caused by projection effects.
It is important to understand that, in 2.5 D axi-symmetric simulations, the CME is initially a torus
with a plasma density equally distributed in the longitudinal direction (around the Sun). As a result, comparing the mass of the CME determined
with our method and the real mass of the CME is not straightforward.
However, Jacobs et al. (2007) have shown that 2.5 D and 3 D CME simulations give very similar results if the initial
total momentum of the CME is the same.
In other words, we are confident that our new method can be used to determine the total mass of a CME, although it uses 2.5 D axi-symmetric simulations.
Nevertheless, since the density measured by ACE is not perfectly reproduced for this particular CME ejecta (the density peak is 2.7 times too high),
the total mass determined is this study (
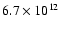 kg) might be overestimated.
kg) might be overestimated.
In this letter, we have demonstrated that reproducing the in situ data observed
by a spacecraft at 1 AU is possible to an acceptable level, even with a simple
2.5 D model. Of course, in order to one day be able to predict the data at L1,
accurate information about CMEs when they are still close to the Sun should be available.
The direction of propagation and the speed of the CMEs, the magnetic polarity, and
magnitude, the total mass of the CMEsshould be precisely known to
make accurate predictions. The STEREO mission, for instance, already allows us
to get rid of the projection effects.
Our goal in this Letter was not to predict the data at L1, but to try to reproduce them
in order to derive information about the initial state of the CME.
We have demonstrated the method and its capabilities by applying it to the halo CME
of 2000 April 4. We were able to reproduce
the data at L1 with unprecedented precision, and we concluded that the CME had
an initial maximal magnetic field of
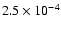 T, and a total mass of
T, and a total mass of
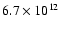 kg and that the linear speed of the CME up to 30
kg and that the linear speed of the CME up to 30 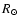 was 1524 km s-1.
was 1524 km s-1.
Acknowledgements
These results were obtained in the framework of the projects
GOA/2004/01 (K.U. Leuven), G.0304.07 (FWO-Vlaanderen), and
C 90205 (ESA Prodex 9).
Financial support by the European Commission through the SOLAIRE
Network (MTRN-CT-2006-035484) is gratefully acknowledged.
The numerical results were obtained on the HPC cluster VIC of the
K.U. Leuven.
We thank the ACE teams for making the data available.
We acknowledge use of the LASCO CME catalogue generated and maintained at
the CDAW Data Center by NASA and the Catholic University
of America in cooperation with the Naval Research Laboratory.
- Amari, T.,
Luciani, J. F., Mikic, Z., & Linker, J. 2000, ApJ, 529,
L49 [NASA ADS] [CrossRef]
- Antiochos,
S. K. 1998, ApJ, 502, L181 [NASA ADS] [CrossRef]
- Arge, C. N.,
& Pizzo, V. J. 2000, J. Geophys. Res., 105,
10465 [NASA ADS] [CrossRef]
(In the text)
- Chané, E.,
Jacobs, C., van der Holst, B., Poedts, S., & Kimpe, D. 2005,
A&A, 432, 331 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Chané, E.,
van der Holst, B., Jacobs, C., Poedts, S., & Kimpe, D. 2006,
A&A, 447, 727 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Chen, P. F.,
& Shibata, K. 2000, ApJ, 545, 524 [NASA ADS] [CrossRef]
- Dubey, G., van
der Holst, B., & Poedts, S. 2006, ApJ, 459, 927 [NASA ADS]
- Gallagher,
P. T., Mathioudakis, M., Keenan, F. P., Phillips,
K. J. H., & Tsinganos, K. 1999, ApJ, 524, L133 [NASA ADS] [CrossRef]
(In the text)
-
Gopalswamy, N., Lara, A., Yashiro, S., Kaiser, M. L., &
Howard, R. A. 2001, J. Geophys. Res., 106,
29207 [NASA ADS] [CrossRef]
(In the text)
- Groth,
C. P. T., De Zeeuw, D. L., Gombosi, T. I.,
& Powell, K. G. 2000, J. Geophys. Res., 105,
25053 [NASA ADS] [CrossRef]
(In the text)
- Huttunen,
K. E. J., Koskinen, H. E. J., Pulkkinen,
T. I., et al. 2002, J. Geophys. Res., 107,
1440 [CrossRef]
(In the text)
- Jacobs, C.,
Poedts, S., & van der Holst, B. 2006, A&A, 450, 793 [NASA ADS] [CrossRef] [EDP Sciences]
- Jacobs, C.,
Poedts, S., Van der Holst, B., & Chané, E. 2005, A&A,
430, 1099 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Jacobs, C., van
der Holst, B., & Poedts, S. 2007, A&A, 470, 359 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Jadav,
R. M., Iyer, K. N., Joshi, H. P., & Vats,
H. O. 2005, Planet. Space Sci., 53, 671 [NASA ADS] [CrossRef]
(In the text)
- Low, B. C. 1977,
ApJ, 212, 234 [NASA ADS] [CrossRef]
- Lugaz, N.,
Manchester, IV, W. B., Roussev, I. I., Tóth, G.,
& Gombosi, T. I. 2007, ApJ, 659, 788 [NASA ADS] [CrossRef]
- Mikic, Z., Barnes,
D. C., & Schnack, D. D. 1988, ApJ, 328, 830 [NASA ADS] [CrossRef]
- Odstrcil,
D., Pizzo, V. J., & Arge, C. N. 2005, J. Geophys.
Res., Space Phys., 110, 2106
-
Ruohoniemi, J. M., Barnes, R. J., Greenwald, R. A.,
& Shepherd, S. G. 2001, J. Geophys. Res., 106,
30085 [NASA ADS] [CrossRef]
- Tóth, G. 1996,
Astrophys. Lett. Commun., 34, 245
(In the text)
- Tóth, G., De
Zeeuw, D. L., Gombosi, T. I., et al. 2007, Space
Weather, 5, 6003 [CrossRef]
- van
Ballegooijen, A. A., & Martens, P. C. H. 1989,
ApJ, 343, 971 [NASA ADS] [CrossRef]
- van
der Holst, B., Jacobs, C., & Poedts, S. 2007, ApJ, 671,
L77 [NASA ADS] [CrossRef]
- Wang, Y.-M., &
Sheeley, Jr., N. R. 1990, ApJ, 355, 726 [NASA ADS] [CrossRef]
- Wang, Y.-M., &
Sheeley, Jr., N. R. 1991, ApJ, 372, L45 [NASA ADS] [CrossRef]
- Wu, C.-C., Fry,
C. D., Wu, S. T., Dryer, M., & Liou, K. 2007, J.
Geophys. Res., Space Phys., 112, 9104
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[angle=90,width=7.4cm,clip]{1022fig1.eps}
\end{figure}](/articles/aa/full/2008/47/aa11022-08/Timg6.gif)
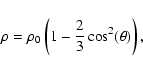
![\begin{figure}
\par\includegraphics[angle=90,width=8.4cm,clip]{1022fig2.eps}
\end{figure}](/articles/aa/full/2008/47/aa11022-08/Timg12.gif)
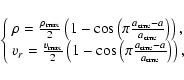
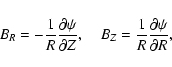
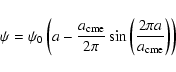
![\begin{figure}
\par\includegraphics[trim=0mm 0mm 0mm 0mm,clip,width=7.8cm,angle=90]{1022fig3.eps}
\end{figure}](/articles/aa/full/2008/47/aa11022-08/Timg19.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{1022fig4.eps}
\end{figure}](/articles/aa/full/2008/47/aa11022-08/Timg25.gif)
![\begin{figure}
\par {\hspace*{8mm}\includegraphics[width=7.7cm]{1022fig5.eps}\hs...
...vspace*{3mm}
\includegraphics[width=8.7cm,angle=90]{1022fig6.eps}
\end{figure}](/articles/aa/full/2008/47/aa11022-08/Timg26.gif)