A&A 492, 401-410 (2008)
DOI: 10.1051/0004-6361:200810447
New two-colour light curves of Q0957+561:
time delays and the origin of intrinsic variations
V. N. Shalyapin1 - L. J. Goicoechea2 - E. Koptelova3,4 - A. Ullán5 - R. Gil-Merino6
1 - Institute for Radiophysics and Electronics, National Academy of Sciences of Ukraine,
12 Proskura St., Kharkov 61085, Ukraine
2 -
Departamento de Física Moderna, Universidad de Cantabria,
Avda. de Los Castros s/n, 39005 Santander, Spain
3 -
Sternberg Astronomical Institute, Universitetski pr. 13, 119992 Moscow, Russia
4 -
Graduate Institute of Astronomy, Jhongli City, Taoyuan County 320, Taiwan
5 -
Robotic Telescopes Group, Centro de Astrobiología (CSIC-INTA), associated to the
NASA Astrobiology Institute, Ctra de Ajalvir, km 4, 28850 Torrejón de Ardoz, Madrid,
Spain
6 -
Instituto de Física de Cantabria (CSIC-UC), Avda. de Los Castros s/n, 39005
Santander, Spain
Received 23 June 2008 / Accepted 24 September 2008
Abstract
Aims. We extend the gr-band time coverage of the gravitationally lensed double quasar Q0957+561. New gr light curves permit us to detect significant intrinsic fluctuations, to determine new time delays, and thus to gain perspective on the mechanism of intrinsic variability in Q0957+561.
Methods. We use new optical frames of Q0957+561 in the g and r passbands from January 2005 to July 2007. These frames are part of an ongoing long-term monitoring with the Liverpool robotic telescope. We also introduce two photometric pipelines that are applied to the new gr frames of Q0957+561. The transformation pipeline incorporates zero-point, colour, and inhomogeneity corrections to the instrumental magnitudes, so final photometry to the 1-2% level is achieved for both quasar components. The two-colour final records are then used to measure time delays.
Results. The gr light curves of Q0957+561 show several prominent events and gradients, and some of them (in the g band) lead to a time delay between components
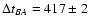 d (1
d (1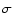 ). We do not find evidence of extrinsic variability in the light curves of Q0957+561. We also explore the possibility of a delay between a large event in the g band and the corresponding event in the r band. The gr cross-correlation reveals a time lag
). We do not find evidence of extrinsic variability in the light curves of Q0957+561. We also explore the possibility of a delay between a large event in the g band and the corresponding event in the r band. The gr cross-correlation reveals a time lag
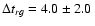 d (1
d (1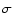 ;
the g-band event is leading) that confirms a previous claim of the existence of a delay between the g and r band in this lensed quasar.
;
the g-band event is leading) that confirms a previous claim of the existence of a delay between the g and r band in this lensed quasar.
Conclusions. The time delays (between quasar components and between optical bands) from the new records and previous ones in similar bands indicate that most observed variations in Q0957+561 (amplitudes of  100 mmag and timescales of
100 mmag and timescales of  100 d) are very probably due to reverberation within the gas disc around the supermassive black hole.
100 d) are very probably due to reverberation within the gas disc around the supermassive black hole.
Key words: techniques: photometric - gravitational lensing - black hole physics - quasars: individual: Q0957+561
Studies of optical continuum variability in gravitationally lensed quasars (GLQs) have a main
advantage: one is usually able to disentangle intrinsic from extrinsic signal in GLQs
(e.g., Paraficz et al. 2006; Kundic et al. 1997; Goicoechea et al. 2008, Paper I). Following the original idea by Refsdal (1964),
intrinsic variations in brightness records of GLQs have mainly been used to estimate global time
delays between components, and to discuss the structure of galaxy mass halos and the expansion
rate of the Universe (e.g., Kochanek et al. 2004, and references therein). Less effort has been devoted
to investigating the nature of intrinsic fluctuations, which are generated by mechanisms of
variability in lensed quasars. This can be done by measuring time delays between components
and between optical bands, using prominent events in segments of long-term light curves. Time
delays between two given components of a GLQ (determined from different pairs of twin features)
arise from gravitational lensing of flares in the variable source. While the flaring of a
well-defined emission region (e.g., a ring of the accretion disc) produces a set of similar
delays, the existence of flares in some widely separated zones can lead to important time
delay differences (Yonehara 1999). For either of the two components, time delays between optical
bands (or interband time delays) refer to time lags arising from physical phenomena within the
quasar.
The gravitationally lensed double quasar Q0957+561 at z = 1.41 (Walsh et al. 1979) has been
monitored photometrically in different optical bands with different telescopes. To derive a
global time delay between quasar components, some previous studies used large data sets
incorporating all kinds of fluctuations, i.e., noisy or poorly sampled features as well as
noticeable gradients and events on several timescales. These large data sets are based on frames
that were taken in the 1980s and 90s, and they lead to a global delay of about 423-425 d
(Ovaldsen et al. 2003a; Oscoz et al. 2001). The Apache Point Observatory (APO) experiment permitted investigators to
follow-up the variability in the g and r bands during the 1995 and 1996 seasons, i.e.,
covering 1.5 years (Kundic et al. 1997). This monitoring programme with the APO 3.5 m telescope produced
accurate light curves of both components Q0957+561A and Q0957+561B, which show
sharp intrinsic features with high signal-to-noise ratio (
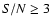 ). From the APO main twin
events in the g band (a prominent event in A and the replica event in B;
). From the APO main twin
events in the g band (a prominent event in A and the replica event in B;
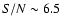 ),
Kundic et al. (1997) also reported a gravitational lens time delay of 417
+3-4 d (95%
confidence interval). Complementary to this result, Collier (2001) found that the r-band main
twin events lag with respect to the ones in the g-band by 3.4
+1.5-1.4 d (68%
confidence interval), and this interband delay was interpreted as clear evidence for reprocessing
in the accretion disc of the quasar.
),
Kundic et al. (1997) also reported a gravitational lens time delay of 417
+3-4 d (95%
confidence interval). Complementary to this result, Collier (2001) found that the r-band main
twin events lag with respect to the ones in the g-band by 3.4
+1.5-1.4 d (68%
confidence interval), and this interband delay was interpreted as clear evidence for reprocessing
in the accretion disc of the quasar.
Goicoechea (2002) reanalysed the APO g-band data set to obtain two different gravitational lens
time delays of
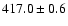 d (68% confidence interval) and
d (68% confidence interval) and
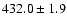 d (68%
confidence interval) depending on the features taken as reference. The longest delay corresponds
to the APO secondary twin events (
d (68%
confidence interval) depending on the features taken as reference. The longest delay corresponds
to the APO secondary twin events (
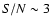 )
and it clearly disagrees with the 417-day value.
The APO main and secondary twin events in the g band are associated with a main flare and
a secondary flare in the variable source, respectively. From the time delay difference of
)
and it clearly disagrees with the 417-day value.
The APO main and secondary twin events in the g band are associated with a main flare and
a secondary flare in the variable source, respectively. From the time delay difference of 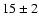 days (68% confidence interval) and using standard cosmological parameters (
days (68% confidence interval) and using standard cosmological parameters (
 ,
,
 ), one can also determine a minimum size for the variable source (minimum
distance between both flares) of 300 pc (Yonehara et al. 2003; Goicoechea 2002; Yonehara 1999). Several physical sources are
consistent with this spatial constraint (from multiple gravitational lens delays) and the
interband delay for the main twin events, but either a nuclear accretion disc plus a
circumnuclear stellar region or a nuclear accretion disc plus an optical jet are the most
probable ones (e.g., Hutchings 2003). We note that the 424-d global time delay between
components (Ovaldsen et al. 2003a; Oscoz et al. 2001) coincides with the average of both APO gravitational lens time
delays. This suggests the presence of two or more gravitational lens delays in the current large
data sets (for alternative explanations, see Hirv et al. 2007; Schild 2005).
), one can also determine a minimum size for the variable source (minimum
distance between both flares) of 300 pc (Yonehara et al. 2003; Goicoechea 2002; Yonehara 1999). Several physical sources are
consistent with this spatial constraint (from multiple gravitational lens delays) and the
interband delay for the main twin events, but either a nuclear accretion disc plus a
circumnuclear stellar region or a nuclear accretion disc plus an optical jet are the most
probable ones (e.g., Hutchings 2003). We note that the 424-d global time delay between
components (Ovaldsen et al. 2003a; Oscoz et al. 2001) coincides with the average of both APO gravitational lens time
delays. This suggests the presence of two or more gravitational lens delays in the current large
data sets (for alternative explanations, see Hirv et al. 2007; Schild 2005).
In the present study, we substantially extend the gr-band time coverage of
Q0957+561. The key idea is to use new gr light curves to detect prominent intrinsic
events similar to the APO ones. These new features should allow us to determine new time delays
and to improve our understanding of the mechanism causing the intrinsic variability. The paper
is organised as follows: in Sect. 2, we present new data of Q0957+561 based on recent
observations with the Liverpool 2 m telescope (LT) in the g and r bands, spanning 2.5 years.
We describe the observations, the pre-processing, and the photometric procedure for determining
calibrated and corrected magnitudes of field stars and quasar components. This last reduction
procedure consists of two new pipelines specially designed for the LT. In Sect. 3 we study the
time delays between the two components of Q0957+561 as well as the possible delays
between the g and r band in the new data set. In Sect. 4 we summarize our results.
From the APO and LT delays of Q0957+561, we also discuss the origin of the observed
variations with an amplitude of  100 mmag and lasting
100 mmag and lasting  100 d.
100 d.
Liverpool Quasar Lens Monitoring (LQLM) I is the first phase of an optical follow-up of lensed
quasars, undertaken using the RATCam optical CCD camera on the Liverpool robotic telescope
(Steele et al. 2004) between January 2005 and July 2007. The first scientific output of LQLM I was
reported in Paper I, and we concentrate here on the observations of Q0957+561 in the
g and r filters. The field of view and the pixel scale (binning 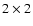 )
were
)
were 
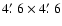 and
and
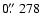 ,
respectively. The exposure times were 100-200 s (g band) and 120 s (r band). We obtained 286 frames in the g band and 264 frames in the r
band. The LT observed for a total science time of
,
respectively. The exposure times were 100-200 s (g band) and 120 s (r band). We obtained 286 frames in the g band and 264 frames in the r
band. The LT observed for a total science time of  22.6 h during the 2.5-year programme of
Q0957+561.
22.6 h during the 2.5-year programme of
Q0957+561.
A pre-processing pipeline is applied to all RATCam frames![[*]](/icons/foot_motif.gif) . This performs three basic
instrumental reductions: bias subtraction, trimming of the overscan regions, and flat fielding.
We also apply a bad-pixel mask (made available by the Angstrom project; Kerins et al. 2006), and
correct bad pixels on the CCD. The next step is the pre-selection of frames, based on individual
inspection, to assure that exposures verify some elemental conditions (e.g., that the telescope
pointing was accurate enough so that the lens system was included in the field of view, that
there is no strongly degraded signal, etc.), and that seeing (FWHM) and sky level (background) values do not exceed reasonable bounds. We only consider frames with
. This performs three basic
instrumental reductions: bias subtraction, trimming of the overscan regions, and flat fielding.
We also apply a bad-pixel mask (made available by the Angstrom project; Kerins et al. 2006), and
correct bad pixels on the CCD. The next step is the pre-selection of frames, based on individual
inspection, to assure that exposures verify some elemental conditions (e.g., that the telescope
pointing was accurate enough so that the lens system was included in the field of view, that
there is no strongly degraded signal, etc.), and that seeing (FWHM) and sky level (background) values do not exceed reasonable bounds. We only consider frames with
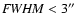 due to
the separation between the two quasar components (A and B) of
due to
the separation between the two quasar components (A and B) of 
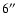 .
The pre-selected
database contains 199 frames in the g band and 210 frames in the r band. This means that
.
The pre-selected
database contains 199 frames in the g band and 210 frames in the r band. This means that
 75% of the original LT frames were initially useful.
75% of the original LT frames were initially useful.
In a first step, we take a reference frame, i.e., a high-quality frame with small FWHM and large
signal-to-noise ratio (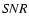 ). We then measure the positions (with respect to the left bottom corner
of the reference frame) of seven reference stars and both quasar images. We select the 7 brightest
stars in the Sloan Digital Sky Survey (SDSS) catalog
). We then measure the positions (with respect to the left bottom corner
of the reference frame) of seven reference stars and both quasar images. We select the 7 brightest
stars in the Sloan Digital Sky Survey (SDSS) catalog![[*]](/icons/foot_motif.gif) (e.g., Adelman-McCarthy et al. 2007). These stars, having g(SDSS) and r(SDSS)
magnitudes below 18 and 17, respectively, were labeled as X, G, F, H, D, E, and R stars in Fig. 1 and Table 1 of Ovaldsen et al. (2003a). Several Image Reduction and Analysis Facility (IRAF)
(e.g., Adelman-McCarthy et al. 2007). These stars, having g(SDSS) and r(SDSS)
magnitudes below 18 and 17, respectively, were labeled as X, G, F, H, D, E, and R stars in Fig. 1 and Table 1 of Ovaldsen et al. (2003a). Several Image Reduction and Analysis Facility (IRAF)![[*]](/icons/foot_motif.gif) tasks are also used to identify the available reference objects (in general, less than 7 stars) and the quasar components in the rest of the frames.
tasks are also used to identify the available reference objects (in general, less than 7 stars) and the quasar components in the rest of the frames.
In a second step, our photometric pipeline performs aperture photometry of bright field stars and
quasar images. This IRAF procedure is used to estimate initial instrumental fluxes (sources and their associated backgrounds) and to improve the initial source positions on each frame. The pipeline also cuts the original frames in order to produce square subframes with 64 pixels per side: the system subframe (around the centre of the lens system) and subframes of stars (around the bright stars), and makes a PSF subframe containing the clean 2D profile of the H star (removing the local background). This last empirical PSF is required when performing PSF fitting. The point-like sources (quasar components and stars) are modelled by means of the empirical PSF, whereas the extended source (lensing elliptical galaxy) is modelled by a de Vaucouleurs profile convolved with the empirical PSF. After obtaining all subframes for a given frame, PSF photometry on the stellar and system (crowed field) subframes is performed with IMFITFITS software (McLeod et al. 1998). The pipeline is written in the Python programming language![[*]](/icons/foot_motif.gif) , and incorporates the capabilities of IRAF (through the PyRAF interface) and IMFITFITS, as well as additional numerical and graphical tools.
, and incorporates the capabilities of IRAF (through the PyRAF interface) and IMFITFITS, as well as additional numerical and graphical tools.
To determine accurate quasar fluxes, one needs to use a set of constraints. For Q0957+561,
the most relevant constraints were obtained from Hubble Space Telescope (HST) frames
(Kochanek et al. 2008; Bernstein et al. 1997; Keeton et al. 1998): positions of the B component and the lensing galaxy relative to the A
component, and the optical structure of the galaxy, i.e., effective radius, ellipticity, and position angle (a de Vaucouleurs profile was fitted to HST images). Due to the relatively low brightness of the lensing galaxy in the frames and the proximity of the B component to the galaxy, we determine the galaxy-to-H star ratio (GAL/H) in the gr bands from the best LT frames, in terms of FWHM and 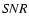 values. The H star is relatively bright and it is present in all frames. We then apply the pipeline to all frames (whatever their qualities) in each optical filter, by setting the galaxy fluxes to those derived from the GAL/H ratio and H star fluxes, and allowing the remaining free parameters to vary.
values. The H star is relatively bright and it is present in all frames. We then apply the pipeline to all frames (whatever their qualities) in each optical filter, by setting the galaxy fluxes to those derived from the GAL/H ratio and H star fluxes, and allowing the remaining free parameters to vary.
![\begin{figure}
\par\includegraphics[angle=0,width=7cm]{10447_f1.eps}\end{figure}](/articles/aa/full/2008/47/aa10447-08/Timg23.gif) |
Figure 1:
Observations of Q0957+561 with the Liverpool robotic telescope in the g band. We display
system subframes ( left panels), model subframes ( middle panels), and residual subframes ( right panels) for five frames taken during the 2.5-year monitoring period (see main text). |
| Open with DEXTER |
The photometry pipeline output includes the system subframes, their model subframes (best fits) and
the associated residual subframes (system subframes after subtracting model subframes). In
Fig. 1 we show system subframes (left panels), model subframes (middle panels), and residual subframes (right panels) corresponding to five frames in the g band. From top to bottom:
March 16, 2005 (
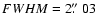 ,
,
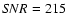 ,
,
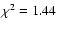 ), November 9, 2005 (
), November 9, 2005 (
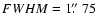 ,
,
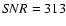 ,
,
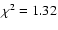 ), April 26, 2006 (
), April 26, 2006 (
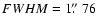 ,
,
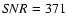 ,
,
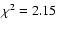 ), October 21, 2006 (
), October 21, 2006 (
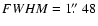 ,
,
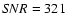 ,
,
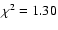 ), and May 28, 2007 (
), and May 28, 2007 (
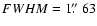 ,
,
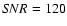 ,
,
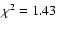 ), where the
), where the 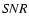 values are inferred from the A images (having fluxes similar to those of B images) and the
values are inferred from the A images (having fluxes similar to those of B images) and the 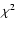 values quantitatively describe the quality of the fits (i.e., these represent the standard reduced
values quantitatively describe the quality of the fits (i.e., these represent the standard reduced 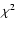 for the best fits). All subframes in Fig. 1 have been expanded by a factor of 2. The visual comparison between left and middle panels as well as the inspection of patterns of residual brightness (right panels) indicate that the photometric method works well. The pipeline also produces a basic data release file containing values of all relevant instrumental fluxes (stars and quasar images) and relative instrumental magnitudes of both quasar components, e.g.,
gA* - gE* and
gB* - gE* in the g band. To check the reliability of our PSF fitting procedure, we applied a deconvolution technique (Koptelova et al. 2005) to two sets of frames in October-December 2005 (gr bands). The relative instrumental magnitudes from the deconvolution method agreed with the records from the PSF fitting technique (see Fig. 3 of Goicoechea et al. 2007).
for the best fits). All subframes in Fig. 1 have been expanded by a factor of 2. The visual comparison between left and middle panels as well as the inspection of patterns of residual brightness (right panels) indicate that the photometric method works well. The pipeline also produces a basic data release file containing values of all relevant instrumental fluxes (stars and quasar images) and relative instrumental magnitudes of both quasar components, e.g.,
gA* - gE* and
gB* - gE* in the g band. To check the reliability of our PSF fitting procedure, we applied a deconvolution technique (Koptelova et al. 2005) to two sets of frames in October-December 2005 (gr bands). The relative instrumental magnitudes from the deconvolution method agreed with the records from the PSF fitting technique (see Fig. 3 of Goicoechea et al. 2007).
We use a transformation pipeline (in the Python programming language) to obtain SDSS magnitudes from instrumental magnitudes that are corrected for systematic effects. The whole calibration-correction
process is outlined in Appendix A. Only frames with
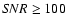 over Q0957+561A are taken into account (see however Sect. 3). In the g band, this selection leads to 170 frames. In the r band, besides the
over Q0957+561A are taken into account (see however Sect. 3). In the g band, this selection leads to 170 frames. In the r band, besides the 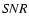 based selection, the surviving frames from the first season (January-June 2005) are also removed. Several of these
based selection, the surviving frames from the first season (January-June 2005) are also removed. Several of these  10 r-band frames with
10 r-band frames with 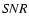 above 100 (first season) are characterized by an anomalous image formation. Thus, the high-quality data set in the r band includes 167 frames.
above 100 (first season) are characterized by an anomalous image formation. Thus, the high-quality data set in the r band includes 167 frames.
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm]{10447_f2.eps}\end{figure}](/articles/aa/full/2008/47/aa10447-08/Timg41.gif) |
Figure 2:
Colour coefficient in the g band. The values are distributed around the central discontinuous
line (average coefficient), and most of them are placed between the top and bottom discontinuous lines
(filled circles). Only seven extreme values (triangles and open circles) exceed these limits. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm]{10447_f3.eps}\end{figure}](/articles/aa/full/2008/47/aa10447-08/Timg42.gif) |
Figure 3:
Inhomogeneity map in the g band. The zero inhomogeneity level is described by means of a
continuous line that crosses the centre of the
 camera. Pixels inside this zero level contour have a positive inhomogeneity of a few mmag, whereas the rest of the pixels have a negative inhomogeneity that varies between a few mmag and tens of mmag. We explicitly show contours of -10, -20, -30, -40, -50, -60, and -70 mmag.
camera. Pixels inside this zero level contour have a positive inhomogeneity of a few mmag, whereas the rest of the pixels have a negative inhomogeneity that varies between a few mmag and tens of mmag. We explicitly show contours of -10, -20, -30, -40, -50, -60, and -70 mmag. |
| Open with DEXTER |
The transformation pipeline fits the deviations between instrumental and standard g magnitudes of the 7 reference stars to the transformation model that incorporates a zero-point term (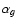 ), a colour coefficient (
), a colour coefficient (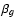 ), and inhomogeneity coefficients (
), and inhomogeneity coefficients (
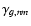 ). Equation (A.11) shows the relationship between the observed magnitude deviation and the model to describe it. The zero-point term and the colour coefficient are allowed to vary over time because the atmospheric and instrumental conditions significantly evolve during the 2.5 years of monitoring. The last ingredient of the model is a linear-quadratic inhomogeneity term, which is related to the 2D position on the CCD and tries to correct the possible inhomogeneous response over the camera area (e.g., Magnier & Cuillandre 2004; Manfroid et al. 2001). Each source occupies different positions on the CCD area during the robotic monitoring period, so this could complicate the collecting of accurate brightness records.
With respect to the least squares fit, in Fig. 2 we plot the solution of
). Equation (A.11) shows the relationship between the observed magnitude deviation and the model to describe it. The zero-point term and the colour coefficient are allowed to vary over time because the atmospheric and instrumental conditions significantly evolve during the 2.5 years of monitoring. The last ingredient of the model is a linear-quadratic inhomogeneity term, which is related to the 2D position on the CCD and tries to correct the possible inhomogeneous response over the camera area (e.g., Magnier & Cuillandre 2004; Manfroid et al. 2001). Each source occupies different positions on the CCD area during the robotic monitoring period, so this could complicate the collecting of accurate brightness records.
With respect to the least squares fit, in Fig. 2 we plot the solution of 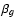 .
The
.
The
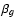 values are distributed around an average colour coefficient
values are distributed around an average colour coefficient
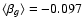 (central discontinuous line in Fig. 2), which is close to the typical coefficient (see comments in Appendix A). The scatter is
(central discontinuous line in Fig. 2), which is close to the typical coefficient (see comments in Appendix A). The scatter is
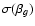 = 0.033, and the
= 0.033, and the
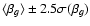 limits also appear in Fig. 2 (top and bottom discontinuous lines). In relation to the average coefficient, there are seven extreme values representing changes from 100%, i.e., values around either -0.2 or 0.0 (triangles and open circles in Fig. 2). The first two triangles and the first open circle correspond to the first night after a realuminisation of the mirror and other maintenance works, and very probably, the telescope was not performing optimally that night. The rest of the extreme values (around day 3770) are associated with dates close to periods of very bad weather. The highest values of
limits also appear in Fig. 2 (top and bottom discontinuous lines). In relation to the average coefficient, there are seven extreme values representing changes from 100%, i.e., values around either -0.2 or 0.0 (triangles and open circles in Fig. 2). The first two triangles and the first open circle correspond to the first night after a realuminisation of the mirror and other maintenance works, and very probably, the telescope was not performing optimally that night. The rest of the extreme values (around day 3770) are associated with dates close to periods of very bad weather. The highest values of 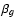 are a consequence of atmospheric-instrumental perturbations during the hard winter in January-February 2006. From the best solutions of
are a consequence of atmospheric-instrumental perturbations during the hard winter in January-February 2006. From the best solutions of
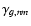 ,
the pipeline also produces the 2D inhomogeneity pattern, i.e.,
,
the pipeline also produces the 2D inhomogeneity pattern, i.e.,
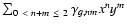 .
This is depicted in Fig. 3. In the transformation procedure, we set the origin of coordinates at the centre of the
.
This is depicted in Fig. 3. In the transformation procedure, we set the origin of coordinates at the centre of the
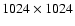 CCD, so it has an inhomogeneity correction equal to zero. In Fig. 3, we see an inhomogeneity amplitude of
CCD, so it has an inhomogeneity correction equal to zero. In Fig. 3, we see an inhomogeneity amplitude of  80 mmag, which is consistent with results from other optical telescopes (e.g., Magnier & Cuillandre 2004; Manfroid et al. 2001). It is evident that the inhomogeneity pattern in Fig. 3 plays a role in achieving 1-2% photometric accuracy.
80 mmag, which is consistent with results from other optical telescopes (e.g., Magnier & Cuillandre 2004; Manfroid et al. 2001). It is evident that the inhomogeneity pattern in Fig. 3 plays a role in achieving 1-2% photometric accuracy.
![\begin{figure}
\par\includegraphics[angle=0,width=7cm]{10447_f4.eps}\end{figure}](/articles/aa/full/2008/47/aa10447-08/Timg50.gif) |
Figure 4:
Final magnitudes of Q0957+561A ( top panel) and Q0957+561B ( bottom panel) in the g band of the SDSS photometric system. These g-SDSS light curves include noticeable fluctuations covering a 2.5-year monitoring period from January 2005 to June 2007. |
| Open with DEXTER |
After the g-band fit, the pipeline computes the calibrated and corrected records of the reference
stars and both quasar images from Eq. (A.13). The 14-15th magnitude stars have a typical scatter of 5 mmag, the 15-16th magnitude stars are characterized by a slightly larger scatter of about 7 mmag, and the faintest  18th magnitude star (R star) has a scatter of about 17 mmag. Although we have several nights with two or three exposures at different times, the standard intranight deviations of the stellar curves do not trace their scatters (see however Paper I). This is not surprising because the intranight variations exclusively correspond to several nights in the second season, which covers a small fraction of the total monitoring period. Thus, after some preliminary test using the stellar records, we find a non-biased estimator of uncertainties (typical errors): stellar scatters are well traced by the standard deviations between adjacent magnitudes that are separated by
18th magnitude star (R star) has a scatter of about 17 mmag. Although we have several nights with two or three exposures at different times, the standard intranight deviations of the stellar curves do not trace their scatters (see however Paper I). This is not surprising because the intranight variations exclusively correspond to several nights in the second season, which covers a small fraction of the total monitoring period. Thus, after some preliminary test using the stellar records, we find a non-biased estimator of uncertainties (typical errors): stellar scatters are well traced by the standard deviations between adjacent magnitudes that are separated by 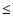 3 d. As this error estimator gives reasonable results, we apply it to the g-SDSS magnitudes of Q0957+561.
3 d. As this error estimator gives reasonable results, we apply it to the g-SDSS magnitudes of Q0957+561.
A final refinement (selection) is taken into account. Our last selection criterion is colour based:
frames with extreme colour coefficients (see the triangles and open circles in Fig. 2) are also removed from the data set. This leads to 163 surviving frames. We obtain uncertainties (see above) of about 16 mmag in both  17th magnitude quasar components, i.e., photometry to the 1-2% is achieved for the lensed quasar. These typical errors are in complete agreement with the stellar scatters, since they are clearly larger than 5-7 mmag (results for the brightest reference stars) and similar to the result for the faintest reference star R. For each component, we also group pairs or trios of magnitudes measured on the same night. The final light curves of Q0957+561A (top panel) and Q0957+561B (bottom panel) are shown in Fig. 4. These g-SDSS light curves include important gradients and prominent events, which resemble those reported by Kundic et al. (1997) using APO observations in the g band. The whole monitoring period consists of three observational seasons: January-June 2005 (first season), October 2005-June 2006 (second season), and October 2006-June 2007 (third season). Besides the three observational seasons, there are two important gaps in the LT monitoring as a consequence of the annual occultation of the lens system.
17th magnitude quasar components, i.e., photometry to the 1-2% is achieved for the lensed quasar. These typical errors are in complete agreement with the stellar scatters, since they are clearly larger than 5-7 mmag (results for the brightest reference stars) and similar to the result for the faintest reference star R. For each component, we also group pairs or trios of magnitudes measured on the same night. The final light curves of Q0957+561A (top panel) and Q0957+561B (bottom panel) are shown in Fig. 4. These g-SDSS light curves include important gradients and prominent events, which resemble those reported by Kundic et al. (1997) using APO observations in the g band. The whole monitoring period consists of three observational seasons: January-June 2005 (first season), October 2005-June 2006 (second season), and October 2006-June 2007 (third season). Besides the three observational seasons, there are two important gaps in the LT monitoring as a consequence of the annual occultation of the lens system.
![\begin{figure}
\par\includegraphics[angle=0,width=7cm]{10447_f5.eps}\end{figure}](/articles/aa/full/2008/47/aa10447-08/Timg52.gif) |
Figure 5:
Final magnitudes of Q0957+561A ( top panel) and Q0957+561B ( bottom panel) in the r band of the SDSS photometric system. The r-SDSS records from October 2005 to June 2007 (two whole seasons) incorporate different prominent features that are also seen in the g-SDSS curves (see
Fig. 4), with the g-SDSS features having a larger amplitude. |
| Open with DEXTER |
The whole procedure in the g band is repeated in the r band. All frames with extreme colour
coefficients are not considered in building the final light curves, so we use a data set incorporating 142 frames. With respect to the quasar brightness records, we achieve  1% photometry (errors of about 12 mmag). The final (grouped) magnitudes are presented in Fig. 5, where the top and bottom panels display the records of Q0957+561A and Q0957+561B, respectively. These r-SDSS light curves
1% photometry (errors of about 12 mmag). The final (grouped) magnitudes are presented in Fig. 5, where the top and bottom panels display the records of Q0957+561A and Q0957+561B, respectively. These r-SDSS light curves![[*]](/icons/foot_motif.gif) trace prominent fluctuations that are weaker than the corresponding fluctuations in g-SDSS (see Fig. 4 and Sect. 3.2). A similar result was claimed by the APO team (Kundic et al. 1995,1997), and some evidence for chromatic variability was also suggested by Ullán et al. (2003) (see also the BVRI variations in Serra-Ricart et al. 1999). The LT records in the red region of the optical spectrum are less noisy than previous curves at red wavelengths (e.g., Kundic et al. 1997; Serra-Ricart et al. 1999), which is due to a combination of an absence of relatively short variations and strict selection procedures.
trace prominent fluctuations that are weaker than the corresponding fluctuations in g-SDSS (see Fig. 4 and Sect. 3.2). A similar result was claimed by the APO team (Kundic et al. 1995,1997), and some evidence for chromatic variability was also suggested by Ullán et al. (2003) (see also the BVRI variations in Serra-Ricart et al. 1999). The LT records in the red region of the optical spectrum are less noisy than previous curves at red wavelengths (e.g., Kundic et al. 1997; Serra-Ricart et al. 1999), which is due to a combination of an absence of relatively short variations and strict selection procedures.
The g-band light curve of A in the second season (October 2005-June 2006) shows significant
fluctuations that are repeated in the g-band light curve of B during the third season (October
2006-June 2007). Taking into account the expected delay range of 415-435 d
(Ovaldsen et al. 2003a; Goicoechea 2002; Kundic et al. 1997; Oscoz et al. 2001), this result is fully consistent with the presence of intrinsic
fluctuations in those records. We use the g-SDSS magnitudes of A and B in the second and third
seasons, respectively, to accurately measure the time delay(s) between both components of
Q0957+561.
About one half of the frames with 80 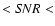 100 correspond to the second season, and thus, they
could help to trace the variability of A and to minimize uncertainties in time delay estimates. Their
photometric outputs (magnitudes of A) are consistent with results from
100 correspond to the second season, and thus, they
could help to trace the variability of A and to minimize uncertainties in time delay estimates. Their
photometric outputs (magnitudes of A) are consistent with results from
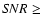 100 frames at
adjacent epochs, so we recover them and expand the g-band record of A in the second season.
In Fig. 6, the A light curve, shifted by 420 d (filled circles), and the unchanged B light
curve (open circles) are plotted. A reference value of 420 d is used to shift in time one component
and to compare it with the other (see above and Introduction). The A record shows two different
features separated by a gap of about 50 d (caused by atmospheric-instrumental problems in
January-February 2006; see Sect. 2.3). The first feature in the A curve consists of an event AE1g and the beginning of another consecutive event AE2g, whereas the second feature is a noisy trend associated with the decline in flux of AE2g. These two consecutive events have an amplitude of about 100 mmag and a duration of 50-150 d, and similar fluctuations BE1g and BE2g are evident in the B record.
100 frames at
adjacent epochs, so we recover them and expand the g-band record of A in the second season.
In Fig. 6, the A light curve, shifted by 420 d (filled circles), and the unchanged B light
curve (open circles) are plotted. A reference value of 420 d is used to shift in time one component
and to compare it with the other (see above and Introduction). The A record shows two different
features separated by a gap of about 50 d (caused by atmospheric-instrumental problems in
January-February 2006; see Sect. 2.3). The first feature in the A curve consists of an event AE1g and the beginning of another consecutive event AE2g, whereas the second feature is a noisy trend associated with the decline in flux of AE2g. These two consecutive events have an amplitude of about 100 mmag and a duration of 50-150 d, and similar fluctuations BE1g and BE2g are evident in the B record.
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm]{10447_f6.eps}\end{figure}](/articles/aa/full/2008/47/aa10447-08/Timg55.gif) |
Figure 6:
Comparison between the g-band light curve of A in the second season (shifted by 420 d; see main text) and the g-band light curve of B in the third season. The A record (filled circles) shows two different features separated by a gap of about 50 d: while the first feature contains an event AE1g and the beginning of another consecutive event AE2g, the second feature describes the (noisy) decline in flux of AE2g. A vertical line is drawn to distinguish between the two events AE1g and AE2g. Replica events BE1g and BE2g are clearly seen in the B record (open circles). |
| Open with DEXTER |
Firstly, we analyse the twin events AE1g-BE1g and AE2g-BE2g. The S/N values for them (the
ratios between their semi-amplitudes and their mean photometric errors) are
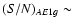 4 and
4 and
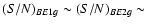 3.4. In spite of the fact that AE2g is a prominent event, it is poorly traced as a consequence of the 50-day gap and the noisy right wing. Thus, we are not able to determine a reliable value of
(S/N)AE2g, and the effective signal-to-noise ratio for AE2g could be significantly less than 3-4. The difficulties in inferring a time delay from the AE2g-BE2g twin events confirm our suspicions. Unfortunately, it is not possible to measure two independent delays, one from AE1g-BE1g and the other from AE2g-BE2g. The only options are the estimation of a delay related to the two flares in the source of intrinsic variability, i.e., using all events in Fig. 6, or a delay corresponding to the first flare, i.e., from AE1g-BE1g.
3.4. In spite of the fact that AE2g is a prominent event, it is poorly traced as a consequence of the 50-day gap and the noisy right wing. Thus, we are not able to determine a reliable value of
(S/N)AE2g, and the effective signal-to-noise ratio for AE2g could be significantly less than 3-4. The difficulties in inferring a time delay from the AE2g-BE2g twin events confirm our suspicions. Unfortunately, it is not possible to measure two independent delays, one from AE1g-BE1g and the other from AE2g-BE2g. The only options are the estimation of a delay related to the two flares in the source of intrinsic variability, i.e., using all events in Fig. 6, or a delay corresponding to the first flare, i.e., from AE1g-BE1g.
Secondly, to calculate the two-flare time delay and magnitude offset (i.e., a constant magnitude
shift between the light curves of the two quasar components), we use two techniques: 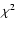 minimization (e.g., Kundic et al. 1997; Ullán et al. 2006) and the minimum dispersion (D2) method (Pelt et al. 1994,1996),
characterized by a bin semisize (
minimization (e.g., Kundic et al. 1997; Ullán et al. 2006) and the minimum dispersion (D2) method (Pelt et al. 1994,1996),
characterized by a bin semisize (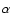 )
and a decorrelation length (
)
and a decorrelation length (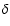 ). The
choice of
). The
choice of
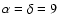 d is a good compromise between the A-B connection and time resolution. Through the
d is a good compromise between the A-B connection and time resolution. Through the 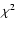 minimization (
minimization (
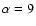 d), we obtain the best solutions of the delay and magnitudeoffset:
d), we obtain the best solutions of the delay and magnitudeoffset:
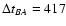 d and
d and
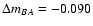 mag (
mag (
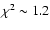 ).The sign ``-'' in the
).The sign ``-'' in the
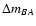 value means that the A component is fainter. The D2 minimization (
value means that the A component is fainter. The D2 minimization (
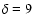 d) gives the best solutions of
d) gives the best solutions of
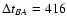 d and
d and
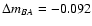 mag. The uncertainties in the magnitude offset and time delay are inferred from 1000 repetitions of the experiment (synthetic light curves based on the observed records). The 1
mag. The uncertainties in the magnitude offset and time delay are inferred from 1000 repetitions of the experiment (synthetic light curves based on the observed records). The 1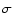 intervals appear in Table 1. Table 1 indicates that the error in time delay from the
intervals appear in Table 1. Table 1 indicates that the error in time delay from the 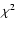 minimization is substantially less than the error from the minimum dispersion method. Both measurements of the two-flare time delay are consistent with the APO main delay in the g band (see Introduction).
minimization is substantially less than the error from the minimum dispersion method. Both measurements of the two-flare time delay are consistent with the APO main delay in the g band (see Introduction).
Table 1:
Magnitude offset and time delay measurements in the g band.
![\begin{figure}
\par\includegraphics[angle=0,width=9cm]{10447_f7.eps}\end{figure}](/articles/aa/full/2008/47/aa10447-08/Timg70.gif) |
Figure 7:
Overlapping periods and difference light curves in the g band. We show the overlap between the A (filled circles) and B (open circles) whole records, when the A magnitudes are shifted by the best solutions of the time delay and the magnitude offset ( left panels). We also draw the difference light curve ( right panels). The three overlap periods cover  20 d ( top panels), 20 d ( top panels),  90 d ( middle panels), and 90 d ( middle panels), and  60 d ( bottom panels). 60 d ( bottom panels). |
| Open with DEXTER |
Thirdly, we exclusively use the AE1g-BE1g twin events. The idea is to accurately measure the
gravitational lens delay associated with only one flare produced in the source of variability. This
time we focus on the 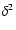 method (see, e.g., Paper I) and the
method (see, e.g., Paper I) and the 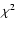 minimization, which
produces a delay error smaller than the delay uncertainty from the minimum dispersion technique (see Table 1). The
minimization, which
produces a delay error smaller than the delay uncertainty from the minimum dispersion technique (see Table 1). The 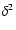 technique obtains the optimal match between the time-shifted
discrete autocorrelation function (DAF) and the discrete cross-correlation function
(DCF; Edelson & Krolik 1988). From the
technique obtains the optimal match between the time-shifted
discrete autocorrelation function (DAF) and the discrete cross-correlation function
(DCF; Edelson & Krolik 1988). From the 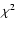 minimization (
minimization (
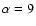 d), the best solutions of the time delay and magnitude offset are 417 d and -0.083 mag, respectively (
d), the best solutions of the time delay and magnitude offset are 417 d and -0.083 mag, respectively (
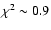 ). From the
). From the 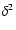 method and 1000 synthetic light curves, the delay measurement (1
method and 1000 synthetic light curves, the delay measurement (1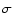 interval) is identical to that derived from the
interval) is identical to that derived from the 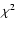 technique (see Table 1). Therefore, the LT first twin events are useful to determine a robust time delay
technique (see Table 1). Therefore, the LT first twin events are useful to determine a robust time delay
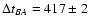 d (1
d (1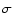 ). This is fully consistent with the APO main delay (Goicoechea 2002; Kundic et al. 1997). The
). This is fully consistent with the APO main delay (Goicoechea 2002; Kundic et al. 1997). The 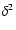 analysis also indicates that
analysis also indicates that
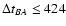 d (99% confidence interval), so the AE1g-BE1g delay is inconsistent (at about the 3
d (99% confidence interval), so the AE1g-BE1g delay is inconsistent (at about the 3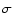 level) with the APO secondary delay (Goicoechea 2002). The r-band curves of AE1-BE1 are not used to determine a time delay because S/N < 3 for these twin events (e.g., Pijpers 1997).
level) with the APO secondary delay (Goicoechea 2002). The r-band curves of AE1-BE1 are not used to determine a time delay because S/N < 3 for these twin events (e.g., Pijpers 1997).
We now check for the possible existence of extrinsic variability in our records. We compute the
difference light curve between the A and B components, since no extrinsic variability should result in a flat difference light curve. To obtain the difference light curve, the magnitude- and time-shifted light curve of image A is subtracted from the light curve of image B (e.g., Gil-Merino et al. 2001; Schmidt & Wambsganss 1998). In Fig. 7 (left panels), we show the overlap between the A (filled circles) and B (open circles) whole records, when the A magnitudes are shifted by the best solutions of the time delay and the magnitude offset. The difference light curve is also plotted in the right panels of Fig. 7. The overlap between A-first season and B-second season covers a very short period of about 20 d (see the top panels of Fig. 7). For this overlap period, the difference curve contains two consecutive deviations from the zero level, which are not significative (e.g., Gil-Merino et al. 2001). The overlap between A-second season and B-third season is much more important than the first overlap (in the top panels). In the middle panels of Fig. 7, we display the situation before the 50-day gap (see above and Fig. 6), where the difference curve has a noisy trend that is consistent with zero. In the bottom panels, the behaviour after the 50-day gap is shown. In this last period, the difference curve is also mainly noise. However, a clear event appears at the beginning of the overlapping period, i.e., six consecutive points are placed above the zero level. Although this naively could be interpreted as the wing of a microlensing event (i.e., extrinsic variability), the A data were obtained at the end of a hard winter in which the colour coefficient strongly deviated (40-70%) from its average value. While some frames with extreme colour coefficients are not considered in the analysis (see the triangles and the open circle around day 3770 in Fig. 2), additional adjacent frames are also unsuitable for fine variability studies. Therefore, bad weather and anomalous behaviour of the LT devices are the most reasonable explanations for the anomalous variation in A that is simultaneously observed in both components. In summary, we do not find evidence of extrinsic variability in the light curves of Q0957+561.
The time delay between optical-UV continuum flux variations at two different wavelengths can be used to test the variability secenario (e.g., Collier et al. 1999). It might be produced by reprocessing of high energy radiation in an accretion disc around a supermassive black hole. The reprocessing hypothesis assumes that the optical-UV variations are the response of the gas in the disc to higher-energy fluctuations in the vecinity of the disc axis. Moreover, the existence of a radiative coupling between the variations is also assumed, i.e., the time delay represents a light-travel time between two disc annuli (see details in Collier et al. 1999). Collier et al. (1999) measured two time lags between fluctuations at two optical wavelengths and the corresponding UV fluctuations (UV variability leading optical variations) in the records of NGC 7469 at z = 0.016, and they found a good agreement between their delay estimates ( 1-2 d) and reverberation within an accretion disc. Sergeev et al. (2005) and Cackett et al. (2007) also explored the thermal reprocessing hypothesis in local active galactic nuclei. For Q0957+561, Collier (2001) reported a delay of about 3.4 d between the r-band and g-band APO main events (g-band events leading those in the r band), which translates into a rest-frame lag of about 1.4 d, in excellent agreement with predictions of the disc reprocessing scenario. This first delay between optical bands for a GLQ requires an independent confirmation as well as new efforts with other GLQs (e.g., Koptelova et al. 2006), and here we try to reach the first goal.
1-2 d) and reverberation within an accretion disc. Sergeev et al. (2005) and Cackett et al. (2007) also explored the thermal reprocessing hypothesis in local active galactic nuclei. For Q0957+561, Collier (2001) reported a delay of about 3.4 d between the r-band and g-band APO main events (g-band events leading those in the r band), which translates into a rest-frame lag of about 1.4 d, in excellent agreement with predictions of the disc reprocessing scenario. This first delay between optical bands for a GLQ requires an independent confirmation as well as new efforts with other GLQs (e.g., Koptelova et al. 2006), and here we try to reach the first goal.
For such a task, we focus on the LT events with highest S/N. The AE1-BE1 twin events are ruled out because (S/N) < 3 in the r band. However, there are two very prominent variations around day 4150 in the top panels of Figs. 4, 5 (A component). These AE3g and AE3r variations last  250 d (the whole light curves of A in the third season are considered as large events) and have signal-to-noise ratios above 6. We use fluxes in arbitrary units
250 d (the whole light curves of A in the third season are considered as large events) and have signal-to-noise ratios above 6. We use fluxes in arbitrary units
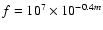 to compare AE3g and AE3r. The use of fluxes (instead of magnitudes m) permits a fair cross-correlation between two records that, apart from a possible delay, differ in a multiplicative constant and an additive constant. On average, the light curves were sampled two times per week. However, there are 20-day gaps around day 4180. Unfortunately, due to a combination of the kind of variability (time asymmetric events consisting of slow rises and rapid declines) and these short gaps close to the maxima, it is not possible to infer a reliable DCF with good time resolution, i.e.,
to compare AE3g and AE3r. The use of fluxes (instead of magnitudes m) permits a fair cross-correlation between two records that, apart from a possible delay, differ in a multiplicative constant and an additive constant. On average, the light curves were sampled two times per week. However, there are 20-day gaps around day 4180. Unfortunately, due to a combination of the kind of variability (time asymmetric events consisting of slow rises and rapid declines) and these short gaps close to the maxima, it is not possible to infer a reliable DCF with good time resolution, i.e.,
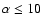 d (see above). For
d (see above). For
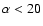 d, 20-day artifacts at lags of
d, 20-day artifacts at lags of 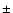 50 d appear in the DCF. This unphysical signal at
50 d appear in the DCF. This unphysical signal at 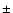 50 d is only avoided using longer bins with
50 d is only avoided using longer bins with
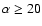 d, so we are forced to take relatively long bins. This is not a problem at all, but the measurement would be more accurate (but not more reliable) with better time resolution. Some DCF (filled circles) and
d, so we are forced to take relatively long bins. This is not a problem at all, but the measurement would be more accurate (but not more reliable) with better time resolution. Some DCF (filled circles) and
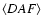 (open circles) trends are shown in Fig. 8. The top, middle, and bottom panels of Fig. 8 contain the results for
(open circles) trends are shown in Fig. 8. The top, middle, and bottom panels of Fig. 8 contain the results for
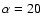 ,
25, and 30 d, respectively. Here,
,
25, and 30 d, respectively. Here,
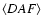 is the average of the gg and rr autocorrelation functions, whereas DCF represents the gr cross-correlation function.
is the average of the gg and rr autocorrelation functions, whereas DCF represents the gr cross-correlation function.
![\begin{figure}
\par\includegraphics[angle=0,width=9cm]{10447_f8.eps}\end{figure}](/articles/aa/full/2008/47/aa10447-08/Timg78.gif) |
Figure 8:
Comparison between the DCF (filled circles) and the
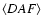 (open circles). Whilethe DCF is the gr cross-correlation function, the
(open circles). Whilethe DCF is the gr cross-correlation function, the
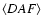 is the average of the gg and rr autocorrelation functions. We use the AE3g-AE3r events (see main text) and three bin semisizes:
is the average of the gg and rr autocorrelation functions. We use the AE3g-AE3r events (see main text) and three bin semisizes:
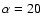 ( top panel), 25 ( middle panel), and 30 ( bottom panel) d.
( top panel), 25 ( middle panel), and 30 ( bottom panel) d. |
| Open with DEXTER |
In Fig. 8, there are no important distortions in the features of the DCF compared to
the features in the
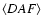 ,
but the existence of a delay of several days is evident. In other words, to get an optimal match, the
,
but the existence of a delay of several days is evident. In other words, to get an optimal match, the
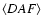 should be shifted by several days. Possible
values of this time shift (
should be shifted by several days. Possible
values of this time shift (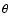 )
versus the associated
)
versus the associated
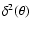 values normalised by its minimum value
values normalised by its minimum value
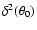 are plotted in Fig. 9. The
are plotted in Fig. 9. The
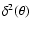 function was defined in Eq. (7) of Serra-Ricart et al. (1999) (see also above), and we use
function was defined in Eq. (7) of Serra-Ricart et al. (1999) (see also above), and we use
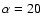 (dotted line), 25 (dashed line), and 30 (solid line) d in Fig. 9. This figure displays relatively narrow peaks centered on 3-4.5 d (best values of the interband delay; AE3g leading AE3r). Uncertainties are again computed by applying the
(dotted line), 25 (dashed line), and 30 (solid line) d in Fig. 9. This figure displays relatively narrow peaks centered on 3-4.5 d (best values of the interband delay; AE3g leading AE3r). Uncertainties are again computed by applying the 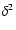 minimization to 1000 synthetic data sets. Through the distributions of delays (
minimization to 1000 synthetic data sets. Through the distributions of delays (
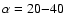 d), five 1
d), five 1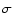 measurements are presented in Table 2. The
measurements are presented in Table 2. The 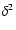 results in Table 2 agree with the previous time lag determination from APO light curves, and we adopt
results in Table 2 agree with the previous time lag determination from APO light curves, and we adopt
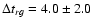 d (using an intermediate bin semisize
d (using an intermediate bin semisize
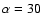 d; the probability of
d; the probability of
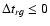 is only 7.5%) as our final 1
is only 7.5%) as our final 1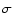 measurement.
measurement.
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm]{10447_f9.eps}\end{figure}](/articles/aa/full/2008/47/aa10447-08/Timg86.gif) |
Figure 9:
Normalised 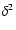 function from the AE3g-AE3r events. We use bin semisizes
function from the AE3g-AE3r events. We use bin semisizes
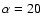 (dotted line), 25 (dashed line), and 30 (solid line) d. In Fig. 8, we can observe the presence of time shifts between the DCF and
(dotted line), 25 (dashed line), and 30 (solid line) d. In Fig. 8, we can observe the presence of time shifts between the DCF and
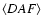 ,
which translate into interband delay peaks centered on 3-4.5 d (AE3g leading AE3r). ,
which translate into interband delay peaks centered on 3-4.5 d (AE3g leading AE3r). |
| Open with DEXTER |
Table 2:
Time lag measurements from the AE3g-AE3r events.
Liverpool Quasar Lens Monitoring is a long-term project to follow the optical (gri bands) variability of 10-20 GLQs with the Liverpool robotic telescope (Steele et al. 2004). The first phase of this project (LQLM I) was conducted between January 2005 and July 2007. While in Paper I we mainly studied the intrinsic variability of Q0909+532 in the r band, in this paper we present the monitoring programme of Q0957+561 in the gr bands. A main goal of our project (LQLM) is to considerably increase the public database of GLQs. Thus, all LQLM I pre-processed frames of Q0909+532 and Q0957+561 are publicly available on the Lens Image Archive of the German Astrophysical Virtual Observatory![[*]](/icons/foot_motif.gif) .
.
We have fully developed two photometric pipelines through the 3 years of observations and analyses. The transformation pipeline incorporates zero-point, colour, and inhomogeneity corrections in the
instrumental fluxes, so photometry to the 1-2% is achieved for Q0957+561A and
Q0957+561B. We detect an inhomogeneous response over the CCD area, which has an amplitude of  80 mmag (from maximum to minimum) and is consistent with studies in other optical telescopes (e.g., Magnier & Cuillandre 2004; Manfroid et al. 2001). Moreover, the colour coefficient is allowed to vary through time, because the atmospheric-instrumental conditions signicantly evolve through 2.5 years of monitoring. Due to atmospheric-instrumental problems at some epochs, the colour coefficient reaches anomalous values, i.e., we obtain dramatic deviations with respect to the average coefficient. Thus, the frames corresponding to an anomalous coefficient are removed or not considered.
80 mmag (from maximum to minimum) and is consistent with studies in other optical telescopes (e.g., Magnier & Cuillandre 2004; Manfroid et al. 2001). Moreover, the colour coefficient is allowed to vary through time, because the atmospheric-instrumental conditions signicantly evolve through 2.5 years of monitoring. Due to atmospheric-instrumental problems at some epochs, the colour coefficient reaches anomalous values, i.e., we obtain dramatic deviations with respect to the average coefficient. Thus, the frames corresponding to an anomalous coefficient are removed or not considered.
The LT gr light curves of Q0957+561 show several prominent events and gradients, and some of them (in the g band) are used to infer a time delay between components
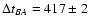 d (1
d (1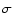 ). This gravitational lens delay from new g-band events is in agreement with the delay from the previous APO g-band main events (Kundic et al. 1997), so the associated UV flares in the variable source (APO and LT events) probably originate in the same emission region (Yonehara 1999). Taking into account that the previous APO gr-band main events are plausibly due to reverberation within an irradiated accretion disc (Collier 2001), the new gr-band events are likely related to flares in the central accretion disc. In addition, the delay between the two new LT large events in the g and r bands:
). This gravitational lens delay from new g-band events is in agreement with the delay from the previous APO g-band main events (Kundic et al. 1997), so the associated UV flares in the variable source (APO and LT events) probably originate in the same emission region (Yonehara 1999). Taking into account that the previous APO gr-band main events are plausibly due to reverberation within an irradiated accretion disc (Collier 2001), the new gr-band events are likely related to flares in the central accretion disc. In addition, the delay between the two new LT large events in the g and r bands:
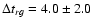 d (1
d (1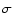 ;
the g-band event is leading), coincides with the estimation by Collier (2001) and agrees with flares generated during reprocessing in the accretion disc. Therefore, most APO-LT variations in the g and r bands are very probably associated with the gas disc around the supermassive black hole (only the APO secondary events have been associated with flares that were produced far away from the accretion disc; see Introduction). The detection of the same interband delay (between the g and r band) in the two monitoring campaigns (APO and LT) also suggests that the accretion disc reprocessing in Q0957+561 is a usual occurance at different times for different prominent flares. Hence, very likely, most observed variations in the g and r bands (APO and LT fluctuations with an amplitude of
;
the g-band event is leading), coincides with the estimation by Collier (2001) and agrees with flares generated during reprocessing in the accretion disc. Therefore, most APO-LT variations in the g and r bands are very probably associated with the gas disc around the supermassive black hole (only the APO secondary events have been associated with flares that were produced far away from the accretion disc; see Introduction). The detection of the same interband delay (between the g and r band) in the two monitoring campaigns (APO and LT) also suggests that the accretion disc reprocessing in Q0957+561 is a usual occurance at different times for different prominent flares. Hence, very likely, most observed variations in the g and r bands (APO and LT fluctuations with an amplitude of  100 mmag and lasting
100 mmag and lasting  100 d) are associated with reverberation within the gas disc around the supermassive black hole.
100 d) are associated with reverberation within the gas disc around the supermassive black hole.
We add 2.5 years of time coverage to the previous 1.5-year gr-band records of Q0957+561,
and remark that our difference light curves are consistent with zero. Thus, there is no evidence of
extrinsic variations in both APO and LT independent experiments separated by  10 years. These
results disagree with the claim by Schild (2005) that microlenses in the lensing galaxy affect the
observed variability. Therefore, the complex quasar structure suggested by this author is not supported by the gr-band light curves of Q0957+561. We also remark that double replicas in the records of the B component are not detected in the APO and LT experiments. This clearly contradicts previous conclusions by Hirv et al. (2007), which indicated that the full B light curve of the lensed quasar can be decomposed into a sum of two similar and time shifted curves. Finally, the APO-LT combined database of Q0957+561 (together with other monitorings done between both experiments) is a promising tool for studying the quasar structure and the composition of the lensing halo (e.g., Kochanek 2004; Schmidt & Wambsganss 1998).
10 years. These
results disagree with the claim by Schild (2005) that microlenses in the lensing galaxy affect the
observed variability. Therefore, the complex quasar structure suggested by this author is not supported by the gr-band light curves of Q0957+561. We also remark that double replicas in the records of the B component are not detected in the APO and LT experiments. This clearly contradicts previous conclusions by Hirv et al. (2007), which indicated that the full B light curve of the lensed quasar can be decomposed into a sum of two similar and time shifted curves. Finally, the APO-LT combined database of Q0957+561 (together with other monitorings done between both experiments) is a promising tool for studying the quasar structure and the composition of the lensing halo (e.g., Kochanek 2004; Schmidt & Wambsganss 1998).
Acknowledgements
We thank an anonymous referee for several comments that improved the presentation of our results.
We also thank C. Moss for guidance in the preparation of the robotic monitoring project with the
Liverpool telescope. The Liverpool Telescope is operated on the island of La Palma by Liverpool
John Moores University in the Spanish Observatorio del Roque de los Muchachos of the Instituto
de Astrofisica de Canarias with financial support from the UK Science and Technology Facilities
Council. We thank B. McLeod for providing the IMFITFITS software to us. We use information taken
from the Sloan Digital Sky Survey (SDSS) Web site, and we are grateful to the SDSS team for doing
that public database. This research has been supported by the Spanish Department of Education and
Science grants AYA2004-08243-C03-02 and AYA2007-67342-C03-02, University of Cantabria funds, grant
for young scientists of the President of the Russian Federation (number MK-2637.2006.2), Deutscher
Akademischer Austausch Dienst (DAAD) grant number A/05/56557 and grant of Russian Foundation for
Basic Research (RFBR) 06-02-16857. EK holds the Taiwan National Research Councils grant No.
96-2811-M-008-058. RGM holds a grant of the ESP2006-13608-C02-01 project financed by the Spanish
Department of Science and Innovation.
The initial transformation equations for a given reference star are
| g*(tj) = g + Ag(tj) + Cg(tj)(g - r) , |
|
|
(A.1) |
| r*(tk) = r + Ar(tk) + Cr(tk)(r - i) , |
|
|
(A.2) |
where g* and r* are the instrumental magnitudes of the star, g, r, and i are its
standard magnitudes, Ag and Ar are the zero-point terms (including instrumental
and atmospheric corrections), and Cg and Cr are the colour coefficients. The zero-point
terms and the colour coefficients are expected to significantly change during the 2.5-year
monitoring period, so we explicitly consider their time evolution. Here, tj and tk denote
observation times in the g and r bands, respectively. As we are initially interested in
the usual systematic corrections, Eqs. (A.1, A.2) do not include other possible terms (see here below). Instead of the LT photometric system (
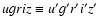 ), we want to use the SDSS
``natural'' system, since accurate standard magnitudes are available in this SDSS 2.5 m system
(e.g., Stoughton et al. 2002; Smith et al. 2002). SDSS magnitudes are also suitable for comparing our results with
future data of Q0957+561 using different facilities and/or SDSS quasar studies/databases
(e.g., Schneider et al. 2007; Vanden Berk et al. 2004). From equations for transforming LT magnitudes to magnitudes in the
SDSS system
), we want to use the SDSS
``natural'' system, since accurate standard magnitudes are available in this SDSS 2.5 m system
(e.g., Stoughton et al. 2002; Smith et al. 2002). SDSS magnitudes are also suitable for comparing our results with
future data of Q0957+561 using different facilities and/or SDSS quasar studies/databases
(e.g., Schneider et al. 2007; Vanden Berk et al. 2004). From equations for transforming LT magnitudes to magnitudes in the
SDSS system![[*]](/icons/foot_motif.gif) :
:
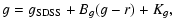 |
|
|
(A.3) |
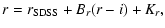 |
|
|
(A.4) |
and equations that relate LT and SDSS colours:
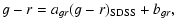 |
|
|
(A.5) |
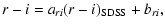 |
|
|
(A.6) |
it is possible to rewrite Eqs. (A.1, A.2) as
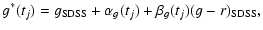 |
|
|
(A.7) |
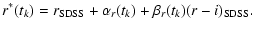 |
|
|
(A.8) |
The 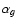 term and the
term and the 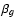 coefficient are given by (it is trivial to write
expressions for
coefficient are given by (it is trivial to write
expressions for 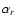 and
and 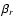 )
)
![$\displaystyle \alpha_g(t_j) = A_g(t_j) + K_g + b_{gr}[B_g + C_g(t_j)] ,$](/articles/aa/full/2008/47/aa10447-08/img96.gif) |
|
|
(A.9) |
![$\displaystyle \beta_g(t_j) = a_{gr}[B_g + C_g(t_j)] .$](/articles/aa/full/2008/47/aa10447-08/img97.gif) |
|
|
(A.10) |
Taking into account typical values of Cg ( -0.029) and Cr (
-0.029) and Cr ( 0.034) reported by
the LT team (on the LT Web site; see main text), the SDSS estimates of Bg (
0.034) reported by
the LT team (on the LT Web site; see main text), the SDSS estimates of Bg (
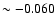 )
and
Br (
)
and
Br ( -0.035) on the SDSS Web site (see here above), and
-0.035) on the SDSS Web site (see here above), and
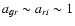 ,
we
expect typical colour coefficients
,
we
expect typical colour coefficients
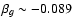 and
and
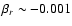 .
On the other
hand, the adopted standard magnitudes of the reference stars (XGFHDER field stars; see main text)
appear in Table A.1. These are PSF magnitudes in the SDSS catalogue2.
.
On the other
hand, the adopted standard magnitudes of the reference stars (XGFHDER field stars; see main text)
appear in Table A.1. These are PSF magnitudes in the SDSS catalogue2.
In order to achieve 1-2% photometric accuracy with the RATCam camera (on the LT), one additional
detail must be taken into account in the transformation Eqs. (A.7, A.8). We introduce an
inhomogeneity term that corrects the flat-field systematic error over the camera area, which might
have a total amplitude of  50 mmag (e.g., Magnier & Cuillandre 2004; Manfroid et al. 2001). For example, this kind of
error could be related to twilight flats. During twilight exposures, some scattered light (within
the dome) would reach the camera, and thus, the illumination would not be homogeneous. This effect
invalidates the basic hypothesis of homogeneous illumination. Here, we assume a second order 2D
polynomial to account for the inhomogeneity term, so the final transformation equations are
50 mmag (e.g., Magnier & Cuillandre 2004; Manfroid et al. 2001). For example, this kind of
error could be related to twilight flats. During twilight exposures, some scattered light (within
the dome) would reach the camera, and thus, the illumination would not be homogeneous. This effect
invalidates the basic hypothesis of homogeneous illumination. Here, we assume a second order 2D
polynomial to account for the inhomogeneity term, so the final transformation equations are
| g*(tj) |
= |
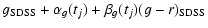 |
|
| |
|
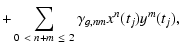 |
(A.11) |
| r*(tk) |
= |
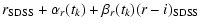 |
|
| |
|
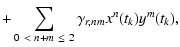 |
(A.12) |
where (x,y) is the 2D position of the star on the CCD. To find the relevant parameters in the
g band, i.e.,
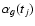 ,
,
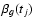 ,
and
,
and
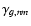 ,
we may fit the observed
magnitude deviations (instrumental - standard) of the seven reference stars to the model
incorporating the three systematic terms: zero-point, colour, and inhomogeneity. Once the fit has
been made, the g-SDSS magnitude of any point-like source (star or quasar) is derived in a
straightforward way:
,
we may fit the observed
magnitude deviations (instrumental - standard) of the seven reference stars to the model
incorporating the three systematic terms: zero-point, colour, and inhomogeneity. Once the fit has
been made, the g-SDSS magnitude of any point-like source (star or quasar) is derived in a
straightforward way:
| g(SDSS) |
= |
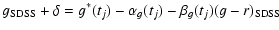 |
|
| |
|
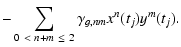 |
(A.13) |
In Eq. (A.13), 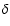 represents the deviation caused by random noise (e.g., photon noise) and
unkown (but presumibly small) systematic corrections. For a non-variable star (e.g., a reference
star), variations in g(SDSS) are generated by noise (
represents the deviation caused by random noise (e.g., photon noise) and
unkown (but presumibly small) systematic corrections. For a non-variable star (e.g., a reference
star), variations in g(SDSS) are generated by noise (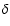 ). However, for variable stars or
quasars, there are two kinds of variability. While true variability is due to time evolution of
). However, for variable stars or
quasars, there are two kinds of variability. While true variability is due to time evolution of
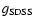 ,
noise is an additional source of fluctuations. The
,
noise is an additional source of fluctuations. The
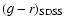 colour of
Q0957+561 might also evolve over time. Thus, the use of an average colour
colour of
Q0957+561 might also evolve over time. Thus, the use of an average colour
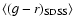 in the colour correction introduces a systematic noise
in the colour correction introduces a systematic noise
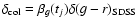 associated with the colour variation. Fortunately, for moderate fluctuations with amplitude of
associated with the colour variation. Fortunately, for moderate fluctuations with amplitude of  25 mmag (e.g., Kundic et al. 1995), the amplitude of the colour noise is only
25 mmag (e.g., Kundic et al. 1995), the amplitude of the colour noise is only  0.2%, well below our accuracy goal. The r-SDSS magnitude of a source is given by an expression similar to Eq. (A.13).
0.2%, well below our accuracy goal. The r-SDSS magnitude of a source is given by an expression similar to Eq. (A.13).
Table A.1:
Adopted standard magnitudes of the reference stars.
- Adelman-McCarthy, J. K.,
Jennifer, K., Agüeros, Marcel A., et al. 2007, ApJS, 172,
634 [NASA ADS] [CrossRef]
(In the text)
- Bernstein, G., Fischer,
P., Tyson, J. A., & Rhee, G. 1997, ApJ, 483, L79 [NASA ADS] [CrossRef]
- Cackett, E. M., Horne,
K., & Winkler, H. 2007, MNRAS, 380, 669 [NASA ADS] [CrossRef]
(In the text)
- Collier, S. 2001, MNRAS,
325, 1527 [NASA ADS] [CrossRef]
(In the text)
- Collier, S., Horne, K.,
Wanders, I., & Peterson, B. M. 1999, MNRAS, 302, L24 [NASA ADS] [CrossRef]
(In the text)
- Edelson, R. A., &
Krolik, J. H. 1988, ApJ, 333, 646 [NASA ADS] [CrossRef]
(In the text)
- Gil-Merino, R.,
Goicoechea, L. J., Serra-Ricart, M., et al. 2001, MNRAS, 322,
397 [CrossRef]
- Goicoechea, L. J. 2002,
MNRAS, 334, 905 [NASA ADS] [CrossRef]
(In the text)
- Goicoechea, L. J.,
et al. 2007, in Highlights of Spanish Astrophysics IV, ed. F.
Figueras, J. M. Girart, M. Hernanz, & C. Jordi (Dordrecht:
Springer), CD-ROM, [arXiv:astro-ph/0609647]
(In the text)
- Goicoechea, L. J.,
Shalyapin, V. N., Koptelova, E., et al. 2008, New A, 13, 182 [NASA ADS] [CrossRef]
(Paper I)
- Hirv, A., Eenmäe,
T., Liimets, T., Liivamägi, L. J., & Pelt, J. 2007,
A&A, 464, 471 [NASA ADS] [CrossRef] [EDP Sciences]
- Hutchings, J. B. 2003,
AJ, 126, 24 [NASA ADS] [CrossRef]
(In the text)
- Keeton, C. R., Kochanek,
C. S., & Falco, E. E. 1998, ApJ, 509, 561 [NASA ADS] [CrossRef]
- Kerins, E., et al.
2006, MNRAS, 365, 1099 [NASA ADS] [CrossRef]
(In the text)
- Kochanek, C.S. 2004,
ApJ, 605, 58 [NASA ADS] [CrossRef]
- Kochanek, C. S.,
Schneider, P., & Wambsganss, J. 2004, StrongGravitational
Lensing, in Proc. 33rd Saas-Fee Advanced Course, ed. G. Meylan, P.
Jetzer, & P. North (Berlin: Springer)
(In the text)
- Kochanek, C. S.,
et al. 2008, The CfA-Arizona Space Telescope LEns Survey
(CASTLES), http://www.cfa.harvard.edu/glensdata/
- Koptelova, E.,
Shimanovskaya, E., Artamonov, B., et al. 2005, MNRAS, 356,
323 [NASA ADS] [CrossRef]
(In the text)
- Koptelova, E. A.,
Oknyanskij, V. L., & Shimanovskaya, E. V. 2006, A&A, 452,
37 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Kundic, T., Colley, W.
N., Gott, J. R., III, et al. 1995, ApJ, 455, L5 [NASA ADS]
- Kundic, T., Turner, E.
L., Colley, W. N., et al. 1997, ApJ, 482, 75 [NASA ADS] [CrossRef]
- Magnier, E. A., &
Cuillandre, J. C. 2004, PASP, 116, 449 [NASA ADS] [CrossRef]
- Manfroid, J., Selman, F.,
& Jones, H. 2001, The Messenger, 104, 16 [NASA ADS]
- McLeod, B. A., Bernstein,
G. M., Rieke, M. J., & Weedman, D. W. 1998, AJ, 115, 1377 [NASA ADS] [CrossRef]
(In the text)
- Oscoz, A., Alcalde, D.,
Serra-Ricart, M., et al. 2001, ApJ, 552, 81 [NASA ADS] [CrossRef]
- Ovaldsen, J. E.,
Teuber, J., Schild, R. E., & Stabell, R. 2003a, A&A, 402,
891 [NASA ADS] [CrossRef] [EDP Sciences]
- Ovaldsen, J. E.,
Teuber, J., Stabell, R., & Evans, A. K. D. 2003b, MNRAS, 345,
795 [NASA ADS] [CrossRef]
- Paraficz, D., Hjorth, J.,
Burud, I., Jakobsson, P., & Elíasdóttir, Á.
2006, A&A, 455, L1 [NASA ADS] [CrossRef] [EDP Sciences]
- Pelt, J., Hoff, W.,
Kayser, R., Refsdal, S., & Schramm, T. 1994, A&A, 286,
775 [NASA ADS]
- Pelt, J., Kayser, R.,
Refsdal, S., & Schramm, T. 1996, A&A, 305, 97 [NASA ADS]
- Pijpers, F.P. 1997,
MNRAS, 289, 933 [NASA ADS]
(In the text)
- Refsdal, S. 1964, MNRAS,
128, 307
(In the text)
- Schild, R. 2005, AJ, 129,
1225 [NASA ADS] [CrossRef]
- Schmidt, R., &
Wambsganss, J. 1998, A&A, 335, 379 [NASA ADS]
- Schneider, D. P., Hall,
P. B., Richards, G. T., et al. 2007, AJ, 134, 102 [NASA ADS] [CrossRef]
- Sergeev, S. G.,
Doroshenko, V. T., Golubinskiy, Y. V., Merkulova, N. I., &
Sergeeva, E. A. 2005, ApJ, 622, 129 [NASA ADS] [CrossRef]
(In the text)
- Serra-Ricart, M., Oscoz,
A., Sanchís, T., et al. 1999, ApJ, 526, 40 [NASA ADS] [CrossRef]
(In the text)
- Smith, J. A., Tucker, D.
L., Kent, S., et al. 2002, AJ, 123, 2121 [NASA ADS] [CrossRef]
- Steele, I. A., Smith, R.
J., Rees, P. C., et al. 2004, Ground-based telescopes, ed. J.
M. Oschmann, Proc. SPIE, 5489, 679
(In the text)
- Stoughton, C., Lupton, R.
H., Bernardi, M., et al. 2002, AJ, 123, 485 [NASA ADS] [CrossRef]
- Ullán, A.,
Goicoechea, L. J., Muñoz, J. A., et al. 2003, MNRAS, 346,
415 [NASA ADS] [CrossRef]
(In the text)
- Ullán, A.,
Goicoechea, L. J., Zheleznyak, A. P., et al. 2006, A&A,
452, 25 [NASA ADS] [CrossRef] [EDP Sciences]
- Vanden Berk, D. E.,
Wilhite, B. C., Kron, R. G., et al. 2004, ApJ, 601, 692 [NASA ADS] [CrossRef]
- Walsh, D., Carswell, R.
F., & Weymann, R. J. 1979, Nature, 279, 381 [NASA ADS] [CrossRef]
(In the text)
- Yonehara, A. 1999, ApJ,
519, L31 [NASA ADS] [CrossRef]
(In the text)
- Yonehara, A., Mineshige,
S., Takei, Y., Chartas, G., & Turner, E. L. 2003, ApJ, 594,
107 [NASA ADS] [CrossRef]
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[angle=0,width=7cm]{10447_f1.eps}\end{figure}](/articles/aa/full/2008/47/aa10447-08/Timg23.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm]{10447_f2.eps}\end{figure}](/articles/aa/full/2008/47/aa10447-08/Timg41.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm]{10447_f3.eps}\end{figure}](/articles/aa/full/2008/47/aa10447-08/Timg42.gif)
![\begin{figure}
\par\includegraphics[angle=0,width=7cm]{10447_f4.eps}\end{figure}](/articles/aa/full/2008/47/aa10447-08/Timg50.gif)
![\begin{figure}
\par\includegraphics[angle=0,width=7cm]{10447_f5.eps}\end{figure}](/articles/aa/full/2008/47/aa10447-08/Timg52.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm]{10447_f6.eps}\end{figure}](/articles/aa/full/2008/47/aa10447-08/Timg55.gif)
![\begin{figure}
\par\includegraphics[angle=0,width=9cm]{10447_f7.eps}\end{figure}](/articles/aa/full/2008/47/aa10447-08/Timg70.gif)
![\begin{figure}
\par\includegraphics[angle=0,width=9cm]{10447_f8.eps}\end{figure}](/articles/aa/full/2008/47/aa10447-08/Timg78.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm]{10447_f9.eps}\end{figure}](/articles/aa/full/2008/47/aa10447-08/Timg86.gif)