A&A 492, 233-243 (2008)
DOI: 10.1051/0004-6361:200810701
Brightness, distribution, and evolution of sunspot umbral dots
T. L. Riethmüller
-
S. K. Solanki
-
V. Zakharov
-
A. Gandorfer
Max-Planck-Institut für Sonnensystemforschung (MPS),
Max-Planck-Str. 2, 37191 Katlenburg-Lindau, Germany
Received 29 July 2008 / Accepted 15 October 2008
Abstract
Context. Umbral Dots (UDs) are thought to be manifestations of magnetoconvection in sunspot umbrae. Recent advances in their theoretical description point to the need for a thorough study of their properties and evolution based on data with the highest currently achievable resolution.
Aims. Our UD analysis aims to provide parameters such as lifetimes, diameters, horizontal velocities, and peak intensities, as well as the evolution of selected parameters.
Methods. We present a 106-min TiO (705.7 nm) time series of high spatial and temporal resolution that contains thousands of UDs in the umbra of a mature sunspot in the active region NOAA 10667 at 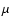 = 0.95. The data were acquired with the 1-m Swedish Solar Telescope (SST) on La Palma. With the help of a multilevel tracking (MLT) algorithm the sizes, brightnesses, and trajectories of 12 836 umbral dots were found and extensively analyzed. The MLT allows UDs with very low contrast to be reliably identified.
= 0.95. The data were acquired with the 1-m Swedish Solar Telescope (SST) on La Palma. With the help of a multilevel tracking (MLT) algorithm the sizes, brightnesses, and trajectories of 12 836 umbral dots were found and extensively analyzed. The MLT allows UDs with very low contrast to be reliably identified.
Results. Inside the umbra we determine a UD filling factor of 11%. The histogram of UD lifetimes is monotonic, i.e. a UD does not have a typical lifetime. Three quarters of the UDs lived for less than 150 s and showed no or little motion. The histogram of the UD diameters exhibits a maximum at 225 km, i.e. most of the UDs are spatially resolved. UDs display a typical horizontal velocity of 420 m s-1 and a typical peak intensity of 51% of the mean intensity of the quiet photosphere, making them on average 20% brighter than the local umbral background. Almost all mobile UDs (large birth-death distance) were born close to the umbra-penumbra boundary, move towards the umbral center, and are brighter than average. Notably bright and mobile UDs were also observed along a prominent UD chain, both ends of which are located at the umbra-penumbra boundary. Their motion started primarily at either of the ends of the chain, continued along the chain, and ended near the chain's center. We observed the splitting and merging of UDs and the temporal succession of both. For the first time the evolution of brightness, size, and horizontal speed of a typical UD could be determined in a statistically significant way. Considerable differences between the evolution of central and peripheral UDs are found, which point to a difference in origin.
Key words: Sun: photosphere - Sun: sunspots - techniques: photometric
The investigation of the complex fine structure of umbrae and penumbrae is crucial to understanding the subsurface energy transport in sunspots. The energy transport from the solar interior to the solar surface outside magnetic features is mainly determined by convection, visible as granulation in images of the quiet photosphere. The strong and nearly vertical umbral magnetic field suppresses normal overturning convection inside the umbra. However, it is believed that some form of residual magnetoconvection is responsible for much of the remaining energy transport and manifests itself in the form of fine structures, such as light bridges (LBs) or umbral dots (UDs). In the present paper we consider UDs, which contribute up to 37% of the radiative umbral flux according to Adjabshirzadeh & Koutchmy (1983). Different models have been proposed to explain the umbral dots. Choudhury (1986) postulated that UDs are thin columns of field-free hot gas between the cluster of small magnetic flux tubes that form the subsurface structure of a sunspot according to Parker (1979). According to this model, a UD is formed when an upwelling brings hot material into the photosphere. An alternative model has been proposed by Weiss et al. (1990) who consider UDs to be spatially modulated oscillations in a strong magnetic field.
A more recent, promising approach is presented by Schüssler & Vögler (2006), who used numerical simulations of three-dimensional radiative magnetoconvection to improve the physical understanding of the umbral fine structure. The simulations exhibit the emergence of small-scale upflow plumes that start off like oscillatory convection columns below the solar surface but turn into narrow overturning cells driven by the strong radiative cooling around optical depth unity. Most of those UDs show a central dark lane. The presence of dark lanes in penumbral and umbral fine structures has already been observed several times, cf. Scharmer et al. (2002); Langhans et al. (2007); Scharmer et al. (2007). The verification of the predicted dark lanes in large UDs by Bharti et al. (2007) and Rimmele (2008),
as well as the verification of the predicted photospheric stratification of bright peripheral UDs
by Riethmüller et al. (2008), support the Schüssler & Vögler model of UDs. There is now a need to learn more about this phenomenon, with a statistically robust analysis of UD properties and evolution being a promising means of achieving this aim.
The most detailed analyses of UDs are more than 10 years old (Sobotka et al. 1997a,b)
and are based on data observed with the 50-cm SVST (Swedish Vacuum Solar Telescope), cf. the
recent reviews of umbral fine structures by Solanki (2003); Thomas & Weiss (2004) and Sobotka (2006).
The more recent papers of Hartkorn & Rimmele (2003); Tritschler & Schmidt (2002) and Sobotka & Hanslmeier (2005) have
concentrated on individual properties and lack, e.g., the determination of UD trajectories.
Furthermore, the possibility of improving the spatial resolution with the help of modern image
reconstruction algorithms is only used by Tritschler & Schmidt (2002). The present paper aims to
overcome these shortcomings, by employing data from the 1-m SST (Swedish Solar Telescope) equipped
with an adaptive optics system, by restoring the data employing MFBD (multi-frame blind
deconvolution), and determining the evolution of UD parameters whenever possible.
The data employed here were acquired on September 7, 2004 with the Swedish Solar Telescope
at the Observatorio del Roque de los Muchachos on La Palma, Spain. Technical details of
the SST are described by Scharmer et al. (2003a). Wavefront aberrations caused by the telescope
and by the turbulent atmosphere of the Earth were partially corrected by the adaptive optics system,
explained in Scharmer et al. (2003b). The science camera was a Kodak Megaplus CCD with a pixel size
of 9 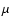 m and a plate scale of 0.041
m and a plate scale of 0.041
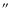 (30 km on the Sun) per pixel. The camera was
equipped with an interference filter at the wavelength of the 705.7 nm of the titanium oxide band head, the FWHM of this filter was 0.71 nm. The theoretical diffraction limit of the telescope at the TiO wavelength is 0.18
(30 km on the Sun) per pixel. The camera was
equipped with an interference filter at the wavelength of the 705.7 nm of the titanium oxide band head, the FWHM of this filter was 0.71 nm. The theoretical diffraction limit of the telescope at the TiO wavelength is 0.18
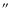 (130 km). Due to the high sensitivity to umbral temperatures of TiO lines, the TiO band head is a good diagnostic wavelength range for imaging umbral features (Berdyugina et al. 2003). A wavelength in the red was chosen also in order to ensure a more homogeneous time series due to the more benign seeing at these wavelengths. Acquisition lasted from
08:27 UT to 10:17 UT, i.e. a total of 110 min. The images were obtained in a frame selection mode that saved only the 8 best images of a 20-s-interval. The exposure time was 10 ms. The telescope pointed to the sunspot of the active region NOAA 10667 at cos
(130 km). Due to the high sensitivity to umbral temperatures of TiO lines, the TiO band head is a good diagnostic wavelength range for imaging umbral features (Berdyugina et al. 2003). A wavelength in the red was chosen also in order to ensure a more homogeneous time series due to the more benign seeing at these wavelengths. Acquisition lasted from
08:27 UT to 10:17 UT, i.e. a total of 110 min. The images were obtained in a frame selection mode that saved only the 8 best images of a 20-s-interval. The exposure time was 10 ms. The telescope pointed to the sunspot of the active region NOAA 10667 at cos 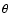 = 0.95, i.e. relatively close to the solar disk center (
= 0.95, i.e. relatively close to the solar disk center (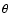 is the heliocentric angle).
is the heliocentric angle).
The data were dark current and flat field corrected, reconstructed via the MFBD technique (Löfdahl 2003), derotated, destretched (November 1988), and subsonic filtered with a cut-off phase velocity of 5 km s-1 (Title et al. 1989). The obtained time series consists of 310 images with a spatial resolution in the range of 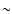 0.18
0.18
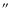 -0.25
-0.25
 ,
as we estimated from radially averaged power spectra. The field of view (FOV) is 37
,
as we estimated from radially averaged power spectra. The field of view (FOV) is 37
 59
59
 and contains the entire considered sunspot whose umbra is divided into two parts by a light bridge. UDs in both
parts of the umbra are analyzed in the next section.
and contains the entire considered sunspot whose umbra is divided into two parts by a light bridge. UDs in both
parts of the umbra are analyzed in the next section.
The detailed analysis of 310 images requires an automated algorithm for the identification of
the thousands of umbral dots they contain. A specific algorithmic challenge is the fact
that UDs as well as the local umbral background between them cover a broad range of intensities.
At a normal contrast (left panel of Fig. 1) UDs are mainly visible near the
penumbra. By displaying the square root of the umbral brightness instead of the brightness itself numerous UDs within the dark umbral background become visible as well (right panel).
![\begin{figure}
\par\includegraphics[width=4.2cm,clip]{0701fig1a.eps}\includegraphics[width=4.2cm,clip]{0701fig1b.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg9.gif) |
Figure 1:
Frame taken at 09:53:20 UT: best quality image plotted at normal contrast ( left panel) and with increased umbral brightness ( right panel). The black contour lines outline the umbra (see text for details). The direction to solar disk center (DC) is indicated by the arrow. Locations of umbral dots (UDs) that are discussed further in the text are marked by the letters A-D. Minor tick marks are given in Mm. |
| Open with DEXTER |
Our automated UD analysis starts with isolating the umbra, which is done by thresholding a lowpass
filtered image (averaging a squared environment of 11  11 pixels) at 35% of the mean
intensity of the quiet photosphere (
11 pixels) at 35% of the mean
intensity of the quiet photosphere (
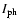 ). From the resulting set of contours we select only
those longer than 3 Mm in order to avoid larger UDs from being connected to the umbral boundary.
In the particular case of the studied penumbra the results are almost identical to identifying
the two longest contours with the umbral boundary. The thus obtained umbral boundary is visible
in the right panel of Fig. 1 as the black contour line. This method for isolating
the umbral boundary automatically ensures that a local brightening at the end of a penumbral fibril
is only considered to be a UD if it is isolated from the penumbra in the sense that the intensity
between the UD and the penumbral fibril falls below the applied threshold of 0.35
). From the resulting set of contours we select only
those longer than 3 Mm in order to avoid larger UDs from being connected to the umbral boundary.
In the particular case of the studied penumbra the results are almost identical to identifying
the two longest contours with the umbral boundary. The thus obtained umbral boundary is visible
in the right panel of Fig. 1 as the black contour line. This method for isolating
the umbral boundary automatically ensures that a local brightening at the end of a penumbral fibril
is only considered to be a UD if it is isolated from the penumbra in the sense that the intensity
between the UD and the penumbral fibril falls below the applied threshold of 0.35
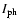 .
.
In the next step the UDs in each of the 310 images (recorded at a cadence of 20.57 s) are detected. For this purpose several algorithms were tested, e.g. a method where, starting from the UD center, 8 equally distributed rays are followed until they reach the UD boundary which is defined as the position where the intensity drops below 50% of the maximum intensity above the local umbral background. The resulting 8 boundary points lead to a polygon that is a good approximation
of the UD boundary. The method does not work properly for UDs with a partly concave boundary and it
cannot easily separate UDs that are close to each other. Finally, the multilevel tracking algorithm of Bovelet & Wiehr (2001), which provided the best results in detecting the UD boundaries, was chosen. First the MLT algorithm determines the global extrema of the umbral intensities and subdivides this range into equidistant levels. Bovelet and Wiehr used MLT to distinguish between granules and intergranular lanes of the quiet Sun and found that three MLT levels are sufficient for their purpose. Since umbral dots cover a broad range of intensities we have to use a noticeably higher number of levels. We normalized our best quality image to
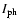 and found an umbral
intensity range from 0.36-0.96
and found an umbral
intensity range from 0.36-0.96
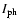 (Note: this range is only valid for the best quality image, other images may reach lower or higher umbral intensities). We found that 25 MLT levels is the optimal compromise between detecting as many UDs as possible and avoiding the misinterpretation
of noise as UDs. Whereas small umbral dots, obtained with this choice of levels, have a typical contrast relative to the local background of about 0.05
(Note: this range is only valid for the best quality image, other images may reach lower or higher umbral intensities). We found that 25 MLT levels is the optimal compromise between detecting as many UDs as possible and avoiding the misinterpretation
of noise as UDs. Whereas small umbral dots, obtained with this choice of levels, have a typical contrast relative to the local background of about 0.05
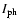 ,
the noise level is about 0.005
,
the noise level is about 0.005
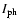 (see Fig. 2 for a typical intensity profile). Starting with the highest intensity level all pixels are found whose intensity exceeds this level. This leads to several bounded two-dimensional structures, that are tagged in a unique way, which is indicated by different colors in the one-dimensional illustration given in Fig. 2. The obtained closed structures are extended pixel by pixel as long as the intensity is greater than the next lower level. After that the algorithm searches through the whole umbra again to find all pixels whose intensity is greater than the next lower level, which may lead to some newly detected closed structures. This procedure is repeated until the minimal intensity level is reached. At the end every umbral pixel belongs to exactly one closed structure. The mode of operation of the
MLT algorithm is illustrated for one dimension in Fig. 2 for the case of 4 levels.
(see Fig. 2 for a typical intensity profile). Starting with the highest intensity level all pixels are found whose intensity exceeds this level. This leads to several bounded two-dimensional structures, that are tagged in a unique way, which is indicated by different colors in the one-dimensional illustration given in Fig. 2. The obtained closed structures are extended pixel by pixel as long as the intensity is greater than the next lower level. After that the algorithm searches through the whole umbra again to find all pixels whose intensity is greater than the next lower level, which may lead to some newly detected closed structures. This procedure is repeated until the minimal intensity level is reached. At the end every umbral pixel belongs to exactly one closed structure. The mode of operation of the
MLT algorithm is illustrated for one dimension in Fig. 2 for the case of 4 levels.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0701fig2.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg10.gif) |
Figure 2:
Illustration of multilevel tracking algorithm with 4 levels applied to a typical intensity profile. |
| Open with DEXTER |
The minimal (
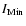 )
and maximal (
)
and maximal (
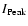 )
intensity of each closed structure is determined and all pixels that have an intensity lower than 50% of this min-max range (white arrows in Fig. 3a) are cut. This leads to a first estimate of the UD boundaries
(see Fig. 3b) that are used to determine the local umbral background intensities (
)
intensity of each closed structure is determined and all pixels that have an intensity lower than 50% of this min-max range (white arrows in Fig. 3a) are cut. This leads to a first estimate of the UD boundaries
(see Fig. 3b) that are used to determine the local umbral background intensities (
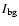 ), i.e. the intensities that would be observed in the absence of all UDs. We applied the method used by Sobotka & Hanslmeier (2005) that approximates the local umbral background by a 2D surface fitted to the grid of local intensity minima, using the method of thin-plate splines
(Barrodale et al. 1993). Since the local umbral background intensities are known now (dashed line in Fig. 3c), we determine the exact UD boundaries by cutting all pixels lower than 50% of the maximum intensity above the local umbral background (see white arrows in
Fig. 3c). Figure 3d illustrates that the resulting UD boundaries are similar to our first estimate in Fig. 3b so that we don't need further iterations (this was the case with most identified UDs). Employing this procedure we found, on average, 323 UDs per image. Sometimes, our algorithm recognizes strong elongated bright structures as UDs that we would not consider as a UD by visual inspection of the images. Via a spot-check on selected images we estimate that the number of misidentifications is lower than 1%. Due to the large number of detected UDs we are not able to remove the misidentifications by hand and
accepted them as noise.
), i.e. the intensities that would be observed in the absence of all UDs. We applied the method used by Sobotka & Hanslmeier (2005) that approximates the local umbral background by a 2D surface fitted to the grid of local intensity minima, using the method of thin-plate splines
(Barrodale et al. 1993). Since the local umbral background intensities are known now (dashed line in Fig. 3c), we determine the exact UD boundaries by cutting all pixels lower than 50% of the maximum intensity above the local umbral background (see white arrows in
Fig. 3c). Figure 3d illustrates that the resulting UD boundaries are similar to our first estimate in Fig. 3b so that we don't need further iterations (this was the case with most identified UDs). Employing this procedure we found, on average, 323 UDs per image. Sometimes, our algorithm recognizes strong elongated bright structures as UDs that we would not consider as a UD by visual inspection of the images. Via a spot-check on selected images we estimate that the number of misidentifications is lower than 1%. Due to the large number of detected UDs we are not able to remove the misidentifications by hand and
accepted them as noise.
Since a UD is an extended structure we determine the coordinates of the brightest pixel (peak intensity) and save them as the UD's position. This method is applicable because the noise was sufficiently reduced by our subsonic filter, as demonstrated by a typical intensity profile in Fig. 2. We also determine the UD's diameter, defined as the diameter of a circle of area equal to that within the boundary of the UD. After the positions of all UDs of every image are known, the motions and trajectories of UDs are determined. The continuation of a trajectory in the image at the next (previous) time step is determined by finding the UD that is closest to the UD's current position. If no UD can be found within a 5 pixel neighborhood (theoretical diffraction limit) of the current UD then the tracking stops. In a loop over all images every UD is tracked backward in time until its birth and forward in time until its death. The tracking must be tolerant to the occasional image with lower image quality in which the UD may not be correctly identified (specially the smaller and fainter ones). In practice we allow for a gap of up to two images. If a UD is present at nearly the same location on both sides of the gap, the tracking is continued. In this manner we found 12 836 UD trajectories that are weakly lowpass filtered in space (averaging the positions of the same UD in 15 consecutive images) in order to further reduce seeing-induced noise. From now, we call such a smoothed trajectory simply
trajectory. We note that 5949 of the 12 836 UDs are only identified in a single image. We decided not to ignore them, because these bright dots in the umbra are detected rather well, even if only for a very short time. We assigned a zero trajectory length and a lifetime of 20.57 s to these 5949 UDs.
A first impression of the temporal evolution of the smallest umbral structures is reached by making
a movie of the reconstructed time series of images. Some interesting phenomena are found by the
visual inspection of this movie and are explained briefly below.
The sunspot has two umbrae, a smaller and a roughly twice larger one separated by a light bridge (LB). The LB contains a clearly visible dark lane in agreement with the observations of, e.g., Berger & Berdyugina (2003). The lane is closer to the limbward edge of the LB. Possibly this is because the sunspot was observed at a heliocentric angle of 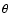 =
=
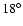 ,
so that projection
effects may cause the observed asymmetry (e.g. Lites et al. 2004). However, the LB also displays another major asymmetry: the movie exhibits many UDs that are born within the LB and move into the larger umbra, i.e. towards the solar disk center (arrow in Fig. 1), while almost no UD leaves the LB into the smaller umbra, i.e. towards the solar limb (antiparallel to the arrow).
,
so that projection
effects may cause the observed asymmetry (e.g. Lites et al. 2004). However, the LB also displays another major asymmetry: the movie exhibits many UDs that are born within the LB and move into the larger umbra, i.e. towards the solar disk center (arrow in Fig. 1), while almost no UD leaves the LB into the smaller umbra, i.e. towards the solar limb (antiparallel to the arrow).
The data clearly show that bright UDs often form chains. The most prominent chains often start
from a penumbral filament and UDs are found to move along the chain until they dissolve. The horizontal motion of the UDs is preferentially along the chain and is directed from the ends
of the chain to its center, where the UDs disappear. Figure 4 displays the
most prominent chain of UDs in the observed umbra. The length of this chain is about 3200 km and
it is about 350 km wide. In the left panel, from 08:58:56 UT, the chain appears as a simple
succession of UDs. One can see the same region in the right panel 28 min later. The appearance
of the chain changed and now the lower part of the chain looks similar to a narrow light bridge.
The typical dark lane of a LB can be seen clearly, even if we degrade the image quality to the
lower level of the left panel by convoluting the image with a point spread function of a circular
pupil (not shown). This degradation was carried out to compensate for the higher spatial resolution
of the later image. High spatial resolution is demonstrated by the presence of dark-cored penumbral
filaments (see Langhans et al. 2007), which are generally observed only at the highest resolution
in the blue. The presence of the dark lane is an indication that the chain eventually evolved into
a fully developed LB some hours after the end of the recording (Katsukawa et al. 2007).
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{0701fig4.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg16.gif) |
Figure 4:
Most prominent chain of umbral dots in the studied umbra, located near label A in Fig. 1 (FOV is 5.4 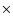 7.4 Mm). The left panel shows the chain composed of several typical UDs along a curved line at 08:58:56 UT. The right panel shows the same chain 28 min later. At this later time the lower half of the chain looks similar to a narrow light bridge. The typical dark lane is clearly recognizable.
7.4 Mm). The left panel shows the chain composed of several typical UDs along a curved line at 08:58:56 UT. The right panel shows the same chain 28 min later. At this later time the lower half of the chain looks similar to a narrow light bridge. The typical dark lane is clearly recognizable. |
| Open with DEXTER |
In some exceptional cases we observe the splitting of a single UD into two parts that continue their
life as independent UDs. Such a splitting is displayed in Fig. 5. It concerns a UD
located close to the penumbra, near point B in Fig. 1. The opposite case, the merging of two UDs into a single one, can also be observed in a few rare cases: see Fig. 6 for an example. Nearly identical phenomena in the temporal evolution of penumbral grains were observed by Hirzberger et al. (2002).
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{0701fig5.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg17.gif) |
Figure 5:
Splitting of an umbral dot near the position B in Fig. 1
(FOV is 1.2 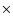 1.2 Mm). The red and yellow lines are the UD boundaries as detected by the
method explained in the main text.
1.2 Mm). The red and yellow lines are the UD boundaries as detected by the
method explained in the main text. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{0701fig6.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg18.gif) |
Figure 6:
Merging of two umbral dots near position C in Fig. 1
(FOV is 1.2 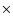 1.2 Mm). 1.2 Mm). |
| Open with DEXTER |
An interesting sequence of events is illustrated in Fig. 7. First the merging of two
UDs can be observed followed immediately afterwards by the splitting of the resulting, unified UD
into two new UDs. The sequence looks similar to an elastic impact in a Newton pendulum consisting of
two balls: the nearly motionless UD 1 is hit by the moving UD 2. The impact of the two UDs brings
the second UD to a standstill while the first UD starts to move roughly in the direction of the first UD. Note that this is simply an empirical description and we do not propose that this is what physically happens (or that the unified UD breaks up into the same parcels of gas which united to form it).
If two UDs come close to each other then the visual impression of a single UD exhibiting a
dark lane can occur, see last panel of Fig. 7 for an example. None of the UDs in our data set seems to stay in such a state for a significant fraction of the UD lifetime. Since the dark lanes as seen in the simulations of Schüssler & Vögler (2006) are visible for most of the UD lifetime, we conclude that we find no clear evidence for such dark lanes. This difference to the results of Bharti et al. (2007) and Rimmele (2008) may stem from the different wavelengths of the analyzed data. The wavelength can have a remarkable effect on the detected fine structure (e.g. Zakharov et al. 2008).
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{0701fig7.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg19.gif) |
Figure 7:
Elastic collision of two umbral dots. The sequence of events is seen near the position marked D in Fig. 1 (FOV is 0.9 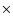 0.9 Mm). UD 2 moves towards UD 1 and merges with it, before separating from it again.
0.9 Mm). UD 2 moves towards UD 1 and merges with it, before separating from it again. |
| Open with DEXTER |
The properties of a UD change along its trajectory. In order to assign a property to the entire
trajectory we either average over all points along the trajectory (which is expressed by introducing an upper index ``Mean'') or we determine the maximum value reached by that parameter over all trajectory points (which is expressed by the upper index ``Max''), e.g.,
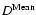 means
the UD diameter averaged along the trajectory, while
means
the UD diameter averaged along the trajectory, while
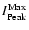 is the maximum value of all peak intensities along a UD trajectory (where the peak intensity is the largest intensity within the UD boundary at a given point in time).
is the maximum value of all peak intensities along a UD trajectory (where the peak intensity is the largest intensity within the UD boundary at a given point in time).
Figure 8 shows the best image with all identified UDs marked by circles. The
circles are centered on the positions of
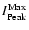 ,
i.e. the position of maximum intensity. In the left panel the circles have a constant radius, while their radii are proportional to
,
i.e. the position of maximum intensity. In the left panel the circles have a constant radius, while their radii are proportional to
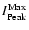 in the right panel. As a result we get an impression of the spatial distribution of UD occurrence as well as of the spatial distribution of UD brightness. Obviously, there is hardly any part of the umbra which does not support umbral dots. Only very localized small voids are visible. The brightness distribution of UDs, however, is rather inhomogeneous, with clear concentrations of bright UDs and regions harboring mainly dark UDs (mainly in the upper right part of the upper umbra and in the lower part of the lower one). Since the UDs of a chain (like the chain close to label A in Fig. 1 and shown in more detail in Fig. 4) appear to move along the chain and hardly in the direction perpendicular to it, there is often a narrow void directly beside the chain.
in the right panel. As a result we get an impression of the spatial distribution of UD occurrence as well as of the spatial distribution of UD brightness. Obviously, there is hardly any part of the umbra which does not support umbral dots. Only very localized small voids are visible. The brightness distribution of UDs, however, is rather inhomogeneous, with clear concentrations of bright UDs and regions harboring mainly dark UDs (mainly in the upper right part of the upper umbra and in the lower part of the lower one). Since the UDs of a chain (like the chain close to label A in Fig. 1 and shown in more detail in Fig. 4) appear to move along the chain and hardly in the direction perpendicular to it, there is often a narrow void directly beside the chain.
![\begin{figure}
\par\includegraphics[width=4.2cm,clip]{0701fig8a.eps}\includegraphics[width=4.2cm,clip]{0701fig8b.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg22.gif) |
Figure 8:
Spatial distribution of UD occurrence ( left panel) and UD maximum brightness ( right panel). Each UD is plotted only once along its entire trajectory, at the position of its maximum brightness. |
| Open with DEXTER |
The filling factor, i.e. the sum of all UD areas relative to the total umbral area, is correlated
to the image quality. Essentially, the filling factor is constant over the entire period of
observations (see Fig. 9), which is important for the later determination of the time dependence of their properties. On average we determine a value of about 11%. Figure 9 shows also the image contrast from an undisturbed granulation area outside the sunspot which demonstrates the high homogeneity of the image quality in our time series.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0701fig9.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg23.gif) |
Figure 9:
Dependence of UD filling factor (dotted blue line) and granulation contrast (solid black line) on the interval of time, t, since the first image of the series was recorded. |
| Open with DEXTER |
The histogram of the UD lifetimes is displayed in Fig. 10 with a logarithmic y axis. One can see that most of the UDs live for a short time. These short-lived UDs move over short distances which leads to physically nonsensical velocities due to the discretization of lifetime and distance. Consequently, when discussing trajectories and velocities of UDs we only consider the 2899 trajectories of UDs with lifetimes greater than 150 s. The histogram is nearly linear for lifetimes between 5 and 60 min, which, due to the logarithmic vertical scale, suggests an exponential distribution of lifetimes. The excess of UDs with short lifetimes may partly be due to seeing. Also given in Fig. 10 is the mean lifetime (180 s) and the median lifetime (41 s). If we consider only the 2899 trajectories of UDs with lifetimes greater than 150 s then we find a mean lifetime of 630 s and a median of 390 s. Note that 281 UDs are already present in the first image and 344 UDs are still present in the last image, whereas only one UD survives the whole sequence. Ignoring those 625 UDs reduces the mean lifetime from 180 s to 152 s. The median lifetime as well as the shape of the histogram do not change, because the number of incomplete UD trajectories is small compared to the total number of UDs. Thus we decided to neglect this effect and consider all 12 836 UDs in the following text.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0701fig10.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg24.gif) |
Figure 10:
Histogram of lifetimes T of all 12 836 UD trajectories (solid line) and their mean and median value (dashed lines and text labels). The bin size is 300 s. |
| Open with DEXTER |
The histogram of the mean UD diameters is plotted in Fig. 11a. The mean UD diameters vary between 50 and 750 km. The UDs have a mean diameter of around 229 km and 95% of the UDs are spatially resolved at our diffraction limit of 130 km. Sobotka & Hanslmeier (2005) found 175 km for the mean UD diameter. They determined the UD boundaries by finding all pixels with downward concavity, whereas we used all pixels whose intensity is greater than 50% of the
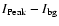 range,
range,
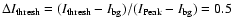 .
As one can see in Fig. 12 we would also find a mean UD diameter of 175 km if a threshold of about
.
As one can see in Fig. 12 we would also find a mean UD diameter of 175 km if a threshold of about
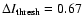 would be used. Nevertheless, we prefer to continue our analysis with a value of 0.5 in analogy to the FWHM definition. Clearly, the employed threshold influences the filling factor as well, roughly quadratically. Remarkably, the histogram is nearly symmetric, which supports the conclusion that most UDs have been resolved.
would be used. Nevertheless, we prefer to continue our analysis with a value of 0.5 in analogy to the FWHM definition. Clearly, the employed threshold influences the filling factor as well, roughly quadratically. Remarkably, the histogram is nearly symmetric, which supports the conclusion that most UDs have been resolved.
The histogram of the mean horizontal velocities, i.e. the quotient of trajectory length and lifetime, is plotted in Fig. 11b and exhibits a broad distribution from 0 to more than 1 km s-1 with a significant maximum at 350 m s-1. The velocity distribution is slightly asymmetric with a small tail to higher velocities. Figure 11c shows the histogram of the mean peak intensities, i.e. the mean of all peak intensities of the points along the trajectory. All intensities are normalized to the mean intensity of the quiet photosphere (
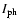 ). Just 3 of the 12 836 UDs reach a brightness greater than that of the quiet Sun, whereas most of the UDs are about half as bright as the quiet photosphere. The distribution is asymmetric, with a tail to higher intensities. Note that these brightnesses are strongly wavelength dependent and cannot be easily compared with values published in the literature (Solanki 2003). Lastly, the histogram of the distances between the UD's birth and death position (
). Just 3 of the 12 836 UDs reach a brightness greater than that of the quiet Sun, whereas most of the UDs are about half as bright as the quiet photosphere. The distribution is asymmetric, with a tail to higher intensities. Note that these brightnesses are strongly wavelength dependent and cannot be easily compared with values published in the literature (Solanki 2003). Lastly, the histogram of the distances between the UD's birth and death position (
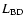 )
is given in Fig. 11d. With increasing distance the number of UDs decreases exponentially, so that only a few UDs travel over long distances in their life, most UDs do not leave the vicinity of their birth position. The maximum observed birth-death distance is 2 Mm, about 20% of the upper umbra's diameter of roughly 10 Mm.
)
is given in Fig. 11d. With increasing distance the number of UDs decreases exponentially, so that only a few UDs travel over long distances in their life, most UDs do not leave the vicinity of their birth position. The maximum observed birth-death distance is 2 Mm, about 20% of the upper umbra's diameter of roughly 10 Mm.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0701fig11a.eps}\hspace*{8m...
...ps}\hspace*{8mm}
\includegraphics[width=8.2cm,clip]{0701fig11d.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg29.gif) |
Figure 11:
Histogram of mean diameters a), mean horizontal velocities b), mean peak intensities c), and distances between birth and death position d). a), c), and d) are plotted for all 12 836 UD trajectories and b) for the 2899 trajectories of UDs that lived longer than 150 s. The location of the maximum, the mean, and the median of the distribution is indicated in each frame. The bin sizes are 30 km for a), 100 m s-1 for b), 0.03
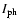 for c), and 90 km for d).
for c), and 90 km for d). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0701fig12.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg30.gif) |
Figure 12:
Mean UD diameter averaged over all trajectories as a function of the intensity threshold
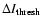 (defined in main text) that is used to determine the UD boundaries (see also Fig. 3 and its explanation).
(defined in main text) that is used to determine the UD boundaries (see also Fig. 3 and its explanation). |
| Open with DEXTER |
A UD size versus UD peak intensity scatterplot (Fig. 13) reveals that there is a weak correlation between UD size and brightness. The brightest UDs are not the biggest ones and large UDs are not the brightest ones. The solid green line connects binned values (obtained by averaging 100 data points with similar intensities) and shows that bright UDs are on average a bit larger than small ones. The relation found by Tritschler & Schmidt (2002) is qualitatively confirmed, although they only considered UD intensities in individual snapshots while we tracked the temporal development of the UDs over their lifetimes.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{0701fig13.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg31.gif) |
Figure 13:
Scatterplot of mean UD diameter versus mean peak intensity. The solid green line connects binned values. |
| Open with DEXTER |
The relation between a UD's mean size (i.e. the size averaged over the lifetime) and its lifetime is
plotted in Fig. 14 (the green curve is obtained after binning over 100 data points). The binned values show an increase in
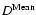 with increasing lifetimes for short-lived UDs. For the longer lived ones size and lifetime do not correlate. The UD sizes scatter more for short lifetimes. All long-lived UDs are of intermediate size of around 290 km. The large, short-lived UDs are all present in the first image of the time series, so that their lifetime would actually be larger if we had started our observation earlier.
with increasing lifetimes for short-lived UDs. For the longer lived ones size and lifetime do not correlate. The UD sizes scatter more for short lifetimes. All long-lived UDs are of intermediate size of around 290 km. The large, short-lived UDs are all present in the first image of the time series, so that their lifetime would actually be larger if we had started our observation earlier.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{0701fig14.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg32.gif) |
Figure 14:
Scatterplot of mean UD size versus lifetime. The solid green line connects binned values. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0701fig15a.eps}\includegraphics[width=7cm,clip]{0701fig15b.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg33.gif) |
Figure 15:
UD trajectories in the upper umbra. The bright ends of the trajectories denote the positions of the UD's birth and the dark ends show the position at death. The black contour line corresponds to the umbral boundary as detected in the best quality image. The left panel shows all UDs whose distance between the birth and the death position was greater than 750 km, the right panel shows all UDs with a birth-death distance smaller than 150 km whose lifetime was greater than 800 s. |
| Open with DEXTER |
In the literature we often find a separation into two UD classes, e.g. Grossmann-Doerth et al. (1986)
find a difference between peripheral and central UDs, i.e. between UDs that are born close to the umbra-penumbra boundary and UDs that are born deep in the umbra, whereas Hartkorn & Rimmele (2003) and Sobotka et al. (1997b) distinguish bright and dark UDs. We use different properties to find reasonable distinctions between types of UDs. E.g. from now on a given UD is called a peripheral UD (PUD) if the UD's birth position is closer than 400 km to the umbral boundary, otherwise it is termed a central UD (CUD). (The selected threshold comes from the histogram of the distances between the UD's birth position and the umbral boundary (not shown) which shows a maximum at around 400 km.) Alternatively, if the distance traveled between birth and death position is larger than 750 km then we call it a mobile UD, otherwise a stationary UD. (We plotted the trajectories of all UDs
whose
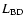 was greater than a threshold, which was determined by starting at a small value and increasing it step by step. We stopped at 750 km which is the smallest
was greater than a threshold, which was determined by starting at a small value and increasing it step by step. We stopped at 750 km which is the smallest
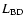 at which no trajectories occurred anymore in the central part of the umbra.) The aim here is not to separate UDs into distinct classes by a single property, e.g. a histogram of
at which no trajectories occurred anymore in the central part of the umbra.) The aim here is not to separate UDs into distinct classes by a single property, e.g. a histogram of
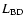 (Fig. 11d) does not show two peaks, even if restricted to long-lived UDs. However, as we shall see below the most mobile UDs are formed near the penumbra, while the least mobile ones are mainly formed deep in the umbra. Such a distinction may help to guide theory towards a better understanding of the origin and evolution of UDs with different properties and at different
locations.
(Fig. 11d) does not show two peaks, even if restricted to long-lived UDs. However, as we shall see below the most mobile UDs are formed near the penumbra, while the least mobile ones are mainly formed deep in the umbra. Such a distinction may help to guide theory towards a better understanding of the origin and evolution of UDs with different properties and at different
locations.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{0701fig16.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg34.gif) |
Figure 16:
Histogram of radial deflection angles
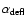 of all UD trajectories (solid black line) and of the mobile UD trajectories (dotted blue line).
of all UD trajectories (solid black line) and of the mobile UD trajectories (dotted blue line). |
| Open with DEXTER |
The strong concentration of bright UDs near the umbral boundary (or along proto-light bridges)
is already clear from Fig. 8 (right panel). Figure 15 shows a separation by birth-death distance. The left panel displays the longest UD trajectories, i.e. only the mobile UDs are shown. These UDs are also relatively long-lived. (Smallest lifetime of this UD class, that contains 85 UDs, is 15 min.) The right panel shows trajectories of long-lived UDs with a small birth-death distance. A clear separation by the birth position is readily identifiable. Almost all trajectories with a large birth-death distance start close to the umbra-penumbra boundary and these UDs move nearly radially into the umbra. A visual inspection of the movie of the reconstructed time series of images shows that many of these UDs are former penumbral grains that broke away from the penumbra. In contrast, many of the UDs with a small birth-death distance are born in the umbral interior and move along a closed loop or jitter around their birth position. We cannot say if this jitter has a physical background or if it is caused by residual seeing-induced noise. As mentioned in Sect. 3 we determined the umbral boundary individually for each image but we show only that corresponding to the best quality image as black contour line in Figs. 15,
17, and 18. Consequently some trajectories (or parts of them) are outside the black contour line, although they are always inside the umbra at the time of their occurrence (see, e.g., the bottom-left corner of the left plot of Fig. 15).
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0701fig17a.eps}\includegraphics[width=7cm,clip]{0701fig17b.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg35.gif) |
Figure 17:
UD trajectories in the upper umbra. The left panel shows all UDs with mean diameter greater than 350 km and the right panel shows all UDs with a mean peak intensity greater than 0.65
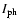 . . |
| Open with DEXTER |
Let us now consider more quantitatively the fact that the mobile UDs prefer to move radially towards the umbral center. Figure 16 displays a histogram of the UD's deflection angles
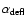 that is defined as angle between the line connecting the umbral center and the UD's birth position and the line connecting the UD's birth and death position. Radially directed inward flow will lead to
that is defined as angle between the line connecting the umbral center and the UD's birth position and the line connecting the UD's birth and death position. Radially directed inward flow will lead to
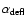 =
= 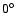 and an outward flow to
and an outward flow to
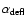 =
=
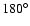 .
Obviously, this definition makes sense only for the 5689 UD trajectories that have different birth and death positions. The solid black line in Fig. 16 shows the histogram for all these UDs and exhibits a clear tendency for a radially directed inward motion (42% of the UDs are found to have a deflection angle lower than
.
Obviously, this definition makes sense only for the 5689 UD trajectories that have different birth and death positions. The solid black line in Fig. 16 shows the histogram for all these UDs and exhibits a clear tendency for a radially directed inward motion (42% of the UDs are found to have a deflection angle lower than
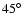 ). This tendency is much more significant if we only consider mobile UDs, see the dotted blue line (88% of the mobile UDs are found to have a deflection angle lower than
). This tendency is much more significant if we only consider mobile UDs, see the dotted blue line (88% of the mobile UDs are found to have a deflection angle lower than
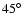 ). However, histograms calculated for central UDs and for peripheral UDs (not shown) lead, in principle, to the same shape as for all UDs, i.e. UDs born close to the penumbra do not show a significantly higher tendency of radially inward directed motion than the central UDs.
). However, histograms calculated for central UDs and for peripheral UDs (not shown) lead, in principle, to the same shape as for all UDs, i.e. UDs born close to the penumbra do not show a significantly higher tendency of radially inward directed motion than the central UDs.
The trajectories of large UDs are drawn in Fig. 17 (left panel). They are born throughout the umbra, with a tendency to cluster in the darker part of the umbra. The vicinity of the light bridge is avoided. This UD class contains long trajectories as well as short ones. The trajectories of the brightest UDs can be seen in the right panel of Fig. 17. These UDs all emerge close to the penumbra, the light bridge, or the prominent UD chain (label A in Fig. 1).
Many UDs with a preferred direction of motion arise near the light bridge. Most of the UDs that emerge on the disk center side of the light bridge (i.e. into the large umbra) move away from the light bridge while many of the limbside UDs (i.e. those formed in the small umbra) move towards the light bridge (see Fig. 18). A high density of UDs is formed by splitting off the light bridge, but all in one direction, in which the LB is corrugated and unsharp (disk center, large umbra side), while on its other straight and sharp side nearly no UDs leave the LB.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0701fig18.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg39.gif) |
Figure 18:
UD trajectories near the light bridge with birth-death distance greater than 300 km. |
| Open with DEXTER |
Table 1:
Characteristic values of UD parameters for different UD classes defined in the main text.
The mean diameter
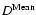 ,
mean horizontal velocity
,
mean horizontal velocity
 ,
mean peak intensity
,
mean peak intensity
 ,
mean intensity contrast
,
mean intensity contrast
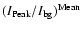 ,
lifetime T, birth-death distance
,
lifetime T, birth-death distance
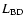 ,
trajectory length
,
trajectory length
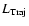 (see definitions of these quantities in the previous text), and the number of UDs N of the types or classes mentioned earlier in this section are summarized in Table 1. We averaged
over all trajectories of a UD class. The standard deviation
(see definitions of these quantities in the previous text), and the number of UDs N of the types or classes mentioned earlier in this section are summarized in Table 1. We averaged
over all trajectories of a UD class. The standard deviation 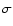 is given after each average value. As mentioned earlier, we consider only UDs that lived longer than 150 s in all cases in which we calculate the mean velocity; only the first line includes all UDs. The last two rows consider only UDs that are close to chain A or the light bridge, respectively. According to Table 1 the difference between peripheral UDs and central UDs is not so large (using the simple categorization described above). The largest relative difference is in the brightness. For all other parameters the difference is less than
is given after each average value. As mentioned earlier, we consider only UDs that lived longer than 150 s in all cases in which we calculate the mean velocity; only the first line includes all UDs. The last two rows consider only UDs that are close to chain A or the light bridge, respectively. According to Table 1 the difference between peripheral UDs and central UDs is not so large (using the simple categorization described above). The largest relative difference is in the brightness. For all other parameters the difference is less than 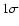 .
In contrast to that, the difference between mobile UDs and stationary UDs is more significant. A relatively large difference of more than
.
In contrast to that, the difference between mobile UDs and stationary UDs is more significant. A relatively large difference of more than 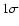 is found for the mean horizontal velocity, for the mean intensity contrast, for the lifetime, and, again for the brightness. On average mobile UDs are brighter, they move faster, and they live longer than stationary UDs but they have similar sizes.
is found for the mean horizontal velocity, for the mean intensity contrast, for the lifetime, and, again for the brightness. On average mobile UDs are brighter, they move faster, and they live longer than stationary UDs but they have similar sizes.
Sometimes one can observe complete chains of successive UDs that are very close to each other (see label A in Fig. 1 and the left panel of Fig. 4). According to Table 1 these UDs are relatively bright and they move along the chain from the endpoints of the chain towards its center, where they disappear. Their mean peak intensity is 0.68
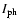 which is significantly higher than 0.51
which is significantly higher than 0.51
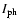 ,
the average of all UDs, but is comparable to that of the peripheral and mobile UDs. The mean diameter as well as the mean velocity of the UDs within the chain is slightly above average. Table 1 also reveals that UDs that are born close to the light bridge show on average a significantly higher brightness and contrast than the mean UD but all other properties do not show remarkable differences.
,
the average of all UDs, but is comparable to that of the peripheral and mobile UDs. The mean diameter as well as the mean velocity of the UDs within the chain is slightly above average. Table 1 also reveals that UDs that are born close to the light bridge show on average a significantly higher brightness and contrast than the mean UD but all other properties do not show remarkable differences.
The umbral background is brightest near the penumbra and gets darker towards the center of the umbra. Figure 19 shows that the UD peak intensity correlates with the umbral background intensity, with the mean ratio
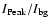 = 1.2
= 1.2 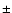 0.1 (intensity contrast). Sobotka & Hanslmeier (2005) found an intensity contrast of 1.8 for a wavelength of 451 nm and 1.6 for the wavelength 602 nm. Obviously, the intensity contrast not only depends on the wavelengths but also on the spatial resolution that can be slightly different even if we compare data from the same telescope. Additionally, the intensity contrast can also be affected by the subsonic filter and the MFBD image restoration we applied. Importantly, however, both binning the points in Fig. 19 (solid green curve) and a linear regression (dotted red curve) indicate that the contrast increases nearly linearly with
0.1 (intensity contrast). Sobotka & Hanslmeier (2005) found an intensity contrast of 1.8 for a wavelength of 451 nm and 1.6 for the wavelength 602 nm. Obviously, the intensity contrast not only depends on the wavelengths but also on the spatial resolution that can be slightly different even if we compare data from the same telescope. Additionally, the intensity contrast can also be affected by the subsonic filter and the MFBD image restoration we applied. Importantly, however, both binning the points in Fig. 19 (solid green curve) and a linear regression (dotted red curve) indicate that the contrast increases nearly linearly with
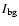 .
A scatter plot of the UD intensity
contrast versus the shortest distance between the UD birth position and the penumbra (not shown) reveals that this UD contrast is not constant over the umbra. The closer the UD is born to the penumbra the higher its intensity contrast, although the contrast does not drop as rapidly from the umbral boundary as the UD brightness does, so that partly, the dependence on distance is due to the dependence on
.
A scatter plot of the UD intensity
contrast versus the shortest distance between the UD birth position and the penumbra (not shown) reveals that this UD contrast is not constant over the umbra. The closer the UD is born to the penumbra the higher its intensity contrast, although the contrast does not drop as rapidly from the umbral boundary as the UD brightness does, so that partly, the dependence on distance is due to the dependence on
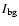 (Fig. 19). We also found that on average the long-lived UDs have a higher contrast than the short-lived ones.
(Fig. 19). We also found that on average the long-lived UDs have a higher contrast than the short-lived ones.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{0701fig19.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg48.gif) |
Figure 19:
UD peak intensity versus umbral background intensity. The solid green line connects binned values. The dashed cyan line displays the theoretical, lower limit of the peak intensities. A linear fit to the data results in the dotted red line. |
| Open with DEXTER |
In a further step we subdivided the umbra into several boxes and determined the probability that a UD is born in such a box. The map obtained in this manner shows a uniform distribution of the UD birth probability (not plotted). Only for very small box sizes do the dark umbral nuclei (see left panel of Fig. 8) become visible as locations of reduced UD production.
Finally, we are interested in the temporal evolution of the UD properties over their lifetimes. To this end we normalize all UD lifetimes to unity and average the temporal evolution of the diameters, peak intensities, intensity contrasts (
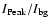 ), and horizontal velocities of the 2899 trajectories with T > 150 s. In order to weight all trajectories equally, i.e. independently of their lifetime, we up-sample all trajectories to 310 points of time via interpolation. (Our time series contains 310 images, so that no trajectory can consist of more than 310 points.) Then we averaged the UD parameters with the help of our binning method, which is applied separately for the 621 PUDs and the 2278 CUDs. Each bin contains 15 000 points for PUDs and 50 000 points for CUDs. The results are plotted in Fig. 20 and show that the mean PUD is smaller, brighter and moves faster than the mean CUD (as could already be deduced from Table 1). More importantly, there are distinct differences in their mean evolution. Whereas both types of UDs share the property that their diameters evolve rather moderately over time (the increase after birth and the decrease before death are less than 10% of the maximum diameter (see panel a), the evolution of their brightness (panel b) and in particular of their contrast (panel c) differ considerably. While the mean CUD displays an initial gentle brightening followed by an equally gentle darkening, the mean PUD darkens continuously. The small magnitude of the change in brightness may be due to the fact that we have averaged over UDs with very different absolute intensity. More information may be gleaned from the contrast, i.e. the peak intensity divided by the local umbral background intensity, plotted in panel (c). The mean PUD initially remains almost constant, exhibiting a slight maximum at around 1/3 of the mean lifetime before dropping rapidly over the remaining portion of its life. The contrast of the CUDs displays a much more symmetric
evolution. The birth velocity of the mean PUD is nearly 50 m s-1 higher than for the mean CUD, while the velocity at death of the two UD types is similar, see panel (d). Both velocity curves show an initial increase, followed by a decrease. As in the case of the contrast the velocity profile is
much more symmetric for the CUDs.
), and horizontal velocities of the 2899 trajectories with T > 150 s. In order to weight all trajectories equally, i.e. independently of their lifetime, we up-sample all trajectories to 310 points of time via interpolation. (Our time series contains 310 images, so that no trajectory can consist of more than 310 points.) Then we averaged the UD parameters with the help of our binning method, which is applied separately for the 621 PUDs and the 2278 CUDs. Each bin contains 15 000 points for PUDs and 50 000 points for CUDs. The results are plotted in Fig. 20 and show that the mean PUD is smaller, brighter and moves faster than the mean CUD (as could already be deduced from Table 1). More importantly, there are distinct differences in their mean evolution. Whereas both types of UDs share the property that their diameters evolve rather moderately over time (the increase after birth and the decrease before death are less than 10% of the maximum diameter (see panel a), the evolution of their brightness (panel b) and in particular of their contrast (panel c) differ considerably. While the mean CUD displays an initial gentle brightening followed by an equally gentle darkening, the mean PUD darkens continuously. The small magnitude of the change in brightness may be due to the fact that we have averaged over UDs with very different absolute intensity. More information may be gleaned from the contrast, i.e. the peak intensity divided by the local umbral background intensity, plotted in panel (c). The mean PUD initially remains almost constant, exhibiting a slight maximum at around 1/3 of the mean lifetime before dropping rapidly over the remaining portion of its life. The contrast of the CUDs displays a much more symmetric
evolution. The birth velocity of the mean PUD is nearly 50 m s-1 higher than for the mean CUD, while the velocity at death of the two UD types is similar, see panel (d). Both velocity curves show an initial increase, followed by a decrease. As in the case of the contrast the velocity profile is
much more symmetric for the CUDs.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0701fig20a.eps}\hspace*{8m...
...ps}\hspace*{8mm}
\includegraphics[width=8.2cm,clip]{0701fig20d.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg49.gif) |
Figure 20:
Temporal evolution of the UD diameter a), UD peak intensity b), intensity contrast c), and velocity d) separated for peripheral UDs (solid red line) and central UDs (dashed blue line). The UD lifetime is normalized to unity. |
| Open with DEXTER |
We have analyzed a time series of images of a mature sunspot close to solar disk center. Due to the excellent image quality we were able to resolve thousands of UDs. Exhaustive UD analyses can be found in earlier papers (Hartkorn & Rimmele 2003; Sobotka et al. 1997a,b; Sobotka & Hanslmeier 2005; Sobotka 2006),
but the present article is the first detailed UD study of a long time series of reconstructed images
with the consistent high resolution of a 1-m telescope.
Trajectories, lifetimes, diameters, horizontal velocities, peak intensities, and distances between
birth and death locations were determined by tracking single UDs over the time series. These
characteristic values were used to look for reasonable separations into UD classes. In the following we summarize the obtained results and compare them with other investigations in the literature:
- 1.
- There is hardly any part of the umbra which does not support UDs, but the UD brightnesses
depend strongly on the location within the umbra, which confirms the previous observation of
Sobotka et al. (1997b).
- 2.
- The histogram of lifetimes shows an exponential distribution, i.e. a UD does not have a typical lifetime. More than 3/4 of all studied UDs lived less than 150 s and their motion was negligible. The exponential distribution is in qualitative agreement with the results obtained
by Sobotka et al. (1997a,1999). Quantitatively, Sobotka et al. (1997a) obtains a median lifetime of 6 min for an umbra of about 6 Mm diameter and a median of 12 min for a 4 Mm pore (Sobotka et al. 1999), whereas we find a median value of 0.7 min for a roughly 10 Mm umbra. Note that these median values depend strongly on algorithmic constraints as well as on the cadence of the time series. For example, the method used by Sobotka et al. (1997a) cannot lead to lifetimes shorter than 1.5 min. If we only consider UDs with lifetimes greater than 1.5 min our median increases to 4.1 min. Irrespectively of which of these two values we use, our results are consistent with the conclusion of Sobotka et al. (1999) that UDs are more stable in a weak magnetic field if we assume a direct correlation between umbral diameter and magnetic field strength (cf. Kopp & Rabin 1992). Alternatively, due to the strong dependence of umbral brightness on umbral size (Mathew et al. 2007) the lifetime may be influenced mainly by the radiative flux or umbral temperature. The scatterplot of the mean umbral background intensities versus the UD lifetimes (not shown) is consistent with both possible explanations mentioned above: UDs live longer in brighter parts of the umbra. Due to the non-linear, monotonically decreasing relation between magnetic field strength and background intensity as observed by Kopp & Rabin (1992) and confirmed by Solanki et al. (1993); Martínez & Vázquez (1993), this implies that UDs live longer in regions of weak field.
- 3.
- The histogram of mean diameters exhibits a maximum at 225 km (0.31
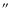 )
and
descends from there towards the diffraction limit, so that we expect the majority of UDs to have
been spatially resolved. This seems not to be the case in many of the earlier papers because there a monotonic decrease was obtained towards higher diameters (see Sobotka et al. 1997a,1999). Sobotka & Hanslmeier (2005) also analyzed data obtained with the 1-m SST. These data lead to a histogram that is qualitatively similar to ours. The mean diameter of 175 km (0.24
)
and
descends from there towards the diffraction limit, so that we expect the majority of UDs to have
been spatially resolved. This seems not to be the case in many of the earlier papers because there a monotonic decrease was obtained towards higher diameters (see Sobotka et al. 1997a,1999). Sobotka & Hanslmeier (2005) also analyzed data obtained with the 1-m SST. These data lead to a histogram that is qualitatively similar to ours. The mean diameter of 175 km (0.24
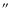 ), as well as the average filling factor of 9% is, however, noticeable smaller. This difference can be explained by the use of a different method to determine the UD boundary. An increase of our brightness threshold to determine the UD boundary leads to smaller diameters and to lower filling factors. Hamedivafa (2008) used an improved method of image segmentation and also found a mean diameter of 230 km and a similar shaped histogram.
), as well as the average filling factor of 9% is, however, noticeable smaller. This difference can be explained by the use of a different method to determine the UD boundary. An increase of our brightness threshold to determine the UD boundary leads to smaller diameters and to lower filling factors. Hamedivafa (2008) used an improved method of image segmentation and also found a mean diameter of 230 km and a similar shaped histogram.
- 4.
- The mean horizontal velocity of those of our UDs that live longer than 150 s is 420 m s-1 which is significantly higher than the 210 m s-1 reported by Molowny-Horas (1994) and higher than the 320 m s-1 found by Sobotka et al. (1999). In both studies the mean horizontal velocity was calculated by means of least-squares linear fits of the x and y coordinates of all trajectory points, which leads to an underestimation of velocity in case of curved trajectories. Our histogram of horizontal velocities shows a maximum at 350 m s-1, whereas some UDs can reach velocities above 1 km s-1. This is in qualitative agreement with the histograms of Kitai (1986), Molowny-Horas (1994), and Hamedivafa (2008) but disagrees with the results of Sobotka et al. (1999,1997b) whose histograms do not exhibit a maximum; they peak at zero velocity and show a monotonic decrease toward higher velocities of up to 1 km s-1. The majority of our UDs moves irregularly around the birth position. However, there are some mobile UDs that travel over long distances within their lifetime. Almost all mobile UDs emerge close to the umbral border, i.e. near the penumbra, they are brighter than the average and their horizontal motion is preferentially directed towards the center of the umbra. The mean velocity of our mobile UDs is 680 m s-1, which is in good agreement with the recent observation of Katsukawa et al. (2007) who found a mean velocity of 700 m s-1.
- 5.
- The relation between mean UD size and lifetime is non-linear. On average, the size of UDs
increases with lifetime, which was also found by Sobotka et al. (1997a), but in contrast to their
work we find a narrow size distribution of around 290 km for long-lived UDs.
- 6.
- UDs that were born close to the penumbra show a significantly higher contrast than the UDs of the umbral interior. The mean UD intensity contrast
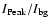 is 1.2 which is
smaller than the value of 1.6 reported by Sobotka & Hanslmeier (2005). This may partly be due to the
longer wavelength of our observation. Additionally, our statistical ensemble contains many more UDs.
In particular we took many UDs with low contrast into account, made possible by the multilevel
tracking technique (Bovelet & Wiehr 2001) we employed to identify UDs. Consequently, we believe that
the lower UD contrast we find is not due to a lower resolution or higher stray light, but rather
to differences in identification of UDs and in particular the difference in wavelength. We stress
that the UD contrast itself depends on the background intensity; the higher the intensity the
stronger the contrast. Also it cannot be ruled out that there could be systematically
different contrasts between different sunspots due to intrinsicly different physical properties of
the spots.
is 1.2 which is
smaller than the value of 1.6 reported by Sobotka & Hanslmeier (2005). This may partly be due to the
longer wavelength of our observation. Additionally, our statistical ensemble contains many more UDs.
In particular we took many UDs with low contrast into account, made possible by the multilevel
tracking technique (Bovelet & Wiehr 2001) we employed to identify UDs. Consequently, we believe that
the lower UD contrast we find is not due to a lower resolution or higher stray light, but rather
to differences in identification of UDs and in particular the difference in wavelength. We stress
that the UD contrast itself depends on the background intensity; the higher the intensity the
stronger the contrast. Also it cannot be ruled out that there could be systematically
different contrasts between different sunspots due to intrinsicly different physical properties of
the spots.
- 7.
- Whereas the temporal variation of the UD diameter is qualitatively similar for UDs formed
close to the penumbra (PUDs) and those formed in the body of the umbra (CUDs), their intensity
contrast and horizontal velocity display contrasting evolutions. The mean PUD shows a continuous
darkening which is in agreement with the results of Kitai et al. (2007) for a single typical PUD.
The typical CUD of Kitai et al. (2007) is found to increase in brightness linearly and then to darken
linearly with time, whereas our results for the mean CUD show a non-linear increase in brightness
until nearby half of the lifetime followed by an again non-linear decrease. The clear difference
between PUDs and CUDs in the behavior of their contrast and mean velocity may be a result of the
different origin of the two types of features (Kitai et al. 2007). We confirm from visual inspection
of a subset of PUDs that PUDs are formed when penumbral grains cross the umbral boundary.
A comparison of the results with the simulations of Schüssler & Vögler (2006) shows a better agreement
with CUDs, than PUDs. For example, the simulated UDs display a gradual increase in contrast followed by a gradual decrease, just as CUDs. They also display little proper motion. This qualitative
agreement further strengthens the interpretation of UDs as localized columns of overturning convection proposed by Schüssler & Vögler (2006). Hinode data had earlier suggested the presence of dark lanes in large UDs (Bharti et al. 2007) and revealed a decrease in the magnetic field strength with depth, as well as an upflow associated with a temperature enhancement (Riethmüller et al. 2008), in good qualitative agreement with the simulations. A detailed analysis of the simulations similar to the one carried out here would allow a more quantitative comparison.
The PUDs have significantly different evolution histories than the simulated features. They start
at a higher speed (Kitai 1986) and in particular display their maximum brightness rightafter the beginning of their life (cf. Kitai et al. 2007). This, combined with the fact that they are born very close to the penumbra, or actually by breaking away from the penumbra (Thomas & Weiss 2004), and move radially towards the umbral center (Kitai 1986) supports that these are two distinct types of UDs based on their origin and evolution, although their physical structure is relatively similar (Riethmüller et al. 2008).
-
Adjabshirzadeh, A., & Koutchmy, S. 1983, A&A, 121, 1 [NASA ADS]
(In the text)
-
Barrodale, I., Skea, D., Berkley, M., Kuwahara, R., & Poeckert,
R. 1993, Pattern Recognition, 26, 375 [CrossRef]
(In the text)
-
Berdyugina, S. V., Solanki, S. K., & Frutiger, C. 2003,
A&A, 412, 513 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Berger, T. E.,
& Berdyugina, S. V. 2003, ApJ, 589, L117 [NASA ADS] [CrossRef]
(In the text)
- Bharti, L.,
Joshi, C., & Jaaffrey, S. N. A. 2007, ApJ, 669,
L57 [NASA ADS] [CrossRef]
(In the text)
- Bovelet, B.,
& Wiehr, E. 2001, Sol. Phys., 201, 13 [NASA ADS] [CrossRef]
(In the text)
-
Choudhury, A. R. 1986, ApJ, 302, 809 [NASA ADS] [CrossRef]
(In the text)
-
Grossmann-Doerth, U., Schmidt, W., & Schröter, E. H.
1986, A&A, 156, 347 [NASA ADS]
(In the text)
-
Hamedivafa, H. 2008, Sol. Phys., in press
(In the text)
- Hartkorn,
K., & Rimmele, T. 2003, in Current Theoretical Models and
Future High-Resolution Solar Observations: Preparing for ATST,
ed. A. A. Pevtsov, & H. Uitenbroek, ASP Conf. Ser.,
286, 281
-
Hirzberger, J., Bonet, J. A., Sobotka, M., Vázquez, M., &
Hanslmeier, A. 2002, A&A, 383, 275 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
Katsukawa, Y., Yokoyama, T., Berger, T. E., et al. 2007, PASJ,
59, S577
(In the text)
- Kitai, R. 1986,
Sol. Phys., 104, 287 [NASA ADS] [CrossRef]
(In the text)
- Kitai, R.,
Watanabe, H., Nakamura, T., et al. 2007, PASJ, 59, S585
(In the text)
- Kopp, G., &
Rabin, D. 1992, Sol. Phys., 141, 253 [NASA ADS] [CrossRef]
(In the text)
- Langhans,
K., Scharmer, G. B., Kiselman, D., & Löfdahl, M. G.
2007, A&A, 464, 763 [NASA ADS] [CrossRef] [EDP Sciences]
- Lites, B. W.,
Scharmer, G. B., Berger, T. E., & Title, A. M. 2004, Sol.
Phys., 221, 65 [NASA ADS] [CrossRef]
(In the text)
-
Löfdahl, M. G. 2003, in Image Reconstruction from Incomplete
Data II, ed. P. J. Bones, M. A. Fiddy, &
R. P. Millane, Proc. SPIE, 4792, 146
(In the text)
-
Martínez Pillet, V., & Vázquez, M. 1993, A&A,
270, 494 [NASA ADS]
- Mathew, S. K.,
Martínez Pillet, V., Solanki, S. K., & Krivova,
N. A. 2007, A&A, 465, 291 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
Molowny-Horas, R. 1994, Sol. Phys., 154, 29 [NASA ADS] [CrossRef]
(In the text)
- November,
L. J., & Simon, G. W. 1988, ApJ, 333, 427 [NASA ADS] [CrossRef]
(In the text)
- Parker, E. N.
1979, ApJ, 234, 333 [NASA ADS] [CrossRef]
(In the text)
-
Riethmüller, T. L., Solanki, S. K., & Lagg, A. 2008, ApJ,
678, L157 [NASA ADS] [CrossRef]
(In the text)
- Rimmele, T.
2008, ApJ, 672, 684 [NASA ADS] [CrossRef]
(In the text)
- Scharmer,
G. B., Gudiksen, B. V., Kiselman, D., Löfdahl, M. G., &
Rouppe van der Voort, L. 2002, Nature, 420, 151 [NASA ADS] [CrossRef]
- Scharmer,
G. B., Bjelksjo, K., Korhonen, T. K., Lindberg, B., &
Petterson, B. 2003a, in Innovative Telescopes and Instrumentation
for Solar Astrophysics, ed. S. L. Keil, & S. V.
Avakyan, Proc. SPIE, 4853, 341
(In the text)
- Scharmer,
G. B., Dettori, P. M., Löfdahl, M. G., & Shand, M. 2003b,
in Innovative Telescopes and Instrumentation for Solar
Astrophysics, ed. S. L. Keil, & S. V. Avakyan,
Proc. SPIE, 4853, 370
(In the text)
- Scharmer,
G. B., Langhans, K., Kiselman, D., & Löfdahl, M. G.
2007, in New Solar Physics with the Solar-B Mission, ed. K.
Shibata, S. Nagata, & T. Sakurai, ASP Conf. Ser., 369, 71
-
Schüssler, M., & Vögler, M. 2006, ApJ, 641, L73 [NASA ADS] [CrossRef]
(In the text)
- Sobotka, M.
2006, Dissertation for Doctor Scientiarum, Acad. Sci. Czech
Republic
(In the text)
- Sobotka, M.,
& Hanslmeier, A. 2005, A&A, 442, 323 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Sobotka,
M., Brandt, P. N., & Simon, G. W. 1997a, A&A, 328,
682 [NASA ADS]
- Sobotka,
M., Brandt, P. N., & Simon, G. W. 1997b, A&A, 328,
689 [NASA ADS]
- Sobotka, M.,
Vázquez, M., Bonet, J. A., Hanslmeier, A., & Hirzberger,
J. 1999, A&A, 511, 436 [NASA ADS]
- Solanki, S.
K. 2003, A&ARv, 11, 153 [NASA ADS]
- Solanki, S.
K., Walther, U., & Livingston, W. 1993, A&A, 277, 639 [NASA ADS]
- Thomas, J. H.,
& Weiss, N. O. 2004, ARA&A, 42, 517 [NASA ADS] [CrossRef]
- Title, A. M.,
Tarbell, T. D., Topka, K. P., Ferguson, S. H., & Shine,
R. A. 1989, ApJ, 336, 475 [NASA ADS] [CrossRef]
(In the text)
-
Tritschler, A., & Schmidt, W. 2002, A&A, 388, 1048 [NASA ADS] [CrossRef] [EDP Sciences]
- Weiss, N. O.,
Brownjohn, D. P., Hurlburt, N. E., & Proctor,
M. R. E. 1990, MNRAS, 245, 434 [NASA ADS]
(In the text)
- Zakharov,
V., Hirzberger, J., Riethmüller, T. L., Solanki, S. K.,
& Kobel, P. 2008, A&A, 488, L17 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=4.2cm,clip]{0701fig1a.eps}\includegraphics[width=4.2cm,clip]{0701fig1b.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg9.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{0701fig4.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg16.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{0701fig7.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg19.gif)
![\begin{figure}
\par\includegraphics[width=4.2cm,clip]{0701fig8a.eps}\includegraphics[width=4.2cm,clip]{0701fig8b.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg22.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0701fig9.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg23.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0701fig10.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg24.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0701fig11a.eps}\hspace*{8m...
...ps}\hspace*{8mm}
\includegraphics[width=8.2cm,clip]{0701fig11d.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg29.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0701fig12.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg30.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{0701fig13.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg31.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{0701fig14.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg32.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0701fig15a.eps}\includegraphics[width=7cm,clip]{0701fig15b.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg33.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{0701fig16.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg34.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0701fig17a.eps}\includegraphics[width=7cm,clip]{0701fig17b.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg35.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{0701fig19.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg48.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0701fig20a.eps}\hspace*{8m...
...ps}\hspace*{8mm}
\includegraphics[width=8.2cm,clip]{0701fig20d.eps}
\end{figure}](/articles/aa/full/2008/46/aa10701-08/Timg49.gif)