A&A 492, 71-80 (2008)
DOI: 10.1051/0004-6361:200810168
A. Corral1,2 - M. J. Page3 - F. J. Carrera1 - X. Barcons1 - S. Mateos4 - J. Ebrero1 - M. Krumpe5 - A. Schwope5 - J. A. Tedds4 - M. G. Watson4
1 - Instituto de Física de Cantabria (CSIC-UC), 39005 Santander, Spain
2 - INAF - Osservatorio Astronomico di Brera, via Brera 28, 20121 Milan, Italy
3 - Mullard Space Science Laboratory, University College London, Holmbury St. Mary, Dorking, Surrey RH5 6NT, UK
4 - X-ray & Observational Astronomy Group, Department of Physics and Astronomy, University of Leicester, Leicester LE1 7RH, UK
5 - Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Postdam, Germany
Received 9 May 2008 / Accepted 17 September 2008
Abstract
Context. One of the most important parameters in the XRB (X-ray background) synthesis models is the average efficiency of accretion onto SMBH (super-massive black holes). This can be inferred from the shape of broad relativistic Fe lines seen in X-ray spectra of AGN (active galactic nuclei). Several studies have tried to measure the mean Fe emission properties of AGN at different depths with very different results.
Aims. We compute the mean Fe emission from a large and representative sample of AGN X-ray spectra up to redshift ![]() 3.5.
3.5.
Methods. We developed a method of computing the rest-frame X-ray average spectrum and applied it to a large sample (more than 600 objects) of type 1 AGN from two complementary medium sensitivity surveys based on XMM-Newton data, the AXIS and XWAS samples. This method makes use of medium-to-low quality spectra without needing to fit complex models to the individual spectra but with computing a mean spectrum for the whole sample. Extensive quality tests were performed by comparing real to simulated data, and a significance for the detection of any feature over an underlying continuum was derived.
Results. We detect with a 99.9![]() significance an unresolved Fe K
significance an unresolved Fe K![]() emission line around 6.4 keV with an EW
emission line around 6.4 keV with an EW ![]() 90 eV, but we find no compelling evidence of any significant broad relativistic emission line in the final average spectrum. Deviations from a power law around the narrow line are best represented by a reflection component arising from cold or low-ionization material. We estimate an upper limit for the EW of any relativistic line of 400 eV at a 3
90 eV, but we find no compelling evidence of any significant broad relativistic emission line in the final average spectrum. Deviations from a power law around the narrow line are best represented by a reflection component arising from cold or low-ionization material. We estimate an upper limit for the EW of any relativistic line of 400 eV at a 3![]() confidence level. We also marginally detect the so-called Iwasawa-Taniguchi effect on the EW for the unresolved emission line, which appears weaker for higher luminosity AGN.
confidence level. We also marginally detect the so-called Iwasawa-Taniguchi effect on the EW for the unresolved emission line, which appears weaker for higher luminosity AGN.
Conclusions. We computed an upper limit for the average relativistic Fe K![]() line contribution that is significantly lower than previously reported values from similar analyses. Our results, however, are in excellent agreement with individual analyses of local AGN samples. We attribute this difference either to our more sophisticated method of modeling the underlying continuum, to intrinsic differences in source populations, and/or to the uneven data quality of the individual spectra of the various samples.
line contribution that is significantly lower than previously reported values from similar analyses. Our results, however, are in excellent agreement with individual analyses of local AGN samples. We attribute this difference either to our more sophisticated method of modeling the underlying continuum, to intrinsic differences in source populations, and/or to the uneven data quality of the individual spectra of the various samples.
Key words: surveys - galaxies: active - X-rays: galaxies - X-rays: general - X-rays: diffuse background
The X-ray background (XRB) has been almost completely resolved into discrete sources at energies up to several keV, using X-ray surveys at different depths (see Gilli et al. 2007, for a recent review). The vast majority of the sources that comprise the XRB at these energies are active galactic nuclei (AGN). The integrated emission of AGN reflects the history of accretion onto super-massive black holes (SMBH) over cosmic time. In order to reproduce the shape and intensity of the XRB, synthesis models are constructed by using a mixture of AGN spectra. The most important physical parameters in these models are the AGN intrinsic column density and accretion-rate distribution and their evolution as a function of luminosity and redshift, as well as the average radiative efficiency of accretion onto SMBH. Since AGN emission comes from accretion onto SMBH, by comparing the energy radiated by distant AGN to the mean mass in local SMBH (Soltan 1982), an estimate of the efficiency of AGN in converting mass to energy - the mean radiative efficiency - can be computed. Following this argument, the mean radiative efficiency has been estimated to range from 10 to 15% (even more than 20% for the most massive systems) from recent studies (Elvis et al. 2002; Yu & Tremaine 2002; Marconi et al. 2005). Although this method suffers from several uncertainties, they can only lead to an underestimate of the radiative efficiency. The accretion efficiency depends on the orbit where most of the accretion material is located, the innermost stable circular orbit (ISCO). The ISCO, in turn, is a function of the SMBH spin. For a non-rotating Schwarzschild BH the efficiency is constrained to be below 6% (Lyden-Bell 1969). To achieve an efficiency stronger than this requires a rapidly rotating SMBH (Thorne 1974).
The mean accretion efficiency can be inferred from the relativistic profile of an emission line emitted close to the SMBH. Emission lines are usually seen in the X-ray spectrum of AGN, the Fe K![]() line (6.4-6.9 keV depending on ionization state) being the best studied
one. If the line is emitted close enough to the SMBH, it shows a broad relativistic profile which is more pronounced for higher SMBH spin due to the ISCO becoming smaller and therefore gravitational redshift (and other General Relativistic effects) being larger (Fabian et al. 1989; Laor 1991).
line (6.4-6.9 keV depending on ionization state) being the best studied
one. If the line is emitted close enough to the SMBH, it shows a broad relativistic profile which is more pronounced for higher SMBH spin due to the ISCO becoming smaller and therefore gravitational redshift (and other General Relativistic effects) being larger (Fabian et al. 1989; Laor 1991).
Early results from the ASCA era suggested that broad relativistic lines might be common in type 1 AGN. Surprisingly, however, they have been significantly detected and characterized in only a small number of sources (Reynolds & Nowak 2003), MCG-6-30-15 being the best studied one (Tanaka et al. 1995; Fabian & Vaughan 2003). The number of counts collected in the AGN X-ray spectra turns out to be the limiting factor, since very accurate modeling of the continuum below the line is critical to properly measure the line properties (Guainazzi et al. 2006). Another possibility, somewhat related to the previous one, is that the extreme
relativistic blurring along with high inclination angles can both widen and weaken the line making it undetectable (Fabian & Miniutti 2005). The direct average Fe line contribution to the XRB is therefore still unknown although it has been estimated to range from 3![]() to 7
to 7![]() (Gilli et al. 1999; Gandhi & Fabian 2003) depending on the assumptions made about the shape and equivalent width (EW). These assumptions affect the spectral templates used to compute the XRB, thus affecting its shape.
(Gilli et al. 1999; Gandhi & Fabian 2003) depending on the assumptions made about the shape and equivalent width (EW). These assumptions affect the spectral templates used to compute the XRB, thus affecting its shape.
Several studies have been performed over samples of local AGN in order to characterize Fe K![]() emission in the local Universe. Nandra et al. (2007) performed a spectral analysis of a sample of 26 type 1 to 1.9 Seyferts galaxies (z < 0.05) observed by XMM-Newton. They found that a relativistic line is significantly detected in half of their sample (54
emission in the local Universe. Nandra et al. (2007) performed a spectral analysis of a sample of 26 type 1 to 1.9 Seyferts galaxies (z < 0.05) observed by XMM-Newton. They found that a relativistic line is significantly detected in half of their sample (54 ![]() 10 per cent) with a mean EW of
10 per cent) with a mean EW of ![]() 80 eV, when fitted as a broad Gaussian. Guainazzi et al. (2006) and de La Calle et al. (in preparation) carried out a similar analysis over a larger sample of local type 1 and 2 radio-quiet AGN, excluding highly obscured type 2 sources. They detected relativistic lines in 25% (50% for well-exposed sources) of
their sample with an EW
80 eV, when fitted as a broad Gaussian. Guainazzi et al. (2006) and de La Calle et al. (in preparation) carried out a similar analysis over a larger sample of local type 1 and 2 radio-quiet AGN, excluding highly obscured type 2 sources. They detected relativistic lines in 25% (50% for well-exposed sources) of
their sample with an EW ![]() 200 eV. Both studies, although computing a similar average EW, found a high dispersion in the individual values. Nevertheless, this kind of analysis cannot be
extended to higher redshifts due to the more limited quality of the spectra of distant AGN. It is, however, at high redshift where the measurement of the accretion efficiency is most relevant to the
synthesis of the XRB.
200 eV. Both studies, although computing a similar average EW, found a high dispersion in the individual values. Nevertheless, this kind of analysis cannot be
extended to higher redshifts due to the more limited quality of the spectra of distant AGN. It is, however, at high redshift where the measurement of the accretion efficiency is most relevant to the
synthesis of the XRB.
Improving the signal to noise ratio (SNR) by averaging as many AGN spectra together as possible is the best solution since spectra of the same type of AGN are expected to display similar spectral characteristics. Recent studies have constructed X-ray averaged spectra for AGN but obtained differing results. In Streblyanska et al. (2005) (hereafter S05) the results of this kind of analysis are presented for 53 type 1 and 41 type 2 AGN in the pencil beam Lockman Hole XMM-Newton field (z < 4.5). They found a broad relativistic line in the final averaged spectra with an EW of 400 and 600 eV for type 2 and type 1 AGN, respectively. Brusa et al. (2005) found qualitatively similar results when stacking the AGN spectra contained in the 1 Ms Chandra Deep Field South in 7 different redshift bins from z = 0.5 to 4.0, the broad line EW being slightly weaker than in S05 but consistent within errors. Longinotti et al. (in preparation), stacked X-ray spectra from a local sample of AGN (extended from the sample of Guainazzi et al. 2006), and found that the EW for the broad relativistic contribution is never larger than 80 eV, either when stacking the whole sample or different sub-samples. Given this apparent divergence of results at high and low redshifts, it is vital to consider carefully and refine the averaging or stacking method applied to faint object spectra.
We present here a new method to construct a rest-frame X-ray averaged spectrum for a large sample of AGN at different redshifts, in order to characterize the mean Fe K![]() emission. We compiled a large sample of spectroscopically identified AGN from two wide angle and large but complementary medium sensitivity surveys: AXIS (An International XMM-Newton Survey; Carrera et al. 2007) in the Northern Hemisphere and XWAS (XMM-Newton Wide Angle Survey;
Tedds et al., in preparation) in the South in order to maximize the total number of counts. Since our sample is composed of low to medium quality X-ray spectra, we developed a method that takes into account the effects of the continuum emission around the emission line and the counting statistics, without needing to fit complex models to the individual spectra, but modelling the underlying continuum using simulations. We have extensively tested this method and a significance
for the emission line detection can be derived from it. Some results using this method were presented by us for a smaller sample of type 2 QSOs in Krumpe et al. (2008), hereafter K08, showing a strong FeK
emission. We compiled a large sample of spectroscopically identified AGN from two wide angle and large but complementary medium sensitivity surveys: AXIS (An International XMM-Newton Survey; Carrera et al. 2007) in the Northern Hemisphere and XWAS (XMM-Newton Wide Angle Survey;
Tedds et al., in preparation) in the South in order to maximize the total number of counts. Since our sample is composed of low to medium quality X-ray spectra, we developed a method that takes into account the effects of the continuum emission around the emission line and the counting statistics, without needing to fit complex models to the individual spectra, but modelling the underlying continuum using simulations. We have extensively tested this method and a significance
for the emission line detection can be derived from it. Some results using this method were presented by us for a smaller sample of type 2 QSOs in Krumpe et al. (2008), hereafter K08, showing a strong FeK![]() emission line in the final averaged spectrum but only for
the low luminosity sources.
emission line in the final averaged spectrum but only for
the low luminosity sources.
The paper is organized as follows: in Sects. 2 and 3 we describe the spectral extraction and the averaging method, respectively. In Sect. 4 we discuss the most important results for the total sample and different sub-samples. Conclusions are presented in Sect. 5. All the quoted errors are at the 1![]() confidence level throughout the paper. We assume H0 = 70
confidence level throughout the paper. We assume H0 = 70
![]() ,
,
![]() = 0.3 and
= 0.3 and
![]() = 0.7.
= 0.7.
We extracted the spectra for the XMS (XMM-Newton Medium Survey) fields within the AXIS sample (![]() 40 XMM-Newton observations) and the complete XWAS sample (
40 XMM-Newton observations) and the complete XWAS sample (![]() 150 XMM-Newton observations), but only included in our analysis those AGN that are optically identified as type 1 AGN in these fields, i.e., those AGN that show broad emission lines (velocity widths
150 XMM-Newton observations), but only included in our analysis those AGN that are optically identified as type 1 AGN in these fields, i.e., those AGN that show broad emission lines (velocity widths ![]() 1500
1500
![]() )
in their optical spectra. We selected only type 1 AGN due
to the larger number of sources and the better quality X-ray spectra for this type of object in both samples. Complete descriptions of both samples can be found in Carrera et al. (2007) and Tedds et al. (in preparation) for the AXIS and XWAS samples, respectively.
)
in their optical spectra. We selected only type 1 AGN due
to the larger number of sources and the better quality X-ray spectra for this type of object in both samples. Complete descriptions of both samples can be found in Carrera et al. (2007) and Tedds et al. (in preparation) for the AXIS and XWAS samples, respectively.
We processed the refinalized ODFs (observation data files) from the XMM-Newton archive using the Science Analysis Software (SAS![]() ) version 6.1.0 for the AXIS sample, and 6.5.0 for the XWAS sample, the latest software
and calibration available at the time of our spectral extraction (2006). We processed the ODFs in order to obtain the calibrated images and event lists using the SAS pipeline chains emchain and epchain for the EPIC-MOS and EPIC-pn data, respectively.
) version 6.1.0 for the AXIS sample, and 6.5.0 for the XWAS sample, the latest software
and calibration available at the time of our spectral extraction (2006). We processed the ODFs in order to obtain the calibrated images and event lists using the SAS pipeline chains emchain and epchain for the EPIC-MOS and EPIC-pn data, respectively.
After filtering out the event lists for high background intervals, we extracted the source spectra in circular regions maximizing the SNR for all detectors via the SAS task eregionanalyse. The
background spectra were taken in annular regions centered on the source position. If any other source falls within this region, we excluded the new source region from the background region. If the resulting background region was too small or fell near bright sources, we substituted it by a circular nearby source-free region. We selected single, double, triple and quadruple events in the MOS1 and MOS2 (pattern ![]() 12) and single and double events in the pn (pattern
12) and single and double events in the pn (pattern ![]() 4). For the pn we selected only high quality events (FLAG==0). We merged MOS1 and MOS2 spectra corresponding to the same source, observation and filter. We also obtained
response matrices for each individual source, camera and observation
via the SAS tasks rmfgen and arfgen.
4). For the pn we selected only high quality events (FLAG==0). We merged MOS1 and MOS2 spectra corresponding to the same source, observation and filter. We also obtained
response matrices for each individual source, camera and observation
via the SAS tasks rmfgen and arfgen.
In some cases, there is more than one observation of the same source. Since we do not expect individual source variability to significantly affect our results, we improved the spectral quality by merging the spectra for the same source, observed with the same EPIC camera, at a similar off-axis angle on the same CCD chip and with the same filter. If filter, CCD chip or off-axis were different the spectra were kept separate. The resulting individual pn and MOS spectra, even if corresponding to the same source, were treated as separate contributions to the final average spectrum.
After the spectral extraction and merging procedure, we selected only the spectra (pn or MOS) containing more than 80 counts in the total band (0.2-12 keV), in order to preserve a minimum spectral quality in the sample. This provided a sample of 606 optically identified type 1 AGN corresponding to more than 1000 individual pn and MOS spectra. Out of these 606 sources, 488 have been observed only once, 78 twice, 16 three times, 6 four times and 18 five times. Note that, having more than one observation does not mean having more than one spectrum, since the final number of spectra used depends on the merging procedure. The counts and redshift distributions, along with the flux distribution in the standard hard (2-10 keV) band, are shown in Fig. 1. It should be noted that we did not intend to construct a complete or flux-limited sample in any way, but to collect as many counts as possible in order to obtain a high SNR averaged spectrum. Therefore the sample comprises objects having a wide range of X-ray luminosities and redshifts. Fluxes are, however, mostly concentrated in the 10-14-10-13 erg cm-2 s-1 flux range, significantly (but not largely) brighter than those in the Lockman Hole sample studied in S05. Luminosities, however, are higher in average for the latter sample due to the redshift distribution peaking close to z=2, whereas it peaks closer to z=1 in our sample. In the stacking analysis presented in K08 all the available spectra are considered in the averaging procedure, no matter how many counts they have. Given that our sample is much larger than the one in K08, we can thus place a much more limiting constraint on the minimum spectral counts threshold so as to improve the quality of our final averaged spectrum.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.4cm,clip]{0168fg01.ps}\par...
...g02.ps}\par\includegraphics[angle=-90,width=7.4cm,clip]{0168fg03.ps}\end{figure}](/articles/aa/full/2008/46/aa10168-08/Timg13.gif) |
Figure 1: Top panel: redshift distribution. Central panel: counts distribution in the total band (0.2-12.0 keV). Bottom panel: flux distribution in the standard hard band (2.0-10.0 keV). |
| Open with DEXTER | |
Having extracted source and background spectra and generated response matrices for each source we next needed to unfold the spectra, i.e. to recover the original source spectra before detection prior to combining the intrinsic spectra from different sources.
To obtain the unfolded spectrum for each source, we used XSPEC v12.4 (Arnaud et al. 1996). We first grouped the spectra to have at least 10 counts per bin (the minimum number of counts required to use the ![]() minimization technique). We then used a single power law model corrected by photoelectric absorption, fixed at the Galactic value for each source position, and intrinsic photoelectric absorption at the source redshift. It should be noted that our intention was not to obtain the best fit parameters but a model good enough to unfold the spectrum without severe biases and to obtain simulated data that represent the actual shape of the
spectra (see Appendix A). In fact the small number of spectral counts for most of the sources did not allow us to fit a more complex model to the data. To avoid the contribution of any soft excesses we fitted each individual spectrum above 1 keV (rest-frame) leaving the intrinsic hydrogen column density, power law slope and normalization as free parameters. Then, we applied this ``best fit model'' to the ungrouped spectrum, obtaining the unfolded spectrum in physical units
(keV cm-2 s-1 keV-1) and free of instrumental effects (eufspec command in XSPEC). Note that given the small number of counts in the spectra presented in K08, their spectral fit was performed over the full energy range (0.2 to 12 keV) and the spectral slope was fixed to 1.9. It is known that performing the spectral fit in this way might introduce some biases, mostly
significant at low energies, that can affect the continuum shape due to the intrinsic absorption although not significantly affecting narrow features.
minimization technique). We then used a single power law model corrected by photoelectric absorption, fixed at the Galactic value for each source position, and intrinsic photoelectric absorption at the source redshift. It should be noted that our intention was not to obtain the best fit parameters but a model good enough to unfold the spectrum without severe biases and to obtain simulated data that represent the actual shape of the
spectra (see Appendix A). In fact the small number of spectral counts for most of the sources did not allow us to fit a more complex model to the data. To avoid the contribution of any soft excesses we fitted each individual spectrum above 1 keV (rest-frame) leaving the intrinsic hydrogen column density, power law slope and normalization as free parameters. Then, we applied this ``best fit model'' to the ungrouped spectrum, obtaining the unfolded spectrum in physical units
(keV cm-2 s-1 keV-1) and free of instrumental effects (eufspec command in XSPEC). Note that given the small number of counts in the spectra presented in K08, their spectral fit was performed over the full energy range (0.2 to 12 keV) and the spectral slope was fixed to 1.9. It is known that performing the spectral fit in this way might introduce some biases, mostly
significant at low energies, that can affect the continuum shape due to the intrinsic absorption although not significantly affecting narrow features.
Below 3 keV, the unfolding process is highly dependent on the model used, due to the shape of the effective area and the limited spectral resolution (FWHM ![]() 80 and 150 eV at 1 and 6.4 keV, respectively), meaning that caution must be applied in deriving any result in our
analysis of the final average spectrum below that energy. Narrow (unresolved) features, both in the model or in the data itself, could also affect the unfolding process above these energies. A narrow
emission (or absorption) line, for example, will be widened during the unfolding process if it is not included in the fitting model. Although less significant than the softer ones, these features should be taken into account very carefully, especially around the position where we
expect the Fe emission line, as they can distort its shape. Absorption edges are not expected to significantly affect the spectral shape at these energies due to the limited amount of absorption for type 1 AGN. Given the quality of our spectra, we cannot fit these features directly from the individual spectra, so we estimate their contribution to the continuum around the emission line position by using simulations, as we explain at the end of this section. Plots
showing the shape of the effective area and the effect of the absorption over a power law can be seen in Appendix A.
80 and 150 eV at 1 and 6.4 keV, respectively), meaning that caution must be applied in deriving any result in our
analysis of the final average spectrum below that energy. Narrow (unresolved) features, both in the model or in the data itself, could also affect the unfolding process above these energies. A narrow
emission (or absorption) line, for example, will be widened during the unfolding process if it is not included in the fitting model. Although less significant than the softer ones, these features should be taken into account very carefully, especially around the position where we
expect the Fe emission line, as they can distort its shape. Absorption edges are not expected to significantly affect the spectral shape at these energies due to the limited amount of absorption for type 1 AGN. Given the quality of our spectra, we cannot fit these features directly from the individual spectra, so we estimate their contribution to the continuum around the emission line position by using simulations, as we explain at the end of this section. Plots
showing the shape of the effective area and the effect of the absorption over a power law can be seen in Appendix A.
Once all the spectra are in physical units we corrected them for Galactic absorption (i.e., we de-absorb the spectrum) via a table model extracted from the phabs XSPEC model, and shift them to their rest frame using the redshifts derived from the optical identifications.
We require that each spectrum contributes with the same weight to the final averaged spectrum and the simplest way to achieve that, without distorting the individual spectral shape, is by dividing each spectrum by a certain value so that every rescaled spectrum has the same flux. Since the differences in spectral shapes could be important, the first issue we have to solve is to select a spectral range to achieve a rescaling not affected by spectral features. It is clear that we
must exclude the energy region where the Fe K![]() line is expected to fall but also exclude lower energy regions due to absorption effects. We also cannot include higher energies to avoid the
contribution of a spectral band where large errors are common. After testing several energy bands within the previous constraints and using simulated data, we selected the 2-5 keV band to rescale the spectra. Tests with our simulations showed that this band recovers the input spectral shape in the most accurate way while minimizing the errors. We then proceeded by computing the fluxes in the 2-5 keV rest-frame band for each spectrum and dividing each spectrum by its corresponding value so that all the rescaled spectra have the same 2-5 keV rest frame flux in units of keV cm-2 s-1.
line is expected to fall but also exclude lower energy regions due to absorption effects. We also cannot include higher energies to avoid the
contribution of a spectral band where large errors are common. After testing several energy bands within the previous constraints and using simulated data, we selected the 2-5 keV band to rescale the spectra. Tests with our simulations showed that this band recovers the input spectral shape in the most accurate way while minimizing the errors. We then proceeded by computing the fluxes in the 2-5 keV rest-frame band for each spectrum and dividing each spectrum by its corresponding value so that all the rescaled spectra have the same 2-5 keV rest frame flux in units of keV cm-2 s-1.
Although now rescaled, each spectrum was expressed on a different energy grid because of the different channel sizes at different energies and shifting to rest-frame. In order to achieve some
uniformity in the errors of the average spectrum across the whole energy band, we constructed a new energy grid for the final averaged rest-frame spectrum ensuring a minimum number of real source counts (![]() 1000) in each new bin. To select these new bins, we used the individual source spectra as measured in counts. We first shifted these spectra in counts to the rest frame, rebinned them to a common energy grid composed of narrow bins (bin widths
1000) in each new bin. To select these new bins, we used the individual source spectra as measured in counts. We first shifted these spectra in counts to the rest frame, rebinned them to a common energy grid composed of narrow bins (bin widths ![]() 40 eV) and added them all together. We then grouped the narrow bins so as to distribute the counts in the most uniform way and so that each new bin contains at least 1000 real source counts. We finally distributed the rescaled flux density values for each individual spectrum among the new energy bins in the following way:
40 eV) and added them all together. We then grouped the narrow bins so as to distribute the counts in the most uniform way and so that each new bin contains at least 1000 real source counts. We finally distributed the rescaled flux density values for each individual spectrum among the new energy bins in the following way:
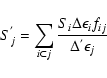 |
(1) |
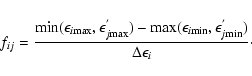 |
(2) |
Once we have the rest frame rescaled and rebinned spectra, we simply averaged them using an un-weighted standard mean. Because of the quite large dispersion in the redshift distribution, high energies are only significantly detected for a few objects. We did not take into account those spectral ranges that were not significantly represented by at least 10 contributing spectra. The individual errors were propagated as Gaussian during the entire process, the final errors being computed in the following way:
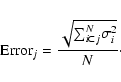 |
(3) |
The resulting averaged spectrum is shown in Fig. 2. We fit a power law between 2 and 10 keV, excluding the 4-7 keV range, obtaining a value of
![]()
![]() 0.02. We clearly see a narrow emission feature around 6.4 keV but also a broad excess of emission
from 5 to 10 keV. Instead of simply fitting a model to the final average spectrum and in order to derive a significance in the detection of the observed features, we decided to construct an
underlying continuum by using simulations. In this manner we could quantify how the results are affected by counting statistics, spectral features due to photoelectric absorption and the averaging method itself. An extensive discussion about the simulations that have been carried
out is presented in Appendix A.
0.02. We clearly see a narrow emission feature around 6.4 keV but also a broad excess of emission
from 5 to 10 keV. Instead of simply fitting a model to the final average spectrum and in order to derive a significance in the detection of the observed features, we decided to construct an
underlying continuum by using simulations. In this manner we could quantify how the results are affected by counting statistics, spectral features due to photoelectric absorption and the averaging method itself. An extensive discussion about the simulations that have been carried
out is presented in Appendix A.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{0168fg04.ps}\end{figure}](/articles/aa/full/2008/46/aa10168-08/Timg22.gif) |
Figure 2: Averaged spectrum along with the power law fit. |
| Open with DEXTER | |
In order to construct the underlying continuum against which we could search for any Fe emission or other spectral components, we simulated each individual source and background spectrum by using the XSPEC command fakeit. Each spectrum was simulated 100 times, including Poisson counting noise and keeping the same 2 to 8 keV observed flux, exposure time and calibration matrices as in the real data. We used the ``best-fit model'' (absorbed power-law) obtained when fitting the individual spectra and we applied to the simulated spectra exactly the same averaging method as for the real data. By simulating 100 times each source we were able to reduce spurious features as well
as to construct 100 absorbed power-law simulated continua. From these 100 simulated continua we could estimate the significance in the detection for any feature in the real averaged spectrum. By removing the 32 and 5 extreme values for each simulated continuum at each energy bin, we computed the normalized flux intervals that encompass 68% and 95% of the simulated values. Therefore, a spectral excursion above or below these limits is detected at the 1![]() or 2
or 2![]() level, respectively. Other spectral components or features, not taken into account in our simulations could contribute to the underlying continuum in the real spectra, but the construction of an
underlying continuum in this way allowed us to build a baseline spectrum that accounted for the absorbed power-law and for all the effects introduced by the averaging process.
level, respectively. Other spectral components or features, not taken into account in our simulations could contribute to the underlying continuum in the real spectra, but the construction of an
underlying continuum in this way allowed us to build a baseline spectrum that accounted for the absorbed power-law and for all the effects introduced by the averaging process.
The averaged spectrum, simulated continuum and 1![]() and 2
and 2![]() limits in each bin are shown in Fig. 3. We clearly see emission features between 5 and 10 keV but only the narrow peak is clearly above the 2
limits in each bin are shown in Fig. 3. We clearly see emission features between 5 and 10 keV but only the narrow peak is clearly above the 2![]() contour. We also see that some apparent deviations from a power law shape present in the averaged spectrum are also present in the simulated continuum. This result emphasizes the importance of properly computing the underlying continuum in order to fit the emission line.
contour. We also see that some apparent deviations from a power law shape present in the averaged spectrum are also present in the simulated continuum. This result emphasizes the importance of properly computing the underlying continuum in order to fit the emission line.
In order to check if a number of ``extreme'' sources are responsible for the observed emission features, we performed a safety test. We removed in each energy bin all the spectra that deviate more than 3 times the standard deviation from the average value. The resulting averaged spectrum shows the same overall shape as for the whole sample, the 5 to 10 keV emission residuals being smaller than the ones in Fig. 3, but consistent within errors. This could be due either to the fact that we are actually removing the sources that show more prominent emission in that range, or we are simply reducing the noise by removing the lowest quality spectra. In any case, the differences found are not significant.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{0168fg05.ps}\par\includegraphics[angle=-90,width=7.4cm,clip]{0168fg06.ps}\end{figure}](/articles/aa/full/2008/46/aa10168-08/Timg23.gif) |
Figure 3:
Top panel: averaged spectrum (error bars) along with the simulated continuum (open circles). Dotted and dashed lines represent the 1 |
| Open with DEXTER | |
Table 1: Best fit parameters.
Assuming the simulated continuum represents the actual underlying continuum below the emission features, we measured a total excess emission with EW of ![]() 600 eV, between 5 and
10 keV. Obviously, this value may correspond to the addition of multiple components in this range. As can be seen in Fig. 3, a relativistic profile is not clearly present in
the resulting averaged spectrum. However, a mixture of different relativistic profiles at different disk inclinations and innermost radii is not expected to result in a straightforward relativistic
profile. In the same way, a mixture of warm absorbers or reflection components should not be perfectly fitted by a one-component model of any of these kind of spectral features.
600 eV, between 5 and
10 keV. Obviously, this value may correspond to the addition of multiple components in this range. As can be seen in Fig. 3, a relativistic profile is not clearly present in
the resulting averaged spectrum. However, a mixture of different relativistic profiles at different disk inclinations and innermost radii is not expected to result in a straightforward relativistic
profile. In the same way, a mixture of warm absorbers or reflection components should not be perfectly fitted by a one-component model of any of these kind of spectral features.
We performed a spectral analysis of the averaged spectrum using XSPEC v12.4. We excluded energies above 15 keV where the errors were very large and also energies below 3 keV to avoid the
contribution of soft features that can be due to the unfolding procedure. As mentioned in Sect. 3.1, the spectral shape below 3 keV is highly dependent on the model used to unfold the spectra. Therefore, the apparent ``soft-excess'' below 2 keV and the ``absorption'' feature around 2.5 keV could be due to the averaging process and we should prevent ourselves from assigning them any physical meaning. In any case, the ``soft-excess'' accounts only for less than 5![]() of
the soft flux, and the ``absorption'' feature is barely significant.
of
the soft flux, and the ``absorption'' feature is barely significant.
We defined a ``baseline model'' composed of the following two components:
It has been claimed that complex absorption and high-density ionized absorbers can mimic the red tail of a broad relativistic line (Reeves et al. 2004; Turner et al. 2005). However, ionized absorbers are often observed in AGN and we find that adding cold (partially or totally covering the primary source) or warm (absori, Zdziarski et al. 1995) absorption does not improve the fit at all.
The next step was to fit a reflected component from neutral material (pexrav model, Magdziarz & Zdziarski 1995). We obtain an improvement on the fit of >3![]() significance level
(
significance level
(![]() /d.o.f. = 14/15), for a reflection fraction R
/d.o.f. = 14/15), for a reflection fraction R ![]() 0.5 (
0.5 (
![]()
![]() 0.5) and inclination angle i
0.5) and inclination angle i ![]() 60
60![]() ,
assuming solar Fe abundance. It should be noted
that we fitted a reflection model for a given inclination angle to a spectrum that corresponds to a mixture of different reflection components with different inclination angles. Unfortunately, the
quality of the averaged spectrum does not allow us to recover the inclination angle distribution for the sample so as to obtain an angle-average model. Leaving the Fe abundance free only results in a
slightly higher value for it and no significant improvement of the
,
assuming solar Fe abundance. It should be noted
that we fitted a reflection model for a given inclination angle to a spectrum that corresponds to a mixture of different reflection components with different inclination angles. Unfortunately, the
quality of the averaged spectrum does not allow us to recover the inclination angle distribution for the sample so as to obtain an angle-average model. Leaving the Fe abundance free only results in a
slightly higher value for it and no significant improvement of the ![]() .
Adding relativistic blurring to the reflected component (kdblur convolution model using a laor profile) did not improve the fit. Note that the amount of reflection along with the measured narrow Fe K
.
Adding relativistic blurring to the reflected component (kdblur convolution model using a laor profile) did not improve the fit. Note that the amount of reflection along with the measured narrow Fe K![]() EW are consistent with reflection from distant Compton-thick matter, such as the torus, for type 1 AGN (Reeves et al. 2003).
EW are consistent with reflection from distant Compton-thick matter, such as the torus, for type 1 AGN (Reeves et al. 2003).
We also tried to fit a reflected component from an ionized disk (reflion model, Ross & Fabian 1993). We obtained quite a good fit (![]() /d.o.f. = 19/16), slightly worse than the previous one, the disk being in a low-ionized state. Modifying it by relativistic blurring, we obtained a similar goodness of fit (
/d.o.f. = 19/16), slightly worse than the previous one, the disk being in a low-ionized state. Modifying it by relativistic blurring, we obtained a similar goodness of fit (![]() /d.o.f. = 15/16, all kdblur parameters fixed to their default values) as derived for the neutral reflection. However, studying this model in detail, we found it provides only an upper limit for the ionization parameter (
/d.o.f. = 15/16, all kdblur parameters fixed to their default values) as derived for the neutral reflection. However, studying this model in detail, we found it provides only an upper limit for the ionization parameter (![]() < 30, neutral to low
ionization disk), that pegs at the lower limit permitted by the model. Moreover, the effect of the relativistic blurring is to smear the emission lines to the point that the resulting shape is almost
identical to the pexrav model. Besides that, the fit does not depend on the remaining disk parameters and, allowing them to vary, results in unreasonable values, like an inclination angle for the disk higher than 60
< 30, neutral to low
ionization disk), that pegs at the lower limit permitted by the model. Moreover, the effect of the relativistic blurring is to smear the emission lines to the point that the resulting shape is almost
identical to the pexrav model. Besides that, the fit does not depend on the remaining disk parameters and, allowing them to vary, results in unreasonable values, like an inclination angle for the disk higher than 60![]() .
Therefore, we cannot distinguish (in terms of
.
Therefore, we cannot distinguish (in terms of
![]() )
between neutral reflection from distant material and ionized reflection from a low-ionization accretion disk. However, the computed parameters for the neutral reflection component, as long
as the central energy for the narrow Fe K
)
between neutral reflection from distant material and ionized reflection from a low-ionization accretion disk. However, the computed parameters for the neutral reflection component, as long
as the central energy for the narrow Fe K![]() line and its EW (6.36 keV and 90 eV, respectively), favor the neutral reflection scenario rather than the ionized one (Reeves et al. 2001; George & Fabian 1991). Furthermore, the relativistically
blurred low-ionization disk reflection just seems to be mimicking the neutral reflection shape instead of actually fitting relativistic effects.
line and its EW (6.36 keV and 90 eV, respectively), favor the neutral reflection scenario rather than the ionized one (Reeves et al. 2001; George & Fabian 1991). Furthermore, the relativistically
blurred low-ionization disk reflection just seems to be mimicking the neutral reflection shape instead of actually fitting relativistic effects.
As a safety test, we checked if the measured reflected component could be due to the dispersion in the power law indices, since a mixture of power laws should not result in a perfect power law shape. To this end, we simulate a Gaussian distribution of power law indices similar to the one presented in Mateos et al. (2005), with a mean spectral slope of 1.9 and an intrinsic dispersion of 0.23. We found that the deviation from a power law shape for the resulting averaged spectrum is too small to account for the observed residuals above 5 keV, thus supporting our refection component hypothesis.
We also attempted to fit the broad residuals by using a relativistic line model (laor model, Laor 1991). Leaving the line energy to vary results in an unreasonable value of ![]() 8 keV so, after trying several values between 6.4 and 6.9 keV, we decided to fix it to 6.4 keV. We found that the fit does not depend on the emissivity index nor the inner or outer radii. The only relevant parameter appears to be the inclination angle, but again, leaving it free to vary results in an unphysical large value (>80
8 keV so, after trying several values between 6.4 and 6.9 keV, we decided to fix it to 6.4 keV. We found that the fit does not depend on the emissivity index nor the inner or outer radii. The only relevant parameter appears to be the inclination angle, but again, leaving it free to vary results in an unphysical large value (>80![]() )
for type 1 AGN. Requiring such a large value for the inclination angle implies that the relativistic line is trying to fit the continuum as well as
the broad residuals. We therefore fixed the inclination angle to 30
)
for type 1 AGN. Requiring such a large value for the inclination angle implies that the relativistic line is trying to fit the continuum as well as
the broad residuals. We therefore fixed the inclination angle to 30![]() ,
a typical value for type 1 AGN (Antonucci 1993; Nandra et al. 2007; Guainazzi et al. 2006). We obtained in this way a barely acceptable fit (
,
a typical value for type 1 AGN (Antonucci 1993; Nandra et al. 2007; Guainazzi et al. 2006). We obtained in this way a barely acceptable fit (![]() /d.o.f. = 26/17), significantly worse than the neutral reflection model.
/d.o.f. = 26/17), significantly worse than the neutral reflection model.
The best-fit parameters corresponding to the models that significantly improve the ``baseline model'' fit are shown in Table 1. The fit corresponding to the ``baseline model'' plus neutral reflection, which seems to be the only physically plausible case, is shown in Fig. 4.
Adding a relativistic line to the ``baseline model'' plus cold reflected component does not improve the fit. We computed an upper limit for the EW of any broad relativistic line (for a Laor line
centered at 6.4 keV) of <400 eV at 3![]() confidence level, a value significantly below the 560 eV reported in S05. The reasons for these differing results could be as follows:
confidence level, a value significantly below the 560 eV reported in S05. The reasons for these differing results could be as follows:
![\begin{figure}
\par\includegraphics[angle=-90,width=7.1cm,clip]{0168fg07.ps}\end{figure}](/articles/aa/full/2008/46/aa10168-08/Timg56.gif) |
Figure 4: Spectral fit corresponding to: baseline model + pexrav. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.1cm,clip]{0168fg08.ps}\par...
...g09.ps}\par\includegraphics[angle=-90,width=7.1cm,clip]{0168fg10.ps}\end{figure}](/articles/aa/full/2008/46/aa10168-08/Timg57.gif) |
Figure 5: Soft (0.5-2.0 keV) Luminosity samples. Top panel: averaged spectrum with Gaussian fit for the low luminosity sample. Central panel: medium luminosity sample. Bottom panel: high luminosity sample. |
| Open with DEXTER | |
Table 2: Luminosity sub-samples.
Given the relatively large number of counts in the final averaged spectrum, we divided the sample into three different bins containing the same number of counts, in order to check for possible averaged spectral variations as a function of redshift, flux or luminosity. We did not detect any significant variation with redshift nor with flux, although we marginally detected a correlation of the narrow emission line EW with luminosity. As can be seen from Fig. 5 and Table 2, the narrow line EW decreases as the luminosity increases, a behaviour previously reported as the Iwasawa-Taniguchi or X-ray Baldwin effect (Iwasawa & Taniguchi 1993), but the errors are too large to extract conclusive results. The results that are presented both in the Fig. 5 and Table 2 correspond to the luminosity sub-samples selected in the soft band (0.5-2.0 keV) but we also observed this behavior when selecting in the hard (2.0-10.0 keV) and XID (0.5-4.5 keV) bands. Note that the tabulated values are very likely higher than the actual values since we are not fitting the reflection component in this case.
A similar result was found in K08. They found that low luminosity sources (0.5-10 keV luminosity <
![]() )
show a prominent emission line at
)
show a prominent emission line at ![]() 6.6 keV with an EW
6.6 keV with an EW ![]() 2 keV whereas high luminosity sources do not show any significant excess
emission in the 4 to 9 keV range.
2 keV whereas high luminosity sources do not show any significant excess
emission in the 4 to 9 keV range.
We developed a new method to obtain an X-ray averaged spectrum for AGN and applied it to the identified type 1 AGN in the XWAS and AXIS samples. We extensively checked this method and performed several tests by using simulated spectra. We also used a large set of simulated spectra to construct an underlying continuum against which the average spectrum is compared. We measured a spectral slope of
![]()
![]() 0.02 in the average spectrum. We significantly detect a narrow line at 6.36
0.02 in the average spectrum. We significantly detect a narrow line at 6.36 ![]() 0.05 keV corresponding to the Fe K
0.05 keV corresponding to the Fe K![]() emission line emitted from neutral (or low-ionization) material, i.e. far from the central engine, with an EW = 90
emission line emitted from neutral (or low-ionization) material, i.e. far from the central engine, with an EW = 90 ![]() 30 eV. This result is in agreement with several studies of local AGN showing that a narrow Fe K
30 eV. This result is in agreement with several studies of local AGN showing that a narrow Fe K![]() emission line, displaying similar characteristics, is almost universally present in the X-ray spectra
of nearby AGN.
emission line, displaying similar characteristics, is almost universally present in the X-ray spectra
of nearby AGN.
We do not significantly detect any significant broad relativistic emission line, although some positive residuals can be seen in the 5 to 10 keV region. We find that the continuum shape is best represented by reflection from neutral or low-ionization material rather than by a relativistic iron line, also consistent with studies of local AGN. The presence of a mixture of low EW relativistic lines is not completely excluded, which might suggest a small amount of emitting material close to the ISCO. We obtained an upper limit for the corresponding EW
of 400 eV at a 3![]() significance level, a value significantly lower than the one presented in Streblyanska et al. (2005). This difference can be attributed either to our more sophisticated treatment of the underlying continuum or to a difference in the source populations themselves. To test these hypotheses, we are increasing the number of sources in our sample and
constructing a large sample of type 2 AGN, by adding data from both deeper and shallower samples. Results from these new samples will be presented in a forthcoming paper.
significance level, a value significantly lower than the one presented in Streblyanska et al. (2005). This difference can be attributed either to our more sophisticated treatment of the underlying continuum or to a difference in the source populations themselves. To test these hypotheses, we are increasing the number of sources in our sample and
constructing a large sample of type 2 AGN, by adding data from both deeper and shallower samples. Results from these new samples will be presented in a forthcoming paper.
Our results are very important for one of the central scientific goals of the XEUS![]() mission, which is to detect growing AGN at significant redshifts (z
mission, which is to detect growing AGN at significant redshifts (z ![]() 5-10). Although XEUS is being designed to have the sensitivity to detect these sources, their identification will not be a trivial task, even in the 2020's with an expected plethora of large observatories at all wavelengths. However, our result that a narrow Fe line is common in type 1 AGN in the distant Universe, with an EW
5-10). Although XEUS is being designed to have the sensitivity to detect these sources, their identification will not be a trivial task, even in the 2020's with an expected plethora of large observatories at all wavelengths. However, our result that a narrow Fe line is common in type 1 AGN in the distant Universe, with an EW ![]() 100 eV, confirms the expectation that redshifts can be obtained for these early AGN from their X-ray spectrum directly.
100 eV, confirms the expectation that redshifts can be obtained for these early AGN from their X-ray spectrum directly.
Acknowledgements
Partial financial support for this work was provided by the Spanish Ministerio de Educación y Ciencia under project ESP2006-13608. A.C. acknowledges financial support from a Spanish Ministerio de Educación y Ciencia fellowship and also from the MIUR and The Italian Space Agency (ASI) grants PRIN-MUR 2006-02-5203 and n. I/088/06/0. M.J.P., S.M., J.A.T. and M.G.W. acknowledge support from the UK STFC research council. M.C. is supported by the Deutsches Zentrumfuer Luft-und Raumfahrl (DLR) GmbH under contract No. FKZ50 OR 0404. We thank the referee, Bev Wills, for useful suggestions.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.4cm,clip]{0168fg11.ps}\end{figure}](/articles/aa/full/2008/46/aa10168-08/Timg68.gif) |
Figure A.1:
Model: po. Simulated average spectrum corresponding to 10 simulated spectrum for each real spectrum and a simple power law model, |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.6cm,clip]{0168fg12.ps}\end{figure}](/articles/aa/full/2008/46/aa10168-08/Timg69.gif) |
Figure A.2:
Model: pha*po. Simulated average spectrum corresponding to 10 simulated spectrum for each real spectrum and a power law ( |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{0168fg13.ps}\par\includegraphics[angle=-90,width=7.25cm,clip]{0168fg14.ps}\end{figure}](/articles/aa/full/2008/46/aa10168-08/Timg70.gif) |
Figure A.3: Top panel: effective area corresponding to an individual observation for pn (solid line) and MOS cameras (dashed line). Bottom panel: pha*po models for different amounts of absorption: no absorption (solid line), 1020 cm-2 (dashed line), 1021 cm-2 (dash-dotted line), 1022 cm-2 (dotted line), 1023 cm-2 (dash-dot-dot-dotted line). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.6cm,clip]{0168fg15.ps}\end{figure}](/articles/aa/full/2008/46/aa10168-08/Timg71.gif) |
Figure A.4:
Model: pha*zpha*po. Simulated average spectrum corresponding to 10 simulated spectrum for each real spectrum and a power law ( |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{0168fg16.ps}\end{figure}](/articles/aa/full/2008/46/aa10168-08/Timg72.gif) |
Figure A.5:
Model: po+gaus: simulations without noise corresponding to E=6.4 keV, |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.6cm,clip]{0168fg17.ps}\par...
...g18.ps}\par\includegraphics[angle=-90,width=7.6cm,clip]{0168fg19.ps}\end{figure}](/articles/aa/full/2008/46/aa10168-08/Timg73.gif) |
Figure A.6: Top panel: model: pha*zpha*(po+gaus): simulated average spectrum corresponding to 10 simulated spectra for each real spectrum (squares) and the ``best-fit model'' continuum (circles). Central panel: simulations pha*zpha*(po+gaus) to power law ratio. Bottom panel: simulations pha*zpha*(po+gaus) to ``best-fit model'' continuum ratio. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.6cm,clip]{0168fg20.ps}\end{figure}](/articles/aa/full/2008/46/aa10168-08/Timg74.gif) |
Figure A.7:
Average continuum with 100 simulations (circles) along with the power law fit (2-10 keV) and the 1 |
| Open with DEXTER | |
In order to distinguish between real spectral features and artifacts from both the averaging process and/or the individual spectral shape around a possible emission line, we carried out extensive quality tests by using simulated spectra. Our strategy can be summarized as follows: we simulate N times each source, including Poisson counting noise, keeping the same 2-8 keV observed flux and exposure time as in the real spectrum along with the same calibrations files. We then applied to the simulated spectra exactly the same averaging method as for the real spectra. We also tested how the spectral model, noise and number of simulations affected the final averaged simulated spectra.
First, we performed 10 simulations for each source, in order to reduce both noise and spurious features, using a simple power law model with ![]() = 1.9 constant (XSPEC model: po). The resulting averaged spectrum is shown in Fig. A.1. We fitted a power law between 2 and
10 keV obtaining a
= 1.9 constant (XSPEC model: po). The resulting averaged spectrum is shown in Fig. A.1. We fitted a power law between 2 and
10 keV obtaining a ![]() (2-10 keV) = 1.89
(2-10 keV) = 1.89 ![]() 0.01 and we did not detect any significant features. We also checked for the effect of not including Poisson noise and increasing the fluxes, obtaining the same result but with smaller errors.
0.01 and we did not detect any significant features. We also checked for the effect of not including Poisson noise and increasing the fluxes, obtaining the same result but with smaller errors.
Our method includes the correction for the Galactic absorption for each source, so we needed to check how this correction affects the average spectrum. We then simulated 10 times each source with a power law model (![]() = 1.9) modified by Galactic absorption (XSPEC model: pha*po). The resulting average spectrum is shown in Fig. A.2. We again measured
= 1.9) modified by Galactic absorption (XSPEC model: pha*po). The resulting average spectrum is shown in Fig. A.2. We again measured ![]() (2-10 keV) = 1.89
(2-10 keV) = 1.89 ![]() 0.01 and did not detect any significant features. We can conclude that the
correction for the Galactic absorption does not affect the results significantly.
0.01 and did not detect any significant features. We can conclude that the
correction for the Galactic absorption does not affect the results significantly.
Once we had tested that the method and the counting statistics do not significantly affect the results, we had to test how narrower spectral features propagate through our averaging and analytic procedures. It is well known that intrinsic absorption, along with warm absorption and reflection components, can significantly affect the continuum below the Fe emission lines. Unfortunately, the spectral quality of most of our spectra did not allow us to fit complex models and subtract them in order to obtain a pure emission line spectrum. Besides, the unfolding procedure itself can also affect the spectra due to the shape of the effective area (see Fig. A.3), although it has been tested that this does not significantly affect the spectral shape above 3 keV.
In order to quantify the effect of intrinsic absorption, we used the ``best fit model'' we obtained for the real spectra (an absorbed power law XSPEC model: pha*zpha*po) and simulated 10 times each source, Fig. A.4. We can see broad features above 4 keV, and we measured a ![]() (2-10 keV) = 1.81
(2-10 keV) = 1.81 ![]() 0.01, thus the average spectrum is affected by the intrinsic absorption above 3 keV and it has to be accounted for very carefully. As an example, in
Fig. A.3 we show the variation in the spectral shape for a power law (
0.01, thus the average spectrum is affected by the intrinsic absorption above 3 keV and it has to be accounted for very carefully. As an example, in
Fig. A.3 we show the variation in the spectral shape for a power law (![]() = 1.9) as the amount of absorption increases from 1020 to 1023 cm-2 (at a typical spectral resolution), although only 5
= 1.9) as the amount of absorption increases from 1020 to 1023 cm-2 (at a typical spectral resolution), although only 5![]() of the type 1 AGN in our sample show an intrinsic
absorption above 1022 cm-2.
of the type 1 AGN in our sample show an intrinsic
absorption above 1022 cm-2.
To test how narrow features are treated by our method, we simulated a power law plus an intrinsically unresolved emission line (![]() = 0). To avoid the contribution from the noise, we did not include Poisson noise this time and increased the source flux by a large factor. We were not interested in effects introduced at these low fluxes or counting statistics but only in the effects due to the process and the redshift distribution over a narrow feature. We simulated once each source, using a power law plus a Gaussian emission line (XSPEC model: po+gaus) with the following parameters:
= 0). To avoid the contribution from the noise, we did not include Poisson noise this time and increased the source flux by a large factor. We were not interested in effects introduced at these low fluxes or counting statistics but only in the effects due to the process and the redshift distribution over a narrow feature. We simulated once each source, using a power law plus a Gaussian emission line (XSPEC model: po+gaus) with the following parameters: ![]() = 1.9, E = 6.4 keV,
= 1.9, E = 6.4 keV, ![]() = 0 and EW = 200 eV, rest-frame
values. The result is presented in Fig. A.5. We can see how the process and the EPIC spectral resolution widen the line giving a value of
= 0 and EW = 200 eV, rest-frame
values. The result is presented in Fig. A.5. We can see how the process and the EPIC spectral resolution widen the line giving a value of ![]()
![]() 100 eV, but we recovered the initial values for the remaining parameters (
100 eV, but we recovered the initial values for the remaining parameters (![]() ,
E and EW). We therefore see that
our averaging method introduces a
,
E and EW). We therefore see that
our averaging method introduces a ![]() 100 eV broadening on narrow features that we subtract in quadrature from fitted values.
100 eV broadening on narrow features that we subtract in quadrature from fitted values.
At this point we still needed to quantify how absorption could affect the shape of an emission line. To achieve this, we added a Gaussian emission line to the ``best fit model'' and ran the
simulations using this model (XSPEC model: pha*zpha*(po+gaus)). Figure A.6 (top) shows the simulations for a Gaussian line centered at E = 6.4 keV with ![]()
![]() 100 eV and EW = 100 eV (rest-frame values) along with the simulations for the ``best-fit model'' (XSPEC model: pha*zpha*po). We can see that the line shape appears distorted towards
low energies mimicking a broad tail, but this feature is also present in the pha*zpha*po simulations. If we fit a power law in the 2-10 keV range, excluding the emission line region (4-7 keV), and compute the ratio between the pha*zpha*(po+gaus) model and this power law, we
obtain the ratio shown in Fig. A.6 (central). The line shape is clearly distorted and some residuals below 6 keV can be seen. Notwithstanding, if we use the simulations without a line as an underlying continuum to obtain the ratio, Fig. A.6 (bottom), we find that the process slightly widens the line due to the unfolding and the different energy resolutions at different energies, but it does not vary the line shape nor its EW, recovering
the input parameters within errors. We also tested if changing the line width, EW and central energy did not affect significantly our conclusions, always recovering the input values within errors when using the pha*zpha*po simulations as the underlying continuum.
100 eV and EW = 100 eV (rest-frame values) along with the simulations for the ``best-fit model'' (XSPEC model: pha*zpha*po). We can see that the line shape appears distorted towards
low energies mimicking a broad tail, but this feature is also present in the pha*zpha*po simulations. If we fit a power law in the 2-10 keV range, excluding the emission line region (4-7 keV), and compute the ratio between the pha*zpha*(po+gaus) model and this power law, we
obtain the ratio shown in Fig. A.6 (central). The line shape is clearly distorted and some residuals below 6 keV can be seen. Notwithstanding, if we use the simulations without a line as an underlying continuum to obtain the ratio, Fig. A.6 (bottom), we find that the process slightly widens the line due to the unfolding and the different energy resolutions at different energies, but it does not vary the line shape nor its EW, recovering
the input parameters within errors. We also tested if changing the line width, EW and central energy did not affect significantly our conclusions, always recovering the input values within errors when using the pha*zpha*po simulations as the underlying continuum.
To minimize the distortion introduced by the averaging method and the intrinsic absorption for a possible emission line, we decide to use this simulated continuum as an underlying continuum for our real average spectrum. Instead of simulating each source 10 times we used 100 simulations per real source, so we were able to construct 100 simulated continua. From these 100 simulated continua we could quantify the significance of any excursion over this continuum by constructing confidence limits, i.e. flux intervals per each energy grid in which a number of simulations is contained (see
Fig. A.7). For the 100-simulations continuum we fitted a power law between 2 and 10 keV obtaining ![]() = 1.96
= 1.96 ![]() 0.01, close to the mean value for the real sample. Although the continuum shape does not show prominent features the confidence contours display an
increasing dispersion towards high energies and around the position where the Fe K
0.01, close to the mean value for the real sample. Although the continuum shape does not show prominent features the confidence contours display an
increasing dispersion towards high energies and around the position where the Fe K![]() line is expected to fall. Therefore, this must be taken into account when fitting a possible broad line as it could be very much affected by these continuum features.
line is expected to fall. Therefore, this must be taken into account when fitting a possible broad line as it could be very much affected by these continuum features.