A&A 492, 185-195 (2008)
DOI: 10.1051/0004-6361:200809996
M. Hareter1 - O. Kochukhov2 - H. Lehmann3 - V. Tsymbal1,4 - D. Huber1 - P. Lenz1 - W. W. Weiss1 - J. M. Matthews5 - S. Rucinski6 - J. F. Rowe6 - R. Kuschnig1 - D. B. Guenther7 - A. F. J. Moffat8 - D. Sasselov9 - G. A. H. Walker6 - A. Scholtz10
1 - Institut für Astronomie, Universität Wien, Türkenschanzstrasse 17, 1180 Vienna, Austria
2 - Department of Physics and Astronomy, Uppsala University, Box 515, 751 20 Uppsala, Sweden
3 - Thüringer Landessternwarte Tautenburg, 07778 Tautenburg, Germany
4 - Tavrian National University, Dep. Astronomy, Simferopol, Ukraine
5 - Department of Physics & Astronomy, University of British Columbia, 6224 Agricultural Road, Vancouver, B.C., V6T 1Z1, Canada
6 - David Dunlap Observatory, Department of Astronomy, University of Toronto, Toronto, Ontario, L4C 4Y6, Canada
7 - Department of Astronomy and Physics, St. Mary's University, Halifax, Nova Scotia, NS B3H 3C3, Canada
8 - Département de physique, Université de Montréal, Montréal, Québec, QC H3C 3J7, Canada
9 - Harvard-Smithsonian Center for Astrophysics, Cambridge, Massachusetts, MA 02138, USA
10 - University of Technology, Institute of Communications and Radio-Frequency Engineering, Gusshausstrasse 25/389, 1040 Vienna, Austria
Received 17 April 2008 / Accepted 3 October 2008
Abstract
Context. A field star, HD 61199 (
![]() ), simultaneously observed with Procyon by the MOST (Microvariability & Oscillations of STars) satellite in continuous runs of 34, 17, and 34 days in 2004, 2005, and 2007, was found to pulsate in 11 frequencies in the
), simultaneously observed with Procyon by the MOST (Microvariability & Oscillations of STars) satellite in continuous runs of 34, 17, and 34 days in 2004, 2005, and 2007, was found to pulsate in 11 frequencies in the ![]() Scuti range with amplitudes from 1.7 down to 0.09 mmag. The photometry also showed variations with a period of about four days. To investigate the nature of the longer period, 45 days of time-resolved spectroscopy was obtained at the Thüringer Landessternwarte Tautenburg in 2004. The radial velocity measurements indicate that HD 61199 is a triple system.
Scuti range with amplitudes from 1.7 down to 0.09 mmag. The photometry also showed variations with a period of about four days. To investigate the nature of the longer period, 45 days of time-resolved spectroscopy was obtained at the Thüringer Landessternwarte Tautenburg in 2004. The radial velocity measurements indicate that HD 61199 is a triple system.
Aims. A ![]() Scuti pulsator with a rich eigenspectrum in a multiple system is promising for asteroseismology. Our objectives were to identify which of the stars in the system is the
Scuti pulsator with a rich eigenspectrum in a multiple system is promising for asteroseismology. Our objectives were to identify which of the stars in the system is the ![]() Scuti variable and to obtain the orbital elements of the system and the fundamental parameters of the individual components, which are constrained by the pulsation frequencies of the
Scuti variable and to obtain the orbital elements of the system and the fundamental parameters of the individual components, which are constrained by the pulsation frequencies of the ![]() Scuti star.
Scuti star.
Methods. Classical Fourier techniques and least-squares multi-sinusoidal fits were applied to the MOST photometry to identify the pulsation frequencies. The groundbased spectroscopy was analysed with least-squares-deconvolution (LSD) techniques, and the orbital elements derived with the KOREL and ORBITX routines. Asteroseismic models were also generated.
Results. The photometric and spectroscopic data are compatible with a triple system consisting of a close binary with an orbital period of 3.57 days and a ![]() Scuti companion (HD 61199 A) as the most luminous component. The
Scuti companion (HD 61199 A) as the most luminous component. The ![]() Scuti star is a rapid rotator with about
Scuti star is a rapid rotator with about ![]() = 130
= 130
![]() and an upper mass limit of about 2.1
and an upper mass limit of about 2.1 ![]() .
For the close binary components, we find they are of nearly equal mass, with lower mass limits of about 0.7
.
For the close binary components, we find they are of nearly equal mass, with lower mass limits of about 0.7 ![]() .
Comparisons to synthetic spectra indicate these stars have a late-F spectral type. The observed oscillation frequencies are compared to pulsation models to further constrain the evolutionary state and mass of HD 61199 A. The orbit frequency of the close binary corresponds to the difference of the two
.
Comparisons to synthetic spectra indicate these stars have a late-F spectral type. The observed oscillation frequencies are compared to pulsation models to further constrain the evolutionary state and mass of HD 61199 A. The orbit frequency of the close binary corresponds to the difference of the two ![]() Scuti frequencies with the highest amplitudes - a coincidence that is remarkable, but not explained.
Scuti frequencies with the highest amplitudes - a coincidence that is remarkable, but not explained.
Key words: binaries: close - stars: variables: ![]() Scuti - techniques: photometric - techniques: spectroscopic - techniques: radial velocities
Scuti - techniques: photometric - techniques: spectroscopic - techniques: radial velocities
The ![]() Scuti variables are stars of intermediate mass located in the classical instability strip near the main sequence, which pulsate in radial and nonradial acoustic (p-) modes driven by opacity effects; see review by Breger (2000). Asteroseismic modelling of
Scuti variables are stars of intermediate mass located in the classical instability strip near the main sequence, which pulsate in radial and nonradial acoustic (p-) modes driven by opacity effects; see review by Breger (2000). Asteroseismic modelling of ![]() Scuti stars has been a challenge, even in cases where dozens of
pulsation frequencies have been identified - e.g., FG Vir Breger et al. (2005) and HD 209775 Matthews (2007) - because the theoretical eigenspectra are so densely populated with frequencies. Constraining the fundamental parameters of a
Scuti stars has been a challenge, even in cases where dozens of
pulsation frequencies have been identified - e.g., FG Vir Breger et al. (2005) and HD 209775 Matthews (2007) - because the theoretical eigenspectra are so densely populated with frequencies. Constraining the fundamental parameters of a ![]() Scuti star in a multiple system through its orbital elements is one possible avenue to a
unique asteroseismic model of the star.
Scuti star in a multiple system through its orbital elements is one possible avenue to a
unique asteroseismic model of the star.
HD 61199 (V = 7.97) was observed by MOST, a Canadian space telescope dedicated to high-precision photometry of bright stars, in 2004, because it happened to lie in the field of MOST's first primary science target, Procyon (Matthews et al. 2004). Little was known about HD 61199 beyond its HD Catalogue classification as an
A3 star. Gatewood & Han (2006) give a parallax of ![]() mas and likely luminosity class of V (see their Table 2, in which HD 61199 corresponds to AO 1098). The 2004 MOST photometry showed clear oscillations with periods in the
mas and likely luminosity class of V (see their Table 2, in which HD 61199 corresponds to AO 1098). The 2004 MOST photometry showed clear oscillations with periods in the ![]() Scuti range, plus an obvious variation with a periodicity near 4 days. If the latter was due to rotational modulation, it would have given the rotation period of the star and helped for more clearly interpreting and modelling any rotational splitting in the pulsation spectrum. Because of this possibility, groundbased spectroscopy was obtained in 2004 from Thüringer Landessternwarte Tautenburg to investigate the HD 61199 system further. The star was again monitored by MOST in 2005 and 2007 as part of subsequent Procyon photometric runs.
Scuti range, plus an obvious variation with a periodicity near 4 days. If the latter was due to rotational modulation, it would have given the rotation period of the star and helped for more clearly interpreting and modelling any rotational splitting in the pulsation spectrum. Because of this possibility, groundbased spectroscopy was obtained in 2004 from Thüringer Landessternwarte Tautenburg to investigate the HD 61199 system further. The star was again monitored by MOST in 2005 and 2007 as part of subsequent Procyon photometric runs.
Photometric indices are available for HD 61199, which can be employed to obtain an initial estimation of the stellar parameters. We have used TempLoggTNG (Kupka & Bruntt 2001; Kaiser 2006) and published Strömgren indices
b-y = 0.125, m1 = 0.192, c1 = 0.931 and
![]() (Hauck & Mermilliod 1998) for various calibrations to calculate values of
(Hauck & Mermilliod 1998) for various calibrations to calculate values of
![]() ranging from
ranging from
![]() to
to
![]() and
and ![]() from 3.94 to 3.80 (see Table 1), based on different calibrations (Napiwotzki et al. 1993; Balona 1984; Ribas et al. 1997; Moon 1986). These values were derived from the combined light of the triple system and imply a spectral type of A7 or A8, significantly later than the HD classification. The uncertainties in the individual temperature determinations are at least 200 K, and in the surface gravities, at least 0.3 dex.
from 3.94 to 3.80 (see Table 1), based on different calibrations (Napiwotzki et al. 1993; Balona 1984; Ribas et al. 1997; Moon 1986). These values were derived from the combined light of the triple system and imply a spectral type of A7 or A8, significantly later than the HD classification. The uncertainties in the individual temperature determinations are at least 200 K, and in the surface gravities, at least 0.3 dex.
Table 1:
![]() and
and ![]() of HD 61199 derived from published Strömgren colours.
of HD 61199 derived from published Strömgren colours.
HD 61199 is kinematically similar to DG Leo (Frémat et al. 2005), where two Am stars form a binary system and a third more distant component is a ![]() Scuti star. This system is bright enough to decide which star is pulsating by means of radial velocity variations, what would need larger telescopes for HD 61199.
Scuti star. This system is bright enough to decide which star is pulsating by means of radial velocity variations, what would need larger telescopes for HD 61199.
The MOST photometry and data reduction is presented in Sect. 2, followed by the frequency analysis in Sect. 3. The spectroscopy and their analyses are described in Sect. 4, and the resulting fundamental parameters and orbital solution are presented. Asteroseismology is attempted in Sect. 5, where the observed pulsation frequencies are compared to models.
The Canadian MOST (Microvariability & Oscillations of STars) microsatellite houses a 15-cm telescope feeding a CCD photometer through a single broadband optical filter. For descriptions of the MOST mission before and after launch, see Walker et al. (2003) and Matthews (2004). MOST's Sun-synchronous 820-km polar orbit (period = 101.4 min) allows uninterrupted observations of a target located in the satellite's continuous viewing zone for up to 8 weeks. MOST now can collect, simultaneously, three types of photometric data: (a) Fabry Imaging - in which the telescope entrance pupil is imaged as an annulus (diameter ![]() 40 pixels), for very bright stars (``Fabry Targets''), minimizing the influence of satellite pointing jitter and cosmic ray strikes on the photometry, and enhancing the total signal (Matthews 2004). (b) Direct Imaging - in which a slightly defocused image of a star (a ``Direct Imaging Target'') is projected directly onto the CCD (Rowe et al. 2006). (c) Guide Star photometry - in which photometry of up to about 30 stars used for MOST's startracking attitude control system is processed on board and downlinked to Earth. Since MOST's launch in June 2003 and its commissioning, the MOST team has improved the pointing performance of the satellite, improving the Direct Imaging photometric performance. The
Guide Star photometry mode was implemented during the mission as well, but was not available during the 2004 observations of HD 61199 presented here.
40 pixels), for very bright stars (``Fabry Targets''), minimizing the influence of satellite pointing jitter and cosmic ray strikes on the photometry, and enhancing the total signal (Matthews 2004). (b) Direct Imaging - in which a slightly defocused image of a star (a ``Direct Imaging Target'') is projected directly onto the CCD (Rowe et al. 2006). (c) Guide Star photometry - in which photometry of up to about 30 stars used for MOST's startracking attitude control system is processed on board and downlinked to Earth. Since MOST's launch in June 2003 and its commissioning, the MOST team has improved the pointing performance of the satellite, improving the Direct Imaging photometric performance. The
Guide Star photometry mode was implemented during the mission as well, but was not available during the 2004 observations of HD 61199 presented here.
HD 61199 was observed simultaneously with Procyon from Jan. 8 to Feb. 9, 2004 and from Jan. 24 to Feb. 10, 2005 as a Direct Imaging Target, and from Jan. 4 to Feb. 12, 2007 as a Guide Star Target. The integration times were about 1 s in the first two runs, while the effective integration time was 24.8 s in the 2007 run (in which short exposures were stacked on board). Table 2 lists details for the photometry. The pointing performance and other aspects of MOST photometry during the 2007 Procyon were the best achieved to that point in the mission, resulting in significantly reduced point-to-point scatter.
Table 2: Details of the MOST photometry of HD 61199.
For the Direct Imaging photometry of HD 61199 in 2004 and 2005, a reduction routine developed by Huber & Reegen (2008) was used, similar to the decorrelation technique developed by Reegen et al. (2006) for MOST Fabry Imaging, but which also takes into account satellite pointing errors. Both techniques decorrelate the signal present in the target pixels with those in the background pixels. The 2007 Guide Star photometry of HD 61199 is handled in a similar way, but for these data, there is no direct information about the background sky in each Guide Star subraster. The on-board Guide Star data processing is performed as follows: a Guide Star is sampled within a
![]() pixel subraster. The subrasters are read out roughly every second and the average of the first and last columns of the subraster are used for an on-board background correction. This procedure is repeated until the final integration time of the Primary Science Target in the field is reached. Then the individual background-corrected pixel intensities are integrated. Only this sum and the Guide Star exposure time are stored in the FITS header of the Primary Science Target data file which is downloaded. Residual stray light due to scattered Earthshine remains in the Guide Star light curves sent to Earth. Fortunately, the modulation of the stray light with the MOST orbital period is well known, and 15 Guide Stars were observed simultaneously with HD 61199 allowing for a modified decorrelation technique using non-variable stars in the field to correct for residual instrumental and
background variations.
pixel subraster. The subrasters are read out roughly every second and the average of the first and last columns of the subraster are used for an on-board background correction. This procedure is repeated until the final integration time of the Primary Science Target in the field is reached. Then the individual background-corrected pixel intensities are integrated. Only this sum and the Guide Star exposure time are stored in the FITS header of the Primary Science Target data file which is downloaded. Residual stray light due to scattered Earthshine remains in the Guide Star light curves sent to Earth. Fortunately, the modulation of the stray light with the MOST orbital period is well known, and 15 Guide Stars were observed simultaneously with HD 61199 allowing for a modified decorrelation technique using non-variable stars in the field to correct for residual instrumental and
background variations.
Figure 1 shows the reduced MOST light curves of HD 61199 for the three observing runs and their respective spectral windows are shown in Fig. 2. The low-amplitude alias sidelobes visible in the spectral window of the 2007 data, spaced by the MOST satellite orbital frequency (164 ![]() Hz
Hz ![]() 14.192 d-1),
are due to our more conservative rejection of outliers in the Guide Star reduction. This procedure is producing more gaps when stray light is highest at certain phases in the MOST orbit than in the 2004 and 2005 Direct Imaging reductions.
14.192 d-1),
are due to our more conservative rejection of outliers in the Guide Star reduction. This procedure is producing more gaps when stray light is highest at certain phases in the MOST orbit than in the 2004 and 2005 Direct Imaging reductions.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9996fig1.eps}
\end{figure}](/articles/aa/full/2008/46/aa09996-08/Timg22.gif) |
Figure 1: MOST light curves of HD 61199 from 2004 ( top panel), 2005, and 2007 ( bottom panel). The solid line shows a running average of 600 data points. |
| Open with DEXTER | |
The decorrelation method reduced the amplitudes of orbitally-modulated background variations in the Guide Star data to about 8% of the raw values. For the final light curve of the 2007 run, a second-order trend (possibly due to long-term stellar variability or subtle instrumental effects) was subtracted. The subtraction of this polynomial fit affects neither the identified frequencies nor their amplitudes, which were checked by comparing the discrete Fourier transform spectra before and after subtraction.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9996fig2.eps}
\end{figure}](/articles/aa/full/2008/46/aa09996-08/Timg23.gif) |
Figure 2: Spectral windows for 2004, 2005 and 2007 from top to bottom. Aliasing is practically not present in the Direct Imaging data of 2004 and 2005. The more restrictive outlier rejection policy in the Guide Star photometry of 2007 affects the spectral window more than the Direct Imaging reduction. |
| Open with DEXTER | |
SigSpec (Reegen 2007) and Period04 (Lenz & Breger 2005) were adopted for the frequency analysis. SigSpec performs iterative prewhitening of the data with the most significant frequency found in each iteration. The iterations end if a specified threshold is reached; the default value is 5.5 in spectral significance (Reegen 2007), corresponding to a signal-to-noise (S/N) ratio in amplitude of about 4. A peak identified with a significance of 5.5 means that a similar peak has a probability of only 10-5.5 of being produced by white noise (i.e., once in
![]() cases).
cases).
Figure 3 shows the Fourier amplitude spectra of the individual observing runs. Frequencies were searched in the range 0-80 d-1, down to a significance limit of 5.5. The final set of 13 adopted frequencies listed in Table 3 includes only those which could be detected in all three runs, where 11 of
the frequencies are in the ![]() Scuti domain, and the other two are close to 0.25 d-1(f3 and f7). The uncertainties of the frequencies and amplitudes are calculated according to the technique of Kallinger et al. (2008). Based on extensive simulations, those authors find that the frequency errors are overestimated when using the classical Fourier T-1 criterion. They propose instead:
Scuti domain, and the other two are close to 0.25 d-1(f3 and f7). The uncertainties of the frequencies and amplitudes are calculated according to the technique of Kallinger et al. (2008). Based on extensive simulations, those authors find that the frequency errors are overestimated when using the classical Fourier T-1 criterion. They propose instead:
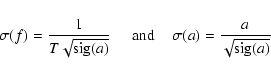
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9996fig3.eps}
\end{figure}](/articles/aa/full/2008/46/aa09996-08/Timg28.gif) |
Figure 3: Fourier amplitude spectra of the 2004 ( top), 2005 ( middle) and 2007 ( bottom) light curves. Power due to the stray light modulation with the MOST orbit is present, but with significantly reduced amplitudes compared to the raw data. The vertical dashed lines indicate the MOST orbital frequency, its harmonics and its 1 d-1 sidelobes. (The MOST Sun-synchronous orbit carries it above nearly the same point on Earth after 1 day, resulting in a secondary modulation of the scattered Earthshine.) |
| Open with DEXTER | |
Table 3: List of identified frequencies and amplitudes in the three MOST data sets.
The amplitudes a in Table 3 were calculated from the combined light of the system, which we know to be triple (see Sect. 4). Therefore, the intrinsic amplitudes are actually higher by the inverse fraction of light of the pulsating component. We show in Sect. 4 that about 80% of the total flux can be attributed to the ![]() Scuti star in the system. Hence, a scaling factor of 1.25 is needed to obtain the intrinsic amplitude. In addition, the pulsation amplitudes do show evidence of variability across the three runs, particularly for f4, as can be seen in Fig. 4. At this stage of the investigation, we can only speculate if this variability is due to unresolved beating frequencies or due to another effect. In a recent study, Breger & Lenz investigated possible explanations for amplitude variability in the
Scuti star in the system. Hence, a scaling factor of 1.25 is needed to obtain the intrinsic amplitude. In addition, the pulsation amplitudes do show evidence of variability across the three runs, particularly for f4, as can be seen in Fig. 4. At this stage of the investigation, we can only speculate if this variability is due to unresolved beating frequencies or due to another effect. In a recent study, Breger & Lenz investigated possible explanations for amplitude variability in the ![]() Scuti star 44 Tau (Breger & Lenz 2008).
Scuti star 44 Tau (Breger & Lenz 2008).
The two close frequencies f9 and f12 in Fig. 4 are spaced 0.063 d-1 (for 2004 data). The frequency errors given for both frequencies in Table 3 are 0.005 and 0.009 respectively. Even the more conservative estimation, the T-1 criterion gives a frequency resolution of 0.029 d-1. Hence the frequencies are resolved. f12 is close to an expected sidelobe with order 5 (i.e.
![]() )
of the first harmonic (28.384 d-1) of the MOST orbit frequency. Sidelobes tend to decrease in amplitude with growing order. No sidelobe has been detected below the orbit harmonic of 28.384 d-1, except for order 1 at 27.387 d-1. Thus, f12 has been adopted in the frequency list (Table 3).
)
of the first harmonic (28.384 d-1) of the MOST orbit frequency. Sidelobes tend to decrease in amplitude with growing order. No sidelobe has been detected below the orbit harmonic of 28.384 d-1, except for order 1 at 27.387 d-1. Thus, f12 has been adopted in the frequency list (Table 3).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9996fig4.eps}
\end{figure}](/articles/aa/full/2008/46/aa09996-08/Timg31.gif) |
Figure 4:
Frequencies in the |
| Open with DEXTER | |
The original 2005 light curve of HD 61199 shows longer-term variability with a period of about 4 days which can be seen by eye (and is not present in the other stars observed in the same field). This timescale was investigated through Phase Dispersion Minimization (PDM, Stellingwerf 1978). The PDM diagrams of the 2004, 2005 and 2007 photometry are plotted in Fig. 5. For this analysis, all significant power at frequencies above 1 d-1 has been prewhitened and the data have been averaged in 1-min bins. The most prominent feature in all three PDM diagrams occurs near a period of about 4 days, or more precisely, of 3.94 ![]() 0.12 days in the 2004 and 2007 data and of 4.15
0.12 days in the 2004 and 2007 data and of 4.15 ![]() 0.24 days in 2005. For those errors, the error estimation of
0.25 T-1 is adopted, which is given by Kallinger et al. (2008) for the case of two closely spaced frequencies. The change in the period is within the errors. Prewhitening of the dominant period in each data set yields the PDM results given in the upper curves in each panel. This reveals clearly in the 2007 data, the stellar system orbital period determined by spectroscopy (3.57 d, shown by the vertical line, see Sect. 4). The period may be present marginally in the PDM analysis of 2004 data, but is absent in the 2005 PDM residuals. The SigSpec and Period04 routines find this latter period (f7 in Table 3) in all three data sets, within the expected frequency uncertainty.
0.24 days in 2005. For those errors, the error estimation of
0.25 T-1 is adopted, which is given by Kallinger et al. (2008) for the case of two closely spaced frequencies. The change in the period is within the errors. Prewhitening of the dominant period in each data set yields the PDM results given in the upper curves in each panel. This reveals clearly in the 2007 data, the stellar system orbital period determined by spectroscopy (3.57 d, shown by the vertical line, see Sect. 4). The period may be present marginally in the PDM analysis of 2004 data, but is absent in the 2005 PDM residuals. The SigSpec and Period04 routines find this latter period (f7 in Table 3) in all three data sets, within the expected frequency uncertainty.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9996fig5.eps}
\end{figure}](/articles/aa/full/2008/46/aa09996-08/Timg32.gif) |
Figure 5: Phase Dispersion Minimization (PDM) diagrams for the 2004 ( top), 2005 ( middle) and 2007 ( bottom) photometry. The lower curve in each panel is the PDM after prewhitening all significant frequencies higher than 1 d-1. Each upper curve shows the PDM of the residuals after prewhitening by the dominant period in the lower curve. The thin vertical line marks the orbital period of the stellar system found spectroscopically (see Sect. 4). |
| Open with DEXTER | |
Prompted by the longer period seen in the 2004 MOST photometry, a spectroscopic follow-up campaign was carried out. A total of 29 high-resolution spectra (R=63 000, wavelength range from 4760-7360 Å) spanning 45 days were obtained with the Coudé-echelle spectrograph attached to the 2-m telescope of the Thüringer Landessternwarte Tautenburg. The Signal to Noise (S/N) of the spectra is between 60 and 180 with a mean value of 130. The S/N was measured in the continuum around 5200 Å.
Table 4: Radial velocities for each component of the HD 61199 system derived from the Tautenburg spectra.
We analysed the dynamics of the HD 61199 system by applying the least-squares deconvolution technique (LSD, Donati et al. 1997) to the spectra. Starting with preliminary estimates for the atmospheric parameters, we extracted from the Vienna Atomic Line Database (VALD, Piskunov et al. 1995; Kupka et al. 1999; Ryabchikova et al. 1997) 700 spectral lines with a residual intensity higher than 0.2 and used this list for the LSD line mask. Based on Table 1, following model parameters have been adopted:
![]() = 7800 K,
= 7800 K, ![]() = 4.0, and solar chemical composition. The relative shape of the LSD profile is rather insensitive to line masks with different parameters.
Thus, because we are using only relative quantities, no additional error is introduced by the difference of
= 4.0, and solar chemical composition. The relative shape of the LSD profile is rather insensitive to line masks with different parameters.
Thus, because we are using only relative quantities, no additional error is introduced by the difference of
![]() of the components. Figure 6 shows the LSD profiles of all 29 spectra with a typical S/N of about 500. A broad - but shallow - line of a rapidly rotating star (to which we refer as component A) is clearly present, superposed on the narrow lines of an obvious binary system (referred to as components Ba and Bb). At some phases (e.g., spectrum #26) a fourth faint narrow component appears at the constant velocity of -26
of the components. Figure 6 shows the LSD profiles of all 29 spectra with a typical S/N of about 500. A broad - but shallow - line of a rapidly rotating star (to which we refer as component A) is clearly present, superposed on the narrow lines of an obvious binary system (referred to as components Ba and Bb). At some phases (e.g., spectrum #26) a fourth faint narrow component appears at the constant velocity of -26
![]() .
At the phase of 0.926 (spectrum #13) it blends the lines of one binary component. For the spectra in which the narrow line component is present, the heliocentric velocity of the observer projected in the direction of HD 61199 varied in the range of -25 to -28
.
At the phase of 0.926 (spectrum #13) it blends the lines of one binary component. For the spectra in which the narrow line component is present, the heliocentric velocity of the observer projected in the direction of HD 61199 varied in the range of -25 to -28
![]() .
Hence, this faint component may well be due to stray moonlight.
The combined light of the system is dominated by the rapidly rotating star, which causes the broad-line component in the LSD profiles. This feature did not change significantly its position and its equivalent line width is much larger than those of the narrow line components.
.
Hence, this faint component may well be due to stray moonlight.
The combined light of the system is dominated by the rapidly rotating star, which causes the broad-line component in the LSD profiles. This feature did not change significantly its position and its equivalent line width is much larger than those of the narrow line components.
![\begin{figure}
\par\includegraphics*[width=12cm,clip]{9996fig6.ps} \end{figure}](/articles/aa/full/2008/46/aa09996-08/Timg36.gif) |
Figure 6: LSD profiles phased with the final derived orbital period of 3.574(4) days. The red solid curve shows the fit of the triple-spectral model. The spectrum numbers (in chronological order) are given on the left of each spectrum, while orbital phase is given on the right. |
| Open with DEXTER | |
We fitted the LSD spectra with a simple model consisting of three superimposed Gaussian profiles, each
broadened with a
![]()
![]() .
The following free model parameters were adjusted using a least-squares procedure:
.
The following free model parameters were adjusted using a least-squares procedure: ![]() ,
radial velocity and intensity. The
LSD profiles were fitted in a window between -140 and +235
,
radial velocity and intensity. The
LSD profiles were fitted in a window between -140 and +235
![]() and the resulting best-fit solution is shown in Fig. 6. The
radial velocities measured from the spectral fits are listed in Table 4. Errors of the LSD profiles were estimated from the discrepancy between the LSD model and observations. Uncertainties of the parameters determined from the fit to LSD profiles are formal errors calculated by a least-squares fitting routine.
and the resulting best-fit solution is shown in Fig. 6. The
radial velocities measured from the spectral fits are listed in Table 4. Errors of the LSD profiles were estimated from the discrepancy between the LSD model and observations. Uncertainties of the parameters determined from the fit to LSD profiles are formal errors calculated by a least-squares fitting routine.
Due to similar line intensities of the components Ba and Bb it is not straightforward to identify their contribution in the composite line profile. Hence a time-dependent observable,
![]() ,
was formed which varies
with twice the orbital frequency of the close binary. Figure 7 (top panel) shows the resulting Fourier amplitude spectrum. The two highest peaks occur at frequencies of 0.4375 and 0.5616 d-1, corresponding to periods of 4.545 and 3.561 days, respectively. Phase plots with both possible periods are shown in the middle and bottom panels of Fig. 7.
A period of 4.55 days leads to discontinuities in the phase diagram, while a period of
3.56 days produces a coherent RV curve. The correct identification of components Ba and Bb appears to fail only for spectrum #13 where the the constant feature at -26
,
was formed which varies
with twice the orbital frequency of the close binary. Figure 7 (top panel) shows the resulting Fourier amplitude spectrum. The two highest peaks occur at frequencies of 0.4375 and 0.5616 d-1, corresponding to periods of 4.545 and 3.561 days, respectively. Phase plots with both possible periods are shown in the middle and bottom panels of Fig. 7.
A period of 4.55 days leads to discontinuities in the phase diagram, while a period of
3.56 days produces a coherent RV curve. The correct identification of components Ba and Bb appears to fail only for spectrum #13 where the the constant feature at -26
![]() interferes, and possibly in spectrum #15 where the LSD profiles of the narrow line components are blended.
interferes, and possibly in spectrum #15 where the LSD profiles of the narrow line components are blended.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{9996fig7.ps}
\end{figure}](/articles/aa/full/2008/46/aa09996-08/Timg39.gif) |
Figure 7: Top panel: Fourier transform of the time-dependent velocity observable, as explained in the text. The two highest peaks correspond to periods of 4.54 and 3.56 days. Note that the radial velocity observable varies with twice the orbit frequency. The middle and bottom panels show the radial velocity curves of the three components of HD 61199 phased with 4.54 and 3.56 days respectively. The filled circles correspond to component Ba (which has systematically stronger spectral lines, as seen in Fig. 6); open circles correspond to component Bb; and the triangles to the fast rotating component A. |
| Open with DEXTER | |
Second, KOREL was applied with the following setup: three stars forming two hierarchical orbits, with components Ba and Bb close together and A in a wide orbit. Spectra of the rapidly rotating B3V star HD 120315 were used to model the spectrum of telluric lines which were subtracted from the broad-lined component to obtain a pure stellar spectrum. Orbital elements were made free parameters in the fit and line strengths were allowed to vary with time. Since the line positions of component A did not change measurably during the period of observations, we assumed the period of the wide orbit to lie in the range 1000-20 000 d. For 12 different long trial periods, we detected only marginal changes in the disentangled spectra and in the resulting orbital elements. 20 000 d is the upper limit to observe any changes in the KOREL solution.
KOREL determines simultaneously orbital elements, line strengths of each component and disentangled spectra. Radial velocities are not determined from the input spectra but are calculated from the orbital solution. The KOREL code finds several local minima that all give zero RMS of the obtained RVs (shifts applied by KOREL to the individual spectra), i.e. the RVs are identical to those calculated from the simultaneously obtained orbital elements. We searched for the best solution nearest to that obtained with ORBITX, using the wavelength interval 4895-5680 Å. For an error estimation we then divided this interval into 10 parts of equal lengths and applied KOREL to each of them. In this way we obtained 10 orbital solutions, mean and standard deviation, which we weighted by the total equivalent width included in each subspectrum. There was no significant difference between the values obtained from the full wavelength interval and the weighted means.
The disentangled spectra and the combined spectrum are shown in Fig. 8. KOREL provides no information about the individual continua of the stars, because the disentangled spectra are normalised to the common continuum of the observed composite spectrum. To renormalise the KOREL output spectra, one must either use information about the luminosity ratios of the stars or, as we did, scale the stellar spectra by comparison to synthetic spectra.
KOREL has difficulties disentangling the H![]() region, where the RV shifts are much smaller than the intrinsic line width. For this reason the disentangled spectra cannot be used for
region, where the RV shifts are much smaller than the intrinsic line width. For this reason the disentangled spectra cannot be used for
![]() estimation from H
estimation from H![]() .
.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{9996fig8.eps}
\end{figure}](/articles/aa/full/2008/46/aa09996-08/Timg41.gif) |
Figure 8: Disentangled spectra of the components Ba (1), Bb (2), A (3, from top to bottom) and the combined spectrum. |
| Open with DEXTER | |
Table 5 gives the orbital elements for the close system obtained by KOREL and ORBITX, respectively. The epoch T refers to the time of the maximum positive velocity of component Ba. In the ORBITX analysis, the eccentricity was found to be insignificant and was therefore fixed to zero, whereas in the KOREL analysis the eccentricity is small, but significant. Figure 9 shows the orbit solution obtained by ORBITX for the narrow-line pair (circles) and the velocity of the broad-line component (triangles) phased with the ephemeris (HJD = 2 453 069.089(3) + 3.574(4)E) of the close orbit.
For HD 61199 Ba and Bb, lower limits on the masses can be derived via the equation given by Aitken (1935)
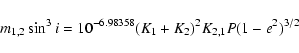
Aitken's formula for the masses of binaries allows us to constrain the inclination angle of the close binary orbit. A conservative mass range for F type stars ranging from 1.1 to 1.6 ![]() yields a range for the inclination angle of the orbital plane between 47 and 57 degrees.
yields a range for the inclination angle of the orbital plane between 47 and 57 degrees.
Table 5: Results for the orbit solution of the close binary.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{9996fig9.ps}
\end{figure}](/articles/aa/full/2008/46/aa09996-08/Timg45.gif) |
Figure 9: Radial velocity curves of the HD 61199 system phased with the final orbit solution. The filled circles, open circles and triangles are the measured radial velocities of the components Ba, Bb and A, respectively. The solid and dashed lines show the orbital solution of components Ba and Bb in the close binary. The phase is based on the ephemeris derived by the ORBITX solution. |
| Open with DEXTER | |
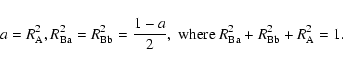
By comparing fits of synthetic triple-star spectra across a wide parameter space, we estimate for component A an effective temperature of
![]() = (8000
= (8000 ![]() 200) K and for each component of the close binary
200) K and for each component of the close binary
![]() = (6400
= (6400![]() 400) K. The rather large uncertainties of the temperatures for the close binary is caused by the uncertainty in
400) K. The rather large uncertainties of the temperatures for the close binary is caused by the uncertainty in ![]() and the fact that its contribution to the total light is small compared to the dominant A component. Figure 10 illustrates the quality of the best fit and the accuracy to which fundamental
parameters of the three components can be determined from existing data. The black wiggly lines represent four out of 29 observed spectra in the range around H
and the fact that its contribution to the total light is small compared to the dominant A component. Figure 10 illustrates the quality of the best fit and the accuracy to which fundamental
parameters of the three components can be determined from existing data. The black wiggly lines represent four out of 29 observed spectra in the range around H![]() and the smooth blue line corresponds to a synthetic spectrum with
and the smooth blue line corresponds to a synthetic spectrum with
![]() = 8000 K and
= 8000 K and ![]() = 4.2, plus two stars with 6800 K (4.4) and 6600 K (4.4). Another model with 8000 K (4.0) plus two stars (each with
= 4.2, plus two stars with 6800 K (4.4) and 6600 K (4.4). Another model with 8000 K (4.0) plus two stars (each with
![]() = 6000 K and
= 6000 K and ![]() = 4.2) also agrees with the observed spectra within the resolution. The radial velocity values for these fits were taken from our orbital solution (see Table 5).
The chosen parameters for the triple system give also a good fit to the metal line spectrum as is illustrated in Fig. 11.
Based on evolutionary tracks published by Schaller et al. (1992), Fig. 12 shows that a triple system with log(age) between 8.8 and 8.9 is compatible with our observations of HD 61199.
= 4.2) also agrees with the observed spectra within the resolution. The radial velocity values for these fits were taken from our orbital solution (see Table 5).
The chosen parameters for the triple system give also a good fit to the metal line spectrum as is illustrated in Fig. 11.
Based on evolutionary tracks published by Schaller et al. (1992), Fig. 12 shows that a triple system with log(age) between 8.8 and 8.9 is compatible with our observations of HD 61199.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{9996fy10.ps}
\end{figure}](/articles/aa/full/2008/46/aa09996-08/Timg55.gif) |
Figure 10:
Fits to the H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=12cm,clip]{9996fy11.ps} \end{figure}](/articles/aa/full/2008/46/aa09996-08/Timg56.gif) |
Figure 11:
Comparison of our best-fitting synthetic spectrum to an observed spectrum of HD 61199 with high S/N during a phase of large separation of components in the close binary, in a wavelength range with many metal lines. The model parameters for the synthesis are
|
| Open with DEXTER | |
The determination of the fundamental parameters was also performed on the disentangled spectra.
A grid of model spectra ranging from 6000 to 8600 K with stepwidth of 200 K and ![]() of 3.6, 4.0, 4.4, respectively, was compared to the disentangled spectra corrected for radial velocity shifts. The model spectra were calculated using the code SynthV (Tsymbal 1996) and NEMO model atmosphere grid (Heiter et al. 2002).
For finding the best fitting spectra two approaches have been used.
First, the standard deviation of the residuals, hereafter referred to as
of 3.6, 4.0, 4.4, respectively, was compared to the disentangled spectra corrected for radial velocity shifts. The model spectra were calculated using the code SynthV (Tsymbal 1996) and NEMO model atmosphere grid (Heiter et al. 2002).
For finding the best fitting spectra two approaches have been used.
First, the standard deviation of the residuals, hereafter referred to as ![]() ,
and second, the
,
and second, the ![]() test were used for evaluating the quality of the fit.
These approaches lead to different best fitting solutions, because the methods differ in weighting the data. The standard deviation of the residuals weights each data point equally, while the
test were used for evaluating the quality of the fit.
These approaches lead to different best fitting solutions, because the methods differ in weighting the data. The standard deviation of the residuals weights each data point equally, while the ![]() test weights the data according to the relative line strength. Hence the
test weights the data according to the relative line strength. Hence the ![]() test prefers better fits of line cores. Solar chemical composition was assumed, based on the good fit obtained by the direct method (see Fig. 11).
test prefers better fits of line cores. Solar chemical composition was assumed, based on the good fit obtained by the direct method (see Fig. 11).
The standard deviation of the residuals and ![]() was calculated the following way:
was calculated the following way:
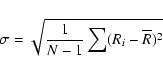
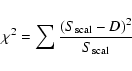
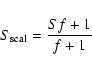
Table 8 shows the results of both analyses, disentangled spectra and H![]() fitting of the combined spectrum. The most likely parameters are printed bold face. For the fainter components large uncertainties in the parameters are evident.
fitting of the combined spectrum. The most likely parameters are printed bold face. For the fainter components large uncertainties in the parameters are evident.
Theoretical pulsation frequencies of HD 61199 were computed with updated codes for stellar evolution (Paczynski 1969) and oscillation (Dziemblowski 1977), where rotation is taken into account to second order (Dziembowski & Goode 1992). Standard Mixing Length Theory (MLT) for convection (Böhm-Vitense 1958) was used and the simplest convection - pulsation treatment (the assumption of frozen convective flux). Since envelope convection becomes less efficient for stars closer to the hot border of the classical instability
strip,
![]() can be expected to be smaller for HD 61199 than for the
can be expected to be smaller for HD 61199 than for the ![]() Scuti star FG Vir. For that star, the MLT parameter
Scuti star FG Vir. For that star, the MLT parameter
![]() was found to be 0.5 (Daszynska-Daszkiewicz et al. 2005).
was found to be 0.5 (Daszynska-Daszkiewicz et al. 2005).
Direct mode identification based on our photometric and spectroscopic data is not possible, so we instead investigate period ratios. The values of radial-pulsation period ratios depend mainly on metallicity and rotation (Suarez et al. 2006) and also slightly on the evolutionary stage of the star. Table 7 shows the predicted values for radial period ratios of a ![]() Scuti star model with Z = 0.018 and 0.02 and
Scuti star model with Z = 0.018 and 0.02 and
![]() (ZAMS) = 150
(ZAMS) = 150
![]() and 180
and 180
![]() .
.
![\begin{figure}
\par\includegraphics[angle=90,width=7.8cm,clip]{9996fy12.ps} \end{figure}](/articles/aa/full/2008/46/aa09996-08/Timg64.gif) |
Figure 12:
Evolutionary tracks from Schaller et al. (1992) for masses |
| Open with DEXTER | |
For convenience, the radial fundamental mode is hereafter referred to as F, the first overtone as 1H, and so on. The observed pulsation frequencies in Table 3 were examined to identify possible period ratios for radial modes in HD 61199. (The two long periods given in Table 3 have been excluded because they are not due to ![]() Scuti pulsation.) Our temperature estimate indicates that the star is located close to the hot border of the instability strip of radially pulsating
Scuti pulsation.) Our temperature estimate indicates that the star is located close to the hot border of the instability strip of radially pulsating ![]() Scuti stars (Pamyatnykh 2000). Under the assumption that radial modes are observed, we find five possibilities:
Scuti stars (Pamyatnykh 2000). Under the assumption that radial modes are observed, we find five possibilities:
(a) f4 / f5 (1H/2H) = 0.819
(b) f8 / f11 (2H/3H) = 0.837
(c) f12 / f5 (2H/3H) = 0.846
(d) f2 / f10 (2H/3H) = 0.841
(e) f11 / f1 (4H/5H) = 0.884.
In fast rotating stars, nonradial modes usually dominate (Breger 2000), and this may also be the case for HD 61199. Unfortunately, fitting the observed frequencies to model frequencies with a least-squares technique does not result in a unique solution, because models predict a very dense spectrum of frequencies of which only a few (in this case, 11) are detected. Hence we concentrated our modelling efforts on explaining the observed frequency range of
18.69-29.70 d-1. Figure 14 shows the region in the
![]() diagram where pulsation models are consistent with the frequency range observed in HD 61199.
The inner polygons are calculated with Z = 0.018 and Z = 0.02 and represent the area in which all observed frequencies lie in the theoretically predicted range of excited modes. Due to uncertainties in stellar modelling and potentially incomplete opacity data the frequency range of unstable modes may be larger than predicted by our codes. The outer polygons shows the range of models where the observed frequency range is 3 d-1 larger than the theoretically predicted range of unstable modes.
diagram where pulsation models are consistent with the frequency range observed in HD 61199.
The inner polygons are calculated with Z = 0.018 and Z = 0.02 and represent the area in which all observed frequencies lie in the theoretically predicted range of excited modes. Due to uncertainties in stellar modelling and potentially incomplete opacity data the frequency range of unstable modes may be larger than predicted by our codes. The outer polygons shows the range of models where the observed frequency range is 3 d-1 larger than the theoretically predicted range of unstable modes.
Table 6: Results for the individual spectra obtained by KOREL.
Table 7: Expected period ratios from models.
Table 8: Summary of fundamental parameters derived with different techniques and proposed solution.
The models (a) to (e) mentioned above are also included in the figure. Models (b), (c) and (d) lie outside the errorbox, model (a) is close to the edge of the
error box, while (e) is inside. In model (e) the period ratio of the fourth overtone and the fifth overtone of the radial fundamental would match the theoretical ratio given in Table 7. However, the unstable modes range from 19.6 d-1 to 27.3 d-1, which is too small by 1 d-1 on the lower frequency border and 2.3 d-1on the higher frequency border, respectively. The model parameters are
![]() = 8050 K,
= 8050 K, ![]() = 3.86, M = 2.1
= 3.86, M = 2.1 ![]() .
This model
is compatible to the derived parameters for HD 61199 in Sect. 4. The amplitude of the presumably radial mode in model (e), f11, is 0.16 mmag and did not change significantly, while the amplitude of the presumably consecutive radial mode, f1, is about 1.5 mmag and was clearly variable. Considering that f11 is close to the detection limit while f1 has the highest amplitude, it is questionable, if the identification with radial modes is correct in this case.
.
This model
is compatible to the derived parameters for HD 61199 in Sect. 4. The amplitude of the presumably radial mode in model (e), f11, is 0.16 mmag and did not change significantly, while the amplitude of the presumably consecutive radial mode, f1, is about 1.5 mmag and was clearly variable. Considering that f11 is close to the detection limit while f1 has the highest amplitude, it is questionable, if the identification with radial modes is correct in this case.
The error box in Fig. 14 is based on the assumption, that HD 61199 forms a physical triple system, where for component A ![]() = 4.0 was adopted.
Models hotter than
= 4.0 was adopted.
Models hotter than ![]()
![]() = 3.92 cannot explain the observed frequency range, nor can models with masses larger than 2.1
= 3.92 cannot explain the observed frequency range, nor can models with masses larger than 2.1 ![]() .
Note, however, that models generated for FG Vir tend to be too cool by 200 to 300 K, when comparing the best-fitting models to the spectroscopically determined temperatures.
.
Note, however, that models generated for FG Vir tend to be too cool by 200 to 300 K, when comparing the best-fitting models to the spectroscopically determined temperatures.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{9996fy13.eps}
\end{figure}](/articles/aa/full/2008/46/aa09996-08/Timg68.gif) |
Figure 13:
Model spectra compared to the disentangled spectra. From top to bottom the comparison is shown for component Ba, Bb and A respectively. The full line corresponds to the best fitting model spectrum using |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{9996fy14.eps} \end{figure}](/articles/aa/full/2008/46/aa09996-08/Timg69.gif) |
Figure 14:
Region in the |
| Open with DEXTER | |
HD 61199 was discovered to be a multiperiodic ![]() Scuti pulsator from MOST photometry in 2004. Analysis of these data, and MOST data
collected in 2005 and 2007, reveal 11 pulsation frequencies, with amplitudes as low as 90 ppm in the total flux of the system. Subsequent Tautenburg spectroscopy demonstrates that HD 61199 is a triple system, where the two form a close binary with a period of 3.57 days, and the
Scuti pulsator from MOST photometry in 2004. Analysis of these data, and MOST data
collected in 2005 and 2007, reveal 11 pulsation frequencies, with amplitudes as low as 90 ppm in the total flux of the system. Subsequent Tautenburg spectroscopy demonstrates that HD 61199 is a triple system, where the two form a close binary with a period of 3.57 days, and the ![]() Scuti star (which we dub the A component and which contributes 80% of the total flux) is either in a much wider orbit or is incidentally in the line of sight. The system does not exhibit
eclipses, but variations with the period of the close binary orbit are evident in the 2007 MOST photometry.
Another period of about 4 days is present in all three epochs of photometry.
The origin of this period remains unknown.
The high
Scuti star (which we dub the A component and which contributes 80% of the total flux) is either in a much wider orbit or is incidentally in the line of sight. The system does not exhibit
eclipses, but variations with the period of the close binary orbit are evident in the 2007 MOST photometry.
Another period of about 4 days is present in all three epochs of photometry.
The origin of this period remains unknown.
The high ![]() of the
of the ![]() Scuti star, and its likely radius, mean
that its rotation period must be about 1 day. The only way we know to
associate a 4-day period with the
Scuti star, and its likely radius, mean
that its rotation period must be about 1 day. The only way we know to
associate a 4-day period with the ![]() Scuti star is through an
isolated high-overtone g-mode. It could be a hybrid pulsator, with both
Scuti star is through an
isolated high-overtone g-mode. It could be a hybrid pulsator, with both
![]() Doradus g-modes and
Doradus g-modes and ![]() Scuti p-modes. However, the expected
range of high order g-mode periods is about 0.3-3 d, and most
Scuti p-modes. However, the expected
range of high order g-mode periods is about 0.3-3 d, and most ![]() Dor periods
are closer to 0.8 d. Thus the hybrid explanation is unlikely, and we conclude
the 4-day period originates in one or both components of the close binary.
However, the stars in the close binary are almost certainly tidally locked,
so it is unlikely that the 4-day period represents evidence for rotation in that system.
If the rotation axes of the two components were
significantly misaligned, we would be able to measure the difference in
Dor periods
are closer to 0.8 d. Thus the hybrid explanation is unlikely, and we conclude
the 4-day period originates in one or both components of the close binary.
However, the stars in the close binary are almost certainly tidally locked,
so it is unlikely that the 4-day period represents evidence for rotation in that system.
If the rotation axes of the two components were
significantly misaligned, we would be able to measure the difference in
![]() between the two stars in the spectra, and we do not see such a
difference.
between the two stars in the spectra, and we do not see such a
difference.
An additional puzzle in the system is the fact that the orbital frequency of the close binary is equal to the difference between the two ![]() Scuti frequencies with the highest amplitudes. The separation of the
Scuti frequencies with the highest amplitudes. The separation of the ![]() Scuti star from the close binary is large enough that there should be no significant tidal influence. The observed frequency coincidence is remarkable, but we have no explanation for it.
Scuti star from the close binary is large enough that there should be no significant tidal influence. The observed frequency coincidence is remarkable, but we have no explanation for it.
Considering the various estimates for the fundamental astrophysical
parameters of the three components we conclude that (
![]() /
/![]() )
A:
8000/4.0, Ba and Bb: 6400/4.4, are the best compromise within the uncertainties
given in Table 8. This conclusion is also supported by the fact that
synthetic spectra of a triple system computed for various combinations
in the mentioned parameter space overlap within the observational
uncertainties of our spectroscopy. The H
)
A:
8000/4.0, Ba and Bb: 6400/4.4, are the best compromise within the uncertainties
given in Table 8. This conclusion is also supported by the fact that
synthetic spectra of a triple system computed for various combinations
in the mentioned parameter space overlap within the observational
uncertainties of our spectroscopy. The H![]() line profiles are rather insensitive to
line profiles are rather insensitive to ![]() for stars with
for stars with
![]() < 8500 K, hence the large uncertainty for
< 8500 K, hence the large uncertainty for ![]() given in the table are estimated from the metal lines of the disentangled spectra.
given in the table are estimated from the metal lines of the disentangled spectra.
The parallax given by Gatewood & Han (2006) is consistent with the A component being a ![]() Scuti star with an absolute magnitude of
Scuti star with an absolute magnitude of
![]() .
For both fainter components, Ba and Bb, we derive
.
For both fainter components, Ba and Bb, we derive
![]() and 4.2, respectively, based on our model of the triple system.
and 4.2, respectively, based on our model of the triple system.
![]() Scuti models enable us to estimate upper limits on the effective temperature (about
Scuti models enable us to estimate upper limits on the effective temperature (about
![]() )
and mass (2.1
)
and mass (2.1 ![]() )
of HD 61199 A. Based on the orbit solution, we set lower mass limits of about 0.7
)
of HD 61199 A. Based on the orbit solution, we set lower mass limits of about 0.7 ![]() for the close binary components, Ba and Bb.
However, given the expected masses for F-type stars (between 1.1 and 1.6
for the close binary components, Ba and Bb.
However, given the expected masses for F-type stars (between 1.1 and 1.6 ![]() ), we can exploit the upper limit to constrain the inclination of the orbital plane to
), we can exploit the upper limit to constrain the inclination of the orbital plane to
![]() .
.
Acknowledgements
This project was supported by the Austrian Fonds zur Förderung der wissenschaftlichen Forschung (FWF, project The Core of the HR diagram, P17580-N02), and the Bundesministerium für Verkehr, Innovation und Technologie (BM.VIT) via the Austrian Agentur für Luft- und Raumfahrt (FFG-ALR). V.T. also kindly acknowledges the Ukrainian grant FRSF F25.2/074 for partial financial support. J.M.M., J.F.R., S.R., D.B.G., and A.F.J.M. received research support from NSERC (Natural Sciences & Engineering Research Council) Canada. R.K. was partly funded by the Canadian Space Agency.