A&A 491, 923-927 (2008)
DOI: 10.1051/0004-6361:200810504
J.-Ch. Hamilton1 - R. Charlassier1 - C. Cressiot1 - J. Kaplan1 - M. Piat1 - C. Rosset2
1 - APC, Université Denis Diderot-Paris 7, CNRS/IN2P3, CEA, Observatoire de Paris; 10 rue A. Domon & L. Duquet, Paris, France
2 -
LAL, Laboratoire de l'accélérateur Linéaire, Université Paris-Sud 11, CNRS/IN2P3; Bâtiment 200, 91898 Orsay Cedex, France
Received 2 July 2008 / Accepted 27 August 2008
Abstract
Context. The search for B-mode polarization fluctuations in the Cosmic Microwave Background is one of the main challenges of modern cosmology. The expected level of the B-mode signal is very low and therefore requires the development of highly sensitive instruments with low systematic errors. An appealing possibility is bolometric interferometry.
Aims. We compare in this article the sensitivity on the CMB angular power spectrum achieved with direct imaging, heterodyne and bolometric interferometry.
Methods. Using a simple power spectrum estimator, we calculate its variance leading to the counterpart for bolometric interferometry of the well known Knox formula for direct imaging.
Results. We find that bolometric interferometry is less sensitive than direct imaging. However, as expected, it is finally more sensitive than heterodyne interferometry due to the low noise of the bolometers. It therefore appears as an alternative to direct imagers with different and possibly lower systematic errors, mainly due to the absence of an optical setup in front of the horns.
Key words: cosmology: cosmic microwave background - cosmology: early Universe - methods: data analysis
The detection of primordial gravity waves through B-mode polarization anisotropies in the Cosmic Microwave Backgroud is one of the most exciting challenges of modern cosmology. It could provide direct information on the energy scale of inflation, possibly associated with GUT (Liddle & Lyth 2000). It would also allow one to investigate the standard cosmological model in detail through consistency tests involving the spectral indices of scalar and tensor perturbations and their amplitude ratio (Langlois 2004).
Despite the weakness of the expected signal, many teams have decided to join the quest for the B-modes and to construct dedicated instruments that must combine exquisite sensitivity and precise control of systematic effects. Most of the projects proposed up to now use direct imagers, a concept that has proven to be very sensitive. However they might be affected by significant systematic effects such as ground-pickup and beam differences that would less affect an interferometer having no optics before the entry horns. Thus, we investigate the possibility of developing a high sensitivity interferometer dedicated to B-mode searches. A bolometric interferometer would combine the high sensitivity of bolometers with the clean optics of an interferometer and could complement the ongoing imaging projects.
In this article we investigate the sensitivity achieved by such an instrument and compare it with direct imagers and heterodyne interferometers. In Sect. 1 we review useful quantities regarding interferometry in general and the reconstruction of visibilities with a bolometric interferometer. We define in Sect. 2 a simple power spectrum estimator under the assumption that E and B visibilities can be extracted from Q and U Stokes parameter visibilities (this is in itself an important issue and is beyond the scope of this article). From this estimator we derive a formula for the ![]() uncertainty with a bolometric interferometer equivalent to the famous one derived in Knox (1997) for imagers. We compare the sensitivities achieved with imagers and bolometric and heterodyne interferometers in Sect. 3. We discuss our results in Sect. 4.
uncertainty with a bolometric interferometer equivalent to the famous one derived in Knox (1997) for imagers. We compare the sensitivities achieved with imagers and bolometric and heterodyne interferometers in Sect. 3. We discuss our results in Sect. 4.
Here, we discuss basic definitions regarding interferometry in general and bolometric interferometry in particular. An interferometer observes the visibilities of an incoming radiation field
![]() that are defined as:
that are defined as:
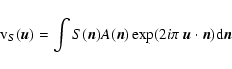 |
(1) |
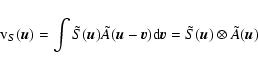 |
(2) |
| (3) |
| (4) |
| (5) |
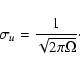 |
(6) |
| (7) |
In a heterodyne interferometer, the visibilities are directly obtained using a correlator that gives as an output the correlated signal
![]() coming from two antennae in a coherent way. Bolometers are incoherent detectors that measure the time averaged incoming power. Bolometric interferometers are therefore additive interferometers where the visibilities are obtained from squaring the sum of the signal coming from two horns:
coming from two antennae in a coherent way. Bolometers are incoherent detectors that measure the time averaged incoming power. Bolometric interferometers are therefore additive interferometers where the visibilities are obtained from squaring the sum of the signal coming from two horns:
![]() =
=
![]() .
When a large number of horns are used, the signal detected by the bolometers is a linear combination of all available visibilities. The use of phase shifters on each of the input channels allows one to reconstruct the complex visibilities of the four Stokes parameters
.
When a large number of horns are used, the signal detected by the bolometers is a linear combination of all available visibilities. The use of phase shifters on each of the input channels allows one to reconstruct the complex visibilities of the four Stokes parameters ![]() ,
,
![]() ,
,
![]() and
and ![]() .
We have shown (Charlassier et al. 2008) that this reconstruction is done optimally when the phase-shifting scheme is such that equivalent baselines
.
We have shown (Charlassier et al. 2008) that this reconstruction is done optimally when the phase-shifting scheme is such that equivalent baselines![]() are summed coherently - they correspond to the same phase difference. In this case, the noise covariance matrix on the complex reconstructed visibilities is diagonal and has the form:
are summed coherently - they correspond to the same phase difference. In this case, the noise covariance matrix on the complex reconstructed visibilities is diagonal and has the form:
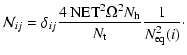 |
(8) |
In the flat-sky approximation, the E and B polarization fields are related to the Stokes parameters by a simple rotation of angle ![]() ,
the angle between
,
the angle between ![]() and the ux axis (Zaldarriaga 2001). In terms of visibilities, this can be written:
and the ux axis (Zaldarriaga 2001). In terms of visibilities, this can be written:
![\begin{displaymath}%
\left\{\begin{array}{lll}
{\rm V}_Q(\vec{u})&=& \displaysty...
...] \tilde{A}(\vec{u}-\vec{v}){\rm d}\vec{v}. \end{array}\right.
\end{displaymath}](/articles/aa/full/2008/45/aa10504-08/img41.gif) |
(9) |
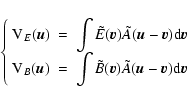 |
(10) |
| |
= | (11) | |
| = | (12) | ||
| = | (13) |
In the presence of noise and assuming the power to be flat enough to be taken out of the integral (recall that
![]() ):
):
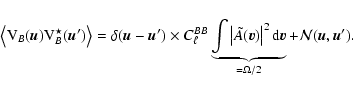 |
(14) |
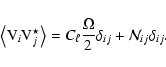 |
(15) |
From the above equation, it is obvious that the simplest unbiased estimator of the power spectrum is:
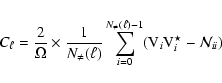 |
(16) |
| |
= | (17) | |
| = | ![$\displaystyle \left(\frac{2}{\Omega N_\neq(\ell)}\right)^2 \left< \left[ \sum_i ({\rm V}_i{\rm V}^\star_i-\mathcal{N}_{ii})\right]^2\right> -{\rm C}_\ell^2$](/articles/aa/full/2008/45/aa10504-08/img62.gif) |
(18) | |
| = | 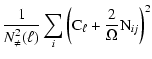 |
(19) |
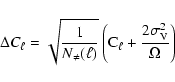 |
(20) |
| (21) |
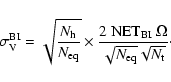 |
(23) |
The above expression is the same for both heterodyne interferometry and direct imaging, only the expression of
![]() changes. For heterodyne interferometry, if the noise equivalent temperature of one of the two input channels of the correlator is
changes. For heterodyne interferometry, if the noise equivalent temperature of one of the two input channels of the correlator is
![]() ,
the noise on the reconstructed Stokes parameter visibility calculated with
,
the noise on the reconstructed Stokes parameter visibility calculated with ![]() time samples and averaged over
time samples and averaged over
![]() equivalent baselines is given by:
equivalent baselines is given by:
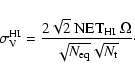 |
(24) |
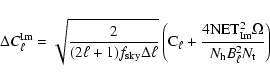 |
(25) |
As the sample variance term is exactly the same whatever technique is used (as expected), we are only interested in comparing the noise terms. We assume in the following that we are comparing three instruments observing the same fraction of the sky
![]() from the ground for the same duration:
from the ground for the same duration:
For the bolometric interferometer, one gets:
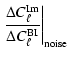 |
= | 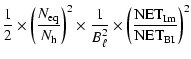 |
(26) |
| = | 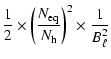 |
(27) |
For heterodyne interferometry, one gets:
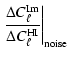 = = 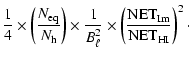 |
(28) |
| |
Figure 1:
Approximate formula (red line) from Eq. (30) and actual values (black dots) for the number of equivalent baselines as a function of
|
| Open with DEXTER | |
The number of equivalent baselines for a square horn array is:
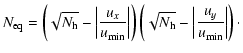 |
(29) |
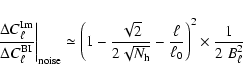 |
(31) |
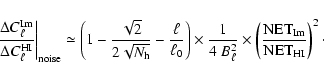 |
(32) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0504fig2.eps}\hspace*{6mm}
\includegraphics[width=8cm,clip]{0504fig3.eps}\end{figure}](/articles/aa/full/2008/45/aa10504-08/Timg102.gif) |
Figure 2:
Power spectrum error bar ratio between an imager and a bolometric interferometer (red solid) and between an imager and a heterodyne interferometer (blue dashed). The thick lines only include the noise contribution while the thin lines also include sample variance (with a tensor to scalar ratio of 0.1). In each case we have assumed 256 horns, a sky fraction defined by the 20 degrees FWHM primary beam of the interferometers. The left panel corresponds to a 10 arcmin resolution imager and the right one to a one degree imager. The points are obtained with a precise measurement of the number of equivalent baselines and the lines are from the approximate expression given above. The green dotted line shows the region where the relative sample variance
|
| Open with DEXTER | |
The sensitivities of the three different techniques only differ in the way the instrument filters the multipoles observed in the sky. An imager is affected by its resolution on the sky while an interferometer is affected by the ratio between the number of equivalent baselines and the number of horns as a function of multipoles. All of these filtering factors are less than one. However, imagers are usually operated in such a way that they are not limited by their angular resolution in the multipole region of interest, in that case
![]() ,
and the imager is always more sensitive than an interferometer (bolometric or heterodyne). From the strict point of view of sensitivity, interferometers can therefore only compete with low angular resolution imagers.
,
and the imager is always more sensitive than an interferometer (bolometric or heterodyne). From the strict point of view of sensitivity, interferometers can therefore only compete with low angular resolution imagers.
There is a large difference in sensitivity between bolometric and heterodyne interferometers compared to an imager: the ratio
![]() acts quadratically on the variance for a bolometric interferometer while it acts linearly for a heterodyne instrument.
This is due to the fact that with a heterodyne interferometer, equivalent baselines are averaged after their measurement, resulting in a
acts quadratically on the variance for a bolometric interferometer while it acts linearly for a heterodyne instrument.
This is due to the fact that with a heterodyne interferometer, equivalent baselines are averaged after their measurement, resulting in a
![]() factor on the variances. In a bolometric interferometer, the signals from all
factor on the variances. In a bolometric interferometer, the signals from all ![]() horns are added together multiplying the noise variance by
horns are added together multiplying the noise variance by ![]() while the coherent summation of equivalent baselines performs an efficient
while the coherent summation of equivalent baselines performs an efficient
![]() reduction of the noise. This finally results in a factor
reduction of the noise. This finally results in a factor
![]() for the variance of a bolometric interferometer relative to a heterodyne one.
This is largely compensated by the difference in NET between bolometric instruments and coherent ones. When comparing them, the ratio of their NET also appears quadratically and favours bolometric instruments that are dominated by the photon noise rather than by that of the amplifiers. This situation may change in the future with the improvements of the HEMT technologies but at frequencies around and above 100 GHz we are unlikely to face photon noise limited HEMTs in the near future. The difference between the NET would be even greater in space where the bolometers NET would drop as the background temperature while that of the coherent instruments would remain roughly constant.
for the variance of a bolometric interferometer relative to a heterodyne one.
This is largely compensated by the difference in NET between bolometric instruments and coherent ones. When comparing them, the ratio of their NET also appears quadratically and favours bolometric instruments that are dominated by the photon noise rather than by that of the amplifiers. This situation may change in the future with the improvements of the HEMT technologies but at frequencies around and above 100 GHz we are unlikely to face photon noise limited HEMTs in the near future. The difference between the NET would be even greater in space where the bolometers NET would drop as the background temperature while that of the coherent instruments would remain roughly constant.
With the present technologies of bolometers and coherent amplifiers, the hierarchy in terms of sensitivity between the three techniques (and layout) studied here is very clear for the multipole range
![]() where the primordial B-mode signal is expected to be maximal. Imagers are the most sensitive, bolometric interferometers have a lower sensitivity, the ratio dropping quadratically with the multipole considered. Heterodyne interferometers have an even lower sensitivity but the ratio with an imager drops less rapidly. They remain however less sensitive than bolometric interferometers in the range of multipoles considered here, where the largest primordial B-mode signal is expected and where the lensing of the E-modes into B-modes is still low. At higher multipoles however, the bandwidth smearing effect and loss of coherence would be a real issue for bolometric interferometers while in a heterodyne interferometer, the separation into small bands would prevent the sensitivity from dropping.
where the primordial B-mode signal is expected to be maximal. Imagers are the most sensitive, bolometric interferometers have a lower sensitivity, the ratio dropping quadratically with the multipole considered. Heterodyne interferometers have an even lower sensitivity but the ratio with an imager drops less rapidly. They remain however less sensitive than bolometric interferometers in the range of multipoles considered here, where the largest primordial B-mode signal is expected and where the lensing of the E-modes into B-modes is still low. At higher multipoles however, the bandwidth smearing effect and loss of coherence would be a real issue for bolometric interferometers while in a heterodyne interferometer, the separation into small bands would prevent the sensitivity from dropping.
The main remaining question is whether the gain in terms of systematic effects is worth the price of this sensitivity reduction if one builds an interferometer instead of an imager. In terms of optics for instance, an interferometer directly observes the sky. The primary beam is therefore only set by that of the horns, while in an imager, the telescope (mirror or lenses) produces sidelobes inducing poorly predictible ground pickup that often prevent one from reaching the nominal sensitivity. An interferometer is also completely insensitive to spatially uniform polarized signals that vary with time such as polarized atmospheric contamination. These could also prevent an imager from reaching its nominal sensitivity by adding some spread in the noise. These examples mitigate the statistical sensitivity loss of an interferometer with respect to an imager. The differences in terms of systematic effects between imagers and bolometric and heterodyne interferometers are not obvious and deserve a detailed quantitative study in continuation of the work done by Bunn (2007).
Acknowledgements
The authors thank Ken Ganga for fruitful discussions and all the participants of the ``Bolometric Interferometry for the B-mode search'' workshop held in Paris in June 2008 for the many stimulating discussions that took place. We also thank Sarah Church, Keith Grainge and Mike Jones for their explanations concerning heterodyne interferometry.