A&A 491, 633-641 (2008)
DOI: 10.1051/0004-6361:200810578

SATLAS: spherical versions of the ATLAS stellar atmosphere program

J. B. Lester1 - H. R. Neilson2


1 - Department of Chemical and Physical Sciences, University of Toronto Mississauga, Canada
2 - Department of Astronomy and Astrophysics, University of Toronto, Canada

Received 11 July 2008/ Accepted 30 August 2008

Abstract
Context. The current stellar atmosphere programs still cannot match some fundamental observations of the brightest stars, and with new techniques, such as optical interferometry, providing new data for these stars, additional development of stellar atmosphere codes is required.
Aims. To modify the open-source model atmosphere program ATLAS to treat spherical geometry, creating a test-bed stellar atmosphere code for stars with extended atmospheres.
Methods. The plane-parallel ATLAS has been changed by introducing the necessary spherical modifications in the pressure structure, in the radiative transfer and in the temperature correction.
Results. Several test models show that the spherical program matches the plane-parallel models in the high surface gravity regime, and matches spherical models computed by PHOENIX and by MARCS in the low gravity case.

Key words: stars: atmospheres - methods: numerical - radiative transfer

1 Introduction

ATLAS (Kurucz 1979,1970) is a well-documented, well-tested, robust, open-source computer program for computing static, plane-parallel stellar atmospheres in local thermodynamic equilibrium (LTE). Since ATLAS came to maturity in the 1970s, stellar atmosphere codes have progressed in a number of directions to include important additional physics. For example, the PHOENIX program (Hauschildt et al. 1999) includes advances such as the massive use of statistical equilibrium (NLTE) in place of LTE, spherically symmetric extension in place of plane-parallel geometry, the inclusion of the dust opacities needed for brown dwarf temperatures, and the ability to include blast wave velocity fields.

These advances, while obviously moving toward greater reality, have not eliminated some persistent problems. For example, a detailed study of Arcturus using PHOENIX models (Short & Hauschildt 2003) found that their spherical NLTE models increased the discrepancy between the observed and computed spectral irradiance. A similar analysis of models with solar parameters (Short & Hauschildt 2005) also concluded that important opacity and/or other physics is still missing.

This evidence that the significant improvements contained in the state-of-the-art programs have not achieved closer agreement with the observations of these fundamental, bright stars indicates a need to continue exploring additional physics. This is a valuable role that ATLAS can play because it is open source and freely available from Kurucz's web page (http://kurucz.harvard.edu), where anyone can download the code and use it as the starting point for studying other possible improvements. An example of the advantage provided by this starting point is the work of Kupka (1996) who explored convection as represented by the full spectrum of turbulence (Canuto et al. 1996; Canuto & Mazzitelli 1991) as an alternative to the standard mixing length theory. More recently, Sbordone et al. (2007) have developed a GNU-Linux port of ATLAS for use in a range of applications. In that spirit, we have developed versions of the ATLAS program that replace the assumption of plane-parallel geometry by spherical symmetry. These codes, comparable to the LTE, spherical version of PHOENIX or of the spherical version of MARCS (Gustafsson et al. 2008), can serve as the basis for the study of additional physics needed to understand luminous stars that are cool enough that NLTE effects are not dominant. Such continued studies are certainly necessary given the revolutionary achievements of optical interferometry in imaging the surfaces of stars, thus providing powerful new observational tests of models of stellar atmospheres.

2 From ATLAS9 and ATLAS12 to ATLAS_ODF and ATLAS_OS

In addition to including a wide range of continuous opacities, ATLAS also incorporates the opacity of tens of millions of ionic, atomic and molecular lines. The original treatment of these lines was via pre-computed opacity distribution functions (ODF) in the ATLAS9 program. Later, ATLAS12 was developed to use opacity sampling (OS) of the same extensive line lists, and Kurucz continues to expand and improve the opacities for these codes. There are small parts of the two ATLAS codes that must be different to handle the different line treatments, but the majority of the codes are not affected by the line treatment, and these can be identical. However, as inevitably happens, small differences between the two codes develop over time; these can be seen by differencing the two source files. Therefore, before beginning our conversion to spherical geometry, we rationalized the two versions of ATLAS to be identical in every way except where they must be different for the line treatments. Where there are differences not associated with the treatment of the line opacity, we have adopted the ATLAS12 routine, under the assumption that it is likely to be newer and undergoing more active development than the older ATLAS9 code. We have also converted our codes to current Fortran 2003 standards. To distinguish our programs from the Kurucz originals, we use the name ATLAS_ODF for our version of ATLAS9, and ATLAS_OS for our version of ATLAS12.

To test the accuracy of our conversions, we computed a model of the solar atmosphere, starting from the input model asunodfnew.dat dated 2 April 2008 in the Kurucz directory /grids/gridp00odfnew. We learned later that this model was computed by Castelli as part of her collaboration with Kurucz (Castelli & Kurucz 2004). We used the opacity distribution function bdfp00fbig2.dat located Kurucz's directory /opacities/dfp00f, which uses the solar iron abundance = -4.51. After 20 iterations, the flux errors are all $\leq$0.2% and the flux derivative errors are all $\leq$2.8%; most errors of both kinds are smaller than our output resolution of 0.1%. Figure 1 compares the temperature and pressure structures of the solar model computed with ATLAS_ODF and the starting ATLAS9 model.


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{0578fg1.eps}\end{figure} Figure 1: A comparison of the temperature structures for two solar atmospheric models. The top panel displays the temperatures as a function of $\log_{10} (P_{{\rm gas}})$. The solid line is the model computed with ATLAS_ODF and the dashed line is the solar model atmosphere asunodfnew.dat from the Kurucz web page. The bottom panel shows the percentage difference between the temperatures of the two models, also as a function of the gas pressure. The differences are entirely due to the conversion to Fortran 2003 and to using consistent, modern values of fundamental parameters throughout the ATLAS_ODF code. The numerical methods are the same for the two models.
Open with DEXTER

Starting from the ATLAS_ODF code, we removed those components that used the opacity distribution functions and replaced them with the components needed to do opacity sampling. At this point we introduced several changes that are not present in ATLAS12. Depending on the effective temperature of the star, ATLAS12 adjusts the index of the starting wavelength, variable nustart, to eliminate wavelengths were the flux is negligibly small. In anticipation of future applications of the code, we have removed this adjustment to always begin at the shortest wavelength, independent of the effective temperature. This change has been propagated back to the ATLAS_ODF version. Second, ATLAS12 always computes 30 000 wavelengths with a wavelength spacing equal to a constant spectral resolving power of 104. We have modified this to be able to specify a spectral resolving power ${\leq}10^4$, and have the number of wavelengths adjust automatically. We did this to test the dependence of the computed model on the spectral resolving power. Third, in assembling the master file of lines to be sampled, ATLAS12 uses a sorting routine from the computer's operating system, which is outside of the source code. We have modified the subroutine prelinop, to perform this sort within the ATLAS source code, making it self-contained.


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{0578fg2.eps}\end{figure} Figure 2: A comparison of the temperature structures for two solar atmospheric models. The top panel displays the temperatures as a function of $\log_{10} (P_{{\rm gas}})$. The solid line is for the model computed with ATLAS_OS and the dashed line is the model computed with ATLAS_ODF. The bottom panel shows the percentage difference between the temperatures of the two models, also as a function of the gas pressure. The differences are entirely due to the way in which line opacity is included. Both codes use Fortran 2003, the same fundamental parameters and the same numerical methods.
Open with DEXTER

To test ATLAS_OS, we computed a model of the solar atmosphere, again starting from the input model asunodfnew.dat. We used Kurucz's files lowlines, hilines and bnltelines8 for the atomic and ionic lines, as well as the molecular files diatomic, tiolines and h2ofast. After eliminating lines that did not contribute at the temperatures of the solar atmosphere, the number of sampled lines used in the calculation was about two million. Figure 2 compares the temperature structure of the solar model computed with ATLAS_OS and the model computed with ATLAS_ODF. The differences between the models using the two methods of including line opacity are comparable to the differences between our ATLAS_ODF and the original ATLAS9 shown in Fig. 1. Therefore, the joint agreements displayed in Figs. 1 and 2 show that our ATLAS_OS code matches the ATLAS9 structure. As an additional test of the two line treatments, we have used our modification to the opacity-sampled code mentioned earlier to vary the spectral resolving power. The opacity-sampled model shown in Fig. 2 used the default spectral resolving power of 30 000. Our tests found that repeating the calculation with spectral resolving powers of 10 000 and 3000 produced almost no change in the resulting model structure.

As an additional test, Kurucz (private communication) provided us with a new ATLAS12 (opacity-sampled) solar model that we compare with our ATLAS_OS model in Fig. 3. It is apparent that the agreement is very good.


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{0578fg3.eps}\end{figure} Figure 3: A comparison of the temperature structures for two solar atmospheric models. The top panel displays the temperature as a function of $\log_{10} (P_{{\rm gas}})$. The solid line is the model computed with ATLAS_OS, and the dashed line is an ATLAS12 model provided by Kurucz (private communication). The bottom panel shows the percentage difference between the temperatures of the two models, also as a function of the gas pressure.
Open with DEXTER

3 From ATLAS_ODF to SATLAS_ODF

The spherically symmetric version of the code, SATLAS_ODF, was created from ATLAS_ODF. Plane-parallel models are labeled with the parameters effective temperature, $T_{{\rm eff}}$, and surface gravity, usually given as $\log ~ g$ in cgs units. For spherical models these two parameters are degenerate because the same value of $\log ~ g$ is produced by different combinations of the stellar mass and radius. Therefore, we have elected to use the three fundamental physical parameters luminosity, $L_{\ast}$, mass, $M_{\ast}$, and radius, $R_{\ast}$. These can be supplied in cgs units or as multiples or fractions of the solar values, $L_{\ast}$/ $L_{\hbox{$\odot$ }}$, $M_{\ast}$/ $M_{\hbox{$\odot$ }}$ and $R_{\ast}$/ $R_{\hbox{$\odot$ }}$, where the values of $L_{\hbox{$\odot$ }}$, $M_{\hbox{$\odot$ }}$ and $R_{\hbox{$\odot$ }}$ are available throughout the source code via a Fortran 2003 module routine.

The radius, of course, will vary with depth in the extended atmosphere. Therefore we have chosen to define the radius where the radial Rosseland mean optical depth, $\tau_{{\rm R}}$, has the value of 2/3 because a photon has a probability of about 50% of escaping the atmosphere from that depth. Other choices could be made, such as $\tau_{{\rm R}} = 1$ (Gustafsson et al. 2008), or $\tau_{500} = 1$ (Hauschildt et al. 1999), but these differences are nearly negligible.

With the three basic parameters defined, there are three modifications to the code: pressure structure, radiative transfer and temperature correction.

3.1 Pressure structure

ATLAS9 and ATLAS12 both solve for the pressure structure in two locations. After reading in the starting model, the pressure structure is solved from the initial temperature structure as a function of Rosseland mean optical depth, $T(\tau_{{\rm R}})$, in the subroutine ttaup. After the first iteration the total gas pressure is computed by integrating the simple equation

\begin{displaymath}\textrm{d} P_{{\rm tot}}/\textrm{d}m = g, \end{displaymath} (1)

where m is the mass column density defined as

 \begin{displaymath} \textrm{d}m = - \rho \textrm{d}r, \end{displaymath} (2)

and g is the constant gravitational acceleration in the plane-parallel atmosphere.

In a spherical atmosphere there are three potential depth variables: mass column density, m, radius, r, and radial Rosseland mean optical depth, $\tau_{{\rm R}}$. As discussed by Mihalas & Hummer (1974), there is no clear preference for any of these variables. Therefore, we have elected to adopt the radial Rosseland mean optical depth as our primary variable, and then use $T(\tau_{{\rm R}})$ to solve for the pressure structure by modifying the subroutine ttaup. This is done in the initialization of the calculation and for each iteration.

The modifications to the subroutine ttaup include allowing the surface gravity to vary with the radial distance from the center of the star,

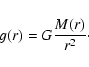\begin{displaymath}g(r) = G \frac{M(r)}{r^2}\cdot \end{displaymath} (3)

Because the mass of the atmosphere is negligible compared to the mass of the star, it is an excellent approximation to set $M(r) = M_{\ast}$, giving

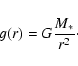\begin{displaymath}g(r) = G \frac{M_{\ast}}{r^2}\cdot \end{displaymath} (4)

If the starting model is a spherical model, there will be initial values for r. If the starting model is plane parallel, we solve for r from the defining differential equation

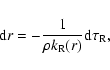\begin{displaymath}\textrm{d} r = - \frac{1}{\rho k_{{\rm R}}(r)} \textrm{d} \tau_{{\rm R}}, \end{displaymath} (5)

in its logarithmic form to minimize numerical errors. Here $\rho(r)$ is the mass density, and $k_{{\rm R}}(r)$ is the Rosseland mean opacity, the sum of absorption, $\kappa$, and scattering, $\sigma$, per unit mass as a function of depth, both of which are available from the input model. This solution begins by assuming an initial value for the atmosphere's extension, $r(1)/R_{\ast}$, after which the solution is performed using the Bulirsch-Stoer method given in Numerical Recipes in Fortran 90 (Press et al. 1996). The fifth-order Runga-Kutta method, also from Numerical Recipes in Fortran 90, was also investigated, and is built into the source code, but we found the results from the two methods to be identical. After finishing the solution for r, the atmospheric extension, $r(1)/R_{\ast}$, is checked against the initial assumption. If the extension differs by more than 10-6 from the starting assumption, the starting assumption is updated and the solution is iterated until the extension converges to <10-6.

Using g(r), the equation of spherical hydrostatic equilibrium is

 \begin{displaymath} \frac{\textrm{d} P_{{\rm tot}}}{\textrm{d} \tau_{{\rm R}}} = \frac{g(r)}{k_{{\rm R}}(r)}\cdot \end{displaymath} (6)

The solution begins at the upper boundary by assuming an initial value of $k_{{\rm R}}(1)$. Then, following Mihalas & Hummer (1974), we assume all properties, except pressure and density, are constant above r(1), and that these variables decrease with a constant scale height. This leads to

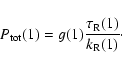\begin{displaymath}P_{{\rm tot}}(1) = g(1) \frac{\tau_{{\rm R}}(1)}{k_{{\rm R}}(1)}\cdot \end{displaymath} (7)

The gas pressure, $P_{{\rm g}}(1)$, is derived from the total pressure by subtracting values for radiation pressure, $P_{{\rm r}}(1)$, and turbulent pressure, $P_{{\rm t}}(1)$, if these are known. The gas pressure and the temperature are then used to interpolate an updated value for $k_{{\rm R}}(1)$ from the input model. This procedure is iterated until the upper boundary pressure converges to <10-6.

With the upper boundary condition established, Eq. (6) is integrated for $P_{{\rm tot}}$, again using the Bulirsch-Stoer method. At each step the gas pressure is found as described above, and the gas pressure and temperature are used to interpolate the corresponding value for the Rosseland mean opacity.

This method of solving the hydrostatic equilibrium is also applicable to the plane-parallel atmosphere with g(r) = g and without solving for the radius. To test our implementation, we have incorporated the modified version of subroutine ttaup, with both the Bulirsh-Stoer and the fifth-order Runga-Kutta routines, into ATLAS_ODF and ATLAS_OS. The maximum difference between the Bulirsch-Stoer (or the fifth-order Runga-Kutta) method and the original Hamming method was less than our output numerical resolution of 1 part in 104 at all but two of the 72 depth points. Therefore, the percentage difference between the methods is zero except at these two depths, where the differences are only 0.021% and $0.014\%$. It is clear that the pressure solution is being done correctly.


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{0578fg4.eps}\end{figure} Figure 4: The geometry used for the Rybicki (1971) method of radiative transfer. The rays are distributed over the core in equal steps of 0.1 in $\mu $.
Open with DEXTER

3.2 Radiative transfer

ATLAS9 and ATLAS12 solve the radiative transfer using the integral equation method. The complication introduced by a geometrically extended, spherically symmetric atmosphere is that the angle between a ray of light and the radial direction varies with depth. Numerous methods are available for solving this problem, of which we have chosen to use the Rybicki (1971) reorganization of the Feautrier (1964) method.

Following the approach described by Mihalas (1978), we solve the radiative transfer along a set of rays parallel to the central ray directed toward the distant observer, as shown in Fig. 4. A subset of these rays intersect the ``core'' of the star, defined as the deepest radial optical depth, which we usually set to be $\tau_{{\rm R}} = 100$. We sample the surface of the core using 10 rays. We tried both equal steps of $\mu = \cos \theta$ covering the interval $1.0 \leq \mu \leq 0.1$ in steps of $\Delta \mu = 0.1$, which is shown in Fig. 4, and a finer spacing toward the edge of the core by distributing the rays as $\mu = 1.0$, 0.85, 0.7, 0.55, 0.4, 0.25, 0.2, 0.15, 0.1, 0.05. We found the results to be almost identical, so we chose to use the equal $\mu $ spacing.

For the core rays, the lower boundary condition of the radiative transfer is the diffusion approximation. From the core to the surface we follow the convention used by Kurucz in his plane-parallel models by having 72 depth points. For the central ray these depth points are distributed eight per decade with equal steps of the $\Delta \log \tau_{{\rm R}} = 0.125$ from $\log \tau_{{\rm R}} = 2$ to -6.875. For the off-center core rays the steps will be different, depending on the projection.

The tangent rays are those that terminate at the radius perpendicular to the central ray, and which are tangent to a particular atmospheric shell at that point, as shown in Fig. 4. The radial spacing between the shells is set by the central ray, and these spacings define the impact parameters of all the tangent rays. With this geometry, we calculated values of $\mu $ at the intersection of each ray toward the distant observer with each atmospheric depth, and from these we compute the integration weights at each point over the surface of each atmospheric shell at every depth. The lower boundary condition for the radiative transfer of the tangent rays is the assumption of symmetry at the perpendicular radius. At the surface of the atmosphere the rays toward the distant observer have $\mu $ values that depend on the steps described above. When we want to use these surface intensities, such as to predict the observable center-to-limb variation, we map the computed $I(\mu)$ onto a specified set of $\mu $-values using a cubic spline interpolation.


  \begin{figure} \par\includegraphics[width=8cm,clip]{0578fg5.eps}\end{figure} Figure 5: A comparison of the temperature structures for two solar atmospheric models, both using the ATLAS_ODF code. The solid line used the Rybicki (1971) method to compute the radiative transfer, and the dashed line used the original ATLAS9 integral equation method.
Open with DEXTER

This solution with the Rybicki (1971) organization uses exactly the same equations as the original Feautrier (1964) method. Therefore, in the plane-parallel case, in which both can be used, the results must be exactly the same. To test this, we created two alternative radiative transfer routines for the plane-parallel codes ATLAS_ODF and ATLAS_OS, one new routine having the original Feautrier organization and the other having the Rybicki organization, and we select which of the radiative transfer routines we want by using an input instruction at run time, holding everything else the same. The result of the comparison is shown in Fig. 5.

Using the Feautrier (1964) organization gives exactly the same result (the output files have zero differences), as it should. The tiny temperature drop at the top of the atmosphere shown in Fig. 5 is entirely due to the precise form of implementing the surface boundary condition. We explored different implementations (changing one statement) that were logically equivalent, and we found the result shown to be the closest match to the original ATLAS integral equation solution. The other implementations gave the same temperature at the top depth of the atmosphere, $T(\tau_1)$, but have a slower convergence to the temperature derived using the integral equation method.

A note about the relative run times of the same code using the three different radiative transfer routines: the time per iteration using the Feautrier method is about half the time of the original integral equation method, while with the Rybicki method the time per iteration is about ten times longer than the original integral equation method.

The difference in the execution time of the Feautrier and the Rybicki methods, which use the same equations, is due to the sizes of the matrices that must be inverted. The Feautrier method computes the radiation field for all $\mu $ values at each atmospheric depth, where the $\mu $ values are the double-Gauss angles found to be superior by Sikes (1951). The computing time to invert the matrices scales as the cube of the number of $\mu $ values, M3. We use three angle points because our tests using four and eight angle points are insignificantly different ( $\Delta T < 1$ K) from the three-angle solution, while the computing time is certainly increased.

The Rybicki method computes the radiation for each individual ray over all atmospheric depths. The number of depth points ranges from just two for the tangent ray that penetrates just one atmospheric depth, up to 72 depth points for the rays that reach the core. The need to invert these larger matrices causes the execution of the Rybicki method to be longer.

3.3 Temperature correction

ATLAS9 and ATLAS12 perform the temperature correction using the Avrett-Krook method (Avrett 1964; Avrett & Krook 1963) modified to include convection (Kurucz 1970). While the other spherical atmosphere programs (PHOENIX and MARCS) use their own methods to perform temperature corrections, it is our experience (Tycner & Lester 2002) that the Avrett-Krook method is extremely robust, capable of achieving temperature convergence $\leq$1 mK. Therefore, we have chosen to modify the Avrett-Krook temperature correction routine in the original ATLAS codes to include spherically symmetric extension.

We start with the time-independent equation of radiative transfer in spherical geometry (Mihalas 1978),

 \begin{displaymath} \mu \frac{\partial I(\nu)}{\partial r} + \frac{1 - \mu^2}{r} \frac{\partial I(\nu)}{\partial \mu} = k(\nu) [S(\nu) - I(\nu)], \end{displaymath} (8)

where $S(\nu)$ is the source function given by

 \begin{displaymath} S(\nu, T) = \sigma(\nu) J(\nu) + [1 - \sigma(\nu)] B(\nu, T). \end{displaymath} (9)

To be consistent with the approach in ATLAS, we express Eq. (8) in terms of the mass column density (Eq. (2)) to obtain

 \begin{displaymath} - \rho \mu \frac{\partial I(\nu)}{\partial m} + \frac{1 - \... ...rac{\partial I(\nu)}{\partial \mu} = k(\nu) [S(\nu) - I(\nu)]. \end{displaymath} (10)

In general, Eq. (10) does not conserve the luminosity with depth because the atmospheric temperature structure is wrong, but we assume that small perturbations to the current structure will produce a constant luminosity with depth. That is, we introduce the perturbations

 \begin{displaymath} m = m_0 + \delta m, \end{displaymath} (11)


 \begin{displaymath} r = r_0 + \delta r, \end{displaymath} (12)


 \begin{displaymath} T = T_0 + \delta T, \end{displaymath} (13)

and

 \begin{displaymath} I(\nu) = I_0(\nu) + \delta I(\nu), \end{displaymath} (14)

where the subscript 0 refers to the current structure. We also use the subscript 0 for the current extinction, $k_0(\nu)$, and the current source function, $S_0(\nu)$.

The extinction and the source function are expanded to first order as

 \begin{displaymath} k(\nu) = k_0(\nu) + \frac{\partial k_0(\nu)}{\partial m} \cdot \delta m, \end{displaymath} (15)

and

 \begin{displaymath} S(\nu) = S_0(\nu) + \frac{\partial S_0(\nu)}{\partial m} \cd... ...delta m + \frac{\partial S_0(\nu)}{\partial T} \cdot \delta T. \end{displaymath} (16)

To simplify the notation further, we represent $\partial k_0(\nu) / \partial m = k_0^\prime(\nu)$, $\partial S_0(\nu) / \partial m = S_0^\prime(\nu)$, and $\partial S_0(\nu) / \partial T = \dot{S}_0(\nu)$.

Using Eq. (11) we can write

 \begin{displaymath} \frac{\textrm{d} m}{\textrm{d} m_0} = 1 + \frac{\textrm{d} \delta m}{\textrm{d} m_0} \end{displaymath} (17)

or

 \begin{displaymath} \textrm{d} m = \textrm{d} m_0(1 + \delta m^{\prime}), \end{displaymath} (18)

where

 \begin{displaymath} \delta m^{\prime} = \frac{\textrm{d} \delta m}{\textrm{d} m_0}\cdot \end{displaymath} (19)

Therefore, the derivative in the first term in Eq. (10) becomes

\begin{displaymath}\frac{\partial I(\nu)}{\partial m} = \frac{\partial I(\nu)}{\partial m_0} (1 + \delta m^{\prime})^{-1}. \end{displaymath} (20)

In the second term in Eq. (10) there is $r^{-1} = (r_0 + \delta r)^{-1}$. Because we assume that $\delta r \ll r_0$, we can perform a binomial expansion of r-1, keeping only the first two terms, to get

 \begin{displaymath} \frac{1}{r} = \frac{1}{r_0 + \delta r} \approx \frac{1}{r_0... ... = \frac{1}{r_0} \left (1 + \frac{\delta m}{\rho r_0} \right ) \end{displaymath} (21)

by using Eq. (2).

Using these, the spherical radiative transfer equation, including perturbations, becomes

 
$\displaystyle {\frac{- \rho \mu}{1 + \delta m^\prime}\frac{\partial[I_0(\nu) + ... ...{\rho r_0} \right) \frac{\partial [I_0(\nu) + \delta I(\nu)]}{\partial \mu} = }$
    $\displaystyle [k_0(\nu) + k_0^\prime(\nu) \cdot \delta m] [S_0(\nu) + S_0^\prime(\nu) \cdot \delta m + \dot{S}_0(\nu) \cdot \delta T$  
    $\displaystyle {}- I_0(\nu) - \delta I(\nu)].$ (22)

Clearing the $1/(1 + \delta m^{\prime})$ term and expanding Eq. (22), ignoring terms with second-order perturbations, gives
 
$\displaystyle { - \rho \mu \frac{\partial I_0(\nu)}{\partial m_0} - \rho \mu \f... ...rtial \mu} + \frac{1 - \mu^2}{r_0} \frac{\partial \delta I(\nu)}{\partial \mu}}$
    $\displaystyle {} + \frac{1 - \mu^2}{r_0} \left ( \delta m^{\prime} + \frac{\del... ...right ) \frac{\partial I_0(\nu)}{\partial \mu} = k_0(\nu) [S_0(\nu) - I_0(\nu)]$  
    $\displaystyle {}\quad + [k_0(\nu) \cdot \delta m^\prime + k_0^\prime \cdot \delta m] [S_0(\nu) - I_0(\nu)]$  
    $\displaystyle {} \quad + k_0(\nu) [S_0^\prime(\nu) \cdot \delta m + \dot{S}_0(\nu) \cdot \delta T - \delta I(\nu)].$ (23)

Note that the left hand side of Eq. (23) contains

 \begin{displaymath} - \rho \mu \frac{\partial I_0(\nu)}{\partial m_0} + \frac{1 - \mu^2}{r_0}\frac{\partial I_0(\nu)}{\partial \mu}, \end{displaymath} (24)

and the right hand side has

 \begin{displaymath} k_0(\nu) [S_0(\nu) - I_0(\nu)], \end{displaymath} (25)

and these equal each other because they are just the two sides of Eq. (10) for the current structure. Canceling these out of Eq. (23) leaves the first-order perturbation of the spherical equation of radiative transfer
 
$\displaystyle {- \rho \mu \frac{\partial \delta I(\nu)}{\partial m_0} + \frac{1... ... + \frac{\delta m}{\rho r_0} \right ) \frac{\partial I_0(\nu)}{\partial \mu}= }$
    $\displaystyle [k_0(\nu) \cdot \delta m^{\prime} + k_0^{\prime}(\nu) \cdot \delta m] [S_0(\nu) - I_0(\nu)]$  
    $\displaystyle {} + k_0(\nu) [S_0^{\prime}(\nu) \cdot \delta m + \dot{S_0}(\nu) \cdot \delta T - \delta I(\nu)].$ (26)

The first angular moment of the first-order perturbation equation is obtained by multiplying Eq. (26) by $\mu $ and integrating over all $\mu $, to get
 
$\displaystyle {- \rho \frac{\partial \delta K(\nu)}{\partial m_0} + \frac{1}{r_0} [3 \delta K(\nu) - \delta J(\nu)] = }$
    $\displaystyle {} - [k_0(\nu) \cdot \delta m^{\prime} + k_0^\prime(\nu) \cdot \delta m] H_0(\nu) - k_0(\nu) \delta H(\nu)$  
    $\displaystyle {} - \frac{1}{r_0} \left (\delta m^{\prime} + \frac{\delta m}{\rho r_0} \right ) [3K_0(\nu) - J_0(\nu)].$ (27)

Dividing Eq. (27) by $k_0(\nu)$ and integrating over all frequencies, we obtain
 
$\displaystyle {\int_0^{\infty}\frac{1}{k_0(\nu)} \left [ \frac{3 \delta K(\nu) ... ...} - \rho \frac{\partial \delta K(\nu)}{\partial m_0} \right ] \textrm{d} \nu =}$
    $\displaystyle {} - \delta m^{\prime} \int_0^{\infty} H_0(\nu) \textrm{d} \nu - ... ...0(\nu) } H_0(\nu) \textrm{d} \nu - \int_0^{\infty} \delta H(\nu) \textrm{d} \nu$  
    $\displaystyle {} - \frac{1}{r_0} \left (\delta m^{\prime} + \frac{\delta m}{\rh... ...right ) \int_0^{\infty} \frac{[3K_0(\nu) - J_0(\nu)]}{k_0(\nu)} \textrm{d} \nu.$ (28)

We now assume that the correct choice of $\delta m$ will make the left hand side of Eq. (28) go to zero. That is, we assume that the perturbations of the radiation field, $\delta K$ and $\delta J$, vanish when the correct atmospheric structure is obtained. These assumptions are equivalent to the assumptions used in Avrett (1964), Eq. (25), and in Kurucz (1970), Eq. (7.5). This leaves the right hand side of Eq. (28) as a differential equation for $\delta m$,

 \begin{displaymath} a_0 \delta m^{\prime} + b_0 \delta m + c_0 = 0, \end{displaymath} (29)

where

 \begin{displaymath} a_0 = H_0 + \frac{1}{r_0} \int_0^{\infty} \frac{[3K_0(\nu) - J_0(\nu)]} {k_0(\nu)} \textrm{d} \nu, \end{displaymath} (30)


 \begin{displaymath} b_0 = \int_0^{\infty} \frac{k_0^{\prime}(\nu)}{k_0(\nu)}H_0(... ...infty} \frac{[3K_0(\nu) - J_0(\nu)]} {k_0(\nu)} \textrm{d} \nu \end{displaymath} (31)

and

 \begin{displaymath} c_0 = \int_0^{\infty} \delta H(\nu) \textrm{d} \nu = \delta H = \mathcal{H} - H_0, \end{displaymath} (32)

with

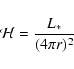\begin{displaymath}\mathcal{H} = \frac{L_{\ast}}{(4 \pi r)^2} \end{displaymath} (33)

being the radially dependent Eddington flux that we need to achieve. The general solution to Eq. (29) is

 \begin{displaymath} \delta m = - \exp \left [-\int \frac{b_0(\tilde{m})} {a_0(\t... ...m})}{a_0(\tilde{m})} {\rm d} \tilde{m}} \textrm{d} \tilde{m}, \end{displaymath} (34)

where $\tilde{m}$ is an integration variable.

The correction for the mass column density found above has assumed that all the energy is carried by radiation. If the atmospheric temperature is cool enough, significant amounts of energy can also be carried by convection in the deeper, less transparent levels of the atmosphere. ATLAS calculates the convective energy transport by the mixing length approximation. The equations in Kurucz (1970) do not contain the radial variable explicitly, but they do contain the surface gravity, g, which now varies with r. However, the implementation of those equations replaces g in terms of the total pressure, which now implicitly includes the geometry. Therefore, there is no need to modify the original ATLAS code to include convection in the spherical temperature correction, and Eq. (29) remains the same, with the addition of convective terms in the coefficients a0, b0 and c0 as follows:

 
                          a0 = $\displaystyle H_0({\rm rad}) + \frac{1}{r_0} \int_0^{\infty} \frac{[3K_0(\nu) - J_0(\nu)]} {k_0(\nu)} \textrm{d} \nu$  
    $\displaystyle {} + H_0({\rm conv}) \frac{3 \nabla}{2(\nabla - \nabla_{{\rm ad}})} \left (1 + \frac{D}{D + \nabla - \nabla_{{\rm ad}}} \right )$ (35)


 
$\displaystyle {b_0 = \int_0^{\infty} \frac{k_0^{\prime}(\nu)}{k_0(\nu)}H_0(\nu)... ...r_0^2} \int_0^{\infty} \frac{[3K_0(\nu) - J_0(\nu)]} {k_0(\nu)} \textrm{d} \nu}$
    $\displaystyle {}\quad + H_0({\rm conv}) \frac{\textrm{d} T}{\textrm{d} m} \frac{1}{T} \left [ 1 - \frac{9 D}{D + \nabla - \nabla_{{\rm ad}}} \right .$  
    $\displaystyle \left . {} \quad + \frac{3}{2(\nabla - \nabla_{{\rm ad}})} \frac{... ...textrm{d} m}\left ( 1 + \frac{D}{D + \nabla - \nabla_{{\rm ad}}} \right)\right]$ (36)

and

 \begin{displaymath} c_0 = \mathcal{H} - H_0({\rm rad}) - H_0({\rm conv}). \end{displaymath} (37)

In Eqs. (35) and (36) the $\nabla$ is

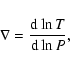\begin{displaymath}\nabla = \frac{\textrm{d} \ln T}{\textrm{d} \ln P}, \end{displaymath} (38)

D is from Kurucz (1970), and in Eq. (36) the $H_0(\nu)$ is the radiative flux. Solving Eq. (34) for $\delta m$, using the coefficients in Eqs. (35), (36) and (37), the corresponding temperature change based on conserving the flux is

 \begin{displaymath} \delta T_{{\rm flux}} = \frac{\partial T}{\partial m} \delta m. \end{displaymath} (39)

ATLAS uses two additional temperature corrections near the surface, where the flux error loses sensitivity. One correction is based on the flux derivative. Because this correction applies high in the atmosphere where the gas is quite transparent, radiation will carry almost all the energy, and it is a good approximation to ignore convective energy transport. The zeroth angular moment of the spherical radiative transfer equation (Eq. (10)) is

 \begin{displaymath} \frac{\partial [r^2 H(\nu)]}{\partial m} = r^2 k(\nu) [J(\nu) - S(\nu)]. \end{displaymath} (40)

Replacing $J(\nu)$ by $\Lambda[S(\nu)]$, expanding the Planck function in $S(\nu)$ in terms of T, integrating over frequency and retaining just the diagonal terms of the $\Lambda$ operator, the resulting temperature correction becomes

 \begin{displaymath} \delta T_{\Lambda} = \frac{ \frac{1}{r^2} \left \{ \frac{\pa... ...u)] \frac{\partial B(\nu, T)}{\partial T} \textrm{d} \nu}\cdot \end{displaymath} (41)

The term $\Lambda_{{\rm dia}}$ is approximated by the plane-parallel expression given in Kurucz (1970), assuming it has minimal dependence on the geometry.

A third temperature correction is used in the original ATLAS code to smooth the region of overlap between the first two corrections. This is

 \begin{displaymath} \delta T_{{\rm surf}} = \frac{T \delta H}{4 \cal{H}}, \end{displaymath} (42)

and this is retained here. The total temperature correction is therefore,

 \begin{displaymath} \delta T = \delta T_{{\rm flux}} + \delta T_{\Lambda} + \delta T_{{\rm surf}}. \end{displaymath} (43)

4 Comparisons between SATLAS_ODF and ATLAS_ODF

One test of the validity of the spherical code is to compute a spherical solar atmosphere, which should be nearly identical to the plane-parallel model. For both models we used the Kurucz file asunodfnew.dat for the starting model and the file bdfp00fbig2.dat for the opacity distribution function. To eliminate other possible sources of differences, we used the Bulirsch-Stoer solution to solve for the pressure structures and the Rybicki method for the radiative transfer in the plane-parallel model as well as for the spherical calculations. The spherical model used the atmospheric parameters $L_{\hbox{$\odot$ }} = 3.8458~ \times~~ 10^{33}$ erg/s, $M_{\hbox{$\odot$ }} = 1.9891 ~\times~~ 10^{33}$ g, and $R_{\hbox{$\odot$ }} = 6.95508 \times 10^{10}$ cm. These correspond to $T_{{\rm eff}} = 5779.5$ K and $\log g = 4.43845$, which are slightly different from the canonical values used by Kurucz. Therefore, we computed the plane-parallel model with the consistent values of $T_{{\rm eff}}$ and $\log g$. The comparison is shown in Fig. 6.

The $\vert\Delta T \vert$ is $\leq 0.25\%$ until $\log_{10}~P_{{\rm gas}} < 2$, where the temperature of the spherical model begins to trend lower than the plane-parallel model. The dip in the temperature difference down to -2.4% is due to the kink in the temperature structure of the plane-parallel model. This feature was discussed earlier in connection with Fig. 5. However, in this case the Rybicki (1971) method is used to compute the radiative transfer in both models, using the same surface boundary condition in both codes. Therefore, this difference cannot be due to a coding difference between the two routines. This feature might be due to the number of rays used in the calculation of the radiative transfer. The Rybicki solution for the plane-parallel code uses three rays for each depth, whereas the same method in the spherical code uses $\approx$80 rays for the layers approaching the surface. Perhaps this finer griding produces a smoother temperature profile in these layers. There is, however, no physical significance to the temperature differences near the surface because these layers are located in the solar chromosphere (Fontenla et al. 2006), well above the temperature minimum, where other physics is completely dominant.


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{0578fg6.eps}\end{figure} Figure 6: A comparison of the temperature structures for two solar atmospheric models. The top panel displays the temperatures as a function of $\log_{10} (P_{{\rm gas}})$. The solid line is computed using spherical geometry and the dashed line is using the traditional plane-parallel geometry. The radiative transfer and the pressure structures of both models were computed using the same numerical techniques. The bottom panel shows the percentage difference between the temperatures of the two models, also as a function of the gas pressure.
Open with DEXTER

A test where larger differences are expected is for the coolest model ( $T_{{\rm eff}} = 3500$ K, $\log g = 0.0$) in the grid /grids/gridp00odfnew/ap00k2odfnew.dat (computed by Castelli) on the Kurucz web site. Because $T_{{\rm eff}}$ and $\log g$ really represent the three parameters L, M and R, there is a degeneracy that must be broken. To do this, we have assumed the star has  $M = 1~M_{\hbox{$\odot$ }}$, which leads to $L_{\ast} = 3690~L_{\hbox{$\odot$ }}$ and $R = 166~R_{\hbox{$\odot$ }}$. The comparison of the atmospheric structures is shown in Fig. 7. While the plane-parallel model was taken from the grid on Kurucz's web site, that model served only as the starting point for computing the model structure using our ATLAS_ODF code to ensure that it reflects the same numerical routines. In particular, we used the Rybicki routine for the radiative transfer of both the plane-parallel and the spherical models so that the resulting differences must come from the atmosphere's geometry, and not the method of solution.

The spherical model is cooler than the plane-parallel model throughout most of the atmosphere, and it becomes progressively cooler with increasing height. The distance from r(1) to $r(\tau_{{\rm R}} = 2/3) = R_{\ast}$ is $2.12 \times 10^7$ km, giving an atmospheric extension, defined in Sect. 3.1, of 0.18. In the plane-parallel model the corresponding distance d(1)- $d(\tau_{{\rm R}} = 2/3) = 1.85 \times 10^7$ km. Deep in the atmosphere the spherical model becomes systematically hotter than the planer-parallel model as the core makes a greater contribution.


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{0578fg7.eps}\end{figure} Figure 7: A comparison of the temperature structures of two red giant atmospheric models. The top panel displays the temperatures as a function of $\log_{10} (P_{{\rm gas}})$. The solid line is a spherical model with the parameters $L = 3690~L_{\hbox{$\odot$ }}$, $M = 1~M_{\hbox{$\odot$ }}$ and $R = 166~R_{\hbox{$\odot$ }}$. These values were chosen to match the parameters of the plane-parallel model having $T_{{\rm eff}} = 3500$ K and $\log g = 0.0$, computed using ATLAS_ODF, shown by the dashed line. The bottom panel shows the percentage difference between the temperatures of the two models, also as a function of the gas pressure.
Open with DEXTER

Because of the degeneracy of the atmospheric parameters, we tried another combination of luminosity, mass and radius that also match $T_{{\rm eff}} = 3500$ K and $\log g = 0.0$, namely, $L_{\ast} = 2952~L_{\hbox{$\odot$ }}$, $M = 0.8~M_{\hbox{$\odot$ }}$ and $R = 148~R_{\hbox{$\odot$ }}$. The comparison of the two spherical models, both computed with SATLAS_ODF, is shown in Fig. 8. The structures are so similar that they seem identical in the top panel. In the bottom panel, where the differences in the structures are plotted, it is easier to see that the less massive and luminous star has a slightly steeper temperature profile, as is expected.


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{0578fg8.eps}\end{figure} Figure 8: A comparison of the structures of two spherical red giant atmospheric models, both equivalent to $T_{{\rm eff}} = 3500$ K and $\log g = 0.0$. The top panel displays the temperatures as a function of $\log_{10} (P_{{\rm gas}})$. The solid line is a spherical model having $L = 3690~L_{\hbox{$\odot$ }}$, $M = 1~M_{\hbox{$\odot$ }}$ and $R = 166~R_{\hbox{$\odot$ }}$. The dashed line, which is nearly coincident with the solid line, represents the model having the parameters $L = 2952~L_{\hbox{$\odot$ }}$, $M = 0.8~M_{\hbox{$\odot$ }}$ and $R = 148~R_{\hbox{$\odot$ }}$. The bottom panel shows the percentage difference between the temperatures of the two models, also as a function of the gas pressure. The sense of the differences is the less massive and luminous model minus the more massive and luminous model.
Open with DEXTER

5 Comparison with other programs

The PHOENIX program (Hauschildt et al. 1999) can also compute LTE, line-blanketed, spherically extended models, and a comparisons with those models is appropriate. The PHOENIX web site (http://www.hs.uni-hamburg.de/EN/For/ThA/phoenix/index.html) contains the NG-giant grids, in which the model that is closest to the examples used above is the one with $T_{{\rm eff}} = 3600$ K, $\log g = 0.0$ and $M = 2.5~M_{\hbox{$\odot$ }}$. To compare with this model, we have computed a spherical model with $L = 10~324~L_{\hbox{$\odot$ }}$, $M = 2.5~M_{\hbox{$\odot$ }}$ and $R = 262~R_{\hbox{$\odot$ }}$, again starting from the same plane-parallel model with $T_{{\rm eff}} = 3500$ K and $\log g = 0.0$ that we used earlier. The comparison is shown in Fig. 9. Now the differences are somewhat larger than in the previous comparisons, which is to be expected because the detailed calculations are nearly totally independent. Overall, however, the comparison is very similar, showing that the two models have essentially the same structures, although we note that the NextGen model has a temperature bulge compared with our model in the pressure range $-1 < \log_{10} P_{{\rm gas}} < + 1.5$. We have not observed this kind of feature in the comparisons we have made with the Kurucz models or between our spherical and plane-parallel models.

A note about the relative run times of the two codes: the time per iteration running SATLAS_ODF on our single-processor desktop workstation is just 5% of the time per iteration given in the header files of the NG-giant model.


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{0578fg9.eps}\vspace*{2mm} \end{figure} Figure 9: A comparison of the temperature structures of an SATLAS_ODF atmosphere (solid line) with the structure of a model from the NG-giant grid computed with the PHOENIX code (dashed line). The SATLAS model has the atmospheric parameters $L = 10~324~L_{\hbox{$\odot$ }}$, $M = 2.5~M_{\hbox{$\odot$ }}$ and $R = 262~R_{\hbox{$\odot$ }}$, corresponding to the NextGen parameters $T_{{\rm eff}} = 3600$ K, $\log g = 0.0$ and $M = 2.5~M_{\hbox{$\odot$ }}$.
Open with DEXTER

The MARCS program (Gustafsson et al. 2008) is another well established code that has the ability to compute LTE, line-blanketed, spherical model atmospheres. From the MARCS web site (http://marcs.astro.uu.se/) the model with parameters $T_{{\rm eff}} = 4000$ K, $\log g = 0.0$ and $M = 1~M_{\hbox{$\odot$ }}$ is closest the the examples we have been using. This model also has solar abundances and a microturbulent velocity of 2 km s-1. The header lines in the model gives the spherical parameters $L = 6390~L_{\hbox{$\odot$ }}$ and $R = 1.1550 \times 10^{13}~\textrm{cm} = 166~R_{\hbox{$\odot$ }}$. MARCS defines the radius at $\tau_{{\rm R}} = 1.0$, not at $\tau_{{\rm R}} = 2/3$ that we use, but this is a small difference. Therefore, we have started from the model with $T_{{\rm eff}} = 4000$ K, $\log g = 0.0$ and microturbulence = 2 km s-1 in the same grid (/grids/gridp00odfnew/ap00k2odfnew.dat) used earlier, and we have computed a spherical model with the luminosity, mass and radius of the MARCS model. The comparison is shown in Fig. 10. The models agree very well in the range $\log_{10} P_{{\rm gas}} < + 1.5$, where the NextGen model displayed a temperature bulge. But, the spherical MARCS model appears to have a pressure inversion at T > 6500 K, something that is not present in the comparison with the PHOENIX model. Overall, however, the structures are in substantial agreement.

6 Conclusions

We have modified the robust, open-source, plane-parallel model atmosphere program ATLAS to treat spherically extended geometry. The resulting spherical code, SATLAS, which is available in both opacity distribution function and opacity sampling versions, was used to compute several test models. At high surface gravity the spherical model structure is essentially identical to the plane-parallel model structure. At low surface gravity, the SATLAS models agree very well with the spherical model structures computed by PHOENIX and by MARCS. The SATLAS program, which runs easily on a desktop workstation, offers a viable alternative for modeling the atmospheres of low surface gravity stars.


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{0578fg10.eps} \end{figure} Figure 10: A comparison of the temperature structures of an SATLAS_ODF atmosphere (solid line) with a spherical MARCS model (dashed line). The SATLAS model has the atmospheric parameters $L = 6390~L_{\hbox{$\odot$ }}$, $M = 1.0~M_{\hbox{$\odot$ }}$ and $R = 166~R_{\hbox{$\odot$ }}$, corresponding to the MARCS parameters $T_{{\rm eff}} = 4000$ K, $\log g = 0.0$ and $M = 1.0~M_{\hbox{$\odot$ }}$.
Open with DEXTER

As an example of the utility of SATLAS, we have used it to compute more than 2500 models to create model cubes with fine parameter spacing covering the specific $L_{\ast}$, $M_{\ast}$ and $R_{\ast}$ values needed for an analysis of the optical interferometry of just three stars (Neilson & Lester 2008). We are in the process of computing more models for our own application. These codes and models are available at http://www.astro.utoronto.ca/~lester/Programs/.

Acknowledgements
This work is built on the development of the original ATLAS programs by Robert Kurucz, and his generosity in making his source codes, line lists and opacity distribution functions freely available. Our modifications have benefited greatly from the many times that he has answered our questions and from the test models he has provided. We also gratefully acknowledge the comments and sample models provided by Fiorella Castelli that have aided our efforts. We also thank the anonymous referee for asking numerous questions that prompted us to provide more thorough explanations of our results.

This work has been supported by a research grant from the Natural Sciences and Engineering Research Council of Canada. H.R.N. has received financial support from the Walter John Helm OGSST and the Walter C. Sumner Memorial Fellowship.

References

 
Copyright ESO 2008