Recent VLT SINFONI observations of the close environments (
A&A 491, 441-453 (2008)
DOI: 10.1051/0004-6361:200810446
B. Vollmer1 - T. Beckert2 - R. I. Davies3
1 - CDS, Observatoire astronomique de Strasbourg, UMR 7550,
11 rue de l'université, 67000 Strasbourg, France
2 -
Max Planck Institut für Radioastronomie,
Auf dem Hügel 69, 53121 Bonn, Germany
3 -
Max Planck Insitut für extraterrestrische Physik, Postfach 1312,
85741 Garching, Germany
Received 23 June 2008 / Accepted 15 September 2008
Abstract
Recent VLT SINFONI observations of the close environments (![]() 30 pc) of nearby AGNs have shown that thick gas tori and starbursts with ages between 10 and 150 Myr are frequently found. By applying these observations to a previously established analytical model of clumpy accretion disks, we suggest an evolutionary sequence for starburst and AGN phases. Whereas the observed properties of the gas tell us about the current state of the torus, the starburst characteristics provide information on the history of the torus. In the suggested evolution, a torus passes through 3 different phases predetermined by an external mass accretion rate. Started by an initial, short, and massive gas infall, a turbulent and stellar wind-driven
30 pc) of nearby AGNs have shown that thick gas tori and starbursts with ages between 10 and 150 Myr are frequently found. By applying these observations to a previously established analytical model of clumpy accretion disks, we suggest an evolutionary sequence for starburst and AGN phases. Whereas the observed properties of the gas tell us about the current state of the torus, the starburst characteristics provide information on the history of the torus. In the suggested evolution, a torus passes through 3 different phases predetermined by an external mass accretion rate. Started by an initial, short, and massive gas infall, a turbulent and stellar wind-driven ![]() disk is formed in which the starburst proceeds. Once the supernovae explode the intercloud medium is removed, leaving a massive, geometrically thick, collisional disk with a decreasing, but still high-mass accretion rate. When the mass accretion rate has significantly decreased, the collisional torus becomes thin and transparent as the circumnuclear disk in the Galactic center of the Milky Way. Variations on this scenario are possible either when there is a second short and massive gas infall, in which case the torus may switch back into the starburst mode, or when there is no initial short massive gas infall. All observed tori up to now have been collisional and thick. The observations show that this phase can last more than 100 Myr. During this phase the decrease in the mass accretion rate within the torus is slow (a factor of 4 within 150 Myr). The collisional tori also form stars, but with an efficiency of about 10% when compared to a turbulent disk.
disk is formed in which the starburst proceeds. Once the supernovae explode the intercloud medium is removed, leaving a massive, geometrically thick, collisional disk with a decreasing, but still high-mass accretion rate. When the mass accretion rate has significantly decreased, the collisional torus becomes thin and transparent as the circumnuclear disk in the Galactic center of the Milky Way. Variations on this scenario are possible either when there is a second short and massive gas infall, in which case the torus may switch back into the starburst mode, or when there is no initial short massive gas infall. All observed tori up to now have been collisional and thick. The observations show that this phase can last more than 100 Myr. During this phase the decrease in the mass accretion rate within the torus is slow (a factor of 4 within 150 Myr). The collisional tori also form stars, but with an efficiency of about 10% when compared to a turbulent disk.
Key words: galaxies: active - galaxies: nuclei - ISM: clouds - ISM: structure - ISM: kinematics and dynamics
In the unification scheme for active galactic nuclei (AGN) the central massive black hole is surrounded by a geometrical thick gas and dust torus (see, e.g., Antonucci 1993). If the observer's line-of-sight crosses the torus material, the AGN is entirely obscured from near-IR to soft X-rays and only visible at X-ray energies if the gas column density is not too high (Seyfert 2 galaxies). On the other hand, if the torus is oriented face-on with respect to the observer, the central engine is visible (Seyfert 1 galaxies). The spectral energy distributions (SEDs) of most quasars and AGN in Seyfert galaxies have a pronounced secondary peak in the mid-infrared (mid-IR) (e.g. Sanders et al. 1989; Elvis et al. 1994), which is interpreted as thermal emission by hot dust in the torus. The dust is heated by the primary optical/ultraviolet (UV) continuum radiation, and the torus extends from the dust sublimation radius outwards (Barvainis 1987).
The geometrical thickness of the torus in the gravitational potential of the galactic nucleus
implies a vertical velocity dispersion of about
50-100 km s-1. If one assumes that the disk is continuous, i.e. thermally supported,
this corresponds to a temperature of ![]() 105 K. Since this is beyond the dust
sublimation temperature (
105 K. Since this is beyond the dust
sublimation temperature (![]() 103 K), thick tori have to be clumpy
or must be supported by additional forces other than thermal pressure.
Krolik & Begelman (1988) proposed a clumpy torus model where the clumps have supersonic velocities.
Vollmer et al. (2004) and Beckert & Duschl (2004) elaborated this model
in which orbital motion can be randomized if magnetic fields permit the cloud collisions
to be sufficiently elastic. Vollmer et al. (2004) found that the
circumnuclear disk (CND) in the
Galactic center (Güsten et al. 1987) and obscuring tori share the same gas physics,
where the mass of clouds is in the range 20-50
103 K), thick tori have to be clumpy
or must be supported by additional forces other than thermal pressure.
Krolik & Begelman (1988) proposed a clumpy torus model where the clumps have supersonic velocities.
Vollmer et al. (2004) and Beckert & Duschl (2004) elaborated this model
in which orbital motion can be randomized if magnetic fields permit the cloud collisions
to be sufficiently elastic. Vollmer et al. (2004) found that the
circumnuclear disk (CND) in the
Galactic center (Güsten et al. 1987) and obscuring tori share the same gas physics,
where the mass of clouds is in the range 20-50 ![]() and
their density close to the limit of disruption by tidal shear.
A change in matter supply and the dissipation of kinetic energy can turn a torus into a
CND-like structure and vice versa.
Any massive torus will naturally lead to sufficiently high mass accretion
rates to feed a luminous AGN.
and
their density close to the limit of disruption by tidal shear.
A change in matter supply and the dissipation of kinetic energy can turn a torus into a
CND-like structure and vice versa.
Any massive torus will naturally lead to sufficiently high mass accretion
rates to feed a luminous AGN.
If and how efficient these clumpy tori form stars is an open question.
The large majority of observational studies probed the nuclear star formation
on scales of a few hundred parsecs (see, e.g., Sarzi et al. 2007; Asari et al. 2007;
Gonzáles Delgado & Cid Fernandes 2005; Cid Fernandes et al. 2004).
These studies resulted in a general view that about 30%-50% of
the sample AGNs are associated with recent (ages less than a few 100 Myr) star formation
on these scales. Thanks to the high spatial resolution of the near-infrared adaptive optics
integral field spectrograph SINFONI, it has only recently become possible to study the
environments of AGN on the 10 pc scale. Davies et al. (2007) analyzed star formation
in the nuclei of nine Seyfert galaxies at spatial resolutions down to 0.085''.
They found recent, but no longer active, starbursts in the central regions
which occurred 10-300 Myr ago. Moreover,
Hicks et al. (2008) were able to measure
the rotation and dispersion velocity of the molecular gas
in these galaxies using the 2.12 ![]() m
H2 (1-0)S(1) line. Surprisingly, all molecular gas tori have high velocity dispersions
and are therefore geometrically thick.
m
H2 (1-0)S(1) line. Surprisingly, all molecular gas tori have high velocity dispersions
and are therefore geometrically thick.
In this article we compare
the observations of Davies et al. (2007) and Hicks et al. (2008)
with the expectations of
analytical models of clumpy
accretion disks developed in Vollmer & Beckert (2002, 2003) and Vollmer et al. (2004).
In a first step, we test
whether these models are able to describe observations.
In a second step, these models allow us to investigate the scenario hypothesized by
Davies et al. (2007) where sporadic, short-lived
starbursts are due to short massive accretion events in the central region,
followed by more quiescent phases until there is another episode of accretion.
This scenario is corroborated by a closer look at the nucleus of NGC 3227
where Davies et al. (2006) found signs of a past starburst (![]() 40 Myr ago)
and a presently quiescent gas torus with a Toomre parameter Q>1.
40 Myr ago)
and a presently quiescent gas torus with a Toomre parameter Q>1.
Within the framework of Vollmer & Beckert (2002, 2003) and Vollmer et al. (2004)
clumpy accretion disks are divided into two categories:
(i) turbulent and (ii) collisional disks. In case (i) the ISM is regarded as
a single entity which changes phase (molecular, atomic, ionized) according
to internal (gas density, pressure, magnetic field) and external (gravitation,
radiation field, winds) conditions. Energy is injected into a turbulent cascade
at the driving length scale (large scale) and dissipated
at the dissipation length scale (small scale). We identify the dissipation length scale with
the characteristic size of selfgravitating clouds.
These clouds decouple from the the turbulent cascade and constitute the first energy sink.
The source of energy which is injected at the driving scale to maintain turbulence
can be either (i) mass accretion in the gravitational
potential of the galactic center (fully gravitational FG model)
or (ii) supernova explosions (SN model).
In the collisional case energy is also supplied in the process of mass accretion in the gravitational
potential of the galactic center and dissipated via partially
inelastic cloud-cloud collisions. The actual dissipation rate in individual collisions is largely unknown.
The disk evolution is mainly driven by the external mass accretion rate.
Since these models are equilibrium models, we assume that the mass accretion rate
is constant throughout the region of interest when averaged for a sufficiently long time
(![]()
![]() ;
here
;
here ![]() is the angular velocity of circular orbits in the gravitational
potential of the galatic nucleus) and maintained for at least the turnover timescale
is the angular velocity of circular orbits in the gravitational
potential of the galatic nucleus) and maintained for at least the turnover timescale
![]() of gas in the disk, where R is the distance from the center of the galaxy and
of gas in the disk, where R is the distance from the center of the galaxy and
![]() the
characteristic speed of turbulent eddies.
All models give access to the global parameters of the disk
and the local parameters of the most massive clouds (see Table 1).
The free parameters of the models are the Toomre parameter Q, the disk transparency
the
characteristic speed of turbulent eddies.
All models give access to the global parameters of the disk
and the local parameters of the most massive clouds (see Table 1).
The free parameters of the models are the Toomre parameter Q, the disk transparency ![]() (Eq. (7)), and the mass accretion rate
(Eq. (7)), and the mass accretion rate ![]() .
Other parameters are fixed using the Galactic
values (Vollmer & Beckert 2002, 2003). Each model has an associated star formation rate.
In the following we describe these models in more detail.
.
Other parameters are fixed using the Galactic
values (Vollmer & Beckert 2002, 2003). Each model has an associated star formation rate.
In the following we describe these models in more detail.
Table 1: Model parameters and their meaning.
In Vollmer & Beckert (2002, Paper I) we developed an analytical model for clumpy accretion disks and included a simplified description of turbulence in the disk. In contrast to classical accretion disk theory (see, e.g., Pringle 1981), we eliminated the ``thermostat'' mechanism, which implies a direct coupling between the heat produced by viscous friction and the viscosity itself. The viscosity is usually assumed to be proportional to the thermal sound speed. Thus, the (gas) heating rate depends itself on the gas temperature. This leads to an equilibrium corresponding to a thermostat mechanism. Instead, we use energy flux conservation, where the potential energy that is gained through mass accretion and differential rotation is cascaded by turbulence from large to small scales and dissipated there.
One fundamental approximation is that the kinetic energy is
dissipated (removed from the turbulent cascade) when the gas clouds become self-gravitating.
Turbulence transfers the energy from the driving wavelength
![]() to the
dissipation wavelength
to the
dissipation wavelength
![]() ,
which corresponds to the size of the largest selfgravitating clouds.
The two length scales are linked by the scaling parameter
,
which corresponds to the size of the largest selfgravitating clouds.
The two length scales are linked by the scaling parameter ![]() .
For a Kolmogorov-like turbulent energy spectrum
.
For a Kolmogorov-like turbulent energy spectrum
![]() .
In addition, the
modeled disks have a constant Toomre-Q parameter:
.
In addition, the
modeled disks have a constant Toomre-Q parameter:
Furthermore, we use the following prescription for the viscosity:
In a second step we included the energy input due to supernova (SN)
explosions (Vollmer & Beckert 2003, Paper II).
The energy flux provided by SNe is
transfered by turbulence to smaller scales where it is again dissipated.
The SN energy flux is assumed to be proportional
to the local star formation rate. The local star formation
rate
![]() is taken to be proportional
to the mean density and inversely proportional to the local free fall
time of the clouds. These clouds have sizes that are a factor
is taken to be proportional
to the mean density and inversely proportional to the local free fall
time of the clouds. These clouds have sizes that are a factor ![]() smaller than the driving length scale.
The factor of proportionality is the probability to find
a self-gravitating cloud, i.e. the volume filling factor.
The integration length in the vertical z direction is assumed to be the turbulent
driving scale length, i.e. the vertical height in the disk where self-gravitating clouds are found:
smaller than the driving length scale.
The factor of proportionality is the probability to find
a self-gravitating cloud, i.e. the volume filling factor.
The integration length in the vertical z direction is assumed to be the turbulent
driving scale length, i.e. the vertical height in the disk where self-gravitating clouds are found:
![]() .
The SN energy per unit time
.
The SN energy per unit time
![]() per area
per area ![]() is
therefore proportional to the local star formation rate
is
therefore proportional to the local star formation rate
![]() :
:
In the FG model the energy transported through the turbulent cascade is
supplied by mass accretion, which leads to an energy flux equation of the form
If the selfgravitating clouds are stable, their collisions will give rise to angular
momentum redistribution again described by an effective viscosity.
An equilibrium disk can be formed if there are fragmenting
collisions or partially elastic collisions (the clouds are supposed to be magnetized).
If the collisional timescale
![]() is longer or
equal to the dynamical timescale, the resulting viscosity can be written as
is longer or
equal to the dynamical timescale, the resulting viscosity can be written as
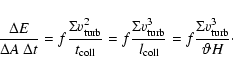 |
(8) |
Since in the FG model
![]() ,
the FG model and the collisional model
are formally equivalent.
We can thus use Eq. (1)-(3) replacing
,
the FG model and the collisional model
are formally equivalent.
We can thus use Eq. (1)-(3) replacing ![]() by
by ![]() to describe
the collisional model.
Nonetheless the interpretation of
to describe
the collisional model.
Nonetheless the interpretation of ![]() and
and ![]() is completely different.
is completely different.
The cloud size
![]() and the volume filling factor
and the volume filling factor
![]() of clouds
can be derived using their mean free path (see Vollmer et al. 2004)
of clouds
can be derived using their mean free path (see Vollmer et al. 2004)
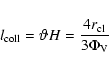 |
(9) |
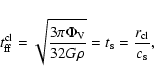 |
(10) |
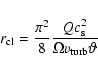 |
(11) |
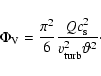 |
(12) |
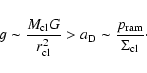 |
(14) |
Following Paper II we assume that the star formation rate is proportional to the mean
density of the disk and the inverse of
the characteristic timescale for the cloud collapse, i.e.
the non-averaged local free fall time
![]() :
:
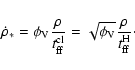 |
(16) |
For the collisional disk we assume that the star formation rate is
proportional to the overall density ![]() and the cloud collision
frequency
and the cloud collision
frequency
![]() :
:
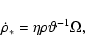 |
(18) |
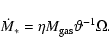 |
(19) |
The theoretical model described in the previous sections can now
be applied to recent near-IR high-spatial resolution SINFONI observations
of nearby AGN.
Davies et al. (2007) showed that there had been recent
star formation in the central few tens of parsecs in a sample of nearby AGN.
Following on from this, Hicks et al. (2008) showed that distribution
and kinematics of the central concentrations of gas were similar to
those of the stars, and was geometrically thick with
![]() .
They argued that this gas comprised the large scale
structure of the tori, implying that tori can form stars.
And they gave an estimate for the gas mass in this region as 10% of
the dynamical mass.
Before we derive the physical disk parameters for the individual AGNs observed
by Davies et al. (2007), we give an overview over the different types of thick tori.
Note that
.
They argued that this gas comprised the large scale
structure of the tori, implying that tori can form stars.
And they gave an estimate for the gas mass in this region as 10% of
the dynamical mass.
Before we derive the physical disk parameters for the individual AGNs observed
by Davies et al. (2007), we give an overview over the different types of thick tori.
Note that ![]() is the disk transparency, i.e.
is the disk transparency, i.e.
![]() implies an opaque disk
whereas a large
implies an opaque disk
whereas a large ![]() results in a transparent disk.
For a generic galactic center we assume a dynamical mass
(which for radii R larger
than a few pc is dominated by the stellar content),
of
results in a transparent disk.
For a generic galactic center we assume a dynamical mass
(which for radii R larger
than a few pc is dominated by the stellar content),
of
![]()
![]() and a gas mass of
and a gas mass of
![]()
![]() ,
both within a radius of R=20 pc. The enclosed mass leads to
a rotation velocity of 150 km s-1 at this radius. In addition, we adopt a cloud internal sound speed
of
,
both within a radius of R=20 pc. The enclosed mass leads to
a rotation velocity of 150 km s-1 at this radius. In addition, we adopt a cloud internal sound speed
of
![]() km s-1.
The value for the sound speed corresponds to
a cloud temperature of
km s-1.
The value for the sound speed corresponds to
a cloud temperature of ![]() 500 K when only thermal gas pressure is considered.
The sound speed is a measure of the pressure support against self-gravity and additional
contributions to the pressure gradient inside clouds like magnetic fields may contribute.
The adopted sound speed leads to cloud masses of
500 K when only thermal gas pressure is considered.
The sound speed is a measure of the pressure support against self-gravity and additional
contributions to the pressure gradient inside clouds like magnetic fields may contribute.
The adopted sound speed leads to cloud masses of
![]() .
The disk is stable with a Toomre parameter of Q=4.7
for a turbulent velocity supporting the vertical thickness of
.
The disk is stable with a Toomre parameter of Q=4.7
for a turbulent velocity supporting the vertical thickness of
![]() km s-1.
Moreover, we assume a star formation rate of
km s-1.
Moreover, we assume a star formation rate of
![]() yr-1.
This can be considered an upper limit to the current star
formation rate in the central few tens of parsecs.
Davies et al. (2007) showed that while star formation had occured
there recently, it has now ceased.
Based on the exponentially decaying starburst model they used and the
time averaged star formation rates they estimated, the current rates
are expected to be below this limit.
yr-1.
This can be considered an upper limit to the current star
formation rate in the central few tens of parsecs.
Davies et al. (2007) showed that while star formation had occured
there recently, it has now ceased.
Based on the exponentially decaying starburst model they used and the
time averaged star formation rates they estimated, the current rates
are expected to be below this limit.
In the following we generate
a generic set of models which (i) can describe
different evolutionary phases of a ![]() 20 pc scale gas disk in terms
of mass accretion rate, disk thickness/transparency, and star formation rate
and (ii) can reproduce the observations at a generic time
in the evolutionary sequence.
We first compare different disk models, representing evolutionary stages, to
the observations of
the current state of the disk (Sects. 4.1-4.5).
It is shown that a massive accretion event leads to a relatively thin turbulent
disk which forms stars at a high rate (SN model). Once the SN explode the
intercloud medium is blown out, leaving only dense, compact clouds. This results in a
collisional disk that may assume one of
several states (Sects. 4.2-4.5)
depending on the external
mass accretion rate
20 pc scale gas disk in terms
of mass accretion rate, disk thickness/transparency, and star formation rate
and (ii) can reproduce the observations at a generic time
in the evolutionary sequence.
We first compare different disk models, representing evolutionary stages, to
the observations of
the current state of the disk (Sects. 4.1-4.5).
It is shown that a massive accretion event leads to a relatively thin turbulent
disk which forms stars at a high rate (SN model). Once the SN explode the
intercloud medium is blown out, leaving only dense, compact clouds. This results in a
collisional disk that may assume one of
several states (Sects. 4.2-4.5)
depending on the external
mass accretion rate ![]() ,
the Toomre Q, and transparency
,
the Toomre Q, and transparency ![]() parameters.
In Sect. 5 we then investigate the evolution of the collisional disk.
parameters.
In Sect. 5 we then investigate the evolution of the collisional disk.
We first try applying the turbulent SN disk model. With
the parameters described above it would have a mass accretion rate
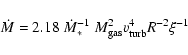 |
(20) |
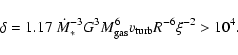 |
(21) |
On the other hand, if we assume that a turbulent SN disk is responsible for the
starburst with a star formation rate of
![]() yr-1
(comparable to the initial rate inferred by Davies et al. 2007) and that
the turbulent
velocity was lower (
yr-1
(comparable to the initial rate inferred by Davies et al. 2007) and that
the turbulent
velocity was lower (
![]() km s-1) than the present collisional disk,
we find a mass accretion rate of
km s-1) than the present collisional disk,
we find a mass accretion rate of
![]() yr-1 and
yr-1 and
![]() .
These values are close to the values for the large-scale Galactic disk (see Paper II).
A typical cloud has a radius of
.
These values are close to the values for the large-scale Galactic disk (see Paper II).
A typical cloud has a radius of
![]() pc and a mass of
pc and a mass of
![]() .
This kind of disk contains about a thousand clouds within R=20 pc.
.
This kind of disk contains about a thousand clouds within R=20 pc.
We conclude that a viable turbulent massive gas disk has a rather low turbulent velocity and is
therefore moderately thin with
![]() .
It then
yields large star formation rates of the order of one solar mass per year.
This represents a starburst which subsequently will destroy the disk once the
supernovae explode after about 10 Myr. These explosions do not cause any harm to the
densest and most massive clouds, but they clear the space between the clouds, i.e.
they remove the initial intercloud medium. We are then left with a collisional disk.
.
It then
yields large star formation rates of the order of one solar mass per year.
This represents a starburst which subsequently will destroy the disk once the
supernovae explode after about 10 Myr. These explosions do not cause any harm to the
densest and most massive clouds, but they clear the space between the clouds, i.e.
they remove the initial intercloud medium. We are then left with a collisional disk.
The collisional disks can be distinguish by their Q and ![]() parameters.
We start with collisional and opaque disks, i.e. the mean free path of the
clouds is about the height of the disk H. This implies that along a vertical path through
the disk there is on average one intervening cloud. Along a path in the disk midplane towards
the center there are typically
parameters.
We start with collisional and opaque disks, i.e. the mean free path of the
clouds is about the height of the disk H. This implies that along a vertical path through
the disk there is on average one intervening cloud. Along a path in the disk midplane towards
the center there are typically ![]() clouds blocking the direct view. Collisions are
frequent in such a torus or disk.
This yields a mass accretion rate of
clouds blocking the direct view. Collisions are
frequent in such a torus or disk.
This yields a mass accretion rate of
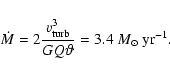 |
(22) |
The large mass accretion rate in the above model (Sect. 4.2)
depends linearly on the collision rate and is a consequence of the low transparency.
If the disk is more transparent,
![]() ,
the mass accretion rate is therefore
,
the mass accretion rate is therefore
![]() yr-1, the volume filling factor of the clouds is
yr-1, the volume filling factor of the clouds is
![]() ,
and
the clouds have typical radii
of
,
and
the clouds have typical radii
of
![]() pc and masses of
pc and masses of
![]() .
We see that for the same Toomre-Q a larger transparency implies smaller and
less massive clouds with smaller volume filling factors.
.
We see that for the same Toomre-Q a larger transparency implies smaller and
less massive clouds with smaller volume filling factors.
If clouds are large and less dense we can have a disk which is light but still optically
opaque due to dust in the clouds.
For this disk class we assume a gas mass of only ![]() of the dynamical mass, i.e.
of the dynamical mass, i.e.
![]() .
This yields a mass accretion rate of
.
This yields a mass accretion rate of
![]() yr-1.
The volume filling factor is
yr-1.
The volume filling factor is
![]() ,
and the typical cloud radii and masses
are
,
and the typical cloud radii and masses
are
![]() pc and
pc and
![]() .
.
The last disk class is transparent,
![]() ,
and has a small gas mass,
,
and has a small gas mass,
![]() .
It has the lowest mass accretion rate,
.
It has the lowest mass accretion rate,
![]() yr-1, and a low
volume filling factor,
yr-1, and a low
volume filling factor,
![]() .
The cloud radii and masses are the same as
those of the massive, opaque disk (
.
The cloud radii and masses are the same as
those of the massive, opaque disk (
![]() pc and
pc and
![]() ).
).
We conclude that (i) a high mass accretion leads to a massive, opaque disk and (ii)
a (Q=5,
![]() )-disk and a (Q=50,
)-disk and a (Q=50,
![]() )-disk share clouds
of the same mass and size. These clouds are very similar to those found in the Galactic Center
(see Vollmer et al. 2004). We thus can draw up a disk evolution in which a massive, opaque
disk evolves with time into a light, transparent disk.
)-disk share clouds
of the same mass and size. These clouds are very similar to those found in the Galactic Center
(see Vollmer et al. 2004). We thus can draw up a disk evolution in which a massive, opaque
disk evolves with time into a light, transparent disk.
For the rest of the article we assume that the cloud mass of all disks is
![]() .
This is equivalent to
a common column density of all clouds
of
.
This is equivalent to
a common column density of all clouds
of
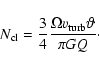 |
(23) |
The collisional disks described above can be identified with the observed 30 pc-scale gas concentrations observed by Davies et al. (2007) and Hicks et al. (2008) which arguably correspond to the large scale structure of AGN tori.
It is now investigated how a collisional torus can evolve from a massive to a less massive state.
To do so we assume that the gas mass of the torus is proportional to its mass accretion rate
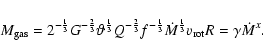 |
(24) |
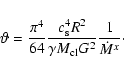 |
(25) |
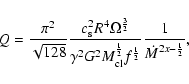 |
(26) |
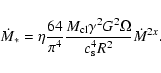 |
(28) |
Whenever the disk thickness stays the same during its evolution,
![]() const. in time,
and subsequently
const. in time,
and subsequently
![]() (Eq. (27)),
this implies that the external mass accretion rate stays at a high level.
The gas mass, star formation rate,
(Eq. (27)),
this implies that the external mass accretion rate stays at a high level.
The gas mass, star formation rate, ![]() ,
and the Toomre Q parameter depend on the mass accretion rate
,
and the Toomre Q parameter depend on the mass accretion rate
![]() in the following way:
in the following way:
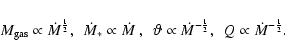 |
(29) |
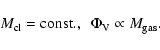 |
(31) |
Alternatively, at later stages when the mass accretion rate is low and changes little,
the torus mass may stay constant,
![]() ,
and subsequently x=0 (Eq. (27)).
The turbulent velocity dispersion, star formation rate,
,
and subsequently x=0 (Eq. (27)).
The turbulent velocity dispersion, star formation rate, ![]() ,
and the Toomre depend on the mass accretion rate
,
and the Toomre depend on the mass accretion rate
![]() now in the following way:
now in the following way:
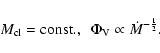 |
(33) |
An interesting result is that during both types of torus evolution - at constant turbulent velocity and at constant gas mass - the cloud mass does not change.
In the picture of quasi-stationary equilibrium disks driven by cloud collisions the evolution will be determined by the external mass accretion rate, i.e. the mass inflow from distances >100 pc. We divide the torus evolution into three phases:
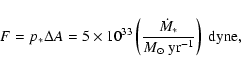 |
(34) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10446fig1.ps} \end{figure}](/articles/aa/full/2008/44/aa10446-08/Timg177.gif) |
Figure 1:
Schematic of torus evolution scenarios: Torus mass accretion rate ( |
| Open with DEXTER | |
The scenarios of Sect. 6 derived from our analytical models can now be compared
with the VLT SINFONI observations of Davies et al. (2007)
and Hicks et al. (2008).
As has been shown in Sect. 4.1 the present state of the disk
can only be described consistently by a collisional disk model.
The comparison with observations will allow us to derive the parameters of (i) the
present torus; (ii) the initial torus immediately after Phase I; (iii) the massive (![]() )
turbulent gas disk that gave rise to the initial starburst (scenario II and III),
and (iii) the star formation efficiency of the collisional phase.
)
turbulent gas disk that gave rise to the initial starburst (scenario II and III),
and (iii) the star formation efficiency of the collisional phase.
The observables, i.e. the input parameters for our analytical model, are the
radius from the galactic center R, the rotation velocity
![]() ,
the turbulent velocity
dispersion
,
the turbulent velocity
dispersion
![]() ,
the gas mass
,
the gas mass
![]() ,
the peak star formation rate during the initial starburst
,
the peak star formation rate during the initial starburst
![]() ,
and
the age of the initial starburst
,
and
the age of the initial starburst
![]() .
We assume for all AGN, except NGC 1097, a starburst duration of 10 Myr,
i.e. the the starburst continues until the first SN explode.
We only apply our model to a subsample of 6 nearby AGNs from Davies et al. (2007) for which
these input parameters are sufficiently well known.
The parameters for these objects can be found in Table 2.
For each object, the table gives its Seyfert type and the radius
within which the subsequent parameters apply.
The dispersion
.
We assume for all AGN, except NGC 1097, a starburst duration of 10 Myr,
i.e. the the starburst continues until the first SN explode.
We only apply our model to a subsample of 6 nearby AGNs from Davies et al. (2007) for which
these input parameters are sufficiently well known.
The parameters for these objects can be found in Table 2.
For each object, the table gives its Seyfert type and the radius
within which the subsequent parameters apply.
The dispersion
![]() is the value measured from the data (after
accounting for instrumental broadening), while the rotation velocity
is the value measured from the data (after
accounting for instrumental broadening), while the rotation velocity
![]() is a Keplerian equivalent value.
This means that it represents the rotation velocity that would be
needed if ordered circular motions in a single plane supported the entire
dynamical mass.
It is therefore significantly greater than the measured rotation speed.
The gas mass
is a Keplerian equivalent value.
This means that it represents the rotation velocity that would be
needed if ordered circular motions in a single plane supported the entire
dynamical mass.
It is therefore significantly greater than the measured rotation speed.
The gas mass
![]() is difficult to derive.
Hicks et al. (2008) estimated it from a combination of diagnostics,
including the 1.3 mm CO luminosity, the 2.12
is difficult to derive.
Hicks et al. (2008) estimated it from a combination of diagnostics,
including the 1.3 mm CO luminosity, the 2.12 ![]() m H2 1-0 S(1)
luminosity, and a
comparison to the gas-to-dynamical mass ratios in other spiral and
starburst galaxies.
The peak star formation rates
m H2 1-0 S(1)
luminosity, and a
comparison to the gas-to-dynamical mass ratios in other spiral and
starburst galaxies.
The peak star formation rates
![]() are derived
from the starburst models used in Davies et al. (2007).
They are simply the star formation rates required to form the young
stars in a timescale of 10 Myr (in contrast to the time-averaged rates
given in that paper).
The only exception is NGC 3783, for which we have adopted a
2-starburst model with ages of 110 Myr and 30 Myr.
Such models were not considered by Davies et al. (2007) because of the
limited number of diagnostics.
In our scenario with stronger theoretical constraints on the models we need
these additional degrees of freedom to reproduce the observations.
The final column gives the age
are derived
from the starburst models used in Davies et al. (2007).
They are simply the star formation rates required to form the young
stars in a timescale of 10 Myr (in contrast to the time-averaged rates
given in that paper).
The only exception is NGC 3783, for which we have adopted a
2-starburst model with ages of 110 Myr and 30 Myr.
Such models were not considered by Davies et al. (2007) because of the
limited number of diagnostics.
In our scenario with stronger theoretical constraints on the models we need
these additional degrees of freedom to reproduce the observations.
The final column gives the age
![]() of the most recent
starburst.
All equations to derive the properties of the present collisional torus,
the massive
of the most recent
starburst.
All equations to derive the properties of the present collisional torus,
the massive
![]() turbulent gas disk, and the initial collisional torus
are given in Table 3.
turbulent gas disk, and the initial collisional torus
are given in Table 3.
Table 2: Input parameters from Davies et al. (2007) and Hicks et al. (2008); see Sect. 7 for details.
Table 3:
Equations to derive the disk/torus properties from observations.
Velocities are in units of km s-1, radii in pc,
masses in ![]() ,
and star formation rates in
,
and star formation rates in ![]() yr-1.
yr-1.
We recall the assumption that all gas clouds have
a constant mass of
![]() .
Moreover
the sound speed within the clouds is set to
.
Moreover
the sound speed within the clouds is set to
![]() km s-1.
The Toomre Q parameter of the present disks is directly calculated from Eq. (1).
We then use the following expressions for
km s-1.
The Toomre Q parameter of the present disks is directly calculated from Eq. (1).
We then use the following expressions for ![]() and the mass accretion rate
and the mass accretion rate ![]() which follow from the expression derived for the turbulent velocity dispersion in Paper I
which follow from the expression derived for the turbulent velocity dispersion in Paper I
![]() and Eq. (13)
and Eq. (13)
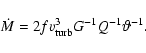 |
(36) |
All tori show Toomre Q parameters between 4 and 6, i.e. they are massive thick tori.
Moreover, 3 AGNs (Circinus, NGC 3227, and NGC 1068) have opaque tori (
![]() ),
2 AGNs (NGC 1097 and NGC 7469) show moderately transparent tori (
),
2 AGNs (NGC 1097 and NGC 7469) show moderately transparent tori (
![]() ),
and 1 AGN (NGC 3783) has a transparent torus (
),
and 1 AGN (NGC 3783) has a transparent torus (
![]() ).
It is worth noting that two out of the 3 AGNs with opaque tori are classified as Sy2.
We find the smallest mass accretion rate for NGC 3783. The highest mass accretion
rates (NGC 3227 and NGC 1068) are several ten times higher than that of NGC 3783.
).
It is worth noting that two out of the 3 AGNs with opaque tori are classified as Sy2.
We find the smallest mass accretion rate for NGC 3783. The highest mass accretion
rates (NGC 3227 and NGC 1068) are several ten times higher than that of NGC 3783.
Table 4: Parameters of the present collisional tori.
We now derive the parameters of the initial massive turbulent gas disk which gave
rise to the initial starburst.
For this we apply the SN model (see Sect. 2) where
the energy source for maintaining turbulence in the disk are
stellar winds. Their energy input is comparable to that of SN explosions
(MacLow & Klessen 2004). Therefore we do not need to change the
formalism of the SN model.
We further assume that the mass accretion rate equals the peak star formation rate
given by Davies et al. (2007) (Table 2) and
![]() ,
which is the Galactic value (Vollmer & Beckert 2003).
,
which is the Galactic value (Vollmer & Beckert 2003).
We assume that for all AGNs, except for Circinus and NGC 3783, scenario II is valid.
For Circinus we argue below that scenario I applies, because its peak star formation rate is
a factor of more than
10 lower when compared to
the other starbursts.
This does not imply
that star formation is not occurring, just that there was no initial
massive accretion event.
For NGC 3783 scenario III is more applicable,
because a single starburst
leads to an enormously high initial mass accretion rate compared to the present value,
which we think is implausible.
The double starburst we have adopted for NGC 3783, which is consistent with the observations of
Davies et al. (2007), requires a first intense burst with
![]() yr-1 to have occurred 110 Myr ago, followed by a
second distinct burst with
yr-1 to have occurred 110 Myr ago, followed by a
second distinct burst with
![]() yr-1 only
30 Myr ago.
yr-1 only
30 Myr ago.
The Toomre Q parameter, the total gas mass, and the turbulent
velocity dispersion can then be calculated using the following expressions:
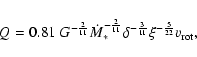 |
(37) |
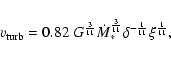 |
(39) |
Using a peak star formation rate of
![]() yr-1 for Circinus
leads to a gas mass of the massive turbulent disk which is smaller than that of the present
collisional torus. We therefore conclude that scenario II (Fig. 1) does not apply
to this AGN. Instead, scenario I yields more appropriate results.
The nuclear disk in Circinus did not experience a turbulent, supernovae and stellar wind driven
yr-1 for Circinus
leads to a gas mass of the massive turbulent disk which is smaller than that of the present
collisional torus. We therefore conclude that scenario II (Fig. 1) does not apply
to this AGN. Instead, scenario I yields more appropriate results.
The nuclear disk in Circinus did not experience a turbulent, supernovae and stellar wind driven ![]() disk.
disk.
The gas masses of the turbulent starburst disks is between ![]() and
and ![]() higher than the gas mass of the corresponding present collisional torus,
except for Circinus. In the course of torus evolution
(Fig. 1) the loss of gas mass in the disk is moderate (up to a factor of 2;
Tables 2 and 5).
The star forming disks are moderately thin (
higher than the gas mass of the corresponding present collisional torus,
except for Circinus. In the course of torus evolution
(Fig. 1) the loss of gas mass in the disk is moderate (up to a factor of 2;
Tables 2 and 5).
The star forming disks are moderately thin (
![]() )
and their
Toomre Q parameter is close to unity.
)
and their
Toomre Q parameter is close to unity.
Table 5:
Parameters of the initial massive (![]() )
turbulent gas disk
that gave rise to the initial starburst.
)
turbulent gas disk
that gave rise to the initial starburst.
Since all observed tori are thick (Table 2), they
are all in Phase II of their evolution (see Sect. 6), i.e.
they evolve at constant thickness or velocity dispersion.
This implies the following relation between the gas mass and
the mass accretion rate:
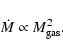 |
(40) |
For all other AGN a continuous transition from phase I to II provides
the mass accretion rate of the initial
collisional torus. The Q and ![]() parameters can then be
calculated using the following expressions (see Sect. 5):
parameters can then be
calculated using the following expressions (see Sect. 5):
 |
(41) |
Table 6: Parameters of the initial collisional tori.
In this section we investigate the evolution of the torus mass accretion rate with time in Phase II (see Sect. 6). For this we plot in Fig. 2 the fraction between the mass accretion rate of the present collisional torus and that of the initial collisional torus (end of Phase I and beginning of Phase II) as a function of time for our sample. To determine the time that a given torus passed in Phase II, we place ourselves in scenario II (Fig. 1) and adopt the starburst ages of Davies et al. (2007) for all AGNs except NGC 3783. We assume scenario III for this galaxy, i.e. the occurrence of two distinct starbursts. This leads to an estimated age of the most recent starburst of 30 Myr. The solid line is meant to guide the eye. Based on this plot we conclude that the mass accretion rate shows a slow monotonic decrease with time. It decreases to one fourth of its initial value in about 150 Myr.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10446fig2.ps} \end{figure}](/articles/aa/full/2008/44/aa10446-08/Timg215.gif) |
Figure 2:
Ratio between the mass accretion
rate of the present collisional torus and that of the initial collisional torus
(end of Phase I and beginning of Phase II) as a function of time.
The zero point in time is the end of Phase I (
|
| Open with DEXTER | |
Star formation in collisional disks is expected (see Sect. 3) to be proportional to the
cloud collision rate
![]() :
:
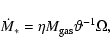 |
(42) |
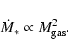 |
(43) |
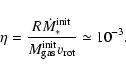 |
(44) |
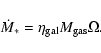 |
(45) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10446fig3a.eps}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{10446fig3b.eps} \end{figure}](/articles/aa/full/2008/44/aa10446-08/Timg228.gif) |
Figure 3:
Projected mean number of clouds |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10446fig4.eps} \end{figure}](/articles/aa/full/2008/44/aa10446-08/Timg229.gif) |
Figure 4:
Ratio between the extinction-free starburst emission to the emission
with cloud absorption
|
| Open with DEXTER | |
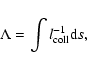 |
(46) |
Figure 4 shows the ratio between the extinction-free starburst emission and the emission
with obscuration by intervening clouds in the mixed case
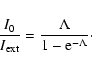 |
(47) |
The screen and the mixed models can be regarded as two extreme cases and the reality maybe somewhere in between these two models. Most probably the starburst will be significantly obscured at galactocentric radii smaller than 1 pc. The extinction of star formation at the 10 pc scale by torus clouds is so low that additional extinction by extended dust lanes at larger radii (>100 pc) in the galaxies is possible. We can therefore conclude that our torus model is consistent with the small observed extinction of the central starburst.
The inner edge of the torus is thought to be set by the dust sublimation radius which is located at
about 0.1-0.5 pc from the central black hole. In Sect. 7
we have derived the mass accretion rate of the tori, i.e. the mass transport rate arriving at these inner
edges. It is not clear what happens between the inner edge of the torus and
the thin accretion disk around the black hole and what the relation is to the maser emission regions.
These maser disks have sizes of about 0.1 pc. Between 0.1 pc and 0.5 pc from the
central black hole an X-ray heated wind is most likely formed (Krolik & Kriss 1995, 2001).
Less dense and sheared clouds lose their dust by evaporation at the sublimation temperature are consequently
ionized by the AGN X-ray emission, heated, and blown away in a line-driven wind.
What remains of the dust or is newly formed in the wind to obscure the AGN at even higher inclination
angles is undetermined in this scenario. The mass accretion rate onto the central black hole
![]() is thus the difference between the mass accretion within the torus
is thus the difference between the mass accretion within the torus ![]() and the
mass loss due to the AGN wind
and the
mass loss due to the AGN wind
![]() :
:
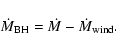 |
(48) |
To investigate the relation between the mass accretion rate onto the central
black hole and the present torus mass accretion rate, we plot their ratio as a function
of the area filling factor
![]() .
The mass accretion rate onto the central black hole
.
The mass accretion rate onto the central black hole
![]() is derived from the AGN luminosity
is derived from the AGN luminosity
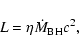 |
(49) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{10446fig5.ps} \end{figure}](/articles/aa/full/2008/44/aa10446-08/Timg248.gif) |
Figure 5:
Ratio between the mass accretion rate onto the central
black hole and the present torus mass accretion rate as a function
the area filling factor, i.e.
|
| Open with DEXTER | |
We observe a tentative trend in the sense that in opaque tori only
![]() of the
torus mass accretion rate feeds the central black hole. On the other hand,
if the torus is transparent,
of the
torus mass accretion rate feeds the central black hole. On the other hand,
if the torus is transparent,
![]() of the torus mass accretion rate
is used to feed the central engine.
of the torus mass accretion rate
is used to feed the central engine.
The main differences between opaque (
![]() )
and transparent tori (
)
and transparent tori (
![]() )
are the cloud collision rate and the cloud mean free path. Since there is no
correlation with the collision rate
)
are the cloud collision rate and the cloud mean free path. Since there is no
correlation with the collision rate
![]() ,
we suspect
the mean free path to be responsible for the accretion efficiency of the tori.
The different mean free paths between the clouds means that in transparent tori
the AGN emission can reach all clouds of the torus, whereas in the opaque case
it only reaches clouds at small galactocentric radii, i.e. close to the central
source. Due to this radiation only the densest clouds can survive, the less denser
clouds being evaporated by a photodissiciation or X-ray dissociation region (PDR/XDR).
Vollmer & Duschl (2001) calculated the location of the ionization fronts in the
cloud of the circumnuclear disk in the Galactic Center. These clouds have about the
same mass as the AGN torus clouds (
,
we suspect
the mean free path to be responsible for the accretion efficiency of the tori.
The different mean free paths between the clouds means that in transparent tori
the AGN emission can reach all clouds of the torus, whereas in the opaque case
it only reaches clouds at small galactocentric radii, i.e. close to the central
source. Due to this radiation only the densest clouds can survive, the less denser
clouds being evaporated by a photodissiciation or X-ray dissociation region (PDR/XDR).
Vollmer & Duschl (2001) calculated the location of the ionization fronts in the
cloud of the circumnuclear disk in the Galactic Center. These clouds have about the
same mass as the AGN torus clouds (
![]() )
and sizes of
)
and sizes of ![]() 0.1 pc. Whereas these clouds are close to the shear limit, the AGN torus
clouds are
0.1 pc. Whereas these clouds are close to the shear limit, the AGN torus
clouds are ![]() 100 times denser.
Note however, that in the
Galactic Center the source of ionization is a central cluster of about 40 O stars
which is much weaker than an AGN.
100 times denser.
Note however, that in the
Galactic Center the source of ionization is a central cluster of about 40 O stars
which is much weaker than an AGN.
Vollmer & Duschl (2001) showed that the cloud radius due to the ionization front
is given by
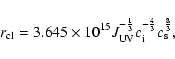 |
(50) |
We scale up the Galactic Center by a factor of 104 and obtain
![]() km s-1,
km s-1,
![]() km s-1 (R/(1 pc))
km s-1 (R/(1 pc))
![]() ,
and
,
and
![]() cm-2 s-1 (R/(1 pc))-2 for a transparent torus.
This leads to a cloud radius of
cm-2 s-1 (R/(1 pc))-2 for a transparent torus.
This leads to a cloud radius of
![]() pc, which is very close to the cloud radius obtained for
our sample of AGN tori (Table 4). Thus, only dense, selfgravitating
clouds can survive in an illuminated environment, i.e. a transparent torus.
On the other hand, if the torus is opaque, less dense and larger clouds can survive.
Since we derive only the properties of the densest and most massive clouds in
our model which determine the physics of the outer torus, less dense and less massive clouds
are still consistent with the model as long as they do not dominate the disk mass.
As a consequence, the transparency values derived for the individual AGNs
and summarized in Table 4 are upper limits.
We therefore suggest that towards the inner edge of opaque tori clouds become
less dense with densities close to the shear limit.
These clouds, however, once they arrive at the inner edge of the torus, are (i) destroyed
easily by the influence of shear and possible winds and are (ii) much easier ionized and
evaporated by the AGN emission.
In addition, for AGN close to the Eddington limit Hönig & Beckert (2007) showed
that dusty clouds experience a strong radiation pressure. For transparent tori only dense
and compact clouds smaller than the shear limit will be found, while for opaque tori shadowing
by clouds at the inner edge allows larger clouds to survive at intermediate distances.
pc, which is very close to the cloud radius obtained for
our sample of AGN tori (Table 4). Thus, only dense, selfgravitating
clouds can survive in an illuminated environment, i.e. a transparent torus.
On the other hand, if the torus is opaque, less dense and larger clouds can survive.
Since we derive only the properties of the densest and most massive clouds in
our model which determine the physics of the outer torus, less dense and less massive clouds
are still consistent with the model as long as they do not dominate the disk mass.
As a consequence, the transparency values derived for the individual AGNs
and summarized in Table 4 are upper limits.
We therefore suggest that towards the inner edge of opaque tori clouds become
less dense with densities close to the shear limit.
These clouds, however, once they arrive at the inner edge of the torus, are (i) destroyed
easily by the influence of shear and possible winds and are (ii) much easier ionized and
evaporated by the AGN emission.
In addition, for AGN close to the Eddington limit Hönig & Beckert (2007) showed
that dusty clouds experience a strong radiation pressure. For transparent tori only dense
and compact clouds smaller than the shear limit will be found, while for opaque tori shadowing
by clouds at the inner edge allows larger clouds to survive at intermediate distances.
This tentative picture leads to two predictions for AGN tori that might be verified in the future:
Up to this point we ignored any possible observational errors. In this section the influence of the quantities derived from observations on the correlations shown in Figs. 2 and 5 is investigated. We assume the following uncertainties:
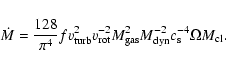 |
(51) |
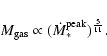 |
(52) |
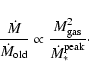 |
(53) |
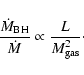 |
(54) |
The starburst ages have uncertainties of a factor of 2.
The area filling factor is proportional to the inverse of the gas mass
![]() (Eq. (35)).
Thus, the associated uncertainty is also a factor of 2.
(Eq. (35)).
Thus, the associated uncertainty is also a factor of 2.
Despite these relatively large uncertainties we believe that the correlations shown in
Figs. 2 and 5 are real.
All systematic errors, like an overestimate of the gas mass, would alter but not destroy
the correlations, as long as the errors for different targets are not random. However, to make
our findings more robust more spectroscopic VLT SINFONI observations with high spatial resolution of
AGNs are needed. Most importantly, future ALMA high resolution CO line observations
are necessary to determine the total gas mass of the tori with an
uncertainty of ![]() 10-30%.
10-30%.
VLT SINFONI observations of the close environments (![]() 30 pc) of a sample of nearby AGNs
by Davies et al. (2007) showed that thick gas tori and recent central starbursts
with ages smaller than 100 Myr are ubiquitous.
We compare different clumpy accretion disk models to these observations:
30 pc) of a sample of nearby AGNs
by Davies et al. (2007) showed that thick gas tori and recent central starbursts
with ages smaller than 100 Myr are ubiquitous.
We compare different clumpy accretion disk models to these observations:
The result of this work is a time sequence for the torus evolution. Present tori appear to be collisional and geometrically thick whereas the tori giving rise to the starburst in the past are of turbulent nature and relatively thin. The torus evolution can be divided into 3 phases depending on the external mass accretion rate:
In addition we conclude that: