Contents

• Chemically peculiar stars and their temperature calibration
• 1 Introduction
• 2 Data collection
• 3 Interstellar reddening
• 4 Photometric temperature calibration
• 5 Bolometric correction
• 6 Conclusions
• References
• 7 Online Material

A&A 491, 545-554 (2008)
DOI: 10.1051/0004-6361:200810325

Chemically peculiar stars and their temperature calibration

M. Netopil¹ - E. Paunzen¹ - H. M. Maitzen¹ - P. North² - S. Hubrig³

1 - Institut für Astronomie der Universität Wien, Türkenschanzstr. 17, 1180 Wien, Austria
2 - Laboratoire d'Astrophysique, École Polytechnique Fédérale de Lausanne (EPFL), Observatoire de Sauverny, 1290 Versoix, Switzerland
3 - European Southern Observatory, Casilla 19001, Santiago, Chile

Received 4 June 2008 / Accepted 3 September 2008

Abstract
Aims. The determination of effective temperature for chemically peculiar (CP) stars by means of photometry is a sophisticated task due to their abnormal colours. Standard calibrations for normal stars lead to erroneous results and, in most cases corrections are necessary.
Methods. In order to specify appropriate corrections, direct temperature determinations for 176 objects of the different subgroups were collected from the literature. This much larger sample than in previous studies therefore allows a more accurate investigation, mostly based on average temperatures.
Results. For the three main photometric systems (UBV, Geneva, Strömgren ${uvby}\beta$), methods to determine effective temperature are presented together with a comparison with former results. Based on the compiled data we provide evidence that He (CP4) objects also need a considerable correction, not noticed in former investigations due to their small number. Additionally, a new relation for the bolometric correction and the capability of standard calibrations to deduce interstellar reddening for magnetic CP stars are shown.

Key words: stars: chemically peculiar - stars: fundamental parameters - techniques: photometric - methods: statistical

1 Introduction

There are only a few direct temperature determinations available of chemically peculiar (CP) stars (results other than from photometry), insufficient to study their evolutionary status. Additionally, photometric standard calibrations for normal stars are mostly inappropriate because of their anomalous properties, e.g. blanketing effects, individual abundances or magnetic fields influencing the photometric colours. Using some peculiar stars with direct temperature determinations, ${\it Geneva}$ and Strömgren photometry was recalibrated by Hauck & North (1993), Napiwotzki et al. (1993), Stepien (1994), or Hauck & Künzli (1996). However, small numbers have often allowed only a vague estimate of the CP stars temperature behaviour, best seen on the basis of the CP3 (HgMn) sample used by Hauck & North (1993) comprising only five objects. Napiwotzki et al. (1993) have included only two stars for comparison, but for the group of CP4 stars insufficient data also were available. Several new temperature determinations having been published, we decided to refine the available corrections and calibrations for the abovementioned photometric systems based on a larger sample. Due to the fact that numerous new CP2 (magnetic group with enhanced Si, Cr, Sr or Eu) objects also have been detected in galactic open clusters or even in the Large Magellanic Cloud (e.g. Netopil et al. 2007; Paunzen et al. 2006), and photometric data in the abovementioned systems are scarce at larger distances, an investigation of the widely used ${\it UBV}$ photometric system is necessary in order to examine the (extra)galactic distribution of CP objects in detail.

   
2 Data collection

Our used starting point was the compilation of chemically peculiar ``standards'' in previous temperature calibration investigations (e.g. Hauck & North 1993). Due to the small number of available direct temperature determinations, most of the same stars have been used for the calibration of the different photometric systems. We consulted the literature to collect more temperatures reported to date and older ones ignored in previous compilations and included only temperature determinations not based on photometry. Results based on averaged values including photometric results were rejected, the same holds for works with no clear description of the method used. Furthermore, the objects were checked for membership of one of the CP groups following the classification scheme by Preston (1974) primarily using the peculiarity types given in Renson et al. (1991) and Bychkov et al. (2003), refined with additional literature values. The He representatives are divided into CP4a (He-weak) and CP4b (He-rich). For the CP3 members subgroups also have been defined (see Sect. 4.3). If a classification was uncertain, the object was rejected. For instance, the star HD 2628 was found to be a nonclassical Am star by Adelman et al. (2000). An exception was made in the case of the stars HD 5737 and HD 125823. Hunger & Groote (1999) classified them as intermediate stars which show He-weak and He-rich behaviour, they were kept as CP4ab. For two cool CP2 stars (HD 29578 and HD 92499, both with $T_{\rm eff} < 8000$) we are unable to calibrate their temperature, since only ${\it Geneva}$ photometry was available and therefore it was not possible to deduce reddening information. Since for these two stars only one temperature determination was found, they were rejected from the sample. In total, 364 individual temperature determinations for 176 CP stars taken from 71 references have been found that fulfil the criteria above. Since we have not noticed significant differences in the overall result between the various methods, no weighting was performed. Some outliers are found, but a rejection was only carried out if more than two determinations were available and a temperature by the same or comparable method was deviated strongly. This was necessary for only about 2% of the nearly 400 individual results. Finally an average and the resulting standard deviation was calculated. For about 92% of the sample the standard deviation does not exceed 5%. Some outliers are based on two references only, or the literature values are spread equally over a large temperature range, making a rejection of individual results difficult.

Photometric data in the studied systems (${\it UBV}$, Strömgren ${uvby}\beta$, ${\it Geneva}$) were collected by using the General Catalogue of Photometric Data (GCPD, Mermilliod et al. 1997). Since the averaged photometry is based on many references with several individual measurements, in addition to wrong photometry, the influence of several kinds of variability is reduced. If no data were found, the literature was consulted in order not to ignore existing measurements. An overview of the number of CP stars compiled can be seen in Table 1.

The compiled references were divided into groups of comparable temperature determination methods. These are (a) the Infrared Flux Method (IRFM) introduced by Blackwell & Shallis (1977); (b) fitting solar/enhanced models to the visual energy distribution; (c) fitting solar/enhanced models to the total energy distribution (from UV to red) as well as (d) fitting (Balmer) line profiles with solar/enhanced models. Three references (e) do not fit into these categories. Stepien & Dominiczak (1989) presented a new method based on visual energy distribution modelling and a correction of the UV flux deficit. Cidale et al. (2007) investigated He peculiar stars using a spectrophotometric system based on the measurement of the continuum energy distribution around the Balmer discontinuity. Since this method was not applicable to their He-rich subsample, non-LTE model atmospheres were used for this CP group. Bruntt et al. (2008) determined for the first time the temperature of HD 128898 using angular diameter and bolometric flux. In Table 8 we present the references for the individual CP stars together with the method used, (a)-(e). This is a rough division, but can serve as a hint to reliability of a particular determination. Falling into group (d) one can find works like Hubrig & Nesvacil (2007), who used iterative processes to minimise the dependence of the average Fe abundance on the excitation potentials of several measured lines, but also several works like Ryabchikova et al. (2004a) using a single line such as H$\alpha$. However, further subdivision will probably result in a confusing number of groups. Several references used combinations of these methods, e.g. in the series by Adelman and collaborators often visual energy distribution modelling plus H$\gamma$ profile fitting were used, which is indicated in Table 8 as bd(+), where the plus sign shows that a model other than a solar one was used. Several objects in the comprehensive list by Adelman & Rayle (2000) have been studied in previous works by Adelman with good agreement. Since it seems that the same data have been used, we only include the results of the latter reference. Furthermore, Adelman & Rayle (2000) used more recent model atmospheres than in the previous studies.

The mean effective temperatures of the compiled CP stars (Tables 4-7) are therefore based on several individual studies, determined mostly with different methods (see Table 8) compensating for the possible disadvantages of a particular method.

   

Table 1: The sample of CP stars used in this study and the available photometric data in the respective systems.

CP class	Starsa	${uvby}\beta$	${\it Geneva}$	${\it UBV}$b
CP1	30/13	29	30	30
CP2	79/51	78	76	63
CP3	28/14	27	27	28
CP4a	20/15	20	20	20
CP4b	17/9	14	16	15
CP4ab	2/2	2	2	2

^a Stars in total / with average temperatures.
^b Number of objects with a complete set is listed.

   
3 Interstellar reddening

   

Table 2: Overview of the temperature calibrations for the individual CP groups and photometric systems determined in this study.

CP type	System	Relation	Errorsa	Restriction	Rb	# Stars
CP1	${\it UBV}$	$\theta_{\rm eff} = 0.527 + 0.515(B-V)_{0}$	0.003/0.013		0.993	24
	${\it Geneva}$	$\theta_{\rm eff} = 0.632 + 0.640(B2-V1)_{0}$c		$-0.160 \leq (B2-V1)_{0} \leq +0.730$
		direct use of TXY		(B2-V1)0 < -0.160
	${uvby}\beta$	direct use of $T_{{uvby}\beta}$
CP2	${\it UBV}$	$\theta_{\rm eff} = 0.541 + 0.389Q$	0.004/0.014	$T_{\rm eff} \ga 9000$	0.982	29
		$\theta_{\rm eff} = 0.572 + 1.177(B-V)_{0}$	0.011/0.089	$-0.20 \leq (B-V)_{0} \leq -0.05$	0.948	21
		$\theta_{\rm eff} = 0.542 + 0.388(B-V)_{0}$	0.005/0.030	$-0.05 \leq (B-V)_{0} \leq 0.40$	0.932	28
	${\it Geneva}$	$\theta_{\rm eff} = 0.835 + 0.458(B2-G)_{0}$d		$T_{\rm eff} \la 9000$
		$T_{\rm eff}=1420 + 0.815T_{XY}$	280/0.023	$T_{\rm eff} \ga 9000$	0.988	30
	${uvby}\beta$	direct use of $T_{{uvby}\beta}$		$T_{{uvby}\beta} < 9000$
		$T_{\rm eff}=2090+0.756T_{{uvby}\beta}$	300/0.025	$T_{{uvby}\beta} \geq 9000$	0.984	31
		$\theta_{\rm eff}=0.234+0.213[u-b]$	0.009/0.008	$T_{\rm eff} \ga 9000$	0.980	33
CP3/4	${\it Geneva}$	$T_{\rm eff}=1120 + 0.892T_{XY}$	350/0.021		0.990	37
CP3/4	${uvby}\beta$	$T_{\rm eff}=2230+0.809T_{{uvby}\beta}$	300/0.018		0.991	37
CP3a	${\it UBV}$	$\theta_{\rm eff} = 0.501 + 0.323Q$	0.007/0.026		0.953	18
	${uvby}\beta$	$\theta_{\rm eff}=0.233+0.196[u-b]$	0.014/0.014		0.965	17
CP3b/4	${\it UBV}$	$\theta_{\rm eff} = 0.540 + 0.418Q$	0.009/0.017		0.980	27
	${uvby}\beta$	$\theta_{\rm eff}=0.173+0.286[u-b]$	0.005/0.008		0.989	27

^a Errors of the linear fits.
^b Correlation Coefficient.
^c Taken from Hauck (1985).
^d Taken from Hauck & North (1982).

For the vast majority of programme stars Hipparcos parallaxes (Perryman et al. 1997) are available. A new reduction of the data (van Leeuwen 2007) has been published, providing more accurate results. These are used for the present study. Since only a limited number of objects was found to be located closer than 50 pc from the sun, interstellar extinction is no longer negligible, especially if examining cooler CP stars in the ${\it Geneva}$ or ${\it UBV}$ photometric system, for which a reddening-free temperature calibration (via ${\it Geneva}$ X/Y or the ${\it UBV}$ Q method) is not possible. Several attempts have been made to now to model the distribution of interstellar extinction. However, these studies should be treated with caution if one intends to deredden individual stars, because such models give only a general trend and do not take local irregularities of the absorbing material into account (Arenou et al. 1992). We therefore rely on reddening estimations based on ${\it UBV}$, ${\it Geneva}$ and ${uvby}\beta$ data. To examine the applicability and accuracy for CP stars because of their anomalous colours, we have chosen the compilation of magnetic CP stars in open clusters by Landstreet et al. (2007). The available listing was reduced by using their flags to limit to at least probable cluster CP objects. We also removed objects within associations and young cluster stars ( $\log t \le 7.0$) to avoid strong differential reddening due to nebulous regions. Averaged cluster ages for the selection and the reddening values for the comparison are taken from Paunzen & Netopil (2006). For clusters not included in their list, we have proceeded analogously. For the remaining 45 CPs in 26 open clusters that have a reddening up to 0.5 mag, we have extracted photometric measurements in the three mentioned systems using the GCPD and the literature. For all objects, data in at least one system are available. Using the Napiwotzki et al. (1993) UVBYBETA calibration, the intrinsic ${\it Geneva}$ colours (Cramer 1982) via the X/Y parameters and the Q method for the ${\it UBV}$ system (Johnson 1958),

E(B-V)=(B-V)-0.332Q

Q=(U-B)-0.72(B-V)-0.05(B-V)²

the colour excesses in the respective systems are determined. However, the latter two systems can be used only for hotter stars. Following the suggestion by North (1998), the correction for hotter CP2 stars in the ${uvby}\beta$ system as defined by Masana et al. (1998) was applied to take the peculiarity effects on c₁ and (b-y) into account. Using this method, negative reddening values are reduced reasonably; the remaining ones are set to zero. Finally, the relations

E(B-V) = 1.43E(b-y) = 0.84E[B-V]

are used to transform reddening values of the different photometric systems to calculate a mean reddening. Square brackets are utilised to distinguish the ${\it Geneva}$ excess from Johnson E(B-V). Note the transformations E(B-V)=1.14E(B2-V1)=0.83E(B2-G) for the additional ${\it Geneva}$ colour excesses. To reduce the influence of differential reddening, which is significantly present in NGC 2516 (see, e.g., Maitzen & Hensberge 1981), the individual determined colour excesses for CP stars $E(B-V)_{\rm CP}$ in a cluster are averaged whenever possible. Figure 1 shows the resulting deviations from the mean cluster reddening ( $\Delta E(B-V) = E(B-V)_{\rm Cluster} - E(B-V)_{\rm CP}$). The CP star HD 127924 in NGC 5662 exhibits the largest difference from the mean cluster reddening (0.06 mag). When inspecting the reddening distribution by Clariá et al. (1991) in this cluster, it is obvious that it lies in a slightly less reddened region.

Figure 1: Histogram of the mean reddening deviations $\Delta E(B-V)$.

The mean deviation was found to be comparable to the errors of the average cluster reddenings ($\sim$0.02 mag). We therefore conclude that the use of the photometrically determined colour excesses is justified and it was applied to the magnetic groups of our sample. However, for objects closer than 50 pc we still assume non reddening. The methods above cannot be used safely in regions with an exotic reddening law.

4 Photometric temperature calibration

For all stars with available Strömgren ${uvby}\beta$ photometry, their initial temperature was obtained using the UVBYBETA calibration by Napiwotzki et al. (1993), hereafter denoted $T_{{uvby}\beta}$. For the hotter stars with ${\it Geneva}$ photometry, the temperature (T_XY) was estimated using the reddening-free X/Y parameters and the calibration by Künzli et al. (1997). For both systems the grids for ${\rm [M/H]}=0$ are used, in order to have the possibility of a direct comparison to former studies. The stars calibratable via X/Y parameters can be selected by using $X \la 1.7+3Y$ and $Y \ga -0.07$ (Hauck & North 1993) as an approximation. For this subsample the ${\it UBV}$ Q-parameter also can be calculated safely. Whenever possible, the best suited relation based on the Strömgren reddening-free indices is given, which is in all cases the [u-b] index.

One crucial point to determine the corrections for the individual CP subgroups and photometric systems is the consideration of errors. Napiwotzki et al. (1993), Stepien (1994) or Lipski & Stepien (2008) have not used errors for the calculations of their [u-b] and [c₁] relations, in contrast to Hauck & North (1993) who assumed 300 K in their ${\it Geneva}$ correction for both axes. Inspecting their results for CP2 stars with and without the use of errors, a non-significant difference can be found. Since the ``real'' errors are unknown, and even the standard deviations of the averaged temperatures cannot be considered as realistic errors, we omitted them.

In Table 2 an overview of all determined relations and the respective errors, their validity range and the correlation coefficient R can be found. In the following sections the individual CP groups are discussed together with a comparison to former results.

4.1 CP1

For the group of Am stars the situation is straightforward, since well known calibrations for normal stars can be used with high accuracy. Although they are metal-rich, solar composition within the UVBYBETA calibration provides the best results ( $\Delta T < 200$ K) without the need for any correction. Using the more realistic assumption of [M/H]=0.5, the temperature is systematically underestimated by $\sim$150 K. In the light of the findings by Hauck & North (1993) that unrecognized binarity (most of the Am stars are SB1 objects) lowers the apparent effective temperature by 2.5-3%, it seems that using a solar composition grid for the photometric calibration balances this effect. However, in the literature it was not always traceable whether binarity was taken into account for the determined effective temperatures.

In contrast to ${uvby}\beta$ photometry, interstellar reddening has to be known if examining cool stars with ${\it Geneva}$ photometry. Except for one star (HD 162132), all objects of our sample are closer than 100 pc, about one third are even members of the nearby non-reddened open cluster Hyades. Examining the reddening determined via ${uvby}\beta$ photometry, one can notice that only three stars exhibit an E(B-V) greater than 0.02 mag. In consideration of these facts and that the mean reddening of the sample is $0.004\pm0.008$ mag, we have omitted a reddening correction (also for ${\it UBV}$), evoking an error of 225 K for the hottest part assuming an error of 0.02 mag in reddening. This is just slightly higher than the mean standard deviation of the individual average effective temperatures (150 K). However, inspecting the reddening determinations via ${uvby}\beta$ for the Hyades stars an excellent agreement with the mean cluster reddening was found.

The easiest and most accurate way to determine effective temperatures via ${\it Geneva}$ photometry is the use of the (B2-V1)₀ relation given in Hauck (1985):

$$\theta_{\rm eff}=0.632+0.640(B2-V1)_{0}$$

for $-0.160 \leq (B2-V1)_{0} \leq +0.730$ ( $\theta_{\rm eff}=5040/T_{\rm eff}$). See also Hauck & North (1993) in this respect. Hauck & Künzli (1996) have proposed, beside the (B2-V1) relation above, also the direct use of the calibration by Künzli et al. (1997), but the resulting temperatures are consistently underestimated by about 200 K for stars cooler than $\sim$9000 K and by the same value too high for the hotter part.

For stars in the temperature domain where the ${\it Geneva}$ reddening-free X/Y parameters can be used directly, no correction of the calibration by Künzli et al. (1997) is necessary. However, the sample of such hot Am representatives is rather small.

In the case of Johnson ${\it UBV}$, a relation based on (B-V) colours for normal stars (e.g. Flower 1996) results in temperatures about 200 K too low, caused by line blanketing due to metallic lines (Feinstein 1974), that has no influence on the ${\it Geneva}$ (B2-V1) index (Hauck & North 1993). To obtain a proper calibration, objects deviating more than 150 K after applying the (B2-V1) relation are rejected to reduce effects of interstellar reddening or other individual variances.

All investigated systems can be used to calibrate effective temperatures at about the same accuracy level ($\sim$200 K). However, ${uvby}\beta$ photometry should be preferred because of the possibility to deduce interstellar reddening. If the colour excess is known or the stars are close by, an average of the three systems results in high precision. Figure 2 shows the histogram of the deviations ( $\Delta T = T_{\rm eff}-\overline{T}_{\rm phot}$); only three stars exhibit a deviation of more than 150 K, whereas $\sim$80% are calibrated to better than 100 K.

Figure 2: Histogram of the temperature deviations for CP1 stars ( $T_{\rm eff} - \overline {T}_{\rm phot}$).

   
4.2 CP2

Several studies in the past dealt with the temperature calibration for the CP2 group, the most recent being by Lipski & Stepien (2008). Since our sample for this peculiar type is rather large (79 objects) compared to previous studies, we are able to restrict it to a selection of the most accurate stars, such CP2s with at least two independent temperature determinations. These 51 objects still cover the complete temperature range of 7000-14 000 K, including several cool roAp stars. A lack of such cool representatives occured in previous attempts. To obtain a more realistic error analysis of the different corrections, these are applied to the whole sample in order to take the different properties and error sources of CP2 stars into account.

Within this limited sample, one star (HD 133880) shows a large discrepancy if comparing effective temperatures and temperatures determined via standard photometric calibrations, and was excluded from the analysis. Stepien (1994) argued that one can find good reasons to reject almost every peculiar star from a sample. However, this star is an exceptional one due to the strong magnetic field and its geometry (Landstreet 1990).

One additional object deserves closer attention. HD 173650 was investigated by two authors (Wolff 1967; Babel 1994), but with different results; they obtained 9000 and 11 000 K, respectively. Since the average value does not affect the correlations in all photometric systems, we decided to keep it in our sample.

In case of the UVBYBETA calibration, stars resulting in temperatures $T_{{uvby}\beta} < 9000$ K can be used without correction. For hotter stars a correction is necessary, listed in Table 2. If both cases are applied properly to the whole sample, an accuracy better than $\sim$500 K can be achieved. Some outliers are present, but it is not possible to distinguish whether they are due to a wrong effective temperature determination or because of individual anomalies.

Adelman & Rayle (2000) proposed a temperature correction for CP2 stars based on results of the UVBYBETA calibration by Napiwotzki et al. (1993). They found $T_{{uvby}\beta} = 1.1984T(sp)-1704$ compared to their spectrophotometrically determined temperatures using 17 stars. Applied to our sample, the cool part ($\la$11 000 K) is reproduced suitably, whereas the hotter stars are overestimated by about 500 K. This can be explained by the large scatter in the results among the hotter ones.

Recently, Lipski & Stepien (2008) presented revised calibrations by means of the reddening free [u-b] and [c₁] indices. They found that a quadratic fit is necessary to take the CP2 properties into account. Based on our sample we cannot confirm these results, although their determined temperatures are included in our sample.

The above defined restricted sample and its [u-b] index is compared to average $\theta _{\rm eff}$ values in Fig. 3. We also included the proposed quadratic fit by Lipski & Stepien (2008). To clarify the discrepancy, especially for the cooler stars, we compare their determined temperatures to our averaged ones excluding their results, which is shown in the lower panel of Fig. 3. One can see that their temperatures for the cooler stars are somewhat underestimated ($\sim$370 K). Since the differences between the averaged values with or without these results are marginal, we keep their results in our sample; a too rigorous treatment probably would exclude nearly the entire dataset.

It can be seen in Fig. 3 (upper panel) that an uncritical application of relations based on [u-b] or [c₁] results in erroneous data for cool stars. The linear fit based on the [u-b] index was therefore limited to stars hotter than about 9000 K. For this group one can achieve an even more accurate result ($\pm$500 K) than after applying the correction of $T_{{uvby}\beta}$. However, without knowledge of additional information like an estimation of temperature via another presented method, it is difficult to separate them. The determined relation is close to former results (Napiwotzki et al. 1993; Stepien 1994), but also to Lipski & Stepien (2008) who included with their quadratic fit a linear correlation for comparison.

Figure 3: The upper panel shows the comparison of the reddening free Strömgren index [u-b] to $\theta _{\rm eff}$. The line represents the quadratic fit given by Lipski & Stepien (2008). the cool stars also are included, although they are not calibratable via the reddening free index. The lower panel shows the discrepancy of the temperatures determined by the authors to our averaged ones without their results. The line gives the one-to-one relation.

Temperatures determinable via ${\it Geneva}$ X/Y parameters have to be corrected according to Table 2, whereas the cooler CP2s can be calibrated using the relation

$$\theta_{\rm eff}=0.835+0.458(B2-G)_0$$

for normal stars by Hauck & North (1982) with good agreement. With these two corrections one can achieve an accuracy better than 500 K for $\sim$85% of the sample.

The correction found for T_XY is closer to the ``original'' one given by Hauck & North (1993) than to the revised relation by Hauck & Künzli (1996), based on the new grids for ${\it Geneva}$ photometry (Künzli et al. 1997) that are also used in the present investigation. The latter one deviates from ours by $\sim$$\pm$400 K, whereas the ``original'' one differs by $\sim$$\pm$150 K only at the hot and cool end, respectively.

Stars expected to be hotter than about 9000 K can be calibrated based on the Q-parameter without the need for reddening information. The found Q dependency is in excellent agreement with that given by Mégessier (1988) based on 11 objects. For cooler stars or if no (U-B) colour information is available, one can also use two relations based on (B-V)₀ (Table 2). We noticed missing ${\it UBV}$ photometry for numerous CP2 objects. For 11 stars we have not found such data, for 5 stars there is only a lack of (U-B).

All photometric systems are capable of estimating effective temperatures of CP2 stars at the same accuracy level with no dependency on temperature. Although it is not possible to separate ``strange'' peculiar objects (like HD 133880) by averaging the results of all possible calibrations, we propose such a method also for the CP2 stars to reduce errors due to photometric uncertainty.

The (B-V)₀ calibration for the hotter stars should be only used as last resort, since the sum of errors of photometry and reddening are not negligible. For intermediate stars ($\sim$11 000 K) 0.02 mag in total already results in a temperature difference of $\sim$600 K. The obtained deviations are presented in Fig. 4 neglecting the mentioned calibration. We are able to calibrate nearly 90% of the whole sample within an error of 500 K, still 75% better than $\sim$300 K.

Figure 4: Histogram of the temperature deviations for CP2 stars ( $T_{\rm eff} - \overline {T}_{\rm phot}$).

Among the strongest deviating stars (see Table 3), the abovementioned object was found, as well as HD 215441 (Babcock's star) or HD 157751 for which Hubrig & Nesvacil (2007) found resolved magnetically split lines and a mean field modulus of 6.6 kG. The photometrically determined temperatures for this object deviate strongly, only the corrected $T_{{uvby}\beta}$ result agrees well, whereas the [u-b] relation supplies a temperature already 1750 K too low. The other star (HD 92499) studied by the authors showing the same effect and even a larger magnetic field modulus is unfortunately among the rejected stars due to the poor photometry available.

To have an additional comparison for a possible magnetic effect on photometric temperatures, the relationship was deduced by means of the (B2-G) relation above. Since this object is located at a distance of $\sim$280 pc, an assumption of E(B-V)=0.05 mag is probably the upper limit that leads to a temperature deviating only by 200 K. For HD 215441, exhibiting the strongest magnetic field, only one direct temperature determination is available to our knowledge (Lipski & Stepien 2008, who discussed the problems of its investigation).

   
4.3 CP3 and CP4

Initially analysed separately, no differences between He-weak, He-rich, and CP3 objects were noticed in the gradient of $T_{{uvby}\beta}$ and T_XY results. Therefore these temperature corrections are valid for all CP3 and CP4 members. For the analysis the sample was reduced to stars with at least two temperature determinations, resulting in 14 CP3, 15 CP4a, 9 CP4b, and the two intermediate CP4 objects (see Sect. 2).

HD 137509 exhibits the second largest magnetic field beside Babcock's star (e.g. Mathys & Hubrig 1997; Kochukhov 2006) and was found to be Si Cr Fe enhanced, but also strongly He underabundant. We therefore included it as a first attempt in the group of He-weak objects. However, like HD 133880 in the CP2 sample, this star was excluded from the analysis because of the large deviation. An inclusion in the CP2 group also would lead to such a rejection. The investigation of HD 137509 by Shulyak et al. (2008) shows that appropriate models should be used for the analysis of stars with such a large magnetic field ( $\left\langle B \right\rangle \sim 29~{\rm kG}$). They suggest a temperature about 1000 K higher for this star than previously published, correcting the temperature in the right way according to its deviation, placing it within the scatter of the other representatives in our sample.

 

 

Table 3: The strongest deviating stars after applying the individual corrections.

HD/DM	CP	$T_{\rm eff} / \sigma$	$\Delta T/\sigma \overline{T}_{\rm phot}$
-27 3748	CP4b	23 000	1120/280
21 699	CP4a	16 000	950/100
23 408	CP3b	11 900/990	-800/90
26 571	CP2	11 750	-1170/200
37 470	CP2	13 000	1340/170
51 688	CP3b	12 500	-880/80
60 344	CP4b	22 500/2120	1490/260
66 522	CP4b	18 000	-1210/90
133 880	CP2	10 700/60	-1230/210
137 509	CP4a	12 680/110	-1350/680
157 751	CP2	11 300	1040/790
215 441	CP2	14 000	-780/390

Although for the He-rich object HD 60344 two independent temperature determinations are available, it was also excluded from the analysis due to the strongly differing results producing a standard deviation of more than 2000 (see Table 3). The same holds for the CP3 star HD 23408, exhibiting an error of more than 8%.

Temperatures for CP4 objects obtained via the UVBYBETA calibration and ${\it Geneva}$ X/Y parameters are found to be overestimated compared to effective temperatures reported in the literature (see Fig. 5). Even for CP3 stars a correction of up to 400 K is necessary, continuing the trend of CP4 stars. A tendency to change with temperature for CP3 and $T_{{uvby}\beta}$ results was already noticed by Adelman & Rayle (2000), and their correction is close to ours.

Former investigations (e.g. Hauck & North 1993) suggested the direct use of ${\it Geneva}$ X/Y temperature for He-weak and HgMn stars, whereas Zboril et al. (1997) noticed an overestimation of ${\it Geneva}$ temperature for He-rich objects. Their proposed correction is in fair agreement with our result. However, in contrast to our study they included similar errors for both axes to determine the relation, but did not list the errors used. In Fig. 5 one can see that a direct use of the ${\it Geneva}$ results significantly overestimates the temperature.

Due to the limited number of available cluster CP3s, a comparison to the photometric colour excess estimations is not significant. Since there are only a few objects closer than 100 pc, a temperature calibration based on the Johnson (B-V) index, very probably affected by interstellar reddening, was not undertaken. For the CP4 group also only the reddening free Q-parameter was investigated, as at such high temperatures even a small reddening error already results in a large deviation (see also Sect. 4.2).

Inspecting the reddening free Q and [u-b] indices, the different properties of CP3 and CP4 stars are apparent. Among the CP3 objects two sequences are noticed, one following the He representatives. Therefore the CP3 sample was divided into two groups, the ``classical'' cooler HgMn stars (CP3a) and predominantly hotter ones (CP3b). Members of the latter group can be mostly considered as PGa objects, the hotter extension of HgMn stars, exhibiting deficient He and strongly overabundant P and Ga (Hubrig & González 2007; Rachkovskaya et al. 2006). We have noticed that several of these objects were studied as pure He-weak objects (e.g. by Cidale et al. 2007). Additional publications helped to clarify their membership to the CP3 (sub)group. However, since the temperature behaviour of CP3b and CP4 members is similar in all investigated systems, an ambiguous classification fortunately does not influence the resulting temperature.

Figure 5: Comparison of temperatures determined via ${\it Geneva}$ photometry to literature values for the restricted CP3 and CP4 samples. The upper line shows the one-to-one relation, the middle one our linear fit, and the bottom line the CP2 relation for comparison. Additionally, the outstanding object HD 137509 is given. The error bars correspond to the standard deviation of the average effective temperatures.

Using the reduced samples mentioned above, the CP4 are combined with the three members of the CP3b group to determine the relations for Q and [u-b]. The exclusion of the latter group does not alter the results listed in Table 2. Due to the limited number of cooler HgMn objects with more than one temperature determination, the whole sample of 18 stars was used for the analysis to better cover the temperature range.

The ${\it UBV}$ and [u-b] calibrations applied to HD 137509 agree well with the temperature of 13 750 K proposed by Shulyak et al. (2008). However, that can be also by chance due to its variability. An amplitude of about 0.1 mag was found in the ${\it Geneva}$ [U] colour by Mathys & Lanz (1997). All other results indicate a consistently higher temperature for this star after the corrections (14 630 and 14 500 K for ${\it Geneva}$ and ${uvby}\beta$ photometry, respectively). See also Sect. 4.4 in this respect.

Figure 6: Histogram of the temperature deviations for CP3 stars ( $T_{\rm eff} - \overline {T}_{\rm phot}$). The dark grey portion represents the ``classical'' HgMn objects.

For the hot CP4b star CPD-62 2124, we noticed large differences between the Strömgren and ${\it UBV}$ results. Since this star agrees very well with the Johnson Q relation, the discrepancy is probably caused by the Strömgren photometry taken from Perry & Landolt (1986), therefore this result is rejected. Unfortunately, no ${\it Geneva}$ photometry is available for a comparison in this system. However, Zboril et al. (1997) noted, that this star shows emission at least in its Balmer lines and the helium abundance is less reliable. Additionally, the emission was not only seen in the star but also in the surrounding sky, caused by a nebula.

The deviations of the determined temperatures compared to literature values are presented in Figs. 6 and 7 for CP3 and CP4 stars respectively. All investigated photometric systems show the same ability to calibrate effective temperatures for the individual subgroups. An average of all results does not provide an improvement in accuracy, but helps to avoid erroneous temperatures due to wrong photometry in a single system. About 85% of the CP3 stars are calibrated to better than 500 K, for the subgroup of HgMn objects even a slightly better result ($\sim$400 K) can be obtained. In the case of CP4 members, one can achieve an accuracy of $\sim$700 K. However, in all groups some stronger deviating objects are found, which are discussed in Sect. 4.4.

Like the Am group, CP3 stars are often part of spectroscopic binaries. Adelman & Rayle (2000), a main contributor to our sample, overcame this problem by studying single objects or those whose companions have not been detected or contribute very little to the optical region fluxes. A restriction to objects studied in this reference (10 stars) reduces the error range to $\sim$300 K. However, this CP group still suffers from a lack of well investigated stars.

In Tables 6 and 7 the compiled data are listed. For some objects, the peculiarity type given by Renson et al. (1991) is misleading. The following references were therefore used for the classification: HD 35497 and HD 77350 (Adelman & Rayle 2000), HD 147550 (López-García & Adelman 1994), HD 19400 (Hubrig et al. 2006), HD 144667 (Castelli & Hubrig 2007).

Figure 7: Histogram of the temperature deviations for CP4 stars ( $T_{\rm eff} - \overline {T}_{\rm phot}$). The dark grey portion represents the He-weak objects.

   
4.4 Strong deviating objects

In Table 3 one can find the strongest deviating stars after applying individual corrections. For the star HD 37470 the standard temperature calibrations result in a much better agreement than the corrected values. The same holds for DM -27 3748 and HD 21699. However, the latter object is a striking helium and silicon variable (Hubrig & Mathys 1994) and the deviation of the other is still below 5%. For HD 51688, showing enhanced Si Mn, but also a He-weak behaviour, the CP2 corrections would reduce the deviation significantly to -290 K. The object HD 66522 also agrees much better as a CP2, although its high temperature excludes it from this group. In Sect. 4.3 large differences between the individual photometric results for the strong magnetic object HD 137509 were noticed, which are not found to such an extent using the CP2 relations. Also the deviation from literature values are noticeably reduced to -720 K, when treating it as CP2. If using the study by Shulyak et al. (2008) for comparison, the temperature difference decreases to +360 K, but the use of the CP4 corrections also results in a good agreement with the reference above. However, the more homogeneous photometric results suggest that this object should be classified as CP2. It seems that strong magnetic fields do not have such a large influence on the photometric temperatures. For the other strong magnetic CP2 stars HD 215441, HD 133880, and HD 157751, an investigation like in Shulyak et al. (2008) would be useful to obtain more comparative values. No influence on the temperature calibrations is given due to probable misclassifications, since none of these objects were used for the calculations. Nevertheless, a spectroscopic re-investigation of the listed stars is necessary, in order to clarify their status and temperature. For most of them only one temperature determination or strongly differing result is found in the literature.

5 Bolometric correction

Two studies (Landstreet et al. 2007; Lipski & Stepien 2008) examined the bolometric correction (BC) for magnetic CP stars. Both investigations presented a relation based on effective temperature, a more appropriate solution than the one by Lanz (1984) on the basis of the ${\it Geneva}$ (B2-G) colour index. While the first reference shows a comparison of published BCs to photometrically determined temperatures, the second authors used their own results for the correlation, whose temperature determinations were discussed in Sect. 4.2. Since we have shown that the former temperature corrections are partially inaccurate, we checked the validity of the two findings using our sample of averaged effective temperatures. For this purpose we collected the integrated fluxes (F_t) for objects in our sample reported in the references above, and some more by Shallis & Blackwell (1979), Shallis et al. (1985), Glushneva (1987), Monier & Mégessier (1992), Cidale et al. (2007), and Bruntt et al. (2008) to build averages whenever possible and calculated a mean BC using

$$BC = -2.5~\log(F_{t})-m_{v}-11.49.$$

In total, we found 85 individual fluxes for 35 CP2, 7 CP3 and 11 CP4 objects. To be as homogeneous as possible, the visual magnitude (m_v) of the ${\it Geneva}$ photometric system was used whenever available, corrected for interstellar absorption by using the determined reddening values and a mean total-to-selective ratio of 3.1.

For HD 22920 we noticed that the integrated flux listed by Lanz (1984) is most likely an error, the value does not correspond to the given bolometric correction. We therefore used the tabulated BC value directly for this star, since it perfectly agrees with the compiled temperature.

Landstreet et al. (2007) argued that the integrated fluxes by Stepien & Dominiczak (1989) are not corrected for reddening and removed the hottest (farthermost) stars from their sample. We therefore checked all objects by means of the determined reddening values. All objects in references with no explicitly given reddening values are not significantly reddened (<0.03 mag), but we rejected four deviating (CP2) objects by comparing the listed E(B-V) values in the work by Lipski & Stepien (2008) to ours. For the remaining 42 magnetic CP objects the second order fit

$$BC = -5.737+18.685~\theta_{\rm eff}-15.135~\theta_{\rm eff}^2,$$

valid for 7500-19 000 K, best represents their behaviour. Even the restriction to nearly non reddened (<0.03 mag) stars or the use of objects with at least two integrated flux measurements does not alter the result significantly, but the cool part especially is not sufficiently covered by such data.

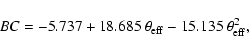
The data are presented in Fig. 8 together with the relation determined above. No difference was noticed between magnetic CP2 and CP4 objects, however only a small temperature overlap between the two groups is available. Within the temperature range of 7500-14 000 K an uncertainty of 0.1 mag applies; for hotter stars up to $\sim$19 000 K a slightly higher value of 0.15 mag has to be taken into account. The discrepancy of -0.16 mag with the result by Landstreet et al. (2007) at the hot end (Fig. 8) is probably caused by the use of overestimated photometric temperatures for He-weak stars in this reference (see Sect. 4.3 and Fig. 5 in this respect) that lowers the resulting slope. However, the large scatter and low number of He objects still prevents a clear conclusion for such hot CP representatives, but at least the main CP2 temperature domain up to 14 000 K seems to be well defined. In contrast to the reference above, the relation by Lipski & Stepien (2008) is shifted to larger negative BC values (see Fig. 8) in this temperature region, placing it close to the BC of normal stars. This can be explained due to the lower temperatures mentioned in Sect. 4.2, by the use of a zero reddening for all stars closer than 100 pc and $E(B-V) \le 0.03$ mag as well as by the difference of the constant used to transform integrated fluxes to the bolometric correction. The bolometric correction for normal stars by Balona (1994) and Flower (1996) is given as a comparison in Fig. 8. The difference in BC between normal and CP stars of same temperature is not larger than about 0.1 mag, in agreement with Kochukhov et al. (2008) who determined using model fluxes a systematic difference of the same value.

Concerning CP3 stars, the situation is even more problematic because of the extremely limited number. For the two closest stars ($\la$50 pc) zero reddening was assumed, for the others the values by Lanz (1984) and Cidale et al. (2007) were adopted. One strongly deviating object (HD 358) can be found in Fig. 8, the others are placed around the normal star relation, but we conclude that the available data has to be increased significantly, which also holds for the magnetic CP types, especially for the hotter representatives.

Figure 8: Bolometric corrections for CP stars together with our fit (solid black line) and the relations for normal stars by Balona (1994) and Flower (1996). For better presentation, the comparison of our fit to Lipski & Stepien (2008) and Landstreet et al. (2007) is shifted by -0.6 mag. Whenever available, the error of BC according to error propagation using the standard deviation of the averaged integrated fluxes and 0.02 mag in reddening is given. Additionally the standard deviation of the averaged temperatures is shown.

6 Conclusions

The literature was consulted to compile a sample of 176 chemically peculiar stars with temperature determinations other than from photometric results, in order to calibrate photometrically determined temperatures. The obtained corrections and relations listed in Table 2 are therefore based on a much larger sample than in previous studies. A clear CP classification is necessary in order to use the proper correction and to obtain the best possible result. Except the (B-V)₀ relation for hot CP2 stars (see Table 2), all presented corrections within the respective CP subgroups are able to determine the effective temperature at about the same accuracy level. However, to avoid erroneous results due to incorrect photometry in a single system, a mean value of all available individual results should be always used.

A comparison to former results showed that He-weak and He-rich objects especially have been overestimated until now, influencing all previous studies (e.g. Landstreet et al. 2007). The new lower temperatures and bolometric corrections will place their hotter (CP4) objects at somewhat older ages, on the border of the adopted errors. These authors also discussed the problems of photometric temperatures (see Sect. 3.2.2 in the reference) referring to the work by Khan & Shulyak (2006) who conclude that photometric temperature calibrations for normal stars are not far from the true values of CP stars. However, the present study confirms that compared to normal stars, sometimes considerable corrections are necessary (except cool Am and CP2 stars), although we cannot exclude effects influencing all compiled temperatures determined via different methods. For example, the effect of strong magnetic fields has to be examined on a much larger sample. On the other hand, the presented results for HD 137509 together with the work by Shulyak et al. (2008) would seem to suggest that photometric temperatures are not significantly affected.

Recently, Bruntt et al. (2008) obtained the first real direct temperature measurement for the roAp HD 128898 by means of angular diameter and integrated flux measurements. Their investigation yields a 480 K lower temperature compared to the spectral analysis by Kupka et al. (1996). For a final solution of the problematic CP temperature calibration, more studies of this kind are needed.

It was shown that photometric standard calibrations can be applied to determine interstellar reddening also for CP2 and CP4 objects. Additionally, a revised bolometric correction for magnetic CP stars is presented. Together with the proposed photometric temperature relations it can serve to study the evolutionary status of these objects to the highest possible accuracy.

Tables 4-7, available in electronic form at A&A, list the compiled objects of the individual CP groups together with average temperature (literature value $\overline{T}_{\rm eff}$ and photometrically determined $\overline{T}_{\rm phot}$), number of literature sources #, the deviation $\Delta T$, visual magnitude m_v, the revised Hipparcos parallaxes $\pi$, and the bolometric corrections found in the literature. The existing photometry is given in the form ${uvby}\beta/{\it Geneva}/{\it UBV}$. For the magnetic subgroups the calculated reddening also is shown. In parentheses the errors of the last significant digits are given. The peculiarity type listed in the CP2-4 sample is taken from Renson et al. (1991). Table 8 lists the references found for the individual stars, as well as the method used for the temperature determination.

Acknowledgements

We are grateful to the referee K. Stepien for valuable comments which helped to improve the paper. This research was performed within the project P17920 of the Austrian Fonds zur Förderung der wissenschaftlichen Forschung (FwF) and has made use of the SIMBAD database, operated at CDS, Strasbourg, France.

References

 
• Adelman, S. J. 1988, MNRAS, 230, 671
   
• Adelman, S. J. 1989, MNRAS, 239, 487
   
• Adelman, S. J. 1994a, MNRAS, 266, 97
   
• Adelman, S. J. 1994b, MNRAS, 271, 355
   
• Adelman, S. J. 1996, MNRAS, 280, 130
   
• Adelman, S. J., & Albayrak, B. 1998, MNRAS, 300, 359
   
• Adelman, S. J., & Rayle, K. E. 2000, A&A, 355, 308
   
• Adelman, S. J., Pyper, D. M., López-García, Z., & Caliskan, H. 1995, A&A, 296, 467
   
• Adelman, S. J., Caliskan, H., Kocer, D., & Bolcal, C. 1997, MNRAS, 288, 470
   
• Adelman, S. J., Caliskan, H., Cay, T., Kocer, D., & Tektanali, H. G. 1999, MNRAS, 305, 591
   
• Adelman, S. J., Caliskan, H., Kocer, D., et al. 2000, MNRAS, 316, 514
   
• Allen, M. S. 1977, ApJ, 213, 121
   
• Arenou, F., Grenon, M., & Gomez, A. 1992, A&A, 258, 104
   
• Babel, J. 1994, A&A, 283, 189
   
• Balona, L. A. 1994, MNRAS, 268, 119
   
• Blackwell, D. E., & Shallis, M. J. 1977, MNRAS, 180, 177
   
• Bolcal, C., Kocer, D., & Duzgelen, A. 1987, Ap&SS, 139, 295
   
• Bruntt, H., North, J. R., Cunha, M., et al. 2008, MNRAS, 386, 2039
   
• Bychkov, V. D., Bychkova, L. V., & Madej, J. 2003, A&A, 407, 631
   
• Caliskan, H., & Adelman, S. J. 1997, MNRAS, 288, 501
   
• Castelli, F., & Hubrig, S. 2007, A&A, 475, 1041
   
• Catanzaro, G. 2006, MNRAS, 368, 247
   
• Catanzaro, G., Leone, F., & Dall, T. H. 2004, A&A, 425, 641
   
• Cayrel, R., Burkhart, C., & van't Veer, C. 1991, in Evolution of Stars: the Photospheric Abundance Connection, ed. G. Michaud, & A. V. Tutukov (Kluwer Acad. Publishers), IAU Symp., 145, 99
   
• Cidale, L. S., Arias, M. L., Torres, A. F., et al. 2007, A&A, 468, 263
   
• Clariá, J. J., Lapasset, E., & Bosio, M. A. 1991, MNRAS, 249, 193
   
• Cramer, N. 1982, A&A, 112, 330
   
• Derman, I. E. 1982, Ap&SS, 88, 135
   
• Feinstein, A. 1974, AJ, 79, 1290
   
• Flower, P. J. 1996, ApJ, 469, 355
   
• Gelbmann, M. J. 1998, Contrib. of the Astron. Obs. Skalnaté Pleso, 27, 280
   
• Gelbmann, M., Kupka, F., Weiss, W. W., & Mathys, G. 1997, A&A, 319, 630
   
• Glagolevskij, Y. V., Leushin, V. V., Chuntonov, G. A., & Shulyak, D. 2006, Astron. Lett., 32, 54
   
• Glushneva, I. N. 1985, SvA, 29, 659
   
• Glushneva, I. N. 1987, SvA, 31, 315
   
• Hauck, B. 1985, in Calibration of fundamental stellar quantities, ed. D. S. Hayes, L. E. Pasinetti, & A. G. D. Philip, IAU Symp., 111, 271
   
• Hauck, B., & Künzli, M. 1996, Baltic Astron., 5, 303
   
• Hauck, B., & North, P. 1982, A&A, 114, 23
   
• Hauck, B., & North, P. 1993, A&A, 269, 403
   
• Hubrig, S., & González, J. F. 2007, A&A, 466, 1083
   
• Hubrig, S., & Mathys, G. 1994, in Pulsation, Rotation and Mass Loss in Early-type Stars, ed. L. A. Balona, H. F. Henrichs, & J. M. Contel, IAU Symp., 162, 167
   
• Hubrig, S., & Nesvacil, N. 2007, MNRAS, 378, 16L
   
• Hubrig, S., North, P., Schöller, M., & Mathys, G. 2006, Astron. Nachr., 327, 289
   
• Hunger, K., & Groote, D. 1999, A&A, 351, 554
   
• Johnson, H. L. 1958, Lowell Observatory, 4, 37
   
• Kato, K. I., & Sadakane, K. 1999, PASJ, 51, 23
   
• Kearsley, A. J., & Wegner, G. 1978, MNRAS, 182, 117
   
• Khan, S. A., & Shulyak, D. V. 2006, A&A, 448, 1153
   
• Kochukhov, O. 2006, A&A, 454, 321
   
• Kochukhov, O., & Shulyak, D. 2008, Contrib. of the Astron. Obs. Skalnaté Pleso, 38, 419
   
• Kochukhov, O., Piskunov, N., Ilyin, I., Ilyina, S., & Tuominen, I. 2002, A&A, 389, 420
   
• Kochukhov, O., Tsymbal, V., Ryabchikova, T., Makaganyk, V., & Bagnulo, S. 2006, A&A, 460, 831
   
• Kupka, F., Ryabchikova, T. A., Weiss, W. W., et al. 1996, A&A, 308, 886
   
• Künzli, M., North, P., Kurucz, R. L., & Nicolet, B. 1997, A&AS, 122, 51
   
• Landstreet, J. D. 1990, ApJ, 352, L5
   
• Landstreet, J. D., Bagnulo, S., Andretta, V., et al. 2007, A&A, 470, 685
   
• Lanz, T. 1984, A&A, 139, 161
   
• Lanz, T. 1985, A&A, 144, 191
   
• Leone, F., & Manfre, M. 1996, A&A, 315, 526
   
• Leone, F., & Manfre, M. 1997, A&A, 320, 257
   
• Leone, F., Catalano, F. A., & Manfre, M. 1993, A&A, 279, 167
   
• Lipski, ., & Stepien, K. 2008, MNRAS, 385, 481
   
• Liubimkov, L. S., & Savanov, I. S. 1983, Izvestiya Ordena Trudovogo Krasnogo Znameni Krymskoj Astrofizicheskoj Observatorii, 67, 3
   
• López-García, Z., & Adelman, S. J. 1994, A&AS, 107, 353
   
• López-García, Z., & Adelman, S. J. 1999, A&AS, 137, 227
   
• López-García, Z., Adelman, S. J., & Pintado, O. I. 2001, A&A, 367, 859
   
• Maitzen, H. M., & Hensberge, H. 1981, A&A, 96, 151
   
• Masana, E., Jordi, C., Maitzen, H. M., & Torra, J. 1998, A&AS, 128, 265
   
• Mathys, G., & Hubrig, S. 1997, A&AS, 124, 475
   
• Mathys, G., & Lanz, T. 1997, A&A, 323, 881
   
• Mégessier, C. 1988, A&AS, 72, 551
   
• Mermilliod, J.-C., Mermilliod, M., & Hauck, B. 1997, A&AS, 124, 349
   
• Mon, M., Hirata, R., & Sadakane, K. 1981, PASJ, 33, 413
   
• Monier, R. 1992, A&A, 263, 175
   
• Monier, R., & Mégessier, C. 1992, A&A, 256, 205
   
• Morossi, C., & Malagnini, M. L. 1985, A&AS, 60, 365
   
• Napiwotzki, R., Schoenberner, D., & Wenske, V. 1993, A&A, 268, 653
   
• Netopil, M., Paunzen, E., Maitzen, H. M., et al. 2007, A&A, 462, 591
   
• North, P. 1998, Highlights of Astronomy, 11a, 657
   
• Paunzen, E., & Netopil, M. 2006, MNRAS, 371, 1641
   
• Paunzen, E., Maitzen, H. M., Pintado, O. I., et al. 2006, A&A, 459, 871
   
• Perry, C. L., & Landolt, A. U. 1986, AJ, 92, 844
   
• Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49
   
• Preston, G. W. 1974, ARA&A, 12, 257
   
• Renson, P., Gerbaldi, M., & Catalano, F. A. 1991, A&AS, 89, 429
   
• Rachkovskaya, T. M., Lyubimkov, L. S., & Rostopchin, S. I. 2006, Astron. Rep., 50, 123
   
• Ramírez, I., & Meléndez, J. 2005, ApJ, 626, 446
   
• Ryabchikova, T., Landstreet, J. D., Gelbmann, M. J., et al. 1997, A&A, 327, 1137
   
• Ryabchikova, T., Piskunov, N., Savanov, I., Kupka, F., & Malanushenko, V. 1999a, A&A, 343, 229
   
• Ryabchikova, T., Malanushenko, V. P., & Adelman, S. J. 1999b, A&A, 351, 963
   
• Ryabchikova, T., Savanov, I. S., Hatzes, A. P., Weiss, W. W., & Handler, G. 2000, A&A, 357, 981
   
• Ryabchikova, T., Leone, F., Kochukhov, O., & Bagnulo, S. 2004a, in The A-Star Puzzle, ed. J. Zverko, W. W. Weiss, J. Ziznovský, & S. J. Adelman, IAU Symp., 224, 580
   
• Ryabchikova, T., Nesvacil, N., Weiss, W. W., Kochukhov, O., & Stütz, Ch. 2004b, A&A, 423, 705
   
• Ryabchikova, T., Leone, F., & Kochukhov, O. 2005, A&A, 438, 973
   
• Ryabchikova, T., Ryabtsev, A., Kochukhov, O., & Bagnulo, S. 2006, A&A, 456, 329
   
• Shallis, M. J., & Blackwell, D. E. 1979, A&A, 79, 48
   
• Shallis, M. J., Booth, A. J., Baruch, J. E. F., & Selby, M. J. 1985, MNRAS, 213, 307
   
• Shulyak, D., Kochukhov, O., & Khan, S. 2008, A&A, 487, 689
   
• Smalley, B. 1993, MNRAS, 265, 1035
   
• Smalley, B., & Dworetsky, M. M. 1993, A&A, 271, 515
   
• Stepien, K. 1994, in Chemically peculiar and magnetic stars, ed. J. Zverko, & J. Ziznovský (Slovak Republic: Tatranska Lomnica), 8
   
• Stepien, K., & Dominiczak, R. 1989, A&A, 219, 197
   
• Takeda, Y. I. 1984, PASJ, 36, 149
   
• van Leeuwen, F. 2007, A&A, 474, 653
   
• van Rensbergen, W., Hensberge, H., & Adelman, S. J. 1984, A&A, 136, 31
   
• van't Veer-Menneret, C., & Mégessier, C. 1996, A&A, 309, 879
   
• Wade, G. A. 1997, A&A, 325, 1063
   
• Wade, G. A., Debernardi, Y., Mathys, G., et al. 2000, A&A, 361, 991
   
• Wade, G. A., Smith, M. A., Bohlender, D. A., et al. 2006, A&A, 458, 569
   
• Wolff, S. C. 1967, ApJS, 15, 21
   
• Zavala, R. T., Adelman, S. J., Hummel, C. A., et al. 2007, ApJ, 655, 1046
   
• Zboril, M., North, P., Glagolevskij, Yu. V., & Betrix, F. 1997, A&A, 324, 949
   
• Zoechling, J., & Muthsam, H. 1987, A&A, 176, 75
  

 

  
7 Online Material

 

 

Table 4: The CP1 (Am) stars.

HD	HIP	mv	$\pi$	$\overline{T}_{\rm phot}$	Phot.	$\overline{T}_{\rm eff}$	#	$\Delta T$
		[mag]	[mas]	[K]		[K]		[K]
27 628	20 400	5.71	22.53(55)	7260(50)	+/+/+	7210(90)	2	-50
27 749	20 484	5.63	20.04(48)	7410(30)	+/+/+	7340(180)	5	-70
27 962	20 648	4.29	21.96(51)	9040(110)	+/+/+	9070(210)	3	30
28 226	20 842	5.71	21.25(41)	7470(100)	+/+/+	7450	1	-20
28 355	20 901	5.02	20.47(28)	7880(70)	+/+/+	7950	1	70
28 527	21 029	4.78	23.15(31)	8110(70)	+/+/+	8000(100)	2	-110
28 546	21 039	5.48	22.27(49)	7640(20)	+/+/+	7640(140)	2	0
29 140	21 402	4.24	20.86(94)	8010(170)	+/+/+	7940	1	-70
29 499	21 670	5.38	20.33(36)	7650(10)	+/+/+	7690	1	40
30 210	22 157	5.35	13.85(38)	8040(120)	+/+/+	8100	1	60
33 204	24 019	5.93	19.04(134)	7490(110)	+/+/+	7650	1	160
33 254	23 983	5.42	18.27(36)	7740(40)	+/+/+	7760(190)	2	20
58 142	36 145	4.60	11.92(24)	9530(170)	+/+/+	9500	1	-30
67 523	39 757	2.82	51.34(15)	6820(70)	+/+/+	6700	1	-120
78 362	45 075	4.65	25.82(54)	7170(100)	+/+/+	7220(230)	2	50
94 334	53 295	4.67	13.22(50)	9950(80)	+/+/+	10 030	1	80
95 418	53 910	2.36	40.89(16)	9560(170)	+/+/+	9600(10)	2	40
95 608	53 954	4.42	25.67(17)	9040(70)	+/+/+	8950(430)	2	-90
97 633	54 879	3.32	19.77(17)	9400(240)	+/+/+	9250(180)	2	-150
141 795	77 622	3.70	46.28(19)	8360(20)	+/+/+	8420	1	60
162 132	87 045	6.47	8.56(40)	8770(50)	+/+/+	8800	1	30
173 648	91 971	4.33	20.88(17)	8040(30)	+/+/+	8160	1	120
182 564	95 081	4.58	14.24(12)	9210(140)	-/+/+	9130	1	-80
188 728	98 103	5.27	14.85(24)	9450(100)	+/+/+	9530	1	80
189 849	98 543	4.66	13.79(20)	8000(120)	+/+/+	7820(110)	3	-180
196 724	101 867	4.80	15.56(52)	10 130(280)	+/+/+	10 200	1	70
206 088	106 985	3.67	20.76(72)	7330(60)	+/+/+	7640	1	310
209 625	108 991	5.28	14.68(30)	7780(70)	+/+/+	7820(100)	3	40
213 320	111 123	4.81	11.27(125)	10 180(50)	+/+/+	10 130	1	-50
214 994	112 051	4.80	10.93(67)	9580(120)	+/+/+	9590(20)	3	10

   

Table 5: The CP2 stars.

HD	HIP	Pec. type	mv	$\pi$	E(B-V)	$\overline{T}_{\rm phot}$	Phot.	$\overline{T}_{\rm eff}$	#	$\Delta T$	BC
			[mag]	[mas]	[mag]	[K]		[K]		[K]	[mag]
8441	6560	Sr	6.69	4.88(59)	0	9140(190)	+/+/+	9200	1	60
9484	7222	Si	6.58	8.54(43)	0(1)	9980(160)	+/+/+	10 200	1	220
12 098		a	7.97		0	7670	+/-/-	7800	1	130
12 767	9677	Si	4.68	8.79(26)	0	12 860(160)	+/+/+	13 000(340)	3	140
15 089	11 569	Sr	4.47	24.55(81)	0	8390(200)	+/+/+	8280(40)	2	-110	0.07
18 610	13 534	Cr Eu Sr	8.15	4.68(54)	0	7680(340)	+/+/-	8100	1	420
19 832	14 893	Si	5.78	6.47(76)	0.02(1)	12 440(120)	+/+/+	12 430(360)	3	-10	-0.70(4)
23 387		Cr Si	7.18		0.05	8420(230)	+/+/+	8250	1	-170
24 155	18 033	Si	6.30	8.13(35)	0.09(1)	13 450(100)	+/+/+	13 780(70)	2	330
24 712	18 339	Sr Eu Cr	5.99	20.32(39)	0	7300(220)	+/+/+	7290(60)	2	-10
25 823	19 171	Sr Si	5.19	7.76(36)	0.01(1)	12 890(90)	+/+/+	12 720(200)	3	-170	-0.67(8)
26 571	19 672	Si	6.13	3.76(44)	0.34(1)	12 920(200)	+/+/+	11 750	1	-1170
27 309	20 186	Si Cr	5.37	9.99(29)	0	12 000(200)	+/+/+	11 930(250)	2	-70	-0.51(7)
32 549	23 607	Si Cr	4.67	8.95(24)	0(1)	9850(150)	+/+/+	9730	1	-120	-0.19
34 452	24 799	Si	5.38	7.91(36)	0	13 980(340)	+/+/+	13 830(810)	2	-150	-0.80
37 470	26 530	Si	8.22	3.41(88)	0.15(2)	11 660(170)	+/+/+	13 000	1	1340	-0.90
37 808	26 728	Si	6.45	4.11(40)	0.01(2)	13 140(190)	+/+/+	12 890(200)	3	-250
40 312	28 380	Si	2.64	19.71(16)	0	10 180(40)	+/+/+	10 180(200)	4	0	-0.23(3)
43 819	30 019	Si	6.27	3.85(79)	0.01(1)	11 240(160)	+/+/+	10 930(290)	4	-310	-0.34
60 435	36 537	Sr Eu	8.90	4.40(76)	0.06	8230(140)	+/+/-	8100	1	-130
62 140	37 934	Sr Eu	6.47	10.35(45)	0.02	7920(180)	+/+/+	7800(140)	2	-120
65 339	39 261	Eu Cr	6.03	10.14(52)	0	8250(160)	+/+/+	8170(150)	3	-80	-0.05(5)
71 866	41 782	Eu Sr Si	6.73	7.52(46)	0	9240(470)	+/+/+	9000	1	-240
75 445	43 257	Sr Eu	7.14	9.23(45)	0	7560(30)	+/+/-	7700	1	140
81 009	45 999	Cr Sr Si	6.52	6.92(60)	0	7970(120)	+/+/+	8250(350)	2	280
90 569	51 213	Sr Cr Si	6.01	7.73(30)	0	9850(150)	+/+/+	10 500	1	650
92 664	52 221	Si	5.50	6.23(24)	0(1)	13 960(70)	+/+/+	14 300(90)	3	340	-1.03(8)
94 427	53 290	Sr	7.37	6.96(62)	0.03	7300(70)	+/+/-	7500	1	200
108 662	60 904	Sr Cr Eu	5.26	13.72(25)	0.01(1)	10 050(200)	+/+/+	10 330(570)	4	280	-0.12
108 945	61 071	Sr	5.45	12.09(27)	0	8870(130)	+/+/+	8700(240)	6	-170	0.03(3)
110 066	61 748	Sr Cr Eu	6.41	7.43(39)	0	9180(350)	+/+/+	9030(60)	3	-150
111 133	62 376	Sr Cr Eu	6.32	3.76(40)	0	9670(280)	+/+/+	9850(220)	2	180
112 185	62 956	Cr Eu Mn	1.75	39.50(20)	0	9190(200)	+/+/+	9350(290)	4	160	-0.06(11)
112 413	63 125	Eu Si Cr	2.84	28.42(89)	0	11 480(200)	+/+/+	11 210(360)	5	-270	-0.34(2)
115 708	64 936	Sr Eu	7.79	8.64(79)	0.01	7660(220)	+/+/+	7760(350)	2	100
116 114	65 203	Sr Cr Eu	7.03	7.71(55)	0.07	7800(60)	+/+/-	7850(210)	2	50
118 022	66 200	Cr Eu Sr	4.92	17.65(20)	0.02(2)	9420(50)	+/+/+	9460(410)	6	40	0.04(3)
120 198	67 231	Eu Cr	5.67	11.23(23)	0	10 090(290)	+/+/+	10 080(330)	3	-10	-0.14(4)
124 224	69 389	Si	4.99	12.63(21)	0(1)	12 120(110)	+/+/+	12 540(300)	6	420	-0.72(8)
125 248	69 929	Eu Cr	5.86	9.81(68)	0.02(2)	9850(230)	+/+/+	9650(260)	4	-200	-0.07(3)
126 515	70 553	Cr Sr	7.09	9.39(62)	0.01(1)	9640(160)	+/+/+	9500	1	-140
128 898	71 908	Sr Eu	3.17	60.36(14)	0	7820(130)	+/+/+	7660(340)	2	-160	0.11
133 029	73 454	Si Cr Sr	6.36	5.89(28)	0	10 750(170)	+/+/+	10 880(300)	4	130	-0.33(6)
133 792	74 181	Sr Cr	6.25	5.50(43)	0	9030(260)	+/+/-	9300(140)	2	270
133 880	74 066	Si	5.78	9.03(33)	0	11 930(210)	+/+/+	10 700(60)	2	-1230
134 305	74 109	Sr Eu Cr	7.24	6.64(67)	0.02	8070(170)	+/+/+	8200	1	130
137 909	75 695	Sr Eu Cr	3.67	29.17(76)	0	7710(260)	+/+/+	8340(360)	4	630
137 949	75 848	Sr Eu Cr	6.66	11.27(67)	0	7420(410)	+/+/+	7530(40)	2	110
140 160	76 866	Sr	5.32	14.83(41)	0	9120(110)	+/+/+	9120(60)	3	0	-0.15
144 897	79 197	Eu Cr	8.60	5.62(103)	0.31(2)	11 140(140)	-/+/+	11 250	1	110
148 112	80 463	Cr Eu	4.58	13.04(64)	0.03	9520(100)	+/+/+	9220(160)	2	-300	-0.04
149 822	81 337	Si Cr	6.38	7.92(38)	0	10 430(250)	+/+/+	10 750	1	320
151 525	82 216	Eu Cr	5.21	8.29(27)	0	9360(130)	+/+/+	9240(130)	2	-120
152 107	82 321	Sr Cr Eu	4.80	18.10(34)	0	8760(30)	+/+/+	8730(230)	3	-30	0.07(6)
153 882	83 308	Cr Eu	6.28	6.15(44)	0.03(3)	9250(190)	+/+/+	9450(580)	3	200
155 102	83 816	Si	6.35	7.38(44)	0	9140(190)	+/-/+	9000	1	-140
157 751	85 372	Si Cr	7.65	6.20(74)	0	10 260(790)	+/+/-	11 300	1	1040
166 473		Sr Eu Sr	7.94		0.04	7500(470)	+/+/-	7850(210)	2	350
168 733	90 074	Ti Sr	5.33	5.84(33)	0.03(1)	12 730(210)	+/+/-	13 320	1	590	-0.92
170 973	90 858	Si Cr Sr	6.42	3.29(40)	0.05(2)	10 830(230)	+/+/+	10 740(20)	2	-90
171 247	90 971	Si	6.41	1.77(41)	0.08(1)	11 630(340)	+/+/+	12 170	1	540
171 782	91 224	Si Cr Eu	7.84	2.00(84)	0.12(2)	11 310(90)	+/-/+	11 500	1	190
173 650	92 036	Si Sr Cr	6.50	4.63(44)	0.09(3)	10 140(160)	+/+/+	10 000(1410)	2	-140
175 744	92 934	Si	6.63	3.22(53)	0.08(1)	12 470(320)	+/+/+	12 620(140)	2	150
176 232	93 179	Sr	5.90	12.76(29)	0.02	7790(190)	+/+/+	7730(140)	4	-60	0.01
183 806	96 178	Cr Eu Sr	5.58	8.22(40)	0.01(1)	9560(30)	+/+/-	9940(190)	2	380
188 041	97 871	Sr Cr Eu	5.63	12.47(36)	0	8090(60)	+/+/+	8580(550)	4	490
191 742	99 340	Sr Cr	8.13	3.28(65)	0.06	8290(80)	+/+/+	8300	1	10
192 678	99 672	Cr	7.36	5.05(36)	0	9420(260)	+/+/+	9000	1	-420	0.09
196 502	101 260	Sr Cr Eu	5.19	8.25(47)	0	8770(80)	+/+/+	8900(360)	3	130	0
201 601	104 521	Sr Eu	4.69	27.55(62)	0	7740(110)	+/+/+	7780(130)	7	40	-0.13
203 932		Sr Eu	8.81		0.02	7520(70)	+/+/-	7450	1	-70
204 411	105 898	Cr	5.30	7.93(24)	0.04	8860(300)	+/+/+	8510(170)	4	-350	-0.03
212 385	110 624	Sr Eu Cr	6.84	7.92(63)	0	8800(530)	+/+/-	9200	1	400
215 441	112 247	Si	8.85	0.65(78)	0.21(2)	14 780(390)	+/+/+	14 000	1	-780
217 522	113 711	Sr Eu Cr	7.52	11.36(79)	0.08	6940(10)	+/+/-	6750	1	-190
220 825	115 738	Cr Sr Eu	4.93	21.25(29)	0	9490(310)	+/+/+	9200(80)	2	-290	-0.10(4)
221 006	115 908	Si	5.65	8.44(29)	0	13 330(130)	+/+/-	13 260(20)	2	-70
223 640	117 629	Si Sr Cr	5.17	10.23(31)	0	12 210(60)	+/+/+	12 240(210)	3	30

^a RoAp according to Ryabchikova et al. (2004b).

 

 

Table 6: The CP3a/b stars.

HD	HIP	Pec. type	mv	$\pi$	$\overline{T}_{\rm phot}$	Phot.	$\overline{T}_{\rm eff}$	#	$\Delta T$	BC
			[mag]	[mas]	[K]		[K]		[K]	[mag]
358	677	Mn Hg	2.08	33.63(35)	13 350(100)	+/+/+	13 830(40)	2	480	-0.55(15)
4335	3604	Hg Mn	6.01	7.63(40)	11 690(100)	+/+/+	12 000	1	310
27 295	20 171	Mn	5.48	12.08(36)	11 790(120)	+/+/+	11 850(210)	2	60
27 376	20 042	Mn Hg	3.54	18.34(15)	12 480(160)	+/+/+	12 300	1	-180
33 904	24 305	Hg Mn	3.29	17.54(55)	12 530(90)	+/+/+	12 160(210)	3	-370	-0.64
35 497	25 428	Si Cr Mn	1.65	24.37(33)	13 320(170)	+/+/+	13 320(100)	2	0
35 548	25 365	Hg Mn	6.54	4.64(58)	11 060(80)	+/+/+	11 500	1	440
58 661	36 348	Hg Mn	5.71	6.71(70)	13 010(50)	-/+/+	13 200	1	190
77 350	44 405	Sr Cr Hg	5.46	8.31(35)	10 490(70)	+/+/+	10 250	1	-240
78 316	44 798	Mn Hg	5.23	6.15(26)	13 100(50)	+/+/+	13 040(230)	3	-60	-0.82
89 822	50 933	Hg Si Sr	4.93	9.61(20)	10 600(40)	+/+/+	10 950(70)	2	350
106 625	59 803	Hg Mn	2.58	21.23(20)	11 940(70)	+/+/+	12 130	1	190
143 807	78 493	Mn Hg	4.97	10.46(24)	11 040(70)	+/+/+	10 930(460)	2	-110
144 206	78 592	Mn Hg	4.71	8.76(18)	11 940(70)	+/+/+	11 740(300)	2	-200	-0.68
145 389	79 101	Mn Hg	4.22	15.99(45)	11 600(70)	+/+/+	11 690(160)	2	90
147 550	80 227	Si?	6.22	7.62(64)	10 430(110)	+/+/+	10 200	1	-230
159 082	85 826	Hg Mn	6.45	7.39(40)	11 200(150)	+/-/+	11 300	1	100
190 229	98 754	Hg Mn	5.65	5.11(32)	12 910(100)	+/+/+	13 190(440)	2	280
4382	3721	Mn P Hg	5.40	4.24(22)	12 820(40)	+/+/+	13 400	1	580
19 400	14 131	He-wk.	5.50	6.34(20)	13 530(100)	+/+/+	13 000	1	-530
23 408	17 573	He-wk. Mn	3.88	8.52(28)	12 700(90)	+/+/+	11 900(990)	2	-800
49 606	32 753	Mn Hg Si/He-wk.	5.85	3.77(42)	13 700(130)	+/+/+	13 500	1	-200
51 688	33 650	Si Mn/He-wk.	6.39	2.72(48)	13 380(80)	+/+/+	12 500	1	-880
144 661	79 031	Mn Hg/He-wk.	6.31	8.38(41)	14 930(90)	+/+/+	15 000	1	-70	-1.10
144 667	79 081	He-wk.	6.64	5.85(56)	13 350(160)	+/+/+	12 900(70)	2	-450	-0.91
144 844	79 098	Mn P Ga/He-wk.	5.84	7.35(31)	12 600(310)	+/+/+	12 430(460)	2	-170	-0.77(8)
202 671	105 143	He-wk. Mn	5.38	6.13(31)	13 430(260)	+/+/+	13 150(70)	2	-280
224 926	145	He-wk. Mn	5.10	7.18(30)	13 670(40)	+/+/+	14 000	1	330

 

 

Table 7: The CP4a/ab/b stars.

HD/DM	HIP	Pec. type	mv	$\pi$	E(B-V)	$\overline{T}_{\rm phot}$	Phot.	$\overline{T}_{\rm eff}$	#	$\Delta T$	BC
			[mag]	[mas]	[mag]	[K]		[K]		[K]	[mag]
21 699	16 470	He-wk. Si	5.48	5.38(31)	0.06(1)	15 050(100)	+/+/+	16 000	1	950	-1.13
22 470	16 803	Si/He-wk.	5.23	6.69(51)	0.01(2)	13 630(200)	+/+/+	13 760(250)	3	130
22 920	17 167	Si/He-wk.	5.52	6.57(48)	0.01(1)	14 440(60)	+/+/+	14 100(260)	3	-340	-0.98
28 843	21 192	He-wk.	5.75	6.86(35)	0.02(2)	14 510(240)	+/+/+	14 830(150)	3	320	-1.18
37 058		He-wk. Sr	7.33		0.05(2)	18 850(200)	+/+/+	19 610	1	760
49 333	32 504	He-wk. Si	6.06	4.13(51)	0.01(1)	15 830(60)	+/+/+	15 810(120)	3	-20
62 712	37 666	He-wk. Si	6.41	5.13(39)	0.01(2)	13 430(220)	+/+/+	13 530(240)	3	100
74 196	42 535	He-wk.	5.55	6.78(26)	0.01(1)	13 530(40)	+/+/+	13 950(350)	2	420
79 158	45 290	He-wk.	5.29	5.60(31)	0.01(1)	13 080(160)	+/+/+	13 250(70)	2	170	-0.85(14)
90 264	50 847	He-wk.	4.96	8.13(18)	0.02(2)	14 230(280)	+/+/+	14 600	1	370
109 026	61 199	He-wk.	3.83	10.04(13)	0.01(1)	15 350(140)	+/+/+	15 500	1	150
137 509	76 011	Si Cr Fe/He-wk.	6.90	5.12(38)	0.04(1)	14 030(680)	+/+/+	12 680(110)	2	-1350
142 301	77 909	He-wk. Si	5.86	6.31(44)	0.11(2)	16 100(200)	+/+/+	15 860(150)	3	-240	-1.36(5)
142 990	78 246	He-wk.	5.41	5.86(24)	0.10(2)	17 040(120)	+/+/+	17 700(1130)	2	660
143 699	78 655	He-wk.	4.88	8.17(30)	0.02(1)	15 100(250)	+/+/+	15 490(410)	2	390	-1.32
144 334	78 877	He-wk.	5.90	6.21(66)	0.09(1)	15 350(70)	+/+/+	14 760(380)	3	-590	-1.26(8)
146 001	79 622	He-wk.	6.04	6.73(40)	0.17(1)	13 510(90)	+/+/+	13 790(300)	2	280
162 374	87 460	He-wk.	5.87	3.85(46)	0.08(1)	16 210(260)	+/+/+	15 900(280)	2	-310	-1.59
175 362	92 989	He-wk. Si	5.36	7.57(27)	0.04(2)	16 890(330)	+/+/+	16 790(620)	3	-100	-1.43
217 833	113 797	He-wk.	6.50	3.84(57)	0.08(3)	15 150(300)	+/+/+	15 450	1	300
5737	4577	He-wk.	4.30	4.19(18)	0.01(1)	13 790(150)	+/+/+	13 970(400)	3	180	-0.83
125 823	70 300	He-wk.	4.40	7.14(17)	0.02(1)	18 240(420)	+/+/+	18 940(500)	3	700	-1.74(5)
-27 3748	34 781	He-rich	9.24	-0.17(112)	0.07(2)	21 880(280)	-/+/+	23 000	1	1120
-46 4639		He-rich	10.02		0.36	22 850	-/+/-	22 500	1	-350
-62 2124		He-rich	11.03		0.33(5)	25 940	+/-/+	26 000	1	60
36 485	25 930	He-rich	6.81	4.72(58)	0.05(1)	17 990(310)	+/+/+	18 000	1	10
37 017	26 233	He-rich	6.55	2.63(73)	0.07(2)	18 970(350)	+/+/+	18 950(640)	2	-20
37 479		He-rich	6.67	4.84(71)	0.07(1)	21 590(310)	+/+/+	22 500(710)	2	910
37 776	26 742	He-rich	6.99	3.04(55)	0.09(2)	21 870(570)	+/+/+	22 270(640)	3	400
58 260	35 830	He-rich	6.73	2.44(32)	0.09(1)	19 030(140)	+/+/+	19 000(0)	3	-30
60 344	36 707	He-rich	7.73	0.25(61)	0.06(2)	21 010(260)	+/+/+	22 500(2120)	2	1490
64 740	38 500	He-rich	4.61	4.29(15)	0.02(1)	22 740(200)	+/+/+	22 270(1100)	3	-470
66 522	39 246	He-rich	7.19	2.27(36)	0.27(1)	19 210(90)	+/+/+	18 000	1	-1210
92 938	52 370	He-rich	4.79	7.19(20)	0.03(1)	14 940(130)	+/+/+	15 000	1	60
96 446	54 266	He-rich	6.69	2.13(45)	0.09(2)	21 620(240)	+/+/+	20 950(640)	2	-670
108 483	60 823	a	3.90	7.92(18)	0.02	18 710(240)	+/+/+	19 200	1	490
133 518	73 966	He-rich	6.38	2.24(44)	0.11(2)	18 700(260)	+/+/+	18 250(1060)	2	-450
260 858		He-rich	9.14		0.31	18 200	-/+/-	18 000	1	-200
264 111	32 581	He-rich	9.64	1.26(37)	0.28(1)	22 330(260)	+/+/+	21 700(990)	2	-630

^a He-rich according to Zboril et al. (1997).

   

Table 8: References of the compiled effective temperatures for CP stars. The different groups of peculiar stars discussed in the text are separated by horizontal lines.

HD/DM	$\overline{T}_{\rm eff}$ [K]	Ref.	HD/DM	$\overline{T}_{\rm eff}$ [K]	Ref.
27 628	7210(90)	(1) a; (2) d+	171 247	12 170	(21) d+
27 749	7340(180)	(1) a; (2),(5) d+; (3),(4) d	171 782	11 500	(26) c+
27 962	9070(210)	(2) d+; (6) d; (7) bd+	173 650	10 000(1410)	(18) b; (25) d+
28 226	7450	(2) d+	175 744	12 620(140)	(23),(24) a
28 355	7950	(2) d+	176 232	7730(140)	(18) b; (28) bd+; (38) a; (51) b+
28 527	8000(100)	(1) a; (2) d+	183 806	9940(190)	(22) b+; (52) bd
28 546	7640(140)	(1) a; (2) d+	188 041	8580(550)	(3) d; (18) b; (22) b+
29 140	7940	(2) d+	191 742	8300	(53) c+
29 499	7690	(2) d+	192 678	9000	(27) e
30 210	8100	(2) d+	196 502	8900(360)	(25) d+; (26) c+; (28) bd+
33 204	7650	(2) d+	201 601	7780(130)	(3) d; (18) b; (20),(28) bd+
33 254	7760(190)	(1) a; (2) d+			(22) b+; (37) a; (50) d+
58 142	9500	(7) bd+	203 932	7450	(54) d+
67 523	6700	(8) a	204 411	8510(170)	(20),(28),(55) bd+; (38) a
78 362	7220(230)	(2),(5) d+	212 385	9200	(22) b+
94 334	10 030	(9) d+	215 441	14 000	(26) c+
95 418	9600(10)	(10) b; (11) bd+	217 522	6750	(50) d+
95 608	8950(430)	(2) d+; (12) bd	220 825	9200(80)	(32),(38) a
97 633	9250(180)	(10) b; (13) a	221 006	13 260(20)	(23),(24) a
141 795	8420	(14) bd	223 640	12 240(210)	(18) b; (23),(24) a
162 132	8800	(15) d+
173 648	8160	(12) bd	358	13 830(40)	(56) cd+; (70) bd+
182 564	9130	(11) bd+	4335	12 000	(3) d
188 728	9530	(9) d+	27 295	11 850(210)	(3) d; (28) bd
189 849	7820(110)	(2) d+; (16) d; (17) bd+	27 376	12 300	(42) a
196 724	10 200	(14) bd	33 904	12 160(210)	(3) d; (28) bd; (32) a
206 088	7640	(18) b	35 497	13 320(100)	(10) b; (28) bd
209 625	7820(100)	(2) d+; (3) d; (17) bd+	35 548	11 500	(3) d
213 320	10 130	(14) bd	58 661	13 200	(3) d
214 994	9590(20)	(3) d; (10) b; (19) bd	77 350	10 250	(28) bd
			78 316	13 040(230)	(23) a; (28) bd; (58) c+
8441	9200	(20) bd+	89 822	10 950(70)	(25) d+; (59) bd+
9484	10 200	(21) d+	106 625	12 130	(28) bd
12 098	7800	(22) b+	143 807	10 930(460)	(3) d; (60) bd
12 767	13 000(340)	(21) d+; (23),(24) a	144 206	11 740(300)	(28) bd; (61) b+
15 089	8280(40)	(25) d+; (26) c+	145 389	11 690(160)	(3) d; (28) bd
18 610	8100	(22) b+	147 550	10 200	(28) bd
19 832	12 430(360)	(26) c+; (27) e; (28) bd+	159 082	11 300	(15) d+
23 387	8250	(26) c+	190 229	13 190(440)	(3) d; (28) bd
24 155	13 780(70)	(23),(24) a
24 712	7290(60)	(29) d; (30) d+	4382	13 400	(3) d
25 823	12 720(200)	(26) c+; (27) e; (31) d	19 400	13 000	(62) e
26 571	11 750	(26) c+	23 408	11 900(990)	(62) e, (63) bd
27 309	11 930(250)	(26) c+; (27) e	49 606	13 500	(62) e
32 549	9730	(32) a	51 688	12 500	(62) e
34 452	13 830(810)	(26) c+; (27) e	144 661	15 000	(62) e
37 470	13 000	(26) c+	144 667	12 900(70)	(64),(65) d+
37 808	12 890(200)	(23),(24) a; (33) d+	144 844	12 430(460)	(26) c+; (62) e
40 312	10 180(200)	(26) c+; (27) e; (32) a; (34) bd+	202 671	13 150(70)	(62) e; (66) d+
43 819	10 930(290)	(20) bd+; (23),(24) a; (26) c+	224 926	14 000	(42) a
60 435	8100	(22) b+
62 140	7800(140)	(22) b+; (25) d+	21 699	16 000	(67) d+
65 339	8170(150)	(25) d+; (26) c+; (27) e	22 470	13 760(250)	(23),(42) a; (62) e
71 866	9000	(25) d+	22 920	14 100(260)	(21) d+; (42) a; (62) e
75 445	7700	(22) b+	28 843	14 830(150)	(23),(42) a; (62) e
81 009	8250(350)	(25) d+; (35) b	37 058	19 610	(23) a
90 569	10 500	(25) d+	49 333	15 810(120)	(23),(42) a; (62) e
92 664	14 300(90)	(23),(24) a; (26) c+	62 712	13 530(240)	(23),(24),(42) a
94 427	7500	(25) d+	74 196	13 950(350)	(42) a; (62) e
108 662	10 330(570)	(18) b; (25) d+; (26) c+; (28) bd+	79 158	13 250(70)	(27) e; (68) cd+
108 945	8700(240)	(18) b; (25) d+; (26) c+; (27) e	90 264	14 600	(42) a
		(28) bd+; (36) a c+	109 026	15 500	(42) a
110 066	9030(60)	(20) bd+; (22) b+; (25) d+	137 509	12 680(110)	(42) a; (69) d+
111 133	9850(220)	(18) b; (25) d+	142 301	15 860(150)	(23),(42) a; (62) e
112 185	9350(290)	(25) d+; (28) bd+; (32),(37) a	142 990	17 700(1130)	(42) a; (62) e
112 413	11 210(360)	(26) c+; (37),(38) a; (39) b+; (40) bd+	143 699	15 490(410)	(23),(42) a
115 708	7760(350)	(25) d+; (29) d	144 334	14 760(380)	(23),(42) a; (62) e
116 114	7850(210)	(22) b+; (25) d+	146 001	13 790(300)	(23),(42) a
118 022	9460(410)	(18) b; (25) d+; (26) c+; (28) bd+	162 374	15 900(280)	(42) a; (62) e
		(32) a; (41) ac+	175 362	16 790(620)	(23),(24) a; (62) e
120 198	10 080(330)	(26) c+; (27) e; (28) bd+	217 833	15 450	(67) d+
124 224	12 540(300)	(23),(24),(32),(42) a; (26) c+; (28) bd+
125 248	9650(260)	(25) d+; (26) c+; (27) e; (41) a c+	5737	13 970(400)	(42) a; (66) d+; (70) b+
126 515	9500	(25) d+	125 823	18 940(500)	(23),(42) a; (62) e
128 898	7660(340)	(43) d+; (44) e
133 029	10 880(300)	(26) c+; (27) e; (28),(45) bd+	-27 3748	23 000	(71) d+
133 792	9300(140)	(46),(47) d+	-46 4639	22 500	(71) d+
133 880	10 700(60)	(23),(24) a	-62 2124	26 000	(71) d+
134 305	8200	(25) d+	36 485	18 000	(71) d+
137 909	8340(360)	(18) b; (22) b+; (25) d+; (28) bd+	37 017	18 950(640)	(42) a; (71) d+
137 949	7530(40)	(22) b+; (25) d+	37 479	22 500(710)	(62) e; (71) d+
140 160	9120(60)	(18) b; (28) bd+; (38) a	37 776	22 270(640)	(42) a; (62) e; (71) d+
144 897	11 250	(48) d+	58 260	19 000(0)	(42) a; (62) e; (71) d+
148 112	9220(160)	(18) b; (38) a	60 344	22 500(2120)	(62) e; (71) d+
149 822	10 750	(28) bd+	64 740	22 270(1100)	(42) a; (62) e; (71) d+
151 525	9240(130)	(18) b; (38) a	66 522	18 000	(71) d+
152 107	8730(230)	(25) d+; (26) c+; (41) ac+	92 938	15 000	(71) d+
153 882	9450(580)	(18) b; (25) d+; (28) bd+	96 446	20 950(640)	(42) a; (71) d+
155 102	9000	(15) d+	108 483	19 200	(71) d+
157 751	11 300	(49) d+	133 518	18 250(1060)	(42) a; (71) d+
166 473	7850(210)	(22) b+; (50) d+	260 858	18 000	(71) d+
168 733	13 320	(23) a	264 111	21 700(990)	(62) e; (71) d+
170 973	10 740(20)	(10) b; (28) bd+

(1) Smalley (1993); (2) Smalley & Dworetsky (1993); (3) Allen (1977); (4) Cayrel et al. (1991); (5) van't Veer-Menneret & Mégessier (1996); (6) Liubimkov & Savanov (1983); (7) Adelman (1994b); (8) Ramírez & Meléndez (2005); (9) Caliskan & Adelman (1997); (10) Morossi & Malagnini (1985); (11) Adelman 1996; (12) Adelman et al. (1999); (13) Glushneva (1985); (14) Adelman & Albayrak (1998); (15) Catanzaro (2006); (16) Takeda (1984); (17) Adelman et al. (1997); (18) Wolff (1967); (19) Adelman (1988); (20) Adelman et al. (1995); (21) Leone & Manfre (1996); (22) Ryabchikova et al. (2004b); (23) Lanz (1985); (24) Mégessier (1988); (25) Babel (1994); (26) Lipski & Stepien (2008); (27) Stepien & Dominiczak (1989); (28) Adelman & Rayle (2000); (29) Wade (1997); (30) Ryabchikova et al. (1997); (31) Bolcal et al. (1987); (32) Glushneva (1987); (33) Leone et al. (1993); (34) van Rensbergen et al. (1984); (35) Wade et al. (2000); (36) Monier & Mégessier (1992); (37) Shallis & Blackwell (1979); (38) Shallis et al. (1985); (39) Ryabchikova et al. (1999a); (40) Kochukhov et al. (2002); (41) Monier (1992); (42) Hunger & Groote (1999); (43) Kupka et al. (1996); (44) Bruntt et al. (2008); (45) López-García & Adelman (1999); (46) Ryabchikova et al. (2004a); (47) Kochukhov et al. (2006); (48) Ryabchikova et al. (2006); (49) Hubrig & Nesvacil (2007); (50) Gelbmann (1998); (51) Ryabchikova et al. (2000); (52) Kearsley & Wegner (1978); (53) Kato & Sadakane (1999); (54) Gelbmann et al. (1997); (55) Ryabchikova et al. (2005); (56) Derman (1982); (57) Ryabchikova et al. (1999b); (58) Zoechling & Muthsam (1987); (59) Adelman (1994a); (60) Adelman (1989); (61) Zavala et al. (2007); (62) Cidale et al. (2007); (63) Mon et al. (1981); (64) Catanzaro et al. (2004); (65) Castelli & Hubrig (2007); (66) Leone & Manfre (1997); (67) Glagolevskij et al. (2006); (68) Wade et al. (2006); (69) Kochukhov (2006); (70) López-García et al. (2001); (71) Zboril et al. (1997)
a: Infrared Flux Method; b: fitting models to visual energy distribution; c: fitting models to total energy distribution; d: (Balmer) line profile fitting; e: methods as described in Sect. 2. The + sign indicates that models different to solar ones were used or the solar model is justified according to abundance analysis or tests as described in the respective reference. References using the same method are combined.