A&A 491, 597-615 (2008)
DOI: 10.1051/0004-6361:200810116
S. M. Leach1,2 - J.-F. Cardoso3,4 - C. Baccigalupi1,2 - R. B. Barreiro5 - M. Betoule3 - J. Bobin6 - A. Bonaldi7,8 - J. Delabrouille3 - G. de Zotti1,7 - C. Dickinson9 - H. K. Eriksen10,11 - J. González-Nuevo1 - F. K. Hansen10,11 - D. Herranz5 - M. Le Jeune3 - M. López-Caniego12 - E. Martínez-González5 - M. Massardi1 - J.-B. Melin13 - M.-A. Miville-Deschênes14 - G. Patanchon3 - S. Prunet15 - S. Ricciardi7,16 - E. Salerno17 - J. L. Sanz5 - J.-L. Starck6 - F. Stivoli1,2 - V. Stolyarov12 - R. Stompor3 - P. Vielva5
1 - SISSA - ISAS, Astrophysics Sector, via Beirut 4, 34014 Trieste, Italy
2 -
INFN, Sezione di Trieste, via Valerio 2, 34014 Trieste, Italy
3 -
CNRS & Université Paris 7, Laboratoire APC, 10 rue A. Domon et L. Duquet, 75205 Paris Cedex 13, France
4 -
Laboratoire de Traitement et Communication de l'Information (CNRS and Telecom ParisTech), 46, rue Barrault, 75634 Paris, France
5 -
Instituto de Física de Cantabria (CSIC-UC), Avda. de los Castros s/n, 39005 Santander, Spain
6 -
CEA - Saclay, SEDI/Service d'Astrophysique, 91191 Gif-Sur-Yvette, France
7 -
INAF - Osservatorio Astronomico di Padova, vicolo dell'Osservatorio 5, 35122 Padova, Italy
8 -
Dipartimento di Astronomia, vicolo dell'Osservatorio 5, 35122 Padova, Italy
9 -
Infrared Processing and Analysis Center, California Institute of Technology, M/S 220-6, 1200 E. California Blvd, Pasadena, 91125, USA
10 -
Institute of Theoretical Astrophysics, University of Oslo, PO Box 1029 Blindern, 0315 Oslo, Norway
11 -
Centre of Mathematics for Applications, University of Oslo, PO Box 1053 Blindern, 0316 Oslo, Norway
12 -
Astrophysics Group, Cavendish Laboratory, J J Thomson Avenue, Cambridge CB3 0HE, UK
13 -
DSM/Irfu/SPP, CEA/Saclay, 91191 Gif-sur-Yvette Cedex, France
14 -
Institut d'Astrophysique Spatiale, Bâtiment 121, 91405 Orsay, France
15 -
Institut d'Astrophysique de Paris, 98 bis Boulevard Arago, 75014 Paris, France
16 -
Space Sciences Laboratory, University of California Berkeley, Computational Cosmology Center, Lawrence Berkeley National Laboratory, CA 94720, USA
17 -
Istituto di Scienza e Technologie dell'Informazione, CNR, Area della ricerca di Pisa, via G. Moruzzi 1, 56124 Pisa, Italy
Received 2 May 2008 / Accepted 17 September 2008
Abstract
Context. The PLANCK satellite will map the full sky at nine frequencies from 30 to 857 GHz. The CMB intensity and polarization that are its prime targets are contaminated by foreground emission.
Aims. The goal of this paper is to compare proposed methods for separating CMB from foregrounds based on their different spectral and spatial characteristics, and to separate the foregrounds into ``components'' with different physical origins (Galactic synchrotron, free-free and dust emissions; extra-galactic and far-IR point sources; Sunyaev-Zeldovich effect, etc.).
Methods. A component separation challenge has been organised, based on a set of realistically complex simulations of sky emission. Several methods including those based on internal template subtraction, maximum entropy method, parametric method, spatial and harmonic cross correlation methods, and independent component analysis have been tested.
Results. Different methods proved to be effective in cleaning the CMB maps of foreground contamination, in reconstructing maps of diffuse Galactic emissions, and in detecting point sources and thermal Sunyaev-Zeldovich signals. The power spectrum of the residuals is, on the largest scales, four orders of magnitude lower than the input Galaxy power spectrum at the foreground minimum. The CMB power spectrum was accurately recovered up to the sixth acoustic peak. The point source detection limit reaches 100 mJy, and about 2300 clusters are detected via the thermal SZ effect on two thirds of the sky. We have found that no single method performs best for all scientific objectives.
Conclusions. We foresee that the final component separation pipeline for PLANCK will involve a combination of methods and iterations between processing steps targeted at different objectives such as diffuse component separation, spectral estimation, and compact source extraction.
Key words: cosmology: cosmic microwave background - methods: data analysis
PLANCK is a European Space Agency space mission whose main objective is to measure the cosmic microwave background (CMB) temperature and polarization anisotropies with high accuracy, high angular resolution and with unprecedented frequency coverage (The Planck Collaboration 2005). In anticipation of the launch, PLANCK is stimulating much research and development into data processing methods that are capable of addressing the ambitious science programme enabled by these multi-frequency observations. It is expected that PLANCK will break new ground in studies of the CMB, of the interstellar medium and Galactic emission mechanisms on scales down to a few arcminutes, as well as of the emission from many extragalactic objects.
The processing of such multi-frequency data depends on both the science goals, as well as on the signal to noise regime and on the overall level and complexity of foreground contamination. This observation is borne out by a brief historical perspective on CMB data processing.
An example of the low foreground level and complexity regime is
provided by the observations made by Boomerang at 145, 245 and 345 GHz (Masi et al. 2006), which targeted a region of sky with
low emission from a single dust foreground. Here the two higher
frequency channels acted as foreground monitors for the 145 GHz CMB
deep survey, and were used to estimate that the foreground
contamination at 145 GHz was at an rms level of less than 10 ![]() K on
angular scales of 11.5' (Table 10, Masi et al. 2006). The
145 GHz CMB maps were then used for the purpose of power spectrum
estimation in both temperature and polarization, after masking away a
handful of compact sources (Jones et al. 2006).
Masi et al. (2006) estimate that the cleanest 40% of the
sky have a level of dust brightness fluctuations similar to those of
the Boomerang observations, and that the cleanest 75% of the sky
have brightness fluctuations less than three times larger.
K on
angular scales of 11.5' (Table 10, Masi et al. 2006). The
145 GHz CMB maps were then used for the purpose of power spectrum
estimation in both temperature and polarization, after masking away a
handful of compact sources (Jones et al. 2006).
Masi et al. (2006) estimate that the cleanest 40% of the
sky have a level of dust brightness fluctuations similar to those of
the Boomerang observations, and that the cleanest 75% of the sky
have brightness fluctuations less than three times larger.
An example of the high foreground level and complexity regime is available with the all-sky observations of the WMAP mission in five frequency channels from 23 to 94 GHz (Hinshaw et al. 2008; Bennett et al. 2003a). In this frequency range, the emission from at least three Galactic components (synchrotron, free-free and dust), as well as contamination by unresolved point sources must be contended with. WMAP also gives a clear example of science goal dependent data processing: CMB maps for use in non-Gaussianity tests are obtained from a noise-weighted sum of frequency maps at differing angular resolution, for which the regions most contaminated by foregrounds are masked (Komatsu et al. 2003); The analysis leading to the WMAP cosmological parameter estimation involves foreground cleaning by template subtraction, masking of the most contaminated 15% of sky, and subtracting a model of the contribution of unresolved point sources from the CMB cross power spectra (Hinshaw et al. 2007,2003). For an improved understanding of galactic emission, the WMAP team have used a number of methods including template fits, internal linear combination (ILC), the maximum entropy method, and the direct pixel-by-pixel fitting of an emission model (Dunkley et al. 2008; Gold et al. 2008).
Component separation is a catch-all term encompassing any data processing that exploits correlations in observations made at separate frequencies, as well as external constraints and physical modeling, as a means of distinguishing between different physical sources of emission.
PLANCK has a number of different scientific objectives: the primary goal is a cosmological analysis of the CMB, but important secondary goals include obtaining a better understanding of the interstellar medium and Galactic emission, measurement of extragalactic sources of emission and the generation of a Sunyaev-Zeldovich (SZ) cluster catalogue. These planned objectives will lead to a set of data products which the PLANCK consortium is committed to delivering to the wider community some time after the completion of the survey. These data products include maps of the main diffuse emissions and catalogues of extragalactic sources, such as galaxies and clusters of galaxies.
In this context, it is worth remembering that PLANCK is designed
to recover the CMB signal at the level of a few microkelvin per
resolution element of 5' (and less than one microkelvin per square degree).
Numbers to keep in mind are the rms of CMB smoothed with a beam of
![]() ,
which is around 70
,
which is around 70 ![]() K, while the rms of white noise at the
same scale is around
K, while the rms of white noise at the
same scale is around ![]() K. This level of sensitivity sets the ultimate goals for data processing - and component separation in particular - if the full scientific potential of PLANCK is to be realised.
However, less stringent requirements may be acceptable for statistical
analyses such as power spectrum estimation, in particular on large
scales where cosmic variance dominates the error of total intensity observations.
K. This level of sensitivity sets the ultimate goals for data processing - and component separation in particular - if the full scientific potential of PLANCK is to be realised.
However, less stringent requirements may be acceptable for statistical
analyses such as power spectrum estimation, in particular on large
scales where cosmic variance dominates the error of total intensity observations.
PLANCK is designed to surpass previous CMB experiments in almost
every respect. Therefore, a complete and timely exploitation of the
data will require methods that improve upon foreground removal via
template subtraction and masking. The development and assessment of such methods is coordinated within the PLANCK ``Component Separation Working Group'' (WG2).
Another working group in the PLANCK collaboration, the ![]() temperature and polarization working group (WG3 or ``CTP''), investigates other
critical data analysis steps, in particular, map-making (Poutanen et al. 2006; Ashdown et al. 2007) and power spectrum
estimation.
temperature and polarization working group (WG3 or ``CTP''), investigates other
critical data analysis steps, in particular, map-making (Poutanen et al. 2006; Ashdown et al. 2007) and power spectrum
estimation.
The present paper reports the results of the WG2 activity in the
framework of a component separation challenge using a common
set of simulated PLANCK data.![]() In turn, this exercise provides valuable feedback and validation during the development of the PLANCK Sky Model.
In turn, this exercise provides valuable feedback and validation during the development of the PLANCK Sky Model.
This is the first time, within the PLANCK collaboration, that an extensive comparison of component separation methods has been attempted on simulated data based on models of sky emissions of representative complexity. As will be seen and emphasised throughout this paper, this aspect is critical for a meaningful evaluation of the performance of any separation method. In this respect, the present work significantly improves on the semi-analytical estimates of foreground contamination obtained by Bouchet & Gispert (1999) for the PLANCK phase A study, as well as on previous work by Tegmark et al. (2000) .
The paper is organised as follows: In Sect. 2 we describe the sky emission model and simulations that were used, and describe the methodology of the Challenge. In Sect. 3 we give an overview of the methods that have been implemented and took part in the analysis. In Sect. 4 we describe the results obtained for CMB component separation and power spectrum estimation. The results for point sources, SZ and Galactic components are described in Sects. 5 and 6 we present our summary and conclusions. In Appendix A we provide a more detailed description of the methods, their implementation details and their strengths and weaknesses.
The objective of the component separation challenge discussed herein is to assess the readiness of the PLANCK collaboration to tackle component separation, based on the analysis of realistically complex simulations. It offers an opportunity for comparing the results from different methods and groups, as well as to develop the expertise, codes, organisation and infrastructure necessary for this task.
This component separation challenge is designed so as to test on realistic simulated data sets, component separation methods and algorithms in a situation as close as possible to what is expected when actual PLANCK data will be analysed. Hence, we assume the availability of a number of ancillary data sets. In particular, we assumed that six-year WMAP observations will be available. Although WMAP is significantly less sensitive than PLANCK, it provides very useful complementary information for the separation of low-frequency Galactic components. This section describes our simulations, the challenge setup, and the evaluation methodology.
Our sky simulations are based on an early development version of the PLANCK Sky Model (PSM, in preparation), a flexible software package developed by PLANCK WG2 for making predictions, simulations and constrained realisations of the microwave sky.
The CMB sky is based on the observed WMAP multipoles up
to ![]() ,
and on a Gaussian realisation assuming the WMAP
best-fit
,
and on a Gaussian realisation assuming the WMAP
best-fit ![]() at higher multipoles. It is the same CMB map used by
Ashdown et al. (2007).
at higher multipoles. It is the same CMB map used by
Ashdown et al. (2007).
The Galactic interstellar emission is described by a three component model of the interstellar medium comprising of free-free, synchrotron and dust emissions. The predictions are based on a number of sky templates which have different angular resolution. In order to simulate the sky at PLANCK resolution we have added small scale fluctuations to some of the templates. The procedure used is the one presented in Miville-Deschênes et al. (2007) which allows to increase the fluctuation level as a function of the local brightness and therefore reproduce the non-Gaussian properties of the interstellar emission.
Free-free emission is based on the model of Dickinson et al. (2003)
assuming an electronic temperature of 7000 K.
The spatial structure of the emission is
estimated using a H![]() template corrected for dust extinction.
The H
template corrected for dust extinction.
The H![]() map is a combination of
the Southern H-Alpha Sky Survey Atlas (SHASSA) and the Wisconsin H-Alpha Mapper (WHAM). The combined map was smoothed to obtain a uniform angular resolution of 1
map is a combination of
the Southern H-Alpha Sky Survey Atlas (SHASSA) and the Wisconsin H-Alpha Mapper (WHAM). The combined map was smoothed to obtain a uniform angular resolution of 1![]() .
For the extinction map we use the E(B-V) all-sky map of
Schlegel et al. (1998) which is a combination of a smoothed IRAS
100
.
For the extinction map we use the E(B-V) all-sky map of
Schlegel et al. (1998) which is a combination of a smoothed IRAS
100 ![]() m map (with resolution of 6.1') and a map at a few degrees
resolution made from DIRBE data to estimate dust temperature and
transform the infrared emission in extinction. As mentioned earlier, small
scales were added in both templates to match the PLANCK resolution.
m map (with resolution of 6.1') and a map at a few degrees
resolution made from DIRBE data to estimate dust temperature and
transform the infrared emission in extinction. As mentioned earlier, small
scales were added in both templates to match the PLANCK resolution.
![\begin{figure}
\par\includegraphics[angle=90,width=8.3cm,clip]{0116fig1a.ps} \includegraphics[angle=90,width=8.3cm,clip]{0116fig1b.ps}\end{figure}](/articles/aa/full/2008/44/aa10116-08/Timg25.gif) |
Figure 1:
Synchrotron and dust (effective powerlaw) spectral indices evaluated between 30 and 44 GHz, and 143 and 217 GHz respectively (in |
| Open with DEXTER | |
Synchrotron emission is based on an extrapolation of the 408 MHz map of Haslam et al. (1982)
from which an estimate of the free-free emission was removed.
The spectral emission law of the synchrotron is assumed to follow a perfect
power law,
![]() .
We use a pixel-dependent spectral index
.
We use a pixel-dependent spectral index ![]() derived from the ratio of the
408 MHz map and the estimate of the synchrotron emission at 23 GHz in the WMAP data obtained by Bennett et al. (2003b) using a Maximum Entropy Method technique. A limitation of this approach is that this synchrotron model
also contains any ``anomalous'' dust correlated emission seen by WMAP at 2 GHz.
derived from the ratio of the
408 MHz map and the estimate of the synchrotron emission at 23 GHz in the WMAP data obtained by Bennett et al. (2003b) using a Maximum Entropy Method technique. A limitation of this approach is that this synchrotron model
also contains any ``anomalous'' dust correlated emission seen by WMAP at 2 GHz.
The thermal emission from interstellar dust is estimated using model
7 of Finkbeiner et al. (1999). This model, fitted to the
FIRAS data (7![]() resolution), makes the hypothesis that each line
of sight can be modelled by the sum of the emission from two dust
populations, one cold and one hot. Each grain population is in thermal
equilibrium with the radiation field and thus has a grey-body
spectrum, so that the total dust emission is modelled as
resolution), makes the hypothesis that each line
of sight can be modelled by the sum of the emission from two dust
populations, one cold and one hot. Each grain population is in thermal
equilibrium with the radiation field and thus has a grey-body
spectrum, so that the total dust emission is modelled as
Table 1:
Characteristics of PLANCK one year simulations ( upper) and WMAP six year simulations ( lower). PLANCK and WMAP hit counts correspond to 1.7' (Healpix
![]() )
and 6.8' (
)
and 6.8' (
![]() ) pixels respectively.
) pixels respectively. ![]() is the white noise level calculated from the inhomogeneous distribution of hits.
is the white noise level calculated from the inhomogeneous distribution of hits.
Point sources are modelled with two main categories: radio and
infra-red. Simulated radio sources are based on the NVSS or SUMSS and GB6 or PMN
catalogues. Measured fluxes at 1 and/or 4.85 GHz are extrapolated to
PLANCK frequencies assuming a distribution in flat and steep
populations. For each of these two populations, the spectral index is
randomly drawn from within a set of values compatible with the typically observed
mean and dispersion.
Infrared sources are based on the IRAS catalogue, and modelled as
dusty galaxies (Serjeant & Harrison 2005). IRAS coverage gaps
were filled by adding simulated sources with a flux distribution consistent with
the mean counts. Fainter sources were assumed to be mostly sub-millimeter
bright galaxies, such as those detected by SCUBA surveys. These were
modelled following Granato et al. (2004) and assumed to be strongly
clustered, with a comoving clustering radius
![]() Mpc. Since such sources have a very high areal density,
they are not simulated individually but make up the sub-mm background.
Mpc. Since such sources have a very high areal density,
they are not simulated individually but make up the sub-mm background.
We also include in the model a map of thermal SZ spectral distortions
from galaxy clusters, based on a simulated cluster catalogue
drawn from a mass-function compatible with present-day observations and with
![]() CDM parameters
CDM parameters
![]() ,
h=0.7 and
,
h=0.7 and
![]() (Colafrancesco et al. 1997; de Zotti et al. 2005).
(Colafrancesco et al. 1997; de Zotti et al. 2005).
Component maps are produced at all PLANCK and WMAP central frequencies. They are then co-added and smoothed with Gaussian beams as indicated in Table 1. A total of fourteen monochromatic maps have been simulated.
Finally, inhomogeneous noise is obtained by simulating the hit counts corresponding to one year of continuous observations by PLANCK, using the Level-S simulations tool (Reinecke et al. 2006). An example of a hit count map is shown in the upper panel of Fig. 2. WMAP six year hit counts, obtained from scaling up the observed WMAP three year hit count patterns, are used to generate inhomogeneous noise in the simulated WMAP observations. The rms noise level per hit for both experiments is given in Table 1.
![\begin{figure}
\par\includegraphics[angle=90,width=8.5cm,clip]{0116fig2a.ps} \includegraphics[angle=90,width=8.5cm,clip]{0116fig2b.ps} \end{figure}](/articles/aa/full/2008/44/aa10116-08/Timg39.gif) |
Figure 2:
Upper panel: hit counts for the 143 GHz channel. The
inhomogeneities at the ecliptic poles are characteristic of
PLANCK's cycloidal scanning strategy.
Lower panel: the masking scheme separating the sky in three
regions of different foreground contamination. The grey region at
high Galactic latitudes is Zone 1, covering
|
| Open with DEXTER | |
The simulated data sets were
complemented by a set of ancillary data including hitmaps and noise
levels, IRAS, 408 MHz, and H![]() templates, as well as catalogues
of known clusters from ROSAT and of known point sources from NVSS, SUMSS, GB6, PMN and IRAS.
templates, as well as catalogues
of known clusters from ROSAT and of known point sources from NVSS, SUMSS, GB6, PMN and IRAS.
The Challenge proceeded first with a blind phase lasting around four months between August and November 2006, when neither the exact prescription used to simulate sky emission from these ancillary data sets, nor maps of each of the input components, were communicated to challenge participants.
After this phase and an initial review of the results at the WG2 meeting in Catania in January 2007, the Challenge moved to an open phase lasting from January to June 2007. In this phase the input data-CMB maps and power spectrum, Galactic emission maps, SZ Compton y parameter map, point source catalogues and maps, noise realisations - were made available to the participating groups.
All of the results presented here have been obtained after several iterations and improvements of the methods, both during the comparison of the results obtained independently by the various teams, and after the input data was disclosed. Hence, the challenge has permitted significant improvement of most of the methods and algorithms developed within the PLANCK collaboration. The analysis of the Challenge results was led by the simulations team, with involvement and discussion from all participating groups.
A set of standard deliverables were defined. These included: a CMB map with 1.7' pixels (Healpix
![]() )
together with a corresponding map of estimated errors;
the effective beam
)
together with a corresponding map of estimated errors;
the effective beam ![]() ,
which describes the total
smoothing of the recovered CMB map due to a combination of
instrumental beams and the filtering induced by the component
separation process; a set of binned CMB power spectrum estimates (band averages of
,
which describes the total
smoothing of the recovered CMB map due to a combination of
instrumental beams and the filtering induced by the component
separation process; a set of binned CMB power spectrum estimates (band averages of
![]() )
and error bars; maps of all the diffuse components identified in the data; catalogues of the infrared and radio sources, and SZ clusters; a map of the SZ Compton y parameter.
)
and error bars; maps of all the diffuse components identified in the data; catalogues of the infrared and radio sources, and SZ clusters; a map of the SZ Compton y parameter.
Different separation methods are likely to perform differently in either foreground-dominated or noise-dominated observations. Also, they may be more or less sensitive to different types of foregrounds. Since the level of foreground contamination varies strongly across the sky, we used a set of standard masks throughout this work, and they are shown in the lower panel of Fig. 2.
The sky is split into three distinct Galactic ``Zones'': Zone 1 is at high
Galactic latitudes and covers ![]() of sky, similar to the WMAP Kp0
mask with smoother edges and small extensions. Zone 2 is at lower
Galactic latitudes and covers
of sky, similar to the WMAP Kp0
mask with smoother edges and small extensions. Zone 2 is at lower
Galactic latitudes and covers ![]() of sky. The remaining
of sky. The remaining ![]() of sky is covered by Zone 3, which is similar to the WMAP Kp12 mask.
of sky is covered by Zone 3, which is similar to the WMAP Kp12 mask.
The point source mask is the product of nine masks, each constructed
by excluding a two FWHM region around every source with a flux greater than 200 mJy at the corresponding PLANCK frequency channel. This point source mask covers ![]() of sky in Zone 1. For comparison, the WMAP point source masks of
Bennett et al. (2003b) excludes a radius of 0.7
of sky in Zone 1. For comparison, the WMAP point source masks of
Bennett et al. (2003b) excludes a radius of 0.7![]() around
almost 700 sources with fluxes greater than 500 mJy, covering a total
of 2% of sky.
around
almost 700 sources with fluxes greater than 500 mJy, covering a total
of 2% of sky.
The SZ mask is constructed by blanking out small circular regions centered on 1625 SZ clusters detected with the needlet-ILC + matched filter method (see Sect. 5.2). For each of them, the diameter of the cut is equal to the virial radius of the corresponding cluster.
A note of caution about these simulations of sky emission is in order. Although the PSM, as described above, has a considerable amount of sophistication, it still makes some simplifying assumptions - and cannot be expected to describe the full complexity of the real sky. This is a critical issue, as component separation methods are very sensitive to these details. We mention four of them.
First, Galactic emission is modelled with only three components, with no anomalous emission at low frequencies. This affects the spectral behaviour of components in the lower frequency bands below 60 GHz where the anomalous emission is thought to be dominant (Bonaldi et al. 2007; Davies et al. 2006; Miville-Deschênes et al. 2008).
Second, even though variable spectral emission laws are used for synchrotron and dust emission, this is still an idealisation: for the synchrotron, the emission law in each pixel is described by a single spectral index without any steepening. For dust, the emission is modelled as a superposition of two populations, with distinct but fixed temperature and emissivity. These approximations impact component separation, since almost perfect estimation of the relevant parameters of a given foreground emission is possible at frequencies where this foreground dominates, thereby allowing perfect subtraction in the cosmological channels.
Third, it is worth mentioning that only low resolution (
![]() )
templates are
available for synchrotron and free-free emissions. Hence, addition of
small-scale power is critical: if such scales were absent from the
simulations, but actually significant in the real sky, one might get
a false impression that no component separation is needed on small
scales. Also, the detection of point sources as well as galaxy
clusters would be significantly easier, hence not representative of
the actual problem.
Here, missing small scale features are simulated using a
non-stationary coloured Gaussian random field. Although quite
sophisticated, this process can not generate for instance, filamentary
or patchy structures known to exist in the real sky.
)
templates are
available for synchrotron and free-free emissions. Hence, addition of
small-scale power is critical: if such scales were absent from the
simulations, but actually significant in the real sky, one might get
a false impression that no component separation is needed on small
scales. Also, the detection of point sources as well as galaxy
clusters would be significantly easier, hence not representative of
the actual problem.
Here, missing small scale features are simulated using a
non-stationary coloured Gaussian random field. Although quite
sophisticated, this process can not generate for instance, filamentary
or patchy structures known to exist in the real sky.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0116fig3a.ps}
\includegraphics[width=8.5cm,clip]{0116fig3b.ps} \end{figure}](/articles/aa/full/2008/44/aa10116-08/Timg46.gif) |
Figure 3:
Spectra of the simulated microwave sky components near the
foreground minimum. CMB, noise with the effect of beam
deconvolution, and the thermal SZ effect are evaluated on the full
sky; point source power is evaluated on Zone 1 + 2 both with and without
sources above 200 mJy masked; the galaxy power spectra are
evaluated on Zone 1 and on Zone 2. The well-known importance of
masking is evident, as is the fact that there is a significant
proportion of sky (Zone 2,
|
| Open with DEXTER | |
Fourth, our simulations are somewhat idealised in the sense that we use perfect Gaussian beams, assume no systematic effects, and assume that the noise is uncorrelated from pixel to pixel and from channel to channel. Also, the effect of the finite bandpass of the frequency channels is not taken into account, and we assume that the calibration and zero levels of each channel is perfectly known.
In spite of these simplifications, component separation remains a difficult task with our simulated data because of pixel-dependent spectral emission laws for dust and synchrotron, and of the presence of more than a million point sources with different emission laws, of hundreds of thousands of unresolved or extended SZ clusters, and of significant emission from a complex IR background. It is fair to say that this simulated sky is far more complex than anything ever used in similar investigations.
In closing this Section, we show in Fig. 3 the angular power spectra of the basic components for the 70 and 100 GHz channels, close to the foreground emission minimum. The spectra of CMB, noise and thermal SZ are compared to the spectra of the total Galactic emission evaluated at high and low Galactic latitudes, on Zone 1 and 2 respectively. The point source spectra are evaluated in Zone 1, both with and without the brightest sources above 200 mJy masked. Figure 3 shows the obvious impact on CMB studies of masking the most foreground-contaminated regions. It also indicates that there is a significant region of sky, Zone 2, for which Galactic emission and CMB power are comparable. In the following sections, results are evaluated independently in both Zones 1 and 2.
In this section we present a brief overview of the methods that have been used in this challenge. The section is divided in three parts, one for diffuse component separation methods, one for point source extraction, and one for SZ cluster extraction.
The spirit of each method tested on the challenge data is outlined here. A more detailed description, including some details of their implementations and a discussion of their strengths and weaknesses is presented in Appendix A.
Table 2: Some characteristics of the diffuse component separation methods used in the challenge.
First we define some relevant terminology. The data model for a given channel ![]() is
is
We now briefly describe each of the methods that performed component separation of the CMB (and possibly other diffuse components), and also mention how the CMB angular power spectrum is estimated.
Note that many different approaches to diffuse component separation are represented here: blind, non-blind, semi-blind; methods based on linear combinations for foreground extraction; likelihood based methods which estimate parameters of a model of the foregrounds and the CMB; a maximum entropy method; methods based on cross correlations; a method based on sparsity. They also rely on very diverse assumptions and models.
In the present challenge, point sources are detected in all PLANCK channels independently. Two methods are used, the first based on a new implementation of matched filtering, and the second using the second member of the Mexican Hat Wavelet Family of filters (González-Nuevo et al. 2006). Point sources are detected by thresholding on the filtered maps.
This corresponds to a first step for effective point source detection. It does not exploit any prior information on the position of candidate sources; Such information can be obtained from external catalogues as in López-Caniego et al. (2007), or from detections in other PLANCK channels. Neither does this approach exploit the coherence of the contaminants throughout PLANCK frequencies, nor try to detect point sources jointly in more than one channel. Hence, there is margin for improvement.
In the present data challenge, we address both the question of building an SZ catalogue, and of making a map of thermal SZ emission.
SZ map: three methods successfully produced SZ maps: ILC in harmonic space, ILC on a needlet frame, and SMICA. For ILC methods, the data are modelled as
SZ catalogue: three main methods were used to obtain the cluster catalogue:
This comparison is being extended to other cluster extraction methods in collaboration with the PLANCK ``Clusters and Secondary Anisotropies'' working group (WG5). Some improvements are obtained using SExtractor as the extraction tool after the component separation step. There is still some margin for other improvements by increasing the studied area to include lower Galactic latitudes and by combining the SZ extraction methods with CMB and Galactic extraction methods more intimately.
We now turn to the presentation and discussion of the results of the challenge, starting with the CMB component. We evaluate performance based on residual errors at the map and spectral level, and on residual errors at the power spectrum estimation level.
The first point to be made is that all methods have produced CMB maps in Zones 1 and 2. Foreground contamination is barely visible. A small patch representative of CMB reconstruction at intermediate Galactic latitude, is shown in Fig. 9. In the following, we focus on the analysis of the reconstruction error (or residual).
Since each method produces a CMB map at a different resolution, the recovered CMB maps are compared both against the input CMB sky smoothed only by the 1.7' pixels, and against a 45' smoothed version, in order to the emphasise errors at large scales.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0116fig4a.ps}\\ [2.5mm]
\includegraphics[width=8.5cm,clip]{0116fig4b.ps} \end{figure}](/articles/aa/full/2008/44/aa10116-08/Timg79.gif) |
Figure 4:
Upper: rms of the residual error of the CMB map,
calculated for each of 18 bands of 10 degrees width in Galactic
latitude. For comparison,
|
| Open with DEXTER | |
Maps of the CMB reconstruction error, with all maps smoothed to a common 45'resolution, are shown in Fig. 5
for all of the methods (excluding Commander, which produced maps at
3![]() resolution).
The remaining Galactic contamination is now visible at various levels for most
methods, and in particular close to regions with the strongest levels of
free-free emission. There is also evidence of contamination by SZ
cluster decrements, which are visible as distinct negative sources
away from the Galactic plane.
As can be seen, significant differences between methods exist.
resolution).
The remaining Galactic contamination is now visible at various levels for most
methods, and in particular close to regions with the strongest levels of
free-free emission. There is also evidence of contamination by SZ
cluster decrements, which are visible as distinct negative sources
away from the Galactic plane.
As can be seen, significant differences between methods exist.
Similarly, the lower panel of Fig. 4 shows
the rms of the smoothed residual errors shown in
Fig. 5.
Depending on the method, the typical level of foreground contamination
(plus noise) has an rms from 2 to 5 ![]() K on this smoothing scale.
For comparison,
K on this smoothing scale.
For comparison,
![]() K
and
K
and
![]() K for the 143 GHz channel.
K for the 143 GHz channel.
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[angle=90,scale=0.35, wi...
...[angle=90,scale=0.35, width=8.5cm,clip]{0116fig5h} \end{tabular}\par\end{figure}](/articles/aa/full/2008/44/aa10116-08/Timg82.gif) |
Figure 5:
CMB reconstruction error smoothed at 45' resolution. These maps are described in Sect. 4.1, and their rms in Galactic latitude
strips of
|
| Open with DEXTER | |
Next we calculate the spectra of the CMB raw residual maps, both on Zone 1 and Zone 2 (high and low Galactic latitudes), with the brightest point sources masked. The results are shown in Fig. 6.
By comparing the spectra of the residuals with the original level of diffuse foreground contamination shown in Fig. 3, we can see that a considerable degree of diffuse foreground cleaning has been attained. There seems however to be a ``floor'' approached by the ensemble of methods, with a spread of about a factor of ten indicating differences in performance. This floor appears to be mostly free of residual CMB signal which would be visible as acoustic oscillations.
Its overall shape is not white: at high Galactic
latitudes the residual spectra bottom out at very roughly
![]() K2, while a low Galactic latitudes the
spectra bottom out at
K2, while a low Galactic latitudes the
spectra bottom out at
![]() K2. This limit
to the level of residuals is considerably higher than the
``foreground-free'' noise limit displayed as a dashed line.
K2. This limit
to the level of residuals is considerably higher than the
``foreground-free'' noise limit displayed as a dashed line.
It is, however, also significantly lower than the CMB cosmic variance, even
with 10% binning in ![]() .
This comforts us in the impression that
component separation is effective enough for CMB power spectrum
estimation (discussed next in this paper), although it may remain a
limiting issue for other type of CMB science. In particular, it
suggests that the component separation residuals, with these channels
and the present methods, will dominate the error in PLANCK CMB
maps.
.
This comforts us in the impression that
component separation is effective enough for CMB power spectrum
estimation (discussed next in this paper), although it may remain a
limiting issue for other type of CMB science. In particular, it
suggests that the component separation residuals, with these channels
and the present methods, will dominate the error in PLANCK CMB
maps.
![\begin{figure}
\par {\includegraphics[width=8cm,clip]{0116fig6a.ps} }\\ [2mm]
{\includegraphics[width=8cm,clip]{0116fig6b.ps} }
\end{figure}](/articles/aa/full/2008/44/aa10116-08/Timg85.gif) |
Figure 6: Spectra of the CMB residual maps, evaluated on Zone 1 ( high Galactic latitudes) and Zone 2 ( low Galactic latitudes), both regions with point sources masked. Comparison with Fig. 3 shows the extent to which the Galactic contamination has been removed from the CMB on large angular scales. |
| Open with DEXTER | |
Recently Huffenberger et al. (2007) performed a reanalysis of the
impact of unresolved point source power in the WMAP three-year
data. They found that cosmological parameter constraints are sensitive
to the treatment of the unresolved point source power spectrum beyond
![]() characterised by a white noise level of
characterised by a white noise level of
![]() K2. By comparison, the residual foreground
contamination obtained in our simulations is as low as
K2. By comparison, the residual foreground
contamination obtained in our simulations is as low as
![]() K2 at
K2 at ![]() .
.
Although not the main focus of effort for the Challenge, each group provided
their own bandpower estimates of the CMB power spectrum,
which in many cases showed obvious acoustic structure out to the
sixth or seventh acoustic peak at
![]() .
As an illustration of this result, we show in the upper and
middle panels of Fig. 7 the power spectrum
estimates from the Commander and SMICA methods respectively.
.
As an illustration of this result, we show in the upper and
middle panels of Fig. 7 the power spectrum
estimates from the Commander and SMICA methods respectively.
To make a quantitative estimate of the accuracy of the power spectrum
estimates ![]() of
of
![]() ,
we calculate the
quantity
,
we calculate the
quantity
In the absence of foregrounds, an approximate lower bound on the relative
standard deviation in estimating the power spectrum is given by
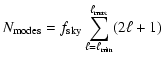 |
(8) |
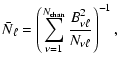 |
(9) | ||
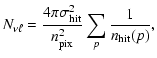 |
(10) |
Ideally, the figure of merit given by Eq. (6) should be
much less than one in the cosmic-variance limited regime (i.e. for
![]() according to Fig. 6).
Significant deviations from zero at low
according to Fig. 6).
Significant deviations from zero at low ![]() and over
and over ![]() at high
at high
![]() are indications of significant departures from optimality. We
display the FoM Eq. (6), calculated for the PSE of each
method in the range
are indications of significant departures from optimality. We
display the FoM Eq. (6), calculated for the PSE of each
method in the range
![]() ,
in the lower panel of
Fig. 7.
,
in the lower panel of
Fig. 7.
Focusing first on the range ![]() we can discern the best
performance from Commander, which models the spatial variation of the
foreground spectral indices, thus improving the subtraction of
foregrounds on large scales. In the range
we can discern the best
performance from Commander, which models the spatial variation of the
foreground spectral indices, thus improving the subtraction of
foregrounds on large scales. In the range
![]() ,
SEVEM,
specifically designed for an estimate of the CMB power spectrum,
performs best among the methods tested on this challenge. Beyond
,
SEVEM,
specifically designed for an estimate of the CMB power spectrum,
performs best among the methods tested on this challenge. Beyond
![]() we see the best performance from SEVEM and SMICA.
we see the best performance from SEVEM and SMICA.
At best, it seems that obtaining PSE with
![]() is
achievable for the multipole range
is
achievable for the multipole range
![]() .
Overall though,
complete convergence between the results from different methods was
not yet achieved.
.
Overall though,
complete convergence between the results from different methods was
not yet achieved.
![\begin{figure}
\par {\includegraphics[width=8cm,clip]{0116fig7a.ps} }
{\include...
....ps} }\\ [2.5mm]
{\includegraphics[width=8cm,clip]{0116fig7c.ps} }
\end{figure}](/articles/aa/full/2008/44/aa10116-08/Timg109.gif) |
Figure 7:
Upper: power spectrum estimates (PSE) using Commander on large angular scales. The diamonds show the |
| Open with DEXTER | |
In closing this section on the results for the CMB component, we make some general observations, and attempt to explain some of the differences in these results, as shown in Fig. 5, and with reference to the characteristics of the analyses as detailed in Table 2.
The most significant foreground contamination, where it exists, is associated with regions where free-free emission is most intense, such as the Gum nebula and Orion A and B, and this is most easily visible in the residual maps of FastICA and WIFIT (which also suffers from some dust contamination). Possibly this can be explained by the more limited frequency range of data exploited in these two analyses.
The WMAP data were used in the separation only by Commander and SMICA. In the Commander case, the inclusion of additional low frequency channels (in particular the 23 GHz band) helps to recover the low frequency foregrounds. For SMICA, the use of the WMAP channels was not really mandatory for extracting the CMB, rather they have been used with the objective of developing a pipeline which uses all observations available. WMAP maps are expected to be useful for the extraction of low frequency galactic components. This specific aspect was not investigated further in the present work, as the simulations used here (which do not include any anomalous dust emission) are not really adequate to address this problem meaningfully.
Table 3: Results of point source detection on the present data challenge.
Additional efforts have been directed towards producing a catalogue of point sources, a catalogue of SZ clusters and maps of the thermal SZ effect and Galactic components.
The detection of point sources is both an objective of PLANCK component separation (for the production of the PLANCK early release compact source catalogue (ERCSC) and of the final point source catalogue), and also a necessity for CMB science, to evaluate and subtract the contamination of CMB maps and power spectra by this population of astrophysical objects (González-Nuevo et al. 2008; Wright et al. 2008).
The matched filter and the Mexican hat wavelet 2 have advantages and drawbacks. In principle, the matched filter is the optimal linear filter. However, it often suffers from inaccurate estimation of the required correlation matrix of the contaminants, and from the difficulty to adapt the filter to the local contamination conditions. On the data from the present challenge, this resulted in excessive contamination of the point source catalogue by small scale Galactic emission, mainly dust at high frequencies.
Table 3 summarises the PS detection achieved by these methods. We found that the Mexican hat wavelet 2 and the matched filter performed similarly in most of the frequency channels, and complement each other in the others. Performance depends on the implementation details, and on properties of the other foregrounds.
It should be noted that, for all channels, the 5![]() detection limit
is somewhat above what would be expected from (unfiltered)
noise alone (by a factor 1.33 for the best case, 44 GHz, to 4.8 for
the worst case, 857 GHz). This is essentially due to the impact of
other foregrounds and the CMB, as well as confusion with
other sources. In particular, this effect is more evident at 545 and
857 GHz, due to high dust contamination but also due to the confusion with
the highly correlated population of SCUBA
sources (Granato et al. 2004; Negrello et al. 2004), which
constitute a contaminant whose impact on point source detection was
until now somewhat underestimated.
detection limit
is somewhat above what would be expected from (unfiltered)
noise alone (by a factor 1.33 for the best case, 44 GHz, to 4.8 for
the worst case, 857 GHz). This is essentially due to the impact of
other foregrounds and the CMB, as well as confusion with
other sources. In particular, this effect is more evident at 545 and
857 GHz, due to high dust contamination but also due to the confusion with
the highly correlated population of SCUBA
sources (Granato et al. 2004; Negrello et al. 2004), which
constitute a contaminant whose impact on point source detection was
until now somewhat underestimated.
The number of detections for each frequency channel in Table 3 has been compared to the predictions made by López-Caniego et al. (2006), properly rescaled for our sky coverage. In general, there is a good agreement between the predictions and the results of this exercise, except for the 857 GHz channel, where the number of detections is roughly half the predicted one. Again, the difference may be due to the confusion of correlated infrared sources, that are now present in the PSM but were not considered by López-Caniego et al. (2006).
The recovery of an SZ map from the challenge data is illustrated in Fig. 8. The recovered full sky SZ is obtained by Wiener-filtering in harmonic space the needlet-ILC map of the SZ y parameter. Wiener filtering enhances the visibility of SZ clusters. We clearly identify by eye the brightest clusters in the map.
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[scale=0.5]{0116fig8a} & \includegraphics[scale=0.5]{0116fig8b}\end{tabular}\par\end{figure}](/articles/aa/full/2008/44/aa10116-08/Timg110.gif) |
Figure 8:
Patch of the recovered needlet-ILC SZ map and input SZ map. For easier comparison of the two maps (
|
| Open with DEXTER | |
One of the main results of this study is the recovery of around 2300 clusters. This is significantly lower than the performance one could expect if the main limitation was the nominal PLANCK noise, and if most detectable clusters were unresolved. Many of the recovered clusters are in fact resolved, and thus emit on scales where the contamination from CMB is not negligible. Small scale Galactic emission and the background of extragalactic sources, now included in the simulations, further complicate the detection. Further study is necessary to find the exact origin of the lack of performance, and improve the detection methods accordingly.
Actual detection performance, limited to 67% of the sky at Galactic latitudes above 20 degrees, is shown in Table 4. The ILC + SExtractor method gives the best result. The ILC+MF approach performs as well as the matched multifilter here. The two implementations of the MMF perform similarly. The difference in the number of detections achieved (about 13.5%), however, suggests that implementation details are important for this task.
Using the detected cluster catalogue obtained with the MMF, we have produced a mask of the detected SZ clusters. For each of the 1625 clusters we masked a region whose radius is given by the corresponding input cluster virial radius (ten times the core radius here).
Table 4:
Performance of the SZ cluster detection methods. The table gives the absolute number of detection for
![]() .
.
For the Challenge, a number of methods were applied for separating out Galactic components. Table 2 lists which Galactic components were obtained by the different methods. Five groups have attempted to separate a high frequency dust-like component. Four groups have attempted separation of synchrotron and free-free at low frequencies.
We compared the reconstructed component maps with their counterpart
input maps, both in terms of the absolute residual error and in terms
of the relative error. Both these measures are computed after
removing the best-fit monopole and dipole from the residual error map (fitted
when excluding a region ![]() 30
30![]() in Galactic latitude).
We then defined a figure of merit
in Galactic latitude).
We then defined a figure of merit ![]() ,
which corresponds to the
fraction of sky where the foreground amplitude is reconstructed with a
relative error of less than 20
,
which corresponds to the
fraction of sky where the foreground amplitude is reconstructed with a
relative error of less than 20![]() .
.
The main results can be summarised as follows:
The dust component was the best reconstructed component with
an
![]() for all methods. The relative error typically
becomes largest at the higher galactic latitudes where the dust emission
is faintest.
The synchrotron component was reconstructed with an
for all methods. The relative error typically
becomes largest at the higher galactic latitudes where the dust emission
is faintest.
The synchrotron component was reconstructed with an
![]() -0.5, with Commander achieving the best results at
-0.5, with Commander achieving the best results at ![]() resolution, but with noticeable errors along the galactic ridge where,
in our simulations, the synchrotron spectral index flattens off.
Free-free emission is detected and identified in regions such as the
Gum Nebula, Orion A and B, and the Ophiucus complex. However, the
reconstruction of the free-free emission at low Galactic latitudes
needs improving.
On the other hand, the total Galactic emission (free-free plus
synchrotron) at low-frequencies is better reconstructed, with
resolution, but with noticeable errors along the galactic ridge where,
in our simulations, the synchrotron spectral index flattens off.
Free-free emission is detected and identified in regions such as the
Gum Nebula, Orion A and B, and the Ophiucus complex. However, the
reconstruction of the free-free emission at low Galactic latitudes
needs improving.
On the other hand, the total Galactic emission (free-free plus
synchrotron) at low-frequencies is better reconstructed, with
![]() -0.8, with the best results from Commander.
-0.8, with the best results from Commander.
In Fig. 9, we show for illustration the recovered total Galactic emission at 23 GHz from Commander, the dust emission at 143GHz from FastICA and, for comparison, the recovered CMB from SMICA on the same patch.
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[angle=90, scale=0.31]{01...
....5]{0116fig9e} & \includegraphics[scale=0.5]{0116fig9f}\end{tabular}\end{figure}](/articles/aa/full/2008/44/aa10116-08/Timg117.gif) |
Figure 9: Example input and recovered total galaxy emission at 23 GHz, dust at 143 GHz and CMB components. |
| Open with DEXTER | |
In this paper we have described a CMB component separation Challenge based on a set of realistic simulations of the PLANCK satellite mission. The simulated data were based on a development version of the PLANCK Sky Model, and included the foreground emission from a three component Galactic model of free-free, synchrotron and dust, as well as radio and infra-red sources, the infra-red background, the SZ effect and PLANCK-like inhomogeneous noise. We have cautioned that the simulations, while complex, still relied on some simplifying assumptions, as discussed in Sect. 2.3. Thus, there is no guarantee that the priors and data models that yielded the best separation on simulations will work equally well on the PLANCK dataset. While this may seem to undercut the main purpose of this paper, we are simply acknowledging that we cannot anticipate in full detail what the PLANCK component separation pipeline will look like and how effective it will be, based on an analysis of present-day simulations. In spite of this, it is clear that methods performing better on the simulated data have in general better chances to work better on the real sky.
As a combined set of tools, the component separation methods developed and tested in this work offer very different ways to address the component separation problem and so comparable performance between different tools, when achieved, provides confidence in the conclusions of this work against some of the simplifications used in the model for simulating the sky emission.
We found that the recovered CMB maps were clean on large scales, in
the sense that the rms of the residual contamination was much less
than the cosmic variance: at best the rms residual of the cleaned CMB
maps was of the order of 2 ![]() K across the sky on a smoothing scale
of 45', with a spectral distribution described by
K across the sky on a smoothing scale
of 45', with a spectral distribution described by
![]() K2 and
K2 and
![]() K2 at
high and low Galactic latitudes respectively. The effectiveness of the
foreground removal is illustrated by comparing the input
foreground power spectra of Fig. 3 with the
residuals shown in Fig. 6. The two panels
of the latter figure show that, with few exceptions, the methods
manage to clean the low Galactic latitude Zone 2, where the foreground
contamination is high,
almost as well as they do for the high Galactic latitude Zone 1, where the CMB
dominates at the frequencies near the foreground minimum. The
amplitude of the power spectrum of residuals is, on the largest
scales, four orders of magnitude lower than that of the input Galaxy
power spectrum at the foreground minimum. This means that the CMB map
could be recovered, at least by some methods, over the whole sky
except for a sky cut at the 5 percent level (see
Fig. 4). The CMB power spectrum was
accurately recovered up to the sixth peak.
K2 at
high and low Galactic latitudes respectively. The effectiveness of the
foreground removal is illustrated by comparing the input
foreground power spectra of Fig. 3 with the
residuals shown in Fig. 6. The two panels
of the latter figure show that, with few exceptions, the methods
manage to clean the low Galactic latitude Zone 2, where the foreground
contamination is high,
almost as well as they do for the high Galactic latitude Zone 1, where the CMB
dominates at the frequencies near the foreground minimum. The
amplitude of the power spectrum of residuals is, on the largest
scales, four orders of magnitude lower than that of the input Galaxy
power spectrum at the foreground minimum. This means that the CMB map
could be recovered, at least by some methods, over the whole sky
except for a sky cut at the 5 percent level (see
Fig. 4). The CMB power spectrum was
accurately recovered up to the sixth peak.
As detailed in Table 2, the outputs of the methods were diverse. While all have produced a CMB map, only a subset of them were used to obtain maps of individual diffuse Galactic emissions. Five (Commander, CCA, FastICA, FastMEM, SMICA) reconstructed thermal dust emission maps at high frequencies, and another five (Commander, CCA, FastMEM, GMCA, SMICA) yielded a map of the low-frequency Galactic emissions (synchrotron and free-free).
It is not surprising that the dust component was more easily reconstructed because it is mapped over a larger frequency range, and benefits from observations at high frequencies where it dominates over all other emissions, except the IR background at high Galactic latitudes. Moreover at high frequencies the noise level is lower and the angular resolution is better. Low frequency Galactic foregrounds suffer from more confusion, with a mixture of several components observed in only few channels, at lower resolution.
The relative errors of the reconstructed foreground maps are larger at
high Galactic latitudes where the foregrounds are fainter. We have
defined a figure of merit ![]() ,
which corresponds to the
fraction of sky where the amplitude of each galactic
component has been reconstructed with a relative error of less than
20
,
which corresponds to the
fraction of sky where the amplitude of each galactic
component has been reconstructed with a relative error of less than
20![]() .
For most methods,
.
For most methods,
![]() was achieved for the dust component,
while
was achieved for the dust component,
while
![]() was achieved for the radio emission, increasing to
was achieved for the radio emission, increasing to
![]() if component separation is performed at a relatively low
resolution of
if component separation is performed at a relatively low
resolution of ![]() .
Clearly, there is ample room and need for
improvement in this area.
.
Clearly, there is ample room and need for
improvement in this area.
The flux limits for extragalactic point source detection are minimum
at 143 and 217 GHz, where they reach ![]() 100 mJy. About 1000
radio sources and about 2600 far-IR sources are detected over about
67% of the sky (
100 mJy. About 1000
radio sources and about 2600 far-IR sources are detected over about
67% of the sky (
![]() ). Over the same region of the sky, the
best methods recover about 2300 clusters.
). Over the same region of the sky, the
best methods recover about 2300 clusters.
In closing, we list areas where work is in progress and improvements are expected: The sky model is being upgraded to include the anomalous emission component and polarization. We are in the process of integrating point source and SZ extraction algorithms together with the diffuse component separation algorithms into a single component separation pipeline. This is expected, on one side, to decrease the contamination of CMB maps on small angular scales, where point and compact sources (including SZ effects) dominate and, on the other side, to achieve a more efficient point and compact source extraction. Assessing this in more detail is part of WG2 work plans for the near future. The SEVEM foreground cleaning step now operates in wavelet space which allows for improved, scale-by-scale removal of foregrounds. In addition the recovery of the power spectrum estimates and error bars at the highest multipoles has been improved by reducing the cross-correlation between modes through the use of an apodised mask. For Commander, work is currently ongoing to extend the foreground sampler to multi-resolution experiments. CCA is being upgraded to fully exploit the estimated spatially-varying spectral indices in the source reconstruction step; SMICA is being improved to model unresolved point source power. The FastICA algorithm is being improved to handle data with a wider frequency coverage. The GMCA framework is being extended to perform a joint separation and deconvolution of the components.
Acknowledgements
The work reported in this paper was carried out by Working Group 2 of the PLANCK Collaboration. PLANCK is a mission of the European Space Agency. The Italian group were supported in part by ASI (contract Planck LFI Phase E2 Activity). The US PLANCK Project is supported by the NASA Science Mission Directorate. The ADAMIS team at APC has been partly supported by the Astro-Map and Cosmostat ACI grants of the French ministry of research, for the development of innovative CMB data analysis methods. The IFCA team acknowledges partial financial support from the Spanish project AYA2007-68058-C03-02. This research used resources of the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the US Department of Energy under Contract No. DE-AC02-05CH11231. D.H., J.L.S. and E.S. would like to acknowledge partial financial support from joint CNR-CSIC research project 2006-IT-0037. R.S. acknowledges support of the E.C. Marie Curie IR Grant (mirg-ct-2006-036614). C.B. was partly supported by the NASA LTSA Grant NNG04CG90G. S.M.L. would like to thank the kind hospitality of the APC, Paris for a research visit where part of this work was completed. We thank Carlo Burigana for a careful reading of the manuscript. We acknowledge the use of the Legacy Archive for Microwave Background Data Analysis (LAMBDA). Support for LAMBDA is provided by the NASA Office of Space Science. The results in this paper have been derived using the HEALPix package (Górski et al. 2005).
``Commander'' is an implementation of the CMB and foregrounds
Gibbs sampler most recently described by Eriksen et al. (2008); This
algorithm maps out the joint CMB-foreground probability distribution, or
``posterior distribution'', by sampling.
The target posterior distribution may be written in terms of the likelihood and
prior using Bayes' theorem,
In the current analysis, the foregrounds are modelled by a sum of
synchrotron, free-free and thermal dust emission, and free monopole
and dipoles at each frequency band. The thermal dust component is
approximated by a single-component modified blackbody with a fixed
dust temperature
![]() .
Thus, the total foreground
model reads
.
Thus, the total foreground
model reads
| |
= | 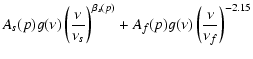 |
|
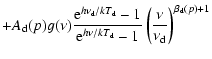 |
|||
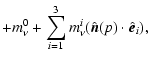 |
(A.2) |
Using the Gibbs (conditional) sampling technique, a set of samples drawn from the posterior distribution. From these samples the marginal posterior mean and rms component maps are derived, as well as the marginal CMB power spectrum posterior distribution.
The code assumes identical beams at all
frequencies, and it is therefore necessary to smooth the data to a
common resolution, limiting the analysis to large angular
scales. For this particular data set, we have chosen a common
resolution of
![]() ,
with 54' pixels (Healpix
Nside=64)
and with
,
with 54' pixels (Healpix
Nside=64)
and with
![]() .
For more details on the
degradation process, see Eriksen et al. (2008). At this resolution,
the CPU time for producing one sample is around one wall-clock minute. A
total of 5400 samples were produced over four independent Markov
chains, of which the first 2400 were rejected due to burn-in. Twelve
frequency bands (covering frequencies between 23 and 353 GHz) were
included, for a total cost of around 1000 CPU h.
.
For more details on the
degradation process, see Eriksen et al. (2008). At this resolution,
the CPU time for producing one sample is around one wall-clock minute. A
total of 5400 samples were produced over four independent Markov
chains, of which the first 2400 were rejected due to burn-in. Twelve
frequency bands (covering frequencies between 23 and 353 GHz) were
included, for a total cost of around 1000 CPU h.
The main advantage of this approach is simply that it provides us with the exact joint CMB and foreground posterior distribution for very general foreground models. From this joint posterior distribution, it is trivial to obtain the exact marginal CMB power spectrum and sky signal posterior distributions. Second, since any parametric foreground model may be included in the analysis, the method is very general and flexible. It also provides maps of the posterior means for individual components, and is therefore a true component separation method, and not only a foreground removal tool.
Currently, the main disadvantage of the approach is the assumption of identical beam profiles at each frequency. This strictly limits the analysis to the lowest resolution of a particular data set. However, this is a limitation of the current implementation, and not of the method as such.
CCA (Bedini et al. 2005) is a semi-blind approach that relies on the second-order statistics of the data to estimate the mixing matrix on sub-patches of the sky. CCA assumes the data model given by Eq. (4), and makes no assumptions about the independence or lack of correlations between pairs of radiation sources. The method exploits the spatial structure of the individual source maps and adopts commonly accepted models for source frequency scalings in order to reduce the number of free parameters to be estimated.
The spatial structures of the maps are accounted for through the
covariance matrices at different shifts. From the data model adopted,
the data covariance matrices at shifts
![]() are given by
are given by
CCA can treat the variability of the spectral properties of each component with the direction of observation by working on sufficiently small sky patches, which must however be large enough to have sufficient constraining power; typically the number of pixels per patch must be around 105. To obtain a continuous distribution of the free parameters of the mixing matrix, CCA is applied to a large number of partially overlapping patches.
A drawback of the present version of CCA is common to many pixel-domain approaches to separation: the data must be smoothed to a common resolution. A Fourier-domain implementation of CCA (Bedini & Salerno 2007) would be able to cope with this problem. Alternatively for the pixel-domain version, the mixing matrix could be estimated from the smoothed maps and then used to separate the sources using the full resolution data.
GMCA (Bobin et al. 2007) is a blind source separation method devised for
separating sources from instantaneous linear mixtures using the model
given by Eq. (4).
The components ![]() are assumed to be sparsely represented
(i.e. have a few significant samples in a specific basis) in
a so-called sparse representation
are assumed to be sparsely represented
(i.e. have a few significant samples in a specific basis) in
a so-called sparse representation ![]() (typically
wavelets). Assuming that the components have a sparse representation
in the wavelet domain is equivalent to assuming that most components
have a certain spatial regularity. These components and their spectral
signatures are then recovered by minimizing the number of significant
coefficients in
(typically
wavelets). Assuming that the components have a sparse representation
in the wavelet domain is equivalent to assuming that most components
have a certain spatial regularity. These components and their spectral
signatures are then recovered by minimizing the number of significant
coefficients in ![]() :
:
| (A.5) |
| (A.6) |
A Wiener filter is applied to provide the denoised CMB estimate. The main advantage of GMCA is its ability to blindly extract strong galactic emission. Indeed, most galactic emission is well represented in a wavelet basis. The main disadvantage is that it relies on the way the deconvolution of the data is performed: an effective beam is used to account for the convolution.
Independent Component Analysis is an approach to component
separation, looking for the components which maximise some
measure of the statistical independence (Hyvarinen 1999).
The FastICA algorithm presented here exploits the fact that
non-Gaussianity is usually a convenient and robust measure of
the statistical independence and therefore it searches for
linear combinations ![]() of the input multi-frequency data,
which maximise some measure of the non-Gaussianity.
In the specific implementation of the idea, employed here,
the non-Gaussianity is quantified by the neg-entropy.
Denoting by
of the input multi-frequency data,
which maximise some measure of the non-Gaussianity.
In the specific implementation of the idea, employed here,
the non-Gaussianity is quantified by the neg-entropy.
Denoting by
![]() the entropy associated with the distribution p, we define
the neg-entropy as,
the entropy associated with the distribution p, we define
the neg-entropy as,
The algorithm has been tested so far as a CMB cleaning procedure, because the hypothesis of statistical independence is expected to be verified at least between CMB and diffuse foregrounds. It produced results on real (BEAST, COBE, WMAP) and simulated total intensity data, as well as on polarization simulations, on patches as well as all sky (see Maino et al. 2007, and references therein). The performance is made possible by two contingencies, i.e. the validity of the assumption of statistical independence for CMB and foregrounds, as well as the high resolution of the present CMB observations, which provides enough of statistical realizations (pixels) for the method to decompose the data into the independent components.
The Maximum Entropy Method (MEM) can be used to separate the CMB signal from astrophysical foregrounds including Galactic synchrotron, dust and free-free emission as well as SZ effects. The particular implementation of MEM used here works in the spherical harmonic domain. The separation is performed mode-by-mode allowing a huge optimisation problem to be split into a number of smaller problems. The solution can thus be obtained more rapidly, giving this implementation its name: FastMEM. This approach is described by Hobson et al. (1999,1998) for Fourier modes on flat patches of the sky and by Stolyarov et al. (2005,2002) for the full-sky case.
If we have a model (or hypothesis) H in which the measured data ![]() is a function of an underlying signal
is a function of an underlying signal ![]() ,
then Bayes' theorem tells
us that the posterior probability
,
then Bayes' theorem tells
us that the posterior probability
![]() is the product of the
likelihood
is the product of the
likelihood
![]() and the prior probability
and the prior probability
![]() ,
divided by the evidence
,
divided by the evidence
![]() ,
,
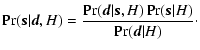 |
(A.8) |
| (A.9) |
| (A.10) |
The prior can be Gaussian, and in this case we recover the Wiener
filter with the well-known analytical solution for the signal s.
However, the astrophysical components have strongly non-Gaussian
distribution, especially in the Galactic plane. Therefore
Hobson et al. (1998) suggested that an entropic prior be used
instead. In this case, maximising the posterior probability is equivalent to the
minimising the following functional for each spherical harmonic mode
| (A.11) |
FastMEM is a non-blind method, so the spectral behaviour of the
components must be known in advance. Since ![]() is fixed, the spectral
properties of the components must be the same everywhere on the sky.
However, small variations in the spectral properties, for example,
dust temperature, synchrotron spectral index or SZ cluster electron
temperature, can be accounted for by introducing additional
components. These additional components correspond to terms in the
Taylor expansion of the frequency spectrum with respect to the
relevant parameter.
is fixed, the spectral
properties of the components must be the same everywhere on the sky.
However, small variations in the spectral properties, for example,
dust temperature, synchrotron spectral index or SZ cluster electron
temperature, can be accounted for by introducing additional
components. These additional components correspond to terms in the
Taylor expansion of the frequency spectrum with respect to the
relevant parameter.
The initial priors on the components are quite flexible and they can be updated by iterating the component separation, especially if the signal-to-noise is high enough.
It is not necessary for all of the input maps to be at the same resolution since FastMEM solves for the most probable solution for unsmoothed signal, deconvolving and denoising maps simultaneously. It is flexible enough to include any datasets with known window function and noise properties. A mask can easily be applied to the input data (the same mask for all frequency channels) and this does not cause problems with the separation.
Since FastMEM uses priors on the signals, the solution for the signals is biased. This is especially evident if the signal-to-noise ratio is low. It is possible to de-bias the power spectrum statistically, knowing the priors and the FastMEM separation errors per mode. However, one can not de-bias the recovered maps since the errors are quadratic and de-biasing will introduce phase errors in the harmonics.
No information about the input components was used in the separation, and the prior power spectra were based solely on the physical properties of the components and templates available in the literature. The prior on the CMB component was set using the best-fit theoretical spectrum, instead of a WMAP-constrained realisation. This has a significant effect at low multipoles.
SEVEM (Martínez-González et al. 2003) tries to recover
only the CMB signal, treating the rest of the emissions as a
generalised noise. As a first step, the cosmological frequency maps,
100, 143 and 217 GHz, are foreground cleaned using an internal
template fitting technique. Four templates are obtained from the
difference of two consecutive frequency channels, which are smoothed
down to the same resolution if necessary, to avoid the presence of
CMB signal in the templates. In particular, we construct maps of (30-44), (44-70), (545-353) and (857-545) differences. The central frequency
channels are then cleaned by subtracting a linear combination of these
templates. The coefficients of this combination are obtained
minimising the variance of the final clean map outside the considered
mask. The second step consists of estimating the power spectrum of
the CMB from the three cleaned maps using the method (based on the
Expectation-Maximization algorithm) described in
Martínez-González et al. (2003), which has been adapted to deal
with spherical data. Using simulations of CMB plus noise, processed in
the same way as the Challenge data, we obtain the bias and statistical
error of the estimated power spectrum and construct an unbiased
version of the ![]() 's of the CMB. This unbiased power spectrum
is used to recover the CMB map from the three clean channels through
Wiener filter in harmonic space. Finally, we estimate the noise per
pixel of the reconstructed map using CMB plus noise simulations.
's of the CMB. This unbiased power spectrum
is used to recover the CMB map from the three clean channels through
Wiener filter in harmonic space. Finally, we estimate the noise per
pixel of the reconstructed map using CMB plus noise simulations.
One of the advantages of SEVEM is that it does not need any external
data set or need to make any assumptions about the frequency dependence or
the power spectra of the foregrounds, other than the fact that they
are the dominant contribution at the lowest and highest frequency
channels. This makes the method very robust and, therefore, it is
expected to perform well for real PLANCK data. Moreover, SEVEM
provides a good recovery of the power spectrum up to relatively hig ![]() and a small error in the CMB map reconstruction. In addition
the method is very fast, which allows one to characterise the errors
of the CMB power spectrum and map using simulations. The cleaning of
the data takes around 20 mn, while the estimation of the power
spectrum and map requires around 15 and 30 mn respectively. In
fact, the whole process described, including producing simulations to
estimate the bias and errors, takes around 30 h on one single CPU.
Regarding weak points, the method reconstructs only the CMB
and does not try to recover any other component of the microwave sky
although it could be generalised to reconstruct simultaneously the
both the CMB and the thermal SZ effect. Also, the reconstructed CMB map is not
full-sky, since the method does not aim to remove the strong
contamination at the centre of the Galactic plane or at the point
source positions. In any case, the masked region excluded for the
analysis is relatively small.
and a small error in the CMB map reconstruction. In addition
the method is very fast, which allows one to characterise the errors
of the CMB power spectrum and map using simulations. The cleaning of
the data takes around 20 mn, while the estimation of the power
spectrum and map requires around 15 and 30 mn respectively. In
fact, the whole process described, including producing simulations to
estimate the bias and errors, takes around 30 h on one single CPU.
Regarding weak points, the method reconstructs only the CMB
and does not try to recover any other component of the microwave sky
although it could be generalised to reconstruct simultaneously the
both the CMB and the thermal SZ effect. Also, the reconstructed CMB map is not
full-sky, since the method does not aim to remove the strong
contamination at the centre of the Galactic plane or at the point
source positions. In any case, the masked region excluded for the
analysis is relatively small.
The principle of SMICA can be summarised in three steps:
1) compute spectral statistics; 2) fit a component-based model to them;
3) use the result to implement a Wiener filter in harmonic space.
More specifically, an idealised operation goes as follows.
Denote
![]() the column vector whose ith entry contains
the observation in direction
the column vector whose ith entry contains
the observation in direction ![]() for the i-th channel and denote
for the i-th channel and denote
![]() the vector of same size (the number of frequency
channels) in harmonic space.
This is modelled as the superposition of C components
the vector of same size (the number of frequency
channels) in harmonic space.
This is modelled as the superposition of C components
![]() .
In Step 1), we compute spectral matrices
.
In Step 1), we compute spectral matrices
![]() .
In Step 2) we model the ensemble-averaged spectral matrix
.
In Step 2) we model the ensemble-averaged spectral matrix
![]() as the superposition of C uncorrelated components:
as the superposition of C uncorrelated components:
![]() and, for each component, we postulate
a parametric model, that is, we let the matrix set
and, for each component, we postulate
a parametric model, that is, we let the matrix set
![]() be a function of a
parameter vector
be a function of a
parameter vector ![]() .
This parameterization embodies our prior knowledge about a given
component. For instance, for the CMB component, we take
.
This parameterization embodies our prior knowledge about a given
component. For instance, for the CMB component, we take
![]() where ei is the known CMB
emmission coefficient for channel i and
where ei is the known CMB
emmission coefficient for channel i and ![]() is the unknown
angular power spectrum at frequency
is the unknown
angular power spectrum at frequency ![]() .
The parameter vector for CMB
would then be
.
The parameter vector for CMB
would then be
![]() .
All unknown parameters for all components are then estimated by fitting the
model to the spectral statistics, i.e. by solving
.
All unknown parameters for all components are then estimated by fitting the
model to the spectral statistics, i.e. by solving
![]() where
where
![]() is a measure of mismatch between two covariance matrices
is a measure of mismatch between two covariance matrices
![]() and
and
![]() .
The resulting values
.
The resulting values
![]() provide estimates
provide estimates
![]() of
of
![]() .
The Wiener filter estimate of
.
The Wiener filter estimate of
![]() can be expressed
as
can be expressed
as
![]() .
In practice, we use the fitted spectral matrices estimated at the previous step: component c is estimated as
.
In practice, we use the fitted spectral matrices estimated at the previous step: component c is estimated as
| (A.12) |
For processing the current data set, we have used a model containing four components: the CMB, the SZ component, a 4-dimensional Galactic component and a noise component.
The actual processing includes several modifications with respect to
this outline: a) beam correction applied to each spectral matrix
![]() ;
b) spectral binning by which the (beam corrected)
spectral matrices are averaged over bins of increasing lengths; c)
localization implemented via aopdised masks, by which the SMICA
process is conducted independently over two different sky zones.
;
b) spectral binning by which the (beam corrected)
spectral matrices are averaged over bins of increasing lengths; c)
localization implemented via aopdised masks, by which the SMICA
process is conducted independently over two different sky zones.
Strengths: a) no prior information used regarding Galactic emission; b) accurate recovery of the CMB via Wiener filtering; c) it is a relatively fast algorithm; d) built-in goodness of fit.
Weaknesses: a) the results reported here do not account for the contribution of point sources for which a convenient model is lacking; b) localization in two zones is probably too crude; c) no separation of Galactic components.
WI-FIT (Hansen et al. 2006) is based on fitting and subtraction of internal templates. Regular (external) template fitting uses external templates of Galactic components based on observations at frequencies different from the ones used to study the CMB. These templates are fitted to CMB data, the best fit coefficients for each component are found and the templates are subtracted from the map using these coefficients in order to obtain a clean CMB map. WI-FIT differs from this procedure in two respects: (1) it does not rely on external observations of the galaxy but forms templates by taking the difference of CMB maps at different channels. The CMB temperature is equal at different frequencies whereas the Galactic components are not. For this reason, the difference maps contain only a sum of Galactic components. A set of templates are constructed from difference maps based on different combinations of channels; (2) the fitting of the templates are done in wavelet space where the uncertainty on the foreground coefficients is much lower than a similar pixel based approach (in the pixel based approach, no pixel-pixel correlations are taken into account since the correlation matrix will become to large for PLANCK-like data sets. In the wavelet based approach, a large part of these correlations are taken into account in scale-scale covariance matrices).
For calibration purposes, a set of 500 simulated CMB maps need to be produced and the full wavelet fitting procedure applied to all maps. This is where most CPU time goes. For PLANCK resolution maps, around 1 Gb of memory is necessary to apply WI-FIT and a total of around 400 CPU h are required.
The strength of WI-FIT is that it relies on very few assumptions about the Galactic components. WI-FIT does however assume that the spectral indices do not vary strongly from pixel to pixel within the frequency range used in the analysis. If this assumption is wrong then WI-FIT leaves residuals in the areas where there are strongly varying spectral indices.
Another advantage of WI-FIT is that it is easy to apply and is completely linear, i.e. the resulting map is a linear combination of frequency channels with well known noise and beam properties. This will in general result in increased noise variance in the cleaned map. In order to avoid this, we smooth the internal templates in order to make the noise at small scales negligable and at the same time not make significant changes to the shape of the diffuse foregrounds. If the diffuse foregrounds turn out to be important at small scales l>300, the smoothing of the internal templates will significantly reduce the ability of WI-FIT to perform foreground cleaning at these scales. Tests on the WMAP data have shown that diffuse foregrounds do not seem to play an important role at such small scales. This is valid for the frequency range observed by WMAP (i.e. at LFI-frequencies), similar tests will need to be made for the PLANCK HFI data.
Finally, WI-FIT does not do anything to the point sources, which need to be masked.