A&A 490, 1103-1107 (2008)
DOI: 10.1051/0004-6361:20079004
The role of the stellar rotation on the internal constitution of PV Cassiopeiae
(Research Note)
A. Claret
Instituto de Astrofísica de Andalucía, CSIC, Apartado 3004, 18080 Granada, Spain
Received 6 November 2007 / Accepted 23 August 2008
Abstract
Aims. It has been suggested that the observed apsidal-motion of PV Cas agrees with theoretical predictions. However, this view is not supported by other investigations of the same system. By using standard and rotating models, we re-analyse the evolutionary status of PV Cas, which is poorly established, especially its apsidal-motion.
Methods. We computed standard (without rotation) stellar models for the precise observed masses of PV Cas by considering a moderate amount of core overshooting (
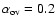 ). Rotating models - assuming solid-body rotation and local conservation of angular momentum - were also computed to verify the influence of rotation on the astrophysical properties of the system.
). Rotating models - assuming solid-body rotation and local conservation of angular momentum - were also computed to verify the influence of rotation on the astrophysical properties of the system.
Results. Considering the limitations of the theoretical models, rotation does not appear to have a significant influence on the modelling of PV Cas. Rotating, in addition to standard models, are able to reproduce the the masses, radii, and TR (effective temperature ratio) of PV Cas without a rapidly rotating core, surrounded by a slowly rotating envelope. Although our rotating models provide more mass-concentrated configurations, the improvement is insufficient to reproduce the observed apsidal-motion rate. Given the error bars, the discrepancy between theory and observation, in terms of apsidal-motion, appears to be real.
Key words: stars: binaries: eclipsing - stars: evolution - stars: rotation - stars: interiors
The double-lined eclipsing binary system (DLEBS) PV Cas has been the subject
of systematic investigations, mainly concerning its apsidal-motion.
The first robust determination of its absolute dimensions was achieved by Popper
(1987), who, using 29 spectrograms, was able to derive mean error bars of 2% in mass
and radius. The system also showed apsidal-motion (Giménez & Margrave 1982).
It was therefore found to be interesting to compare its observational data with the theoretical predictions of evolutionary
models. A number of comparisons have been completed for PV Cas with specific consideration of its apsidal-motion rate
(Claret &
Gimenez 1993; Barembaum & Etzel 1995; Claret & Willems 2002).
A systematic difference between the observed apsidal motion constant and that
theoretically predicted was detected in the sense that the models seems to be less
mass-concentrated than indicated by the observational data. Even considering the
effects of the dynamic tides and rotation (Claret & Willems 2002) such
a discrepancy cannot be removed. A more recent analysis of PV Cas (Svaricek et al. 2008)
supports this trend.
Yildiz (2005) presented an alternative analysis of PV Cas, which
appears to provide closer agreement between the observed and theoretical apsidal-motion
rates. His numerical procedure is similar to that used to analyse EK Cep
(Yildiz 2003). Given that the evolutionary status of PV Cas appears to be insufficiently clear - especially its apsidal-motion - we complete a reanalysis by adopting both standard and rotating stellar models.
The observed masses, radii, and effective temperatures of DLEBS are often used to test
stellar models. However, effective temperatures are not directly
measured. They depend on calibrations, based on atmosphere models, which are dependent on the
adopted opacities, plane-parallel approach, and the extinction law. A clear example of this problem is the case of EK Cep (Claret 2006). This does not appear to be an isolated case because
observational data of eclipsing binaries are found to exhibit significant internal scatter in relations used to provide distance indicators, as
pointed out by Alves (2004). This may indicate that
a serious and systematic problem may be present in the derivation of the effective
temperature of these stars. The corresponding error bars also appear to be, in some cases,
too optimistic. For the particular case of PV Cas, Barembaum & Etzel (1995) suggested the presence of a spot on one of its components, and Popper (1987) reported an effective temperature excess
relative to calibrated
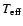 scales.
scales.
To avoid these problems we therefore decided to adopt the effective temperature
ratio
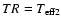 /
/
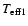 ,
instead of their absolute values, because this ratio was determined far more
accurately from the light curve analysis and is not dependent on calibrations. The relevant
astrophysical data for PV Cas that will be used in this paper are presented in
Table 1.
,
instead of their absolute values, because this ratio was determined far more
accurately from the light curve analysis and is not dependent on calibrations. The relevant
astrophysical data for PV Cas that will be used in this paper are presented in
Table 1.
Table 1:
Astrophysical parameters for PV Cas (solar, K units).
The code that we use in this investigation was described by Claret (2004) and more
details can be found in that paper.
The only novelty is the incorporation of nuclear reaction
14N(p, 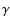 )15O measurements from Runkle (2003) and Formicola et al. (2004).
To derive the theoretical apsidal-motion constants kj, we must integrate
the Radau differential equation.
Kopal (1978) showed that the apsidal-motion constants kj can be written in
a simpler form if we consider that the mass is centrally concentrated (see
for example, Claret & Giménez 1989).
However, the models have finite degree of mass concentration and the use of
the Kopal equation is limited. Claret & Giménez (1989) and Claret (2006) used more realistic models than polytropes, to show that the hypothesis formulated by Kopal is
highly arbitrary and a systematic deviation is detected if it is adopted instead
of the appropriate Radau differential equation. This systematic
effect, as we see in the following sections, is critical to the interpretation
of the apsidal-motion of PV Cas.
)15O measurements from Runkle (2003) and Formicola et al. (2004).
To derive the theoretical apsidal-motion constants kj, we must integrate
the Radau differential equation.
Kopal (1978) showed that the apsidal-motion constants kj can be written in
a simpler form if we consider that the mass is centrally concentrated (see
for example, Claret & Giménez 1989).
However, the models have finite degree of mass concentration and the use of
the Kopal equation is limited. Claret & Giménez (1989) and Claret (2006) used more realistic models than polytropes, to show that the hypothesis formulated by Kopal is
highly arbitrary and a systematic deviation is detected if it is adopted instead
of the appropriate Radau differential equation. This systematic
effect, as we see in the following sections, is critical to the interpretation
of the apsidal-motion of PV Cas.
More accurate observational data and the modern input physics for the evolutionary models
are responsible for the improvement in the comparison between theory and observations of
DLEBS, including the apsidal-motion rate (Claret & Giménez 1993; Pols et al. 1997;
Lastennet & Valls-Gabaud 2002; Claret & Willems 2002). Among the evolutionary code developments that have refined the theoretical calculations are new opacity tables and the introduction of moderate core overshooting. Concerning the apsidal-motion rates,
Yildiz (2005) concluded that the introduction of core overshooting increases the
discrepancies between theory and observation. However, this conclusion is not
suppported by several studies (see for example, Claret & Giménez 1993;
Southworth et al. 2004; Claret & Willems 2002; Claret 2007).
Given that core overshooting appears necessary to reproduce the observations of
DLEBS and the colour-magnitude diagram of
clusters (VandenBerg et al. 2006; Paunzen et al. 2006, and references therein) we
adopt for the models of PV Cas the value of
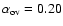 .
For PV Cas, we use
(X, Z) = (0.70, 0.02), which
represents the average chemical composition derived by using several DLEBS. As previously
mentioned, we adopt the effective temperature ratio as a constraint to avoid systematic effects (see Sect. 2) that may affect, for example, the inferred chemical composition.
However, it is interesting to compare our predictions of the absolute effective temperatures for
both components of PV Cas. We found that the differences between the observed and the theoretical values are of the order of -0.04 dex. This is certainly a significant discrepancy,
which could be reduced by using models with higher metal content. It would be invaluable to have new determinations of absolute effective temperatures to compare with our theoretical predictions.
.
For PV Cas, we use
(X, Z) = (0.70, 0.02), which
represents the average chemical composition derived by using several DLEBS. As previously
mentioned, we adopt the effective temperature ratio as a constraint to avoid systematic effects (see Sect. 2) that may affect, for example, the inferred chemical composition.
However, it is interesting to compare our predictions of the absolute effective temperatures for
both components of PV Cas. We found that the differences between the observed and the theoretical values are of the order of -0.04 dex. This is certainly a significant discrepancy,
which could be reduced by using models with higher metal content. It would be invaluable to have new determinations of absolute effective temperatures to compare with our theoretical predictions.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pvcas1.eps}\end{figure}](/articles/aa/full/2008/42/aa9004-07/Timg22.gif) |
Figure 1:
Theoretical standard models for PV Cas. The upper panel shows the effective temperature ratio TR as a function of time (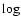 (age)). The middle panel shows the radii of the models as a function of the log (age) (continuous line represents the primary and dashed line denotes the secondary). The two vertical dotted lines illustrate the influence of the radius error bars in the age determination. The horizontal dashed lines indicate the error bars for the primary while the horizontal dotted lines denote the same for the secondary. The bottom panel presents the mean apsidal-motion constant for PV Cas (continuous: Radau equation and short-dashed: Kopal approach). The horizontal lines represent the observational value affected by the error bars (
(age)). The middle panel shows the radii of the models as a function of the log (age) (continuous line represents the primary and dashed line denotes the secondary). The two vertical dotted lines illustrate the influence of the radius error bars in the age determination. The horizontal dashed lines indicate the error bars for the primary while the horizontal dotted lines denote the same for the secondary. The bottom panel presents the mean apsidal-motion constant for PV Cas (continuous: Radau equation and short-dashed: Kopal approach). The horizontal lines represent the observational value affected by the error bars (
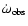 was taken from Svaricev et al. 2008).
was taken from Svaricev et al. 2008). |
| Open with DEXTER |
Figure 1 shows the results for both components of PV Cas.
The first panel illustrates the behaviour of TR versus time, while the second shows the time variation in radius. These plots indicate that PV Cas is not a system that has
evolved too significantly, following the models, the components burnt only about 20% of their
initial hydrogen content. The inferred age is
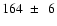 Myr.
The most important consequence of the first two panels of Fig. 1 is that there is
no need to assume a rapidly rotating core surrounded by a slowly rotating envelope, as adopted by Yildiz (2005). We return to this point in the next subsection.
Myr.
The most important consequence of the first two panels of Fig. 1 is that there is
no need to assume a rapidly rotating core surrounded by a slowly rotating envelope, as adopted by Yildiz (2005). We return to this point in the next subsection.
The components of PV Cas are similar (2.81 and 2.76 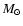 )
and the
individual contribution of each component to the total apsidal-motion rate is
also similar. In the third panel of Fig. 1, we can see the time variation in mean
)
and the
individual contribution of each component to the total apsidal-motion rate is
also similar. In the third panel of Fig. 1, we can see the time variation in mean 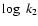 for the two components obtained by integrating
the Radau differential equation (continuous line).
To compute the corresponding
c2 i in Eq. (6) by Claret (2006),
we used the observed rotational velocities provided by Popper (1987).
The observed value was corrected
with the relativistic contribution following Levi-Civita (1937).
The apsidal-motion rate was also corrected for the effects of stellar
rotation (Stothers 1974; Claret 1999), and for dynamic tides (Claret & Willems 2002). Both contributions equalled about 0.02 dex.
The effect of rotation on the theoretical
for the two components obtained by integrating
the Radau differential equation (continuous line).
To compute the corresponding
c2 i in Eq. (6) by Claret (2006),
we used the observed rotational velocities provided by Popper (1987).
The observed value was corrected
with the relativistic contribution following Levi-Civita (1937).
The apsidal-motion rate was also corrected for the effects of stellar
rotation (Stothers 1974; Claret 1999), and for dynamic tides (Claret & Willems 2002). Both contributions equalled about 0.02 dex.
The effect of rotation on the theoretical 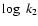 has previously investigated
by Stothers (1974) and Claret (1999) who found that
has previously investigated
by Stothers (1974) and Claret (1999) who found that
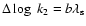 where b was determined by Sothers to be 0.7, b by Claret to be 0.9, and
where b was determined by Sothers to be 0.7, b by Claret to be 0.9, and
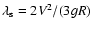 and V is the
rotational velocity. It is interesting to note that Yildiz (2005) found
differences between the corrections in
and V is the
rotational velocity. It is interesting to note that Yildiz (2005) found
differences between the corrections in 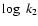 ,
due to rotation, introduced by Stothers and Claret. Since the respective factors differed only in 0.2, the net difference in
,
due to rotation, introduced by Stothers and Claret. Since the respective factors differed only in 0.2, the net difference in
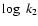 is only about
0.002 dex. Given that Yildiz did not indicate his
value of b and that b determined by Claret is similar to that of Sothers, it is difficult to understand how the Yildiz b value is closer to the
Stother value. To be able to discriminate between values of b that are close (0.7 and 0.9) using the Kopal approach (when we used the Radau equation) is surprising. Unfortunately, Yildiz did not provide a complete report of his results and a more careful comparison with the results of Stothers and Claret is impossible.
is only about
0.002 dex. Given that Yildiz did not indicate his
value of b and that b determined by Claret is similar to that of Sothers, it is difficult to understand how the Yildiz b value is closer to the
Stother value. To be able to discriminate between values of b that are close (0.7 and 0.9) using the Kopal approach (when we used the Radau equation) is surprising. Unfortunately, Yildiz did not provide a complete report of his results and a more careful comparison with the results of Stothers and Claret is impossible.
As can be noted,
there is a discrepancy between the observed and theoretical predicted
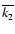 of 0.07 dex.
This is in clear contradiction with the results by Yildiz (2005), who found good agreement with the observed value.
As previously mentioned, the approximation by Kopal (1978) is
inadequate for computing accurately the theoretical k2: calculations that use such an equation provides
more artificially mass-concentrated configurations (smaller k2). Yildiz (2005) applied
his Eq. (9) to evaluate
the apsidal-motion rate. This explains why he found good agreement between
of 0.07 dex.
This is in clear contradiction with the results by Yildiz (2005), who found good agreement with the observed value.
As previously mentioned, the approximation by Kopal (1978) is
inadequate for computing accurately the theoretical k2: calculations that use such an equation provides
more artificially mass-concentrated configurations (smaller k2). Yildiz (2005) applied
his Eq. (9) to evaluate
the apsidal-motion rate. This explains why he found good agreement between
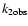 and
and
 .
If we use the Kopal approach, we also find good agreement between
the observed and theoretical apsidal-motion rates (short-dashed line in the third panel of Fig. 1) but
without the need to include a rapidly rotating core.
However, as we have emphasized before, this is an inadequate procedure and the discrepancy
of 0.07 cannot be removed. This result is in good agreement with those found by Claret & Giménez (1993), Barembaum & Etzel (1995), Claret & Willems (2002) and Svaricek et al. (2008).
.
If we use the Kopal approach, we also find good agreement between
the observed and theoretical apsidal-motion rates (short-dashed line in the third panel of Fig. 1) but
without the need to include a rapidly rotating core.
However, as we have emphasized before, this is an inadequate procedure and the discrepancy
of 0.07 cannot be removed. This result is in good agreement with those found by Claret & Giménez (1993), Barembaum & Etzel (1995), Claret & Willems (2002) and Svaricek et al. (2008).
It is well known, all stars rotate. Rotating models are therefore more realistic than standard models in comparing theory and observations.
In the particular case of PV Cas, the effects of rotation or tidal distortions do not to be appear important because no
significant oblateness in the light curves was reported (Popper 1987; Barembaum & Etzel 1995). In addition, the similar components of PV Cas are well within their
Roche lobes (relative radii  0.2 and
0.2 and
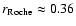 ). They are also no very rapid rotators since
). They are also no very rapid rotators since
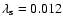 .
Given all of these characteristics, we expect that the effects of rotation are not too important in the case of PV Cas. However, for completeness we explore the capability of rotating models to predict its absolute dimensions and apsidal-motion rate.
.
Given all of these characteristics, we expect that the effects of rotation are not too important in the case of PV Cas. However, for completeness we explore the capability of rotating models to predict its absolute dimensions and apsidal-motion rate.
We adopt a different procedure from that used by Yildiz (2005) to simulate rotation.
The main differences are in how the differential equations of the stellar structure and evolution are modified. Since we describe the method in previous papers, we refer the readers interested in the numerical details to the investigations by Kippenhahn & Thomas (1970); Endal & Sofia (1976); Claret (1999, 2006).
To follow the evolution of the angular velocity, we must integrate a fourth-order differential equation. The results of this equation are between two possibilities:
1) solid-body rotation; and 2) local conservation of angular momentum.
These laws provide limits because for the former one the redistribution
of the angular momentum is complete, while for the second there is no redistribution.
Both laws therefore serve as a reasonable control of the present calculations.
Note that the transport of angular momentum due to rotationally-induced instabilities is not considered because the related diffusion equation is coupled to the differential equation for the evolution of the angular velocity.
Yildiz (2005) proposed that only rotating models - with a rapidly
rotating core - could explain the
physical properties of PV Cas.
His method of introducing rotation may have been inadequate because the only differential equation of the stellar structure that is altered is the hydrostatic one.
All equations of the stellar structure are changed by rotation, and by altering the hydrostatic equation alone, the effects of oblateness can be neglected.
As we have shown in the previous subsection, the standard models
are also able to reproduce the absolute dimensions of PV Cas (and also the apsidal-motion if we adopt the Koppal approach) at a similar age.
Case 1) In order to get an rotating model displaying the observed
rotational velocity of each component of PV Cas, we computed
models with trial initial angular velocities until
the equatorial velocity was similar to that observed. For the observed rotational velocities, we adopted
the values given by Popper (1987), which was 65 km s-1 for both components.
The remaining input physics was the same as that used
in Fig. 1. The value of the angular velocity at the ZAMS was
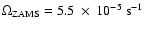 .
The agreement between the observed TR and R (first two panels of Fig. 2)
is reassuring because both parameters
are described by the same isochrone simultaneously. The derived age was
.
The agreement between the observed TR and R (first two panels of Fig. 2)
is reassuring because both parameters
are described by the same isochrone simultaneously. The derived age was
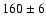 Myr.
Myr.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{pvcas2.eps} \end{figure}](/articles/aa/full/2008/42/aa9004-07/Timg36.gif) |
Figure 2:
The same as for Fig. 1 but taking into account solid rotation.
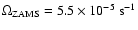 . .
|
| Open with DEXTER |
Figure 2 also illustrates that rotation does not
change drastically the properties of PV Cas since the derived age does not differ significantly from that derived by using
standard models. Obviously, we correct the apsidal-motion rate in the third panel only for the effects of dynamical tides. As expected, rotating models provide more mass-concentrated configurations. However, the improvement is insufficient to describe the observations. The detected discrepancy between the observed and theoretical
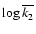 is 0.06.
is 0.06.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{pvcas3.eps} \end{figure}](/articles/aa/full/2008/42/aa9004-07/Timg39.gif) |
Figure 3:
The same as for Fig. 1 but taking into account rotation with local conservation of the angular momentum.
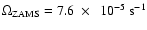 . . |
| Open with DEXTER |
Case 2) We have also computed other series of models by assuming local conservation of
the angular momentum. The results are shown in Fig. 3. The value of
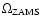 was
was
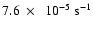 .
Again, the models were able to reproduce the radii and TR of PV Cas for the same isochrone. The derived age did not differ significantly from previous estimates,
.
Again, the models were able to reproduce the radii and TR of PV Cas for the same isochrone. The derived age did not differ significantly from previous estimates, 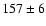 Myr and the ratio
Myr and the ratio
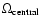 /
/
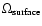 for this isochrone is 1.8. The apsidal-motion rate was found to differ by 0.05 dex, unless the (inappropriate) Kopal approach was adopted (short-dashed line). An example of the systematic
differences between k2 computed using the Kopal approach and those
calculated by integrating the Radau equation is given in Fig. 4. We plotted
log k2 computed by either integrating the Radau equation (continuous line) and adopting
the Kopal approach (dashed line) for several profiles, represented by the ratio
for this isochrone is 1.8. The apsidal-motion rate was found to differ by 0.05 dex, unless the (inappropriate) Kopal approach was adopted (short-dashed line). An example of the systematic
differences between k2 computed using the Kopal approach and those
calculated by integrating the Radau equation is given in Fig. 4. We plotted
log k2 computed by either integrating the Radau equation (continuous line) and adopting
the Kopal approach (dashed line) for several profiles, represented by the ratio
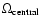 /
/
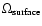 .
The differences are of the order of 0.08 dex and they are
almost independent of
.
The differences are of the order of 0.08 dex and they are
almost independent of
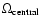 /
/
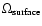 .
These methods only
provide similar results for very evolved configurations, which was not the case for PV Cas.
The profiles connecting
.
These methods only
provide similar results for very evolved configurations, which was not the case for PV Cas.
The profiles connecting
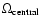 and
and
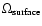 were almost flat, at least in our region of interest. For very evolved configurations, the increase in
were almost flat, at least in our region of interest. For very evolved configurations, the increase in 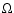 in the central part was more pronounced and for the outer layers the profile was rather flat.
in the central part was more pronounced and for the outer layers the profile was rather flat.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{pvcas4.eps}\end{figure}](/articles/aa/full/2008/42/aa9004-07/Timg46.gif) |
Figure 4:
The apsidal-motion constant as a function of the ratio between the central and surface rotational velocities. Continuous line represents the calculations by integrating the Radau differential equation while dashed one denotes the Kopal approach. Model with 1.81 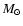 ,
local conservation of the angular momentum and ,
local conservation of the angular momentum and
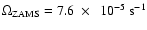 . . |
| Open with DEXTER |
The present results relative to
radii, effective temperature ratio, and apsidal-motion rate are similar,
regardless of whether we adopt models without rotation, with solid rotation, or local
conservation of the angular momentum. This indicates that the models for PV Cas are not affected significantly by rotation, in contrast to the results
of Yildiz (2005). Case 2
can be used to check the ratio of core/envelope rotation ratio and the discontinuity in
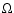 obtained by this
author. The main differences between our rotating models and those by Yildiz (2005) - apart
from the method of introducing rotation - are: 1) no discontinuities in the angular velocities inside any configuration are detected in our models; 2) We have not
detected differences as significant as a factor of 20 between the envelope and nucleus (see his Fig. 8). Only for more evolved models we have found such a high ratio, but without discontinuities in
obtained by this
author. The main differences between our rotating models and those by Yildiz (2005) - apart
from the method of introducing rotation - are: 1) no discontinuities in the angular velocities inside any configuration are detected in our models; 2) We have not
detected differences as significant as a factor of 20 between the envelope and nucleus (see his Fig. 8). Only for more evolved models we have found such a high ratio, but without discontinuities in 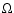 being detected.
For the currently observed radius of PV Cas at an age of 157 Myr, the ratio between central and surface angular velocity is 1.8, which is one order of magnitude smaller than found by Yildiz (2005).
being detected.
For the currently observed radius of PV Cas at an age of 157 Myr, the ratio between central and surface angular velocity is 1.8, which is one order of magnitude smaller than found by Yildiz (2005).
The only direct observational indication of stellar internal rotation is that derived from observations of the Sun (Schou et al. 1998; Chaplin et al. 1999, for a review see Thompson et al. 2003). Although this profile cannot be directly compared with the case of PV Cas, it
does not agree with the profile found by Yildiz. As commented in our paper on EK Cep (Claret 2006), the profiles of internal rotation derived by Yildiz (2005) also yield additional
difficulties. In the boundary core-envelope, the drastic change
in the angular velocity (see his Fig. 8) may introduce some
kind of instability. This rapidly rotating nucleus would possibly
alter the dynamics of the system, changing the rate of apsidal-motion.
Considering the above results and comments, we have been able to
conclude that:
- 1)
- Rotation
appears to have no significant influence on the modeling of PV Cas.
- 2)
- Rotating and standard models are able to fit the radii and TR
of PV Cas without the need to postulate a very fast rotating core,
surrounded by a slow rotator envelope.
- 3)
- The adoption
of Kopal's approach to computing the theoretical k2, in place of the integration of the differential equation of Radau, is an inappropriate procedure because the differences can amount to 0.10-0.20 dex in unevolved systems, as in the case of PV Cas and EK Cep.
- 4)
- Concerning apsidal-motion, the improvement introduced by the rotating models is insufficient to
remove the discrepancy between theory and observation. This discrepancy seems to be real and the components of PV Cas are more mass-concentrated than theoretically predicted.
We have not considered the solutions presented here to be definitive ones; more observations are needed to determine the absolute dimensions (mainly the effective temperatures) of PV Cas as well as the rate of its apsidal-motion. Concerning theoretical models, the introduction of the effects of induced mixing by rotation could shed some light on the evolutionary status of PV Cas. Furthermore, the tidal evolution of PV Cas must be followed in detail. The investigattion of how the external layers decelerate with time is an interesting point beyond the scope of this paper that we plan to study in the future.
Acknowledgements
The Spanish MEC (AYA2006-06375) is gratefully
acknowledged for its support during the development of this work.
- Alves, D. R.
2004, New Astron. Rev., 48, 659 [NASA ADS] [CrossRef]
(In the text)
-
Barembaum, M. J., & Etzel, P. B. 1995, AJ, 109, 2680 [NASA ADS] [CrossRef]
(In the text)
- Chaplin, W.
J., Christensen-Dalsgaard, J., Elsworth, Y., et al. 1999, MNRAS,
308, 405 [NASA ADS] [CrossRef]
(In the text)
- Claret, A. 1999, A&A, 350,
56 [NASA ADS]
- Claret, A.
2004, A&A, 424, 919 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Claret, A.
2006, A&A, 445, 1061 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Claret, A.
2007, A&A, 475, 1019 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Claret, A.,
& Giménez, A. 1989, A&AS, 81, 1 [NASA ADS]
(In the text)
- Claret, A.,
& Giménez, A. 1993, A&A, 277, 487 [NASA ADS]
(In the text)
- Claret, A.,
& Willems, B. 2002, A&A, 388, 518 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Endal, A. S.,
& Sofia, S. 1976, ApJ, 210, 184 [NASA ADS] [CrossRef]
(In the text)
-
Formicola, A., Imbriani, G., Costantini, H., et al. 2004, Phys.
Lett. B, 591, 61 [NASA ADS] [CrossRef]
(In the text)
- Giménez,
A., & Margrave, T. E. 1982, AJ, 93, 672
(In the text)
-
Kippenhahn, R., & Thomas, R. C. 1970, in Stellar Rotation, ed.
A. Slettebak (Gordon and Breach Science Publishers), 20
(In the text)
- Kopal, Z. 1978,
Dynamics of Close Binary System (Dordrecht/Holland: Reidel)
(In the text)
-
Lastennet, E., & Valls-Gabaud, D. 2002, A&A, 396, 551 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Levi-Civita, T.
1937, Amer. J. Math., 59, 225 [CrossRef]
(In the text)
- Paunzen, E.,
Netopil, M., Iliev, I. Kh., et al. 2006, A&A, 454, 171 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Pols, O. R., Tout,
C. A., Schroder, K.-P., Eggleton, P. P., & Manners, J. 1997,
MNRAS, 289, 869 [NASA ADS]
(In the text)
- Popper, D. M.
1987, AJ, 93, 672 [NASA ADS] [CrossRef]
(In the text)
- Runkle, R. C.
2003, Ph. D. Thesis, University of North Carolina, unpublished
(In the text)
- Schou, J., Antia,
H. M., Basu, S., et al. 1998, ApJ, 505, 390 [NASA ADS] [CrossRef]
(In the text)
-
Southworth, J., Maxted, P. F. L., & Smalley, B. 2004, MNRAS,
351, 1277 [NASA ADS] [CrossRef]
(In the text)
- Stothers,
R. 1974, ApJ, 194, 651 [NASA ADS] [CrossRef]
(In the text)
- Svaricek,
P., Wolf, M., Claret, A., et al. 2008, A&A, 477, 615 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Thompson,
M. J., Christensen-Dalsgaard, J., Miesch, M. S., & Toomre, J.
2003, ARA&A, 41, 599 [NASA ADS] [CrossRef]
(In the text)
-
VandenBerg, D. A., Bergbusch, P. A., & Dowler, P. D. 2006,
ApJS, 162, 375 [NASA ADS] [CrossRef]
(In the text)
- Yildiz, M.
2003, A&A, 409, 689 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Yildiz, M.
2005, MNRAS, 363, 967 [NASA ADS] [CrossRef]
(In the text)
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pvcas1.eps}\end{figure}](/articles/aa/full/2008/42/aa9004-07/Timg22.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{pvcas2.eps} \end{figure}](/articles/aa/full/2008/42/aa9004-07/Timg36.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{pvcas3.eps} \end{figure}](/articles/aa/full/2008/42/aa9004-07/Timg39.gif)
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{pvcas4.eps}\end{figure}](/articles/aa/full/2008/42/aa9004-07/Timg46.gif)