A&A 490, 807-810 (2008)
DOI: 10.1051/0004-6361:200810627
Determining parameters of cool giant stars by modeling spectrophotometric and interferometric observations using the SATLAS program
(Research Note)
H. R. Neilson1 - J. B. Lester2
1 - Department of Astronomy & Astrophysics, University of Toronto, Canada
2 - Department of Chemical and Physical Sciences, University of Toronto Mississauga, Canada
Received 16 July 2008 / Accepted 12 September 2008
Abstract
Context. Optical interferometry is a powerful tool for observing the intensity structure and angular diameter of stars. When combined with spectroscopy and/or spectrophotometry, interferometry provides a powerful constraint for model stellar atmospheres.
Aims. The purpose of this work is to test the robustness of the spherically symmetric version of the ATLAS stellar atmosphere program, SATLAS, using interferometric and spectrophotometric observations.
Methods. Cubes (three dimensional grids) of model stellar atmospheres, with dimensions of luminosity, mass, and radius, are computed to fit observations for three evolved giant stars, 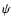 Phoenicis,
Phoenicis, 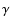 Sagittae, and
Sagittae, and 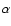 Ceti. The best-fit parameters are compared with previous results.
Ceti. The best-fit parameters are compared with previous results.
Results. The best-fit angular diameters and values of 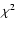 are consistent with predictions using PHOENIX and plane-parallel ATLAS models. The predicted effective temperatures, using SATLAS, are about 100 to 200
are consistent with predictions using PHOENIX and plane-parallel ATLAS models. The predicted effective temperatures, using SATLAS, are about 100 to 200 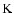 lower, and the predicted luminosities are also lower due to the differences in effective temperatures.
lower, and the predicted luminosities are also lower due to the differences in effective temperatures.
Conclusions. It is shown that the SATLAS program is a robust tool for computing models of extended stellar atmospheres that are consistent with observations. The best-fit parameters are consistent with predictions using PHOENIX models, and the fit to the interferometric data for 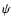 Phe differs slightly, although both agree within the uncertainty of the interferometric observations.
Phe differs slightly, although both agree within the uncertainty of the interferometric observations.
Key words: stars: atmospheres - stars: fundamental parameters - stars: late-type
Optical interferometry accurately measures the combination of the angular diameter and the structure of the intensity distribution of a stellar disk. The combination of interferometry with spectroscopy and/or spectrophotometry is a powerful tool for determining effective temperatures and other properties of stars, and the growth of optical interferometry is testing theoretical models of stellar atmospheres in new ways.
In a series of articles, Wittkowski et al. (2006a,2004,2006b) fit Very Large Telescope Interferometer (VLTI) observations of cool giants using the VINCI instrument with spherically symmetric stellar atmosphere models in local thermodynamic equilibrium (LTE) computed with the PHOENIX program (Hauschildt et al. 1999), and with plane parallel models from PHOENIX and ATLAS (Kurucz 1970,1993). The authors demonstrated that optical interferometry can detect the wavelength-dependent limb-darkening of cool giants and that the limb-darkening can be used to constrain model stellar atmospheres. These works are based on observations of three stars: 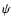 Phoenicis (M4 III),
Phoenicis (M4 III), 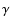 Sagittae (M0 III), and
Sagittae (M0 III), and 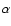 Ceti (M1.5 III) also called Menkar.
Ceti (M1.5 III) also called Menkar.
The purpose of this note is to model these interferometric observations using the new spherically symmetric version of the ATLAS program (SATLAS) developed by Lester & Neilson (2008) and to determine fundamental parameters of the three stars. There are two versions of the SATLAS program, one using opacity distribution functions while the other uses opacity sampling; in this work we use the first version. The radiation field is computed using the method suggested by Rybicki (1971), which is a reorganization of the Feautrier (1964) method.
In this work we compute cubes (three dimensional grids) of spherically symmetric stellar atmospheres with dimensions of luminosity, mass, and radius to model interferometric visibilities to fit the VLTI/VINCI observations and broadband spectrophotometry from Johnson & Mitchell (1975). This will provide a robust test of the program and a comparison to the results predicted using spherically symmetric PHOENIX models. In the next section, we outline the method for computing synthetic visibilities and predicting radii, effective temperatures, luminosities, masses, and gravities. We present the results in the third section and the discussion in the fourth section.
The goal of this note is to determine the global properties of the three observed stars. Interferometric observations are ideal for measuring the angular diameter, and with the HIPPARCOS parallax (Perryman & ESA 1997) one can find the linear radii of the stars. The visibility (Tango & Davis 2002; Davis et al. 2000) at wavelength 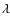 is
is
![\begin{displaymath}%
V_{\rm {LD}}(\lambda) = \int_0^1S_\lambda I_\lambda(\mu)J_0...
..._{\rm {LD}}(B/\lambda)(1 - \mu^2)^{1/2}\right] \mu \rm {d}\mu.
\end{displaymath}](/articles/aa/full/2008/41/aa10627-08/img35.gif) |
(1) |
In this equation, 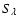 is the sensitivity function of the instrument (VINCI in this case) (Kervella et al. 2000), J0 is the zeroth-order Bessel function, B is the length of the baseline of the interferometer, and
is the sensitivity function of the instrument (VINCI in this case) (Kervella et al. 2000), J0 is the zeroth-order Bessel function, B is the length of the baseline of the interferometer, and 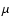 is the cosine of the angle between the center of the stellar disk and a distance from the center. The center of the disk corresponds to
is the cosine of the angle between the center of the stellar disk and a distance from the center. The center of the disk corresponds to 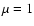 and the edge of the disk is
and the edge of the disk is 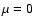 as seen from the center of the star. To match the broadband VLTI/VINCI observations, the monochromatic model visibilities must be integrated and squared to get the squared visibility amplitudes,
as seen from the center of the star. To match the broadband VLTI/VINCI observations, the monochromatic model visibilities must be integrated and squared to get the squared visibility amplitudes,
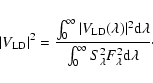 |
(2) |
The denominator of Eq. (2) normalizes the visibilities, where 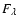 is the flux of model. For a given model atmosphere, we can find the best-fit angular diameter with a minimum
is the flux of model. For a given model atmosphere, we can find the best-fit angular diameter with a minimum 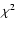 value.
value.
The next step is to use the model stellar atmospheres to fit spectrophotometric observations. The purpose of fitting spectrophotometry is to constrain the effective temperature and the stellar flux; however, the effective temperature is dependent on the angular diameter. The modeled flux is scaled using the same method and assumptions as in Wittkowski et al. (2004) to fit the broadband data from Johnson & Mitchell (1975). The best-fit effective temperature is determined using the best-fit angular diameter from the interferometric fit to break the degeneracy.
The linear radius of the star is determined using the best-fit angular diameter and HIPPARCOS parallax, and the luminosity is calculated using the radius and the effective temperature. The mass and gravity are constrained by comparing the predicted effective temperature and luminosity with theoretical stellar evolution tracks (Girardi et al. 2000).
For each of the three stars, we compute a cube of models with luminosity, mass, and radius as input parameters. The metallicity is assumed to be solar, consistent with the conclusions of Feast et al. (1990), and the microturbulence is zero. These assumptions can be tested, but for this work variations of metallicity and microturbulence are ignored. The range of values for the input mass, luminosity and radius are chosen based on the results of Wittkowski et al. (2006a,2004,2006b).
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0627f5.eps}\\
\includegraphics[width=6.5cm,clip]{0627f1a.eps}
\end{figure}](/articles/aa/full/2008/41/aa10627-08/Timg42.gif) |
Figure 1:
Values of minimum 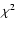 for each model stellar atmosphere for fitting the interferometric data of
for each model stellar atmosphere for fitting the interferometric data of 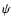 Phe as a function of (top)
Phe as a function of (top)
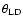 and (bottom)
and (bottom)
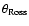 . . |
| Open with DEXTER |
For 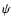 Phe, the mass range is chosen to be 0.6 to
Phe, the mass range is chosen to be 0.6 to
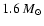 in steps of
in steps of
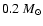 ;
the luminosity range is 630 to
;
the luminosity range is 630 to
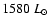 in steps of
in steps of
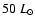 and the radius range is 60 to
and the radius range is 60 to
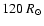 in steps of
in steps of
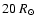 .
There are 480 models computed for
.
There are 480 models computed for 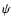 Phe. The mass range for
Phe. The mass range for 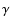 Sge is 1.0 to
Sge is 1.0 to
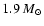 in steps of
in steps of
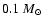 ,
the luminosity range is 400 to
,
the luminosity range is 400 to
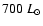 in steps of
in steps of
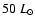 and the radius range is 30 to
and the radius range is 30 to
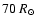 in steps of
in steps of
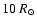 ,
leading to 350 models for this star. There are 1680 models computed for
,
leading to 350 models for this star. There are 1680 models computed for 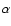 Cet to provide a larger range of parameters and a more robust test of the SATLAS program. The mass range is 1.5 to
Cet to provide a larger range of parameters and a more robust test of the SATLAS program. The mass range is 1.5 to
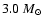 in steps of
in steps of
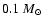 ,
the luminosity range is 103 to
,
the luminosity range is 103 to
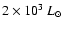 in steps of
in steps of
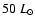 and the radius range is 60 to
and the radius range is 60 to
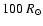 in steps of
in steps of
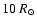 .
.
We fit the limb-darkened angular diameter,
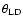 ,
to the interferometric observations of each star and find a minimum value of
,
to the interferometric observations of each star and find a minimum value of 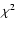 .
The limb-darkened angular diameter is the angular diameter to the edge of the stellar disk corresponding to the the layer where
.
The limb-darkened angular diameter is the angular diameter to the edge of the stellar disk corresponding to the the layer where 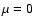 ,
and from the stellar atmosphere models we determine the Rossland angular diameter by multiplying
,
and from the stellar atmosphere models we determine the Rossland angular diameter by multiplying
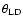 by the ratio of radius of the stellar atmosphere model at
by the ratio of radius of the stellar atmosphere model at
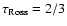 to the radius of the outermost shell of that model, although this outermost shell is determined by an arbitrary choice of the minimum
to the radius of the outermost shell of that model, although this outermost shell is determined by an arbitrary choice of the minimum
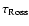 when the model is computed. The quality of fit to the interferometric data is sensitive to the Rossland angular diameter, as was noted by Wittkowski et al. (2004). The minimum
when the model is computed. The quality of fit to the interferometric data is sensitive to the Rossland angular diameter, as was noted by Wittkowski et al. (2004). The minimum 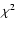 values are shown in Fig. 1 as a function of limb-darkened and Rossland angular diameter for each model for the case of
values are shown in Fig. 1 as a function of limb-darkened and Rossland angular diameter for each model for the case of 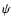 Phe. The best-fit Rossland angular diameter is well constrained by interferometry and the values of the Rossland and limb-darkened angular diameters, along with the uncertainty of the fit, for each star is given in Table 1. The Rossland angular diameter has a smaller uncertainty than the limb-darkened angular diameter for each star because the fits to the interferometric data produce less variation of the Rossland angular diameter than the limb-darkened angular diameter. This variation is clearly shown in Fig. 1.
Phe. The best-fit Rossland angular diameter is well constrained by interferometry and the values of the Rossland and limb-darkened angular diameters, along with the uncertainty of the fit, for each star is given in Table 1. The Rossland angular diameter has a smaller uncertainty than the limb-darkened angular diameter for each star because the fits to the interferometric data produce less variation of the Rossland angular diameter than the limb-darkened angular diameter. This variation is clearly shown in Fig. 1.
Table 1:
Best-fit parameters of the three stars.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0627f2a.eps}\par\includegraphics[width=6.5cm,clip]{0627f2b.eps}
\end{figure}](/articles/aa/full/2008/41/aa10627-08/Timg100.gif) |
Figure 2:
(Top) The visibilities calculated for three SATLAS models and the interferometric data for 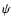 Phe. (Bottom) Close-up of the second lobe of the visibility amplitude. The dotted line refers to the model stellar atmosphere for
Phe. (Bottom) Close-up of the second lobe of the visibility amplitude. The dotted line refers to the model stellar atmosphere for
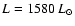 , ,
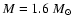 ,
and ,
and
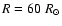 ,
the dot-dashed line represents a model with ,
the dot-dashed line represents a model with
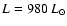 , ,
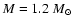 ,
and ,
and
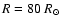 ,
and the dashed line is for ,
and the dashed line is for
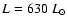 , ,
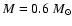 ,
and ,
and
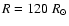 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0627f3.eps}
\end{figure}](/articles/aa/full/2008/41/aa10627-08/Timg110.gif) |
Figure 3:
The visibilities calculated for three SATLAS models and the interferometric data for 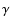 Sge. The dotted line refers to the model stellar atmosphere for
Sge. The dotted line refers to the model stellar atmosphere for
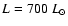 , ,
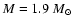 ,
and ,
and
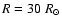 ,
the dot-dashed line represents a model with ,
the dot-dashed line represents a model with
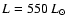 , ,
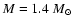 ,
and ,
and
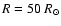 ,
and the dashed line is for ,
and the dashed line is for
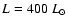 , ,
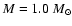 ,
and ,
and
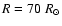 . . |
| Open with DEXTER |
The model visibilities are shown in Fig. 2 for 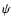 Phe, with a close-up of the second lobe, Fig. 3 for
Phe, with a close-up of the second lobe, Fig. 3 for 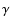 Sge, and Fig. 4 for
Sge, and Fig. 4 for 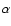 Ceti with a close-up of the second lobe shown. The displayed model visibilities are chosen to be the smallest, middle and largest luminosity and gravity from each cube of models. The model visibilities for
Ceti with a close-up of the second lobe shown. The displayed model visibilities are chosen to be the smallest, middle and largest luminosity and gravity from each cube of models. The model visibilities for 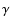 Sge and
Sge and 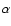 Cet agree with the results of Wittkowski et al. (2006a,b). For
Cet agree with the results of Wittkowski et al. (2006a,b). For 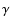 Sge, there is not enough information to test the limb-darkening of the model atmospheres. While the model visibilities using SATLAS and PHOENIX both fit the observed interferometric data well within the uncertainties of the observations, the minimum value of the
Sge, there is not enough information to test the limb-darkening of the model atmospheres. While the model visibilities using SATLAS and PHOENIX both fit the observed interferometric data well within the uncertainties of the observations, the minimum value of the 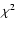 from fitting the SATLAS models is smaller than that using the PHOENIX models. This implies that there are small differences in the model atmosphere intensity structures predicted from each program. It is not obvious why the predictions using PHOENIX models and SATLAS models differ in this case.
from fitting the SATLAS models is smaller than that using the PHOENIX models. This implies that there are small differences in the model atmosphere intensity structures predicted from each program. It is not obvious why the predictions using PHOENIX models and SATLAS models differ in this case.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0627f4a.eps}\par\includegraphics[width=6.7cm,clip]{0627f4b.eps}
\end{figure}](/articles/aa/full/2008/41/aa10627-08/Timg118.gif) |
Figure 4:
(Top) The visibilities calculated for three SATLAS models and the interferometric data for 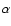 Cet. (Bottom) Close-up of the second lobe of the visibility amplitude. The dotted line refers to the model stellar atmosphere for
Cet. (Bottom) Close-up of the second lobe of the visibility amplitude. The dotted line refers to the model stellar atmosphere for
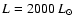 , ,
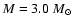 ,
and ,
and
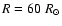 ,
the dot-dashed line represents a model with ,
the dot-dashed line represents a model with
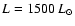 , ,
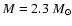 ,
and ,
and
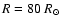 ,
and the dashed line is for ,
and the dashed line is for
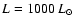 , ,
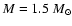 ,
and ,
and
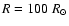 . .
|
| Open with DEXTER |
Having fit the interferometric data, we next fit the broadband spectrophotometric data. One concern about fitting stellar atmosphere models to spectrophotometry is that the effective temperature and Rossland angular diameter are related. In Fig. 5, we compare the best-fit values of Rossland angular diameter as a function of the best-fit effective temperature for each model for fitting 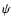 Phe. The predicted angular diameter is almost constant with respect to effective temperature for the fit to interferometry. Therefore the interferometric fit of the Rossland angular diameter is used to constrain the predicted effective temperature. This process is repeated for the other two stars and the best-fit effective temperatures are given in Table 1.
Phe. The predicted angular diameter is almost constant with respect to effective temperature for the fit to interferometry. Therefore the interferometric fit of the Rossland angular diameter is used to constrain the predicted effective temperature. This process is repeated for the other two stars and the best-fit effective temperatures are given in Table 1.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0627f1b.eps}
\end{figure}](/articles/aa/full/2008/41/aa10627-08/Timg119.gif) |
Figure 5:
The best-fit effective temperature as a function of Rossland angular diameter found by fitting spectrophotometry (+'s) and interferometry (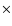 's) for 's) for 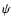 Phe.
Phe. |
| Open with DEXTER |
The next step is to calculate the linear radius and luminosity of the stars. Using the HIPPARCOS parallax with the predicted Rossland angular diameter, we determine the radius of each star, the values of the parallax and radius are given in Table 1. The stellar luminosity is determined using the effective temperature and radius,
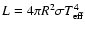 .
The best-fit effective temperature and luminosity for each star is plotted in Fig. 6 along with evolutionary tracks from Girardi et al. (2000) to determine the mass and gravity of each star.
.
The best-fit effective temperature and luminosity for each star is plotted in Fig. 6 along with evolutionary tracks from Girardi et al. (2000) to determine the mass and gravity of each star.
![\begin{figure}
\par\includegraphics[]{0627f6.eps}
\end{figure}](/articles/aa/full/2008/41/aa10627-08/Timg121.gif) |
Figure 6:
Comparison of the derived effective temperatures and luminosities of the three stars relative the derived parameters from previous analyses. The lines are evolutionary tracks from Girardi et al. (2000), the points given by 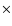 's are the predicted effective temperatures and luminosities found using the SATLAS models and the plusses are the values found using PHOENIX models. 's are the predicted effective temperatures and luminosities found using the SATLAS models and the plusses are the values found using PHOENIX models. |
| Open with DEXTER |
The purpose of this work is to test the spherical version of the ATLAS program. By fitting interferometric and spectrophotometric observations using model stellar atmospheres, we derive the properties of 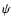 Phe,
Phe, 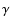 Sge, and
Sge, and 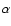 Cet. The derived parameters are compared to earlier results. The angular diameters that are determined by fitting model stellar atmospheres to interferometric observations are the same, except for
Cet. The derived parameters are compared to earlier results. The angular diameters that are determined by fitting model stellar atmospheres to interferometric observations are the same, except for 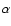 Cet, for which we predict an angular diameter that is 0.1 mas smaller. The differences in predicted angular diameter are likely due to differences in limb-darkening of the model atmospheres generated using SATLAS and PHOENIX. Also our minimum
Cet, for which we predict an angular diameter that is 0.1 mas smaller. The differences in predicted angular diameter are likely due to differences in limb-darkening of the model atmospheres generated using SATLAS and PHOENIX. Also our minimum 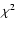 value of the fit of the limb-darkened angular diameter for
value of the fit of the limb-darkened angular diameter for 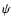 Phe, 1.66, is smaller than the predicted value of
Phe, 1.66, is smaller than the predicted value of 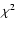 from the spherically symmetric PHOENIX models, 1.8. The SATLAS models for
from the spherically symmetric PHOENIX models, 1.8. The SATLAS models for 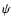 Phe that best fit the interferometric data have effective temperatures in the range of 4000 to 4500 K, while the PHOENIX models from Wittkowski et al. (2004) are all 3550 and 3600 K. The fit of the SATLAS models to spectrophotometric observations predict an effective temperature of 3415 K conflicting with the prediction of a higher temperature. For the effective temperature range of 3400 to 3800 K, the minimum
Phe that best fit the interferometric data have effective temperatures in the range of 4000 to 4500 K, while the PHOENIX models from Wittkowski et al. (2004) are all 3550 and 3600 K. The fit of the SATLAS models to spectrophotometric observations predict an effective temperature of 3415 K conflicting with the prediction of a higher temperature. For the effective temperature range of 3400 to 3800 K, the minimum 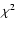 values predicted by fitting SATLAS models are 1.70 to 1.72, similar to the values found using plane-parallel ATLAS models.
values predicted by fitting SATLAS models are 1.70 to 1.72, similar to the values found using plane-parallel ATLAS models.
The fit of the SATLAS models to broadband spectrophotometric observations are used to determine the effective temperatures of the three stars because spectrophotometry is much more sensitive to the effective temperature than interferometry. The predicted effective temperatures are smaller than those found in the previous works, but this difference is due to the methods used for determining the effective temperature, not differences in the stellar atmosphere programs. If we use the method from Wittkowski et al. (2004) where the bolometric flux
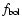 is calculated by integrating the spectrophotometric data and then
is calculated by integrating the spectrophotometric data and then
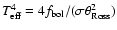 ,
we would predict similar effective temperatures. Any variation in that case would be due to differences in the calculation of the bolometric flux and differences in the angular diameter. This suggests the effective temperatures here would differ by at most
,
we would predict similar effective temperatures. Any variation in that case would be due to differences in the calculation of the bolometric flux and differences in the angular diameter. This suggests the effective temperatures here would differ by at most 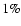 .
Our results also differ because of the spectrophotometric data used. The difference is smallest for
.
Our results also differ because of the spectrophotometric data used. The difference is smallest for 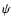 Phe because the PHOENIX and SATLAS fits both use the same spectrophotometric data for the fitting and agree within the uncertainty. For
Phe because the PHOENIX and SATLAS fits both use the same spectrophotometric data for the fitting and agree within the uncertainty. For 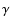 Sge, Wittkowski et al. (2006b) complement the Johnson & Mitchell (1975) data with narrow-band data from Alekseeva et al. (1997) while for
Sge, Wittkowski et al. (2006b) complement the Johnson & Mitchell (1975) data with narrow-band data from Alekseeva et al. (1997) while for 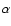 Cet, Wittkowski et al. (2006a) use optical (Glushneva et al. 1998b,a) and infrared (Cohen et al. 1996) spectrophotometry. The effective temperature difference for the remaining two stars are about 150 to 200 K.
Cet, Wittkowski et al. (2006a) use optical (Glushneva et al. 1998b,a) and infrared (Cohen et al. 1996) spectrophotometry. The effective temperature difference for the remaining two stars are about 150 to 200 K.
Because the angular diameters are similar, the predicted radii are also similar for both fits with SATLAS and PHOENIX. Therefore the differences between predicted luminosities are due to differences in effective temperatures and thus due to the different methods for determining the effective temperatures. The lower effective temperatures and luminosities imply lower masses when compared to Girardi et al. (2000) evolutionary tracks and smaller gravities.
The SATLAS models are consistent with previous results. Fitting the models to interferometric and spectrophotometric observations have provided a robust test of the spherically symmetric version of the ATLAS program and have shown that the SATLAS program is a powerful tool for studies of stellar atmospheres.
-
Alekseeva, G. A., Arkharov, A. A., Galkin, V. D.,
et al. 1997, Baltic Astron., 6, 481 [NASA ADS]
(In the text)
- Cohen, M.,
Witteborn, F. C., Carbon, D. F., et al. 1996, AJ,
112, 2274 [NASA ADS] [CrossRef]
(In the text)
- Davis, J., Tango,
W. J., & Booth, A. J. 2000, MNRAS, 318, 387 [NASA ADS] [CrossRef]
- Feast,
M. W., Whitelock, P. A., & Carter, B. S. 1990,
MNRAS, 247, 227 [NASA ADS]
(In the text)
-
Feautrier, P. 1964, C.R. Acad. Sci. Paris, 258, 3189 [NASA ADS]
(In the text)
- Girardi, L.,
Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141,
371 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
Glushneva, I. N., Doroshenko, V. T., Fetisova,
T. S., et al. 1998a, VizieR Online Data Catalog, 3208,
0
-
Glushneva, I. N., Doroshenko, V. T., Fetisova,
T. S., et al. 1998b, VizieR Online Data Catalog, 3207,
0
-
Hauschildt, P. H., Allard, F., Ferguson, J., Baron, E., &
Alexander, D. R. 1999, ApJ, 525, 871 [NASA ADS] [CrossRef]
(In the text)
- Johnson,
H. L., & Mitchell, R. I. 1975, Rev. Mex. Astron.
Astrofis., 1, 299 [NASA ADS]
(In the text)
- Kervella,
P., Coude du Foresto, V., Glindemann, A., & Hofmann, R. 2000,
in Interferometry in Optical Astronomy, ed. P. J. Lena, &
A. Quirrenbach, Proc. SPIE, 4006, 31
(In the text)
- Kurucz,
R. L. 1970, SAO Special Report, 309 [NASA ADS]
- Kurucz,
R. L. 1993, in Peculiar versus Normal Phenomena in A-type and
Related Stars, ed. M. M. Dworetsky, F. Castelli, &
R. Faraggiana, IAU Colloq., 138, ASP. Conf. Ser., 44, 87
- Lester, J.,
& Neilson, H. 2008, A&A, accepted
(In the text)
- Perryman,
M. A. C., & ESA (ed.) 1997, The HIPPARCOS and TYCHO
catalogues. Astrometric and photometric star catalogues, derived
from the ESA HIPPARCOS Space Astrometry Mission, ESA SP, 1200
(In the text)
- Rybicki,
G. B. 1971, J. Quant. Spectroscopy Radiative Trans., 11,
589 [NASA ADS] [CrossRef]
(In the text)
- Tango,
W. J., & Davis, J. 2002, MNRAS, 333, 642 [NASA ADS] [CrossRef]
-
Wittkowski, M., Aufdenberg, J. P., & Kervella, P. 2004,
A&A, 413, 711 [NASA ADS] [CrossRef] [EDP Sciences]
-
Wittkowski, M., Aufdenberg, J. P., Driebe, T., et al.
2006a, A&A, 460, 855 [NASA ADS] [CrossRef] [EDP Sciences]
-
Wittkowski, M., Hummel, C. A., Aufdenberg, J. P., &
Roccatagliata, V. 2006b, A&A, 460, 843 [NASA ADS] [CrossRef] [EDP Sciences]
Copyright ESO 2008
![\begin{displaymath}%
V_{\rm {LD}}(\lambda) = \int_0^1S_\lambda I_\lambda(\mu)J_0...
..._{\rm {LD}}(B/\lambda)(1 - \mu^2)^{1/2}\right] \mu \rm {d}\mu.
\end{displaymath}](/articles/aa/full/2008/41/aa10627-08/img35.gif)
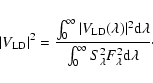
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0627f5.eps}\\
\includegraphics[width=6.5cm,clip]{0627f1a.eps}
\end{figure}](/articles/aa/full/2008/41/aa10627-08/Timg42.gif)
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0627f2a.eps}\par\includegraphics[width=6.5cm,clip]{0627f2b.eps}
\end{figure}](/articles/aa/full/2008/41/aa10627-08/Timg100.gif)
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0627f3.eps}
\end{figure}](/articles/aa/full/2008/41/aa10627-08/Timg110.gif)
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0627f4a.eps}\par\includegraphics[width=6.7cm,clip]{0627f4b.eps}
\end{figure}](/articles/aa/full/2008/41/aa10627-08/Timg118.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0627f1b.eps}
\end{figure}](/articles/aa/full/2008/41/aa10627-08/Timg119.gif)
![\begin{figure}
\par\includegraphics[]{0627f6.eps}
\end{figure}](/articles/aa/full/2008/41/aa10627-08/Timg121.gif)