A&A 490, 695-706 (2008)
DOI: 10.1051/0004-6361:200810443

SiO line emission from interstellar jets and outflows: silicon-containing mantles and non-stationary shock waves

A. Gusdorf^1,2 - G. Pineau des Forêts^2,3,4 - S. Cabrit³ - D. R. Flower¹

1 - Physics Department, The University, Durham DH1 3LE, UK
2 - Institut d'Astrophysique Spatiale (IAS), Bâtiment 121, 91405 Orsay, France
3 - LERMA (UMR 8112 du CNRS), Observatoire de Paris, 61 Avenue de l'Observatoire, 75014 Paris, France
4 - Université Paris-Sud 11 and CNRS (UMR 8617), France

Received 23 June 2008 / Accepted 29 August 2008

Abstract
Context. We study the production and emission of SiO and H₂ in the gas phase of molecular outflows, extending previous work in which we considered steady-state C-type shock waves and assumed the silicon to be present only in the cores of silicate grains.
Aims. We place constraints on the physical parameters of the pre-shock region, using recent observations of SiO and observations of molecular hydrogen. We show the effects of introducing SiO-containing mantles and of varying the age of the shock wave. We consider simultaneously the emission of SiO and H₂ from the young L1157 outflow.
Methods. The molecular outflows are studied by means of a code that can generate stationary C- and J-type shock models and approximate non-stationary solutions, which combine these two types of shock wave. The emission of molecular hydrogen is computed by this code, whereas the SiO emission is computed by means of a separate LVG model, which uses the calculated physical and chemical profiles. A grid of models has been computed, with shock speeds in the range $10~\leq~v_{\rm s}~\leq~35$ km s^-1 and pre-shock gas densities $10^4 \leq n_{\rm H}~\leq~10^6$ cm^-3. A wide range of magnetic field strengths has been investigated, from $45~\mu$G to about $600~\mu$G.
Results. We illustrate our results by means of observational data obtained on the blue lobe of the L1157 outflow. Given the combinations of pre-shock densities and shock velocities necessary to fit the H₂ observations, we find that the erosion only of the silicate material in the grains cores cannot account for the observed SiO line intensities. We investigate the possiblity that a fraction of the SiO is present initially in the grain mantles, and we succeed in constraining this fraction. Introducing even a few percent of the silicon (as SiO) into the mantles is sufficient to increase the SiO line widths and fluxes by an order of magnitude. With this assumption, it is possible to find a non-stationary shock model that provides a reasonable fit of the observations of both H₂ and SiO.
Conclusions. With a few percent of the silicon present initially in the grain mantles, good agreement is obtained with recent observations of SiO line integrated line intensities for a pre-shock density $n_{\rm H} = 10^4$ cm^-3 and a shock speed $v_{\rm s} = 20$ km s^-1. The magnetic field strength and the shock age are not well constrained by the observations of either H₂ or SiO. We show that CO observations (in particular, with the Herschel satellite) could provide further discrimination between the models.

Key words: astrochemistry - magnetohydrodynamics (MHD) - molecular processes - ISM: jets and outflows - infrared: ISM - radio lines: ISM

   
1 Introduction

In a previous article (Gusdorf et al. 2008, henceforth G08), we investigated the SiO emission from steady-state C-type shock waves, in an attempt at accounting for recent observations of SiO emission lines in the L1157 and L1448 molecular outflows. Simulations of stationary shocks were performed by means of a one-dimensional dynamical and chemical code, whose outputs were used in an LVG model, in order to calculate the SiO emission. In this stationary C-type shock model, grain erosion is a consequence of ambipolar diffusion: the grains are predominantly negatively charged in the shock wave and are impacted by the neutrals at the ion-neutral drift velocity. When the shock speed is sufficiently high, this process releases Si into the gas phase, where oxidation reactions lead to the formation and thence the emission of SiO. G08 made the assumption that elemental silicon was solely in the form of silicates (in practice, olivine) in the grain cores. The code and its recent updates, as well as our implementation of the LVG technique, are described in G08. We use rate coefficients for rotational transitions in SiO, induced by He and by para-H₂, from the recent work of Dayou & Balança (2006).

The gas-phase reactions leading to the formation of SiO were discussed by G08. Neutral Si reacts either with OH or O₂ to form SiO, and so the fractional abundance of O₂ in the pre-shock gas is an important parameter. In our previous study, we considered two scenarios, relating to the initial distribution of oxygen:

• molecular oxygen formed in the gas phase was adsorbed subsequently on to the grains, where it remained as O₂ ice in the pre-shock medium, with a fractional abundance which was taken to be of $1.3 \times 10^{-5}$, relative to elemental hydrogen. (We note that the initial abundance of water ice is an order of magnitude larger than that of O₂ ice.)

• atomic oxygen was adsorbed on to the grains before O₂ was synthesized in the gas phase and was hydrogenated to water ice in the mantles of the grains in the cold pre-shock medium. As a consequence, the fractional abundance of H₂O ice increases by 25%, to $1.3 \times 10^{-4}$.

In both cases, the initial gas-phase fractional abundance of molecular oxygen is n(O₂)/n(H₂) = 10^-7, consistent with satellite observations by Pagani et al. (2003) and Larsson et al. (2007). In our previous study (of C-type shocks), we found that the results were not sensitive to the scenario which was adopted, particularly at high shock speeds, as Si can be oxidized in the gas phase by both O₂ and OH. Accordingly, we make the first assumption in the present work.

G08 computed a grid of C-type shock models and compared the calculated SiO line intensities and profiles with observations. With respect to the line intensities, the agreement with the observations was satisfactory, for rotational transitions up to SiO(11-10). However, the line profiles predicted under these assumptions were narrower than observed, with predicted widths of 0.5-2 km s^-1, as compared with the observed widths of 5-20 km s^-1, in 3 $^{\prime \prime }$-10 $^{\prime \prime }$ beams. Partly with this discrepancy in mind, we consider now the possibility that SiO may be present in the grain mantles, where the corresponding binding energy is much lower than that of the Si in the silicate grain cores. We transfer a small percentage (1%, 5%, or 10%) of the Si, and the corresponding amounts of oxygen, from the cores to the mantles. If this process is mediated by the passage of shock waves, our calculations indicate that the dominant form of silicon in the mantle is likely to be SiO; see, for example, Fig. 1 of G08. The SiO is then released directly into the gas phase, through sputtering by the most abundant neutrals, H, H₂ and He in a subsequent shock wave. Such sputtering processes were incorporated already for known mantle constituents, such as water and carbon monoxide. The sputtering rate of SiO was calculated using the same parameters as for CO. Adopting the parameters appropriate to a more polar species, such as H₂O, has no significant influence on the results, as the mantle species are, in either case, sputtered rapidly (in the magnetic precursor).

In steady-state C-type shock waves, the SiO emission peaks in the post-shock gas, owing to the chemical delay introduced by the oxidation of Si to SiO and also to the larger line optical depths at low velocity gradients. In view of the small dynamical ages (<5000 yr) of several outflows and jets, we consider how the SiO emission is affected when the C-type shock wave has not yet reached steady-state, and its precursor is truncated by an embedded J-discontinuity.

It has been shown previously (Flower et al. 2003; Giannini et al. 2004, 2006) that non-stationary shock waves are favoured by observations of rovibrational emission lines of H₂ in outflows. Stationary C-type models are unable to fit simultaneously the column densities of both the vibrationally excited levels and the rotational levels of the vibrational ground state. It is conceivable that a combination of C-type shock models with appropriate parameters, including filling factors, could be found which fits the observations of H₂; but it is not possible for single or even multiple C-type shock models to reproduce also the observations of SiO, if it is assumed that the only source of Si in the gas phase is the erosion of the grain cores.

In the following Sect. 2, we summarize the results obtained for stationary C-type shock waves. Section 3 contains an initial discussion of non-stationary (CJ-type) models and is followed, in Sect. 4, by more detailed considerations of using such models to interpret the H₂ and SiO emission line observations of the L1157 B1 outflow. Our concluding remarks are made in Sect. 5.

   
2 Stationary C-type shock waves with SiO present in the grain mantles

Figure 1: The temperature of the neutral fluid, $T_{\rm n}$, and the fractional abundances of OH and O2 ( top panels) and of Si, SiO, and silicon in the grain mantles, $\Sigma$ Si* ( bottom panels), as functions of the flow time of the charged fluid, for two reference C-type shock models: $n_{\rm H} = 10^4$ cm-3, b = 1, $v_{\rm s} = 25$ km s-1 ( left-hand panels) and 50 km s-1 ( right-hand panels). In both models, it is assumed that 5% of the elemental silicon is initially in the mantles, in the form of SiO.

Open with DEXTER

G08 assumed that Si was present in grains in the form of silicates, contained in the cores, with an initial fractional abundance of $3.37 \times 10^{-5}$, relative to elemental H. We consider now two particular C-type shock models, for which the pre-shock density $n_{\rm H} = 10^4$ cm^-3, the shock velocity $v_{\rm s} = 25$ and 50 km s^-1, respectively, and b = 1; in our models, b is a parameter that scales the transverse magnetic field, B, such that $B = b\sqrt{n_{\rm H}}$, where B is in $\mu$G and $n_{\rm H}$ in cm^-3. At 25 km s^-1, the velocity of the C-type shock model is inadequate for significant erosion of the grain cores to take place, and this model failed to produce enough SiO to account for the observations. On the other hand, the higher velocity (50 km s^-1) shock yielded good agreement with the SiO observations of L1157 B1, in terms of the integrated line intensities. In both cases, Si is released into the gas phase through erosion of the grain cores. Because of the time required to oxidize Si in the gas phase, the SiO emission peaks in the post-shock region. When $v_{\rm s} = 50$ km s^-1, the fractional abundance of SiO attains $7 \times 10^{-7}$, before decreasing, owing to adsorption on to the grains.

We introduce now an alternative scenario, in which the silicon is initially in the mantles, in the form of SiO. If the silicon in the mantles was assumed to be in atomic form instead, we found that the SiO line intensities were underestimated (because of the chemical delay in oxidizing the atomic silicon to SiO in the gas phase) in the lower speed shock wave models which fit satisfactorily the observations of H₂; see Sect. 4 below. Owing to the rapidity with which the mantles are eroded during the passage of a shock wave, another possibility - that the atomic silicon is already present in the gas phase, following its release from the grains by an earlier shock - gave very similar results. Accordingly, we consider now an example in which 5% of the silicon is assumed to be initially in the form of SiO in the mantles.

Figure 1 shows the neutral temperature profiles and the fractional abundances of Si-containing species, for the models with $v_{\rm s} = 25$ and 50 km s^-1. In both cases, essentially all of the SiO which is initially in the mantles is released into the gas phase by sputtering, subsequently freezing back on to grains in the cold, post-shock gas. The more SiO is initially present in the grain mantles, the higher is the maximum fractional abundance of SiO in the gas phase. At the lower shock speed, the SiO produced following erosion of Si from the grain cores is negligible, compared with SiO sputtered directly from the mantles. Even at the higher shock speed of $v_{\rm s} = 50$ km s^-1, only about 5% of the silicon is released from the grain cores: see G08, Fig. 2, and the curve marked Si in the lower right hand panel of Fig. 1 of the present paper.

When comparing the models with the observations of SiO, we consider first the integrated intensity of the SiO(5-4) line, $\int {T{\rm d}v}(5-4)$ K km s^-1, and then the integrated intensities of rotational transitions up to (11-10), expressed relative to SiO(5-4).

• The variation of the integrated intensity of the SiO(5-4) line with the percentage of SiO initially in the mantles is shown in Fig. 2. Observational data relating to L1448 and L1157, compiled by Nisini et al. (2007), are displayed also. Our calculations show that the observed line intensities can be reproduced when only of the order of 1% of the elemental silicon is initially in the grain mantles, as SiO. Core erosion alone is sufficient only at the higher shock speed, 50 km s^-1; Fig. 2 confirms the efficacy of mantle sputtering at lower speeds.

  
  

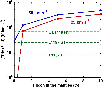  Figure 2: The integrated intensity of the SiO(5-4) line, $\int {T{\rm d}v}(5-4)$, as a function of the percentage of SiO initially in the grain mantles, for both of the C-type shock models: $n_{\rm H} = 10^4$ cm-3, b = 1, $v_{\rm s} = 25$ km s-1 ( lower curve) and 50 km s-1 ( upper curve). At the lower shock speed, the erosion of Si from the grain cores is negligible compared with the release of SiO from the mantles. The SiO(5-4) intensities observed in L1157 and L1448 are indicated by the horizontal lines.

  Open with DEXTER

  
  

• Figure 3 presents the integrated intensities of other rotational transitions, relative to the (5-4) line; observational data relating to L1157 B1 are shown also. At the lower shock speed, only the SiO sputtered from the mantles contributes significantly to the line emission. Furthermore, as the SiO is released into regions of high temperature, the emission in the high rotational transitions becomes stronger as the amount of SiO in the mantles increases. At the lower shock speed, 5% seems adequate to fit the relative line intensities; but this model predicts a value of the (5-4) line intensity which is 3-10 times higher than observed in L1448-L1157 (cf. Fig. 2). A low effective surface filling factor of 0.3-0.1 would then be required to reconcile this model with the observations, and this is incompatible with the typical sizes of the SiO knots observed by Nisini et al. (2007), which are comparable with the thickness of the SiO emitting layer in the model. On the other hand, at the higher speed, models with less than 1% of silicon in the mantles fit satisfactorily both the relative and the absolute line intensities.

  
  

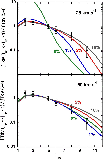  Figure 3: The integrated intensities of rotational transitions of SiO, relative to the (5-4) line, in stationary C-type shock waves: $n_{\rm H} = 10^4$ cm-3, b = 1, $v_{\rm s} = 25$ km s-1 ( upper panel) and 50 km s-1 ( lower panel). The observational data relate to L1157 B1. The initial fraction of silicon in the form of SiO in the grain mantles varies from 0% to 10%, as indicated. In the lower limit, the SiO which is seen in this figure arises from the erosion of silicates in the grain cores.

  Open with DEXTER

  
  

The motivation for considering SiO being present in grain mantles was its possible consequences for the widths of the emission lines. Figure 4 displays the line profiles obtained when 5% of elemental silicon is initially in the mantles. As SiO is now present in the gas phase over the full width of the shock wave, the lines are much broader than predicted when assuming that Si is released by erosion of the grain cores only; cf. G08, Fig. 8. However, the computed profiles vary considerably from line to line, whereas they are observed to be similar (see, for example, Fig. 9 of Nisini et al. 2007). Furthermore, as noted by Nisini et al. (2007), the line profiles in L1157 B1, considered below, are reversed relative to those in the outflow L1448: in the former object, the maximum SiO line intensities occur close to the LSR velocity, with weaker emission from the higher velocity (more blue-shifted) gas. If the shock in L1157 B1 is moving towards the observer, the profiles plotted in Fig. 4 would correspond to maximum intensities at high blue shifts, as in L1448 but not as in L1157 B1. A possible explanation is that the SiO emission in L1157 B1 arises in a reverse shock. We shall return to the issue of line profiles in Sect. 3.3 below.

Figure 4: Profiles of the SiO rotational transitions (2-1), (3-2), (5-4), (6-5), (8-7), and (10-9) computed in stationary C-type shock waves, for $n_{\rm H} = 10^4$ cm-3, b = 1, $v_{\rm s} = 25$ km s-1 ( left panel) and 50 km s-1 ( right panel). 5% of the elemental silicon is assumed to be initially in the grain mantles, in the form of SiO. The flow speed is in the reference frame of the preshock gas. $T_{\rm n}$ is the temperature of the neutral fluid.

Open with DEXTER

   
3 Non-stationary shock waves

In the case of the SiO emission, stationary C-type shock waves have been shown to be able to account for the observed rotational line intensities (G08). However, the dynamical age of the blue lobe of the L1157 outflow, inferred from observations (see Gueth et al. 1998), is 2000-3000 yr, which is less than the time (of the order of 10⁴ yr) required for a typical C-type shock wave to attain a steady state. Furthermore, previous studies (see, for example, Flower et al. 2003; Giannini et al. 2004, 2006) have demonstrated the necessity of considering non-stationary shock waves in order to account successfully for both the pure rotational and the rovibrational emission of molecular hydrogen observed in molecular outflows. The difficulty which has to be faced is that a single C-type shock fails to reproduce simultaneously the column densities of both the high (v, j) levels of H₂ and the column densities of the low (v = 0, j) levels. Accordingly, we proceed to consider non-stationary shock waves, which have developed a magnetic precursor but which retain a J-type discontinuity; see Chièze et al. (1998), Lesaffre et al. (2004b). We simulate such shock waves by introducing a discontinuity into the flow (by switching on artificial viscosity terms; see Flower & Pineau des Forêts 1999) at a given value of the fluid flow time, which becomes a parameter of the model. In practice, we introduce the discontinuity at one half of the flow time of the charged fluid (cf. Lesaffre et al. 2004b) to the point at which the flow is terminated; see Appendix C. We refer to such models as ``CJ-type'', as they possess both C- and J-type characteristics.

   
3.1 Molecular hydrogen cooling

Figure 5: Profiles of the CJ-type shocks specified in Sect. 3.1. The corresponding steady-state C-type shock models are shown also. Left-hand panels: $v_{\rm s} = 25$ km s-1; right-hand panels: $v_{\rm s} = 50$ km s-1. In the middle panels, the full curves correspond to the neutrals and the broken curves to the ions. In the bottom panels, the full curves correspond to the compression factor, and the broken curves to the fractional abundance of H2.

Open with DEXTER

By way of illustration, we consider the following models:

• $n_{\rm H} = 10^4$ cm^-3, b = 1, $v_{\rm s} = 25$ km s^-1; ages of 175 and 500 yr (and the limit of steady-state);

• $n_{\rm H} = 10^4$ cm^-3, b = 1, $v_{\rm s} = 50$ km s^-1; ages of 10 and 500 yr (and the limit of steady-state).

As the fractional abundance of SiO remains low, it plays only a minor role in the cooling of the medium. It follows that the choice of the initial repartition of silicon has negligible influence on the temperature profiles and on the fractional abundances of species other than those containing silicon. Accordingly, we assume initially that there is no elemental silicon in the grain mantles, i.e. that the silicon is in the form of silicates in the grain cores.

In Fig. 5, the neutral temperature profile, fluid velocities (charged and neutral), the compression factor, and the fractional abundance of molecular hydrogen are plotted against the flow time of the charged fluid, $t_{\rm i} = \int (1/v_{\rm i}){\rm d}z$, for the models specified above. It may be seen that the lower age, of 175 yr or 10 yr, respectively, is insufficient for a significant magnetic precursor to develop at the corresponding shock speed. In all cases, the initial rise in temperature is followed by radiative cooling and compression of the gas as it evolves towards its final state. The younger the shock, the higher is the compression factor and hence the initial, adiabatic increase in temperature at the J-discontinuity. Thus, even at 25 km s^-1, the CJ-type shock wave is sufficiently energetic to dissociate partially the ambient molecular hydrogen. At the higher shock speed, a much larger fraction of the H₂ is dissociated. The cooling of the gas occurs mainly through rovibrational transitions of H₂ and, in the region where the fractional abundance of molecular hydrogen is low, through fine-structure transitions of atomic oxygen. The compression of the gas and its falling temperature are accompanied by partial re-formation of H₂, on the grains. In the steady-state C-type shock models, H₂ remains the principal coolant throughout the shock wave, as the maximum temperature which is attained is not high enough to give rise to significant dissociation. The flow time required for full compression of the gas to be attained is approximately $5\times 10^3$ yr when $v_{\rm s} = 50$ km s^-1 and 10⁴ yr when $v_{\rm s} = 25$ km s^-1, as may be seen in the bottom panels of Fig. 5.

   
3.2 H₂ excitation diagrams

In molecular shock waves, H₂ is not only the major coolant but also comprises most of the mass and helps to define the chemical state of the gas. For these reasons, our numerical simulations include a detailed treatment of the physics of H₂, whose level populations are computed in parallel with the dynamical and chemical equations which determine the evolution of the shock wave: see Le Bourlot et al. (2002). At each point of the shocked region, the population densities of the rovibrational levels of molecular hydrogen are calculated. The corresponding column densities are determined by numerical quadrature.

Our analysis of the H₂ line emission from shocks makes use of excitation diagrams, which are plots of ln( N_vj/g_j) against $E_{vj}/k_{\rm B}$, where N_vj (cm^-2) is the column density of the rovibrational level (v, J), $E_{vj}/k_{\rm B}$ is its excitation temperature and g_j = (2j+1)(2I+1) its statistical weight. The nuclear spin quantum number is I = 1 for ortho-H₂ and I = 0 for para-H₂. If the gas is thermalized at a single temperature, all the points in the diagram lie on a straight line. In practice, thermalization is rarely realized, and the line is curved; then, the local values of the gradient of the curve provide an indication of the kinetic temperatures in the corresponding emitting regions. Our calculations incorporated all significant collisional and radiative transitions between rovibrational levels up to an excitation energy of almost 40 000 K. In partially dissociated gas, rovibrational excitation of H₂ can be dominated by collisions with H. For this process, we use the rate coefficients computed recently by Wrathmall & Flower (2007).

The excitation diagrams for the models specified above are plotted in Fig. 6. The younger the shock, the higher is its maximum temperature (and the smaller is its width). It follows that levels of high excitation energy tend to be more populated, relative to low levels, in younger shock waves. It is clear that the comparison of observed and calculated excitation diagrams has the potential for evolutionary age discrimination.

   
3.3 SiO emission

Our aim is to find a model that accounts for the observational data pertaining to both SiO and H₂, on the assumption that their emission is generated by the same non-stationary shock wave(s). The predictions of the SiO line intensities are not affected by our choice of shock termination point, which is taken to be twice the flow time at the J-discontinuity. The highly compressed gas behind the J-discontinuity does not contribute significantly to the line intensities.

We discuss first the emission from SiO which occurs following the erosion of Si from the grain cores, and then the corresponding results obtained on assuming that a small percentage of the silicon is initially in the form of SiO in the grain mantles.

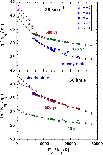	Figure 6: Synthetic H2 excitation diagrams for the CJ-type shocks specified in Sect. 3.1.
Open with DEXTER

3.3.1 SiO absent from the grain mantles

The erosion of Si from the grain cores occurs in the magnetic precursor of the CJ-type shock, where there is a non-zero drift velocity between charged and neutral species. We have noted already in Sect. 2 that core erosion is significant only in the case of the high-velocity shock, $v_{\rm s} = 50$ km s^-1, and so this is the model which we consider. In order to enhance the extent of the region in which the flow velocities of the charged and the neutral fluids are decoupled, we consider evolved shock waves, with ages $\ge$500 yr. We recall that the pre-shock parameters are $n_{\rm H} = 10^4$ cm^-3 and b = 1.

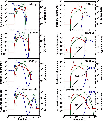Figure 7: The temperature of the neutral fluid, $T_{\rm n}$, and the fractional abundances of OH and O2 ( left-hand panels) and of Si, SiO, and silicon in the grain mantles, $\Sigma$ Si* (right-hand panels), as functions of the flow time of the charged fluid, for the CJ-type shock model in which $n_{\rm H} = 10^4$ cm-3, b = 1, and $v_{\rm s} = 50$ km s-1. The shock age increases from top to bottom: 500, 1800, 3800 yr, and steady-state. In these calculations, there is no SiO in the grain mantles, and the gas-phase silicon is produced solely by erosion of the silicate grain cores.

Open with DEXTER

Figure 7 illustrates the production of SiO in CJ-type shock waves with ages of 500, 1800 and 3800 yr; the corresponding stationary shock is shown also. There is a chemical delay to the formation of SiO, following the release of Si into the gas phase, due to the time required for oxidation to take place; this delay is significant in the case of non-stationary models, as it is comparable with the evolutionary ages being considered, i.e. of the order of 10³ yr. Consequently, the maximum fractional abundance of SiO tends to increase with the shock age. In the CJ-type models, the flow speed becomes almost constant behind the J-discontinuity; this has consequences for the predicted SiO emission, as will be seen below.

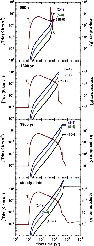Figure 8: The integrated intensities, $\int {T{\rm d}v}$, of the SiO (2-1), (5-4) and (10-9) rotational transitions, as functions of the flow time of the charged fluid, for the CJ-type shock model in which $n_{\rm H} = 10^4$ cm-3, b = 1, and $v_{\rm s} = 50$ km s-1. The shock age increases from top to bottom: 500, 1800, 3800 yr, and steady-state. The temperature of the neutral fluid, $T_{\rm n}$, is plotted also. In these calculations, there is no SiO in the grain mantles, and the gas-phase silicon is produced solely by erosion of the silicate grain cores.

Open with DEXTER

Figure 8 shows the contributions to the intensities of three lines of SiO, (2-1), (5-4), and (10-9), as functions of the flow time of the charged fluid, for the CJ-type model specified above. In the magnetic precursor, Si is eroded from the grain cores and then oxidized to SiO in the gas phase, resulting in rotational line emission whose intensity increases through the shock wave. The emission saturates behind the discontinuity, owing to the low fluid velocity gradient. In the CJ-type models (top three panels of Fig. 8), the populations of excited rotational levels, and the intensity of, in particular, the (10-9) line, are given a boost whose significance increases with the temperature jump at the J-discontinuity, i.e. towards lower evolutionary ages; this explains the variations of the relative line intensities with the shock age, seen in Fig. 9. The younger the CJ-type shock, the larger is the temperature jump and the stronger are the lines from high rotational levels, relative to low levels.

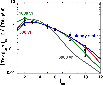Figure 9: Integrated SiO line intensities, relative to the (5-4) transition, for the CJ-type shock model in which $n_{\rm H} = 10^4$ cm-3, b = 1, and $v_{\rm s} = 50$ km s-1. The shock ages are 500, 1800, 3800 yr, and the corresponding steady-state results are plotted also. In these calculations, there is no SiO in the grain mantles, and the gas-phase silicon is produced solely by erosion of the silicate grain cores. The observed points, with error bars, relate to L1157 B1.

Open with DEXTER

In the case of the stationary (C-type) shock model, emission arises over almost the full width of the shock wave, including the SiO fractional abundance peak; this explains why all the lines have higher final integrated intensities. In addition, as the j = 10 level lies only 115 K above the ground state, it can be excited right through to the point where the fluid velocity reaches its (constant) post-shock value and the compression is highest, which accounts for the high relative integrated intensity of the (10-9) transition in the stationary shock model. On the other hand, at an age of 3800 yr, the J-discontinuity gives rise to a temperature blip which is followed by rapid cooling (see Fig. 8) to temperatures such that the highly rotationally excited levels, such as j = 10, become energetically inaccessible; this accounts for the deviation of the relative line intensities from the steady-state values, seen in Fig. 9.

Figure 9 shows that either a stationary C-type shock or young CJ-type shocks provide the best fits to the observations of L1157 B1. However, the lower panel of Fig. 10 shows that the absolute SiO(5-4) line intensity is substantially underestimated by the young CJ-type shock models, if it is assumed that there is no SiO in the grain mantles and the gas-phase silicon is produced exclusively by erosion of the silicate grain cores. In this case, only the stationary shock model is a good candidate to fit the SiO observations.

3.3.2 SiO present in the grain mantles

We turn now to non-stationary shock models in which SiO is supposed to be present in the grain mantles; the fraction of the elemental silicon which is initially in the mantles is varied from 0% to 10%. As in Sect. 2, we consider the following model parameters: $n_{\rm H} = 10^4$ cm^-3, b = 1, $v_{\rm s} = 25$ and 50 km s^-1.

First, we compare the computed values of the integrated SiO(5-4) line intensity with those observed in L1157 and L1448; see Fig. 10. As expected, the line emission increases with the amount of SiO in the grains mantles. We see also that the line intensity tends to increase with the evolutionary age of the shock, owing to the greater velocity extent of the emitting region. Exceptions to this general trend are young, high-velocity CJ-type shocks (cf. lower panel of Fig. 10), for which the temperature rise at the J-discontinuity is sufficient to cause partial dissociation of molecular hydrogen. Consequent to the reduction in the efficiency of H₂ cooling, the width of the cooling zone, behind the discontinuity, is greater and the SiO line intensity is enhanced.

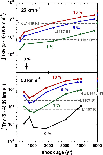Figure 10: The integrated intensity of the SiO(5-4) line, $\int {T{\rm d}v}(5-4)$, as a function of the age of the shock wave and the percentage of silicon initially in the form of SiO in the grain mantles; $n_{\rm H} = 10^4$ cm-3, b = 1, $v_{\rm s} = 25$ km s-1 ( upper panel) and 50 km s-1 ( lower panel). The points corresponding to the limit of steady-state are plotted on the right-hand y-axis. The SiO(5-4) intensities observed in L1157 and L1448 are indicated by the horizontal lines.

Open with DEXTER

Figure 10 shows that agreement can be found between the observed and calculated (5-4) line intensity for almost every model in which there is some SiO in the grain mantles. With a view to finding a means of discriminating between the models, we plot, in Fig. 11, the integrated SiO line intensities, relative to the (5-4) transition. In the calculations shown in this figure, it was assumed that 5% of the elemental silicon was initially in the form of SiO in the grain mantles.

At the lower shock speed, the populations of the high rotational levels are greater when the shock is young, owing to the larger jump in temperature at the J-discontinuity. The oldest shock (4000 yr) remains far from the steady-state limit. On the other hand, at the higher shock speed, the 3800 years-old CJ-type shock has almost attained steady state. The cooling efficiency behind the J-discontinuity in the youngest shock (with an age of 500 yr) is reduced by the partial dissociation of molecular hydrogen. Reasonable agreement with the observations is found for evolutionary ages of the order of a thousand years.

Owing to the presence of the embedded J-discontinuity, the profiles of the SiO lines predicted by CJ-type models are compressed in velocity space, as compared with the steady-state C-type models discussed in Sect. 2. The younger the shock wave, the greater is the fraction of the emission that is contributed by the gas immediately behind the discontinuity. As the flow velocity of this gas becomes approximately constant, the lines become narrower than in the steady-state limit. The predicted widths decrease to the assumed turbulent width, which is smaller than the observed widths of 5-20 km s^-1, in 3 $^{\prime \prime }$-10 $^{\prime \prime }$ beams. In this respect, the CJ-type models face a problem which is analogous to that encountered by G08, and for which, in Sect. 5, we advance the same tentative explanation.

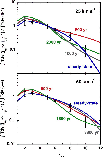Figure 11: Integrated SiO line intensities, relative to the (5-4) transition, for the CJ-type shock models in which $n_{\rm H} = 10^4$ cm-3, b = 1, and $v_{\rm s} = 25$ km s-1 ( upper panel) and $v_{\rm s} = 50$ km s-1 ( lower panel). The evolutionary ages of the shocks are indicated, and the corresponding steady-state results are plotted also. In these calculations, 5% of the elemental silicon is assumed to be initially in the grain mantles, in the form of SiO. The observed points, with error bars, relate to L1157 B1. The highest rotational level for which observations are available, $j_{\rm up} = 10$, lies 115 K above the ground state.

Open with DEXTER

In the following Section, we consider the observations of L1157 B1 in more detail, considering both the H₂ and SiO emission lines.

   
4 A test case: L1157 B1

Observations of pure rotational lines of SiO (up to the (10-9) transition) in the L1157 outflow have been reported recently by Nisini et al. (2007). Caratti o Garatti et al. (2006) compiled observations of a large number of rovibrational lines of H₂, whereas Cabrit et al. (1999) observed pure rotational lines of molecular hydrogen, using ISO; see Appendix A. L1157 is a Class 0 object, at a distance of approximately 440 pc. The jet is highly collimated and inclined relative to the line of sight. L1157 is an example of a ``chemically active outflow'' (see Bachiller et al. 2001) and is an appropriate object with which to compare our simulations of H₂ and SiO emission from shock waves.

Nisini et al. (2007) studied the excitation of SiO in various knots of the blue and red lobes of L1157, whereas Caratti o Garatti et al. (2006) concentrated on the H₂ rovibrational lines in its blue lobe. Therefore, we focus our analysis on the B1 region; this refers to the SiO observations and corresponds approximately to the A1 and A2 regions observed in molecular hydrogen.

In order to compare with the observations of H₂ and SiO, a grid of models was computed, with the following ranges of parameters:

• shock speeds $10~\le~v_{\rm s}~\le~45$ km s^-1;

• preshock densities $10^4~\le~n_{\rm H}~\le~10^6$ cm^-3;

• preshock transverse magnetic field strengths determined by $0.1 \le b \le 2.0$.

In addition, we varied both the evolutionary age of the (CJ-type) shocks and the fraction of silicon that was initially in the grain mantles, as SiO.

Although the parameter space was not covered uniformly, i.e. not all possible combinations of the parameters above were used, the grid of C- and J-type models that was generated was sufficient to make meaningful comparisons with the observations. The grid will be made accessible from http://massey.dur.ac.uk/drf/outflows/

   
4.1 H₂ emission lines

We present in Fig. 12 the excitation diagram which derives from the H₂ rovibrational line intensities listed in Caratti o Garatti et al. (2006) and the pure rotational line intensities observed by Cabrit et al. (1999). When correcting the data for reddening, we adopted a visual extinction $A_{\rm V} = 2$, which is an upper limit from Caratti o Garatti et al. (2006), and the interstellar extinction law of Rieke & Lebofsky (1985). Results are plotted for two single-pixel (``pix1'' and ``pix2'') ISO measurements of the pure rotational line intensities (see Appendix A), and for the two regions, A1 and A2, observed in the near-infrared rovibrational lines. We note that the effects of the reddening correction on the observational points plotted in this diagram are minor.

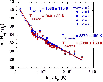	Figure 12: Composite H2 excitation diagrams, corrected for reddening with $A_{\rm V} = 2$; see text, Sect. 4.1. The excitation temperatures deduced from each set of observations are indicated.
Open with DEXTER

Rotational and rovibrational temperatures, deduced from the excitation diagrams for each set of data, are compiled in Table 1. The excitation temperatures deduced for pix1 and pix2, and for A1 and A2, are similar. Furthermore, the reddening correction has only minor significance. Unsurprisingly, the rovibrational transitions trace hotter gas than the pure rotational transitions; cf. Le Bourlot et al. (2002), Giannini et al. (2006). There is no persuasive evidence for non-thermal values of the ortho:para H₂ ratio from the observational points in the excitation diagram. In the models, an initial (statistical) value of 3:1 was assumed, and the computed value of the ortho:para ratio remained unchanged (to better than 10%) through the shock wave. The timescale for thermalization under the conditions of the cold, preshock gas (via proton exchange reactions with H⁺ or H₃⁺) approaches 10⁶ yr, which is much larger than the dynamical age of L1157 B1. Thermalization in the hot gas of the shock wave occurs more rapidly, via hydrogen atom exchange reactions: see Wilgenbus et al. (2000).

Table 1: Excitation temperatures inferred from observations of H₂ rotational (pix1 and pix2) and rovibrational (A1 and A2) transitions in L1157.

We have already noted in Sect. 3 that previous studies (see, for example, Flower et al. 2003; Giannini et al. 2004, 2006) have suggested that only CJ-type shock waves can account for the molecular hydrogen emission observed in molecular outflows. Our preliminary investigations of L1157 B1 confirmed this conclusion: stationary C-type shocks cannot reproduce the observed H₂ excitation diagram. Accordingly, we concentrate on CJ-type models, for which the parameters to be varied include $n_{\rm H}$, $v_{\rm s}$, b, and the age of the shock wave. It follows that a procedure which restricts the range of the search of the parameter space is desirable, even essential.

Figures 6 and 12 show that most of the column density of H₂ is contributed by the rotational levels of the vibrational ground state. Consequently, the first restriction is to models that can reproduce the observed rotational excitation temperature (cf. Table 1), to within a reasonable tolerance. Adopting even a wide tolerance of 400 K restricts the parameter ranges to the following:

• $n_{\rm H} = 10^4$ cm^-3, $15~\le~v_{\rm s}~\le~35$ km s^-1, and $0.45~\le~b~\le~2.00$;
• $n_{\rm H} = 10^{5}$ cm^-3, $10~\le~v_{\rm s}~\le~20$ km s^-1, and $0.30~\le~b~\le~2.00$.

With $n_{\rm H} = 10^{6}$ cm^-3, only models with evolutionary ages less than a few hundred years are able to fit the observed rotational temperature. We excluded such models on the grounds that the dynamical age deduced empirically is in the range 2000-3000 yr Gueth et al. (1998). The magnetic field parameter, b, is poorly constrained by the rotational line observations. A lower limit to the magnetic field strength is imposed by the requirement that the ion magnetosonic speed should exceed the shock speed, a necessary condition for a magnetic precursor to develop; see Flower & Pineau des Forêts (2003), Le Bourlot et al. (2002), Guillet et al. (2007).

In order to constrain the evolutionary age of the shock wave, we are guided by the rotational line spectrum, and initially by the 0-0 S(5) transition. In Fig. 13 is plotted the flux in this rotational line against the mean rotational excitation temperature in the vibrational ground state, v = 0. We show results for series of C- and J-type models, for the parameters specified and ranges of the shock speed, $v_{\rm s}$, and of CJ-type models with $v_{\rm s} = 25$ km s^-1 and varying ages. The fluxes observed in L1157 B1 (pix1 and pix2) are shown also. The evolution of J-type models into C-type, through CJ-type of increasing ages, is well represented in this figure. It is clear that only CJ-type models provide a fit to the observations, a result which is consistent with earlier studies of ouflows, cited above, and which will receive further confirmation below. The steady-state C-type models consistently overestimate the intensity of the 0-0 S(5) transition, whatever value of b is adopted. Whilst the discrepancy might be resolved by assuming a small filling factor, this assumption would result in the intensities of lines from vibrational levels v > 0 being underestimated. When optimizing the values of the CJ-type model parameters, we shall make use of the entire H₂ excitation diagram, incorporating the emission observed from vibrationally excited levels.

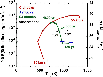Figure 13: The observed and calculated values of the H2 0-0 S(5) emission line flux, plotted as functions of the mean excitation temperature of the rotational lines within the v = 0 vibrational ground state. The corresponding values of the column density per magnetic sub-level are given on the right-hand axis for the (v = 0, j = 7) emitting level, whose degeneracy is g7 = 45. Results are given for L1157 B1, as observed by ISO (two separate pixels, pix1 and pix2) and for a series of models of (stationary) C-type (b = 1) shock waves (red curve) for ranges of the shock speed, $v_{\rm s}$, in steps of 5 km s-1 between the limiting values indicated. Also shown are the results for an evolutionary sequence of non-stationary CJ-type (b = 1) models (green curve), for $v_{\rm s} = 25$ km s-1, and for J-type (b = 0.1) models (blue curve) with $v_{\rm s} = 20$, 25 and 30 km s-1. In all cases, the pre-shock density is $n_{\rm H} = 10^4$ cm-3.

Open with DEXTER

We compute a small grid of CJ-type (non-stationary) shock models around our initial estimation of the shock age. The range of ages is sufficient to ensure that we do not exclude models which might yield acceptable excitation diagrams.

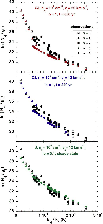Figure 14: Three models of the H2 excitation diagram of L1157 B1: CJ-type $n_{\rm H} = 10^4$ cm-3, $v_{\rm s} = 20$ km s-1, b = 1, age 850 yr ( top panel); CJ-type $n_{\rm H} = 10^{5}$ cm-3, $v_{\rm s} = 12$ km s-1, b = 1, age 240 yr ( middle panel); J-type $n_{\rm H} = 10^{5}$ cm-3, $v_{\rm s} = 12$ km s-1, b = 0.1 ( bottom panel). The observations are from Caratti o Garatti et al. (2006) and Cabrit et al. (1999); see also Appendix A.

Open with DEXTER

CJ-type shocks with a pre-shock density $n_{\rm H} = 10^4$ cm^-3, shock velocities $v_{\rm s} = 20$, 22, and 25 km s^-1, and $n_{\rm H} = 10^{5}$ cm^-3, $v_{\rm s} = 12$ and 15 km s^-1 were found to give reasonable fits to the H₂ observations. In Fig. 14, we compare the H₂ excitation diagram derived from the observations of L1157 B1 with the predictions of two CJ-type models with pre-shock densities $n_{\rm H} = 10^4$ and 10⁵ cm^-3. We show also the results from the best-fitting J-type shock model. None of the models provides a completely satisfactory fit to the observations. As the shock evolves towards stationary C-type, i.e. as its age increases, the intensities of the rovibrational transitions decrease, relative to the pure rotational transitions within the vibrational ground state, v = 0. Thus, the J-type shock underestimates substantially the column densities of the v = 0 rotational levels. As these levels contribute most of the H₂ column density, we eliminate the J-type model from further consideration. On the other hand, the CJ-type shocks tend to underestimate the column densities of some of the vibrationally excited rotational levels. We defer further discussion of these remaining discrepancies until comparisons with the observations of the rotational transitions of SiO have been made.

   
4.2 SiO emission lines

After an initial selection of model parameters, based on H₂ observations, we proceed to comparisons with the observed SiO rotational line intensities. There is now an additional parameter, namely, the fraction of silicon present as SiO in the grain mantles.

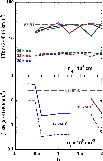Figure 15: The integrated intensity of the SiO(5-4) line, $\int {T{\rm d}v}(5-4)$, against the magnetic field parameter, b, for CJ-type shocks of various ages in which the pre-shock density $n_{\rm H} = 10^4$ cm-3, the shock velocity $v_{\rm s} = 20$, 22, and 25 km s-1 ( upper panel), and $n_{\rm H} = 10^{5}$ cm-3, $v_{\rm s} = 12$ and 15 km s-1 ( lower panel). Results were obtained assuming either 10% (full curves) or 1% (broken curves) of the silicon is initially SiO in the grain mantles.

Open with DEXTER

As in Sect. 3.3, we consider first the integrated intensity of the SiO(5-4) line. It is clear that, for the low shock speeds which were derived from the analysis of the H₂ rovibrational spectrum, some silicon must be present in the grain mantles: grain-core erosion alone would not give rise to a sufficient amount of gas-phase SiO to account for the observations of its rotational lines. We assume that either 1% or 10% of the silicon is SiO in the mantles.

In Fig. 15 is plotted the SiO(5-4) integrated line intensity against the magnetic field parameter, b, for CJ-type shocks with a pre-shock density $n_{\rm H} = 10^4$ cm^-3, shock velocities $v_{\rm s} = 20$, 22, and 25 km s^-1 (in the upper panel), and $n_{\rm H} = 10^{5}$ cm^-3, $v_{\rm s} = 12$ and 15 km s^-1 (in the lower panel). We recall that these models were found to give acceptable fits to the H₂ observations. We note that the evolutionary age was varied simultaneously with b, in order to optimize the fits to the observed H₂ excitation diagram, giving rise to the variations which are seen in the (5-4) line intensity. This variation is particularly striking in the results for a pre-shock density of 10⁵ cm^-3 and shock velocity of 12 km s^-1: the model for which b = 0.45 (age 75 yr) incorporates a significant magnetic precursor, whereas, when b = 0.6 (age 75 yr), the precursor is negligible. In the latter case, there is much less sputtering of SiO from the grain mantles, and the SiO emission is correspondingly weaker. The results in Fig. 15 may be seen to support the higher percentage (10%) of silicon being present in the mantles.

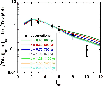	Figure 16: The best-fitting models of the H2 and SiO observations of L1157 B1: CJ-type shocks for which $n_{\rm H} = 10^4$ cm-3 and $v_{\rm s} = 20$ km s-1; the magnetic field parameter, b and the evolutionary age are varied simultaneously. 10% of the silicon is initially SiO in the grain mantles.
Open with DEXTER

Finally, we compare the integrated line intensities, relative to the (5-4) transition, with the observations. This comparison eliminates the models with $n_{\rm H} = 10^{5}$ cm^-3, which are found to overestimate the intensities of the lines from high rotational levels. On the other hand, as may be seen from Fig. 16, a range of combinations of b and the shock age remains compatible with the relative line intensities for $n_{\rm H} = 10^4$ cm^-3 and the optimal shock speed of $v_{\rm s} = 20$ km s^-1. The only observational point that is not well fitted by the models (the (10-9) transition) could be more closely approached by reducing the amount of SiO assumed to be initially in the mantles. The evolutionary ages of the models in Fig. 16 lie in the range 500-2000 yr, as compared with the dynamical age estimate of 2000-3000 yr, derived empirically (Gueth et al. 1998). The models which fit the observations of H₂ and SiO have been found to be compatible with the integrated intensities of rotational lines of CO: see Appendix B.

   
5 Concluding remarks

We have extended a previous study (G08) of the emission of SiO from shock waves in molecular outflows by considering the possibility that a small percentage of the silicon is present, as SiO, in the grain mantles, rather than exclusively as silicates in the grain cores. The lower binding energy of the mantle material ensures that the constituents are rapidly sputtered by the light but abundant neutral species, H₂, He and H, which impact the grains (most of which are negatively charged, and hence flow with the charged fluid) at the ion-neutral drift speed. The sputtering process ensures that SiO emission occurs over the full width of the magnetic precursor and hence over a wide range of flow speeds. This situation contrasts with that studied by G08, in which Si was sputtered from the grain cores by the impact of heavy but scarce neutral species, such as CO, and subsequently oxidized to SiO in the gas phase. As a consequence, the SiO rotational line profiles predicted by steady-state C-type shock waves (see Fig. 4, above) are much broader than in our previous study (G08, Fig. 8) and, in this respect, in much better agreement with the observed line profiles. However, the computed profiles vary significantly with the emitting rotational level, $j_{\rm up}$, whereas the observed profiles are seen to be similar from line to line (see Fig. 9 of Nisini et al. 2007).

Additional constraints on the nature of the shock waves are provided by observations of molecular hydrogen. Previous comparisons with observed H₂ excitation diagrams for Cepheus A West, Orion OMC-1, and various Herbig-Haro objects have suggested that non-stationary (CJ-type) shock waves are required to reproduce simultaneously the column densities of the ground and the excited vibrational levels of H₂. This conclusion is confirmed by the present study. Furthermore, the derived evolutionary ages of the order of a thousand years are consistent with the empirically-derived dynamical age of L1157, the object that we have studied in most detail. We derive a pre-shock gas density $n_{\rm H} = 10^4$ cm^-3 and a shock speed $v_{\rm s} = 20$ km s^-1; approximately 10% of the elemental silicon is initially in the form of SiO in the grain mantles. The initial (transverse) magnetic field strength is not well constrained by the observations but is broadly compatible with the values derived by Crutcher (1999) from Zeeman measurements. The predictions of this model are found to be consistent also with the rotational line emission of CO (Appendix B). We consider that the level of agreement between the model predictions and the observations of H₂, SiO and CO is encouraging, though certainly not perfect. The optimal model (pre-shock density $n_{\rm H} = 10^4$ cm^-3 and shock speed $v_{\rm s} = 20$ km s^-1) tends to underestimate the column densities of the v = 1 and v = 2 vibrationally excited levels of H₂ and overestimate the emission from the j = 10 rotational level of SiO.

It would be naive to believe that a single plane-parallel shock wave could be completely successful in accounting for the emission from what is undoubtedly a complex flow. In order to explain the fact that the calculated SiO line widths were an order of magnitude smaller than observed, G08 proposed that the observed lines are attributable to several shocks within the telescope beam, which appear spread out in radial velocity, owing to a range of inclination angles or propagation speeds (in the reference frame of the observer). In the case of CJ-type models, the discrepancy between the calculated and observed line widths is at least as great as in G08; but as the dimension of the emitting region is also reduced by the presence of the J-discontinuity, we may invoke the same explanation in this case, namely that there are several shocks within the telescope beam.

Acknowledgements

This study is based in part on observations with ISO, an ESA project with instruments funded by ESA Member States (especially the PI countries: France, Germany, the Netherlands and the United Kingdom) with the participation of ISAS and NASA. Antoine Gusdorf and the University of Durham acknowledge the support of the European Commission under the Marie Curie Research Training Network ``The Molecular Universe'' MRTN-CT-2004-512302. We thank Brunella Nisini for helpful correspondence relating to the SiO observations of Nisini et al. (2007), Emmanuel Dartois for discussions of the possibility of detecting SiO in grain mantles, and Malcolm Walmsley for his comments on the manuscript.

References

• Bachiller, R., & Pérez Gutiérez, M. 1997, ApJ, 487, L93 [NASA ADS] [CrossRef]
• Bachiller, R., Pérez Gutiérez, M., Kumar, M. S. N., & Tafalla, M. 2001, A&A, 372, 899 [NASA ADS] [CrossRef] [EDP Sciences]
• Balakrishnan, N., Yan, M., & Dalgarno, A. 2002, ApJ, 568, 443 [NASA ADS] [CrossRef] (In the text)
• Cabrit, S., Bontemps, S., Lagage, P. O., et al. 1999, in the Universe as seen by ISO, ed P. Cox, & M. F. Kessler, 449 (In the text)
• Caratti o Garatti, A., Giannini, T., Nisini, B., & Lorenzetti, D. 2006, A&A, 449, 1077 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Cecchi-Pestellini, C., Bodo, E., Balakrishnan, N., & Dalgarno, A. 2002, ApJ, 571, 1015 [NASA ADS] [CrossRef] (In the text)
• Chièze, J.-P., Pineau des Forêts, G., & Flower, D. R. 1998, MNRAS, 295, 672 [NASA ADS] [CrossRef] (In the text)
• Crutcher, R. M. 1999, ApJ, 520, 706 [NASA ADS] [CrossRef] (In the text)
• Davis, C. J., & Eisloeffel, J. 1995, A&A, 300, 851 [NASA ADS] (In the text)
• Dayou, F., & Balança, C. 2006, A&A, 459, 297 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Flower, D. R. 2001, J. Phys. B, 34, 2731 [NASA ADS] [CrossRef] (In the text)
• Flower, D. R., & Pineau des Forêts, G. 1999, MNRAS, 308, 271 [NASA ADS] [CrossRef]
• Flower, D. R., & Pineau des Forêts, G. 2003, MNRAS, 343, 390 [NASA ADS] [CrossRef] (In the text)
• Flower, D. R., Le Bourlot, J., Pineau des Forêts, G., & Cabrit, S. 2003, MNRAS, 341, 70 [NASA ADS] [CrossRef]
• Giannini, T., Nisini, B., & Lorenzetti, D. 2001, ApJ, 555, 40 [NASA ADS] [CrossRef] (In the text)
• Giannini, T., McCoey, C., Caratti o Garatti, A., et al. 2004, A&A, 419, 999 [NASA ADS] [CrossRef] [EDP Sciences]
• Giannini, T., McCoey, C., Nisini, B., et al. 2006, A&A, 459, 821 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Guillet, V., Pineau des Forêts, G., & Jones, A. 2007, A&A, 476, 263 [NASA ADS] [CrossRef] [EDP Sciences]
• Gueth, F., Guilloteau, S., & Bachiller, R. 1998, A&A, 333, 287 [NASA ADS] (In the text)
• Gusdorf, A., Cabrit, S., Flower, D. R., & Pineau des Forêts, G. 2008, A&A, 482, 809 [NASA ADS] [CrossRef] [EDP Sciences]
• Larsson, B., Liseau, R., Pagani, L., et al. 2007, A&A, 466, 999 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Le Bourlot, J., Pineau des Forêts, G., Flower, D. R., & Cabrit, S. 2002, MNRAS, 332, 985 [NASA ADS] [CrossRef] (In the text)
• Lesaffre, P., Chièze, J.-P., Cabrit, S., & Pineau des Forêts, G. 2004a, A&A, 427, 147 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Lesaffre, P., Chièze, J.-P., Cabrit, S., & Pineau des Forêts, G. 2004b, A&A, 427, 157 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Nisini, B., Codella, C., Giannini, T., et al. 2007, A&A, 462, 163 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Pagani, L., Olofsson, A. O. H., Bergman, P., et al. 2003, A&A, 402, L77 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618 [NASA ADS] [CrossRef] (In the text)
• Schilke, P., Pineau des Forêts, G., Walmsley, C. M., & Martín-Pintado, J. 2001, A&A, 372, 291 [NASA ADS] [CrossRef] [EDP Sciences]
• Tafalla, M., & Bachiller, R. 1995, ApJ, 443, L37 [NASA ADS] [CrossRef]
• Van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences]
• Walmsley, C. M., Pineau des Forêts, G., & Flower, D. R. 1999, A&A, 342, 542 [NASA ADS]
• Wilgenbus, D., Cabrit, S., Pineau des Forêts, G., & Flower, D. R., 2000, A&A, 356, 1010 [NASA ADS]
• Wrathmall, S. A., & Flower, D. R., 2007, J. Phys. B, 40, 3221 [NASA ADS] [CrossRef] (In the text)
• Zhang, Q., Ho, P. T. P., Wright, M. C. H., & Wilner, D. J. 1995, ApJ, 451, L71 [NASA ADS] [CrossRef]
• Zhang, Q., Ho, P. T. P., & Wright, M. C. H. 2000, AJ, 119, 1345 [NASA ADS] [CrossRef]

 

  
Online Material

   
Appendix A: H₂ rotational lines observed with ISO

In order to illustrate the morphology of the H₂ emission, we show, in Fig. A.1, the map of the L1157 outflow obtained by Cabrit et al. (1999) with ISOCAM in a narrow filter ( $R \approx 40$) centered on the 0-0 S(5) line at 6.9 $\mu$m, superposed on the CO map of Bachiller & Pérez-Guttiérez (1997). A curving chain of knots is seen along the outflow axis, coinciding with previously known shocked regions, traced by interferometric mapping in SiO (Gueth et al. 1998; Zhang et al. 1995, 2000) and NH₃ (Tafalla & Bachiller 1995), and in 2.12 $\mu$m H₂ro-vibrational emission (Davis & Eisloeffel 1995). As may be seen in Fig. A.2, there is good spatial correspondence between the H₂ v = 0-0 lines and the SiO and rovibrational H₂ towards the southern blue lobe. The peak of H₂ v = 0-0 coincides with the brightest regions in SiO and 2.12 $\mu$m H₂. A second SiO knot at the tip of the southern lobe appears only in the longer wavelength LW3 filter that covers the 0-0 S(1) and 0-0 S(2) lines, indicating a lower degree of excitation.

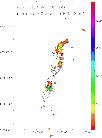	Figure A.1: A map of the L1157 outflow (Cabrit et al. 1999) obtained with ISOCAM in a narrow filter ( $R \approx 40$), centered on the 0-0 S(5) line at 6.9 $\mu$m, and superposed on the CO map of Bachiller & Pérez-Guttiérez (1997).
Open with DEXTER

Individual line fluxes of the 0-0 S(2) to 0-0 S(7) lines towards the peak were extracted from a full ISOCAM/CVF scan of this region obtained with 6 $^{\prime \prime }$ per pixel resolution. By comparing the fluxes in the broad and the narrow filters, we established that there was negligible continuum contamination. The data were analyzed using ``CIA'', a joint development by the ESA Astrophysics Division and the ISOCAM Consortium led by the ISOCAM PI, C. Cesarsky, Direction des Sciences de la Matière, C.E.A., France. The most important sources of uncertainty are, in decreasing order, transient effect corrections, flat-field errors, and photometric conversion factors, giving a total uncertainty of $\pm$20-30%. The observed fluxes after transient correction are listed in Table A.1.

	Figure A.2: Left panel: the LW3 ISOCAM image of the southern blue lobe of L1157 superposed on the SiO (2-1) contours of Gueth et al. (1998). Right panel: the LW2 ISOCAM image of the southern blue lobe of L1157 superposed on the contours of the H2 2.12 $\mu$m (plus continuum) emission from Davis & Eisloeffel (1995).
Open with DEXTER

Table A.1: Values of $\ln(N_{\rm up}/g_{\rm up})$, derived from ISOCAM observations of H₂ rotational lines in L1157 (uncorrected for reddening), for the two brightest pixels of the knot B1 and also for a $3\times 3$ pixel area which comprises the two peaks. The pixel size is 6 $^{\prime \prime }$, which corresponds to 2600 AU at the distance of L1157.

   
Appendix B: CO integrated line intensities

The treatment of the radiative transfer of the rotational lines of CO was completely analogous to that of SiO. In particular, the expression for the escape probability and the numerical implementation were identical; for more complete information, see G08, Appendix A. The Einstein A-values and the rotational constant for the ground vibrational state of ¹²C¹⁶O ( B₀ = 57635.96828 MHz, corresponding to $hB_0/k_{\rm B} = 2.766$ K) were taken from the NIST database (http://www.nist.gov/data/).

In the case of CO, rate coefficients for collisional excitation by H₂, He and H are available. We used the following sets of collisional data:

• collisions with H from Balakrishnan et al. (2002) for the 8 lowest rotational levels of CO and $5 \le T \le 100$ K, and also for the 17 lowest levels and $100 \le T \le 300$ K;

• collisions with He from Cecchi-Pestellini et al. (2002) for the 15 lowest rotational levels of CO and $5 \le T \le 500$ K;

• collisions with ortho-H₂ and para-H₂ from Flower (2001): the 20 lowest levels of CO for collisions with ortho-H₂, and the 29 lowest levels of CO for collisions with para-H₂; $5 \le T \le 400$.

At temperatures higher than the specified upper limits, we assumed the rate coefficients to be constant.

Our code was tested against the online version of RADEX (http://www.sron.rug.nl/vdtak/radex/radex.php), which is appropriate to a turbulent homogeneous sphere (Van der Tak et al. 2007), adopting their expression for the escape probability and assuming that H₂ is the only collision partner; discrepancies never exceeded a few percent. As anticipated, the initial distribution of elemental oxygen (see Sect. 1 and G08) and of elemental silicon (see above) had no influence on the CO emission from the shock wave.

As in the case of SiO, we computed the CO integrated line intensities for all models which simulated the H₂ emission satisfactorily. Models for which $n_{\rm H} = 10^{5}$ cm^-3 generated too much emission from the high rotational levels, relative to the low levels. CJ-type shock models with a preshock density  $n_{\rm H} = 10^4$ cm^-3 provided better fits to the observations. Figure B.1 shows a comparison between observed and calculated (absolute) integrated line intensities; the observations were compiled by Giannini et al. (2001). The model for which results are displayed is the same as in Fig. 16 and corresponds to $n_{\rm H} = 10^4$ cm^-3 and $v_{\rm s} = 20$ km s^-1; there are various combinations of the magnetic field strength parameter, b, and the shock age. The shape of the theoretical curves in this Fig. B.1 is in good agreement with that observed, although there remains a discrepancy in the absolute values which may indicate an overestimation of the beam filling factor, for which we adopted a value of 1/16, corresponding to a beam diameter of 80 $^{\prime \prime }$ and a source diameter of 20 $^{\prime \prime }$. Figure B.1 suggests that the rotational transitions which were observed by ISO are not ideal discriminants of the models.

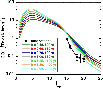	Figure B.1: The integrated intensities of the CO rotational lines, $\int {T{\rm d}v}$, for CJ-type shocks for which $n_{\rm H} = 10^4$ cm-3 and $v_{\rm s} = 20$ km s-1; the magnetic field parameter, b and the evolutionary age are varied simultaneously.
Open with DEXTER

   
Appendix C: The age of a CJ-type shock wave

In the CJ-type models considered above, the termination point of the flow was determined such that the (ion) flow time in theC part of the shock wave, i.e. up to the J-discontinuity, and the flow time behind the discontinuity were equal. In so far as the models are perceived as a set of quasi-time-dependent simulations of the flow, the termination point should correspond to the location of the ``piston'' which drives the shock wave.

Let $u_{\rm p}$ be the speed of the piston (which is also the speed of the gas at the surface of the piston) and u₀ be the speed of the gas immediately upstream of the discontinuity, with these speeds being expressed in the shock frame. If $\rho _{\rm p}$ and $\rho _0$ are the corresponding mass densities, then

$$\rho _{\rm p} u_{\rm p} = \rho _0 u_0$$

from the equation of continuity. Hence

$$u_{\rm p} = \rho _0 u_0 / \rho _{\rm p}.$$

The discontinuity advances at u₀ relative to the gas immediately in front of it, and the velocity of the piston, relative to this same gas, is $(u_0 - u_{\rm p})$. Thus, the speed of the discontinuity minus the speed of the piston is $u_{\rm p}$. In other words, the discontinuity moves away from the piston at speed $u_{\rm p}$. As the discontinuity coincides with the surface of the piston at time t = 0, the age of the shock wave is

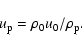
$$t_{\rm s} = \int _0^p [(\rho _{\rm p} / \rho _0) / u_0] {\rm d}z = [(\rho _{\rm p} / \rho _0) / u_0] \Delta z$$

where z is the position coordinate and $\Delta z$ is the current distance between the discontinuity and the piston; $t_{\rm s}$ is the time required for the discontinuity to move to its current position from its initial position, at the surface of the piston.

Using $t_{\rm s}$ as defined above to define the shock age has the advantage of removing the ambiguity of the two flow times (ion and neutral): behind the discontinuity, $u_{\rm i} = u_{\rm n}$. Because the flow speed rapidly attains its postshock value $({=} u_{\rm p})$ behind the discontinuity, the flow time behind the discontinuity is approximately equal to $t_{\rm s}$. In the time $t_{\rm s}$ required for the discontinuity to separate from the piston and reach its current position, a magnetic precursor develops simultaneously upstream of the discontinuity.

Note, however, that the expression above for $t_{\rm s}$ does not give the shock age exactly, as it assumes that the speed of the discontinuity relative to the piston, $u_{\rm p}$, remains constant, whereas Fig. 3d of Lesaffre et al. (2004a) shows that $u_{\rm p}$ decreases steadily as cooling sets in and the size of the velocity jump at the discontinuity decreases, following the growth of the precursor. A more accurate estimate of the age, under the (generally valid) condition that the width of the region downstream of the J-discontinuity is much smaller than the width of the C part of the shock wave, upstream of the discontinuity (i.e. the ``magnetic precursor''), is the time of flow of the charged fluid through the precursor (Lessaffre et al. 2004b, Eq. (60)). It is this determination of the shock age that has been adopted in the present paper.