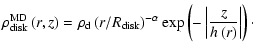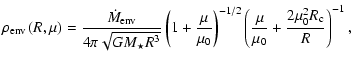A&A 490, 673-684 (2008)
DOI: 10.1051/0004-6361:200809901
HK-band imaging polarimetry and radiative transfer modeling
of the massive young stellar object CRL 2136
K. Murakawa -
T. Preibisch -
S. Kraus
-
G. Weigelt
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69, 53121 Bonn, Germany
Received 3 April 2008 / Accepted 6 August 2007
Abstract
Aims. We investigate the physical properties of the dust environment of the massive proto-stellar object CRL 2136 by means of two-dimensional radiative transfer modeling, which combines fitting of the spectral energy distribution, the intensity images, and the polarization images.
Methods. We obtained polarimetric images of CRL 2136 in the H and K bands using the CIAO instrument on the 8 m Subaru telescope. We developed a new Monte Carlo code which can deal with multiple-grain models and computes the SED, the dust temperature, and the Stokes IQUV images. With this code, we performed two-dimensional modeling of CRL 2136's circumstellar disk and envelope.
Results. Our images show a compact infrared source, two bright lobes extending towards the south and east, and two faint lobes extending towards the northwest and west. The polarization images show a polarization disk near the central star with a position angle of 
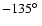 ,
a polarization vector alignment approximately parallel to the polarization disk, and a region with low polarization between the eastern and the southern lobes. In our modeling, we assume three grain models: bare grains, warm grains with a crystalline water ice mantle, and cold grains with an amorphous water ice mantle. We obtained a maximum grain core size of 0.45
,
a polarization vector alignment approximately parallel to the polarization disk, and a region with low polarization between the eastern and the southern lobes. In our modeling, we assume three grain models: bare grains, warm grains with a crystalline water ice mantle, and cold grains with an amorphous water ice mantle. We obtained a maximum grain core size of 0.45  m. We found that the CRL 2136 disk has a low disk mass of 0.007
m. We found that the CRL 2136 disk has a low disk mass of 0.007  ,
a large radius of 2000 AU, a scale height of 1.0, and a low accretion rate of
,
a large radius of 2000 AU, a scale height of 1.0, and a low accretion rate of
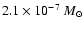 yr-1 compared to an envelope mass infall rate of
yr-1 compared to an envelope mass infall rate of
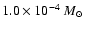 yr-1.
yr-1.
Conclusions. The predicted environment of the disk and the envelope is consistent with a scenario in which the central star forms rapidly (
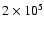 yr), with a high mass infalling rate, and nearly isotropically (large disk scale height) in the early phase. Then, the accretion of the disk matter is prevented by the strong radiation pressure from the luminous central star, resulting in a low disk mass and a low accretion rate.
yr), with a high mass infalling rate, and nearly isotropically (large disk scale height) in the early phase. Then, the accretion of the disk matter is prevented by the strong radiation pressure from the luminous central star, resulting in a low disk mass and a low accretion rate.
Key words: stars: circumstellar matter -
radiative transfer - polarization - stars: imaging
CRL 2136 (=IRAS 18196-1331 = OH 17.6+0.2) is a massive
star-forming region consisting of the near-infrared (NIR) source IRS 1 and a
bipolar reflection nebula located at a distance of 2 kpc (Kastner et al. 1992).
IRS 1 possesses a protostar with a luminosity of 
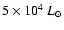 ,
and its mass was estimated to be higher than
,
and its mass was estimated to be higher than
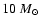 (Kastner et al. 1992).
Previous NIR imaging polarimetry (e.g. Kastner et al. 1992; Minchin et al. 1991) detected
two bright lobes of nebulosity extending east and south with respect to IRS 1.
Their polarization data shows a centro-symmetrically aligned pattern in the
nebulosities surrounding IRS 1 and a linear alignment near IRS 1 with a
position angle (PA) of
(Kastner et al. 1992).
Previous NIR imaging polarimetry (e.g. Kastner et al. 1992; Minchin et al. 1991) detected
two bright lobes of nebulosity extending east and south with respect to IRS 1.
Their polarization data shows a centro-symmetrically aligned pattern in the
nebulosities surrounding IRS 1 and a linear alignment near IRS 1 with a
position angle (PA) of  45
45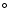 .
Low resolution spectroscopy has detected
deep absorption features of silicate at 9.7
.
Low resolution spectroscopy has detected
deep absorption features of silicate at 9.7  m (
m (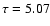 )
and water ice
at 3.07
)
and water ice
at 3.07  m (
m (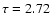 )
(Willner et al. 1982). A CO emission line map shows
blue- and red-shifted outflow components extending toward the southeast
(
)
(Willner et al. 1982). A CO emission line map shows
blue- and red-shifted outflow components extending toward the southeast
( 135
135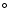 )
and the northwest (
)
and the northwest (
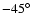 ), respectively,
approximately perpendicular to the direction of aligned polarization vectors
near the central star (Kastner et al. 1994). The above-mentioned observational
results are strong evidence for an optically thick torus, possibly a disk, and
an envelope structure.
), respectively,
approximately perpendicular to the direction of aligned polarization vectors
near the central star (Kastner et al. 1994). The above-mentioned observational
results are strong evidence for an optically thick torus, possibly a disk, and
an envelope structure.
In recent years, some observational insights into the circumstellar environment
of massive protostars have been obtained by high-resolution NIR imaging
(e.g. Kraus et al. 2006; Alvarez et al. 2004; Weigelt et al. 2006; Preibisch et al. 2003) and radio interferometry
(e.g. Steinacker et al. 2006; Menten & van der Tak 2004; Patel et al. 2005). Furthermore, the circumstellar
environment of young stellar objects (YSOs) is also known to be a
molecule-forming region. Various absorption features, such as water ice,
formaldehyde, and methanol, have been detected in the circumstellar environment
(e.g. van Dishoeck 2004; Gibb et al. 2004). These molecules are thought to form on
dust grains, which work as a catalyst to promote chemical reactions
(e.g. Jones & Williams 1984). The chemical reactions (or molecule formation) depend on
physical conditions such as the dust temperature and the dust and gas densities.
Therefore, investigating the physical properties of the dusty environment
around young stellar objects is important in order to obtain a better
understanding of the formation of massive stars as well as the chemical
evolution in their surroundings.
Imaging polarimetry in the optical to NIR regime is a powerful technique to
probe the dust environment because scattered polarized light may contain
important information on the dust properties. Previous radiative transfer
modeling successfully explained a polarization disk around the central star
and a centro-symmetric polarization vector pattern in the envelope, which are
often detected in the observed data of YSOs, applying disk and envelope
geometries (e.g. Bastien & Ménard 1988; Lucas & Roche 1998; Whitney et al. 1997; Kenyon et al. 1993b; Fischer et al. 1996; Whitney & Hartman 1993).
Furthermore, polarization analysis allows us to constrain the grain size,
particularly in the nebula on a large scale better than using the SED and the
intensity images (e.g. Murakawa et al. 2008a,2007; Pendleton et al. 1990; Dougados et al. 1990).
In this work, we obtain NIR polarimetric images of the massive protostar
CRL 2136 using the 8 m Subaru telescope and apply the above method. Although
the above previous polarization analyses have mainly reproduced the intensity
and polarization images, we attempt to fit the SED in our experiment as well.
This allows us to better constrain the disk structure and grain size and to
analyze the dust temperature distribution, particularly in the disk. We have
already performed a similar technique for the proto-planetary nebula Frosty Leo
(Murakawa et al. 2008a). In Sect. 2, we present our observational
results. For our radiative transfer modeling, we developed a Monte Carlo code
which can analyze polarized light and handle multiple-grain models that are
distributed arbitrarily within the model geometry. We summarize the algorithms
of our code in Sect. 3. In Sect. 4, the details of our
modeling and the results are presented.
2 HK-band imaging polarimetry
We obtained H- and K-band polarimetric images using the NIR camera CIAO
on the 8 m Subaru telescope on 2005 June 28. The central wavelengths and
the band widths of the H- and K-band filters are
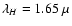 m
and
m
and
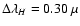 m, and
m, and
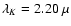 m and
m and
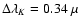 m, respectively. We used a medium resolution camera
with a pixel scale of 0.0217 arcsec pix-1. The natural seeing was
m, respectively. We used a medium resolution camera
with a pixel scale of 0.0217 arcsec pix-1. The natural seeing was
 0
0
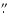 4 at R band. Since the target is faint at the wavelength for
wavefront sensing (mR>16 mag) and there is no bright single star near
the target, we did not apply the adaptive optics correction. In order to
measure linear polarization, we obtained four sets of images with half-wave
plate (HWP) orientations of 0
4 at R band. Since the target is faint at the wavelength for
wavefront sensing (mR>16 mag) and there is no bright single star near
the target, we did not apply the adaptive optics correction. In order to
measure linear polarization, we obtained four sets of images with half-wave
plate (HWP) orientations of 0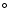 ,
45
,
45 ,
22.5
,
22.5 ,
and 67.5
,
and 67.5 .
At each orientation of the HWP, two frames with 30 s exposure times and
five frames with 3 s were obtained, and 8 and 12 jitter positions were
applied in the H and K bands, respectively. The total integration times
were 32 min for the H band and 12 min. for the K band. Although we also
obtained intensity images in the J band, we do not discuss the results due to
their poor image quality. For flux and polarization calibrations, we observed
Elias 2-14 and BS 6141. We found an offset of
.
At each orientation of the HWP, two frames with 30 s exposure times and
five frames with 3 s were obtained, and 8 and 12 jitter positions were
applied in the H and K bands, respectively. The total integration times
were 32 min for the H band and 12 min. for the K band. Although we also
obtained intensity images in the J band, we do not discuss the results due to
their poor image quality. For flux and polarization calibrations, we observed
Elias 2-14 and BS 6141. We found an offset of
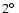 in position angle of
the polarization orientation and a difference of 0.3% in the degree of
polarization, which are both within the measurement errors.
in position angle of
the polarization orientation and a difference of 0.3% in the degree of
polarization, which are both within the measurement errors.
We reduced the observed data following the procedure described in our previous
papers (Murakawa et al. 2004,2005). After subtraction of the dark frame and
flat-fielding, we obtained the Stokes IQU images, the degree of linear
polarization (P), the polarization position angle (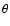 ), as well as their
error images. We found signal-to-noise ratios of the Stokes I (intensity)
images of 30-120 per pixel and an error of linear polarization of <15%
per pixel in the region with surface brightnesses higher than
), as well as their
error images. We found signal-to-noise ratios of the Stokes I (intensity)
images of 30-120 per pixel and an error of linear polarization of <15%
per pixel in the region with surface brightnesses higher than

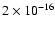 and
and

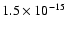 Wm
Wm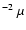 m-1 arcsec-2 in the H and
K bands, respectively. The uncertainty on the polarization position angle per
pixel is <
m-1 arcsec-2 in the H and
K bands, respectively. The uncertainty on the polarization position angle per
pixel is <
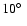 in these regions. The average PSF size is measured to be
0
in these regions. The average PSF size is measured to be
0
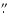 35 in the H and K bands from several point-source-like features
detected in our images.
35 in the H and K bands from several point-source-like features
detected in our images.
Figure 1 presents the intensity images overlaid with polarization
vector lines and the degree of polarization images in the H (left) and K(right) bands. The field of view (FOV) is
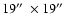 .
Figure 2 shows a sketch of CRL 2136, which illustrates some
components detected in our data and a CO emission line observation and inferred
from our modeling. Our images show the bright infrared source IRS 1,
fan-shaped nebulosities extending toward the south, east, west, and northwest,
and several point sources. The polarimetric data shows a centro-symmetric
vector pattern in the nebulosities. The degree of polarization reaches values
up to
.
Figure 2 shows a sketch of CRL 2136, which illustrates some
components detected in our data and a CO emission line observation and inferred
from our modeling. Our images show the bright infrared source IRS 1,
fan-shaped nebulosities extending toward the south, east, west, and northwest,
and several point sources. The polarimetric data shows a centro-symmetric
vector pattern in the nebulosities. The degree of polarization reaches values
up to  30% in the H band and
30% in the H band and  50% in the K bands.
Near IRS 1, we see a polarization disk extending at a position angle (PA) of
50% in the K bands.
Near IRS 1, we see a polarization disk extending at a position angle (PA) of

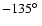 ,
but it is not clear in the northeast. In this region,
polarization vector lines are systematically aligned along a PA of
,
but it is not clear in the northeast. In this region,
polarization vector lines are systematically aligned along a PA of
 30
30 .
However, in the K band data, they converge at a point, i.e.
the polarization null point, in the southwest. These features are consistent
with previous results and they led authors to support the disk hypothesis
(Kastner et al. 1992; Minchin et al. 1991).
.
However, in the K band data, they converge at a point, i.e.
the polarization null point, in the southwest. These features are consistent
with previous results and they led authors to support the disk hypothesis
(Kastner et al. 1992; Minchin et al. 1991).
![\begin{figure}
\par\includegraphics[width=16.5cm,keepaspectratio]{9901fig1.eps}
\end{figure}](/articles/aa/full/2008/41/aa09901-08/Timg34.gif) |
Figure 1:
Polarimetric images of CRL 2136. The top panels are the obtained
intensity (Stokes I) images in the H ( left) and K ( right)
bands with the polarization vector lines. The field of view is
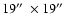 .
The bottom panels show the degree of
linear polarization images in the H ( left) and K
( right) bands.
The position of the central star is indicated with the offset of
(0 .
The bottom panels show the degree of
linear polarization images in the H ( left) and K
( right) bands.
The position of the central star is indicated with the offset of
(0
 0, 0 0, 0
 0). 0). |
| Open with DEXTER |
Our images clearly resolve the southern component into two lobes; i.e.
the west S1 and the east S2 lobes. While high polarizations are detected in
the S1 and E lobes (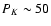 %), the S2 lobe as well as a fan-shaped
region between the E and S1 lobe have low polarizations of
%), the S2 lobe as well as a fan-shaped
region between the E and S1 lobe have low polarizations of 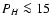 % and
% and
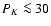 %. If we assume an envelope with a polar cavity structure, the E
and S1 lobes and the fan-shaped region correspond to the projected edges and
inner part of the cavity, respectively. Furthermore, we measured the
polarizations to be PH=32% and PK=21% at IRS 1 using a 0
%. If we assume an envelope with a polar cavity structure, the E
and S1 lobes and the fan-shaped region correspond to the projected edges and
inner part of the cavity, respectively. Furthermore, we measured the
polarizations to be PH=32% and PK=21% at IRS 1 using a 0
 7
diameter aperture, and
7
diameter aperture, and 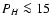 % and
% and 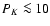 % south-west of IRS 1 in
the polarization disk. We stress that the H-band polarization in these
regions is higher than in the K band, in contrast to the envelope.
These results are in rough agreement with previous 3
% south-west of IRS 1 in
the polarization disk. We stress that the H-band polarization in these
regions is higher than in the K band, in contrast to the envelope.
These results are in rough agreement with previous 3  m spectropolarimetry
(Holloway et al. 2002; Hough et al. 1989). Details of our interpretation of the above
observational results based on our radiative transfer modeling will be
discussed in Sect. 4.2.2.
m spectropolarimetry
(Holloway et al. 2002; Hough et al. 1989). Details of our interpretation of the above
observational results based on our radiative transfer modeling will be
discussed in Sect. 4.2.2.
3 Radiative transfer code
We developed a new Monte Carlo radiative transfer code stsh
(StrahlungsTransportcode für Staubige Hüllen) and used it to
investigate the physical properties of the CRL 2136 nebula. Our code is
designed to simulate scattering, absorption, and reemission of radiation in the
model dust shell under local thermal equilibrium. It can treat transfer of
polarized light and multiple-grain models in a model geometry. The code
computes the SED and the dust temperature for multiple-grain models and
generates the Stokes
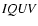 images. The principles of radiative transfer and
the Monte Carlo method have already been discussed in several papers
(e.g. Lucy 1999; Bjorkman & Wood 2001; Ivezic & Elitzur 1997; Yusef-Zadeh et al. 1984; Cashwell & Everett 1959; Niccolini et al. 2003; Witt 1977).
In this section, we summarize the algorithms of our code.
images. The principles of radiative transfer and
the Monte Carlo method have already been discussed in several papers
(e.g. Lucy 1999; Bjorkman & Wood 2001; Ivezic & Elitzur 1997; Yusef-Zadeh et al. 1984; Cashwell & Everett 1959; Niccolini et al. 2003; Witt 1977).
In this section, we summarize the algorithms of our code.
The model geometry consists of cells in one-dimensional (1-D) spherically
symmetric coordinates, two-dimensional (2-D) axi-symmetric coordinates, or
three-dimensional (3-D) spherical coordinates. For each cell, the dust density
can be specified for each grain model. Our code currently treats spherical
grains with an MRN- (Mathis et al. 1977) or KMH-like (Kim et al. 1994) size distribution
with or without a single-layered mantle. Cross sections of
absorption, scattering, and extinction, as well as scattering amplitude matrix
elements are calculated using Mie's scattering theory. For bare grains, we use
the algorithm reported by Wolf & Voshchinnikov (2004), which can handle grains with size
parameter![[*]](/icons/foot_motif.gif) values up to
values up to  107. For coated grains, we use the algorithm by
Wiscombe (1980) and Nussenzveig & Wiscombe (1980), which can treat a coating material even with
high absorption. We combined this algorithm with Wolf & Voshcninnikov's
algorithm in order to treat a very large size parameter value. In each grain
model, the cross sections and scattering amplitude matrix elements are averaged
in size with a size distribution function
107. For coated grains, we use the algorithm by
Wiscombe (1980) and Nussenzveig & Wiscombe (1980), which can treat a coating material even with
high absorption. We combined this algorithm with Wolf & Voshcninnikov's
algorithm in order to treat a very large size parameter value. In each grain
model, the cross sections and scattering amplitude matrix elements are averaged
in size with a size distribution function
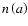 and in chemical
composition with a specified fraction.
and in chemical
composition with a specified fraction.
 |
Figure 2:
Cartoon of CRL 2136 illustrating the features detected in our data,
the direction of the CO outflow, as well as our interpretation of
a disk and envelope structure. The polarization disk on the
northeastern side of IRS 1 is not visible in our data. |
| Open with DEXTER |
The radiation from the radiation source is split into several photon packets.
The spectrum of the radiation source is given by a black-body spectrum with
an effective temperature
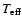 or by an arbitrary SED specified with
an external file. The former case is used for a single stellar system. When
a photon packet is emitted, the wavelength is determined following
Eqs. (14)-(16)
in the paper by Bjorkman & Wood (2001). The latter case is used for a non-black-body
radiation source, such as close multiple stellar systems and active galactic
nuclei (AGNs). The radiation from the source is assumed to be unpolarized and
to be emitted isotropically.
or by an arbitrary SED specified with
an external file. The former case is used for a single stellar system. When
a photon packet is emitted, the wavelength is determined following
Eqs. (14)-(16)
in the paper by Bjorkman & Wood (2001). The latter case is used for a non-black-body
radiation source, such as close multiple stellar systems and active galactic
nuclei (AGNs). The radiation from the source is assumed to be unpolarized and
to be emitted isotropically.
A photon packet propagates straight ahead in the model geometry to the next
interacting point, which is chosen by
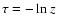 with a uniformly distributed
random number
with a uniformly distributed
random number ![$z\in(0,1]$](/articles/aa/full/2008/41/aa09901-08/img46.gif) .
At an interacting point, a grain model to interact
is determined. The probability of choosing the jth grain model is given by
.
At an interacting point, a grain model to interact
is determined. The probability of choosing the jth grain model is given by
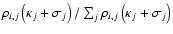 ,
where the quantities of
,
where the quantities of 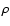 ,
,
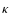 ,
and
,
and 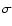 are the dust number density and the cross sections of
absorption and scattering, respectively. Then, with the albedo
are the dust number density and the cross sections of
absorption and scattering, respectively. Then, with the albedo
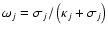 of the selected grain
model, absorption (
of the selected grain
model, absorption (
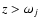 )
or scattering (
)
or scattering (
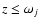 )
is determined
with a random number
)
is determined
with a random number 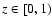 .
When the scattering event is chosen, the
direction of the photon propagation is changed. Our code uses Fischer's
algorithm (Fischer et al. 1996), which determines the direction of scattered light
depending on the polarization status before scattering. The Stokes parameters
after scattering are updated with the scattering Mueller matrix (Bohren & Huffmann 1983).
When the absorption event is chosen, the dust temperature is updated and a new
wavelength of reemitted light is determined. Our code employs
Bjorkman & Wood's method (Bjorkman & Wood 2001). After the interaction, the photon
packet performs further random walks until it leaves the model geometry or the
number of times of interaction reaches the specified limit. If the photon
packet reaches the outer boundary of the model geometry and the direction of
the ray points towards the observer, the SED and/or the Stokes images
are/is updated with the photon information. Then, a new photon packet is
emitted from the radiation source. The above procedures are repeated until all
photon packets are examined.
.
When the scattering event is chosen, the
direction of the photon propagation is changed. Our code uses Fischer's
algorithm (Fischer et al. 1996), which determines the direction of scattered light
depending on the polarization status before scattering. The Stokes parameters
after scattering are updated with the scattering Mueller matrix (Bohren & Huffmann 1983).
When the absorption event is chosen, the dust temperature is updated and a new
wavelength of reemitted light is determined. Our code employs
Bjorkman & Wood's method (Bjorkman & Wood 2001). After the interaction, the photon
packet performs further random walks until it leaves the model geometry or the
number of times of interaction reaches the specified limit. If the photon
packet reaches the outer boundary of the model geometry and the direction of
the ray points towards the observer, the SED and/or the Stokes images
are/is updated with the photon information. Then, a new photon packet is
emitted from the radiation source. The above procedures are repeated until all
photon packets are examined.
It is well known that the images generated by the above algorithm (hereafter
the standard full interacting mode) suffer from severe Monte Carlo noise in
most actual experiments. In order to relieve this problem, the concept of
weighted photons and its applications of the forced first scattering
(Cashwell & Everett 1959; Witt 1977) and peeling off (Gordon et al. 2001; Yusef-Zadeh et al. 1984; Wood & Reynolds 1999) have
been proposed. Dramatic improvements of the quality of the model images are
expected in cases of models with a high extinction (e.g. 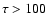 )
and
a large scale height value (e.g. H>0.5) or with a 3-D geometry. Our code
uses these algorithms.
)
and
a large scale height value (e.g. H>0.5) or with a 3-D geometry. Our code
uses these algorithms.
We have tested our code by comparing several model results with those obtained
using the DUSTY code (Ivezic & Elitzur 1997) for the 1-D case and the
mcsim_mpi code (Ohnaka et al. 2006) for the 2-D case. The 3-D case was
tested by choosing an axi-symmetric model geometry which can be compared with
the results obtained in a 2-D simulation. In all cases, we found that the
results of SED, dust temperature, and Stokes
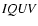 images produced by our code
are in good agreement with those obtained using the above codes.
images produced by our code
are in good agreement with those obtained using the above codes.
4 Modeling the CRL 2136 nebula
4.1 Model assumptions
4.1.1 Stellar parameters
The distance to CRL 2136 is not well known. Allen et al. (1977) suggested 5 kpc,
although this result was not well justified. We assume a kinematic distance of
D=2 kpc (Kastner et al. 1992). For this distance, Kastner et al. (1992) estimated
the stellar luminosity to be 
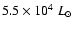 based on the
MIR flux, which dominates the SED. We set the luminosity to be this value.
The stellar temperature is also not well known. Harvey et al. (2000) adopted
based on the
MIR flux, which dominates the SED. We set the luminosity to be this value.
The stellar temperature is also not well known. Harvey et al. (2000) adopted
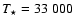 K from theoretical predictions for a zero-age main-sequence
star of the above luminosity (e.g. Yorke & Sonnhalter 2002; Bernasconi & Maeder 1996). However, the star
could be cooler than the above temperature because of the lack of radio
continuum emission (e.g. Harvey et al. 2000) and weak or non-detection of the
H2 1-0 S(1) emission line towards this object (Kastner & Weintraub 1996; Kastner et al. 1992).
They estimated the stellar temperature to be 7000-15 000 K. We set
K from theoretical predictions for a zero-age main-sequence
star of the above luminosity (e.g. Yorke & Sonnhalter 2002; Bernasconi & Maeder 1996). However, the star
could be cooler than the above temperature because of the lack of radio
continuum emission (e.g. Harvey et al. 2000) and weak or non-detection of the
H2 1-0 S(1) emission line towards this object (Kastner & Weintraub 1996; Kastner et al. 1992).
They estimated the stellar temperature to be 7000-15 000 K. We set 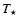 to be 20 000 K, which is an intermediate value of the above estimates.
An uncertainty of
to be 20 000 K, which is an intermediate value of the above estimates.
An uncertainty of  10 thousand Kelvins is possible. Even such a large
uncertainty does not affect the model results much because the wavelength
ranges in the NIR or longer are in the Rayleigh-Jeans law regime. We adopt
a stellar mass of
10 thousand Kelvins is possible. Even such a large
uncertainty does not affect the model results much because the wavelength
ranges in the NIR or longer are in the Rayleigh-Jeans law regime. We adopt
a stellar mass of
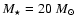 ,
which is expected from the
above-mentioned theoretical predictions.
,
which is expected from the
above-mentioned theoretical predictions.
4.1.2 Dust grains
Dust in star formation regions is often modeled similarly to the interstellar
matter (ISM); i.e. two major chemical compositions of silicate and graphite and
a power law size distribution (Kim et al. 1994; Draine & Lee 1984; Mathis et al. 1977). However, variations of
grain properties from region to region and even within one region have been
reported (e.g. Larson & Whittet 2005; Cardelli et al. 1989; Clayton et al. 2003). Since the dust in
CRL 2136 has not yet been investigated in detail, we assume a DL-MRN model;
i.e. a mixture of grain cores of astronomical silicate and of graphite with
fractions of 62.5% and 37.5%, respectively (Draine & Lee 1984). Although some
evidence for the presence of non-spherical grains has been reported
(Holloway et al. 2002; Hough et al. 1989), we assume spherical grains for simplicity.
We assume a size distribution with a power index given by
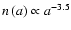 .
The minimum grain size
.
The minimum grain size
 does
not affect the SED and the polarization properties much, whereas the maximum
size
does
not affect the SED and the polarization properties much, whereas the maximum
size
 can have a strong influence. Therefore, we set a fixed
value of
can have a strong influence. Therefore, we set a fixed
value of
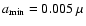 m, (corresponding to the diffuse ISM
population, Mathis et al. 1977) and estimate
m, (corresponding to the diffuse ISM
population, Mathis et al. 1977) and estimate
 from our modeling.
from our modeling.
Numerous molecules such as H2O (Willner et al. 1982), CH3OH (Skinner et al. 1992),
cyano group (often referred to as ``XCN'', Whittet et al. 2001; Pendleton et al. 1999),
and CO (Skinner et al. 1992) have been detected towards CRL 2136. These volatile
molecules are thought to form on the grain surface and cover the refractory
grain core as a mixture or ``dirty icy'' mantles (e.g. Jones & Williams 1984; Tielens & Hagen 1982; Herbst & Leung 1985).
Water ice is the major component and is an important tracer that allows us
to derive information about the dust temperature and grain size from
spectroscopic data. To reduce complexity, we consider only water ice as grain
mantles. It is known that water ice stays in a crystalline form at temperatures
between  80 K and the sublimation temperature of
80 K and the sublimation temperature of  140 K or in an
amorphous form below
140 K or in an
amorphous form below  80 K (Leger et al. 1983; Hagen et al. 1981). Therefore, we take
into account three grain species: grains with an amorphous ice mantle, grains
with a crystalline ice mantle, and bare grains at temperatures between
80 K (Leger et al. 1983; Hagen et al. 1981). Therefore, we take
into account three grain species: grains with an amorphous ice mantle, grains
with a crystalline ice mantle, and bare grains at temperatures between
 140 K and the dust sublimation temperature of
140 K and the dust sublimation temperature of  1500 K.
Details about our grain modeling are described in Sect. 4.2.1.
1500 K.
Details about our grain modeling are described in Sect. 4.2.1.
4.1.3 Disk and envelope geometries
As discussed in Sect. 2, several observational results of
CRL 2136 can be explained qualitatively with a disk and envelope structure.
Therefore, we applied both of these geometries in our radiative transfer
modeling using a dust density distribution given,
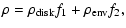 |
|
|
(1) |
where f1 and f2 are Fermi-type filter functions to guarantee a smooth
transition between the disk and the envelope components (Fischer et al. 1996).
For the disk structure, we examine a Keplerian rotating disk in hydrodynamical
equilibrium (labeled ``SH'', Pringle 1981; Shakura & Sunyaev 1973). Using the 2-D cylindrical
coordinate (r, z), the density structure is given by
![$\displaystyle \rho^{\rm SH}_{\rm disk}\left(r,z\right)=
\rho_{\rm d}\left(r/R_{...
...alpha}
\exp\left(-\frac{\pi}{4}\left[\frac{z}{h\left(r\right)}\right]^2\right),$](/articles/aa/full/2008/41/aa09901-08/img63.gif) |
|
|
(2) |
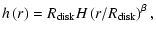 |
|
|
|
where
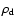 and H are the mass density at the disk
radius
and H are the mass density at the disk
radius
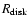 in the equatorial plane and the scale height of the
disk, respectively. The mass density coefficient
in the equatorial plane and the scale height of the
disk, respectively. The mass density coefficient
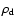 is
determined with the disk mass
is
determined with the disk mass
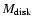 .
The values of
.
The values of 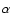 and
and 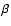 are 15/8 and 9/8, respectively. While the above model has a flared
shape because of
are 15/8 and 9/8, respectively. While the above model has a flared
shape because of 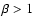 ,
Lazareff et al. (1990) proposed another disk model
(massive disk, ``MD'') which is a potential model for proto-stellar objects.
The density distribution is given by
,
Lazareff et al. (1990) proposed another disk model
(massive disk, ``MD'') which is a potential model for proto-stellar objects.
The density distribution is given by
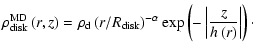 |
|
|
(3) |
This model is classified into four sub classes, depending on the values
of 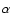 and
and 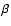 .
These are characterized by azimuthal velocity and the
surface density
.
These are characterized by azimuthal velocity and the
surface density 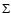 and have
and have
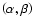 values of (2, 1),
(1, 1), (0, 1), and (0, 0) for the Toomre model (TO), the Larson model (LA), the
rigid body model (RB), and the infinite isothermal slab model (SL), respectively
(Larson et al. 1984; Toomre 1982; Fischer et al. 1996).
values of (2, 1),
(1, 1), (0, 1), and (0, 0) for the Toomre model (TO), the Larson model (LA), the
rigid body model (RB), and the infinite isothermal slab model (SL), respectively
(Larson et al. 1984; Toomre 1982; Fischer et al. 1996).
In our model, the inner radius
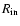 is set to be the dust sublimation
radius of 30 AU, which is appropriate for a star with an estimated luminosity of
is set to be the dust sublimation
radius of 30 AU, which is appropriate for a star with an estimated luminosity of
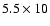 4
4 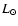 (e.g. Monnier & Millan-Gabet 2002). We determine the three
other free parameters of the disk radius
(e.g. Monnier & Millan-Gabet 2002). We determine the three
other free parameters of the disk radius
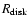 ,
the disk
mass
,
the disk
mass
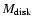 ,
and the disk scale height H from our modeling.
,
and the disk scale height H from our modeling.
For the envelope, we use the model of the slowly rotating, infalling envelope
(Terebey et al. 1984; Ulrich 1976; Cassen & Moosman 1981). The mass density distribution is given by
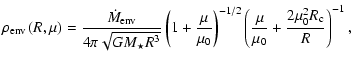 |
|
|
(4) |
where R, G,
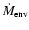 ,
and
,
and 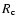 are the radial
distance from the central star, the gravitational constant, the envelope mass
infall rate, and the centrifugal radius, respectively. Beyond
are the radial
distance from the central star, the gravitational constant, the envelope mass
infall rate, and the centrifugal radius, respectively. Beyond 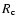 ,
the dust density of this envelope is approximately proportional to R-1.5.
An FIR observation and modeling satisfies this result (Harvey et al. 2000). The
quantity
,
the dust density of this envelope is approximately proportional to R-1.5.
An FIR observation and modeling satisfies this result (Harvey et al. 2000). The
quantity  is the cosine of the polar angle
is the cosine of the polar angle
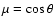 ,
and
,
and 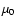 is the angle of a stream line as related through the equation
is the angle of a stream line as related through the equation
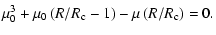 |
|
|
(5) |
The polar cavity is the region for 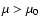 .
The density inside the cavity
is reduced to 0.001 compared to the surrounding envelope.
.
The density inside the cavity
is reduced to 0.001 compared to the surrounding envelope.
If we assume for CRL 2136 that the E and S1 lobes represent the cavity edge,
the opening angle is
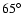 ,
i.e.
,
i.e.
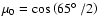 .
The centrifugal radius
.
The centrifugal radius  is set to be
is set to be
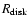 .
The outer
radius
.
The outer
radius
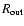 of the envelope affects mainly the fluxes in the FIR
and longer wavelengths and was estimated to be 0.3 pc, which is about the
extension of the submillimeter continuum at 800
of the envelope affects mainly the fluxes in the FIR
and longer wavelengths and was estimated to be 0.3 pc, which is about the
extension of the submillimeter continuum at 800  m (Kastner et al. 1994).
Therefore, we began to use 0.3 pc as the initial value and changed it later in
the course of the modeling process. A free parameter in our modeling is the
envelope mass infall rate
m (Kastner et al. 1994).
Therefore, we began to use 0.3 pc as the initial value and changed it later in
the course of the modeling process. A free parameter in our modeling is the
envelope mass infall rate
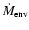 .
The value is searched around
an order of
.
The value is searched around
an order of
 yr-1, which is the typical value for massive
YSOs (Wolfire & Cassinelli 1986).
yr-1, which is the typical value for massive
YSOs (Wolfire & Cassinelli 1986).
4.2 Numerical simulations
Although some of the dust and geometry parameters were estimated in earlier
studies, a large number of parameters still have not been determined.
Because it is unrealistic to scan the whole parameter space, we follow the
following procedure. First, we constrain the dust grain parameters by fitting
the polarization maps and the spectrum. Then, with the best grain model, we
compute SEDs in order to obtain some potential solutions. We produce the
intensity and polarization images of these models and, finally, choose a good
model.
4.2.1 Grain model
As described in Sect. 4.1.2, we take into account three grain species:
cold grains (with an amorphous water ice mantle), warm grains (with a
crystalline water ice mantle), and bare grains. We first examine the cold
grains, which probably exist in the low-temperature envelope at large distances
from the central star. While the color information in our H- and K-band
intensity images depends on the grain size and the dust density (or the optical
depth), the degree of polarization is mostly governed by only the grain size
since the scattering angle dependence vanishes towards the projected cavity,
i.e. the E and S1 lobes, by integrating along the line of sight. Furthermore,
the degree of polarization varies the most as a function of the size
parameter x around 1, which corresponds to submicron-sized grains at NIR wavelengths.
Such grain sizes are very likely in the envelope. Therefore, we determine the
grain size
 by polarization fit. We compare the polarization
data in the above regions, where the dust density distribution in the plane
which crosses the central star the scattering matter (i.e. dust), and the
observer, can be approximated with a 1-D spherically symmetric geometry.
In addition, the polarization vectors are aligned centro-symmetrically in the
above E and S1 lobes. Thus, we apply a single scattering analysis
(Dougados et al. 1990). In this modeling, light emitted from the central star is
scattered only once in a 1-D dust shell and contributes to the observed
1-D image. The degree of polarization is calculated, using the Stokes IQparameters, by -Q/I. Although the grains in the nebula are expected to be
covered with a water ice mantle, the mantle does not affect the scattering
properties much if the mantle is not too thick compared to the grain core
radius or the considered wavelength is not at the absorption bands, e.g.
3.1
by polarization fit. We compare the polarization
data in the above regions, where the dust density distribution in the plane
which crosses the central star the scattering matter (i.e. dust), and the
observer, can be approximated with a 1-D spherically symmetric geometry.
In addition, the polarization vectors are aligned centro-symmetrically in the
above E and S1 lobes. Thus, we apply a single scattering analysis
(Dougados et al. 1990). In this modeling, light emitted from the central star is
scattered only once in a 1-D dust shell and contributes to the observed
1-D image. The degree of polarization is calculated, using the Stokes IQparameters, by -Q/I. Although the grains in the nebula are expected to be
covered with a water ice mantle, the mantle does not affect the scattering
properties much if the mantle is not too thick compared to the grain core
radius or the considered wavelength is not at the absorption bands, e.g.
3.1  m. Therefore, we modeled bare grains and examined values for
m. Therefore, we modeled bare grains and examined values for
 between 0.2 and 1.0
between 0.2 and 1.0  m in increments of 0.1
m in increments of 0.1  m.
For the geometry parameters, we set the inner radius
m.
For the geometry parameters, we set the inner radius
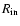 ,
the outer
radius
,
the outer
radius
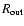 ,
and the power index of the dust density distribution
to be 30 AU, 0.3 pc, and -1.5, respectively. Because the polarization at
a large separation from the central star varies little in optically thin cases,
we set the optical depth at V band to be 1. Figure 3 shows the
degree of polarization
,
and the power index of the dust density distribution
to be 30 AU, 0.3 pc, and -1.5, respectively. Because the polarization at
a large separation from the central star varies little in optically thin cases,
we set the optical depth at V band to be 1. Figure 3 shows the
degree of polarization
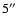 from the central star as a function of grain
size
from the central star as a function of grain
size
 .
We find that a grain model with
.
We find that a grain model with
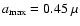 m reproduces our observational results of
m reproduces our observational results of
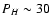 % and
% and
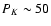 % quite well.
% quite well.
 |
Figure 3:
The degree of polarization dependence on the grain size
(
 ). The polarization is calculated by means of
a single scattering modeling with a spherically symmetric dust shell.
For simplicity, bare grains are assumed in this modeling. The minimum
grain size ). The polarization is calculated by means of
a single scattering modeling with a spherically symmetric dust shell.
For simplicity, bare grains are assumed in this modeling. The minimum
grain size
 and the power index of the size
distribution are fixed to be 0.005
and the power index of the size
distribution are fixed to be 0.005  m and -3.5, respectively. m and -3.5, respectively. |
| Open with DEXTER |
We determine the thickness of water ice mantles of the cold and warm dust and
the grain core size of the warm dust by fitting the 3  m spectrum.
It is well known that the 3
m spectrum.
It is well known that the 3  m water ice absorption feature suggests the
dust temperature from the width of the absorption feature, the chemical
composition from the 3.4
m water ice absorption feature suggests the
dust temperature from the width of the absorption feature, the chemical
composition from the 3.4  m feature, and the dust grain size from the
bottom position in the wavelength (e.g. Smith et al. 1989). In principle, it is
possible to investigate these parameters with the 3
m feature, and the dust grain size from the
bottom position in the wavelength (e.g. Smith et al. 1989). In principle, it is
possible to investigate these parameters with the 3  m spectroscopic data.
However, we simplified our modeling to treat only water ice. Thus, our modeling
fits only the shape of the spectrum near 3.08
m spectroscopic data.
However, we simplified our modeling to treat only water ice. Thus, our modeling
fits only the shape of the spectrum near 3.08  m and estimates the fractions
of cold and warm water ice mantles and the grain sizes. Although bare grains
are expected to exist in the line of sight towards the central star, their
optical properties affect the water ice absorption feature only marginally.
Thus, we model a mixture of the cold and warm dust. The mantle thickness of
water ice is obtained with the mantle/core volume ratio of
m and estimates the fractions
of cold and warm water ice mantles and the grain sizes. Although bare grains
are expected to exist in the line of sight towards the central star, their
optical properties affect the water ice absorption feature only marginally.
Thus, we model a mixture of the cold and warm dust. The mantle thickness of
water ice is obtained with the mantle/core volume ratio of  for
the cold grains and
for
the cold grains and  for the warm grains, respectively. We use
optical constants provided by Bertie et al. (1969) for crystalline and Leger et al. (1983)
for amorphous water ice. We calculate the extinction spectra as a function of
wavelength of the model grains and compare them with observations reported by
Holloway et al. (2002). The best grain model was found to be
for the warm grains, respectively. We use
optical constants provided by Bertie et al. (1969) for crystalline and Leger et al. (1983)
for amorphous water ice. We calculate the extinction spectra as a function of
wavelength of the model grains and compare them with observations reported by
Holloway et al. (2002). The best grain model was found to be
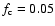 ,
,
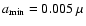 m,
m,
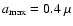 m,
m,
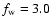 ,
and
the fraction of the cold grains w=0.1. Figure 4 compares the
observed 3
,
and
the fraction of the cold grains w=0.1. Figure 4 compares the
observed 3  m water ice absorption feature with our model result. The model
profile at
m water ice absorption feature with our model result. The model
profile at
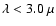 m and
m and
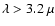 m is wider than the
observation. This discrepancy is mainly due to contamination by other
molecules in the real grain mantles such as the C-H group, i.e. ``dirty ice''
(Preibisch et al. 1993; Merrill et al. 1976; d'Hendecourt & Allamandola 1986; Duley & Williams 1981). A range of
m is wider than the
observation. This discrepancy is mainly due to contamination by other
molecules in the real grain mantles such as the C-H group, i.e. ``dirty ice''
(Preibisch et al. 1993; Merrill et al. 1976; d'Hendecourt & Allamandola 1986; Duley & Williams 1981). A range of
 up to 0.8 and
up to 0.8 and
 down to 1.0 provides acceptable fits. This estimation is in
rough agreement with the one provided by Dartois et al. (2002). Since the estimated
size of warm grains does not sufficiently differ from the grain size of the
cold grains, we adopt 0.45
down to 1.0 provides acceptable fits. This estimation is in
rough agreement with the one provided by Dartois et al. (2002). Since the estimated
size of warm grains does not sufficiently differ from the grain size of the
cold grains, we adopt 0.45  m for our further modeling. We also assume the
same core size for bare grains. This will be revisited later if necessary.
Figure 5 shows cross sections of the modeled grains. Black, red,
and blue lines denote the bare grains, warm grains, and cold grains,
respectively. Scattering cross sections dominate up to 3
m for our further modeling. We also assume the
same core size for bare grains. This will be revisited later if necessary.
Figure 5 shows cross sections of the modeled grains. Black, red,
and blue lines denote the bare grains, warm grains, and cold grains,
respectively. Scattering cross sections dominate up to 3  m.
In each profile, silicate features at 10
m.
In each profile, silicate features at 10  m and 18
m and 18  m are seen.
Warm grains with a crystalline ice mantle exhibit the characteristic
feature at 62
m are seen.
Warm grains with a crystalline ice mantle exhibit the characteristic
feature at 62  m, which does not appear in the amorphous form.
m, which does not appear in the amorphous form.
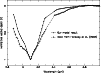 |
Figure 4:
Comparison of the normalized optical depths of 3  m water ice
absorption feature of the model result (filled triangles with dashed
line) with an observational result (filled circles with solid line).
The observational data was scanned from the paper by
Holloway et al. (2002). m water ice
absorption feature of the model result (filled triangles with dashed
line) with an observational result (filled circles with solid line).
The observational data was scanned from the paper by
Holloway et al. (2002). |
| Open with DEXTER |
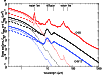 |
Figure 5:
Cross sections of extinction (solid line), scattering (dashed line),
and absorption (dotted line) of the modeled grains as a function of
wavelength. Black, red, and blue lines denote the bare grains
(
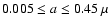 m), warm grains with a crystalline ice
mantle ( m), warm grains with a crystalline ice
mantle (
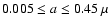 m, m,
 )
(multiplied
by a factor of 5), and cold grains with an amorphous ice mantle
( )
(multiplied
by a factor of 5), and cold grains with an amorphous ice mantle
(
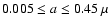 m, m,
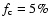 )
(multiplied by
a factor of 0.1), respectively. )
(multiplied by
a factor of 0.1), respectively. |
| Open with DEXTER |
4.2.2 Monte Carlo experiments
Because the real CRL 2136 nebula exhibits highly complicated features, we do not
expect our 2-D model to explain every aspect of the observed SED and intensity
and polarimetric images. Instead, we attempt to reproduce features which
characterize important structures of the modeled disk and envelope.
Before scanning parameter spaces, we examined some parameter sets in order to
obtain rough solutions and to investigate the effects of the parameters on
the model results. From this study, we determined the following parameter
ranges: a disk radius
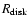 between 1000 and 5000 AU in increments
of 1000 AU; a disk mass
between 1000 and 5000 AU in increments
of 1000 AU; a disk mass
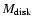 of 0.007, 0.01, 0.02, 0.03, 0.05,
0.07, and 0.1
of 0.007, 0.01, 0.02, 0.03, 0.05,
0.07, and 0.1 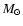 ;
a disk scale height H of 0.2, 0.5, 1.0, and 2.0;
and an envelope mass infall rate
;
a disk scale height H of 0.2, 0.5, 1.0, and 2.0;
and an envelope mass infall rate
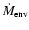 of
of
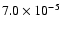 ,
,
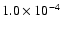 ,
,
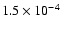 ,
and
,
and
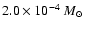 yr-1. The gas-to-dust mass ratio is assumed
to be 100. For the outer radius
yr-1. The gas-to-dust mass ratio is assumed
to be 100. For the outer radius
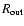 ,
we examine 0.3, 0.5, and
1.0 pc to find which value provides a better fit of the flux in the bipolar
lobes in the H- and K-band images and those in the submillimeter wavelength
range. The viewing angles
,
we examine 0.3, 0.5, and
1.0 pc to find which value provides a better fit of the flux in the bipolar
lobes in the H- and K-band images and those in the submillimeter wavelength
range. The viewing angles
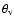 were chosen to be 60
were chosen to be 60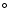 ,
70
,
70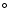 ,
75
,
75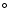 ,
80
,
80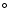 ,
and
,
and
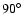 (edge-on). The dust temperature in the
inner radius is estimated to be about 1500 K, which is consistent with the dust
sublimation temperature. The radii where the dust temperature reaches 140 K and
80 K were found to be
(edge-on). The dust temperature in the
inner radius is estimated to be about 1500 K, which is consistent with the dust
sublimation temperature. The radii where the dust temperature reaches 140 K and
80 K were found to be  1500 AU (SH, TO),
1500 AU (SH, TO),  1800 AU (LA), and
1800 AU (LA), and
 5000 AU for all disk models. Because these values vary only
insignificantly in the above-examined parameter space, we fixed them in our
subsequent simulations. For the above 1680 parameter sets for each disk model,
we computed the SEDs to constrain the above parameters. This SED fitting
was done by eye. From this survey, we found that a large disk radius
(
5000 AU for all disk models. Because these values vary only
insignificantly in the above-examined parameter space, we fixed them in our
subsequent simulations. For the above 1680 parameter sets for each disk model,
we computed the SEDs to constrain the above parameters. This SED fitting
was done by eye. From this survey, we found that a large disk radius
(
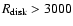 AU), a low disk mass
(
AU), a low disk mass
(
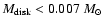 ), or a low disk scale height (H<1.0) result
in a too shallow 10
), or a low disk scale height (H<1.0) result
in a too shallow 10  m silicate feature or a too high flux in the optical
and NIR because of a too low optical depth. On the other hand, a small disk
radius (
m silicate feature or a too high flux in the optical
and NIR because of a too low optical depth. On the other hand, a small disk
radius (
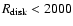 AU) or a high disk mass
(
AU) or a high disk mass
(
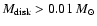 )
causes the opposite results. For the envelope
parameters, the lower the infalling rate or smaller the outer radius is, the
lower the FIR to submillimeter fluxes and the lower surface brightness in the
nebulosity in the NIR become. The viewing angle affects the optical depth in
the line of sight towards the central star and the appearances of the lobes and
the polarization distribution, particularly in the projected inner part of the
cavity. A viewing angle close to
)
causes the opposite results. For the envelope
parameters, the lower the infalling rate or smaller the outer radius is, the
lower the FIR to submillimeter fluxes and the lower surface brightness in the
nebulosity in the NIR become. The viewing angle affects the optical depth in
the line of sight towards the central star and the appearances of the lobes and
the polarization distribution, particularly in the projected inner part of the
cavity. A viewing angle close to
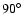 fits better in polarization, but the
optical and NIR fluxes become too low if the viewing angle is larger
than 75
fits better in polarization, but the
optical and NIR fluxes become too low if the viewing angle is larger
than 75 .
On the other hand, a viewing angle of
.
On the other hand, a viewing angle of
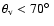 causes 10
causes 10  m silicate features to be too shallow. Furthermore, the SH, TO,
and LA disk models produce acceptable results, but the RB and SL fail, as
discussed in Sect. 4.2.3. The reasonable parameters were found to be
m silicate features to be too shallow. Furthermore, the SH, TO,
and LA disk models produce acceptable results, but the RB and SL fail, as
discussed in Sect. 4.2.3. The reasonable parameters were found to be
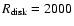 -3000 AU,
-3000 AU,
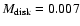 -0.07
-0.07 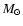 ,
H=1.0-2.0,
,
H=1.0-2.0,
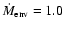 -
-
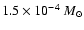 yr-1,
and
yr-1,
and
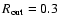 -0.5 pc, and
-0.5 pc, and
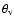 of 70
of 70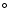 -75
-75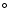 .
We generated Stokes IQUV images in the H and K bands and, finally,
selected a parameter set for each disk model which reproduces the characteristic
features seen in the observed intensity and polarization images. The parameters
of the selected model for each disk model are:
.
We generated Stokes IQUV images in the H and K bands and, finally,
selected a parameter set for each disk model which reproduces the characteristic
features seen in the observed intensity and polarization images. The parameters
of the selected model for each disk model are:
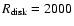 AU,
AU,
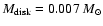 (SH, TO) and 0.05
(SH, TO) and 0.05  (LA),
H=2.0 (SH) and H=1.0 (TO, LA),
(LA),
H=2.0 (SH) and H=1.0 (TO, LA),
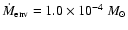 yr-1,
yr-1,
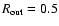 pc, and
pc, and
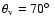 .
In these disk models,
we found that the TO model is favorable. We also estimated the disk accretion
rate
.
In these disk models,
we found that the TO model is favorable. We also estimated the disk accretion
rate
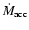 and the total envelope mass to be
and the total envelope mass to be
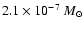 yr-1 using Eq. (5) in Whitney et al. (2003)
and 177
yr-1 using Eq. (5) in Whitney et al. (2003)
and 177 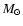 ,
respectively, and the visual optical depth towards the
central star at the chosen viewing angle to be 66 (SH), 77 (TO), and 78 (LA).
The parameters, the adopted values, and the ranges of uncertainty are
summarized in Table 1.
,
respectively, and the visual optical depth towards the
central star at the chosen viewing angle to be 66 (SH), 77 (TO), and 78 (LA).
The parameters, the adopted values, and the ranges of uncertainty are
summarized in Table 1.
Table 1:
Parameters of our 2-D radiative transfer model of CRL 2136.
 |
Figure 6:
Mass density distribution ( top panels) and dust temperature
distribution ( bottom panels). The results of three potential disk
models of the SH, TO, and LA are shown in the left, middle, and
right columns, respectively. The dust temperature distribution
maps are generated with the standard full interacting mode and
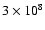 photon packets. Although the dust temperature in
several cells in the polar direction still suffers from Monte Carlo
noise, this does not affect the resulting SED significantly since the
noise appears mainly in the low density region (cf. the corresponding
mass density distribution maps). photon packets. Although the dust temperature in
several cells in the polar direction still suffers from Monte Carlo
noise, this does not affect the resulting SED significantly since the
noise appears mainly in the low density region (cf. the corresponding
mass density distribution maps). |
| Open with DEXTER |
 |
Figure 7:
Comparisons of SEDs of the acceptable, SH, TO, and LA disk models
( top panel) and the rejected, RB and SL disk models
( bottom panel)
with observations. The results of these three disk models are
indicated with violet, black, and blue curves, respectively.
For the TO disk model, fluxes due to the thermal emission and dust
scattering are also shown with a dotted-dashed line and dotted line,
respectively. The attenuated stellar flux is not presented because
it is less than 10-14 Wm-2. The observed data is obtained
from Allen et al. (1977) for the JHK band photometry, Willner et al. (1982)
for the spectrum from 2.0  m to 15 m to 15  m, IRAS photometry at 12,
25, 60, and 100 m, IRAS photometry at 12,
25, 60, and 100  m, and Kastner et al. (1994) for the photometry in
sub-millimeter wavelength. An estimated interstellar extinction of
3.2 mag at V-band is dereddened in the observations. m, and Kastner et al. (1994) for the photometry in
sub-millimeter wavelength. An estimated interstellar extinction of
3.2 mag at V-band is dereddened in the observations. |
| Open with DEXTER |
4.2.3 Dust temperature and SED
Figure 6 displays the mass density distribution maps (top panels)
and the dust temperature distribution maps (bottom panels) of the SH, TO, and
LA disk models, which are presented in the left, middle, and right columns,
respectively. The dust density distribution of the disk determines the
temperature structure. CRL 2136's disk has a very puffed-up or even a spherical
shell-like structure with a thin polar hole (H=1) and is extended
(
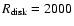 AU). Thus, the disk is heated nearly isotropically and
efficiently even in the midplane. Although the SH model has a flared structure,
the effect is seen only slightly in the polar region. An H2O maser
observation of this object obtained evidence for a warm dust environment in
the inner part of the disk (Menten & van der Tak 2004). In their maser maps, most maser
spots are seen within 200 AU (=0
AU). Thus, the disk is heated nearly isotropically and
efficiently even in the midplane. Although the SH model has a flared structure,
the effect is seen only slightly in the polar region. An H2O maser
observation of this object obtained evidence for a warm dust environment in
the inner part of the disk (Menten & van der Tak 2004). In their maser maps, most maser
spots are seen within 200 AU (=0
 1), where the estimated dust temperature
reaches
1), where the estimated dust temperature
reaches  350 K in our model. This is in good agreement with a prediction of
350 K in our model. This is in good agreement with a prediction of
 400 K by an excitation calculation (Elitzur et al. 1989). Furthermore,
the above dust temperature and density distributions also affect the formation
and growth of icy molecules. While the estimated dust temperature in the disk
is
400 K by an excitation calculation (Elitzur et al. 1989). Furthermore,
the above dust temperature and density distributions also affect the formation
and growth of icy molecules. While the estimated dust temperature in the disk
is  100 K and the optical depth of grains with a water ice mantle at
3.08
100 K and the optical depth of grains with a water ice mantle at
3.08  m in the disk is found to be only 0.14, the residual large fraction
is calculated to be
m in the disk is found to be only 0.14, the residual large fraction
is calculated to be  11 and occurs in the envelope. Thus, only a little
water ice exists in the disk, which is consistent with the argument by
Holbrook & Temi (1998). The above-mentioned disk properties of CRL 2136 are contrast with
those of the T Tauri and Herbig Ae stars
(e.g. Calvet et al. 1994; Chiang et al. 2001; Kenyon et al. 1993a).
11 and occurs in the envelope. Thus, only a little
water ice exists in the disk, which is consistent with the argument by
Holbrook & Temi (1998). The above-mentioned disk properties of CRL 2136 are contrast with
those of the T Tauri and Herbig Ae stars
(e.g. Calvet et al. 1994; Chiang et al. 2001; Kenyon et al. 1993a).
Figure 7 presents comparisons of SEDs of the three potential (top panel)
and two rejected (bottom panel) disk models with observations. The interstellar
extinction is taken into account because CRL 2136 is located towards the
Galactic plane (
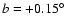 ). We estimate the visual extinction
). We estimate the visual extinction 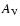 to be 3.2 mag from a model of the general Galactic interstellar extinction
(Allen 1973) for the distance of 2 kpc. The observed SED was corrected for
this value by applying an extinction correction using the cross sections of the
MRN grain model for the interstellar diffuse cloud (Mathis et al. 1977). The effects
of aperture size should be considered. The aperture size of the
JHK band photometry obtained by Allen et al. (1977) is not specified. However,
the 2.2
to be 3.2 mag from a model of the general Galactic interstellar extinction
(Allen 1973) for the distance of 2 kpc. The observed SED was corrected for
this value by applying an extinction correction using the cross sections of the
MRN grain model for the interstellar diffuse cloud (Mathis et al. 1977). The effects
of aperture size should be considered. The aperture size of the
JHK band photometry obtained by Allen et al. (1977) is not specified. However,
the 2.2  m flux is within the error compared to that obtained using
a
m flux is within the error compared to that obtained using
a
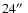 aperture (Kastner et al. 1992), which probably captures the greatest
fraction of flux from the source. Thus, we believe that Allen's photometric
data suggests the real flux. Since the flux of Willner's spectrum at 2.2
aperture (Kastner et al. 1992), which probably captures the greatest
fraction of flux from the source. Thus, we believe that Allen's photometric
data suggests the real flux. Since the flux of Willner's spectrum at 2.2  m
is in good agreement with Allen's K band photometry, we also use this data
without a flux correction. An infinite aperture size is applied in the
computation of our model SED. It is thus also valid to directly compare our
model SED to the above observations.
m
is in good agreement with Allen's K band photometry, we also use this data
without a flux correction. An infinite aperture size is applied in the
computation of our model SED. It is thus also valid to directly compare our
model SED to the above observations.
Because the dust temperature in the disk is higher than about 100 K, the fluxes
in the wavelengths shorter than 30  m are mainly determined by the dust
density structure of the disk. We see the effect on the SEDs of the examined
disk models. In the order of the TO, SH, LA, RB, and SL disk models, the dust
concentrates towards the central star more, so that the mass of the higher
temperature dust component is higher. Thus, the 4 to 10
m are mainly determined by the dust
density structure of the disk. We see the effect on the SEDs of the examined
disk models. In the order of the TO, SH, LA, RB, and SL disk models, the dust
concentrates towards the central star more, so that the mass of the higher
temperature dust component is higher. Thus, the 4 to 10  m flux of the
TO model was obtained to be higher than the flux of other models, as seen in
Fig. 7 (top panel). In the RB and SL models, we find that a model with
a
m flux of the
TO model was obtained to be higher than the flux of other models, as seen in
Fig. 7 (top panel). In the RB and SL models, we find that a model with
a
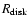 of 2000 AU, a H of 1, and a
of 2000 AU, a H of 1, and a
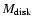 of
0.07
of
0.07 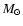 results in less discrepancy in the examined 1680 models.
However, a sufficient MIR flux is not obtained in these two models (see
Fig. 7, bottom panel) for the above-mentioned reason.
Thus, we reject these two disk models.
results in less discrepancy in the examined 1680 models.
However, a sufficient MIR flux is not obtained in these two models (see
Fig. 7, bottom panel) for the above-mentioned reason.
Thus, we reject these two disk models.
The 3  m and 10
m and 10  m features would obtain better fits if the chemical
compositions of water ice, methanol (see also Skinner et al. 1992), and silicate,
and their fractions were more precisely chosen. The model flux around a
wavelength of 60
m features would obtain better fits if the chemical
compositions of water ice, methanol (see also Skinner et al. 1992), and silicate,
and their fractions were more precisely chosen. The model flux around a
wavelength of 60  m depends on the stellar luminosity but not on the above
parameters much. Thus, our model result confirms that the estimated stellar
luminosity of
m depends on the stellar luminosity but not on the above
parameters much. Thus, our model result confirms that the estimated stellar
luminosity of
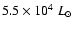 (
(
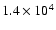 [d/kpc]2
[d/kpc]2 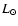 )
is reasonable at a distance of
2 kpc.
)
is reasonable at a distance of
2 kpc.
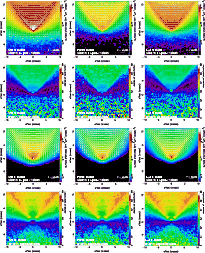 |
Figure 8:
Our model results for the intensity images, polarization vector
lines, and the degree of polarization images.
The top two rows
represent the H band and the bottom two rows the K-band.
The left, middle, and right columns are results of the SH, TO, and
LA disk models, respectively. In these calculations, the scattering
mode with the peeling-off technique and
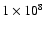 photon
packets were applied. All images were convolved with a Gaussian
function with a full width at half maximum of 0 photon
packets were applied. All images were convolved with a Gaussian
function with a full width at half maximum of 0
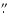 35, which
corresponds to the PSF size of our observations. 35, which
corresponds to the PSF size of our observations. |
| Open with DEXTER |
4.2.4 Intensity and polarization images
Figure 8 presents the intensity images and the degree of
polarization images in the H and K bands for the SH, TO, and LA disk models.
The polarization vectors are overlaid on the intensity images. In the intensity
images, the central star feature and a V-shaped feature due to the
cavity wall, which corresponds to the E and S1 lobes in our intensity images in
Fig. 1, are reproduced. Although Fischer et al. (1996) reported that the
appearance of the nebulosity near the central star differs depending on the
disk form, our results show less difference, unlike the SED. This is probably
due to the fact that Fischer's modeling made the comparisons using a constant
mass density coefficient. In contrast, our modeling uses parameters which
provide a good fit in the SED. A detailed analysis of the SED is also important
in order to derive the disk geometry, as is being done to distinguish flat,
flared, or self-shadowed structures in low mass and Herbig Ae stars
(e.g. Dullemond & Dominik 2004; Meeus et al. 2001). While the absolute fluxes in the V-shaped
feature and towards the central star are in rough agreement with our
observations, the model flux in the projected inner part of the cavity is
higher than in the observations. This is obviously due to an asymmetric
structure in the real CRL 2136 nebula. The lobe expected at the bottom is not
visible in our model results because of the inclination effect.
In the polarization images, the degree of polarization is enhanced along the
V-shaped feature, as seen in our observations. The value is consistent
with the observational results in the H and K bands, suggesting that our
single scattering modeling provides a reasonable estimation of the grain sizes
in the nebula. The centro-symmetric polarization vector pattern in the lobes
and the polarization disk along the equatorial plane are reproduced in our
models. However, the polarization vector alignment across the central star is
not reproduced in our model. Three possible mechanisms have been proposed so
far; (1) the PSF smoothing effect (Piirola et al. 1992); (2) multiple scattering
at the boundaries of a geometrically thin disk (Bastien & Ménard 1988); and (3) linear
dichroism by aligned non-spherical grains (Hough et al. 1989). Because (1) our
model images are convolved with a Gaussian function with the estimated PSF size
in our observations; and (2) the immediate surrounding nebulosity of the central
star looks somewhat spherical instead of a butterfly-like shape with a dark
lane, the PSF smoothing effect can probably be ruled out. Furthermore,
the possibility of multiple scattering at disk boundaries can also be ruled out
in the case of CRL 2136 because the presence of a geometrically thin, optically
thick disk is not expected based on our modeling. A third possibility remains.
A higher polarization in the H band (PH=32%) is present at IRS 1
compared to the K band (PK=21%). This can be explained by dichroic
absorption due to aligned, non-spherical grains in such a high extinction
(
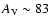 )
environment (e.g. Whittet et al. 2008) but not by scattering or
the PSF smoothing effect. Therefore, for CRL 2136, we favor the explanations
by Hough et al. (1989).
)
environment (e.g. Whittet et al. 2008) but not by scattering or
the PSF smoothing effect. Therefore, for CRL 2136, we favor the explanations
by Hough et al. (1989).
Interestingly, our high-resolution 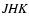 -band imaging polarimetry of the Herbig
Be star R Mon (Murakawa et al. 2008b) and the low mass protostar
HL Tau (Murakawa et al. 2008c) show polarization behaviors very different
from the above result of the massive star CRL 2136. In these objects, the
polarization disk has significantly lower polarizations of PJ=7% and
PH,K<2% for R Mon and
PJ,H,K<3% for HL Tau. Such low
polarizations are probably due to large grains (micron-sized or even larger)
in the disks of these objects, while high polarizations in CRL 2136 are a result
of small grains (
-band imaging polarimetry of the Herbig
Be star R Mon (Murakawa et al. 2008b) and the low mass protostar
HL Tau (Murakawa et al. 2008c) show polarization behaviors very different
from the above result of the massive star CRL 2136. In these objects, the
polarization disk has significantly lower polarizations of PJ=7% and
PH,K<2% for R Mon and
PJ,H,K<3% for HL Tau. Such low
polarizations are probably due to large grains (micron-sized or even larger)
in the disks of these objects, while high polarizations in CRL 2136 are a result
of small grains (
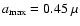 m).
m).
We presented H- and K-band polarimetric images of the massive proto-stellar
object CRL 2136 obtained using the Subaru telescope. The intensity images
present two bright lobes extending east and south and two faint lobes extending
west and northwest, with respect to the central star IRS 1. The polarization
images show (1) centro-symmetrically aligned polarization vectors in all the
lobes surrounding the central star; (2) high polarizations of 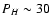 %
and
%
and 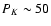 % in the two bright lobes and low polarizations of PH<15%
and PK<30% in the fan-shaped region between IRS 1 and the eastern and
southern lobes; and (3) a polarization disk around the central star oriented
along the PA of
% in the two bright lobes and low polarizations of PH<15%
and PK<30% in the fan-shaped region between IRS 1 and the eastern and
southern lobes; and (3) a polarization disk around the central star oriented
along the PA of  45
45
 ;
i.e. perpendicular to the direction of
CO outflow. These results are consistent with previous observations
(Kastner et al. 1992; Minchin et al. 1991) but are detected more clearly due to a higher
angular resolution in our data. These signatures are convincing evidence that
the central star of CRL 2136 is surrounded by an optically thick dust disk and
an envelope with a polar cavity. Furthermore, our polarization data also show
that the polarization vectors are aligned along the disk direction and gives a
degree of polarization of 32% in the H band and 21% in the K band at
IRS 1.
;
i.e. perpendicular to the direction of
CO outflow. These results are consistent with previous observations
(Kastner et al. 1992; Minchin et al. 1991) but are detected more clearly due to a higher
angular resolution in our data. These signatures are convincing evidence that
the central star of CRL 2136 is surrounded by an optically thick dust disk and
an envelope with a polar cavity. Furthermore, our polarization data also show
that the polarization vectors are aligned along the disk direction and gives a
degree of polarization of 32% in the H band and 21% in the K band at
IRS 1.
In order to investigate the physical properties of the dust environment of
CRL 2136, we performed radiative transfer modeling with 2-D disk and envelope
geometries using our newly developed Monte Carlo code. Assuming three grain
models with a DL-type chemistry with or without a water ice mantle, depending
on the dust temperature, we found the maximum grain core size of
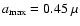 m for all grain species, volume ratios of amorphous
water ice of 0.05 for cold grains (
m for all grain species, volume ratios of amorphous
water ice of 0.05 for cold grains (
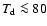 K),
and crystalline water ice of 3.0 for warm grains (
K),
and crystalline water ice of 3.0 for warm grains (
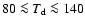 K).
For the disk model, we found that the TO model, where the dust concentrates
towards the central star the most, is the favored. Our modeling predicts that
the disk has a low mass (
K).
For the disk model, we found that the TO model, where the dust concentrates
towards the central star the most, is the favored. Our modeling predicts that
the disk has a low mass (
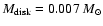 ), puffed up (H=1.0),
and expanded (
), puffed up (H=1.0),
and expanded (
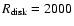 AU) structure. With our grain models
assuming spherical shapes, the polarization vector alignment and high
polarization in the polarization disk were not reproduced. The most plausible
reason would be dichroic absorption of aligned, non-spherical grains, which
probably exist in the equatorial, high-density region in the inner part of the
envelope. Further detailed studies involving treatment of spheroidal grains
would provide important clues about the magnetic field structure in the disk as
well as the envelope.
AU) structure. With our grain models
assuming spherical shapes, the polarization vector alignment and high
polarization in the polarization disk were not reproduced. The most plausible
reason would be dichroic absorption of aligned, non-spherical grains, which
probably exist in the equatorial, high-density region in the inner part of the
envelope. Further detailed studies involving treatment of spheroidal grains
would provide important clues about the magnetic field structure in the disk as
well as the envelope.
Our model results provide new information about the dust environment of
CRL 2136. Previous observations of massive stars reported disk mass ranges of
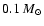 to
to  1
1  ;
e.g. Ori IRc2;
Blake et al. (1996); Plambeck et al. (1995), Cep A; Patel et al. (2005), and M 17;
Steinacker et al. (2006). These results might have implications for the evolutionary
stage of the system, although some of these differences could be due to the use
of different methods to estimate the disk parameters (e.g. a rotating component
from a radio continuum, a flux distribution from mid-IR images, and radiative
transfer modeling). A massive disk of
;
e.g. Ori IRc2;
Blake et al. (1996); Plambeck et al. (1995), Cep A; Patel et al. (2005), and M 17;
Steinacker et al. (2006). These results might have implications for the evolutionary
stage of the system, although some of these differences could be due to the use
of different methods to estimate the disk parameters (e.g. a rotating component
from a radio continuum, a flux distribution from mid-IR images, and radiative
transfer modeling). A massive disk of  1
1  (
( 10% of the
central object) is likely due to gravitational instability in the early phase
of star formation (e.g. Krumholz et al. 2005). In contrast, CRL 2136 has a low
mass, a puffed-up disk, and a low disk accretion rate. This can be interpreted
as follows: (1) the central star of 20
10% of the
central object) is likely due to gravitational instability in the early phase
of star formation (e.g. Krumholz et al. 2005). In contrast, CRL 2136 has a low
mass, a puffed-up disk, and a low disk accretion rate. This can be interpreted
as follows: (1) the central star of 20  formed rapidly
(
formed rapidly
(
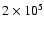 yr) with a high infalling rate and nearly isotropically
(
yr) with a high infalling rate and nearly isotropically
(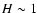 )
in the beginning of the star formation process; (2) Then, after
ignition of the central star, the strong radiation pressure from the luminous
central star halted the accretion of the disk matter, resulting in a low mass,
sparse disk structure keeping a nearly constant mass. Furthermore, these disk
properties also affect the grain growth. In order for grains to grow in the
disk, they have to undergo several grain-grain collisions in a high-density
region. While it is believed that the disks around T Tauri stars and Herbig Ae
stars provide such an environment, this does not seem to be the case for
CRL 2136, according to our analysis. Therefore, grain growth is unlikely in
CRL 2136's disk.
)
in the beginning of the star formation process; (2) Then, after
ignition of the central star, the strong radiation pressure from the luminous
central star halted the accretion of the disk matter, resulting in a low mass,
sparse disk structure keeping a nearly constant mass. Furthermore, these disk
properties also affect the grain growth. In order for grains to grow in the
disk, they have to undergo several grain-grain collisions in a high-density
region. While it is believed that the disks around T Tauri stars and Herbig Ae
stars provide such an environment, this does not seem to be the case for
CRL 2136, according to our analysis. Therefore, grain growth is unlikely in
CRL 2136's disk.
Acknowledgements
Our HK-band imaging polarimetry using the Subaru telescope was carried out on
the Director's Discretionary Time. We would like to thank Prof. H. Karoji for
providing us with the valuable opportunity. We also wish to thank the
observatory staff for supporting our observations.
- Allen, C. W. 1973,
Astrophysical Quantities, 3r [NASA ADS]d edn. (London: Athlone Press),
263
(In the text)
- Allen, D. A., Hyland,
A. R., Longmore, A. J., et al. 1977, ApJ, 217, 108 [NASA ADS] [CrossRef]
(In the text)
- Alvarez, C.,
Hoare, M., & Lucas, P. 2004, A&A, 419, 203 [NASA ADS] [CrossRef] [EDP Sciences]
- Bastien, P., &
Ménard, F. 1988, ApJ, 326, 334 [NASA ADS] [CrossRef]
- Beckwith, S. V. W., &
Sargent, A. I. 1991, ApJ, 381, 250 [NASA ADS] [CrossRef]
- Bernasconi, P. A., &
Maeder, A. 1996, A&A, 307, 829 [NASA ADS]
- Bertie, J. E.,
Labbé, H. J., & Whalley, E. 1969, J. Chem. Phys., 50,
4501 [NASA ADS] [CrossRef]
(In the text)
- Bohren, C. F., &
Huffmann, D. R. 1983, Absorption and scattering of light by small
particles (New York: John Wiley & Sons)
(In the text)
- Bjorkman, J.
E., & Wood, K. 2001, ApJ, 554, 615 [NASA ADS] [CrossRef]
- Blake, G. A., Mundy,
L. G., Garlstrom, J. E., et al. 1996, ApJ, 472, L49 [NASA ADS] [CrossRef]
- Brooke, T. Y.,
Sellgren, K., & Geballe, T. R. 1999, ApJ, 517, 883 [NASA ADS] [CrossRef]
- Calvet, N.,
Hartmann, L., Kenyon, S. J., & Whitney, B. A. 1994, ApJ, 434,
330 [NASA ADS] [CrossRef]
- Cardelli, J.
A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef]
- Cashwell, E.
D., & Everett, C. J. 1959, A Practical Manual on the Monte
Carlo Method for Random Walk Problems (New York: Pergamon
Press)
- Cassen, P., & Moosman,
A. 1981, Icarus, 48, 353 [NASA ADS] [CrossRef]
- Chiang, E. I.,
Joung, M. K., Creech-Eakman, M. J., et al. 2001, ApJ, 547,
1077 [NASA ADS] [CrossRef]
- Clayton, G. C.,
Wolff, M. J., Sofia, U. T., Gordon, K. D., & Misselt, K. A.
2003, ApJ, 588, 871 [NASA ADS] [CrossRef]
- Dartois, E.,
d'Hendecourt, L., Thi, W., Pontoppidan, K. M., & van Dischoeck,
E. F. 2002, A&A, 394, 1057 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- d'Hendecourt, L. B., &
Allamandola, L. J. 1986, A&AS, 64, 453 [NASA ADS]
- Dougados, C.,
Rouan, D., Lacombe, F., Tiphene, D., & Forveille, T. 1990,
A&A, 227, 437 [NASA ADS]
- Draine, B. T., & Lee,
H. M. 1984, ApJ, 285, 89 [NASA ADS] [CrossRef]
- Duley, W. W., &
Williams, D. A. 1981, MNRAS, 196, 269 [NASA ADS]
- Dullemond, C. P., &
Dominik, C. 2004, A&A, 417, 159 [NASA ADS] [CrossRef] [EDP Sciences]
- Elitzur, M.,
Hollenbach, D. J., & McKee, C. F. 1989, ApJ, 346, 983 [NASA ADS] [CrossRef]
(In the text)
- Fischer, O.,
Henning, Th., & Yorke, H. W. 1996, A&A, 308, 863 [NASA ADS]
- Gibb, E. L., Whittet,
D. C. B., Boogert, A. C. A., & Tielens, A. G. G. M. 2004, ApJS,
151, 35 [NASA ADS] [CrossRef]
- Gordon, K. D.,
Misselt, K. A., Witt, A. N., & Clayton, G. C. 2001, ApJ, 551,
269 [NASA ADS] [CrossRef]
- Hagen, W., Tielens,
A. G. G. M., & Greenberg, J. M. 1981, Chem. Phys., 56, 367 [CrossRef]
- Harvey, P. M.,
Butner, H. M., Colome, C., Francesco, J. D., & Smith, B. 2000,
ApJ, 534, 846 [NASA ADS] [CrossRef]
(In the text)
- Herbst, E., & Leung, C.
1985, MNRAS, 222, 689 [NASA ADS]
- Holbrook, J. C., &
Temi, P. 1998, ApJ, 496, 280 [NASA ADS] [CrossRef]
(In the text)
- Holloway, R.
P., Chrysostomou, A., Aitken, D. K., Hough, J. H., & McCall, A.
2002, MNRAS, 336, 425 [NASA ADS] [CrossRef]
- Hough, J. H.,
Whittet, D. C. B., Sato, S., et al. 1989, MNRAS, 241, 71 [NASA ADS]
- Ivezic, Z., & Elitzur,
M. 1997, MNRAS, 287, 799 [NASA ADS]
- Jones, A. P., &
Williams, D. A. 1984, MNRAS, 209, 955 [NASA ADS]
(In the text)
- Kastner, J. H., &
Weintraub, D. A. 1996, ApJ, 466, L103 [NASA ADS] [CrossRef]
- Kastner, J. H.,
Weintraub, D. A., & Aspin, C. 1992, ApJ, 389, 357 [NASA ADS] [CrossRef]
(In the text)
- Kastner, J. H.,
Weintraub, D. A., Snell, R. L., et al. 1994, ApJ, 425,
695 [NASA ADS] [CrossRef]
(In the text)
- Kenyon, S. J.,
Calvet, N., & Hartmann, L. 1993a, ApJ, 414, 676 [NASA ADS] [CrossRef]
- Kenyon, S. J.,
Whitney, B. A., Gomez, M., & Hartmann, L. 1993b, ApJ, 414,
773 [NASA ADS] [CrossRef]
- Kim, S.-H., Martin, P.
G., & Hendry, P. D. 1994, ApJ, 422, 164 [NASA ADS] [CrossRef]
(In the text)
- Kraus, S., Balega,
Y., Elitzur, M., et al. 2006, A&A, 455, 521 [NASA ADS] [CrossRef] [EDP Sciences]
- Krumholz, M.
R., McKee, C. F., & Klein, R. I. 2005, ApJ, 618, L33 [NASA ADS] [CrossRef]
(In the text)
- Larson, R. B. 1984,
MNRAS, 206, 197 [NASA ADS]
- Larson, K. A.,
& Whittet, D. C. B. 2005, ApJ, 623, 897 [NASA ADS] [CrossRef]
- Lazareff, B.,
Pudritz, R. E., & Monin, J.-L. 1990, ApJ, 358, 170 [NASA ADS] [CrossRef]
(In the text)
- Leger, A., Gauthier,
S., Defourneau, D., & Rouan, D. 1983, A&A, 117, 164 [NASA ADS]
- Lucas, P. W., & Roche,
P. F. 1998, MNRAS, 299, 699 [NASA ADS] [CrossRef]
- Lucy, L. B. 1999,
A&A, 344, 282 [NASA ADS]
- Mathis, J. S., Rumpl, W.,
& Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef]
(In the text)
- Meeus, G., Waters, L.
B. F. M., Bouwan, J., et al. 2001, A&A, 365, 476 [NASA ADS] [CrossRef] [EDP Sciences]
- Menten, K. M.,
& van der Tak, F. F. S. 2004, A&A, 414, 289 [NASA ADS] [CrossRef] [EDP Sciences]
- Merrill, K. M., Russell,
R. W., & Soifer, B. T. 1976, ApJ, 207, 763 [NASA ADS] [CrossRef]
- Minchin, N. R.,
Hough, J. H., Burton, M. G., & Yamashita, T. 1991, MNRAS, 251,
522 [NASA ADS]
- Monnier, J. D.,
& Millan-Gabet, R. 2002, ApJ, 579, 694 [NASA ADS] [CrossRef]
(In the text)
- Murakawa, K.,
Suto, H., Tamura, M., et al. 2004, PASJ, 56, 509 [NASA ADS]
- Murakawa, K.,
Suto, H., Oya, S., et al. 2005, A&A, 436, 601 [NASA ADS] [CrossRef] [EDP Sciences]
- Murakawa, K.,
Nakashima, J., Ohnaka, K., & Deguchi, S. 2007, A&A, 470,
957 [NASA ADS] [CrossRef] [EDP Sciences]
- Murakawa, K.,
Ohnaka, K., Driebe, T., et al. 2008a, A&A, 489, 195 [NASA ADS] [CrossRef] [EDP Sciences]
- Murakawa, K.,
Preibisch, T., Kraus, S., & Weigelt, G. 2008b, A&A, 488,
L75 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Murakawa, K.,
Oya, S., Pyo, T.-S., & Ishii, M. 2008c, A&A, submitted
(In the text)
- Niccolini,
G., Woitke, P., & Lopez, B. 2003, A&A, 399, 703 [NASA ADS] [CrossRef] [EDP Sciences]
- Nussenzveig, H. M., &
Wiscombe, W. J. 1980, , 45, 1490
(In the text)
- Ohnaka, K., Driebe,
T., Hofmann, K.-H., et al. 2006, A&A, 445, 1015 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Patel, N. A.,
Salvador, C., Sridharan, T. K., et al. 2005, Nature, 437,
109 [NASA ADS] [CrossRef]
- Pendleton, Y.
J., Tielens, A. G. G. M., & Werner, M. W. 1990, ApJ, 349,
107 [NASA ADS] [CrossRef]
- Pendleton, Y.
J., Tielens, A. G. G. M., Tokunaga, A. T., & Bernstein, M. P.
1999, ApJ, 513, 294 [NASA ADS] [CrossRef]
- Plambeck, R.
L., Wright, M. C. H., Mundy, L. G., & Looney, L. W. 1995, ApJ,
455, L189 [NASA ADS] [CrossRef]
- Piirola, V.,
Scaltriti, F., & Coyne, G. V. 1992, Nature, 359, 339 [CrossRef]
(In the text)
- Preibisch,
T., Ossenkopf, V., Yorke, H. W., & Henning, T. 1993, A&A,
279, 577 [NASA ADS]
- Preibisch,
T., Balega, Y. Y., Schertl, D., & Weigelt, G. 2003, A&A,
412, 735 [NASA ADS] [CrossRef] [EDP Sciences]
- Pringle, J. E.
1981, ARA&A, 19, 137 [NASA ADS] [CrossRef]
- Shakura, N. I., &
Sunyaev, R. A. 1973, A&A, 24, 337
- Skinner, C. J.,
Tielens, A. G. G. M., Barlow, M. J., & Justtanont, K. 1992,
ApJ, 399, L79 [NASA ADS] [CrossRef]
(In the text)
- Smith, R. G.,
Sellgren, K., & Tokunaga, A. T. 1989, ApJ, 344, 413 [NASA ADS] [CrossRef]
(In the text)
- Steinacker,
J., Chini, R., Nielbock, M., et al. 2006, A&A, 456,
1013 [NASA ADS] [CrossRef] [EDP Sciences]
- Terebey, S., Shu,
F. H., & Cassen, P. 1984, ApJ, 286, 529 [NASA ADS] [CrossRef]
- Tielens, A. G. G. M., &
Hagen, W. 1982, A&A, 114, 245 [NASA ADS]
- Toomre, A. 1982,
ApJ, 259, 535 [NASA ADS] [CrossRef]
- Ulrich, R. K. 1976,
ApJ, 210, 377 [NASA ADS] [CrossRef]
- van
Dishoeck, E. F. 2004, ARA&A, 42, 119 [NASA ADS] [CrossRef]
- Weigelt, G.,
Beuther, H., Hofmann, K.-H., et al. 2006, A&A, 447,
655 [NASA ADS] [CrossRef] [EDP Sciences]
- Whitney, B. A., &
Hartman, L. 1993, ApJ, 402, 605 [NASA ADS] [CrossRef]
- Whitney, B. A.,
Kenyon, S. L., & Gomez, M. 1997, ApJ, 485, 703 [NASA ADS] [CrossRef]
- Whitney, B. A.,
Wood, K., Bjorkman, J. E., & Wolf, M. J. 2003, ApJ, 591,
1049 [NASA ADS] [CrossRef]
(In the text)
- Whittet, D. C.
B., Pendleton, Y. J., Gibb, E. L., et al. 2001, ApJ, 550,
793 [NASA ADS] [CrossRef]
- Whittet, D. C.
B., Hough, J. H., Lazarian, A., & Hoang, T. 2008, ApJ, 674,
304 [NASA ADS] [CrossRef]
(In the text)
- Willner, S. P.,
Gillett, F. C., Herter, T. L., Jones, B., et al. 1982, ApJ,
253, 174 [NASA ADS] [CrossRef]
(In the text)
- Wiscombe, W. J.
1980, Appl. Opt., 19, 1505 [NASA ADS]
(In the text)
- Witt, A. N. 1977, ApJS,
35, 1 [NASA ADS] [CrossRef]
- Wolf, S., &
Voshchinnikov, N. V. 2004, CoPhC, 162, 113 [NASA ADS]
(In the text)
- Wollfire, M. G., &
Cassinelli, J. P. 1986, ApJ, 310, 207 [NASA ADS] [CrossRef]
(In the text)
- Wood, K., &
Reynolds, R. J. 1999, ApJ, 525, 799 [NASA ADS] [CrossRef]
- Yorke, H., &
Sonnhalter, C. 2002, ApJ, 569, 846 [NASA ADS] [CrossRef]
- Yusef-Zadeh, F.,
Morris, M., & White, R. L. 1984, ApJ, 278, 186 [NASA ADS] [CrossRef]
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=16.5cm,keepaspectratio]{9901fig1.eps}
\end{figure}](/articles/aa/full/2008/41/aa09901-08/Timg34.gif)

![$\displaystyle \rho^{\rm SH}_{\rm disk}\left(r,z\right)=
\rho_{\rm d}\left(r/R_{...
...alpha}
\exp\left(-\frac{\pi}{4}\left[\frac{z}{h\left(r\right)}\right]^2\right),$](/articles/aa/full/2008/41/aa09901-08/img63.gif)