A&A 490, 835-842 (2008)
DOI: 10.1051/0004-6361:200809865
Collisional and dynamical evolution of Plutinos
G. C. de Elía - A. Brunini - R. P. Di Sisto
Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata,
Paseo del Bosque S/N (1900), La Plata, Argentina
IALP-CONICET, Argentina
Received 27 March 2008 / Accepted 22 July 2008
Abstract
Aims. In this paper, we analyze the collisional and dynamical evolution of the population of Plutinos.
Methods. To do this, we test different collisional parameters and include a dynamical treatment that takes into account the stability and instability zones of the 3:2 mean motion resonance with Neptune. This procedure allows us to estimate the size distribution of Plutinos, to study their mean collisional lifetimes, to analyze the formation of families, to obtain ejection rates of fragments from the resonance and to discuss their possible contribution to the ecliptic comet population. Our simulations are developed assuming the existence of one Pluto-sized object in the 3:2 Neptune resonance.
Results. The Plutino population larger than a few kilometers in diameter is not significantly altered by catastrophic collisions over the age of the Solar System. Thus, we infer that the break suggested by previous works at a diameter D near 40-80 km in the Plutino cumulative size distribution should be primordial and not a result of the collisional evolution. The existence of such a break is still a matter of debate. On the other hand, our analysis indicates that one large family was formed in the 3:2 Neptune resonance over the Solar System history. Concerning Plutino removal, we find that one object with a diameter D > 1 km is ejected from the 3:2 resonance with Neptune every 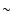 300-1200 yr. Then, we study the sensitivity of our results to the number of Pluto-sized objects in the 3:2 Neptune resonance. Our simulations suggest that the larger the number of Pluto-sized bodies, the higher the ejection rate of fragments from that resonant region and the number of families formed over 4.5 Gyr. Thus, if a maximum of 5 Pluto-sized objects are assumed to be in the 3:2 Neptune resonance, one body with a diameter D > 1 km is ejected every tens of years while
300-1200 yr. Then, we study the sensitivity of our results to the number of Pluto-sized objects in the 3:2 Neptune resonance. Our simulations suggest that the larger the number of Pluto-sized bodies, the higher the ejection rate of fragments from that resonant region and the number of families formed over 4.5 Gyr. Thus, if a maximum of 5 Pluto-sized objects are assumed to be in the 3:2 Neptune resonance, one body with a diameter D > 1 km is ejected every tens of years while 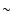 30 large families are formed over the Solar System history. From these estimates, we conclude that it is necessary to specify the number of Pluto-sized objects present in the 3:2 Neptune resonance to determine if this region can be considered an important source of ecliptic comets. Finally, we find that the current orbital distribution of the Plutinos does not offer a strong constraint on the dynamical origin of this population.
30 large families are formed over the Solar System history. From these estimates, we conclude that it is necessary to specify the number of Pluto-sized objects present in the 3:2 Neptune resonance to determine if this region can be considered an important source of ecliptic comets. Finally, we find that the current orbital distribution of the Plutinos does not offer a strong constraint on the dynamical origin of this population.
Key words: Kuiper Belt - methods: numerical - solar system: formation
The 3:2 mean motion resonance with Neptune, located at 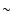 39.5 AU, is the most densely populated one in the Kuiper Belt. The residents of this resonant region are usually called Plutinos because of the analogy of their orbits with that of Pluto, which is its most representative member. Aside from Pluto and its largest moon Charon, the Minor Planet Center (MPC) database contains 207 Plutino candidates.
39.5 AU, is the most densely populated one in the Kuiper Belt. The residents of this resonant region are usually called Plutinos because of the analogy of their orbits with that of Pluto, which is its most representative member. Aside from Pluto and its largest moon Charon, the Minor Planet Center (MPC) database contains 207 Plutino candidates.
Although the Scattered Disk is assumed to be the primary source of Centaurs and Jupiter-family comets (Duncan & Levison 1997; Di Sisto & Brunini 2007), several authors have also suggested the existence of some connection between the Plutinos and comets.
Duncan et al. (1995) analyzed the dynamical structure of the trans-Neptunian region and found that in the 3:2 mean motion resonance with Neptune there are currently unstable orbits that may be related to the origin of the observed Jupiter-family comets. Motivated by these results, Morbidelli (1997) studied the dynamics of the 3:2 Neptune resonance at small inclinations and showed the existence of a slow chaotic diffusion
region at moderate amplitudes of libration, which should be an active source of comets at present. On the other hand, Morbidelli (1997) estimated that about 4.5  108 comet-sized objects should presently be trapped in the 3:2 resonance to reproduce the observed flux of Jupiter-family comets in the inner Solar System. This number seems to indicate that the Plutinos should represent a collisionally evolved population.
108 comet-sized objects should presently be trapped in the 3:2 resonance to reproduce the observed flux of Jupiter-family comets in the inner Solar System. This number seems to indicate that the Plutinos should represent a collisionally evolved population.
Melita & Brunini (2000) showed that the 3:2 resonance presents a very robust stable zone primarily at low inclinations, where most of the observed Plutinos are distributed. Moreover, they suggested that the existence of Plutinos in very unstable regions can be explained by physical collisions or gravitational encounters with other Plutinos. At the same time, Nesvorný & Roig (2000) determined the most important inner resonances within the 3:2 Neptune resonance. Moreover, these authors estimated that the current number of Plutinos larger than 1-3 km in diameter is 6 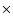 108.
108.
Later, Dell'Oro et al. (2001) computed the values of the intrinsic collision probability and the mean impact velocity for some minor body populations, including the Plutinos.
Some years later, Bernstein et al. (2004), Elliot et al. (2005) and
Petit et al. (2006) carried out several detailed surveys which allowed them to obtain results concerning the mass and size distribution parameters for the different dynamical classes of the trans-Neptunian region. Kenyon et al. (2007) summarized and discussed the main predictions derived from those surveys and analyzed the formation and collisional evolution of the Kuiper Belt objects.
In this paper, we present the first study aimed at describing the collisional evolution of the Plutinos. The main purposes of this work are to estimate the size distribution of Plutinos, to
study their collisional lifetimes, to analyze the formation of families, to obtain ejection rates of fragments from the 3:2 Neptune resonance and to discuss a possible connection between such fragments and the population of ecliptic comets. To do this, we use the numerical code developed by de Elía & Brunini (2007a,b), which allows us to test different collisional parameters and to include a dynamical treatment that takes into account the stability and instability regions of the 3:2 mean motion resonance with Neptune.
In Sect. 2 we give a brief description of the main parameters of our collisional model, while the major dynamical features present in the 3:2 Neptune resonance are discussed in Sect. 3. In Sect. 4 we construct the populations of the model from recent observational surveys. In Sect. 5 we describe the full numerical model. Section 6 shows the most important results derived from the collisional and dynamical evolution of the Plutinos. Conclusions are given in the last section.
In order to describe the outcome of a collision between two bodies, we use the collisional algorithm developed by de Elía & Brunini (2007a,b) which is based on the method performed by Petit & Farinella (1993) with the corrections made by O'Brien & Greenberg (2005). Such an algorithm considers catastrophic collisions and cratering events as well as the escape and reaccumulation of the fragments resulting from those impacts.
There are three fundamental quantities for any collisional evolution study:
- the impact strength law of the colliding bodies;
- the mean impact velocity
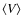 ;
and
;
and
- the intrinsic collision probability
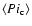 .
.
Concerning the impact strength, two different definitions are generally adopted: the shattering impact specific energy 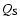 and the dispersing impact specific energy
and the dispersing impact specific energy 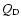 .
.
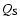 represents the amount of energy per unit target mass needed to catastrophically fragment a body, such that the largest resulting fragment has half the mass of the original target, regardless of reaccumulation of fragments. On the other hand,
represents the amount of energy per unit target mass needed to catastrophically fragment a body, such that the largest resulting fragment has half the mass of the original target, regardless of reaccumulation of fragments. On the other hand, 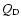 represents the amount of energy per unit mass needed to fragment a body and disperse half of its mass. For small bodies,
with diameters D
represents the amount of energy per unit mass needed to fragment a body and disperse half of its mass. For small bodies,
with diameters D 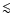 1 km, the gravitational binding energy is negligible and then
1 km, the gravitational binding energy is negligible and then 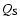 and
and 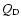 have the same value. For larger bodies,
have the same value. For larger bodies, 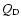 must be larger than
must be larger than 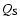 ,
since gravity is important and can therefore impede the dispersal of fragments.
Thus, for large bodies, with diameters D
,
since gravity is important and can therefore impede the dispersal of fragments.
Thus, for large bodies, with diameters D 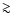 1 km, the
1 km, the 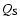 and
and 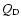 curves show a gap between them according to the terminology used by O'Brien & Greenberg (2005).
On the other hand, associated with
curves show a gap between them according to the terminology used by O'Brien & Greenberg (2005).
On the other hand, associated with 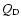 ,
there exists an inelasticity parameter
,
there exists an inelasticity parameter
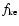 which determines which fraction of the energy received by a body is transferred to the kinetic energy of the fragments.
which determines which fraction of the energy received by a body is transferred to the kinetic energy of the fragments.
The impact velocity V and the shattering impact specific energy 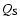 determine, for a given body, if the collision must be studied in the catastrophic regime or in the cratering regime.
determine, for a given body, if the collision must be studied in the catastrophic regime or in the cratering regime.
Finally, the intrinsic collision probability
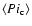 describes how frequently collisions occur, allowing us to study the evolution in time of the population.
describes how frequently collisions occur, allowing us to study the evolution in time of the population.
In this work, we adopt constant values of the intrinsic collision probability
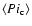 and the mean impact velocity
and the mean impact velocity
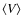 for Plutinos derived by Dell'Oro et al.'s (2001) algorithm, that takes into account the resonant behavior of bodies.
Based on a sample of 46 Plutinos and taking into account the libration of the critical argument
for Plutinos derived by Dell'Oro et al.'s (2001) algorithm, that takes into account the resonant behavior of bodies.
Based on a sample of 46 Plutinos and taking into account the libration of the critical argument
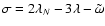 around 180
around 180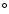 ,
Dell'Oro et al. (2001) computed values of
,
Dell'Oro et al. (2001) computed values of
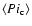 and
and
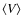 of 4.44
of 4.44 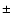 0.04
0.04  10-22 km-2 yr-1 and 1.44
10-22 km-2 yr-1 and 1.44 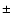 0.71 km s-1, respectively.
0.71 km s-1, respectively.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9865fig1.eps}\end{figure}](/articles/aa/full/2008/41/aa09865-08/Timg15.gif) |
Figure 1:
Strength impact. The dashed line represents the 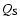 law used in our simulations while the law used in our simulations while the 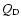 law from Benz & Asphaug (1999) for icy bodies at 3 km s-1 is plotted as a solid line. law from Benz & Asphaug (1999) for icy bodies at 3 km s-1 is plotted as a solid line. |
| Open with DEXTER |
O'Brien & Greenberg (2005) showed that the general shape of the final evolved asteroid population is determined primarily by 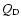 ,
but variations in
,
but variations in 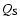 and
and
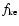 can affect such a final population even if
can affect such a final population even if 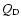 is held the same.
According to these arguments, we decide to choose a combination of the
parameters
is held the same.
According to these arguments, we decide to choose a combination of the
parameters 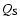 and
and
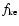 that yield the
that yield the 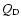 law from
Benz & Asphaug (1999) for icy bodies at 3 km s-1.
law from
Benz & Asphaug (1999) for icy bodies at 3 km s-1.
In a recent paper concerning the L4 Trojan asteroids, de Elía & Brunini (2007b) analyzed the dependence of their numerical simulations on the shattering impact specific energy 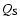 .
This work indicates that the smallest gaps between
.
This work indicates that the smallest gaps between
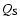 and
and 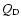 curves lead to the smallest wave amplitudes in the size distribution of the final evolved population as well as to the highest ejection rates of fragments. Moreover, that study also allows us to infer that the formation of families is more effective for the simulations with a small gap between
curves lead to the smallest wave amplitudes in the size distribution of the final evolved population as well as to the highest ejection rates of fragments. Moreover, that study also allows us to infer that the formation of families is more effective for the simulations with a small gap between 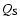 and
and 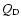 laws. Following these arguments, in this work we decide to use an only
laws. Following these arguments, in this work we decide to use an only 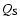 law with a small gap with respect
to the
law with a small gap with respect
to the 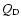 law from Benz & Asphaug (1999) for icy bodies at 3 km s-1. This procedure allows us to obtain upper values of the ejection rate of fragments from the 3:2 Neptune resonance and to maximize the number of families that may be found in this resonant region.
law from Benz & Asphaug (1999) for icy bodies at 3 km s-1. This procedure allows us to obtain upper values of the ejection rate of fragments from the 3:2 Neptune resonance and to maximize the number of families that may be found in this resonant region.
The 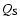 law used in our simulations is shown in Fig. 1 as a dashed line and can be represented by an expression of the form
law used in our simulations is shown in Fig. 1 as a dashed line and can be represented by an expression of the form
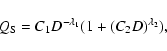 |
(1) |
where C1, C2,
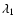 ,
and
,
and
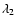 are constant coefficients whose values are 24, 1.2, 0.39 and 1.75, respectively. The
are constant coefficients whose values are 24, 1.2, 0.39 and 1.75, respectively. The 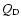 law from Benz & Asphaug (1999) for icy bodies at 3 km s-1 is shown in Fig. 1 as a solid line.
law from Benz & Asphaug (1999) for icy bodies at 3 km s-1 is shown in Fig. 1 as a solid line.
Once the 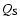 law is specified, we adjust the ineslaticity parameter
law is specified, we adjust the ineslaticity parameter
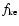 to get the Benz & Asphaug (1999)
to get the Benz & Asphaug (1999) 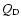 law. Many authors have suggested that
law. Many authors have suggested that
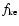 may vary with size (Davis et al. 1995; O'Brien & Greenberg 2005), with impact speed and probably with the material properties. Thus, according
to O'Brien & Greenberg (2005), we express the parameter
may vary with size (Davis et al. 1995; O'Brien & Greenberg 2005), with impact speed and probably with the material properties. Thus, according
to O'Brien & Greenberg (2005), we express the parameter
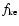 as
as
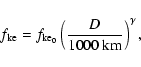 |
(2) |
where
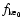 is the value of
is the value of
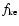 at 1000 km and
at 1000 km and 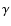 is a given exponent.
Our simulations indicate that the
is a given exponent.
Our simulations indicate that the 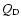 law from Benz & Asphaug (1999) for icy bodies at 3 km s-1 is obtained with good accuracy from the combination of the selected
law from Benz & Asphaug (1999) for icy bodies at 3 km s-1 is obtained with good accuracy from the combination of the selected
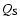 law and
law and
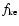 ,
with
,
with
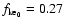 and
and
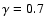 .
Such values are consistent with those discussed by
Davis et al. (1989) and O'Brien & Greenberg (2005).
.
Such values are consistent with those discussed by
Davis et al. (1989) and O'Brien & Greenberg (2005).
In order to study the orbital space occupied by the Plutino population, we develop a numerical integration of 197 Plutino candidates extracted from the Minor Planet Center database with semimajor
axes between 39 and 40 AU. These objects are assumed to be massless particles subject to the gravitational field of the Sun (including the masses of the terrestrial planets) and the perturbations of the four giant planets. The simulation is performed
with the simplectic code EVORB from Fernández et al. (2002) using a timestep of 0.25 years. The evolution of the test particles is followed for 107 years which is a timescale greater than any secular period found in this resonance (Morbidelli 1997).
From this evolution we construct 3D niches within the boundaries of the 3:2 resonance
with widths of 0.02 AU, 0.0125 and 1.125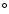 in semimajor axis a, eccentricity e and inclination i, respectively. In each of these niches, we calculate the fraction of time each niche is occupied normalized to the total time that all the Plutinos spend within the boundaries of the resonance. This process allows us to build a map of the distribution of Plutinos in the orbital element planes (a, e) and (a, i). These maps are shown in Figs. 2a and b.
Such plots indicate the regions where the Plutinos spend their time. We assume that the color zones in those maps are regions with different degrees of probability where a Plutino can be found, and they will be called ``stability niches'' in this work. On the contrary the empty zones are regions where a Plutino could not survive for a long time (remember that the neighborhoods of the resonance are rather unstable regions). These empty regions will be called ``instability niches'' in this work. They correspond to unstable zones where objects are quickly ejected from the 3:2 resonance, losing the resonance protecting mechanism and encountering Neptune on a timescale of less than some 107 years (Morbidelli 1997; Nesvorný & Roig 2000).
in semimajor axis a, eccentricity e and inclination i, respectively. In each of these niches, we calculate the fraction of time each niche is occupied normalized to the total time that all the Plutinos spend within the boundaries of the resonance. This process allows us to build a map of the distribution of Plutinos in the orbital element planes (a, e) and (a, i). These maps are shown in Figs. 2a and b.
Such plots indicate the regions where the Plutinos spend their time. We assume that the color zones in those maps are regions with different degrees of probability where a Plutino can be found, and they will be called ``stability niches'' in this work. On the contrary the empty zones are regions where a Plutino could not survive for a long time (remember that the neighborhoods of the resonance are rather unstable regions). These empty regions will be called ``instability niches'' in this work. They correspond to unstable zones where objects are quickly ejected from the 3:2 resonance, losing the resonance protecting mechanism and encountering Neptune on a timescale of less than some 107 years (Morbidelli 1997; Nesvorný & Roig 2000).
Section 5 describes how the stability and instability niches shown in Fig. 2 are included in our numerical algorithm in order to model the dynamical treatment of the code. We discuss in Sect. 6.5 the sensitivity of our results to the way those niches are constructed as well as the dependence of our simulations on the initial orbital element distribution of the population.
Recently, Kenyon et al. (2007) used the Minor Planet Center database and the main results from Bernstein et al. (2004), Elliot et al. (2005) and Petit et al. (2006) and found clear evidence of physical differences among the dynamical classes of the trans-Neptunian region. Particularly, their analysis indicates that the cumulative size distribution of the resonant population shows a break at a diameter D near 40-80 km, which is in agreement with Bernstein et al. (2004). Moreover, for larger resonant objects, the population seems to have a shallow size distribution with a cumulative power-law index of 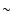 3. On the other hand, Kenyon et al. (2007) suggested that the resonant population has
3. On the other hand, Kenyon et al. (2007) suggested that the resonant population has 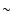 0.01-0.05
0.01-0.05
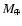 in objects with
in objects with 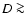 20-40 km. Petit et al. (2006) proposed that there is no evidence of a break in the Kuiper Belt population, indicating that a single power-law luminosity function fits their data.
20-40 km. Petit et al. (2006) proposed that there is no evidence of a break in the Kuiper Belt population, indicating that a single power-law luminosity function fits their data.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{9865fig2.eps}\end{figure}](/articles/aa/full/2008/41/aa09865-08/Timg26.gif) |
Figure 2:
Normalized distribution of Plutinos obtained from the dynamical evolution of 197 Plutino candidates extracted from the Minor Planet Center database with semimajor axes between 39 and 40 AU in the planes (a, e) a) and (a, i) b). The color scale depicts the expected density of Plutinos. Blue colors indicate where the Plutinos are statistically most likely to spend their time. |
| Open with DEXTER |
Considering for large objects (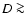 40-80 km) in the resonant population a cumulative power-law index of
40-80 km) in the resonant population a cumulative power-law index of 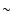 3 for the size distribution and a lower limit of 0.01
3 for the size distribution and a lower limit of 0.01
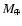 for the mass in objects with
for the mass in objects with 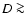 20-40 km, we obtain one Pluto-sized object in the resonant population. Assuming that this object is in the 3:2 mean motion resonant we have one Pluto-sized object, Pluto itself. But considering the upper limit of 0.05
20-40 km, we obtain one Pluto-sized object in the resonant population. Assuming that this object is in the 3:2 mean motion resonant we have one Pluto-sized object, Pluto itself. But considering the upper limit of 0.05
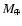 for the mass in resonant objects with
for the mass in resonant objects with
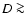 20-40 km, we infer the existence of 5 Pluto-sized objects in the whole resonant population. If these 5 Pluto-sized objects were all in the 3:2 mean motion resonance we would have an upper limit for the large objects in this resonance. This is (though optimistic) a real possibility from the studies mentioned above, and even though only Pluto
has been observed up to now, more Pluto-sized objects in the 3:2 resonance may remain to be discovered. Brown (2008), based on the completeness of the current surveys argues that two or three more large KBOs are likely awaiting discovery. We will consider the limit of 5 Pluto-sized objects in the 3:2 resonance only as an upper limit for the calculations
and results addressing this subject in Sect. 6.4.
In the following we assume the existence of one Pluto-sized object in the 3:2 resonance.
20-40 km, we infer the existence of 5 Pluto-sized objects in the whole resonant population. If these 5 Pluto-sized objects were all in the 3:2 mean motion resonance we would have an upper limit for the large objects in this resonance. This is (though optimistic) a real possibility from the studies mentioned above, and even though only Pluto
has been observed up to now, more Pluto-sized objects in the 3:2 resonance may remain to be discovered. Brown (2008), based on the completeness of the current surveys argues that two or three more large KBOs are likely awaiting discovery. We will consider the limit of 5 Pluto-sized objects in the 3:2 resonance only as an upper limit for the calculations
and results addressing this subject in Sect. 6.4.
In the following we assume the existence of one Pluto-sized object in the 3:2 resonance.
In order to take into account the possible existence of a break in the resonant population,
the initial size distribution for 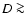 60 km is assumed to follow a cumulative power-law index with a value of 3, while for
60 km is assumed to follow a cumulative power-law index with a value of 3, while for 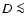 60 km, we assign a cumulative power-law index p in order to reproduce a given initial mass. From this, the general form of the cumulative initial population used in our model to study the collisional and dynamical evolution of the Plutinos can be written as follows
60 km, we assign a cumulative power-law index p in order to reproduce a given initial mass. From this, the general form of the cumulative initial population used in our model to study the collisional and dynamical evolution of the Plutinos can be written as follows
| |
|
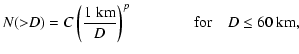 |
|
| |
|
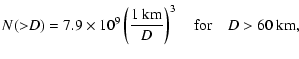 |
(3) |
where C = 7.9  109 (60)p-3 by continuity for D = 60 km. Given the uncertainty in the parameters of the Plutino size distribution at small sizes, we decide to use in our model three different initial populations, which are defined as follows
These initial cumulative size distributions are shown in Fig. 3. Note that the Initial Population 1 does not show a break, in agreement with Petit et al. (2006). On the other hand, the Initial Populations 2 and 3 have a double power-law functional form according to Bernstein et al. (2004) and Kenyon et al. (2007).
109 (60)p-3 by continuity for D = 60 km. Given the uncertainty in the parameters of the Plutino size distribution at small sizes, we decide to use in our model three different initial populations, which are defined as follows
These initial cumulative size distributions are shown in Fig. 3. Note that the Initial Population 1 does not show a break, in agreement with Petit et al. (2006). On the other hand, the Initial Populations 2 and 3 have a double power-law functional form according to Bernstein et al. (2004) and Kenyon et al. (2007).
In Sect. 6 we discuss the dependence of our simulations on the initial population.
Moreover, in Sect. 6.4 we study the sensitivity of our results to the number of Pluto-sized objects in the 3:2 resonance with Neptune.
In order to simulate the collisional and dynamical evolution of the Plutinos, our numerical code evolves in time the number of bodies residing in a set of 135 discrete logarithmic size bins, whose central values range from D1 = 10-10 km to D135 = 2816.1 km in diameter, in such a way that from one bin to the next, the mass of the bodies changes by a factor of 2 and the diameter changes by a factor of 21/3, adopting a density of 1 g cm-3.
In each timestep, a characteristic orbit is generated at random for each collision between Plutinos of diameters D1 and D2 in the 3:2 resonance. The generated orbits are not used to
compute new values of the mean impact velocity
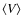 and the intrinsic collision
probability
and the intrinsic collision
probability
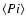 (see Sect. 2.1). The main goals of this treatment are to analyze the final fate of the fragments resulting from impacts and to obtain more reliable estimates of the collisional ejection rates of Plutinos from the 3:2 Neptune resonance.
(see Sect. 2.1). The main goals of this treatment are to analyze the final fate of the fragments resulting from impacts and to obtain more reliable estimates of the collisional ejection rates of Plutinos from the 3:2 Neptune resonance.
From Figs. 2a and b, we have the normalized distribution of Plutinos in each niche
previously defined in Sect. 3, what is equivalent to a probability distribution function f(a,e,i). Then, we assign to our initial fictitious Plutinos orbital elements a, e, i,
following the probability distribution function f(a,e,i) by von Neumann's acceptance-rejection method (Knuth 1981). This technique indicates that if a set of numbers a*, e* and i* is selected randomly from a uniform distribution over the domain of the function f (namely, a*, e* and i* between 39 and 40 AU, 0 and 0.5 and 0 and 45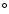 ,
respectively), and another set of numbers f* is given uniformly at random from the range of such a function (namely, f* between 0 and 0.0012), the condition
,
respectively), and another set of numbers f* is given uniformly at random from the range of such a function (namely, f* between 0 and 0.0012), the condition
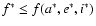 will generate a distribution for
(a*,e*,i*)
whose density is
will generate a distribution for
(a*,e*,i*)
whose density is
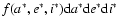 .
Such
(a*,e*,i*) values will be accepted as possible initial conditions for the semimajor axis, eccentricity and inclination of the Plutinos, in agreement with the observational data and the numerical integration developed in Sect. 3. In mean motion resonances, the evolution of a,e and i is coupled. However, here, we are treating them as uncorrelated variables. Nevertheless, a more rigorous treatment would be very difficult, and we believe that the results would be not too different to the ones found here. Finally, since we do not compute Neptune's orbit in our simulations, it is not necessary to include constraints on the resonant argument of the Plutinos. Thus, given uniformly at random the longitude of ascending node
.
Such
(a*,e*,i*) values will be accepted as possible initial conditions for the semimajor axis, eccentricity and inclination of the Plutinos, in agreement with the observational data and the numerical integration developed in Sect. 3. In mean motion resonances, the evolution of a,e and i is coupled. However, here, we are treating them as uncorrelated variables. Nevertheless, a more rigorous treatment would be very difficult, and we believe that the results would be not too different to the ones found here. Finally, since we do not compute Neptune's orbit in our simulations, it is not necessary to include constraints on the resonant argument of the Plutinos. Thus, given uniformly at random the longitude of ascending node 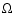 ,
the argument of pericentre
,
the argument of pericentre 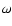 and the mean anomaly M between 0 and 360
and the mean anomaly M between 0 and 360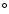 ,
an orbit can be assigned and from this, a position-velocity pair can be derived for each of the
colliding Plutinos.
,
an orbit can be assigned and from this, a position-velocity pair can be derived for each of the
colliding Plutinos.
Once a typical orbit has been computed for each body participating in a given collision, the next step is to carry out the collisional treatment (including the analysis of the reaccumulation process) from the algorithm developed by de Elía & Brunini (2007a,b). In order to determine the final fate of the fragments escaping from the gravitational field of the two colliding bodies, it is necessary to calculate their orbital elements once they are ejected with a relative velocity with respect to the parent body. Immediately before the collision, the barycentric position and velocity of the fragments are assumed to be those associated with their parent body. After the collision, we consider that the barycentric position of the
fragments does not change while the relative velocities with respect to their parent body are assumed to be equally partitioned between the three components.
Once the barycentric position and velocity of the fragments after the collision have been obtained, it is possible to calculate their orbital elements and their final fates.
To define if the fragments remain or are ejected from the resonance
we use the following criterion:
- 1.
- The fragments remain in the 3:2 resonance if the combinations of (a, e) and (a, i) values are associated with some of the stability niches shown in Figs. 2a and b.
- 2.
- Otherwise, the fragments are ejected from the 3:2 resonance and no longer participate in the
collisional evolution if any of the following conditions is fulfilled:
- -
- eccentricity
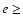 1;
1;
- -
- eccentricity e < 1 but (a, e, i) values exceed the boundaries of the 3:2 resonance (see Sect. 3);
- -
- eccentricity e < 1 but (a, e) and (a, i) values are associated with some of the instability niches shown in Figs. 2a and b, respectively, previously defined in Sect. 3.
To study the evolution in time of the Plutino population, the timestep 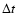 is calculated in such a way that the change in the number of objects in any size bin is always smaller than a given amount, which is generally chosen as 1
is calculated in such a way that the change in the number of objects in any size bin is always smaller than a given amount, which is generally chosen as 1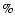 of the original number of bodies.
of the original number of bodies.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{9865fig4.eps}\end{figure}](/articles/aa/full/2008/41/aa09865-08/Timg40.gif) |
Figure 4:
Our estimates of the Plutino cumulative size distribution after 4.5 Gyr of evolution obtained from the different initial populations proposed in Sect. 4. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{9865fig5.eps}\end{figure}](/articles/aa/full/2008/41/aa09865-08/Timg41.gif) |
Figure 5:
Mean collisional lifetimes of Plutinos obtained using the different initial populations defined in Sect. 4. The horizontal short-dashed line represents the age of the Solar System. |
| Open with DEXTER |
Figure 4a shows our estimate of the Plutino cumulative size distribution after 4.5 Gyr of evolution obtained from the Initial Population 1 (see Sect. 4) which follows a cumulative power-law index equal to 3 at all sizes. From this, we find that it is not possible to reproduce the break suggested by Bernstein et al. (2004) and Kenyon et al. (2007) at 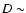 40-80 km using a single-slope power law to describe the starting population. On the contrary, the final evolved population just shows a break at a diameter D near 2 km
while the larger objects are not significantly altered by collisions over the age of the Solar System. In fact, the solid line in Fig. 5 represents our results concerning the mean collisional lifetimes of Plutinos obtained from the Initial Population 1. This indicates that Plutinos with diameters greater than
40-80 km using a single-slope power law to describe the starting population. On the contrary, the final evolved population just shows a break at a diameter D near 2 km
while the larger objects are not significantly altered by collisions over the age of the Solar System. In fact, the solid line in Fig. 5 represents our results concerning the mean collisional lifetimes of Plutinos obtained from the Initial Population 1. This indicates that Plutinos with diameters greater than 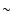 2 km have mean lifetimes longer
than the age of the Solar System, which implies that such objects have likely survived unaltered by catastrophic impacts over the Solar System history. The confirmation of the existence of a break at
2 km have mean lifetimes longer
than the age of the Solar System, which implies that such objects have likely survived unaltered by catastrophic impacts over the Solar System history. The confirmation of the existence of a break at 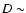 40-80 km in the Plutino cumulative size distribution should rule out a single-slope power law distribution as a possible initial population.
40-80 km in the Plutino cumulative size distribution should rule out a single-slope power law distribution as a possible initial population.
On the other hand, Fig. 4b shows our estimate of the Plutino cumulative size distribution after 4.5 Gyr, starting from the Initial Population 2 (see Sect. 4) which presents a break at a diameter D near 60 km and follows a cumulative power-law index of 2.7 for smaller sizes. Our results indicate that the final evolved population produces a break at 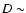 2 km while the larger bodies do not suffer a significant collisional evolution over the Solar System
age, representing a primordial population. In fact, the long-dashed line in Fig. 5 indicates that the mean collisional lifetimes of Plutinos larger than
2 km while the larger bodies do not suffer a significant collisional evolution over the Solar System
age, representing a primordial population. In fact, the long-dashed line in Fig. 5 indicates that the mean collisional lifetimes of Plutinos larger than 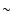 2 km in diameter are longer than the age of the Solar System. In the same way, Fig. 4c presents our results concerning the Plutino cumulative size distribution after 4.5 Gyr, using the Initial Population 3 (see Sect. 4), which has a break at
2 km in diameter are longer than the age of the Solar System. In the same way, Fig. 4c presents our results concerning the Plutino cumulative size distribution after 4.5 Gyr, using the Initial Population 3 (see Sect. 4), which has a break at 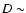 60 km and follows a cumulative power-law index of 2.4
for smaller sizes. In this case, the final evolved population shows a slight break at a diameter D near 1 km. Moreover, the short-dashed line in Fig. 5 allows us to infer that Plutinos with diameters greater than 1 km are primordial since their mean collisional lifetimes are longer than the age of the Solar System.
60 km and follows a cumulative power-law index of 2.4
for smaller sizes. In this case, the final evolved population shows a slight break at a diameter D near 1 km. Moreover, the short-dashed line in Fig. 5 allows us to infer that Plutinos with diameters greater than 1 km are primordial since their mean collisional lifetimes are longer than the age of the Solar System.
Our simulations indicate that the existence of a break at 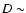 40-80 km in the
Plutino cumulative size distribution should be a primordial feature of the population and not the result of the collisional evolution. This strongly agrees with the results derived by Charnoz & Morbidelli (2007) who argued that the knee at 50 km in the distribution of the Kuiper Belt objects should be primordial.
40-80 km in the
Plutino cumulative size distribution should be a primordial feature of the population and not the result of the collisional evolution. This strongly agrees with the results derived by Charnoz & Morbidelli (2007) who argued that the knee at 50 km in the distribution of the Kuiper Belt objects should be primordial.
The existence of families in a given region represents a natural result of the collisional activity.
We study the existence of families in the 3:2 resonance with Neptune formed from the breakup of parent bodies with diameters greater than 100 km that disperse fragments in such a way that the diameter of the largest one is larger than 30-40 km.
Our simulations indicate that the formation of large Plutino families does not depend strongly on the starting population. In fact, from any of the three initial populations proposed in Sect. 4, one large family is formed in the 3:2 resonance with Neptune over the age of the Solar System.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{9865fig6.eps}\end{figure}](/articles/aa/full/2008/41/aa09865-08/Timg43.gif) |
Figure 6:
Ejection rate of fragments from the 3:2 mean motion resonance with Neptune with diameters greater than 1 km per Myr obtained from the different initial populations defined in Sect. 4. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9865fig7.eps}\end{figure}](/articles/aa/full/2008/41/aa09865-08/Timg44.gif) |
Figure 7:
Representative values of semimajor axis, eccentricity and inclination for the fragments ejected from the 3:2 mean motion resonance with Neptune. |
| Open with DEXTER |
Figure 6 shows the number of bodies ejected from the 3:2 Neptune resonance with diameters greater than 1 km per Myr as a function of time over the age of the Solar System, obtained from the different initial populations defined in Sect. 4. In order to study the contribution of the Plutinos to the current population of ecliptic comets, we estimate a mean ejection rate of fragments from the 3:2 resonance for each of our simulations over the last 500 Myr of evolution, where the number of bodies removed per time unit is more or less constant and the data sample is statistically significant. Our results indicate that the maximum ejection rates starting with the Initial Populations 1-3 (see Sect. 4) are of 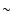 3.5
3.5 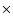 103, 1.7
103, 1.7 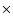 103 and 8.6
103 and 8.6 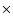 102 objects larger than 1 km in diameter per Myr from the 3:2 resonance, respectively. Thus, we would expect a maximum of 1 ecliptic comet with a diameter D > 1 km every
102 objects larger than 1 km in diameter per Myr from the 3:2 resonance, respectively. Thus, we would expect a maximum of 1 ecliptic comet with a diameter D > 1 km every 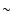 300-1200 yr from the 3:2 resonance with Neptune, while the estimates of
Di Sisto & Brunini (2007) suggest the injection of 4 Centaurs with a radius R > 1 km each year from the Scattered Disk.
300-1200 yr from the 3:2 resonance with Neptune, while the estimates of
Di Sisto & Brunini (2007) suggest the injection of 4 Centaurs with a radius R > 1 km each year from the Scattered Disk.
In Sect. 5 we discussed several criteria to determine the final fate of the Plutino fragments and from this to calculate the ejection rates from the 3:2 mean motion resonance with Neptune.
Our simulations indicate that the ejection of fragments from the 3:2 resonance is due to variations in the a, e and i values, which are associated with some instability
niches shown in Fig. 2 or exceed the boundaries assumed for the resonant region (see Sect. 3). In these cases the fragments have e< 1 (see Sect. 5). From all our numerical experiments, we find that more than 99 percent of the fragments escaping from the 3:2 resonance do it through these two mechanisms, so they have eccentricities e < 1, which rules out parabolic or hyperbolic collisional ejection as a Plutino removal source. Figure 7 shows a representative sample of the distribution of Plutinos ejected from the 3:2 resonance with
respect to semimajor axis, eccentricity and inclination.
On the other hand, for all cases, most of the bodies ejected from the 3:2 mean motion resonance with Neptune with diameters greater than 1 km have diameters ranging from 1 to 5 km. In fact, our results indicate that the ejection rate of fragments with diameters D > 5 km results to be two orders of magnitude smaller than that associated to fragments with diameters D > 1 km.
Moreover, it is interesting to note that the objects ejected from the resonance are fragments resulting from impacts between parent bodies with diameters ranging from 10 to 200 km.
The results discussed so far have been derived assuming the existence of one Pluto-sized object in the 3:2 Neptune resonance. As discussed in Sect. 4, if we consider the upper limit of 0.05
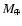 suggested by Kenyon et al. (2007) for the mass of the resonant population in objects with
suggested by Kenyon et al. (2007) for the mass of the resonant population in objects with 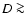 20-40 km, 5 Pluto-sized objects should be found in the whole resonant population according to the size distribution parameters derived by Bernstein et al. (2004) and Kenyon et al. (2007) for such population.
20-40 km, 5 Pluto-sized objects should be found in the whole resonant population according to the size distribution parameters derived by Bernstein et al. (2004) and Kenyon et al. (2007) for such population.
To test the dependence of our results on the number of Pluto-sized objects, we carry out several numerical experiments considering 5 Pluto-sized objects in the 3:2 Neptune resonance.
This number is probably an overestimation (see Sect. 4 for details), but nevertheless our purpose is only to illustrate the effect of the total mass in the population on the Plutinos' collisional history.
Our results suggest that the larger the number of Pluto-sized objects in the 3:2 Neptune resonance, the higher the ejection rate of fragments from that resonant region and the number
of families formed over 4.5 Gyr. In fact, if 5 Pluto-sized objects are assumed to be in the 3:2 Neptune resonance, one body with a diameter D > 1 km is ejected every tens of years while 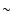 30 large families are formed over the Solar System history. According to the estimates of Di Sisto & Brunini (2007), we conclude that it is necessary to specify the number of Pluto-sized objects present in the 3:2 Neptune resonance to determine if this resonant region can be considered an important source of ecliptic comets.
30 large families are formed over the Solar System history. According to the estimates of Di Sisto & Brunini (2007), we conclude that it is necessary to specify the number of Pluto-sized objects present in the 3:2 Neptune resonance to determine if this resonant region can be considered an important source of ecliptic comets.
The results shown in this paper have been obtained using the stability and instability niches defined in Sect. 3, which present widths of 0.02 AU, 0.0125 and 1.125 in semimajor axis a, eccentricity e and inclination i, respectively. In order to test the dependence of our results on the size of those niches, we carry out several numerical experiments increasing the widths of such regions in a, e and i, which leads to a magnification of the
stability region. In general terms, the larger the area of niches, the smaller the ejection rate of fragments from the 3:2 mean motion resonance with Neptune. In this work, we select small size niches in order to minimize the influence of the lowest density regions shown in Fig. 2.
On the other hand, we find that the results concerning the size distribution of Plutinos, their collisional lifetimes and the formation of families are not sensitive to the size of the stability and instability regions constructed to developed our dynamical treatment.
in semimajor axis a, eccentricity e and inclination i, respectively. In order to test the dependence of our results on the size of those niches, we carry out several numerical experiments increasing the widths of such regions in a, e and i, which leads to a magnification of the
stability region. In general terms, the larger the area of niches, the smaller the ejection rate of fragments from the 3:2 mean motion resonance with Neptune. In this work, we select small size niches in order to minimize the influence of the lowest density regions shown in Fig. 2.
On the other hand, we find that the results concerning the size distribution of Plutinos, their collisional lifetimes and the formation of families are not sensitive to the size of the stability and instability regions constructed to developed our dynamical treatment.
In the same way, we also perform some numerical simulations in order to explore the sensitivity of our results to the initial mass of the population. In fact, the studies developed by Stern (1996), Stern & Colwell (1997a) and Stern & Colwell (1997b) suggest that the mass of the primordial Kuiper Belt between 30 and 50 AU was probably of the order of 10 to 50
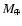 ,
which is
,
which is 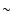 100 times its current value. Moreover, these
authors indicate that once Neptune reached a fraction of its final mass, the disk environment became highly erosive for objects with radii smaller than
100 times its current value. Moreover, these
authors indicate that once Neptune reached a fraction of its final mass, the disk environment became highly erosive for objects with radii smaller than 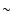 20-30 km, leading to a rapid mass loss on a timescale of
20-30 km, leading to a rapid mass loss on a timescale of 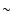 100 Myr. To take into account these results and following O'Brien & Greenberg (2005), we carry out several numerical experiments including a brief period of primordial evolution at the beginning of the simulation. To do this, each of the initial populations defined in Sect. 4 is multiplied by a factor of 100 and then its evolution followed for 100 Myr. Once this phase of primordial evolution ends, the corresponding residual population is reduced by
the same factor and finally its evolution is analyzed for the rest of the 4.5 Gyr. Our results suggest that the size distribution of the Plutinos, their collisional lifetimes, the ejection rate of fragments from the 3:2 mean motion resonance with Neptune and the formation of families do not show relevant changes when this period of primordial evolution is included in the model.
100 Myr. To take into account these results and following O'Brien & Greenberg (2005), we carry out several numerical experiments including a brief period of primordial evolution at the beginning of the simulation. To do this, each of the initial populations defined in Sect. 4 is multiplied by a factor of 100 and then its evolution followed for 100 Myr. Once this phase of primordial evolution ends, the corresponding residual population is reduced by
the same factor and finally its evolution is analyzed for the rest of the 4.5 Gyr. Our results suggest that the size distribution of the Plutinos, their collisional lifetimes, the ejection rate of fragments from the 3:2 mean motion resonance with Neptune and the formation of families do not show relevant changes when this period of primordial evolution is included in the model.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9865fig8.eps}\end{figure}](/articles/aa/full/2008/41/aa09865-08/Timg45.gif) |
Figure 8:
Distribution of 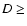 1 km Plutino fragments with respect to semimajor axis a, eccentricity e and inclination i. Time evolution from an initial cold population.
1 km Plutino fragments with respect to semimajor axis a, eccentricity e and inclination i. Time evolution from an initial cold population. |
| Open with DEXTER |
The results presented in this work have been derived generating initial values of semimajor axis a, eccentricity e and inclination i from the dynamical evolution of the 197 test Plutinos shown in Fig. 2. In order to test the dependence of our results on the initial orbital distribution, we develop several simulations starting with a dynamically cold population, with eccentricities and inclinations below 0.05 and 10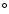 ,
respectively. Such e and i limit values are chosen arbitrarily. Our outcomes show that
,
respectively. Such e and i limit values are chosen arbitrarily. Our outcomes show that 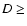 1 km Plutino fragments require timescales of the order of 100 Myr to reach the current dynamical configuration
(see Fig. 8), while the smaller fragments occupy the stability niches very quickly, in only some thousands of years. In addition, we find that the results concerning the size distribution of Plutinos, their collisional lifetimes, the ejection rate of fragments from the 3:2 mean motion resonance with Neptune and the formation of families do not show a strong dependence on the initial distribution of orbital elements. From this analysis, we infer that it is possible to reach the current orbital configuration of the Plutinos starting with a dynamically very different population compared to that presently observed. Thus, we suggest that the current orbital distribution of the Plutinos does not offer a strong constraint on the dynamical origin of this population.
1 km Plutino fragments require timescales of the order of 100 Myr to reach the current dynamical configuration
(see Fig. 8), while the smaller fragments occupy the stability niches very quickly, in only some thousands of years. In addition, we find that the results concerning the size distribution of Plutinos, their collisional lifetimes, the ejection rate of fragments from the 3:2 mean motion resonance with Neptune and the formation of families do not show a strong dependence on the initial distribution of orbital elements. From this analysis, we infer that it is possible to reach the current orbital configuration of the Plutinos starting with a dynamically very different population compared to that presently observed. Thus, we suggest that the current orbital distribution of the Plutinos does not offer a strong constraint on the dynamical origin of this population.
We have presented the first study aimed at analyzing the collisional and dynamical evolution of the Plutinos. Assuming the existence of one Pluto-sized object in the 3:2 Neptune resonance, our main results are the following:
- An initial population described by a single-slope power law does not allow us to reproduce
the break suggested by Bernstein et al. (2004) and Kenyon et al. (2007) at a diameter D near 40-80 km in the Plutino cumulative size distribution after 4.5 Gyr of evolution. Petit et al.'s (2006) results suggest that the existence of a break in the distribution of trans-Neptunian objects is still a matter of debate.
- The population of Plutinos larger than a few kilometers in diameter is not significantly altered by catastrophic impacts over the age of the Solar System. Thus, our simulations indicate that the possible existence of a break at
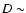 40-80 km in the Plutino cumulative size distribution should be a primordial feature of the population and not
the result of the collisional evolution. This is in agreement with Charnoz & Morbidelli (2007) who argued that the knee at 50 km in the distribution of the Kuiper Belt objects should be primordial.
40-80 km in the Plutino cumulative size distribution should be a primordial feature of the population and not
the result of the collisional evolution. This is in agreement with Charnoz & Morbidelli (2007) who argued that the knee at 50 km in the distribution of the Kuiper Belt objects should be primordial.
- On the other hand, we study the existence of families in the 3:2 resonance with Neptune formed from the breakup of parent bodies with diameters greater than 100 km that disperse fragments so that the diameter of the largest one is larger than 30-40 km. Our simulations indicate that one large family is formed in this resonant region over the age of the Solar System.
- Concerning Plutino removal, our numerical experiments indicate that one object with
a diameter D > 1 km is ejected from the 3:2 resonance with Neptune every
 300-1200 yr. Such ejected objects are D = 1-5 km fragments resulting from impacts between parent bodies with
diameters ranging from 10 to 200 km.
300-1200 yr. Such ejected objects are D = 1-5 km fragments resulting from impacts between parent bodies with
diameters ranging from 10 to 200 km.
- On the other hand, we infer that the current orbital distribution of the Plutinos does not provide a strong constraint on the dynamical origin of this population.
- Finally, we study the dependence of our results on the number of Pluto-sized objects in the 3:2 Neptune resonance. Our simulations suggest that the larger the number of Pluto-sized objects, the higher the ejection rate of fragments from that resonant region and the number of families formed over 4.5 Gyr. In fact, if a maximum of 5 Pluto-sized objects are assumed to be in the 3:2 Neptune resonance (see Sect. 4), one body with a diameter D > 1 km is ejected every tens of years while
 30 large families are formed over the Solar System history.
According to Di Sisto & Brunini (2007), we conclude that it is necessary to specify the number of Pluto-sized objects present in the 3:2 Neptune resonance to determine if this resonant region can be considered an important source of ecliptic comets.
30 large families are formed over the Solar System history.
According to Di Sisto & Brunini (2007), we conclude that it is necessary to specify the number of Pluto-sized objects present in the 3:2 Neptune resonance to determine if this resonant region can be considered an important source of ecliptic comets.
-
Bernstein, G. M., Trilling, D. E., Allen, R. L., et al. 2004, AJ,
128, 1364 [NASA ADS] [CrossRef]
(In the text)
- Benz, W., &
Asphaug, E. 1999, Icarus, 142, 5 [NASA ADS] [CrossRef]
(In the text)
- Brown, M. E.
2008, in The Solar System Beyond Neptune, ed. M. A. Barucci, H.
Boehnhardt, D. P. Cruikshank, & A. Morbidelli (Tucson, USA:
University of Arizona Press), 335
(In the text)
- Charnoz, S.,
& Morbidelli, A. 2007, Icarus, 188, 468 [NASA ADS] [CrossRef]
(In the text)
- Davis, D. R.,
Weidenschilling, S. J., Farinella, P., Paolicchi, P., & Binzel,
R. P. 1989, in Asteroids II, ed. R. P. Binzel, T. Gehrels, & M.
S. Matthews (Tucson, USA: University of Arizona Press), 805
(In the text)
- Davis, D. R., Ryan,
E. V., & Farinella, P. 1995, Lunar and Planetary Sci. Conf.,
26, 319 [NASA ADS] [CrossRef]
(In the text)
- de Elía, G.
C., & Brunini, A. 2007a, A&A, 466, 1159 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- de Elía, G.
C., & Brunini, A. 2007b, A&A, 475, 375 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Dell'Oro, A.,
Marzari, F., Paolicchi, P, & Vanzani, V. 2001, A&A, 366,
1053 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Di Sisto, R. P.,
& Brunini, A. 2007, Icarus, 190, 224 [NASA ADS] [CrossRef]
(In the text)
- Duncan, M. J.,
& Levison, H. F. 1997, Science, 276, 1670 [NASA ADS] [CrossRef]
(In the text)
- Duncan, M. J.,
Levison, H. F., & Budd, S. M. 1995, AJ, 110, 3073 [NASA ADS] [CrossRef]
(In the text)
- Elliot, J. L.,
Kern, S. D., Clancy, K. B., et al. 2005, AJ, 129, 1117 [NASA ADS] [CrossRef]
(In the text)
-
Fernández, J. A., Gallardo, T., & Brunini, A. 2002,
Icarus, 159, 358 [NASA ADS] [CrossRef]
(In the text)
- Kenyon, S. J.,
Bromley, B. C., O'Brien, D. P., & Davis, D. R. 2007, in
press
(In the text)
- Knuth, D. E. 1981,
The Art of Computer Programming, Seminumerical Algorithms, Reading,
Mass. (Addison-Wesley), 2nd edn., 2, 688
(In the text)
- Melita, M. D.,
& Brunini, A. 2000, Icarus, 147, 205 [NASA ADS] [CrossRef]
(In the text)
- Morbidelli,
A. 1997, Icarus, 127, 1 [NASA ADS] [CrossRef]
(In the text)
-
Nesvorný, D., & Roig, F. 2000, Icarus, 148, 282 [NASA ADS] [CrossRef]
(In the text)
- O'Brien, D. P.,
& Greenberg, R. 2005, Icarus, 178, 179 [NASA ADS] [CrossRef]
(In the text)
- Petit, J.-M., &
Farinella, P. 1993, Celest. Mech. Dynam. Astron., 57, 1 [NASA ADS] [CrossRef]
(In the text)
- Petit, J.-M.,
Holman, M. J., Gladman, B. J., et al. 2006, MNRAS, 365, 429 [NASA ADS] [CrossRef]
(In the text)
- Stern, S. A. 1996,
AJ, 112, 1203 [NASA ADS] [CrossRef]
(In the text)
- Stern, S. A., &
Colwell, J. E. 1997a, AJ, 114, 841 [NASA ADS] [CrossRef]
(In the text)
- Stern, S. A., &
Colwell, J. E. 1997b, ApJ, 490, 879 [NASA ADS] [CrossRef]
(In the text)
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9865fig1.eps}\end{figure}](/articles/aa/full/2008/41/aa09865-08/Timg15.gif)
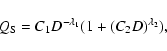
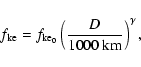
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{9865fig2.eps}\end{figure}](/articles/aa/full/2008/41/aa09865-08/Timg26.gif)
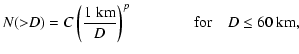
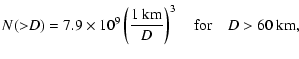
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{9865fig3.eps}\end{figure}](/articles/aa/full/2008/41/aa09865-08/Timg31.gif)
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{9865fig4.eps}\end{figure}](/articles/aa/full/2008/41/aa09865-08/Timg40.gif)
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{9865fig5.eps}\end{figure}](/articles/aa/full/2008/41/aa09865-08/Timg41.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{9865fig6.eps}\end{figure}](/articles/aa/full/2008/41/aa09865-08/Timg43.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9865fig7.eps}\end{figure}](/articles/aa/full/2008/41/aa09865-08/Timg44.gif)
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9865fig8.eps}\end{figure}](/articles/aa/full/2008/41/aa09865-08/Timg45.gif)